CS/CE/SE 6367 Software Testing, Validation and Verification. Lecture 4 Code Coverage (II)
|
|
|
- Joy Peters
- 6 years ago
- Views:
Transcription
1 CS/CE/SE 6367 Softwre Testing, Vlidtion nd Verifiction Lecture 4 Code Coverge (II)
2 2/54 Lst Clss Code coverge Control-flow coverge Sttement coverge Brnch coverge Pth coverge Coverge Collection Tools EclEmm
3 3/54 This Clss Code coverge Dt-flow coverge All-Defs All-Uses All-DU-Pths All-P-Uses/Some-C-Uses All-C-Uses/Some-P-Uses All-P-Uses All-C-Uses
4 4/54 Motivtion t1 t2 Are t1 nd t2 identicl? lthough the pths re the sme, different tests my hve different vrible vlues defined/used Bsic ide: Control-flow grph Existing control-flow coverge criteri only consider the execution pth (structure) In the progrm pths, which vribles re defined nd then used should lso be covered (dt) A fmily of dtflow criteri is then defined, ech providing different degree of dt coverge
5 5/54 Dtflow Coverge Considers how dt gets ccessed nd modified in the system nd how it cn get corrupted Common ccess-relted bugs Using n undefined or uninitilized vrible Dellocting or reinitilizing vrible before it is constructed, initilized, or used Deleting collection object leving its members unccessible (grbge collection helps here) Uninitilized... List l; l.dd("1");... Exception in thred "min" jv.lng.nullpointerexception t dtflow.temp.min(temp.jv:21)
6 6/54 Vrible Definition A progrm vrible is DEFINED whenever its vlue is modified: on the left hnd side of n ssignment sttement e.g., y = 17 in n input sttement e.g., red(y) s n cll-by-reference prmeter in subroutine cll e.g., updte(x, &y);
7 7/54 Vrible Use A progrm vrible is USED whenever its vlue is red: on the right hnd side of n ssignment sttement e.g., y = x+17 s n cll-by-vlue prmeter in subroutine or function cll e.g., y = sqrt(x) in the predicte of brnch sttement e.g., if ( x > 0 ) { }
8 8/54 Vrible Use: p-use nd c-use Use in the predicte of brnch sttement is predicteuse or p-use Any other use is computtion-use or c-use For exmple, in the progrm frgment: if ( x > 0 ) { } print(y); There is p-use of x nd c-use of y
9 9/54 Vrible Use A vrible cn lso be used nd then re-defined in single sttement when it ppers: on both sides of n ssignment sttement e.g., y = y + x s n cll-by-reference prmeter in subroutine cll e.g., increment( &y )
10 10/54 More Dtflow Terms nd Definitions A pth is definition cler ( def-cler ) with respect to vrible v if it hs no vrible re-definition of v on the pth A complete pth is pth whose initil node is entry node nd whose finl node is n exit node p1 p2 p3 red(x,v); if(x>0) x=v+1; v=v+1; p1 is def-cler for v, while p2 is not p1, p2 re not complete, while p3 is return x+v Control-flow grph
11 11/54 Definition-Use Pir (DU-Pir) A definition-use pir ( du-pir ) with respect to vrible v is pir (d,u) such tht d is node defining v u is node or edge using v when it is p-use of v, u is n outgoing edge of the predicte sttement there is def-cler pth with respect to v from d to u def d no def for v c-use u c-use exmple def p-use d no def for v u p-use exmple
12 12/54 DU-Pir: Exmple 1 1. input(a,b) if (B>1) { input(a,b) if(b>1) B>1 2. A = A+7 } B<=1 A=A+7 3. if (A>10) { 4. B = A+B if(a>10) A>10 } A<=10 B=A+B 5. output(a,b) output(a,b)
13 13/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
14 14/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
15 15/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
16 16/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
17 17/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
18 18/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
19 19/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
20 20/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
21 21/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
22 22/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
23 23/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
24 24/54 Identifying DU-Pirs Vrible A 1. du-pir input(a,b) pth(s) (1,2) if (B>1) <1,2> { 2. (1,4) A = A+7 <1,3,4> (1,5) } <1,3,4,5> 3. if (A>10) <1,3,5> { 4. (1,<3,4>) B = A+B <1,3,4> (1,<3,5>) } <1,3,5> 5. (2,4) output(a,b) <2,3,4> (2,5) <2,3,4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 B>1 A=A+7 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> (2,<3,5>) <2,3,5> output(a,b)
25 25/54 Identifying DU-Pirs Vrible B du-pir pth(s) (1,4) <1,2,3,4> <1,3,4> (1,5) <1,2,3,5> <1,3,5> (1,<1,2>) <1,2> (1,<1,3>) <1,3> (4,5) <4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 output(a,b) B>1 A=A+7 A>10 B=A+B
26 26/54 Identifying DU-Pirs Vrible B du-pir pth(s) (1,4) <1,2,3,4> <1,3,4> (1,5) <1,2,3,5> <1,3,5> (1,<1,2>) <1,2> (1,<1,3>) <1,3> (4,5) <4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 output(a,b) B>1 A=A+7 A>10 B=A+B
27 27/54 Dtflow Test Coverge Criteri All-Defs for every progrm vrible v, t lest one def-cler pth from every definition of v to t lest one c-use or one p-use of v must be covered
28 28/54 Dtflow Test Coverge Criteri Consider test cse executing pth: t1: <1,2,3,4,5> Identify ll def-cler pths covered (i.e., subsumed) by this pth for ech vrible Are ll definitions for ech vrible ssocited with t lest one of the subsumed def-cler pths?
29 29/54 Def-Cler Pths subsumed by <1,2,3,4,5> for Vrible A du-pir pth(s) (1,2) <1,2> (1,4) <1,3,4> (1,5) <1,3,4,5> <1,3,5> input(a,b) if(b>1) B<=1 B>1 A=A+7 (1,<3,4>) <1,3,4> (1,<3,5>) <1,3,5> (2,4) <2,3,4> (2,5) <2,3,4,5> if(a>10) A<=10 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> output(a, (2,<3,5>) <2,3,5>
30 30/54 Def-Cler Pths Subsumed by <1,2,3,4,5> for Vrible B du-pir pth(s) (1,4) <1,2,3,4> <1,3,4> (1,5) <1,2,3,5> <1,3,5> (1,<1,2>) <1,2> (1,<1,3>) <1,3> (4,5) <4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 output(a, B>1 A=A+7 A>10 B=A+B
31 31/54 Dtflow Test Coverge Criteri Since <1,2,3,4,5> covers t lest one def-cler pth from every definition of A or B to t lest one c-use or p-use of A or B, All-Defs coverge is chieved
32 32/54 Dtflow Test Coverge Criteri All-Uses: for every progrm vrible v, t lest one def-cler pth from every definition of v to every c-use nd every p-use (including ll outgoing edges of the predicte sttement) of v must be covered Requires tht ll du-pirs covered Consider dditionl test cses executing pths: t2: <1,3,4,5> t3: <1,2,3,5> Do ll three test cses provide All-Uses coverge?
33 33/54 Def-Cler Pths Subsumed by <1,3,4,5> for Vrible A du-pir pth(s) (1,2) <1,2> (1,4) <1,3,4> (1,5) <1,3,4,5> <1,3,5> input(a,b) if(b>1) B<=1 B>1 A=A+7 (1,<3,4>) <1,3,4> (1,<3,5>) <1,3,5> (2,4) <2,3,4> (2,5) <2,3,4,5> if(a>10) A<=10 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> output(a, (2,<3,5>) <2,3,5>
34 34/54 Def-Cler Pths Subsumed by <1,3,4,5> for Vrible B du-pir pth(s) (1,4) <1,2,3,4> <1,3,4> (1,5) <1,2,3,5> <1,3,5> (1,<1,2>) <1,2> (1,<1,3>) <1,3> (4,5) <4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 output(a, B>1 A=A+7 A>10 B=A+B
35 35/54 Def-Cler Pths Subsumed by <1,2,3,5> for Vrible A du-pir pth(s) (1,2) <1,2> (1,4) <1,3,4> (1,5) <1,3,4,5> <1,3,5> input(a,b) if(b>1) B<=1 B>1 A=A+7 (1,<3,4>) <1,3,4> (1,<3,5>) <1,3,5> (2,4) <2,3,4> (2,5) <2,3,4,5> if(a>10) A<=10 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> output(a, (2,<3,5>) <2,3,5>
36 36/54 Def-Cler Pths Subsumed by <1,2,3,5> for Vrible A du-pir pth(s) (1,2) <1,2> (1,4) <1,3,4> (1,5) <1,3,4,5> <1,3,5> input(a,b) if(b>1) B<=1 B>1 A=A+7 (1,<3,4>) <1,3,4> (1,<3,5>) <1,3,5> (2,4) <2,3,4> (2,5) <2,3,4,5> if(a>10) A<=10 A>10 B=A+B <2,3,5> (2,<3,4>) <2,3,4> output(a, (2,<3,5>) <2,3,5>
37 37/54 Def-Cler Pths Subsumed by <1,2,3,5> for Vrible B du-pir pth(s) (1,4) <1,2,3,4> <1,3,4> (1,5) <1,2,3,5> <1,3,5> (1,<1,2>) <1,2> (1,<1,3>) <1,3> (4,5) <4,5> input(a,b) if(b>1) B<=1 if(a>10) A<=10 output(a, B>1 A=A+7 A>10 B=A+B
38 38/54 Dtflow Test Coverge Criteri None of the three test cses covers the du-pir (1,<3,5>) for vrible A, All-Uses Coverge is not chieved
39 39/54 DU-Pir: More Complicted Exmple 1. input(x,y) 2. while (Y>0) { 3. if (X>0) 4. Y := Y-X else 5. input(x) 6. } 7. output(x,y) input(x,y) while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 Y:=Y-X input(x) n6 } n7 output(x,y)
40 40/54 du-piridentifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> input(x,y) (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 <5,6,2,3,4,(6,2,3,4)*> Y:=Y-X input(x) (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> n6 n7 } output(x,y
41 41/54 du-pir Identifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> input(x,y) while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 Y:=Y-X input(x) n6 n7 } output(x,y
42 42/54 du-piridentifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> input(x,y) (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 <5,6,2,3,4,(6,2,3,4)*> Y:=Y-X input(x) (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> n6 n7 } output(x,y
43 43/54 ()* mens will be repeted for >=1 times du-piridentifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> input(x,y) (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 <5,6,2,3,4,(6,2,3,4)*> Y:=Y-X input(x) (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> n6 n7 } output(x,y
44 44/54 du-piridentifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> input(x,y) (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 <5,6,2,3,4,(6,2,3,4)*> Y:=Y-X input(x) (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> n6 n7 } output(x,y
45 du-pir Identifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> Infesible! input(x,y) while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 Y:=Y-X input(x) n6 n7 } output(x,y 45/54 Note tht the definition of dupir does not require the existence of fesible def-cler pth from d to u
46 46/54 du-piridentifying pth(s) DU-Pirs Vrible X (1,4) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,7) <1,2,7> <1,2,(3,4,6, 2)*,7> input(x,y) (1,<3,4>) <1,2,3,4> <1,2,3,4,(6,2,3,4)*> (1,<3,5>) <1,2,3,5> <1,2,3,5,(6,2,3,5)*> (5,4) <5,6,2,3,4> while(y>0) Y>0 Y<=0 if(x>0) X>0 X<=0 <5,6,2,3,4,(6,2,3,4)*> Y:=Y-X input(x) (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5> n6 n7 } output(x,y
47 47/54 More Dtflow Terms nd Definitions A pth (either prtil or complete) is simple if ll edges within the pth re distinct, i.e., different A pth is loop-free if ll nodes within the pth re distinct, i.e., different
48 48/54 Simple nd Loop-Free Pths pth Simple? Loop-free? <1,3,4,2> <1,2,3,2> <1,2,3,1,2> <1,2,3,2,4>
49 49/54 DU-Pth A pth <,,...,nj,nk> is du-pth with respect to vrible v, if v is defined t node nd either: there is c-use of v t node nk nd <,,...,nj,nk> is def-cler simple pth, or there is p-use of v t edge <nj,nk> nd <,,...nj> is def-cler loop-free pth. NOTE!
50 50/54 Identifying DU-Pths du-pir pth(s) du-pth? (5,4) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,7) <5,6,2,7> <5,6,2,(3,4,6,2)*,7> (5,<3,4>) <5,6,2,3,4> <5,6,2,3,4,(6,2,3,4)*> (5,<3,5>) <5,6,2,3,5> <5,6,2,(3,4,6,2)*,3,5>
51 51/54 Another Dtflow Test Coverge Criterion All-DU-Pths: for every progrm vrible v, every du-pth from every definition of v to every c-use nd every p-use of v must be covered p1 2 def 1 3 p2 p1 stisfies ll-defs nd ll-uses, but not ll-du-pths p1 nd p2 together stisfy ll-du-pths 4 c-use node 1 is the only def node, nd 4 is the only use node for v
52 52/54 More Dtflow Test Coverge Criteri All-P-Uses/Some-C-Uses: for every progrm vrible v, t lest one def-cler pth from every definition of v to every p-use of v must be covered If no p-use of v is vilble, t lest one def-cler pth to c-use of v must be covered All-C-Uses/Some-P-Uses: for every progrm vrible v, t lest one def-cler pth from every definition of v to every c-use of v must be covered If no c-use of v is vilble, t lest one def-cler pth to p-use of v must be covered
53 53/54 More Dtflow Test Coverge Criteri (2) All-P-Uses: for every progrm vrible v, t lest one def-cler pth from every definition of v to every p-use of v must be covered All-C-Uses: for every progrm vrible v, t lest one def-cler pth from every definition of v to every c-use of v must be covered
54 54/54 Summry Pth Coverge All-DU-Pths All-Uses All-P-Uses/Some-C-Uses All-C-Uses/Some-P-Uses All-P-Uses All-Defs All-C-Uses Brnch Coverge Sttement Coverge
55 55/54 Suggested Redings Sndr Rpps nd Eline J. Weyuker. Selecting Softwre Test Dt Using Dt Flow Informtion. IEEE Trnsctions on Softwre Engineering, 11(4), April 1985, pp tp=&rnumber= P. Frnkl nd E. Weyuker. An Applicble Fmily of Dt Flow Testing Criteri. IEE Trnsction on softwre eng., vol.14, no.10, October E. Weyuker. The evlution of Progrm-bsed softwre test dt dequcy criteri. Communiction of the ACM, vol.31, no.6, June Softwre Testing: A Crftsmn s Approch.2nd CRC publiction, 2002
56 56/54 Thnks
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
We will see what is meant by standard form very shortly
 THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
Here we study square linear systems and properties of their coefficient matrices as they relate to the solution set of the linear system.
 Section 24 Nonsingulr Liner Systems Here we study squre liner systems nd properties of their coefficient mtrices s they relte to the solution set of the liner system Let A be n n Then we know from previous
Section 24 Nonsingulr Liner Systems Here we study squre liner systems nd properties of their coefficient mtrices s they relte to the solution set of the liner system Let A be n n Then we know from previous
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
CS 188: Artificial Intelligence Spring 2007
 CS 188: Artificil Intelligence Spring 2007 Lecture 3: Queue-Bsed Serch 1/23/2007 Srini Nrynn UC Berkeley Mny slides over the course dpted from Dn Klein, Sturt Russell or Andrew Moore Announcements Assignment
CS 188: Artificil Intelligence Spring 2007 Lecture 3: Queue-Bsed Serch 1/23/2007 Srini Nrynn UC Berkeley Mny slides over the course dpted from Dn Klein, Sturt Russell or Andrew Moore Announcements Assignment
Lecture 3 ( ) (translated and slightly adapted from lecture notes by Martin Klazar)
 Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
1.9 C 2 inner variations
 46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
Taylor Polynomial Inequalities
 Tylor Polynomil Inequlities Ben Glin September 17, 24 Abstrct There re instnces where we my wish to pproximte the vlue of complicted function round given point by constructing simpler function such s polynomil
Tylor Polynomil Inequlities Ben Glin September 17, 24 Abstrct There re instnces where we my wish to pproximte the vlue of complicted function round given point by constructing simpler function such s polynomil
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Fundamental Theorem of Calculus
 Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Ordinary Differential Equations- Boundary Value Problem
 Ordinry Differentil Equtions- Boundry Vlue Problem Shooting method Runge Kutt method Computer-bsed solutions o BVPFD subroutine (Fortrn IMSL subroutine tht Solves (prmeterized) system of differentil equtions
Ordinry Differentil Equtions- Boundry Vlue Problem Shooting method Runge Kutt method Computer-bsed solutions o BVPFD subroutine (Fortrn IMSL subroutine tht Solves (prmeterized) system of differentil equtions
Quadratic Forms. Quadratic Forms
 Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
Linearly Similar Polynomials
 Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Reasoning with Bayesian Networks
 Complexity of Probbilistic Inference Compiling Byesin Networks Resoning with Byesin Networks Lecture 5: Complexity of Probbilistic Inference, Compiling Byesin Networks Jinbo Hung NICTA nd ANU Jinbo Hung
Complexity of Probbilistic Inference Compiling Byesin Networks Resoning with Byesin Networks Lecture 5: Complexity of Probbilistic Inference, Compiling Byesin Networks Jinbo Hung NICTA nd ANU Jinbo Hung
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Orthogonal Polynomials
 Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
Math 520 Final Exam Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
( dg. ) 2 dt. + dt. dt j + dh. + dt. r(t) dt. Comparing this equation with the one listed above for the length of see that
 Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
Arc Length of Curves in Three Dimensionl Spce If the vector function r(t) f(t) i + g(t) j + h(t) k trces out the curve C s t vries, we cn mesure distnces long C using formul nerly identicl to one tht we
RELATIONAL MODEL.
 RELATIONAL MODEL Structure of Reltionl Dtbses Reltionl Algebr Tuple Reltionl Clculus Domin Reltionl Clculus Extended Reltionl-Algebr- Opertions Modifiction of the Dtbse Views EXAMPLE OF A RELATION BASIC
RELATIONAL MODEL Structure of Reltionl Dtbses Reltionl Algebr Tuple Reltionl Clculus Domin Reltionl Clculus Extended Reltionl-Algebr- Opertions Modifiction of the Dtbse Views EXAMPLE OF A RELATION BASIC
Automata and Languages
 Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering Lb. The University of Aizu Jpn Grmmr Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Regulr Lnguges Context Free Lnguges Context Sensitive
Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering Lb. The University of Aizu Jpn Grmmr Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Regulr Lnguges Context Free Lnguges Context Sensitive
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
1.1. Linear Constant Coefficient Equations. Remark: A differential equation is an equation
 1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
CS 314 Principles of Programming Languages
 C 314 Principles of Progrmming Lnguges Lecture 6: LL(1) Prsing Zheng (Eddy) Zhng Rutgers University Ferury 5, 2018 Clss Informtion Homework 2 due tomorrow. Homework 3 will e posted erly next week. 2 Top
C 314 Principles of Progrmming Lnguges Lecture 6: LL(1) Prsing Zheng (Eddy) Zhng Rutgers University Ferury 5, 2018 Clss Informtion Homework 2 due tomorrow. Homework 3 will e posted erly next week. 2 Top
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
CMPSCI 250: Introduction to Computation. Lecture #31: What DFA s Can and Can t Do David Mix Barrington 9 April 2014
 CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
IN GAUSSIAN INTEGERS X 3 + Y 3 = Z 3 HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A2 IN GAUSSIAN INTEGERS X + Y = Z HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH Elis Lmpkis Lmpropoulou (Term), Kiprissi, T.K: 24500,
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 (2008), #A2 IN GAUSSIAN INTEGERS X + Y = Z HAS ONLY TRIVIAL SOLUTIONS A NEW APPROACH Elis Lmpkis Lmpropoulou (Term), Kiprissi, T.K: 24500,
Calculus of Variations
 Clculus of Vritions Com S 477/577 Notes) Yn-Bin Ji Dec 4, 2017 1 Introduction A functionl ssigns rel number to ech function or curve) in some clss. One might sy tht functionl is function of nother function
Clculus of Vritions Com S 477/577 Notes) Yn-Bin Ji Dec 4, 2017 1 Introduction A functionl ssigns rel number to ech function or curve) in some clss. One might sy tht functionl is function of nother function
The Fundamental Theorem of Calculus. The Total Change Theorem and the Area Under a Curve.
 Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
CS 275 Automata and Formal Language Theory
 CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) Anton Setzer (Bsed on book drft by J. V. Tucker nd K. Stephenson)
CS 275 Automt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Problem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) Anton Setzer (Bsed on book drft by J. V. Tucker nd K. Stephenson)
1.2. Linear Variable Coefficient Equations. y + b "! = a y + b " Remark: The case b = 0 and a non-constant can be solved with the same idea as above.
 1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
Designing finite automata II
 Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
CS 330 Formal Methods and Models
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
Finite Automata. Informatics 2A: Lecture 3. John Longley. 22 September School of Informatics University of Edinburgh
 Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
2D1431 Machine Learning Lab 3: Reinforcement Learning
 2D1431 Mchine Lerning Lb 3: Reinforcement Lerning Frnk Hoffmnn modified by Örjn Ekeberg December 7, 2004 1 Introduction In this lb you will lern bout dynmic progrmming nd reinforcement lerning. It is ssumed
2D1431 Mchine Lerning Lb 3: Reinforcement Lerning Frnk Hoffmnn modified by Örjn Ekeberg December 7, 2004 1 Introduction In this lb you will lern bout dynmic progrmming nd reinforcement lerning. It is ssumed
Pre-Session Review. Part 1: Basic Algebra; Linear Functions and Graphs
 Pre-Session Review Prt 1: Bsic Algebr; Liner Functions nd Grphs A. Generl Review nd Introduction to Algebr Hierrchy of Arithmetic Opertions Opertions in ny expression re performed in the following order:
Pre-Session Review Prt 1: Bsic Algebr; Liner Functions nd Grphs A. Generl Review nd Introduction to Algebr Hierrchy of Arithmetic Opertions Opertions in ny expression re performed in the following order:
Chapter 5 Plan-Space Planning
 Lecture slides for Automted Plnning: Theory nd Prctice Chpter 5 Pln-Spce Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Stte-Spce Plnning Motivtion g 1 1 g 4 4 s 0 g 5 5 g 2
Lecture slides for Automted Plnning: Theory nd Prctice Chpter 5 Pln-Spce Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Stte-Spce Plnning Motivtion g 1 1 g 4 4 s 0 g 5 5 g 2
The steps of the hypothesis test
 ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
AUTOMATA AND LANGUAGES. Definition 1.5: Finite Automaton
 25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
CS 275 Automata and Formal Language Theory
 CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
UNIT 1 FUNCTIONS AND THEIR INVERSES Lesson 1.4: Logarithmic Functions as Inverses Instruction
 Lesson : Logrithmic Functions s Inverses Prerequisite Skills This lesson requires the use of the following skills: determining the dependent nd independent vribles in n exponentil function bsed on dt from
Lesson : Logrithmic Functions s Inverses Prerequisite Skills This lesson requires the use of the following skills: determining the dependent nd independent vribles in n exponentil function bsed on dt from
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
USA Mathematical Talent Search Round 1 Solutions Year 21 Academic Year
 1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
1/1/21. Fill in the circles in the picture t right with the digits 1-8, one digit in ech circle with no digit repeted, so tht no two circles tht re connected by line segment contin consecutive digits.
University of Texas MD Anderson Cancer Center Department of Biostatistics. Inequality Calculator, Version 3.0 November 25, 2013 User s Guide
 University of Texs MD Anderson Cncer Center Deprtment of Biosttistics Inequlity Clcultor, Version 3.0 November 5, 013 User s Guide 0. Overview The purpose of the softwre is to clculte the probbility tht
University of Texs MD Anderson Cncer Center Deprtment of Biosttistics Inequlity Clcultor, Version 3.0 November 5, 013 User s Guide 0. Overview The purpose of the softwre is to clculte the probbility tht
Jim Lambers MAT 169 Fall Semester Lecture 4 Notes
 Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Section 14.3 Arc Length and Curvature
 Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Finite Automata. Informatics 2A: Lecture 3. Mary Cryan. 21 September School of Informatics University of Edinburgh
 Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
Student Activity 3: Single Factor ANOVA
 MATH 40 Student Activity 3: Single Fctor ANOVA Some Bsic Concepts In designed experiment, two or more tretments, or combintions of tretments, is pplied to experimentl units The number of tretments, whether
MATH 40 Student Activity 3: Single Fctor ANOVA Some Bsic Concepts In designed experiment, two or more tretments, or combintions of tretments, is pplied to experimentl units The number of tretments, whether
Jim Lambers MAT 280 Spring Semester Lecture 26 and 27 Notes
 Jim Lmbers MAT 280 pring emester 2009-10 Lecture 26 nd 27 Notes These notes correspond to ection 8.6 in Mrsden nd Tromb. ifferentil Forms To dte, we hve lerned the following theorems concerning the evlution
Jim Lmbers MAT 280 pring emester 2009-10 Lecture 26 nd 27 Notes These notes correspond to ection 8.6 in Mrsden nd Tromb. ifferentil Forms To dte, we hve lerned the following theorems concerning the evlution
Introduction to Group Theory
 Introduction to Group Theory Let G be n rbitrry set of elements, typiclly denoted s, b, c,, tht is, let G = {, b, c, }. A binry opertion in G is rule tht ssocites with ech ordered pir (,b) of elements
Introduction to Group Theory Let G be n rbitrry set of elements, typiclly denoted s, b, c,, tht is, let G = {, b, c, }. A binry opertion in G is rule tht ssocites with ech ordered pir (,b) of elements
Generalized Fano and non-fano networks
 Generlized Fno nd non-fno networks Nildri Ds nd Brijesh Kumr Ri Deprtment of Electronics nd Electricl Engineering Indin Institute of Technology Guwhti, Guwhti, Assm, Indi Emil: {d.nildri, bkri}@iitg.ernet.in
Generlized Fno nd non-fno networks Nildri Ds nd Brijesh Kumr Ri Deprtment of Electronics nd Electricl Engineering Indin Institute of Technology Guwhti, Guwhti, Assm, Indi Emil: {d.nildri, bkri}@iitg.ernet.in
Fall 2017 Exam 1 MARK BOX HAND IN PART PIN: 17
 Fll 7 Exm problem MARK BOX points HAND IN PART 3-5=x5 NAME: Solutions PIN: 7 % INSTRUCTIONS This exm comes in two prts. () HAND IN PART. Hnd in only this prt. () STATEMENT OF MULTIPLE CHOICE PROBLEMS.
Fll 7 Exm problem MARK BOX points HAND IN PART 3-5=x5 NAME: Solutions PIN: 7 % INSTRUCTIONS This exm comes in two prts. () HAND IN PART. Hnd in only this prt. () STATEMENT OF MULTIPLE CHOICE PROBLEMS.
New data structures to reduce data size and search time
 New dt structures to reduce dt size nd serch time Tsuneo Kuwbr Deprtment of Informtion Sciences, Fculty of Science, Kngw University, Hirtsuk-shi, Jpn FIT2018 1D-1, No2, pp1-4 Copyright (c)2018 by The Institute
New dt structures to reduce dt size nd serch time Tsuneo Kuwbr Deprtment of Informtion Sciences, Fculty of Science, Kngw University, Hirtsuk-shi, Jpn FIT2018 1D-1, No2, pp1-4 Copyright (c)2018 by The Institute
For a continuous function f : [a; b]! R we wish to define the Riemann integral
![For a continuous function f : [a; b]! R we wish to define the Riemann integral For a continuous function f : [a; b]! R we wish to define the Riemann integral](/thumbs/77/75581142.jpg) Supplementry Notes for MM509 Topology II 2. The Riemnn Integrl Andrew Swnn For continuous function f : [; b]! R we wish to define the Riemnn integrl R b f (x) dx nd estblish some of its properties. This
Supplementry Notes for MM509 Topology II 2. The Riemnn Integrl Andrew Swnn For continuous function f : [; b]! R we wish to define the Riemnn integrl R b f (x) dx nd estblish some of its properties. This
4 7x =250; 5 3x =500; Read section 3.3, 3.4 Announcements: Bell Ringer: Use your calculator to solve
 Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
Properties of the Riemann Integral
 Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
CS 330 Formal Methods and Models Dana Richards, George Mason University, Spring 2016 Quiz Solutions
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
Spring 2017 Exam 1 MARK BOX HAND IN PART PIN: 17
 Spring 07 Exm problem MARK BOX points HAND IN PART 0 5-55=x5 0 NAME: Solutions 3 0 0 PIN: 7 % 00 INSTRUCTIONS This exm comes in two prts. () HAND IN PART. Hnd in only this prt. () STATEMENT OF MULTIPLE
Spring 07 Exm problem MARK BOX points HAND IN PART 0 5-55=x5 0 NAME: Solutions 3 0 0 PIN: 7 % 00 INSTRUCTIONS This exm comes in two prts. () HAND IN PART. Hnd in only this prt. () STATEMENT OF MULTIPLE
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
MAA 4212 Improper Integrals
 Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
19 Optimal behavior: Game theory
 Intro. to Artificil Intelligence: Dle Schuurmns, Relu Ptrscu 1 19 Optiml behvior: Gme theory Adversril stte dynmics hve to ccount for worst cse Compute policy π : S A tht mximizes minimum rewrd Let S (,
Intro. to Artificil Intelligence: Dle Schuurmns, Relu Ptrscu 1 19 Optiml behvior: Gme theory Adversril stte dynmics hve to ccount for worst cse Compute policy π : S A tht mximizes minimum rewrd Let S (,
Reasoning and programming. Lecture 5: Invariants and Logic. Boolean expressions. Reasoning. Examples
 Chir of Softwre Engineering Resoning nd progrmming Einführung in die Progrmmierung Introduction to Progrmming Prof. Dr. Bertrnd Meyer Octoer 2006 Ferury 2007 Lecture 5: Invrints nd Logic Logic is the sis
Chir of Softwre Engineering Resoning nd progrmming Einführung in die Progrmmierung Introduction to Progrmming Prof. Dr. Bertrnd Meyer Octoer 2006 Ferury 2007 Lecture 5: Invrints nd Logic Logic is the sis
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Example Sheet 6. Infinite and Improper Integrals
 Sivkumr Exmple Sheet 6 Infinite nd Improper Integrls MATH 5H Mteril presented here is extrcted from Stewrt s text s well s from R. G. Brtle s The elements of rel nlysis. Infinite Integrls: These integrls
Sivkumr Exmple Sheet 6 Infinite nd Improper Integrls MATH 5H Mteril presented here is extrcted from Stewrt s text s well s from R. G. Brtle s The elements of rel nlysis. Infinite Integrls: These integrls
Lecture 3: Equivalence Relations
 Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
12 TRANSFORMING BIVARIATE DENSITY FUNCTIONS
 1 TRANSFORMING BIVARIATE DENSITY FUNCTIONS Hving seen how to trnsform the probbility density functions ssocited with single rndom vrible, the next logicl step is to see how to trnsform bivrite probbility
1 TRANSFORMING BIVARIATE DENSITY FUNCTIONS Hving seen how to trnsform the probbility density functions ssocited with single rndom vrible, the next logicl step is to see how to trnsform bivrite probbility
Review of Riemann Integral
 1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
Speech Recognition Lecture 2: Finite Automata and Finite-State Transducers
 Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
Best Approximation in the 2-norm
 Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
38 Riemann sums and existence of the definite integral.
 38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
Topic 1 Notes Jeremy Orloff
 Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Normal Distribution. Lecture 6: More Binomial Distribution. Properties of the Unit Normal Distribution. Unit Normal Distribution
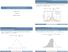 Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
1 2-D Second Order Equations: Separation of Variables
 Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
CS5371 Theory of Computation. Lecture 20: Complexity V (Polynomial-Time Reducibility)
 CS5371 Theory of Computtion Lecture 20: Complexity V (Polynomil-Time Reducibility) Objectives Polynomil Time Reducibility Prove Cook-Levin Theorem Polynomil Time Reducibility Previously, we lernt tht if
CS5371 Theory of Computtion Lecture 20: Complexity V (Polynomil-Time Reducibility) Objectives Polynomil Time Reducibility Prove Cook-Levin Theorem Polynomil Time Reducibility Previously, we lernt tht if
Read section 3.3, 3.4 Announcements:
 Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
11.1 Finite Automata. CS125 Lecture 11 Fall Motivation: TMs without a tape: maybe we can at least fully understand such a simple model?
 CS125 Lecture 11 Fll 2016 11.1 Finite Automt Motivtion: TMs without tpe: mybe we cn t lest fully understnd such simple model? Algorithms (e.g. string mtching) Computing with very limited memory Forml verifiction
CS125 Lecture 11 Fll 2016 11.1 Finite Automt Motivtion: TMs without tpe: mybe we cn t lest fully understnd such simple model? Algorithms (e.g. string mtching) Computing with very limited memory Forml verifiction
A Matrix Algebra Primer
 A Mtrix Algebr Primer Mtrices, Vectors nd Sclr Multipliction he mtrix, D, represents dt orgnized into rows nd columns where the rows represent one vrible, e.g. time, nd the columns represent second vrible,
A Mtrix Algebr Primer Mtrices, Vectors nd Sclr Multipliction he mtrix, D, represents dt orgnized into rows nd columns where the rows represent one vrible, e.g. time, nd the columns represent second vrible,
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Definite integral. Mathematics FRDIS MENDELU
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
