Probability theory and mathematical statistics:
|
|
|
- Malcolm Cooper
- 6 years ago
- Views:
Transcription
1 N.I. Lobachevsky State Uiversity of Nizhi Novgorod Probability theory ad mathematical statistics: Law of Total Probability. Associate Professor A.V. Zorie Law of Total Probability. 1 / 14
2 Theorem Let H 1, H 2,..., H,... be a fiite or deumerable sequece of mutualually exclusive evets with positive probability each, ad A H 1 H 2... H.... The P(A) = P(H 1 )P(A H 1 ) + P(H 2 )P(A H 2 ) P(H )P(A H ) +... Proof. Evets A H 1, A H 2,..., A H,... are mutually exclusive ad A = (A H 1 ) (A H 2 )... (A H ).... The P(A) = P((A H 1 ) (A H 2 )... (A H )...) = P(A H 1 ) + P(A H 2 ) P(A H ) +... = P(H 1 )P(A H 1 ) + P(H 2 )P(A H 2 ) +... P(H )P(A H ) +... Law of Total Probability. 2 / 14
3 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Law of Total Probability. 3 / 14
4 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by classical formula We ca use classical formula here. A outcome is a arragemet of two balls without repetitios. Favorable outcome are those with the secod ball of the blue color. The first ball ca be either blue or red. N(Ω) = A 2 m+ = (m + )(m + 1), N(A) = ( 1) + m, So, P(A) = ( 1) + m (m + )(m + 1) = m + Law of Total Probability. 3 / 14
5 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Law of Total Probability. 4 / 14
6 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by law of total probability. Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = m m +, Law of Total Probability. 4 / 14
7 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by law of total probability. Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = m m +, P(A H 1) = m + 1 Law of Total Probability. 4 / 14
8 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by law of total probability. Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = P(H 2 ) = m m +, P(A H 1) = m +, m + 1 Law of Total Probability. 4 / 14
9 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by law of total probability. Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = P(H 2 ) = m m +, P(A H 1) = m + 1 m +, P(A H 2) = 1 m + 1 Law of Total Probability. 4 / 14
10 Example. There are m red balls ad blue balls i a ur. Two balls are take out oe by oe without replacemet. What s the probability the secod ball is blue (evet A)? Solutio by law of total probability. Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. The P(H 1 ) = P(H 2 ) = m m +, P(A H 1) = m + 1 m +, P(A H 2) = 1 m + 1 P(A) = P(H 1 )P(A H 1 ) + P(H 2 )P(A H 2 ) = m + m m m + 1 m + 1 = m + Law of Total Probability. 4 / 14
11 Example. There 5 urs, two of them cotai 2 red balls ad 1 blue ball, aother two cotai 3 red balls ad 1 blue ball, ad the last oe cotais 10 blue balls. A ur is picked at radom ad oe ball is take out. What s the probability that the ball is red? Law of Total Probability. 5 / 14
12 Example. There 5 urs, two of them cotai 2 red balls ad 1 blue ball, aother two cotai 3 red balls ad 1 blue ball, ad the last oe cotais 10 blue balls. A ur is picked at radom ad oe ball is take out. What s the probability that the ball is red? Solutio. Let evet H 1 occur whe oe of the first two urs is chose, H 2 occur whe the third or the fourth urs is chose, H 3 occur whe the fifth ur is chose. P(H 1 ) = 2 5, P(H 2) = 2 5, P(H 3) = 1 5, P(A H 1) = 2 3, P(A H 2 ) = 3 4, P(A H 3) = 0. The P(A) = = Law of Total Probability. 5 / 14
13 There are m red balls ad blue balls i a ur. r balls are take out oe by oe without replacemet, r m +. Prove that the probability for the last ball to be blue is m+. Law of Total Probability. 6 / 14
14 There are m red balls ad blue balls i a ur. r balls are take out oe by oe without replacemet, r m +. Prove that the probability for the last ball to be blue is m+. Deote by π(r; m, ) the probability i questio. It s obvious that Now assume that π(1; m, ) = m +. π(2; m, ) = π(3; m, ) =... = π(r 1; m, ) = We have to prove that π(r; m, ) = m + m + Law of Total Probability. 6 / 14
15 Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = m + m, P(H 2) = m + Law of Total Probability. 7 / 14
16 Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = m + m, P(H 2) = m + If H 1 occurs, the oly + m 1 balls left, of them are blue, ad we still have to take r 1 balls out, so the coditioal probability that the last ball is blue give that the first is red equals π(r 1; m 1, ). Law of Total Probability. 7 / 14
17 Let evet H 1 occur whe the first ball is red ad H 2 occur whe the first ball is blue. P(H 1 ) = m + m, P(H 2) = m + If H 1 occurs, the oly + m 1 balls left, of them are blue, ad we still have to take r 1 balls out, so the coditioal probability that the last ball is blue give that the first is red equals π(r 1; m 1, ). If H 2 occurs, the oly + m 1 balls left, 1 of them are blue, ad we are to take r 1 balls out, so the coditioal probability that the last ball is blue give that the first is blue equals π(r 1; m, 1). Law of Total Probability. 7 / 14
18 By assumptio, π(r 1; m 1, ) = m + 1, π(r 1; m, 1) = 1 m + 1. Accordig to the law of total probability, π(r; m, ) = P(H 1 )π(r 1; m 1, ) + P(H 2 )π(r 1; m, 1) = m + m m m + 1 m + 1 = m + Law of Total Probability. 8 / 14
19 Rui problem Law of total probability Assume A ad Bart play Heads ad Tails. If A wis, she pays oe rouble to Bart. If Bart wis, he pays oe rouble to A. I the begiig A has a roubles, Bart has b roubles. What s the probability A loses all her moey? A s rui meas that A has o more roubles. The same holds for Bart s rui. Law of Total Probability. 9 / 14
20 Rui problem Law of total probability Assume A ad Bart play Heads ad Tails. If A wis, she pays oe rouble to Bart. If Bart wis, he pays oe rouble to A. I the begiig A has a roubles, Bart has b roubles. What s the probability A loses all her moey? A s rui meas that A has o more roubles. The same holds for Bart s rui. The total sum of roubles is a + b. Deote by π(x) probabilty of A s rui havig x roubles iitially. If she wis a toss, her fortue becomes x + 1 roubles, otherwise x 1 roubles. She wis a toss with probability 1 2 ad loses with probability 1 2. If has x roubles ad she wis a toss, whether she gets ruied or ot is defied oly by the future tosses which are idepedet of the past tosses, so the rui probability after that is π(x + 1). Law of Total Probability. 9 / 14
21 By the total probability formula, besides that, From (1), for a costat c, ad Usig (2), obtai π(a) = 1 2 π(x + 1) + 1 π(x 1) (1) 2 π(0) = 1 ad π(a + b) = 0. (2) π(x) π(x 1) = π(x + 1) π(x) = c π(x) = π(0) + xc. π(x) = 1 x a + b Thus, A gets ruied with probability π(a) = b a+b. Law of Total Probability. 10 / 14
22 A problem i rus I ay ordered sequece of elemets of two kids, each maximal subsequece of elemets of like kid is called a ru. For example, the sequece xxxyxxyyyx opes with a x ru of legth 3; it is followed by rus of legth 1, 2, 3, 1, respectively. Law of Total Probability. 11 / 14
23 A problem i rus I ay ordered sequece of elemets of two kids, each maximal subsequece of elemets of like kid is called a ru. For example, the sequece xxxyxxyyyx opes with a x ru of legth 3; it is followed by rus of legth 1, 2, 3, 1, respectively. Let α ad β be positive itegers, ad cosider a potetially ulimited sequece i idepedet trials, such as tossig a coi or throwig dice. Symbol x occurs i a sigle trial with probability p, symbol y occurs i a sigle trial with probability q = 1 p. What s the probability that a ru of α cosecutive x s will occur before a ru of β cosecutive y s? Law of Total Probability. 11 / 14
24 Sice the trials are idepedet, the probability of the sequece xxxyxxyyyx equals p p p q p p q q q p = p 6 q 4. Law of Total Probability. 12 / 14
25 Sice the trials are idepedet, the probability of the sequece xxxyxxyyyx equals p p p q p p q q q p = p 6 q 4. Let A be the evet that a ru of α cosecutive x s occurs before a ru of β cosecutive y s. Deote x = P(A). Let The u = P(A the first trial results i x ), v = P(A the first trial results i y ). x = pu + qv. Law of Total Probability. 12 / 14
26 Suppose that the first trial results i x. I this case the evet A ca occur i α mutually exclusive ways: 1 The followig α 1 trials result i x s; the probability for this is p α 1. Law of Total Probability. 13 / 14
27 Suppose that the first trial results i x. I this case the evet A ca occur i α mutually exclusive ways: 1 The followig α 1 trials result i x s; the probability for this is p α 1. 2 The first y occurs at the rth trial where 2 r α. Let this evet be H r. The P(H r ) = p r 2 q, ad P(A H r ) = v. Hece u = p α 1 + qv(1 + p p α 2 ) Law of Total Probability. 13 / 14
28 Suppose that the first trial results i x. I this case the evet A ca occur i α mutually exclusive ways: 1 The followig α 1 trials result i x s; the probability for this is p α 1. 2 The first y occurs at the rth trial where 2 r α. Let this evet be H r. The P(H r ) = p r 2 q, ad P(A H r ) = v. Hece u = p α 1 + qv(1 + p p α 2 ) = p α 1 + v(1 p α ). Law of Total Probability. 13 / 14
29 Suppose that the first trial results i x. I this case the evet A ca occur i α mutually exclusive ways: 1 The followig α 1 trials result i x s; the probability for this is p α 1. 2 The first y occurs at the rth trial where 2 r α. Let this evet be H r. The P(H r ) = p r 2 q, ad P(A H r ) = v. Hece u = p α 1 + qv(1 + p p α 2 ) = p α 1 + v(1 p α ). If the first trial results i y, a similar argumet leads to v = pu(1 + q q β 2 ) Law of Total Probability. 13 / 14
30 Suppose that the first trial results i x. I this case the evet A ca occur i α mutually exclusive ways: 1 The followig α 1 trials result i x s; the probability for this is p α 1. 2 The first y occurs at the rth trial where 2 r α. Let this evet be H r. The P(H r ) = p r 2 q, ad P(A H r ) = v. Hece u = p α 1 + qv(1 + p p α 2 ) = p α 1 + v(1 p α ). If the first trial results i y, a similar argumet leads to v = pu(1 + q q β 2 ) = q(1 q β 1 ). Law of Total Probability. 13 / 14
31 We have two equatios for the two ukow u ad v: u = p α 1 + v(1 p α ), v = qu(1 q β 1 ). Law of Total Probability. 14 / 14
32 We have two equatios for the two ukow u ad v: Solutio is u = p α 1 + v(1 p α ), u = v = v = qu(1 q β 1 ). p α q pq β + p α (q q β ), p α (q q β ) pq β + p α (q q β ). Law of Total Probability. 14 / 14
33 We have two equatios for the two ukow u ad v: u = p α 1 + v(1 p α ), v = qu(1 q β 1 ). Solutio is u = v = p α q pq β + p α (q q β ), p α (q q β ) pq β + p α (q q β ). Fially, x = pu + qv = p α 1 1 p α p α 1 + q β 1 p α 1 q β 1 Law of Total Probability. 14 / 14
34 We have two equatios for the two ukow u ad v: u = p α 1 + v(1 p α ), v = qu(1 q β 1 ). Solutio is u = v = p α q pq β + p α (q q β ), p α (q q β ) pq β + p α (q q β ). Fially, x = pu + qv = p α 1 1 p α p α 1 + q β 1 p α 1 q β 1 For example, i tossig a coi (p = 1 2 ) the probability that a ru of two heads appears before a ru of three tails is 0,7. Law of Total Probability. 14 / 14
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Sets and Probabilistic Models
 ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
UNIT 2 DIFFERENT APPROACHES TO PROBABILITY THEORY
 UNIT 2 DIFFERENT APPROACHES TO PROBABILITY THEORY Structure 2.1 Itroductio Objectives 2.2 Relative Frequecy Approach ad Statistical Probability 2. Problems Based o Relative Frequecy 2.4 Subjective Approach
UNIT 2 DIFFERENT APPROACHES TO PROBABILITY THEORY Structure 2.1 Itroductio Objectives 2.2 Relative Frequecy Approach ad Statistical Probability 2. Problems Based o Relative Frequecy 2.4 Subjective Approach
Discrete Mathematics and Probability Theory Summer 2014 James Cook Note 15
 CS 70 Discrete Mathematics ad Probability Theory Summer 2014 James Cook Note 15 Some Importat Distributios I this ote we will itroduce three importat probability distributios that are widely used to model
CS 70 Discrete Mathematics ad Probability Theory Summer 2014 James Cook Note 15 Some Importat Distributios I this ote we will itroduce three importat probability distributios that are widely used to model
Sets and Probabilistic Models
 ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal iversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
ets ad Probabilistic Models Berli Che Departmet of Computer ciece & Iformatio Egieerig Natioal Taiwa Normal iversity Referece: - D. P. Bertsekas, J. N. Tsitsiklis, Itroductio to Probability, ectios 1.1-1.2
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
Random Models. Tusheng Zhang. February 14, 2013
 Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
Radom Models Tusheg Zhag February 14, 013 1 Radom Walks Let me describe the model. Radom walks are used to describe the motio of a movig particle (object). Suppose that a particle (object) moves alog the
PUTNAM TRAINING PROBABILITY
 PUTNAM TRAINING PROBABILITY (Last udated: December, 207) Remark. This is a list of exercises o robability. Miguel A. Lerma Exercises. Prove that the umber of subsets of {, 2,..., } with odd cardiality
PUTNAM TRAINING PROBABILITY (Last udated: December, 207) Remark. This is a list of exercises o robability. Miguel A. Lerma Exercises. Prove that the umber of subsets of {, 2,..., } with odd cardiality
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
CS 70 Second Midterm 7 April NAME (1 pt): SID (1 pt): TA (1 pt): Name of Neighbor to your left (1 pt): Name of Neighbor to your right (1 pt):
 CS 70 Secod Midter 7 April 2011 NAME (1 pt): SID (1 pt): TA (1 pt): Nae of Neighbor to your left (1 pt): Nae of Neighbor to your right (1 pt): Istructios: This is a closed book, closed calculator, closed
CS 70 Secod Midter 7 April 2011 NAME (1 pt): SID (1 pt): TA (1 pt): Nae of Neighbor to your left (1 pt): Nae of Neighbor to your right (1 pt): Istructios: This is a closed book, closed calculator, closed
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
Discrete Mathematics for CS Spring 2005 Clancy/Wagner Notes 21. Some Important Distributions
 CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
CS 70 Discrete Mathematics for CS Sprig 2005 Clacy/Wager Notes 21 Some Importat Distributios Questio: A biased coi with Heads probability p is tossed repeatedly util the first Head appears. What is the
Discrete Mathematics and Probability Theory Spring 2016 Rao and Walrand Note 19
 CS 70 Discrete Mathematics ad Probability Theory Sprig 2016 Rao ad Walrad Note 19 Some Importat Distributios Recall our basic probabilistic experimet of tossig a biased coi times. This is a very simple
CS 70 Discrete Mathematics ad Probability Theory Sprig 2016 Rao ad Walrad Note 19 Some Importat Distributios Recall our basic probabilistic experimet of tossig a biased coi times. This is a very simple
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
UC Berkeley Department of Electrical Engineering and Computer Sciences. EE126: Probability and Random Processes
 UC Berkeley Departmet of Electrical Egieerig ad Computer Scieces EE26: Probability ad Radom Processes Problem Set Fall 208 Issued: Thursday, August 23, 208 Due: Wedesday, August 29, 207 Problem. (i Sho
UC Berkeley Departmet of Electrical Egieerig ad Computer Scieces EE26: Probability ad Radom Processes Problem Set Fall 208 Issued: Thursday, August 23, 208 Due: Wedesday, August 29, 207 Problem. (i Sho
Conditional Probability. Given an event M with non zero probability and the condition P( M ) > 0, Independent Events P A P (AB) B P (B)
 Coditioal robability Give a evet M with o zero probability ad the coditio ( M ) > 0, ( / M ) ( M ) ( M ) Idepedet Evets () ( ) ( ) () ( ) ( ) ( ) Examples ) Let items be chose at radom from a lot cotaiig
Coditioal robability Give a evet M with o zero probability ad the coditio ( M ) > 0, ( / M ) ( M ) ( M ) Idepedet Evets () ( ) ( ) () ( ) ( ) ( ) Examples ) Let items be chose at radom from a lot cotaiig
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
ACO Comprehensive Exam 9 October 2007 Student code A. 1. Graph Theory
 1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
Putnam Training Exercise Counting, Probability, Pigeonhole Principle (Answers)
 Putam Traiig Exercise Coutig, Probability, Pigeohole Pricile (Aswers) November 24th, 2015 1. Fid the umber of iteger o-egative solutios to the followig Diohatie equatio: x 1 + x 2 + x 3 + x 4 + x 5 = 17.
Putam Traiig Exercise Coutig, Probability, Pigeohole Pricile (Aswers) November 24th, 2015 1. Fid the umber of iteger o-egative solutios to the followig Diohatie equatio: x 1 + x 2 + x 3 + x 4 + x 5 = 17.
STAT Homework 1 - Solutions
 STAT-36700 Homework 1 - Solutios Fall 018 September 11, 018 This cotais solutios for Homework 1. Please ote that we have icluded several additioal commets ad approaches to the problems to give you better
STAT-36700 Homework 1 - Solutios Fall 018 September 11, 018 This cotais solutios for Homework 1. Please ote that we have icluded several additioal commets ad approaches to the problems to give you better
0, otherwise. EX = E(X 1 + X n ) = EX j = np and. Var(X j ) = np(1 p). Var(X) = Var(X X n ) =
 PROBABILITY MODELS 35 10. Discrete probability distributios I this sectio, we discuss several well-ow discrete probability distributios ad study some of their properties. Some of these distributios, lie
PROBABILITY MODELS 35 10. Discrete probability distributios I this sectio, we discuss several well-ow discrete probability distributios ad study some of their properties. Some of these distributios, lie
Discrete Mathematics and Probability Theory Spring 2012 Alistair Sinclair Note 15
 CS 70 Discrete Mathematics ad Probability Theory Sprig 2012 Alistair Siclair Note 15 Some Importat Distributios The first importat distributio we leared about i the last Lecture Note is the biomial distributio
CS 70 Discrete Mathematics ad Probability Theory Sprig 2012 Alistair Siclair Note 15 Some Importat Distributios The first importat distributio we leared about i the last Lecture Note is the biomial distributio
Downloaded from
 ocepts ad importat formulae o probability Key cocept: *coditioal probability *properties of coditioal probability *Multiplicatio Theorem o Probablity *idepedet evets *Theorem of Total Probablity *Bayes
ocepts ad importat formulae o probability Key cocept: *coditioal probability *properties of coditioal probability *Multiplicatio Theorem o Probablity *idepedet evets *Theorem of Total Probablity *Bayes
CS284A: Representations and Algorithms in Molecular Biology
 CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Lecture Chapter 6: Convergence of Random Sequences
 ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
CS 171 Lecture Outline October 09, 2008
 CS 171 Lecture Outlie October 09, 2008 The followig theorem comes very hady whe calculatig the expectatio of a radom variable that takes o o-egative iteger values. Theorem: Let Y be a radom variable that
CS 171 Lecture Outlie October 09, 2008 The followig theorem comes very hady whe calculatig the expectatio of a radom variable that takes o o-egative iteger values. Theorem: Let Y be a radom variable that
Math 104: Homework 2 solutions
 Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Lecture 2. The Lovász Local Lemma
 Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
On a Smarandache problem concerning the prime gaps
 O a Smaradache problem cocerig the prime gaps Felice Russo Via A. Ifate 7 6705 Avezzao (Aq) Italy felice.russo@katamail.com Abstract I this paper, a problem posed i [] by Smaradache cocerig the prime gaps
O a Smaradache problem cocerig the prime gaps Felice Russo Via A. Ifate 7 6705 Avezzao (Aq) Italy felice.russo@katamail.com Abstract I this paper, a problem posed i [] by Smaradache cocerig the prime gaps
CS 330 Discussion - Probability
 CS 330 Discussio - Probability March 24 2017 1 Fudametals of Probability 11 Radom Variables ad Evets A radom variable X is oe whose value is o-determiistic For example, suppose we flip a coi ad set X =
CS 330 Discussio - Probability March 24 2017 1 Fudametals of Probability 11 Radom Variables ad Evets A radom variable X is oe whose value is o-determiistic For example, suppose we flip a coi ad set X =
f X (12) = Pr(X = 12) = Pr({(6, 6)}) = 1/36
 Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probability that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c}) Pr(X c) = Pr({s S X(s)
Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probability that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c}) Pr(X c) = Pr({s S X(s)
Massachusetts Institute of Technology
 Solutios to Quiz : Sprig 006 Problem : Each of the followig statemets is either True or False. There will be o partial credit give for the True False questios, thus ay explaatios will ot be graded. Please
Solutios to Quiz : Sprig 006 Problem : Each of the followig statemets is either True or False. There will be o partial credit give for the True False questios, thus ay explaatios will ot be graded. Please
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
STAT 516 Answers Homework 6 April 2, 2008 Solutions by Mark Daniel Ward PROBLEMS
 STAT 56 Aswers Homework 6 April 2, 28 Solutios by Mark Daiel Ward PROBLEMS Chapter 6 Problems 2a. The mass p(, correspods to either o the irst two balls beig white, so p(, 8 7 4/39. The mass p(, correspods
STAT 56 Aswers Homework 6 April 2, 28 Solutios by Mark Daiel Ward PROBLEMS Chapter 6 Problems 2a. The mass p(, correspods to either o the irst two balls beig white, so p(, 8 7 4/39. The mass p(, correspods
Homework 9. (n + 1)! = 1 1
 . Chapter : Questio 8 If N, the Homewor 9 Proof. We will prove this by usig iductio o. 2! + 2 3! + 3 4! + + +! +!. Base step: Whe the left had side is. Whe the right had side is 2! 2 +! 2 which proves
. Chapter : Questio 8 If N, the Homewor 9 Proof. We will prove this by usig iductio o. 2! + 2 3! + 3 4! + + +! +!. Base step: Whe the left had side is. Whe the right had side is 2! 2 +! 2 which proves
First Year Quantitative Comp Exam Spring, Part I - 203A. f X (x) = 0 otherwise
 First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
Chapter 6 Conditional Probability
 Lecture Notes o robability Coditioal robability 6. Suppose RE a radom experimet S sample space C subset of S φ (i.e. (C > 0 A ay evet Give that C must occur, the the probability that A happe is the coditioal
Lecture Notes o robability Coditioal robability 6. Suppose RE a radom experimet S sample space C subset of S φ (i.e. (C > 0 A ay evet Give that C must occur, the the probability that A happe is the coditioal
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
Discrete probability distributions
 Discrete probability distributios I the chapter o probability we used the classical method to calculate the probability of various values of a radom variable. I some cases, however, we may be able to develop
Discrete probability distributios I the chapter o probability we used the classical method to calculate the probability of various values of a radom variable. I some cases, however, we may be able to develop
Math 152. Rumbos Fall Solutions to Review Problems for Exam #2. Number of Heads Frequency
 Math 152. Rumbos Fall 2009 1 Solutios to Review Problems for Exam #2 1. I the book Experimetatio ad Measuremet, by W. J. Youde ad published by the by the Natioal Sciece Teachers Associatio i 1962, the
Math 152. Rumbos Fall 2009 1 Solutios to Review Problems for Exam #2 1. I the book Experimetatio ad Measuremet, by W. J. Youde ad published by the by the Natioal Sciece Teachers Associatio i 1962, the
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
f X (12) = Pr(X = 12) = Pr({(6, 6)}) = 1/36
 Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probablity that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c} Pr(X c) = Pr({s S X(s)
Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probablity that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c} Pr(X c) = Pr({s S X(s)
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
SEQUENCES AND SERIES
 Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
The multiplicative structure of finite field and a construction of LRC
 IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
Random Variables, Sampling and Estimation
 Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Problems from 9th edition of Probability and Statistical Inference by Hogg, Tanis and Zimmerman:
 Math 224 Fall 2017 Homework 4 Drew Armstrog Problems from 9th editio of Probability ad Statistical Iferece by Hogg, Tais ad Zimmerma: Sectio 2.3, Exercises 16(a,d),18. Sectio 2.4, Exercises 13, 14. Sectio
Math 224 Fall 2017 Homework 4 Drew Armstrog Problems from 9th editio of Probability ad Statistical Iferece by Hogg, Tais ad Zimmerma: Sectio 2.3, Exercises 16(a,d),18. Sectio 2.4, Exercises 13, 14. Sectio
SEQUENCE AND SERIES NCERT
 9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
On Random Line Segments in the Unit Square
 O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
Expectation and Variance of a random variable
 Chapter 11 Expectatio ad Variace of a radom variable The aim of this lecture is to defie ad itroduce mathematical Expectatio ad variace of a fuctio of discrete & cotiuous radom variables ad the distributio
Chapter 11 Expectatio ad Variace of a radom variable The aim of this lecture is to defie ad itroduce mathematical Expectatio ad variace of a fuctio of discrete & cotiuous radom variables ad the distributio
CS / MCS 401 Homework 3 grader solutions
 CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
CS / MCS 401 Homework 3 grader solutios assigmet due July 6, 016 writte by Jāis Lazovskis maximum poits: 33 Some questios from CLRS. Questios marked with a asterisk were ot graded. 1 Use the defiitio of
2) 3 π. EAMCET Maths Practice Questions Examples with hints and short cuts from few important chapters
 EAMCET Maths Practice Questios Examples with hits ad short cuts from few importat chapters. If the vectors pi j + 5k, i qj + 5k are colliear the (p,q) ) 0 ) 3) 4) Hit : p 5 p, q q 5.If the vectors i j
EAMCET Maths Practice Questios Examples with hits ad short cuts from few importat chapters. If the vectors pi j + 5k, i qj + 5k are colliear the (p,q) ) 0 ) 3) 4) Hit : p 5 p, q q 5.If the vectors i j
IIT JAM Mathematical Statistics (MS) 2006 SECTION A
 IIT JAM Mathematical Statistics (MS) 6 SECTION A. If a > for ad lim a / L >, the which of the followig series is ot coverget? (a) (b) (c) (d) (d) = = a = a = a a + / a lim a a / + = lim a / a / + = lim
IIT JAM Mathematical Statistics (MS) 6 SECTION A. If a > for ad lim a / L >, the which of the followig series is ot coverget? (a) (b) (c) (d) (d) = = a = a = a a + / a lim a a / + = lim a / a / + = lim
M A T H F A L L CORRECTION. Algebra I 1 4 / 1 0 / U N I V E R S I T Y O F T O R O N T O
 M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
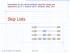 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Probability and Statistics
 robability ad Statistics rof. Zheg Zheg Radom Variable A fiite sigle valued fuctio.) that maps the set of all eperimetal outcomes ito the set of real umbers R is a r.v., if the set ) is a evet F ) for
robability ad Statistics rof. Zheg Zheg Radom Variable A fiite sigle valued fuctio.) that maps the set of all eperimetal outcomes ito the set of real umbers R is a r.v., if the set ) is a evet F ) for
Final Review for MATH 3510
 Fial Review for MATH 50 Calculatio 5 Give a fairly simple probability mass fuctio or probability desity fuctio of a radom variable, you should be able to compute the expected value ad variace of the variable
Fial Review for MATH 50 Calculatio 5 Give a fairly simple probability mass fuctio or probability desity fuctio of a radom variable, you should be able to compute the expected value ad variace of the variable
Lecture 6 Simple alternatives and the Neyman-Pearson lemma
 STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
STATS 00: Itroductio to Statistical Iferece Autum 06 Lecture 6 Simple alteratives ad the Neyma-Pearso lemma Last lecture, we discussed a umber of ways to costruct test statistics for testig a simple ull
Lecture 1 Probability and Statistics
 Wikipedia: Lecture 1 Probability ad Statistics Bejami Disraeli, British statesma ad literary figure (1804 1881): There are three kids of lies: lies, damed lies, ad statistics. popularized i US by Mark
Wikipedia: Lecture 1 Probability ad Statistics Bejami Disraeli, British statesma ad literary figure (1804 1881): There are three kids of lies: lies, damed lies, ad statistics. popularized i US by Mark
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Different kinds of Mathematical Induction
 Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
ARITHMETIC PROGRESSION
 CHAPTER 5 ARITHMETIC PROGRESSION Poits to Remember :. A sequece is a arragemet of umbers or objects i a defiite order.. A sequece a, a, a 3,..., a,... is called a Arithmetic Progressio (A.P) if there exists
CHAPTER 5 ARITHMETIC PROGRESSION Poits to Remember :. A sequece is a arragemet of umbers or objects i a defiite order.. A sequece a, a, a 3,..., a,... is called a Arithmetic Progressio (A.P) if there exists
PRACTICE PROBLEMS FOR THE FINAL
 PRACTICE PROBLEMS FOR THE FINAL Math 36Q Fall 25 Professor Hoh Below is a list of practice questios for the Fial Exam. I would suggest also goig over the practice problems ad exams for Exam ad Exam 2 to
PRACTICE PROBLEMS FOR THE FINAL Math 36Q Fall 25 Professor Hoh Below is a list of practice questios for the Fial Exam. I would suggest also goig over the practice problems ad exams for Exam ad Exam 2 to
Mathematical Statistics - MS
 Paper Specific Istructios. The examiatio is of hours duratio. There are a total of 60 questios carryig 00 marks. The etire paper is divided ito three sectios, A, B ad C. All sectios are compulsory. Questios
Paper Specific Istructios. The examiatio is of hours duratio. There are a total of 60 questios carryig 00 marks. The etire paper is divided ito three sectios, A, B ad C. All sectios are compulsory. Questios
Introduction to Probability and Statistics Twelfth Edition
 Itroductio to Probability ad Statistics Twelfth Editio Robert J. Beaver Barbara M. Beaver William Medehall Presetatio desiged ad writte by: Barbara M. Beaver Itroductio to Probability ad Statistics Twelfth
Itroductio to Probability ad Statistics Twelfth Editio Robert J. Beaver Barbara M. Beaver William Medehall Presetatio desiged ad writte by: Barbara M. Beaver Itroductio to Probability ad Statistics Twelfth
M17 MAT25-21 HOMEWORK 5 SOLUTIONS
 M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
M17 MAT5-1 HOMEWORK 5 SOLUTIONS 1. To Had I Cauchy Codesatio Test. Exercise 1: Applicatio of the Cauchy Codesatio Test Use the Cauchy Codesatio Test to prove that 1 diverges. Solutio 1. Give the series
Topic 8: Expected Values
 Topic 8: Jue 6, 20 The simplest summary of quatitative data is the sample mea. Give a radom variable, the correspodig cocept is called the distributioal mea, the epectatio or the epected value. We begi
Topic 8: Jue 6, 20 The simplest summary of quatitative data is the sample mea. Give a radom variable, the correspodig cocept is called the distributioal mea, the epectatio or the epected value. We begi
This exam contains 19 pages (including this cover page) and 10 questions. A Formulae sheet is provided with the exam.
 Probability ad Statistics FS 07 Secod Sessio Exam 09.0.08 Time Limit: 80 Miutes Name: Studet ID: This exam cotais 9 pages (icludig this cover page) ad 0 questios. A Formulae sheet is provided with the
Probability ad Statistics FS 07 Secod Sessio Exam 09.0.08 Time Limit: 80 Miutes Name: Studet ID: This exam cotais 9 pages (icludig this cover page) ad 0 questios. A Formulae sheet is provided with the
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
SEQUENCES AND SERIES
 9 SEQUENCES AND SERIES INTRODUCTION Sequeces have may importat applicatios i several spheres of huma activities Whe a collectio of objects is arraged i a defiite order such that it has a idetified first
9 SEQUENCES AND SERIES INTRODUCTION Sequeces have may importat applicatios i several spheres of huma activities Whe a collectio of objects is arraged i a defiite order such that it has a idetified first
LECTURE SERIES WITH NONNEGATIVE TERMS (II). SERIES WITH ARBITRARY TERMS
 LECTURE 4 SERIES WITH NONNEGATIVE TERMS II). SERIES WITH ARBITRARY TERMS Series with oegative terms II) Theorem 4.1 Kummer s Test) Let x be a series with positive terms. 1 If c ) N i 0, + ), r > 0 ad 0
LECTURE 4 SERIES WITH NONNEGATIVE TERMS II). SERIES WITH ARBITRARY TERMS Series with oegative terms II) Theorem 4.1 Kummer s Test) Let x be a series with positive terms. 1 If c ) N i 0, + ), r > 0 ad 0
Assignment 5: Solutions
 McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
McGill Uiversity Departmet of Mathematics ad Statistics MATH 54 Aalysis, Fall 05 Assigmet 5: Solutios. Let y be a ubouded sequece of positive umbers satisfyig y + > y for all N. Let x be aother sequece
Statisticians use the word population to refer the total number of (potential) observations under consideration
 6 Samplig Distributios Statisticias use the word populatio to refer the total umber of (potetial) observatios uder cosideratio The populatio is just the set of all possible outcomes i our sample space
6 Samplig Distributios Statisticias use the word populatio to refer the total umber of (potetial) observatios uder cosideratio The populatio is just the set of all possible outcomes i our sample space
Lecture 4 The Simple Random Walk
 Lecture 4: The Simple Radom Walk 1 of 9 Course: M36K Itro to Stochastic Processes Term: Fall 014 Istructor: Gorda Zitkovic Lecture 4 The Simple Radom Walk We have defied ad costructed a radom walk {X }
Lecture 4: The Simple Radom Walk 1 of 9 Course: M36K Itro to Stochastic Processes Term: Fall 014 Istructor: Gorda Zitkovic Lecture 4 The Simple Radom Walk We have defied ad costructed a radom walk {X }
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
GRADE 12 JUNE 2016 MATHEMATICS P1
 NATIONAL SENIOR CERTIFICATE GRADE 1 JUNE 016 MATHEMATICS P1 MARKS: 150 TIME: 3 hours *MATHE1* This questio paper cosists of 14 pages, icludig a iformatio sheet. MATHEMATICS P1 (EC/JUNE 016) INSTRUCTIONS
NATIONAL SENIOR CERTIFICATE GRADE 1 JUNE 016 MATHEMATICS P1 MARKS: 150 TIME: 3 hours *MATHE1* This questio paper cosists of 14 pages, icludig a iformatio sheet. MATHEMATICS P1 (EC/JUNE 016) INSTRUCTIONS
ON POINTWISE BINOMIAL APPROXIMATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
7.1 Convergence of sequences of random variables
 Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
CIS Spring 2018 (instructor Val Tannen)
 CIS 160 - Sprig 2018 (istructor Val Tae) Lecture 5 Thursday, Jauary 25 COUNTING We cotiue studyig how to use combiatios ad what are their properties. Example 5.1 How may 8-letter strigs ca be costructed
CIS 160 - Sprig 2018 (istructor Val Tae) Lecture 5 Thursday, Jauary 25 COUNTING We cotiue studyig how to use combiatios ad what are their properties. Example 5.1 How may 8-letter strigs ca be costructed
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: 2 hours
 THE 06-07 KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: hours Let x, y, ad A all be positive itegers with x y a) Prove that there are
THE 06-07 KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: hours Let x, y, ad A all be positive itegers with x y a) Prove that there are
Let us consider the following problem to warm up towards a more general statement.
 Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Some discrete distribution
 Some discrete distributio p. 2-13 Defiitio (Beroulli distributio B(p)) A Beroulli distributio takes o oly two values: 0 ad 1, with probabilities 1 p ad p, respectively. pmf: p() = p (1 p) (1 ), if =0or
Some discrete distributio p. 2-13 Defiitio (Beroulli distributio B(p)) A Beroulli distributio takes o oly two values: 0 ad 1, with probabilities 1 p ad p, respectively. pmf: p() = p (1 p) (1 ), if =0or
Quick Review of Probability
 Quick Review of Probability Berli Che Departmet of Computer Sciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Refereces: 1. W. Navidi. Statistics for Egieerig ad Scietists. Chapter 2 & Teachig
Quick Review of Probability Berli Che Departmet of Computer Sciece & Iformatio Egieerig Natioal Taiwa Normal Uiversity Refereces: 1. W. Navidi. Statistics for Egieerig ad Scietists. Chapter 2 & Teachig
ABOUT CHAOS AND SENSITIVITY IN TOPOLOGICAL DYNAMICS
 ABOUT CHAOS AND SENSITIVITY IN TOPOLOGICAL DYNAMICS EDUARD KONTOROVICH Abstract. I this work we uify ad geeralize some results about chaos ad sesitivity. Date: March 1, 005. 1 1. Symbolic Dyamics Defiitio
ABOUT CHAOS AND SENSITIVITY IN TOPOLOGICAL DYNAMICS EDUARD KONTOROVICH Abstract. I this work we uify ad geeralize some results about chaos ad sesitivity. Date: March 1, 005. 1 1. Symbolic Dyamics Defiitio
Polynomials with Rational Roots that Differ by a Non-zero Constant. Generalities
 Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
International Contest-Game MATH KANGAROO Canada, Grade 11 and 12
 Part A: Each correct aswer is worth 3 poits. Iteratioal Cotest-Game MATH KANGAROO Caada, 007 Grade ad. Mike is buildig a race track. He wats the cars to start the race i the order preseted o the left,
Part A: Each correct aswer is worth 3 poits. Iteratioal Cotest-Game MATH KANGAROO Caada, 007 Grade ad. Mike is buildig a race track. He wats the cars to start the race i the order preseted o the left,

 1 Solutios of Homework 2. 1. Suppose X Y with E(Y )
1 Solutios of Homework 2. 1. Suppose X Y with E(Y )