Standard Trigonometric Functions
|
|
|
- Dylan Kennedy
- 6 years ago
- Views:
Transcription
1 CRASH KINEMATICS For ngle A: opposite sine A = = hypotenuse djent osine A = = hypotenuse opposite tngent A = = djent For ngle B: opposite sine B = = hypotenuse djent osine B = = hypotenuse opposite tngent B = = djent Stndrd Trigonometri Funtions A C = Sin A = Cos A = Tn A = Sin B = Cos B = Sin B B A= Sin -1 ( ) A= Cos -1 ( ) A= Tn -1 ( ) B= Sin -1 ( ) B= Cos -1 ( ) B= Tn -1 ( ) A = mesured y surveyor = Distne from surveyor to tree Sin A = = sin A + Surveyor height = Height of tree A 1
2 Crsh Fore Computtion Terminology Horizontl Flight Pth Terrin Impt Term Desription Notes The ngle etween the impt surfe nd the horizontl, mesured in the vertil plne of the flight pth. the diretion of the flight is downhill. Terrin Flight Pth Impt The ngle etween the irrft s flight pth nd the horizontl t the moment of impt. The ngle etween the flight pth nd the terrin, mesured in the vertil plne of the flight pth. The lgeri sign of the terrin ngle is positive when the diretion of flight is uphill & negtive when The lgeri sign of the flight pth ngle is positive if the irrft is moving downwrd immeditely prior to impt. The sign is negtive if impt ours while the irrft is moving upwrd. The impt ngle is the lgeri sum of the flight pth ngle plus the terrin ngle. [ Impt = Flight Pth + Terrin ] Airrft Pith Crsh Fore Resultnt Crsh Fore G R Resultnt Crsh Fore G H Horizontl Crsh Fore G V Vertil Crsh Fore Resultnt Term Desription Notes The geometri sum of the horizontl nd vertil rsh fores. Horizontl nd vertil rsh fores re determined on the sis of horizontl nd vertil veloity omponents t impt nd horizontl nd vertil stopping distnes. Attitude t Impt Crsh Fore The irrft ttitude t moment of impt. Pith Nose ove or elow horizon Yw Nose right or left Roll Right or left nk The ngle etween the resultnt rsh fore nd the longitudinl xis of the irrft. Crsh* Resultnt Fore = + * Resultnt ngle mesured from horizontl. Other solutions re possile. Pith The lgeri sign of the Crsh Fore Resultnt ngle is positive when the line of tion of the resultnt is ove the horizontl nd is negtive if the line of tion is elow the horizontl. The lgeri sign of the irrft pith ngle is negtive when the nose of the irrft points elow the horizon nd positive when the nose points ove the horizon. For impts with little lterl omponent of fore the rsh fore ngle is the lgeri sum of the rsh fore resultnt ngle plus the irrft pith ngle. 2
3 V l V l l I V FP Down Hill R = Resultnt CF G ll = G Prllel G l = G Perpendiulr G R = G Resultnt FP T Horizon I = Impt FP = Flight Pth T = Terrin V FP = Veloity Flight Pth = Veloity Vertil V ll = Veloity Prllel = Veloity Perpendiulr V i G l G l l G R R V FP = sin I Tn FP = V l V ll G R = V l = sin I V FP V ll = os I V FP G l = G l sin R Tn R = V l SD G ll = G l G ll V ll SD MPH = Ft/Se KTS 1.69 = Ft/Se is mesured perpendiulr to the Horizon, not the Terrin. V FP Up Hill i fp Horizon V l t V l l G l G R R G l l 3
4 Solve for: Opposite A Sine A = Hypotenuse = B Adjent Cosine A = = Hypotenuse Opposite Tngent A = = Adjent Opposite Sine B = Hypotenuse = Adjent Cosine B = = Hypotenuse Opposite Tngent B = = Adjent Sine of A =.3420 Length of side is 10 feet long Solve for length of side. A = 2 C = 90º Exmple: Solve for length of sides nd if ngle A is 20º nd side is 10 feet long Sine A = = 10 = (0.3420)(10) = feet long Mth Key Cosine of A =.9397 Length of side is 10 feet long Solve for length of side. C B Cosine A = = 10 = (0.9397)(10) = feet long Chek ury of omputtions: = 2 (3.420) 2 + (9.397) 2 = = V = Veloity in feet/seond (f/s) = Vertil Veloity V H = Horizontl Veloity V FP = Veloity of flight pth V(MPH) = V f/s V(KTS) 1.69 = V f/s Grvity (g) = GV = G Lod Vertil GH = G Lod Horizontl SD = Stopping Distne in feet SDV = Stopping Distne Vertil SDH = Stopping Distne Horizontl KE = Keneti Energy in foot/pounds (ft/ls) W = Weight of Ojet h = Height CF = Centrifugl Fore in pounds Rdius = 1/2 dimeter Solve for impt ngle: Impt Opposite Tn A = Adjent = G V = Solve for vertil impt G lod: ( ) 2 g SD V CF = Solve for horizontl imlne: W Rdius (RPM) Solve for vertil veloity, given Solve for horizontl impt G lod: Solve for kineti energy: flight pth veloity (f/s): Sine A = G H = ( ) 2 W KE = 1/2 V 2 V g x SD g H FP (V in fps, nswer in foot/pounds) Solve for horizontl veloity given flight Solve for Veloity: pth veloity (f/s) V H Cosine A = V = 8 h V FP Stopping Distne V2 SD = G s (Ft needed to survive x mount of G s) Sovle for veloity: V 2 = K.E. 1 weight G s = Solve for G s: V SD MPH = Feet/Seond KTS 1.69 = Feet/Seond 4
5 Prolem #1 An irplne impts on level ground fter pssing through the top rnhes of tree. By mesurement, you determine tht the irplne struk the tree 70 feet ove the ground t point 200 feet horizontlly from the point of impt. Find: 1. The ngle of impt. 2. The horizontl nd vertil veloities t impt if the flight pth veloity is 150 feet per seond. 70 A Find the ngle of impt Tn A = A = tn -1 (70 200) = 19.29º 2 The horizontl nd vertil veloities t impt if the flight pth veloity is 150 feet per seond.. Drw sketh of irplne impt ngle A = 19.29º = A = V H. Find nd V H using sine nd osine =, V H = = (sin A = ) sin A = sin (150) = fps V H = (os A = ) os A = os (150) = fps 5
6 Prolem #2 An irrft rshes in level open field. Flight pth ngle is 10 degrees nd the true irspeed is 85 mph. Initil impt ours with the fuselge level (zero pith ngle). The impt uses 2-foot-deep gouge, nd the irrft omes to rest 25 feet from initil impt. The fuselge is rushed 12 inhes vertilly nd 5 feet horizontlly. Find: 1. The irrft ground speed (V H ) nd vertil veloity ( ) in feet per seond. 2. The men vertil nd horizontl elertions, in G s. 3. The mgnitude nd diretion of the men rsh resultnt. 1 To find V H nd. Sketh onditions t impt. Convert 85 mph to ft/se (85 mph)(1.467) = ft/se V H 10 o Answer rounded to ft/se. Determine vertil nd horizontl veloities (Round nswers to nerest 10th for next step) sin 10 o = V FP = V FP sin 10 o = (124.7)(0.174) = ft/se os 10 o = V H V FP V H = V FP os 10 o V H = (124.7)(0.985) = ft/se 2 To find G V nd G H. Determine vertil nd horizontl stopping distnes Vertil stopping distne (S V ) = (2 ft) gouge + (1 ft) struture = 3 ft Horizontl stopping distne (S H ) = (25 ft) gouge + (5 ft) struture = 30 ft. Determine vertil nd horizontl elertions (G s) G = V 2 64S 3 To find R nd G R G V = 2.45G G H = 7.85G G V = (21.7) 2 (64 3) = 2.45 G G H = (122.8) 2 (64 30) = 7.85 G. Sketh the vetor digrm of the impt elertions. Use tngent trig funtion to find diretion of resultnt elertion tn R = G V 2.45 = G H 7.85 = R. Use the osine funtion to find the mgnitude of the resultnt elertion os 17.3º = G R = = 8.22 G G R os 17.3º R = r tn = 17.3º 6
7 Prolem #3 An irrft rshes on level ground t n irspeed of 140 knots. Aident investigtors disover tht the irplne struk the top of tree t point 60 feet ove the ground nd rshed 100 feet from the se of the tree. The irrft me to rest t the end of gouge 32 feet long nd 3 feet deep. Mesurements show tht the irplne ws rushed 60 inhes longitudinlly nd 12 inhes vertilly. Find: 1. Horizontl nd vertil veloities, in feet per seond. 2. Men vertil nd horizontl elertions, in G s. 3. Mgnitude nd diretion of the rsh fore resultnt. 1 To find V H nd. Sketh onditions t impt. Convert 140 knots to ft/se (140 kts)(1.69) = ft/se = 60 = 100 V H d. Determine vertil nd horizontl veloities I. Determine impt ngle tn I = I = tn ( ) = 30.96º 100 (Answer rounded to 31º for next omputtion) (Round nswers to nerest 10th) sin 31 o = V FP = (236.6)(sin 31 o ) = (236.6)(0.515) = ft/se os 31 o = V H V FP V H = (236.6)(os 31 o ) V H = (236.6)(0.857) = ft/se 2 To find G V nd G H. Determine vertil nd horizontl stopping distnes Vertil stopping distne (S V ) = (3 ft) gouge + (1 ft) struture = 4 ft Horizontl stopping distne (S H ) = (32 ft) gouge + (5 ft) struture = 37 ft. Determine vertil nd horizontl elertions (G s) G = V 2 64S 3 To find R nd G R G V = (121.8) 2 (64 4) = G G H = (202.8) 2 (64 37) = G (Round nswers to nerest 10th). Sketh the vetor digrm of the impt elertions. Use tngent trig funtion to find diretion of resultnt elertion G tn R = V 58.0 = = 3.33 G H 17.4 R = tn -1 (3.33) = 73.28º (Round nswer to nerest 10th). Use the osine funtion to find the mgnitude of the resultnt elertion R G H = 17.4 G G sin 73.3º = V = G R = = G G R G R sin73.3º 7
8 Prolem #4 An irrft rshes ginst 10-degree uphill slope. The impt ngle is 20 degrees. At the time of the impt, the irrft vertil veloity ws 1,800 feet per minute. The irplne me to rest fter sliding 80 feet. Mximum depth of the gouge ws 1 foot, nd inspetion reveled tht the irplne struture ws rushed 1 foot vertilly. There ws no horizontl rushing of the struture. Find: 1. Flight pth veloity. 2. Men longitudinl nd vertil elertion, in G s, with respet to the fe of the hill. 3. Men rsh fore resultnt mgnitude nd diretion.. 1 To find flight pth veloity. Sketh onditions t impt. Convert to feet/se 1,800 ft/min 60 = 30 ft/se FP = 10º 10º I = 20º 2 To find G l nd G ll. Determine flight pth veloity sin FP = sin 10º = = V FP = 30 sin 10º V FP 30 V FP = ft/se (Round nswer to nerest 10th). Sketh the known onditions, with respet to the fe of the hill. (This my e inluded in the erlier sketh). I = 20º. Determine veloity prllel to fe of hill nd veloity perpendiulr to fe of hill. (Round nswers to nerest 10th) (1) os 20º = V ll V FP V ll = (V FP )(os 20º) = (172.8)(os 20º) = ft/se (2) sin 20º = V l V FP V l = (V FP )(sin 20º) = (172.8)(sin 20º) = ft/se. Determine stopping distnes prllel to the fe of the hill nd perpendiulr to the fe of the hill. (1) S ll = 80 feet (2) S l = (1 foot) + (1 foot) = 2 feet d. Determine elertions prllel to the slope nd perpendiulr to the slope. G = V 2 64S (1) G ll = (162.4) 2 (64 80) = 5.15 G s (2) G l = (59.1) 2 (64 2) = G s 8
9 Prolem #4 ontinued: 3 To find R nd G R. Sketh the vetor digrm of the men elertions.. Determine R. tn R = G l G = ll 5.15 = 5.29 R = tn -1 (5.29) = 79.29º (Round nswer to nerest 10th). Determine mgnitude of rsh fore resultnt. G ll = 5.15 G G l sin 79.3 = = G R G R = sin 79.3º = G G R 9
10 Prolem #5 (Bsed on Prolem #4: An irrft rshes ginst 10-degree uphill slope. The impt ngle is 20 degrees. At the time of the impt, the irrft vertil veloity ws 1,800 feet per minute. The irplne me to rest fter sliding 80 feet. Mximum depth of the gouge ws 1 foot, nd inspetion reveled tht the irplne struture ws rushed 1 foot vertilly. There ws no horizontl rushing of the struture.) ADD: The longitudinl xis of the irplne is prllel to the flight pth. Find: Longitudinl nd vertil elertions with respet to the irrft xes. 1 Determine longitudinl nd vertil elertions with respet to the irrft xes.. Sketh onditions t impt Airrft Vertil Axis Horizontl Referene 20º. Determine from the sketh tht the G rsh fore resultnt ts t n ngle of 59.3 degrees from the longitudinl xis of the irplne (79.3º - 20º = 59.3º) Therefore, the men longitudinl elertion of the irplne is: G longitudinl = (G R )(os 59.3º) = (27.28)(os 59.3º ) = ft/se And the men vertil elertion of the irplne is: G vertil = (G R )(sin 59.2º) = (27.28)(sin 59.3º ) = ft/se 10
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Topics Covered: Pythagoras Theorem Definition of sin, cos and tan Solving right-angle triangles Sine and cosine rule
 Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Lesson 8.1 Graphing Parametric Equations
 Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Precalculus Notes: Unit 6 Law of Sines & Cosines, Vectors, & Complex Numbers. A can be rewritten as
 Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Forces on curved surfaces Buoyant force Stability of floating and submerged bodies
 Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg) Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
MATH Final Review
 MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
Learning Objectives of Module 2 (Algebra and Calculus) Notes:
 67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Section 13.1 Right Triangles
 Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Alg 3 Ch 7.2, 8 1. C 2) If A = 30, and C = 45, a = 1 find b and c A
 lg 3 h 7.2, 8 1 7.2 Right Tringle Trig ) Use of clcultor sin 10 = sin x =.4741 c ) rete right tringles π 1) If = nd = 25, find 6 c 2) If = 30, nd = 45, = 1 find nd c 3) If in right, with right ngle t,
lg 3 h 7.2, 8 1 7.2 Right Tringle Trig ) Use of clcultor sin 10 = sin x =.4741 c ) rete right tringles π 1) If = nd = 25, find 6 c 2) If = 30, nd = 45, = 1 find nd c 3) If in right, with right ngle t,
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Trigonometry. cosθ. sinθ tanθ. Mathletics Instant Workbooks. Copyright
 Student Book - Series K- sinθ tnθ osθ Mtletis Instnt Workooks Copyrigt Student Book - Series K Contents Topis Topi - Nming te sides of rigt-ngled tringle Topi 2 - Te trigonometri rtios Topi 3 - Using lultor
Student Book - Series K- sinθ tnθ osθ Mtletis Instnt Workooks Copyrigt Student Book - Series K Contents Topis Topi - Nming te sides of rigt-ngled tringle Topi 2 - Te trigonometri rtios Topi 3 - Using lultor
Instructions to students: Use your Text Book and attempt these questions.
 Instrutions to students: Use your Text Book nd ttempt these questions. Due Dte: 16-09-2018 Unit 2 Chpter 8 Test Slrs nd vetors Totl mrks 50 Nme: Clss: Dte: Setion A Selet the est nswer for eh question.
Instrutions to students: Use your Text Book nd ttempt these questions. Due Dte: 16-09-2018 Unit 2 Chpter 8 Test Slrs nd vetors Totl mrks 50 Nme: Clss: Dte: Setion A Selet the est nswer for eh question.
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Solving Right Triangles Using Trigonometry Examples
 Solving Right Triangles Using Trigonometry Eamples 1. To solve a triangle means to find all the missing measures of the triangle. The trigonometri ratios an be used to solve a triangle. The ratio used
Solving Right Triangles Using Trigonometry Eamples 1. To solve a triangle means to find all the missing measures of the triangle. The trigonometri ratios an be used to solve a triangle. The ratio used
CHAPTER 10 PARAMETRIC, VECTOR, AND POLAR FUNCTIONS. dy dx
 CHAPTER 0 PARAMETRIC, VECTOR, AND POLAR FUNCTIONS 0.. PARAMETRIC FUNCTIONS A) Recll tht for prmetric equtions,. B) If the equtions x f(t), nd y g(t) define y s twice-differentile function of x, then t
CHAPTER 0 PARAMETRIC, VECTOR, AND POLAR FUNCTIONS 0.. PARAMETRIC FUNCTIONS A) Recll tht for prmetric equtions,. B) If the equtions x f(t), nd y g(t) define y s twice-differentile function of x, then t
Time : 3 hours 03 - Mathematics - March 2007 Marks : 100 Pg - 1 S E CT I O N - A
 Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Objective: Use the Pythagorean Theorem and its converse to solve right triangle problems. CA Geometry Standard: 12, 14, 15
 Geometry CP Lesson 8.2 Pythgoren Theorem nd its Converse Pge 1 of 2 Ojective: Use the Pythgoren Theorem nd its converse to solve right tringle prolems. CA Geometry Stndrd: 12, 14, 15 Historicl Bckground
Geometry CP Lesson 8.2 Pythgoren Theorem nd its Converse Pge 1 of 2 Ojective: Use the Pythgoren Theorem nd its converse to solve right tringle prolems. CA Geometry Stndrd: 12, 14, 15 Historicl Bckground
9.5 Start Thinking. 9.5 Warm Up. 9.5 Cumulative Review Warm Up
 9.5 Strt Thinking In Lesson 9.4, we discussed the tngent rtio which involves the two legs of right tringle. In this lesson, we will discuss the sine nd cosine rtios, which re trigonometric rtios for cute
9.5 Strt Thinking In Lesson 9.4, we discussed the tngent rtio which involves the two legs of right tringle. In this lesson, we will discuss the sine nd cosine rtios, which re trigonometric rtios for cute
Minnesota State University, Mankato 44 th Annual High School Mathematics Contest April 12, 2017
 Minnesot Stte University, Mnkto 44 th Annul High School Mthemtics Contest April, 07. A 5 ft. ldder is plced ginst verticl wll of uilding. The foot of the ldder rests on the floor nd is 7 ft. from the wll.
Minnesot Stte University, Mnkto 44 th Annul High School Mthemtics Contest April, 07. A 5 ft. ldder is plced ginst verticl wll of uilding. The foot of the ldder rests on the floor nd is 7 ft. from the wll.
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
/ 3, then (A) 3(a 2 m 2 + b 2 ) = 4c 2 (B) 3(a 2 + b 2 m 2 ) = 4c 2 (C) a 2 m 2 + b 2 = 4c 2 (D) a 2 + b 2 m 2 = 4c 2
 SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
Correct answer: 0 m/s 2. Explanation: 8 N
 Version 001 HW#3 - orces rts (00223) 1 his print-out should hve 15 questions. Multiple-choice questions my continue on the next column or pge find ll choices before nswering. Angled orce on Block 01 001
Version 001 HW#3 - orces rts (00223) 1 his print-out should hve 15 questions. Multiple-choice questions my continue on the next column or pge find ll choices before nswering. Angled orce on Block 01 001
Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement. Distance Measurement
 IVL 1101 Surveying - Mesuring Distne 1/5 Distne is one of the most si engineering mesurements Erly mesurements were mde in terms of the dimensions of the ody very old wooden rule - Royl Egyptin uit uits
IVL 1101 Surveying - Mesuring Distne 1/5 Distne is one of the most si engineering mesurements Erly mesurements were mde in terms of the dimensions of the ody very old wooden rule - Royl Egyptin uit uits
Geometry. Trigonometry of Right Triangles. Slide 2 / 240. Slide 1 / 240. Slide 3 / 240. Slide 4 / 240. Slide 6 / 240.
 Slide 1 / 240 Slide 2 / 240 New Jerse enter for Tehing nd Lerning Progressive Mthemtis Inititive This mteril is mde freel ville t www.njtl.org nd is intended for the non-ommeril use of students nd tehers.
Slide 1 / 240 Slide 2 / 240 New Jerse enter for Tehing nd Lerning Progressive Mthemtis Inititive This mteril is mde freel ville t www.njtl.org nd is intended for the non-ommeril use of students nd tehers.
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Applications of trigonometry
 3 3 3 3 3D 3E 3F 3G 3H Review of right-ngled tringles erings Using the sine rule to find side lengths Using the sine rule to find ngles re of tringle Using the osine rule to find side lengths Using the
3 3 3 3 3D 3E 3F 3G 3H Review of right-ngled tringles erings Using the sine rule to find side lengths Using the sine rule to find ngles re of tringle Using the osine rule to find side lengths Using the
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 4 UNIT (ADDITIONAL) Time allowed Three hours (Plus 5 minutes reading time)
 HIGHER SCHOOL CERTIFICATE EXAMINATION 999 MATHEMATICS UNIT (ADDITIONAL) Time llowed Three hours (Plus 5 minutes reding time) DIRECTIONS TO CANDIDATES Attempt ALL questions ALL questions re of equl vlue
HIGHER SCHOOL CERTIFICATE EXAMINATION 999 MATHEMATICS UNIT (ADDITIONAL) Time llowed Three hours (Plus 5 minutes reding time) DIRECTIONS TO CANDIDATES Attempt ALL questions ALL questions re of equl vlue
at its center, then the measure of this angle in radians (abbreviated rad) is the length of the arc that subtends the angle.
 Notes 6 ngle Mesure Definition of Rdin If circle of rdius is drwn with the vertex of n ngle Mesure: t its center, then the mesure of this ngle in rdins (revited rd) is the length of the rc tht sutends
Notes 6 ngle Mesure Definition of Rdin If circle of rdius is drwn with the vertex of n ngle Mesure: t its center, then the mesure of this ngle in rdins (revited rd) is the length of the rc tht sutends
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
MATHEMATICS PAPER & SOLUTION
 MATHEMATICS PAPER & SOLUTION Code: SS--Mtemtis Time : Hours M.M. 8 GENERAL INSTRUCTIONS TO THE EXAMINEES:. Cndidte must write first is / er Roll No. on te question pper ompulsorily.. All te questions re
MATHEMATICS PAPER & SOLUTION Code: SS--Mtemtis Time : Hours M.M. 8 GENERAL INSTRUCTIONS TO THE EXAMINEES:. Cndidte must write first is / er Roll No. on te question pper ompulsorily.. All te questions re
ONLINE PAGE PROOFS. Trigonometry Kick off with CAS 12.2 Trigonometry 12.3 Pythagorean triads
 12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
Stage 11 Prompt Sheet
 Stge 11 rompt Sheet 11/1 Simplify surds is NOT surd ecuse it is exctly is surd ecuse the nswer is not exct surd is n irrtionl numer To simplify surds look for squre numer fctors 7 = = 11/ Mnipulte expressions
Stge 11 rompt Sheet 11/1 Simplify surds is NOT surd ecuse it is exctly is surd ecuse the nswer is not exct surd is n irrtionl numer To simplify surds look for squre numer fctors 7 = = 11/ Mnipulte expressions
Section 11.2: The Law of Sines, from College Trigonometry: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Setion 11.: The Lw of Sines, from College Trigonometry: Correted Edition y Crl Stitz, Ph.D. nd Jeff Zeger, Ph.D. is ville under Cretive Commons Attriution-NonCommeril-ShreAlike 3.0 liense. 013, Crl Stitz.
Setion 11.: The Lw of Sines, from College Trigonometry: Correted Edition y Crl Stitz, Ph.D. nd Jeff Zeger, Ph.D. is ville under Cretive Commons Attriution-NonCommeril-ShreAlike 3.0 liense. 013, Crl Stitz.
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
= x x 2 = 25 2
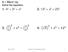 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS WEEK 11 WRITTEN EXAMINATION 2 SOLUTIONS SECTION 1 MULTIPLE CHOICE QUESTIONS
 MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES SECTION MULTIPLE CHOICE QUESTIONS QUESTION QUESTION
MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES SECTION MULTIPLE CHOICE QUESTIONS QUESTION QUESTION
Trigonometric Functions
 Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
HOMEWORK FOR CLASS XII ( )
 HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
Additional Topics in Trigonometry
 dditionl Topis in Trigonometr 6. Lw of Sines 6. Lw of osines 6. Vetors in the Plne 6. Vetors nd Dot Produts 6.5 Trigonometri Form of omple Numer 6 The work done fore, suh s pushing nd pulling ojets, n
dditionl Topis in Trigonometr 6. Lw of Sines 6. Lw of osines 6. Vetors in the Plne 6. Vetors nd Dot Produts 6.5 Trigonometri Form of omple Numer 6 The work done fore, suh s pushing nd pulling ojets, n
5Trigonometric UNCORRECTED PAGE PROOFS. ratios and their applications
 5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Sect 10.2 Trigonometric Ratios
 86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
adjacent side sec 5 hypotenuse Evaluate the six trigonometric functions of the angle.
 A Trigonometric Fnctions (pp 8 ) Rtios of the sides of right tringle re sed to define the si trigonometric fnctions These trigonometric fnctions, in trn, re sed to help find nknown side lengths nd ngle
A Trigonometric Fnctions (pp 8 ) Rtios of the sides of right tringle re sed to define the si trigonometric fnctions These trigonometric fnctions, in trn, re sed to help find nknown side lengths nd ngle
MEP Practice Book ES19
 19 Vectors M rctice ook S19 19.1 Vectors nd Sclrs 1. Which of the following re vectors nd which re sclrs? Speed ccelertion Mss Velocity (e) Weight (f) Time 2. Use the points in the grid elow to find the
19 Vectors M rctice ook S19 19.1 Vectors nd Sclrs 1. Which of the following re vectors nd which re sclrs? Speed ccelertion Mss Velocity (e) Weight (f) Time 2. Use the points in the grid elow to find the
Pythagorean Theorem and Trigonometry
 Ptgoren Teorem nd Trigonometr Te Ptgoren Teorem is nient, well-known, nd importnt. It s lrge numer of different proofs, inluding one disovered merin President Jmes. Grfield. Te we site ttp://www.ut-te-knot.org/ptgors/inde.stml
Ptgoren Teorem nd Trigonometr Te Ptgoren Teorem is nient, well-known, nd importnt. It s lrge numer of different proofs, inluding one disovered merin President Jmes. Grfield. Te we site ttp://www.ut-te-knot.org/ptgors/inde.stml
Additional Topics in Trigonometry
 dditionl Topis in Trigonometr 6 6. Lw of Sines 6. Lw of osines 6. Vetors in the Plne 6. Vetors nd Dot Produts 6.5 Trigonometri Form of omple Numer In Mthemtis Trigonometr is used to sole tringles, represent
dditionl Topis in Trigonometr 6 6. Lw of Sines 6. Lw of osines 6. Vetors in the Plne 6. Vetors nd Dot Produts 6.5 Trigonometri Form of omple Numer In Mthemtis Trigonometr is used to sole tringles, represent
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
2. Topic: Summation of Series (Mathematical Induction) When n = 1, L.H.S. = S 1 = u 1 = 3 R.H.S. = 1 (1)(1+1)(4+5) = 3
 GCE A Level Otober/November 008 Suggested Solutions Mthemtis H (970/0) version. MATHEMATICS (H) Pper Suggested Solutions. Topi: Definite Integrls From the digrm: Are A = y dx = x Are B = x dy = y dy dx
GCE A Level Otober/November 008 Suggested Solutions Mthemtis H (970/0) version. MATHEMATICS (H) Pper Suggested Solutions. Topi: Definite Integrls From the digrm: Are A = y dx = x Are B = x dy = y dy dx
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
15 x. Substitute. Multiply. Add. Find the positive square root.
 hapter Review.1 The Pythagorean Theorem (pp. 3 70) Dynamic Solutions available at igideasmath.com Find the value of. Then tell whether the side lengths form a Pythagorean triple. c 2 = a 2 + b 2 Pythagorean
hapter Review.1 The Pythagorean Theorem (pp. 3 70) Dynamic Solutions available at igideasmath.com Find the value of. Then tell whether the side lengths form a Pythagorean triple. c 2 = a 2 + b 2 Pythagorean
Ch AP Problems
 Ch. 7.-7. AP Prolems. Willy nd his friends decided to rce ech other one fternoon. Willy volunteered to rce first. His position is descried y the function f(t). Joe, his friend from school, rced ginst him,
Ch. 7.-7. AP Prolems. Willy nd his friends decided to rce ech other one fternoon. Willy volunteered to rce first. His position is descried y the function f(t). Joe, his friend from school, rced ginst him,
Review: Velocity: v( t) r '( t) speed = v( t) Initial speed v, initial height h, launching angle : 1 Projectile motion: r( ) j v r
 13.3 Arc Length Review: curve in spce: r t f t i g t j h t k Tngent vector: r '( t ) f ' t i g ' t j h' t k Tngent line t t t : s r( t ) sr '( t ) Velocity: v( t) r '( t) speed = v( t) Accelertion ( t)
13.3 Arc Length Review: curve in spce: r t f t i g t j h t k Tngent vector: r '( t ) f ' t i g ' t j h' t k Tngent line t t t : s r( t ) sr '( t ) Velocity: v( t) r '( t) speed = v( t) Accelertion ( t)
Applications of Trigonometry: Triangles and Vectors
 7 Applitions of Trigonometry: Tringles nd Vetors Norfolk, Virgini Atlnti Oen Bermud Bermud In reent dedes, mny people hve ome to elieve tht n imginry re lled the Bermud Tringle, loted off the southestern
7 Applitions of Trigonometry: Tringles nd Vetors Norfolk, Virgini Atlnti Oen Bermud Bermud In reent dedes, mny people hve ome to elieve tht n imginry re lled the Bermud Tringle, loted off the southestern
Year 12 Trial Examination Mathematics Extension 1. Question One 12 marks (Start on a new page) Marks
 THGS Mthemtics etension Tril 00 Yer Tril Emintion Mthemtics Etension Question One mrks (Strt on new pge) Mrks ) If P is the point (-, 5) nd Q is the point (, -), find the co-ordintes of the point R which
THGS Mthemtics etension Tril 00 Yer Tril Emintion Mthemtics Etension Question One mrks (Strt on new pge) Mrks ) If P is the point (-, 5) nd Q is the point (, -), find the co-ordintes of the point R which
On the diagram below the displacement is represented by the directed line segment OA.
 Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
2) Three noncollinear points in Plane M. [A] A, D, E [B] A, B, E [C] A, B, D [D] A, E, H [E] A, H, M [F] H, A, B
![2) Three noncollinear points in Plane M. [A] A, D, E [B] A, B, E [C] A, B, D [D] A, E, H [E] A, H, M [F] H, A, B 2) Three noncollinear points in Plane M. [A] A, D, E [B] A, B, E [C] A, B, D [D] A, E, H [E] A, H, M [F] H, A, B](/thumbs/74/71214559.jpg) Review Use the points nd lines in the digrm to identify the following. 1) Three colliner points in Plne M. [],, H [],, [],, [],, [],, M [] H,, M 2) Three noncolliner points in Plne M. [],, [],, [],, [],,
Review Use the points nd lines in the digrm to identify the following. 1) Three colliner points in Plne M. [],, H [],, [],, [],, [],, M [] H,, M 2) Three noncolliner points in Plne M. [],, [],, [],, [],,
HW Solutions # MIT - Prof. Kowalski. Friction, circular dynamics, and Work-Kinetic Energy.
 HW Solutions # 5-8.01 MIT - Prof. Kowlski Friction, circulr dynmics, nd Work-Kinetic Energy. 1) 5.80 If the block were to remin t rest reltive to the truck, the friction force would need to cuse n ccelertion
HW Solutions # 5-8.01 MIT - Prof. Kowlski Friction, circulr dynmics, nd Work-Kinetic Energy. 1) 5.80 If the block were to remin t rest reltive to the truck, the friction force would need to cuse n ccelertion
PROBLEM deceleration of the cable attached at B is 2.5 m/s, while that + ] ( )( ) = 2.5 2α. a = rad/s. a 3.25 m/s. = 3.
![PROBLEM deceleration of the cable attached at B is 2.5 m/s, while that + ] ( )( ) = 2.5 2α. a = rad/s. a 3.25 m/s. = 3. PROBLEM deceleration of the cable attached at B is 2.5 m/s, while that + ] ( )( ) = 2.5 2α. a = rad/s. a 3.25 m/s. = 3.](/thumbs/71/66176966.jpg) PROLEM 15.105 A 5-m steel bem is lowered by mens of two cbles unwinding t the sme speed from overhed crnes. As the bem pproches the ground, the crne opertors pply brkes to slow the unwinding motion. At
PROLEM 15.105 A 5-m steel bem is lowered by mens of two cbles unwinding t the sme speed from overhed crnes. As the bem pproches the ground, the crne opertors pply brkes to slow the unwinding motion. At
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
TRIGONOMETRIC FUNCTIONS
 Phone: -649 www.lirntlsses.in. Prove tht:. If sin θ = implies θ = nπ. If os θ = implies θ = (n+)π/. If tn θ = implies θ = nπ. Prove tht: MATHS I & II List of Theorems TRIGONOMETRIC FUNCTIONS. If sin θ
Phone: -649 www.lirntlsses.in. Prove tht:. If sin θ = implies θ = nπ. If os θ = implies θ = (n+)π/. If tn θ = implies θ = nπ. Prove tht: MATHS I & II List of Theorems TRIGONOMETRIC FUNCTIONS. If sin θ
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Static Surface Forces. Forces on Plane Areas: Horizontal surfaces. Forces on Plane Areas. Hydrostatic Forces on Plane Surfaces
 Hdrostti ores on Plne Surfes Stti Surfe ores ores on lne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tes of roblems Horizontl surfes (ressure is ) onstnt
Hdrostti ores on Plne Surfes Stti Surfe ores ores on lne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tes of roblems Horizontl surfes (ressure is ) onstnt
PhysicsAndMathsTutor.com
 1. A uniform circulr disc hs mss m, centre O nd rdius. It is free to rotte bout fixed smooth horizontl xis L which lies in the sme plne s the disc nd which is tngentil to the disc t the point A. The disc
1. A uniform circulr disc hs mss m, centre O nd rdius. It is free to rotte bout fixed smooth horizontl xis L which lies in the sme plne s the disc nd which is tngentil to the disc t the point A. The disc
