Macroeconomic Theory I. Cesar E. Tamayo Department of Economics, Rutgers University
|
|
|
- Katrina Perkins
- 6 years ago
- Views:
Transcription
1 Macroeconomic Theory I Cesar E. Tamayo Department of Economics, Rutgers University ctamayo@econ.rutgers.edu Class Notes: Fall 200
2 Contents I Deterministic models 4 The Solow Model 5. Dynamics Balanced growth The golden rule Quantitative implications Solow growth accounting Optimal growth 9 2. Optimal growth in discrete time Assumptions The sequential method: Lagrange The recursive method: dynamic programming The Envelope Theorem approach Balanced growth and steady state Linearization Equilibrium growth and welfare theorems Extensions to the optimal growth model Assets in the OGM The role of government in OGM Optimal Growth in continuous time Steady State Tobin s q Overlapping generations (OLG) OLG in economies with production (Diamond s) Log-utility and Cobb-Douglas technology Steady state Golden rule and dynamic ine ciency The role of Government Social security Restoring Ricardian equivalence OLG in pure exchange economies (Samuelson s) Homogeneity within generation The role of money Fiscal policy and the La er curve Monetary equilibria with money growth Within generation heterogeneity The real bills doctrine
3 II Stochastic models 4 4 Stochastic Optimal growth Uncertainty in the neoclassical OGM Non-stochastic steady state Stationary distribution Log-linear approximation Solution method : Blanchard-Khan Impulse response functions (IRF) RBC models The baseline RBC model The general case CRRA utility and Cobb-Douglas production The log-linear system Labor productivity (King, Plosser & Rebelo, 988) Solution method 2: Sim s GENSYS Varieties of RBC models Asset pricing models (Lucas, Shiller) Calibration Estimation methods Generalized method of moments (GMM) III Appendixes 56 A The dynamic programming method 57 A. Guess and verify A.2 Value function iteration A.3 Solving for the policy functions A.4 Properties of the BFE A.5 The Envelope Theorem: an application B The Maximum Principle 66 B. Discrete time B.2 Continuous time B.2. Current value vs. present value Hamiltonian C First-Order Di erence Equations and AR() 70 C. The AR() process C.. Representation and properties C..2 Conditional Distribution C..3 Unconditional Distribution C.2 Linear First-Order Di erence Equations (FODE) C.2. Induction & Geometric Series C.2.2 Homogeneous part and General solution C.2.3 Asymptotic Stability C.3 Systems of linear FODE (or VDE) C.3. Asymptotic stability
4 Summary These notes summarize the material of a rst semester graduate course in Macroeconomic theory. The rst sections focus on deterministic growth models and models of overlapping generations (OLG). Later sections are dedicated to stochastic models, including neoclassical growth and real business cycles models. The appendixes cover some mathematical material required for solving simple macro models. The notes are freely based on: Acemoglu (2008), Romer (200), Stokey and Lucas (989), Ljungqvist and Sargent (2004), Dave and De Jong (20), Dixit (990), Levy (992) and lecture notes from Professor Roberto Chang from Rutgers University. Naturally, all errors and omissions are my own. A word on notation: Throughout these notes, x will be used to denote a speci c solution (optima), x will be used for steady states in di erence (di erential) equations and ^x will be used for ln (x=x). When applicable, upper cases will stand for economy-wide values of variables, while lower cases will stand for per-capita (per-e ective labor) variables. Finally, in stochastic models E 0 or simply E will denote unconditional expectations while E t will stand for expectations conditional on information available at t: 3
5 Part I Deterministic models 4
6 Chapter The Solow Model In the original Solow model, time is continuous and the horizon is in nite. Without loss of generality (WLOG) assume that time is indexed t 2 (0; ). At each point in time, there is only one fnal good Y (t). Assumption The nal good is produced with Harrod-neutral or labour augmenting technology: Y (t) = F (K(t); A(t)L(t)) Assumption 2 F () is twice di erentiable and F (K; AL) = F (K; AL). This implies constant returns to scale or no gains from specialization and that one can write the production function in intensive form: K y = f(k) = F AL ; Assumption 3 f(0) = 0; f 0 (k) > 0; f 00 (k) < 0, lim k! f 0 (k) = 0 and lim k!0 f 0 (k) = Assumption 4 Savings are a constant fraction of income. Assumption 5 Existence of a representative household To ilustrate the assumptions about the production technology: Example The Cobb-Douglas production function satis es assumptions -3. To see this consider: F (K(t); A(t)L(t)) = K (AL) K F AL ; = K (AL) AL K = AL f(k) = k and note that f(k) = k = f(k). Also note that f 0 (k) = k > 0 since > 0 and k > 0: Likewise, f 00 (k) = ( ) k 2 < 0 Furthermore lim k = and lim k!0 k! k = 0 since < 0: Remark Notice that: F K (K; AL) = K (AL) = K AL = k = f k (k) 5
7 . Dynamics Suppose that inputs grow as follows: Labor: _ L(t) = nl(t) so that e ln L(t) = L(t) = L(0)e nt Technology: _A(t) = ga(t) so that e ln A(t) = A(t) = A(0)e gt Capital law of motion: _K(t) = sy (t) K(t) To derive the last expression in intensive form apply the quotient rule and the product rule to the expression: d (K=AL) dt the key equation of the Solow model..2 Balanced growth _K(t) K(t) h = A(t)L(t) [A(t)L(t)] 2 sy (t) K(t) = k(t)n k(t)g A(t)L(t) _k(t) = sf(k(t)) k(t) [n + g + ] A(t) L(t) _ + A(t)L(t) _ i Suppose that the economy nds itself in a path in which K(t) and A(t)L(t) are growing at the same rate. This is a special case of balanced growth which itself induces a so-called steady state for k since _ k(t) = 0: Thus sf( k(t)) = k(t) [n + g + ] (.) and one can see that starting from any level of capital per e ective worker, k! k: Furthermore, at the level k one can see that: _k(t) = 0 ) and given the assumption of homogeneity (CRTS): _ K(t) K(t) = n + g _k(t) = 0 ) _y(t) = 0 ) _ Y (t) Y (t) = n + g K(t) nally, note that _ L(t) = g = Y _ (t) L(t). That is, the economy reaches a Balanced Growth Path (BGP), where each variable fy; K; A; Lg is growing at a constant rate..3 The golden rule Suppose starting from the BGP, there s a shift in s. Then k _ jumps since sf(k(t)) > k(t) [n + g + ] and then falls gradually until k! k new : In turn Y (t) L(t) grows by g and k _ > 0 so that Y (t) L(t) jumps but falls gradually too. Consumption C AL, falls by de nition since s jumps: c (t) = ( s) f(k(t)) The generic notion of balanced growth path is a situation in which all variables growth at a constant rate over time (though this rate need not be the same across variables). A special case of a balanced growth path is a steady state, in which the growth rate of all variables is equal to zero. 6
8 To see what happens when the economy reaches the new BGP: and di erentiate w.r.t. s c = ( s) f( k(t)) = f( k(t)) sf( k(t)) = f( k(t)) k(t) [n + g + ] by de nition (s; n; g; ) = f 0 ( k(s; n; g; ) (n + g + k(s; n; g; since the last term is unambiguously positive, the depends on whether f 0 ( k(s; n; g; )? (n + g + ). In fact, the BGP level of capital (per AL) that brings: f 0 ( k(s; n; g; )) = (n + g + ) = 0 (BGP-consumption is at its maximum) is called the golden rule level of capital, k Gold : Therefore, if k > k Gold one has that f 0 ( k) < f 0 ( k Gold ) = (n + g + ) and therefore the economy can increase c by dis-saving. Exercise 2 Suppose that f(k(t)) = k(t). Show that for some, the Solow model can predict overaccumulation of capital in the sense that k > k Gold : Solution. Simply note that (.2) is (s; n; g; ) = k so one needs to show that k one has i (n + g + k(s; n; g; (.2) (.3) (n + g + ) < 0 (and < 0). Using (.) k = s n + g + and replacing k in the golden rule condition, it can be seen that < s ) k > k Gold and the Solow model predicts overaccumulation of capital..4 Quantitative implications In order to quantify the e ect of savings on long-run growth (i.e., = f 0 ( k(s; n; g; to it su ces to di erentiate implicitly the (BGP) equation of _ k = 0: substituting: ds ds f( k) + s df( k) ds f 0 ( k) + f( k) = d k(s; n; g; ) = = d (n + g + ) k(s; n; g; ) + d k(s; n; g; ) (n + g + ) ds ds (n + g + ) f( k) (n + g + ) sf 0 = f 0 ( k)f( k) (n + g + ) sf 0 ( k) 7
9 simplify multiplying by s y obtain: and using y = f( k) and s = k[n+g+] f( k) from the equation _ k = 0 to = = kf 0 ( k)=f( k) kf 0 ( k)=f( k) k k.5 Solow growth accounting To obtain equation () in growth form di erentiate w.r.t. time (recall dy dt rule and omitting the (t): = _ Y ), using the chain _Y Y _Y = F k _K + F k L _ + FA _A _Y = F k K _ + F k L _ Y Y Y + F _ A A Y _Y = KF k _K Y Y K + LF k _L Y L + AF A _A Y A _Y _K = " k Y K + " _L L L + " _A A {z A } _L L = " _K k K + ( " L L ) _ L + X Note that this equation cannot be estimated with data for K and obtaining the residual as X since the residual is correlated (by construction) with capital per worker. Instead, rearrange:! X = _y _K _L " k y K L and now one has everything measurable in the RHS. This is the key equation of growth accounting used to measure Solow s residual. Usually " k is the share of capital on the economy and in a Cobb-Douglas like the example above, " k = : _ K 8
10 Chapter 2 Optimal growth 2. Optimal growth in discrete time Suppose that, savings are not a xed share of income but rather that households decide how much to consume and how much to save on each period. For now, assume that there is neither technical change nor poppulation growth (g = n = 0) so that aggregate production takes the form F (K t ; L t ): As before, suppose that F () is homogeneous of degree one so that production can be written in per labor units: y = f(k) = F K AL ; : Next, suppose there exists a representative household (RH) or, equivalently, that preferences can be aggregated economy-side. Then the RH solves the (discrete-time) problem: max c t;k t+ X t u(c t ) t=0 c t + k t+ f(k t ) + ( s:t: (2.) k 0 given )k t so that the RH chooses a consumption-saving plan fc t ; k t+ g t=0 resource constraint holds at every t = 0; ; ::: under the condition that the 2.2 Assumptions Assumption 6 Assumptions -3 about f() from section. hold. Assumption 7 The objective function u() is continuous, twice di erentiable and satis es the Inada conditions: u(0) = 0; u 0 (k) > 0; u 00 (k) < 0; lim k! u0 (k) = 0 and lim u 0 (k) = k!0 Assumption 8 The constraint set fk t+ j k t+ f(k t ) + ( )k t c t g is compact, convex. Assumption 9 Preferences are additive. This ensures dynamic consistency. Under these assumptions any organization of markets and production will yield the same competitive equilibrium allocation. Hence the competitive equilibrium is unique and the rst and second welfare theorems hold. That is, the competitive equilibrium will be Pareto e cient and the planner s problem can be descentralized as the outcome of a competitive equilibrium as will be shown below. 9
11 2.3 The sequential method: Lagrange The problem above can be approached by the in nite-horizon Lagrange method: X L = t fu(c t ) + t [f(k t ) + ( )k t c t + k t+ ]g t=0 t = 0 =) t u 0 (c t ) = t+ = 0 =) t = t+ (f 0 (k t ) + t+ = 0 =) c t + k t+ = f(k t ) + ( )k t (2.2c) replacing t and using the fact that t+ = t+ u 0 (c t+ ) one obtains the Euler Equation: u 0 (c t ) = u 0 (c t+ ) (f 0 (k t ) + ) (2.3) Along with the resource constraint (F.O.C. (2.2c)) these two di erence equations fully characterize the solution to the optimal plan. The boundary condition required for the solution to (2.2c)-(2.3) to exist is the transversality condition: lim tk t+ = lim t u 0 (c t )k t+ = 0 t! t! 2.4 The recursive method: dynamic programming This problem can also be solved as a discrete time, deterministic, stationary, dynamic programming one. In fact, when the problem is stationary (i.e. the problem faced at every period is identical), the sequential and recursive methods are equivalent. If one separates the problem into periods, each problem depending on the state k t and consisting on choosing controls c t ; k t+ ; the Bellman functional equation (BFE) for the iterated (recursive) one-period optimization problem is: V (k t ) = max c t [u(c t ) + V (k t+ )] s:t: (2.4) y t = c t + i t = f(k t ) k t+ = ( )k t + i t k 0 given In fact, this problem can be seen to have only one control variable since choosing c t is equivalent to choosing k t+ given the combination of the resource constraint and the capital accumulation equation. To be more precise notice that the problem is (2.4) is equivalent to: V (k t ) = max k t+ [u(f(k t ) k t+ ( )k t ) + V (k t+ )] (2.5) V (k t ) = max c t [u(c t ) + V (( )k t + f(k t ) c t )] (2.6) and associated transversality condition: lim t! t+ V 0 (k t+ )k t+ (2.7) 0
12 Under familiar assumptions (see Appendix A), the solution to the Bellman equation, will yield time-invariant, sate-dependent rules for consumtion and capital accumulation, i.e., policy functions: c t = h(k t ) (2.8) k t+ = g(k t ; c t ) = g(k t ; h(k t )) (2.9) and notice that g() is precisely the state-transition function that results after consolidating the two restrictions in (2.4); that is: k t+t = ( )k t + f(k t ) c t = g(k t ; c t ) However, since (2.4) is a functional equation, one needs to solve for V () in order to obtain (2.8)-(2.9). There are mainly three approaches to solve for V (): Guess and verify the value function Value function iteration or method of successive approximations, and, Policy functions iteration or Howard s improvement algorthm. These three approaches are developed in Appendixes A.-A.3, and some examples are provided. The main conditions for the existence of a unique solution, V (); to the BFE (2.4) are: Condition Assumptions -3 at the begining of this chapter hold. Condition 2 The control space and the state space are convex, compact sets, Condition 3 The operator V 7! T (V ) in (2.4) maps the set of continuous, bounded, real-valued functions M into itself. Condition 4 The operator V 7! T (V ) (2.4) is a contraction mapping de ned on a complete metric space of continuous, bounded, real-valued functions M. Condition 3 requires in turn that u () ; f () are continuous and bounded and that the correspondence (k t ) = fc t jc t ( )k t + f(k t ) k t+ g is UHC, LHC, non-? and compact-valued. Appendix A.4 provides the relevant proofs and also proves some additional properties of the operator T () : Condition (iv) requires a contraction mapping; recall that a contraction is a mapping, '; on a metric space (W; d) that satis es d (' (f) ; ' (g)) d (f; g) for all f; g 2 M and some < : Since M above is a complete metric space, conditions (i)-(iv) would su ce for a unique solution to the BFE since the Banach xed point theorem asserts that every contraction mapping on a complete m.s. has a unique xed point, i.e., 9 V such that V = T (V ). Moreover, the sequence de ned by V i+ = T (V i ) converges to the unique xed point V : Now, the Blackwell conditions for an operator to be a contraction mapping are: Monotonicity: ' > (w.r.t. box metric)) T (') > T ( ) whenever '; 2 M. Discounting: for any constant function A = h(), and ' 2 M one has T ('+A) T (')+A for some < : In this case the assumption that V is bounded is redundand since the compactness of the control space ensures this property.
13 Both conditions are easily seen to hold in this case: Assuming that one obtains V () by any of the abovementioned methods, it is easy to obtain the F.O.C. for the problem (2.6): the associated F.O.C. is: and the resource constraint: V (k t ) = max c t [u(c t ) + V (( )k t + f(k t ) c t )] u 0 (c t ) V 0 (k t+ ) = 0 (2.0) c t + k t+ = f(k t ) + ( )k t (2.) At this point one can use the knowledge of V () in order to obtain V 0 () and solve the system of di erence equations (2.0)-(2.). Example 3 (Guess and verify) Cobb-Douglas technology with full depreciation and logarithmic utility. The problem is: the F.O.C is therefore: If one guesses the form of V () as: V (k t ) = max c t;k t+ [ln c t + V (k t+ )] s:t: (2.2) c t + k t+ = k t k 0 given c t = V 0 (k t+ ) kt k t+ = V 0 (k t+ ) V (k t ) = F + G log k t so that one replaces for V 0 (k t+ ) in the F.O.C.: k t = G k t+ and using the resource constraint arrives to the policy functions (with undetermined coe cient G): now using this in the BFE: V (k t ) = F + G log k t = log k t+ = c t = G + G k t k t+ G + G which solving for the undetermined coe cients F,G yields: G = F = k t G G kt + F + G log + G + G k t log ( ) + ( ) log() 2
14 so that nally one can generate optimal plans fc t ; k t+ g t= from the fully speci ed policy functions: c t = ( ) k t k t+ = () k t Finally, note that the transversality condition is satis ed: lim t! t+ V 0 (k t+ )k t+ = lim t+ t! 2.4. The Envelope Theorem approach A di erent avenue that avoids dealing with the value function explicitely is as follows. If conditions -4 above regarding the objects in the problem are satis ed (i.e., concavity, convexity, continuity, compactness, monotonicity, discounting), then the unique solution to the BFE V (), would be continuous, concave, increasing and importantly, di erentiable. Hence, the Envelope theorem applies and one can use the envelope condition for the value function (see the Appendix A for a more elaborate example). To see how the Envelope theorem works in this particular case, recall the policy functions: then the value function becomes: c t = h (k t ) k t+ = g(k t ; c t ) = ( )k t + f(k t ) h (k t ) = 0 V (k t ) = u(h (k t )) + V (( )k t + f(k t ) h (k t )) di erentiating w.r.t. k t : V 0 (k t ) (k (k t ) + V 0 (k t+ ) ( (k t (k t t (k (k t ) + V 0 (k t+ ) ( t) V 0 (k t+ (k (k t t = V 0 (k t+ ) ( t) (k (kt )) V 0 (k t+ (k t ) but the F.O.C. (2.0) (k t (k t ) = u 0 (c t ) = V 0 (k t+ ) and therefore: V 0 (k t ) = V 0 (k t+ ) ( t = u 0 (c t ) ( t and since this holds for every period: V 0 (k t+ ) = u 0 (c t+ ) [f 0 (k t+ ) + ( )] 3
15 replacing in the F.O.C. one obtains once more the system of di erence equations that (under the assumptions above) will characterize the solution to the RH problem: u 0 (c t ) = u 0 (c t+ ) [f 0 (k t+ ) + ( )] (2.3) c t + k t+ = f(k t ) + ( )k t (2.4) Alternatively, one can use the policy functions (2.8)-(2.9) to express the Euler equation in terms of k t : u 0 (g(k t )) = u 0 (g(h(k t ))) [f 0 (h(k t )) + ( )] Finally, note that V 0 (k t+ ) is something similar to a shadow price associated with the resource constraint. Remark 2 Note that in this problem it is the case that 6= and therefore, f 0 (k t ) + = R t. If one was to consider the case where =, as will be the case in some sections below then one would have: f 0 (k t ) = r t = R t : 2.5 Balanced growth and steady state As mentioned earlier, the generic notion of balanced growth path is a situation in which all variables grow at a constant rate over time (though this rate need not be the same across variables). Perhaps the simplest example of balanced growth that solves the optimal growth problem is: Example 4 Consider the so-called AK model.under CRRA utility and full depreciation. The social planner s problem is: the BFE for this problem is: with F.O.C.: and envelope condition: so the Euler equation becomes: or, using the functional form for u (c t ) : max s:t: y t c t + i t X t c t t=0 y t = f (k t ) = Ak t i t = k t+ V (k t ) = max k t+ fu (Ak t k t+ ) + V (k t+ )g u 0 (c t ) + V 0 (k t+ ) = 0 V 0 (k t+ ) = u 0 (c t+ ) A u 0 (c t ) = u 0 (c t+ ) A c t+ c t = A Since c t = Ak t k t+ : (Ak t+ k t+2 ) = A (Ak t k t+ ) 4
16 A second order di erence equation that, without a (on k) that, without a terminal condition has multiple solutions for any given k 0 : The interest is in that which satis es the TVC (2.7) which in this case becomes (using the EC): lim t! t+ V 0 (k t+t ) k t+ = lim t! t+ u 0 (c t+ ) Ak t+ Now to nd conditions that ensure holding of the TVC note that in a BGP capital and consumption grow at the same constant rate so k t+ = k t and c t+ = c t for some : Thus: (c t ) c t = A ) = (A) = which brings positive growth iif > =A. Next, rewrite u 0 (c t+ ) = c t =A and k t+ = t+ k 0 in the TVC: lim t! t+ u 0 (c t+ ) Ak t+ = lim t+ ct t! A At+ k 0 = lim t+ ct t! t+ k 0 = lim t! () t c t k 0 then the TVC holds iif < )if (A) = < : Hence by assuming that < A + one can ensure that there is balanced growth and the TVC holds. A special case of a balanced growth path is a steady state, in which the growth rate of all variables is equal to zero. From (2.3)-(2.4) one can compute the steady state by noting that in the SS, x t = x t+ = x for x = fc; k; yg. Hence: u 0 (c) = u 0 (c) f 0 ( k) + ( ) = f 0 ( k) + ( ) de ning a modi ed golden rule for capital accumulation, and c k = f( k) = y 2.6 Linearization Next it is possible to study the behavior of the model around the steady state (SS). Recall that in the SS, x t = x t+ = x for x = [c; k] 0 and ^x t = (x t x)=x. So, linearize the system around the SS. Recall that to linearize G(x; y) = 0 around the SS (x; y)x ^x t + (x; y)y ^y t = t Linearizing (2.3): ^c t = ^c t+ + ^k t+ (2.5) where division by u 0 (c) on both sides has been used and the fact that = = f 0 ( k) + ( ) from the SS and ; are the elasticities of u 0 () and f 0 (), respectively. Finally, the linear constraint is linearized as: c^c t + k^k t+ = f( k) + ( ) k^kt!^c t + ^k t+ = [ +! + ] ^k t (2.6) 5
17 where! = c y, = k y and is the elasticity of f():now one can suppose that the linearized policy functions are of the form: so that replacing in (2.5)-(2.6) one obtains: ^c t = ^kt ^k t+ = 2^kt = 2 + 2! + 2 = [ +! + ] and one can solve for the undetermined coe cients ; 2 as functions of parameters of the model (;!; ). Note that the rst of these equations will be a cuadratic one so one has two solutions, from which one selects 2 < since this is the only solution that satis es the transversality condition. With this log-linear policy functions and the "true" coe cients as functions of the parameters of the model, one can generate optimal sequences f^c t ; ^k t+ g t=0, that is sequences of the variables in deviation from SS form. 2.7 Equilibrium growth and welfare theorems The solution to the optimal growth model can in fact be deduced as the outcome of a competitive equilbrium. To see this, state the problem of the RH and the rm separately. Households The representative household maximizes lifetime discounted utility subject to its resource constraint. Households own the factors of production k; l and own the rms. For simplicity, suppose there is full depreciation ( = ). At each period, the RH receives income from renting all of its available capital, working all its endowed labor and earning pro ts from the rms. 2 With this income, the RH and decides how much to consume and how much to invest (save): Firms max c t X t u(c t ) t=0 s:t: c t + k h t+ r t k h t + w t l h t + t = y h t Firms produce a single good by renting production factors from the RH and maximize pro ts subject to their production technology: X X max t = max p t y f t w t l f t r t k f t t=0 s:t: t=0 y f t F (k f t ; l f t ) where F () is continuous, di erentiable, strictly increasing and homogeneous of degree one. Since there is only one good in the economy, there are no relative prices and one can set p t =. Also, 2 The assumption that households work their entire endowment of labor re ects the fact that there is no disutility of labor in this model. The RBC models surveyed in the sections below relax this assumption so that labor becomes in fact a choice variable. 6
18 since there is no discounting, lifetime pro ts are maximized, pro ts are maximized at every period t: 3 Equilibrium For simplicity suppose that lt h = : Then a competitive equilibrium consists of a set of prices fp t = ; w t ; r t g t=0 and allocations fk t ; lt = ; yt ; c t g t=0 such that 8 t :. The rm maximizes pro ts. To do so, notethat since F () is strictly increasing, the technology constraint will hold with equality y f t = F (k f t ; l f t ). Thus, the F.O.C.s of the rm f t ; l f t f f t ; l f t f t = 0 =) w t = F l (k f t ; l f t ) = 0 =) r t = F k (k f t ; l f t ) 2. The RH maximizes utility. The F.O.C.s for the RH are, as before: 3. Markets clear in all periods (t = ; 2:::): u 0 (c t ) = u 0 (c t+ )r t+ c t + k h t+ = r t k h t + w t l h t + t y h t = y f t = F (k f t ; l f t ) l h t = l f t = k h t = k f t Next, replace the F.O.C.s for the rm in the pro t function at t and recalling that l t = : t = F (k t ; l t ) F l (k t ; l t ) F k (k t ; l t )k t and because F () is homogeneous of degree one, Euler s theorem (x rf(x) = f(x)) implies that t = 0 so that: w t = F (kt ; lt ) F k (kt ; lt )kt and P t=0 t = 0. Replacing in the F.O.C.s for the RH yields: u 0 (c t ) = u 0 (c t+ )F k (k t ; l t ) and c t + kt+ = F k (kt ; lt )kt + F (kt ; lt ) F k (kt ; lt )kt = F (kt ; lt ) which are of course, the same optimality conditions derived under the centralized approach in the section above. Hence one has found a vector of prices that delivers the (planned) Pareto optimal allocation which results as a solution to (2.3)-(2.4). That is, the optimal allocation has been descentralized as a competitive equilibrium of the economy This is an ilustration of the second fundamental theorem of welfare economics It is straightforward to extend this model to the case where rms discount future pro ts. A natural candidate for discounting would be where R is the gross interest rate (in this economy all assets would earn R). 4 R Recall that the rst welfare theorem states that whenever households are non-satiated, a competitive equilibrium allocation is Pareto optimal. 7
19 2.8 Extensions to the optimal growth model 2.8. Assets in the OGM Recall the budget constraint for the RH is, in general: and if one assumes l t = 8 t: k t+ = ( + r t )k t + w t l t + t c t k t+ = ( + r t ) {z } k t + w t c t + t (2.7) R t = gross return Now, allow for assest a t that HH carry from previous periods. Note that in aggregate a t = k t +b t where we may have b t < 0 at some t. So we can re-write the ow budget constraint as: c t + a t+ = R t a t + w t + t c t + a t+ R t R t = a t + w t + t At this point one carries out forward substitution of a t+ from the equation for a t+2, then substitute the latter from the equation for a t+3 and so on. For some nite T ; the intertemporal budget constraint (IBC) is given by: where: TX t=0 R t c t + a T + R T = ( + r 0 )a 0 + R t = ty R j = j= TX t=0 ty ( + r j ) j= R t (w t + t ) (2.8) But since we re assuming an in nite horizon, we must prevent a T + R T! as T! (build debt forever) which would result in P t=0 R t c t! : So we impose the additional no Ponzi games condition: a T + lim = 0 T! R T so that when the horizon is in nite, taking limits on both sides of (2.8) and using the no-ponzi condition, the IBC can be expressed as: P V X c t R t=0 t {z } = ( + r 0 )a 0 {z } + X (w t + t ) R t=0 t {z } consumption = initial asset income + PV non-asset income (2.9) Note that a stream of consumption that satis es the (IBC) also satis es the ow constraint at each t. To see this, consider a consumption plan f^c t g t=0 that satis es the IBC. At some, by (2.8) the household will have accumulated assets: a + R = ( + r 0 )a 0 + X t=0 R t (w t + t ^c t ) X = ( + r 0 )a 0 + (w t + t ^c t ) + (w + ^c ) (2.20) R t R t=0 8
20 obviously since: a X = ( + r 0 )a 0 + (w t + t ^c t ) R R t=0 t ) X t=0 we can replace this in (2.20) to get: R t (w t + t ^c t ) = ( + r 0 )a 0 + a R a + R = R (w + ^c ) + a R simply multiply this last expression by R on both sides to obtain: a + = w + ^c + R a which is of course the sequential BC for period. Using the IBC just derived, the optimal growth problem can be stated more compactly as: " # X X L = t X u(c t ) + ( + r 0 )a 0 + (w t + t ) c t R t R t t=0 t=0 with associated F.O.C. (noting that in equilibrium t = t t ) t u 0 (c t ) = R t+ t+ ) t+ u 0 (c t+ ) = R t+ so equating them yields the same Euler equation derived earlier: u 0 (c t ) = R t+ u 0 (c t+ ) = u 0 (c t+ )( + r 0 ) which naturally relies on the fact that in equilibrium all rates of return are equilized (so all assets receive and are discounted to the same rate) The role of government in OGM To introduce the government, derive restrictions similar to (2.7) and (2.9): t=0 b t+ = (g t t ) + R t b t where b t+ = debt outstanding at t +, (g t t ) = net income or primary de cit at t and R t b t =debt service in t: [ Note that the same rate of return is used for the government, all nancial assets and capital which is the case if there is no uncertainty (no default risk) and perfect complete nancial markets!]. Next, set up the IBC for the government: X t g t ( + r 0 )b 0 lim b t+ t! R t Naturally, if we allow lim t! R t b t+!, the LHS of this inequality approaches and therefore the government could run primary de cits forever. Hence, the following no-ponzi condition for the Gvt.is imposed: lim b t+ = 0 t! R t 9 t=0 R t R t
21 so that the IBC for the government is: ( + r 0 )b 0 Note that now HH would have to pay taxes so: t=0 X t=0 X t t=0 R t c t = ( + r 0 )a 0 + R t g t R t X wt + t t=0 and replacing PV taxes from the Gvt. IBC: X X wt + t c t = ( + r 0 )a 0 + R t = ( + r 0 )k 0 + t=0 R t X wt + t t=0 R t R t X t=0 X t=0 t R t g t R t ( + r 0 )b 0 g t R t (2.2) where the de nition of assets a 0 = b 0 + k 0 has been used. This is a crucial result, for, it shows that only the (PV) level of government spending matters and not the means through which it is nanced (debt or taxes). This is naturally a Ricardian Equivalence statement. The new IBC for the HH (2.2) can be used again in the Lagrangian as above to derive the system of equilibrium conditions for the optimal growth problem. Furthermore, one can see that for a given initial stock a 0, at any t : k t + b t = a t = R t a 0 and since a 0 is constant, " b t )# k t and/or " R t which are both ways of crowding out. Example 5 (OGM with assets and government) The problem can be stated as: max c t X t u(c t ) t=0 s:t: a t+ = ( + r)a t + w t c t so that the state variable is a t and the control variable again c t : Note that this problem is not well de ned even with the transversality condition: since it may happen that a t+! above: lim t! t+ V 0 (a t+ )a t+ = 0. Therefore, one needs the no-ponzi condition introduced a T+ lim = 0 T! R T so that the TVC holds. With the problem well speci ed, the solution can be found by solving: with F.O.C.: V (a t ) = max fu(( + r)a t + w t a t+ ) + V (a t+ )g u 0 (( + r)a t + w t a t+ ) = V 0 (a t+ ) u 0 (c t ) = V 0 (a t+ ) 20
22 and envelope condition: V 0 (a t+ ) = u 0 (( + r)a t+ + w t a t+2 )( + r) = u 0 (c t+ )( + r) and the usual Euler equation: u 0 (c t ) = u 0 (c t+ )( + r) 2.9 Optimal Growth in continuous time State the problem (2.) in continuous time: max Z c(t);i(t) 0 u(c(t))e t dt s:t: (2.22) c(t) + i (t) f(k(t)) _k(t) = i (t) k(t) (2.23) k(0) given The continuous time problem is actually easier to solve using the tools of optimal control; a review of The Maximum Principle and the Hamiltonian approach is presented in Appendix B. Set up the (present-value) Hamiltonian: H = u(c(t))e t + (t) [f(k(t)) k(t) c(t)] (2.24) where (t) is the co-state variable. The condition for c(t) to maximize the Hamiltonian = 0 =) u0 (c(t))e t = (t) (2.25) solving this yelds c (t) as a function of the co-state and parameters. Next, we can replace c (t) in (2.24) to obtain the maximum value function of the Hamiltonian, H, di erentiate w.r.t. state and co-state variables. Alternatively, simply state the Pontryagin conditions similar to those derived in the Appendix B (B.8)-(B.9): ii) = (t) [f 0 (k(t)) ] (2.26) iii) k(t) = = f(k(t)) k(t) c(t) Conditions (2.25)-(2.26)-(2.27) along with the TCV: lim (t)k(t) = 0 t! are the three di erential equations (and terminal condition) that characterize the solution to the HH problem. Example 6 Suppose that u (c (t)) = ln (c (t)). Then from (2.25): c(t) = e t (t) 2
23 so that replacing in (2.27) we get the two di erential equations on k and that characterize the solution: _k(t) = f(k(t)) k(t) _(t) = (t) [f 0 (k(t)) ] e t (t) Alternatively, one can solve the system in terms of di erential equations in c and k, which is more consistent with the idea of policy rules described in previous sections. To do so, di erentiate (2.25) w.r.t. time: u 00 (c(t))e t _c(t) e t u 0 (c(t)) = _(t) (2.28) and replace in (2.26) to obtain: which upon rearranging: u 00 (c(t))e t _c(t) e t u 0 (c(t)) = (t) [f 0 (k(t)) ] u 00 (c(t))e t _c(t) e t u 0 (c(t)) = e t u 0 (c(t)) [f 0 (k(t)) ] _c(t) c(t) = f 0 (k(t)) [c(t)u 00 (c(t))=u 0 (c(t))] (2.29) where the denominator is naturally, the Arrow-Pratt CRRA coe cient: This condition tells us that whenever f 0 (k(t)) is "large", which happens when k(t) is "low", we have _c=c > 0 so that the HH consumes less today and more in the future. Likewise, _c=c < 0 if is large enough which suggests that the HH is more "patient". Finally, the TVC is: 2.9. Steady State Recall, in SS _c(t) = 0 and _ k(t) = 0. Therefore: lim t! = 0 lim u 0 (c(t))k(t) t! = 0 _c(t) c(t) = 0 =) f 0 ( k) = (2.30) which is, again, a modi ed Golden Rule for capital accumulation and, once more, independent from the shape of u(): Next: _k(t) = 0 =) f( k) c = k so that SS-investment just breaks-even (making _ k(t) = 0). Remark 3 Note that (t) is the shadow price of capital, i.e., it measures the impact of a small increase in k t on the optimal value of the program. By comparison, V (k t ) is the value of of the optimal program from t given the level of capital k t : Therefore, we have that: (t) = V 0 (k t ) and note that _(t) represents the appreciation of capital since its the change in the value of a unit of the state variable. Exercise 7 In order to make meaningful comparisons with the Solow model, reintroduce technical change and poppulation growth. (i) Write the equilibrium conditions of the OGM considerng these features and (ii) Show that along the balanced growth path, k < k Gold where k Gold is the Golden Rule level of (per-e ective-labor) capital in the Solow model. 22
24 Solution. (i) First, derive the analogue to (2.30) after reintroducing poppulation growth and technological progress. To do so, write the constraints in absolute levels: derive the capital accumulation equation: and thus: C (t) + I (t) = F (K (t) ; A (t) L (t)) _K (t) = I (t) K(t) _k(t) = d K (t) = [A (t) L (t)] d dt K (t) K (t) d dt [A (t) L (t)] dt A (t) L (t) [A (t) L (t)] 2 _K (t) _k(t) = k (t) (g + n) A (t) L (t) I (t) K(t) = K (t) (g + n) A (t) L (t) = i (t) ( + g + n) k (t) replace with i (t) = f(k(t)) c (t) so that _ k(t) = f(k(t)) c (t) ( + g + n) k (t) : Therefore conditions (2.26) and (2.29) become: _(t) = _c(t) c(t) (ii) Now, along the BGP _c(t) = 0 so which in turn means that k < k Gold : Tobin = (t) [f 0 (k(t)) g n] = f 0 (k(t)) g n f 0 ( k) = + + g + n > + g + n = k Gold Consider the following model of investment under adjustment costs. Assumptions 2 and 3 in section. are satis ed. There s a single nal good and therefore one can normalize its price to. The problem is that of a RH which must decide how much to consume and how much to invest in the representative rm at each given t. However, installing capital is costly. When there are quadratic investment adjustment costs the problem can be stated as (for simplicity ignore depreciation): max fc(t);i(t)g t=0 s:t. Z 0 e t u(c(t))dt (2.3) _ k(t) = I(t) c(t) + I(t) = f(k(t)) where I(t) is investment and > 0 is a constant: 2 I 2 (t) k(t) 23
25 Note that in this problem, the control variables are c(t) and I(t) (or k t+ in the OGM), while the state variable is k(t). On what follows, the present-value optimization problem is solved and then it is expressed in current value terms since the latter form lends itself to intuitive interpretation. First, we get rid of c(t) by using the second constraint. Notice that we can do this only because the constraint is speci ed with equality. Notice also that after eliminating this constraint, the Lagrangian and the Hamiltonian are obviously the same so that in the language of Appendix B, G () dissapears and L I = H I : Thus, set up the present-value Hamiltonian: H pv = e t u f(k(t)) I(t) The F.O.C. w.r.t. the control is simply obtained: (t) = e t u 0 (c (t)) 2 I 2 (t) k(t) I(t) + k(t) + (t)i(t) (2.32) Next, using the Pontryagin conditions corresponding to the present-value problem (B.8)- (B.9): " _(t) = e t u 0 (c (t)) f 0 (k(t)) + # 2 I(t) (2.33) 2 k(t) _k(t) = I(t) (2.34) Or, using the F.O.C. to solve for I (t) we can rewrite (2.34) as: _k(t) = k (t) e t (t) u 0 (c (t)) And just as in the discrete time problem, the TVC is given by: lim t! (t)k(t): Naturally, with an explicit functional form for u, we could solve for c (t) ; I (t) using the F.O.C. (2.32) and the constraint, replace this in (2.33)-(2.34) to obtain a pair of di erential equations on (t) and k(t) that would characterize the solution to the problem. An interesting avenue to take in this problem is to express the equilibrium conditions in current-value terms. To do so, multiply (2.33) by e t on both sides (the other conditions do not involve (t)) and de ne q(t) = e t (t). Then, since _q(t) = _(t)e t + (t)e t, one has that _(t)e t = _q(t) q(t) and therefore the Pontryagin conditions can be written: " _q(t) q(t) = u 0 (c (t)) f 0 (k(t)) + # 2 I(t) 2 k(t) _k(t) = k (t) q(t) u 0 (c (t)) Finally, using (2.35) we can arrive at: " _q(t) q(t) = u 0 (c (t)) f 0 (k(t)) + # 2 I(t) 2 k(t) 2 3 Z q(t) = e (s t) u 0 (c(s)) 4f 0 (k(t)) + 2 I(t) 5 ds t {z } 2 k(t) {z } (2.35) (2.36) disc. marg. util of output marg. prod. of k - marg. adj cost (2.37) that is, Tobin s q summarizes the informarion of the discounted social bene t of installing an additional unit of capital. 24
26 Chapter 3 Overlapping generations (OLG) 3. OLG in economies with production (Diamond s) Assume that a generation is born in every period of time. Time is discrete indexed t = ; 2::: Each generation lives two periods. Therefore, at each t, there are two generations alive; "young households" and "old households", call them HH types and 2. For completeness, suppose that at period t = a generation is already alive (agent type 0). Therefore generation t is that born in period t: Each new generation is larger than the previous one by a factor of (+n), n 2 (0; ). Therefore: L t = ( + n)l t In its rst year of life, each HH works, saves and consumes. In its second year of life each HH only consumes. Therefore: c ;t! period t consumption of a typical HH from generation t ("youngs") c 2;t+! period t + consumption of a typical HH from generation t ("olds") Production is carried out by the use of capital, technology and "young" agents as the labor force with Harrod-neutral production function: F (K t ; A t L t ) Moreover, production technology satis es assumptions )-3) in section. and utility satis es assumptions 2)-4) in section 2.2. Technology follows an exogenous growth process: A t = ( + g)a t Hence, there are three markets; nal goods, capital goods and labor. Markets are competitive and for simplicity, there is full depreciation ( = ). Acordingly, t = 0, F K = + r t = R t and F L = w t : In period t, each HH from generation t works, receives (technology-enhanced) labor income, consumes and saves : A t w t = c ;t + s t Generation t s savings are rented in the form of capital for production at t + so that capital available is: K t+ = L t s t = S t (3.) Since only "youngs" save on each period, there is no s 2;t ("olds" don t save), to simplify notation s t = s ;t =total savings of the economy at t: 25
27 and are returned with the corresponding rental income. Generation t (i.e. agent type 2 in period t + ) then consumes the proceedings: c 2;t+ = R t+ s t = ( + r t+ )s t = ( + r t+ ) (A t w t c ;t ) Generation t then maximizes its (discounted) lifetime utility from consumption: max U(c) c ;t;c 2;t+ = u(c ;t ) + u(c 2;t+ ) (3.2) s:t: A t w t = c ;t + c 2;t+ R t+ (3.3) alternatively, one the RH solves the unconstrained optimization problem: max c ;t U(c) = u(c ;t ) + u(r t+ (A t w t c ;t )) both yielding the same F.O.C. and Euler equation: u 0 (c ;t ) = u 0 (c 2;t+ )R t+ (3.4) which is analogous to the one found in the OGM. Equations (3.3)-(3.4) are the pair of di erence equations describing the solution to the typical generation t HH problem. Next, note that the Euler equation can be expressed as: u 0 (c ;t ) = (; u 0 (c 2;t+ ); R t+ ) and that u 00 < 0 ) u 0 (c ;t ) = c ;t. Therefore: hence, if one replaces in: u 0 (c ;t ) = u 0 (c 2;t+ ) (; u 0 (c 2;t+ ); R t+ ) c ;t = u 0 (c 2;t+ ) (; u 0 (c 2;t+ ); R t+ ) A t w t = c ;t + s t s t = A t w t u 0 (c 2;t+ ) (; u 0 (c 2;t+ ); R t+ ) s t = (A t w t ; R t+ ) (+) (?) where is called the savings function. Consider a rise in labor income A t w t, then, everything else constant, the properties of u () imply that consumption in both periods would rise, which implies that s t increases; thus the sign t =@A t w t is unambiguous. However, consider a rise in R t+. There are two e ects to consider. First, since the opportunity cost of consumption in t rises, the HH may want to substitute current for future consumption (substitution e ect). Second, a rise in R t+ has an income e ect since each unit saved yields higher return so the HH will want to consume more on both periods. The total e ect is ambiguous as is the sign t =@R t+ : Next, to derive the law of motion of capital come back to (3.): K t+ = L t s t = S t K t+ = L t (A t w t ; R t+ ) = L t (A t w t ; F K ) 26
28 or in per-e ective worker terms (i.e., dividing by A t+ L t+ since we re deriving t + capital): K t+ = L t (A t w t ; F K(t+) ) A t+ L t+ A t+ L t+ (( + g) w t ; f k(t+) ) k t+ = ( + n) k t+ = (( + g) (f f k k t ); f k(t+) ) ( + n) where, in the above derivation one uses the following: ) R t+ t+ = F K(t+) t+ = f k(t+), 2) L : =L t+ = =(+n), 3) A t =A t+ = =(+g) and 4) w t = f l = F F K = f f k by homogeneity of degree one (recall Taylor s theorem):therefore, the key equation for the law of motion of capital in Diamond s model is: ( + n)k t+ = (( + g) (f f k k t ); f k(t+) ) (3.5) at this point one needs to specify some functional form for utility and production since k t+ shows up in both sides of the above equation and cannot be solved for explicitely. 3.. Log-utility and Cobb-Douglas technology Under u(c it ) = log c it and F (K t ; A t L t ) = Kt (A t L t ) ) f(k) = k one can re-write the (generation t HH) problem as: so the Euler eq. can be re-written as: now using the resource constraint: max c ;t;c 2;t+ U(c) = log c ;t + log c 2;t+ s:t: A t w t = c ;t + c 2;t+ R t+ (3.6) = R t+ c ;t c 2;t+ c 2;t+ = c ;t R t+ A t w t = c ;t + c ;tr t+ R t+ c ;t = A tw t + = + k k a policy function for consumption; replacing in the savings function: A t w t = c ;t + s t A t w t s t = A t w t + s t = A t w t + = + k k 27
29 that is, as in the growth models of the sections above, savings are a constant fraction of HH income. Next, using the equation for capital: ( + n)k t+ = = = = k t+ = s t A t+ A t w t A t+ + w t ( + ) ( + g) (kt kt ) ( + ) ( + g) ( ) kt (3.7) ( + ) ( + g)( + n) a policy function for capital accumulation. Equation (3.7) is the key equation of Diamond s model unde log-utility and Cobb-Douglas production Steady state The steady state value for capital can be computed as: k = ( ) ( + ) ( + g)( + n) k = ( ) ( + ) ( + g)( + n) k (3.8) steady state output, is: y = k = ( ) ( + ) ( + g)( + n) To obtain SS consumption rst note that c it is the amount consumed by one typical household of generation i in its rst year of life. Since now the poppulation size is not normalized to as in the growth models of previous sections, in order to nd economy-wide consumption at t one must compute: C t = L t c t + L t c 2t so that total consumption per (e ective) worker in period t: now, using: c t = c t + C t = Y t S t c 2t ( + n) c t = y t s t c = k ( + n) k so that: c = ( ) ( + ) ( + g)( + n) ( + n) ( ) ( + ) ( + g)( + n) 28
30 3..3 Golden rule and dynamic ine ciency As before, the golden rule for capital accumulation will follow: k Gold = arg max k k ( + n) k {z } with F.O.C. as: =c k = + n + n k Gold = (3.9) or, in the general case: f 0 ( k Gold ) = + n R = + n r = n that is, only when the interest rate equals the rate of poppulation growth, capital is at its golden rule level. 2 The possibility of dynamic ine ciency arises by comparing (3.8) with (3.9): ( ) ( + ) ( + g)( + n) k? = k Gold?= + n therefore, if k 6= k Gold the current allocation of resources would be Pareto ine cient and the planner could make every one else by rising/lowering investment (savings) 3..4 The role of Government. Suppose that for some reason the economy nds itself under dynamic ine ciency, i.e., k > k Gold. Then the Government could reallocate resources as follows: spend G t and fund it entirely with (lump-sum) taxes in that same period. Then key equation (3.7) becomes: k t+ = ( ) ( + ) ( + g)( + n) [k t G t ] which unambiguously leads to a lower k: The intuition is as follows: since the taxes are only on t, then generation t is taxed only on its rst year of life. The HH would have to reduce consumption in its rst period but since it wants to smooth consumption (under CRRA) it would have to reduce its savings too, so that consumption in period t falls less than the full amount of taxes. Consequently, savings fall and the economy moves towards k Gold (which maximizes the SS level of consumption). The Government in turn can reallocate the taxes as G t to increase consumption of those hurt and therefore increase economy-wide consumption. Claim 8 In the OLG presented above, the Ricardian equivalence result does not hold in general. 2 Note that if 6= then this condition becomes ( + r ) = + n or r = n: 29
31 To se why, suppose that in period t; Government purchases G t are introduced and funded by issuing one-period bonds b t = G t. In turn, in period t+ the government levies a tax in order to repay for the bonds, so t+ = ( + r t+ )b t : In the OGM the RH would then save whatever the government spends G t, so that it yields reutrn ( + r t+ )G t = t+. Therefore, the consumption plan operates as if the government was funding its purchases via taxes in period t: Hence, the irrelevance of distinguishing between taxes and bonds. On the other hand, in the OLG model, at period t only the young agents care about future taxes; therefore, introducing G t has real e ects on the consumption plan of generation t : 3..5 Social security Consider the problem of social security in the OLG model. "Old" HH receive bene ts b t that are funded by some sort of contriubution d: There are two systems; fully funded social security and pay-as-you-go (PAYGO). Fully funded social security. A HH of generation t contributes d in its rst period of life, this contribution is invested at market rates and then in its second period of life the HH receives ( + R t )d: The HH therefore faces the problem 3 : max u(c t ) + u(c 2t+ ) (3.0) c t;c 2t+ s:t: c ;t + s t + d A t w t (3.) c 2;t+ R t+ (d + s t ) (3.2) Claim 9 Under the above assumptions and de nitions, the HH problem with fully funded social security is equivalent to the simple HH problem (3.2)-(3.3) of section 3. Proof. To see why, rst solve for s t in the constraint (3.2): and next replace in constraint (3.): c 2;t+ = R t+ (d t + s t ) s t = c 2;t+ R t+ c ;t + s t + d = A t w t c2;t+ c ;t + d + d = A t w t R t+ c ;t + c 2;t+ R t+ = A t w t which is exactly the resource constraint (3.3). Hence, the problem is identical to that presented in section 3. The intuition for this result is simple: if contributions are invested at market rates, then they are simply a di erent way of saving. Therefore, the HH only needs to choose how much it wants to save at t, then pay d as contributions and invest the remaining as s t : Note that, depending on the size of d; it may be optimal for the HH to set s t = 0: Also notice that now the amount invested (which matches exactly the amounf of capital available at t + since = ) is s t + d = ( + n)k t+ 3 In this set up it is assumed that each HH of all generations make the same contribution, i.e., the case where d t 6= d t+ is ruled out. This possibility is explored in Acemoglu (2008) and in fact the case where d t is a choice variable is discussed. d 30
Problem Set 3: Proposed solutions Econ Fall 2012 (Prof. Roberto Chang)
 Problem Set 3: Proposed solutions Econ 504 - Fall 01 (Prof. Roberto Chang) Cesar E. Tamayo ctamayo@econ.rutgers.edu Department of Economics, Rutgers University 1 Balanced growth in the OGM Instead of going
Problem Set 3: Proposed solutions Econ 504 - Fall 01 (Prof. Roberto Chang) Cesar E. Tamayo ctamayo@econ.rutgers.edu Department of Economics, Rutgers University 1 Balanced growth in the OGM Instead of going
TOBB-ETU - Econ 532 Practice Problems II (Solutions)
 TOBB-ETU - Econ 532 Practice Problems II (Solutions) Q: Ramsey Model: Exponential Utility Assume that in nite-horizon households maximize a utility function of the exponential form 1R max U = e (n )t (1=)e
TOBB-ETU - Econ 532 Practice Problems II (Solutions) Q: Ramsey Model: Exponential Utility Assume that in nite-horizon households maximize a utility function of the exponential form 1R max U = e (n )t (1=)e
The Ramsey Model. Alessandra Pelloni. October TEI Lecture. Alessandra Pelloni (TEI Lecture) Economic Growth October / 61
 The Ramsey Model Alessandra Pelloni TEI Lecture October 2015 Alessandra Pelloni (TEI Lecture) Economic Growth October 2015 1 / 61 Introduction Introduction Introduction Ramsey-Cass-Koopmans model: di ers
The Ramsey Model Alessandra Pelloni TEI Lecture October 2015 Alessandra Pelloni (TEI Lecture) Economic Growth October 2015 1 / 61 Introduction Introduction Introduction Ramsey-Cass-Koopmans model: di ers
Economic Growth: Lecture 8, Overlapping Generations
 14.452 Economic Growth: Lecture 8, Overlapping Generations Daron Acemoglu MIT November 20, 2018 Daron Acemoglu (MIT) Economic Growth Lecture 8 November 20, 2018 1 / 46 Growth with Overlapping Generations
14.452 Economic Growth: Lecture 8, Overlapping Generations Daron Acemoglu MIT November 20, 2018 Daron Acemoglu (MIT) Economic Growth Lecture 8 November 20, 2018 1 / 46 Growth with Overlapping Generations
Advanced Macroeconomics
 Advanced Macroeconomics The Ramsey Model Marcin Kolasa Warsaw School of Economics Marcin Kolasa (WSE) Ad. Macro - Ramsey model 1 / 30 Introduction Authors: Frank Ramsey (1928), David Cass (1965) and Tjalling
Advanced Macroeconomics The Ramsey Model Marcin Kolasa Warsaw School of Economics Marcin Kolasa (WSE) Ad. Macro - Ramsey model 1 / 30 Introduction Authors: Frank Ramsey (1928), David Cass (1965) and Tjalling
Competitive Equilibrium and the Welfare Theorems
 Competitive Equilibrium and the Welfare Theorems Craig Burnside Duke University September 2010 Craig Burnside (Duke University) Competitive Equilibrium September 2010 1 / 32 Competitive Equilibrium and
Competitive Equilibrium and the Welfare Theorems Craig Burnside Duke University September 2010 Craig Burnside (Duke University) Competitive Equilibrium September 2010 1 / 32 Competitive Equilibrium and
ECON 582: The Neoclassical Growth Model (Chapter 8, Acemoglu)
 ECON 582: The Neoclassical Growth Model (Chapter 8, Acemoglu) Instructor: Dmytro Hryshko 1 / 21 Consider the neoclassical economy without population growth and technological progress. The optimal growth
ECON 582: The Neoclassical Growth Model (Chapter 8, Acemoglu) Instructor: Dmytro Hryshko 1 / 21 Consider the neoclassical economy without population growth and technological progress. The optimal growth
Neoclassical Growth Model / Cake Eating Problem
 Dynamic Optimization Institute for Advanced Studies Vienna, Austria by Gabriel S. Lee February 1-4, 2008 An Overview and Introduction to Dynamic Programming using the Neoclassical Growth Model and Cake
Dynamic Optimization Institute for Advanced Studies Vienna, Austria by Gabriel S. Lee February 1-4, 2008 An Overview and Introduction to Dynamic Programming using the Neoclassical Growth Model and Cake
Solow Growth Model. Michael Bar. February 28, Introduction Some facts about modern growth Questions... 4
 Solow Growth Model Michael Bar February 28, 208 Contents Introduction 2. Some facts about modern growth........................ 3.2 Questions..................................... 4 2 The Solow Model 5
Solow Growth Model Michael Bar February 28, 208 Contents Introduction 2. Some facts about modern growth........................ 3.2 Questions..................................... 4 2 The Solow Model 5
Ramsey Cass Koopmans Model (1): Setup of the Model and Competitive Equilibrium Path
 Ramsey Cass Koopmans Model (1): Setup of the Model and Competitive Equilibrium Path Ryoji Ohdoi Dept. of Industrial Engineering and Economics, Tokyo Tech This lecture note is mainly based on Ch. 8 of Acemoglu
Ramsey Cass Koopmans Model (1): Setup of the Model and Competitive Equilibrium Path Ryoji Ohdoi Dept. of Industrial Engineering and Economics, Tokyo Tech This lecture note is mainly based on Ch. 8 of Acemoglu
problem. max Both k (0) and h (0) are given at time 0. (a) Write down the Hamilton-Jacobi-Bellman (HJB) Equation in the dynamic programming
 1. Endogenous Growth with Human Capital Consider the following endogenous growth model with both physical capital (k (t)) and human capital (h (t)) in continuous time. The representative household solves
1. Endogenous Growth with Human Capital Consider the following endogenous growth model with both physical capital (k (t)) and human capital (h (t)) in continuous time. The representative household solves
ECON607 Fall 2010 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment 2
 ECON607 Fall 200 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment 2 The due date for this assignment is Tuesday, October 2. ( Total points = 50). (Two-sector growth model) Consider the
ECON607 Fall 200 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment 2 The due date for this assignment is Tuesday, October 2. ( Total points = 50). (Two-sector growth model) Consider the
In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now
![In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now In the Ramsey model we maximized the utility U = u[c(t)]e nt e t dt. Now](/thumbs/89/100962140.jpg) PERMANENT INCOME AND OPTIMAL CONSUMPTION On the previous notes we saw how permanent income hypothesis can solve the Consumption Puzzle. Now we use this hypothesis, together with assumption of rational
PERMANENT INCOME AND OPTIMAL CONSUMPTION On the previous notes we saw how permanent income hypothesis can solve the Consumption Puzzle. Now we use this hypothesis, together with assumption of rational
Economics 202A Lecture Outline #3 (version 1.0)
 Economics 202A Lecture Outline #3 (version.0) Maurice Obstfeld Steady State of the Ramsey-Cass-Koopmans Model In the last few lectures we have seen how to set up the Ramsey-Cass- Koopmans Model in discrete
Economics 202A Lecture Outline #3 (version.0) Maurice Obstfeld Steady State of the Ramsey-Cass-Koopmans Model In the last few lectures we have seen how to set up the Ramsey-Cass- Koopmans Model in discrete
Advanced Macroeconomics
 Advanced Macroeconomics The Ramsey Model Micha l Brzoza-Brzezina/Marcin Kolasa Warsaw School of Economics Micha l Brzoza-Brzezina/Marcin Kolasa (WSE) Ad. Macro - Ramsey model 1 / 47 Introduction Authors:
Advanced Macroeconomics The Ramsey Model Micha l Brzoza-Brzezina/Marcin Kolasa Warsaw School of Economics Micha l Brzoza-Brzezina/Marcin Kolasa (WSE) Ad. Macro - Ramsey model 1 / 47 Introduction Authors:
Macroeconomics I. University of Tokyo. Lecture 12. The Neo-Classical Growth Model: Prelude to LS Chapter 11.
 Macroeconomics I University of Tokyo Lecture 12 The Neo-Classical Growth Model: Prelude to LS Chapter 11. Julen Esteban-Pretel National Graduate Institute for Policy Studies The Cass-Koopmans Model: Environment
Macroeconomics I University of Tokyo Lecture 12 The Neo-Classical Growth Model: Prelude to LS Chapter 11. Julen Esteban-Pretel National Graduate Institute for Policy Studies The Cass-Koopmans Model: Environment
Fluctuations. Shocks, Uncertainty, and the Consumption/Saving Choice
 Fluctuations. Shocks, Uncertainty, and the Consumption/Saving Choice Olivier Blanchard April 2002 14.452. Spring 2002. Topic 2. 14.452. Spring, 2002 2 Want to start with a model with two ingredients: ²
Fluctuations. Shocks, Uncertainty, and the Consumption/Saving Choice Olivier Blanchard April 2002 14.452. Spring 2002. Topic 2. 14.452. Spring, 2002 2 Want to start with a model with two ingredients: ²
A simple macro dynamic model with endogenous saving rate: the representative agent model
 A simple macro dynamic model with endogenous saving rate: the representative agent model Virginia Sánchez-Marcos Macroeconomics, MIE-UNICAN Macroeconomics (MIE-UNICAN) A simple macro dynamic model with
A simple macro dynamic model with endogenous saving rate: the representative agent model Virginia Sánchez-Marcos Macroeconomics, MIE-UNICAN Macroeconomics (MIE-UNICAN) A simple macro dynamic model with
Economic Growth: Lecture 7, Overlapping Generations
 14.452 Economic Growth: Lecture 7, Overlapping Generations Daron Acemoglu MIT November 17, 2009. Daron Acemoglu (MIT) Economic Growth Lecture 7 November 17, 2009. 1 / 54 Growth with Overlapping Generations
14.452 Economic Growth: Lecture 7, Overlapping Generations Daron Acemoglu MIT November 17, 2009. Daron Acemoglu (MIT) Economic Growth Lecture 7 November 17, 2009. 1 / 54 Growth with Overlapping Generations
Overlapping Generations Model
 Overlapping Generations Model Yin-Chi Wang The Chinese University of Hong Kong October, 2012 Introduction 1 References: Acemoglu (2009) ch9, Blanchard and Fischer (1989) ch3 Samuelson (1958) and Diamond
Overlapping Generations Model Yin-Chi Wang The Chinese University of Hong Kong October, 2012 Introduction 1 References: Acemoglu (2009) ch9, Blanchard and Fischer (1989) ch3 Samuelson (1958) and Diamond
ECON607 Fall 2010 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment 1 Suggested Solutions
 ECON607 Fall 200 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment Suggested Solutions The due date for this assignment is Thursday, Sep. 23.. Consider an stochastic optimal growth model
ECON607 Fall 200 University of Hawaii Professor Hui He TA: Xiaodong Sun Assignment Suggested Solutions The due date for this assignment is Thursday, Sep. 23.. Consider an stochastic optimal growth model
ECON 582: Dynamic Programming (Chapter 6, Acemoglu) Instructor: Dmytro Hryshko
 ECON 582: Dynamic Programming (Chapter 6, Acemoglu) Instructor: Dmytro Hryshko Indirect Utility Recall: static consumer theory; J goods, p j is the price of good j (j = 1; : : : ; J), c j is consumption
ECON 582: Dynamic Programming (Chapter 6, Acemoglu) Instructor: Dmytro Hryshko Indirect Utility Recall: static consumer theory; J goods, p j is the price of good j (j = 1; : : : ; J), c j is consumption
Lecture 3: Growth with Overlapping Generations (Acemoglu 2009, Chapter 9, adapted from Zilibotti)
 Lecture 3: Growth with Overlapping Generations (Acemoglu 2009, Chapter 9, adapted from Zilibotti) Kjetil Storesletten September 5, 2014 Kjetil Storesletten () Lecture 3 September 5, 2014 1 / 56 Growth
Lecture 3: Growth with Overlapping Generations (Acemoglu 2009, Chapter 9, adapted from Zilibotti) Kjetil Storesletten September 5, 2014 Kjetil Storesletten () Lecture 3 September 5, 2014 1 / 56 Growth
ECON 581: Growth with Overlapping Generations. Instructor: Dmytro Hryshko
 ECON 581: Growth with Overlapping Generations Instructor: Dmytro Hryshko Readings Acemoglu, Chapter 9. Motivation Neoclassical growth model relies on the representative household. OLG models allow for
ECON 581: Growth with Overlapping Generations Instructor: Dmytro Hryshko Readings Acemoglu, Chapter 9. Motivation Neoclassical growth model relies on the representative household. OLG models allow for
4- Current Method of Explaining Business Cycles: DSGE Models. Basic Economic Models
 4- Current Method of Explaining Business Cycles: DSGE Models Basic Economic Models In Economics, we use theoretical models to explain the economic processes in the real world. These models de ne a relation
4- Current Method of Explaining Business Cycles: DSGE Models Basic Economic Models In Economics, we use theoretical models to explain the economic processes in the real world. These models de ne a relation
Capital Structure and Investment Dynamics with Fire Sales
 Capital Structure and Investment Dynamics with Fire Sales Douglas Gale Piero Gottardi NYU April 23, 2013 Douglas Gale, Piero Gottardi (NYU) Capital Structure April 23, 2013 1 / 55 Introduction Corporate
Capital Structure and Investment Dynamics with Fire Sales Douglas Gale Piero Gottardi NYU April 23, 2013 Douglas Gale, Piero Gottardi (NYU) Capital Structure April 23, 2013 1 / 55 Introduction Corporate
New Notes on the Solow Growth Model
 New Notes on the Solow Growth Model Roberto Chang September 2009 1 The Model The firstingredientofadynamicmodelisthedescriptionofthetimehorizon. In the original Solow model, time is continuous and the
New Notes on the Solow Growth Model Roberto Chang September 2009 1 The Model The firstingredientofadynamicmodelisthedescriptionofthetimehorizon. In the original Solow model, time is continuous and the
Slides II - Dynamic Programming
 Slides II - Dynamic Programming Julio Garín University of Georgia Macroeconomic Theory II (Ph.D.) Spring 2017 Macroeconomic Theory II Slides II - Dynamic Programming Spring 2017 1 / 32 Outline 1. Lagrangian
Slides II - Dynamic Programming Julio Garín University of Georgia Macroeconomic Theory II (Ph.D.) Spring 2017 Macroeconomic Theory II Slides II - Dynamic Programming Spring 2017 1 / 32 Outline 1. Lagrangian
Lecture 3, November 30: The Basic New Keynesian Model (Galí, Chapter 3)
 MakØk3, Fall 2 (blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 3, November 3: The Basic New Keynesian Model (Galí, Chapter
MakØk3, Fall 2 (blok 2) Business cycles and monetary stabilization policies Henrik Jensen Department of Economics University of Copenhagen Lecture 3, November 3: The Basic New Keynesian Model (Galí, Chapter
Endogenous Growth Theory
 Endogenous Growth Theory Lecture Notes for the winter term 2010/2011 Ingrid Ott Tim Deeken October 21st, 2010 CHAIR IN ECONOMIC POLICY KIT University of the State of Baden-Wuerttemberg and National Laboratory
Endogenous Growth Theory Lecture Notes for the winter term 2010/2011 Ingrid Ott Tim Deeken October 21st, 2010 CHAIR IN ECONOMIC POLICY KIT University of the State of Baden-Wuerttemberg and National Laboratory
(a) Write down the Hamilton-Jacobi-Bellman (HJB) Equation in the dynamic programming
 1. Government Purchases and Endogenous Growth Consider the following endogenous growth model with government purchases (G) in continuous time. Government purchases enhance production, and the production
1. Government Purchases and Endogenous Growth Consider the following endogenous growth model with government purchases (G) in continuous time. Government purchases enhance production, and the production
Macroeconomics IV Problem Set I
 14.454 - Macroeconomics IV Problem Set I 04/02/2011 Due: Monday 4/11/2011 1 Question 1 - Kocherlakota (2000) Take an economy with a representative, in nitely-lived consumer. The consumer owns a technology
14.454 - Macroeconomics IV Problem Set I 04/02/2011 Due: Monday 4/11/2011 1 Question 1 - Kocherlakota (2000) Take an economy with a representative, in nitely-lived consumer. The consumer owns a technology
ECON 5118 Macroeconomic Theory
 ECON 5118 Macroeconomic Theory Winter 013 Test 1 February 1, 013 Answer ALL Questions Time Allowed: 1 hour 0 min Attention: Please write your answers on the answer book provided Use the right-side pages
ECON 5118 Macroeconomic Theory Winter 013 Test 1 February 1, 013 Answer ALL Questions Time Allowed: 1 hour 0 min Attention: Please write your answers on the answer book provided Use the right-side pages
Economic Growth
 MIT OpenCourseWare http://ocw.mit.edu 14.452 Economic Growth Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 14.452 Economic Growth: Lecture
MIT OpenCourseWare http://ocw.mit.edu 14.452 Economic Growth Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 14.452 Economic Growth: Lecture
u(c t, x t+1 ) = c α t + x α t+1
 Review Questions: Overlapping Generations Econ720. Fall 2017. Prof. Lutz Hendricks 1 A Savings Function Consider the standard two-period household problem. The household receives a wage w t when young
Review Questions: Overlapping Generations Econ720. Fall 2017. Prof. Lutz Hendricks 1 A Savings Function Consider the standard two-period household problem. The household receives a wage w t when young
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics
 STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 202 Answer Key to Section 2 Questions Section. (Suggested Time: 45 Minutes) For 3 of
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 202 Answer Key to Section 2 Questions Section. (Suggested Time: 45 Minutes) For 3 of
1 Jan 28: Overview and Review of Equilibrium
 1 Jan 28: Overview and Review of Equilibrium 1.1 Introduction What is an equilibrium (EQM)? Loosely speaking, an equilibrium is a mapping from environments (preference, technology, information, market
1 Jan 28: Overview and Review of Equilibrium 1.1 Introduction What is an equilibrium (EQM)? Loosely speaking, an equilibrium is a mapping from environments (preference, technology, information, market
Lecture 2 The Centralized Economy: Basic features
 Lecture 2 The Centralized Economy: Basic features Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 41 I Motivation This Lecture introduces the basic
Lecture 2 The Centralized Economy: Basic features Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 41 I Motivation This Lecture introduces the basic
Problem Set 2: Proposed solutions Econ Fall Cesar E. Tamayo Department of Economics, Rutgers University
 Problem Set 2: Proposed solutions Econ 504 - Fall 202 Cesar E. Tamayo ctamayo@econ.rutgers.edu Department of Economics, Rutgers University Simple optimal growth (Problems &2) Suppose that we modify slightly
Problem Set 2: Proposed solutions Econ 504 - Fall 202 Cesar E. Tamayo ctamayo@econ.rutgers.edu Department of Economics, Rutgers University Simple optimal growth (Problems &2) Suppose that we modify slightly
Growth Theory: Review
 Growth Theory: Review Lecture 1.1, Exogenous Growth Topics in Growth, Part 2 June 11, 2007 Lecture 1.1, Exogenous Growth 1/76 Topics in Growth, Part 2 Growth Accounting: Objective and Technical Framework
Growth Theory: Review Lecture 1.1, Exogenous Growth Topics in Growth, Part 2 June 11, 2007 Lecture 1.1, Exogenous Growth 1/76 Topics in Growth, Part 2 Growth Accounting: Objective and Technical Framework
Advanced Macroeconomics II. Real Business Cycle Models. Jordi Galí. Universitat Pompeu Fabra Spring 2018
 Advanced Macroeconomics II Real Business Cycle Models Jordi Galí Universitat Pompeu Fabra Spring 2018 Assumptions Optimization by consumers and rms Perfect competition General equilibrium Absence of a
Advanced Macroeconomics II Real Business Cycle Models Jordi Galí Universitat Pompeu Fabra Spring 2018 Assumptions Optimization by consumers and rms Perfect competition General equilibrium Absence of a
Lecture 6: Competitive Equilibrium in the Growth Model (II)
 Lecture 6: Competitive Equilibrium in the Growth Model (II) ECO 503: Macroeconomic Theory I Benjamin Moll Princeton University Fall 204 /6 Plan of Lecture Sequence of markets CE 2 The growth model and
Lecture 6: Competitive Equilibrium in the Growth Model (II) ECO 503: Macroeconomic Theory I Benjamin Moll Princeton University Fall 204 /6 Plan of Lecture Sequence of markets CE 2 The growth model and
1 The social planner problem
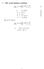 The social planner problem max C t;k t+ U t = E t X t C t () that can be written as: s.t.: Y t = A t K t (2) Y t = C t + I t (3) I t = K t+ (4) A t = A A t (5) et t i:i:d: 0; 2 max C t;k t+ U t = E t "
The social planner problem max C t;k t+ U t = E t X t C t () that can be written as: s.t.: Y t = A t K t (2) Y t = C t + I t (3) I t = K t+ (4) A t = A A t (5) et t i:i:d: 0; 2 max C t;k t+ U t = E t "
Permanent Income Hypothesis Intro to the Ramsey Model
 Consumption and Savings Permanent Income Hypothesis Intro to the Ramsey Model Lecture 10 Topics in Macroeconomics November 6, 2007 Lecture 10 1/18 Topics in Macroeconomics Consumption and Savings Outline
Consumption and Savings Permanent Income Hypothesis Intro to the Ramsey Model Lecture 10 Topics in Macroeconomics November 6, 2007 Lecture 10 1/18 Topics in Macroeconomics Consumption and Savings Outline
Problem 1 (30 points)
 Problem (30 points) Prof. Robert King Consider an economy in which there is one period and there are many, identical households. Each household derives utility from consumption (c), leisure (l) and a public
Problem (30 points) Prof. Robert King Consider an economy in which there is one period and there are many, identical households. Each household derives utility from consumption (c), leisure (l) and a public
Economic Growth: Lectures 5-7, Neoclassical Growth
 14.452 Economic Growth: Lectures 5-7, Neoclassical Growth Daron Acemoglu MIT November 7, 9 and 14, 2017. Daron Acemoglu (MIT) Economic Growth Lectures 5-7 November 7, 9 and 14, 2017. 1 / 83 Introduction
14.452 Economic Growth: Lectures 5-7, Neoclassical Growth Daron Acemoglu MIT November 7, 9 and 14, 2017. Daron Acemoglu (MIT) Economic Growth Lectures 5-7 November 7, 9 and 14, 2017. 1 / 83 Introduction
Lecture 2 The Centralized Economy
 Lecture 2 The Centralized Economy Economics 5118 Macroeconomic Theory Kam Yu Winter 2013 Outline 1 Introduction 2 The Basic DGE Closed Economy 3 Golden Rule Solution 4 Optimal Solution The Euler Equation
Lecture 2 The Centralized Economy Economics 5118 Macroeconomic Theory Kam Yu Winter 2013 Outline 1 Introduction 2 The Basic DGE Closed Economy 3 Golden Rule Solution 4 Optimal Solution The Euler Equation
Lecture 6: Discrete-Time Dynamic Optimization
 Lecture 6: Discrete-Time Dynamic Optimization Yulei Luo Economics, HKU November 13, 2017 Luo, Y. (Economics, HKU) ECON0703: ME November 13, 2017 1 / 43 The Nature of Optimal Control In static optimization,
Lecture 6: Discrete-Time Dynamic Optimization Yulei Luo Economics, HKU November 13, 2017 Luo, Y. (Economics, HKU) ECON0703: ME November 13, 2017 1 / 43 The Nature of Optimal Control In static optimization,
Topic 2. Consumption/Saving and Productivity shocks
 14.452. Topic 2. Consumption/Saving and Productivity shocks Olivier Blanchard April 2006 Nr. 1 1. What starting point? Want to start with a model with at least two ingredients: Shocks, so uncertainty.
14.452. Topic 2. Consumption/Saving and Productivity shocks Olivier Blanchard April 2006 Nr. 1 1. What starting point? Want to start with a model with at least two ingredients: Shocks, so uncertainty.
Suggested Solutions to Homework #3 Econ 511b (Part I), Spring 2004
 Suggested Solutions to Homework #3 Econ 5b (Part I), Spring 2004. Consider an exchange economy with two (types of) consumers. Type-A consumers comprise fraction λ of the economy s population and type-b
Suggested Solutions to Homework #3 Econ 5b (Part I), Spring 2004. Consider an exchange economy with two (types of) consumers. Type-A consumers comprise fraction λ of the economy s population and type-b
Economic Growth: Lecture 9, Neoclassical Endogenous Growth
 14.452 Economic Growth: Lecture 9, Neoclassical Endogenous Growth Daron Acemoglu MIT November 28, 2017. Daron Acemoglu (MIT) Economic Growth Lecture 9 November 28, 2017. 1 / 41 First-Generation Models
14.452 Economic Growth: Lecture 9, Neoclassical Endogenous Growth Daron Acemoglu MIT November 28, 2017. Daron Acemoglu (MIT) Economic Growth Lecture 9 November 28, 2017. 1 / 41 First-Generation Models
Monetary Economics: Solutions Problem Set 1
 Monetary Economics: Solutions Problem Set 1 December 14, 2006 Exercise 1 A Households Households maximise their intertemporal utility function by optimally choosing consumption, savings, and the mix of
Monetary Economics: Solutions Problem Set 1 December 14, 2006 Exercise 1 A Households Households maximise their intertemporal utility function by optimally choosing consumption, savings, and the mix of
Chapter 4. Applications/Variations
 Chapter 4 Applications/Variations 149 4.1 Consumption Smoothing 4.1.1 The Intertemporal Budget Economic Growth: Lecture Notes For any given sequence of interest rates {R t } t=0, pick an arbitrary q 0
Chapter 4 Applications/Variations 149 4.1 Consumption Smoothing 4.1.1 The Intertemporal Budget Economic Growth: Lecture Notes For any given sequence of interest rates {R t } t=0, pick an arbitrary q 0
The Real Business Cycle Model
 The Real Business Cycle Model Macroeconomics II 2 The real business cycle model. Introduction This model explains the comovements in the fluctuations of aggregate economic variables around their trend.
The Real Business Cycle Model Macroeconomics II 2 The real business cycle model. Introduction This model explains the comovements in the fluctuations of aggregate economic variables around their trend.
Lecture 15. Dynamic Stochastic General Equilibrium Model. Randall Romero Aguilar, PhD I Semestre 2017 Last updated: July 3, 2017
 Lecture 15 Dynamic Stochastic General Equilibrium Model Randall Romero Aguilar, PhD I Semestre 2017 Last updated: July 3, 2017 Universidad de Costa Rica EC3201 - Teoría Macroeconómica 2 Table of contents
Lecture 15 Dynamic Stochastic General Equilibrium Model Randall Romero Aguilar, PhD I Semestre 2017 Last updated: July 3, 2017 Universidad de Costa Rica EC3201 - Teoría Macroeconómica 2 Table of contents
Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models
 Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models Prof. George McCandless UCEMA Spring 2008 1 Class 1: introduction and rst models What we will do today 1. Organization of course
Macroeconomics II Dynamic macroeconomics Class 1: Introduction and rst models Prof. George McCandless UCEMA Spring 2008 1 Class 1: introduction and rst models What we will do today 1. Organization of course
Lecture 4 The Centralized Economy: Extensions
 Lecture 4 The Centralized Economy: Extensions Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 36 I Motivation This Lecture considers some applications
Lecture 4 The Centralized Economy: Extensions Leopold von Thadden University of Mainz and ECB (on leave) Advanced Macroeconomics, Winter Term 2013 1 / 36 I Motivation This Lecture considers some applications
Labor Economics, Lecture 11: Partial Equilibrium Sequential Search
 Labor Economics, 14.661. Lecture 11: Partial Equilibrium Sequential Search Daron Acemoglu MIT December 6, 2011. Daron Acemoglu (MIT) Sequential Search December 6, 2011. 1 / 43 Introduction Introduction
Labor Economics, 14.661. Lecture 11: Partial Equilibrium Sequential Search Daron Acemoglu MIT December 6, 2011. Daron Acemoglu (MIT) Sequential Search December 6, 2011. 1 / 43 Introduction Introduction
HOMEWORK #3 This homework assignment is due at NOON on Friday, November 17 in Marnix Amand s mailbox.
 Econ 50a second half) Yale University Fall 2006 Prof. Tony Smith HOMEWORK #3 This homework assignment is due at NOON on Friday, November 7 in Marnix Amand s mailbox.. This problem introduces wealth inequality
Econ 50a second half) Yale University Fall 2006 Prof. Tony Smith HOMEWORK #3 This homework assignment is due at NOON on Friday, November 7 in Marnix Amand s mailbox.. This problem introduces wealth inequality
DYNAMIC LECTURE 5: DISCRETE TIME INTERTEMPORAL OPTIMIZATION
 DYNAMIC LECTURE 5: DISCRETE TIME INTERTEMPORAL OPTIMIZATION UNIVERSITY OF MARYLAND: ECON 600. Alternative Methods of Discrete Time Intertemporal Optimization We will start by solving a discrete time intertemporal
DYNAMIC LECTURE 5: DISCRETE TIME INTERTEMPORAL OPTIMIZATION UNIVERSITY OF MARYLAND: ECON 600. Alternative Methods of Discrete Time Intertemporal Optimization We will start by solving a discrete time intertemporal
Government The government faces an exogenous sequence {g t } t=0
 Part 6 1. Borrowing Constraints II 1.1. Borrowing Constraints and the Ricardian Equivalence Equivalence between current taxes and current deficits? Basic paper on the Ricardian Equivalence: Barro, JPE,
Part 6 1. Borrowing Constraints II 1.1. Borrowing Constraints and the Ricardian Equivalence Equivalence between current taxes and current deficits? Basic paper on the Ricardian Equivalence: Barro, JPE,
Uncertainty Per Krusell & D. Krueger Lecture Notes Chapter 6
 1 Uncertainty Per Krusell & D. Krueger Lecture Notes Chapter 6 1 A Two-Period Example Suppose the economy lasts only two periods, t =0, 1. The uncertainty arises in the income (wage) of period 1. Not that
1 Uncertainty Per Krusell & D. Krueger Lecture Notes Chapter 6 1 A Two-Period Example Suppose the economy lasts only two periods, t =0, 1. The uncertainty arises in the income (wage) of period 1. Not that
Dynamic Optimization Problem. April 2, Graduate School of Economics, University of Tokyo. Math Camp Day 4. Daiki Kishishita.
 Discrete Math Camp Optimization Problem Graduate School of Economics, University of Tokyo April 2, 2016 Goal of day 4 Discrete We discuss methods both in discrete and continuous : Discrete : condition
Discrete Math Camp Optimization Problem Graduate School of Economics, University of Tokyo April 2, 2016 Goal of day 4 Discrete We discuss methods both in discrete and continuous : Discrete : condition
Economic Growth: Lecture 13, Stochastic Growth
 14.452 Economic Growth: Lecture 13, Stochastic Growth Daron Acemoglu MIT December 10, 2013. Daron Acemoglu (MIT) Economic Growth Lecture 13 December 10, 2013. 1 / 52 Stochastic Growth Models Stochastic
14.452 Economic Growth: Lecture 13, Stochastic Growth Daron Acemoglu MIT December 10, 2013. Daron Acemoglu (MIT) Economic Growth Lecture 13 December 10, 2013. 1 / 52 Stochastic Growth Models Stochastic
Housing with overlapping generations
 Housing with overlapping generations Chiara Forlati, Michael Hatcher, Alessandro Mennuni University of Southampton Preliminary and Incomplete May 16, 2015 Abstract We study the distributional and efficiency
Housing with overlapping generations Chiara Forlati, Michael Hatcher, Alessandro Mennuni University of Southampton Preliminary and Incomplete May 16, 2015 Abstract We study the distributional and efficiency
Dynamic Optimization: An Introduction
 Dynamic Optimization An Introduction M. C. Sunny Wong University of San Francisco University of Houston, June 20, 2014 Outline 1 Background What is Optimization? EITM: The Importance of Optimization 2
Dynamic Optimization An Introduction M. C. Sunny Wong University of San Francisco University of Houston, June 20, 2014 Outline 1 Background What is Optimization? EITM: The Importance of Optimization 2
The Solow Model in Discrete Time Allan Drazen October 2017
 The Solow Model in Discrete Time Allan Drazen October 2017 1 Technology There is a single good Y t produced by means of two factors of production capital K t in place at the beginning of the period and
The Solow Model in Discrete Time Allan Drazen October 2017 1 Technology There is a single good Y t produced by means of two factors of production capital K t in place at the beginning of the period and
Macroeconomics Qualifying Examination
 Macroeconomics Qualifying Examination January 2016 Department of Economics UNC Chapel Hill Instructions: This examination consists of 3 questions. Answer all questions. If you believe a question is ambiguously
Macroeconomics Qualifying Examination January 2016 Department of Economics UNC Chapel Hill Instructions: This examination consists of 3 questions. Answer all questions. If you believe a question is ambiguously
Assumption 5. The technology is represented by a production function, F : R 3 + R +, F (K t, N t, A t )
 6. Economic growth Let us recall the main facts on growth examined in the first chapter and add some additional ones. (1) Real output (per-worker) roughly grows at a constant rate (i.e. labor productivity
6. Economic growth Let us recall the main facts on growth examined in the first chapter and add some additional ones. (1) Real output (per-worker) roughly grows at a constant rate (i.e. labor productivity
1 The Basic RBC Model
 IHS 2016, Macroeconomics III Michael Reiter Ch. 1: Notes on RBC Model 1 1 The Basic RBC Model 1.1 Description of Model Variables y z k L c I w r output level of technology (exogenous) capital at end of
IHS 2016, Macroeconomics III Michael Reiter Ch. 1: Notes on RBC Model 1 1 The Basic RBC Model 1.1 Description of Model Variables y z k L c I w r output level of technology (exogenous) capital at end of
The representative agent model
 Chapter 3 The representative agent model 3.1 Optimal growth In this course we re looking at three types of model: 1. Descriptive growth model (Solow model): mechanical, shows the implications of a given
Chapter 3 The representative agent model 3.1 Optimal growth In this course we re looking at three types of model: 1. Descriptive growth model (Solow model): mechanical, shows the implications of a given
1. Using the model and notations covered in class, the expected returns are:
 Econ 510a second half Yale University Fall 2006 Prof. Tony Smith HOMEWORK #5 This homework assignment is due at 5PM on Friday, December 8 in Marnix Amand s mailbox. Solution 1. a In the Mehra-Prescott
Econ 510a second half Yale University Fall 2006 Prof. Tony Smith HOMEWORK #5 This homework assignment is due at 5PM on Friday, December 8 in Marnix Amand s mailbox. Solution 1. a In the Mehra-Prescott
slides chapter 3 an open economy with capital
 slides chapter 3 an open economy with capital Princeton University Press, 2017 Motivation In this chaper we introduce production and physical capital accumulation. Doing so will allow us to address two
slides chapter 3 an open economy with capital Princeton University Press, 2017 Motivation In this chaper we introduce production and physical capital accumulation. Doing so will allow us to address two
1 Two elementary results on aggregation of technologies and preferences
 1 Two elementary results on aggregation of technologies and preferences In what follows we ll discuss aggregation. What do we mean with this term? We say that an economy admits aggregation if the behavior
1 Two elementary results on aggregation of technologies and preferences In what follows we ll discuss aggregation. What do we mean with this term? We say that an economy admits aggregation if the behavior
Comprehensive Exam. Macro Spring 2014 Retake. August 22, 2014
 Comprehensive Exam Macro Spring 2014 Retake August 22, 2014 You have a total of 180 minutes to complete the exam. If a question seems ambiguous, state why, sharpen it up and answer the sharpened-up question.
Comprehensive Exam Macro Spring 2014 Retake August 22, 2014 You have a total of 180 minutes to complete the exam. If a question seems ambiguous, state why, sharpen it up and answer the sharpened-up question.
Lecture 5: The neoclassical growth model
 THE UNIVERSITY OF SOUTHAMPTON Paul Klein Office: Murray Building, 3005 Email: p.klein@soton.ac.uk URL: http://paulklein.se Economics 3010 Topics in Macroeconomics 3 Autumn 2010 Lecture 5: The neoclassical
THE UNIVERSITY OF SOUTHAMPTON Paul Klein Office: Murray Building, 3005 Email: p.klein@soton.ac.uk URL: http://paulklein.se Economics 3010 Topics in Macroeconomics 3 Autumn 2010 Lecture 5: The neoclassical
Suggested Solutions to Problem Set 2
 Macroeconomic Theory, Fall 03 SEF, HKU Instructor: Dr. Yulei Luo October 03 Suggested Solutions to Problem Set. 0 points] Consider the following Ramsey-Cass-Koopmans model with fiscal policy. First, we
Macroeconomic Theory, Fall 03 SEF, HKU Instructor: Dr. Yulei Luo October 03 Suggested Solutions to Problem Set. 0 points] Consider the following Ramsey-Cass-Koopmans model with fiscal policy. First, we
Economic Growth: Lectures 10 and 11, Endogenous Technological Change
 14.452 Economic Growth: Lectures 10 and 11, Endogenous Technological Change Daron Acemoglu MIT December 1 and 6, 2011. Daron Acemoglu (MIT) Economic Growth Lectures 10 end 11 December 1 and 6, 2011. 1
14.452 Economic Growth: Lectures 10 and 11, Endogenous Technological Change Daron Acemoglu MIT December 1 and 6, 2011. Daron Acemoglu (MIT) Economic Growth Lectures 10 end 11 December 1 and 6, 2011. 1
Session 4: Money. Jean Imbs. November 2010
 Session 4: Jean November 2010 I So far, focused on real economy. Real quantities consumed, produced, invested. No money, no nominal in uences. I Now, introduce nominal dimension in the economy. First and
Session 4: Jean November 2010 I So far, focused on real economy. Real quantities consumed, produced, invested. No money, no nominal in uences. I Now, introduce nominal dimension in the economy. First and
Practice Questions for Mid-Term I. Question 1: Consider the Cobb-Douglas production function in intensive form:
 Practice Questions for Mid-Term I Question 1: Consider the Cobb-Douglas production function in intensive form: y f(k) = k α ; α (0, 1) (1) where y and k are output per worker and capital per worker respectively.
Practice Questions for Mid-Term I Question 1: Consider the Cobb-Douglas production function in intensive form: y f(k) = k α ; α (0, 1) (1) where y and k are output per worker and capital per worker respectively.
G Recitation 3: Ramsey Growth model with technological progress; discrete time dynamic programming and applications
 G6215.1 - Recitation 3: Ramsey Growth model with technological progress; discrete time dynamic Contents 1 The Ramsey growth model with technological progress 2 1.1 A useful lemma..................................................
G6215.1 - Recitation 3: Ramsey Growth model with technological progress; discrete time dynamic Contents 1 The Ramsey growth model with technological progress 2 1.1 A useful lemma..................................................
Dynamic (Stochastic) General Equilibrium and Growth
 Dynamic (Stochastic) General Equilibrium and Growth Martin Ellison Nuffi eld College Michaelmas Term 2018 Martin Ellison (Nuffi eld) D(S)GE and Growth Michaelmas Term 2018 1 / 43 Macroeconomics is Dynamic
Dynamic (Stochastic) General Equilibrium and Growth Martin Ellison Nuffi eld College Michaelmas Term 2018 Martin Ellison (Nuffi eld) D(S)GE and Growth Michaelmas Term 2018 1 / 43 Macroeconomics is Dynamic
Problem Set # 2 Dynamic Part - Math Camp
 Problem Set # 2 Dynamic Part - Math Camp Consumption with Labor Supply Consider the problem of a household that hao choose both consumption and labor supply. The household s problem is: V 0 max c t;l t
Problem Set # 2 Dynamic Part - Math Camp Consumption with Labor Supply Consider the problem of a household that hao choose both consumption and labor supply. The household s problem is: V 0 max c t;l t
Introduction to Recursive Methods
 Chapter 1 Introduction to Recursive Methods These notes are targeted to advanced Master and Ph.D. students in economics. They can be of some use to researchers in macroeconomic theory. The material contained
Chapter 1 Introduction to Recursive Methods These notes are targeted to advanced Master and Ph.D. students in economics. They can be of some use to researchers in macroeconomic theory. The material contained
Advanced Economic Growth: Lecture 3, Review of Endogenous Growth: Schumpeterian Models
 Advanced Economic Growth: Lecture 3, Review of Endogenous Growth: Schumpeterian Models Daron Acemoglu MIT September 12, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 3 September 12, 2007 1 / 40 Introduction
Advanced Economic Growth: Lecture 3, Review of Endogenous Growth: Schumpeterian Models Daron Acemoglu MIT September 12, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 3 September 12, 2007 1 / 40 Introduction
Topic 8: Optimal Investment
 Topic 8: Optimal Investment Yulei Luo SEF of HKU November 22, 2013 Luo, Y. SEF of HKU) Macro Theory November 22, 2013 1 / 22 Demand for Investment The importance of investment. First, the combination of
Topic 8: Optimal Investment Yulei Luo SEF of HKU November 22, 2013 Luo, Y. SEF of HKU) Macro Theory November 22, 2013 1 / 22 Demand for Investment The importance of investment. First, the combination of
ECON0702: Mathematical Methods in Economics
 ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
ECON0702: Mathematical Methods in Economics Yulei Luo SEF of HKU January 14, 2009 Luo, Y. (SEF of HKU) MME January 14, 2009 1 / 44 Comparative Statics and The Concept of Derivative Comparative Statics
Macroeconomics I. University of Tokyo. Lecture 13
 Macroeconomics I University of Tokyo Lecture 13 The Neo-Classical Growth Model II: Distortionary Taxes LS Chapter 11. Julen Esteban-Pretel National Graduate Institute for Policy Studies Environment! Time
Macroeconomics I University of Tokyo Lecture 13 The Neo-Classical Growth Model II: Distortionary Taxes LS Chapter 11. Julen Esteban-Pretel National Graduate Institute for Policy Studies Environment! Time
Solutions to Problem Set 4 Macro II (14.452)
 Solutions to Problem Set 4 Macro II (14.452) Francisco A. Gallego 05/11 1 Money as a Factor of Production (Dornbusch and Frenkel, 1973) The shortcut used by Dornbusch and Frenkel to introduce money in
Solutions to Problem Set 4 Macro II (14.452) Francisco A. Gallego 05/11 1 Money as a Factor of Production (Dornbusch and Frenkel, 1973) The shortcut used by Dornbusch and Frenkel to introduce money in
Lecture 2. (1) Aggregation (2) Permanent Income Hypothesis. Erick Sager. September 14, 2015
 Lecture 2 (1) Aggregation (2) Permanent Income Hypothesis Erick Sager September 14, 2015 Econ 605: Adv. Topics in Macroeconomics Johns Hopkins University, Fall 2015 Erick Sager Lecture 2 (9/14/15) 1 /
Lecture 2 (1) Aggregation (2) Permanent Income Hypothesis Erick Sager September 14, 2015 Econ 605: Adv. Topics in Macroeconomics Johns Hopkins University, Fall 2015 Erick Sager Lecture 2 (9/14/15) 1 /
Introduction to Real Business Cycles: The Solow Model and Dynamic Optimization
 Introduction to Real Business Cycles: The Solow Model and Dynamic Optimization Vivaldo Mendes a ISCTE IUL Department of Economics 24 September 2017 (Vivaldo M. Mendes ) Macroeconomics (M8674) 24 September
Introduction to Real Business Cycles: The Solow Model and Dynamic Optimization Vivaldo Mendes a ISCTE IUL Department of Economics 24 September 2017 (Vivaldo M. Mendes ) Macroeconomics (M8674) 24 September
Modern Macroeconomics II
 Modern Macroeconomics II Katsuya Takii OSIPP Katsuya Takii (Institute) Modern Macroeconomics II 1 / 461 Introduction Purpose: This lecture is aimed at providing students with standard methods in modern
Modern Macroeconomics II Katsuya Takii OSIPP Katsuya Takii (Institute) Modern Macroeconomics II 1 / 461 Introduction Purpose: This lecture is aimed at providing students with standard methods in modern
Neoclassical Growth Model: I
 Neoclassical Growth Model: I Mark Huggett 2 2 Georgetown October, 2017 Growth Model: Introduction Neoclassical Growth Model is the workhorse model in macroeconomics. It comes in two main varieties: infinitely-lived
Neoclassical Growth Model: I Mark Huggett 2 2 Georgetown October, 2017 Growth Model: Introduction Neoclassical Growth Model is the workhorse model in macroeconomics. It comes in two main varieties: infinitely-lived
Lecture 5: Competitive Equilibrium in the Growth Model
 Lecture 5: Competitive Equilibrium in the Growth Model ECO 503: Macroeconomic Theory I Benjamin Moll Princeton University Fall 2014 1/17 Competitive Eqm in the Growth Model Recall two issues we are interested
Lecture 5: Competitive Equilibrium in the Growth Model ECO 503: Macroeconomic Theory I Benjamin Moll Princeton University Fall 2014 1/17 Competitive Eqm in the Growth Model Recall two issues we are interested
EC744 Lecture Notes: Economic Dynamics. Prof. Jianjun Miao
 EC744 Lecture Notes: Economic Dynamics Prof. Jianjun Miao 1 Deterministic Dynamic System State vector x t 2 R n State transition function x t = g x 0 ; t; ; x 0 = x 0 ; parameter 2 R p A parametrized dynamic
EC744 Lecture Notes: Economic Dynamics Prof. Jianjun Miao 1 Deterministic Dynamic System State vector x t 2 R n State transition function x t = g x 0 ; t; ; x 0 = x 0 ; parameter 2 R p A parametrized dynamic
1 Recursive Competitive Equilibrium
 Feb 5th, 2007 Let s write the SPP problem in sequence representation: max {c t,k t+1 } t=0 β t u(f(k t ) k t+1 ) t=0 k 0 given Because of the INADA conditions we know that the solution is interior. So
Feb 5th, 2007 Let s write the SPP problem in sequence representation: max {c t,k t+1 } t=0 β t u(f(k t ) k t+1 ) t=0 k 0 given Because of the INADA conditions we know that the solution is interior. So
Lecture 3: Dynamics of small open economies
 Lecture 3: Dynamics of small open economies Open economy macroeconomics, Fall 2006 Ida Wolden Bache September 5, 2006 Dynamics of small open economies Required readings: OR chapter 2. 2.3 Supplementary
Lecture 3: Dynamics of small open economies Open economy macroeconomics, Fall 2006 Ida Wolden Bache September 5, 2006 Dynamics of small open economies Required readings: OR chapter 2. 2.3 Supplementary
Neoclassical Business Cycle Model
 Neoclassical Business Cycle Model Prof. Eric Sims University of Notre Dame Fall 2015 1 / 36 Production Economy Last time: studied equilibrium in an endowment economy Now: study equilibrium in an economy
Neoclassical Business Cycle Model Prof. Eric Sims University of Notre Dame Fall 2015 1 / 36 Production Economy Last time: studied equilibrium in an endowment economy Now: study equilibrium in an economy
Overlapping Generation Models
 Overlapping Generation Models Ömer Özak SMU Macroeconomics II Ömer Özak (SMU) Economic Growth Macroeconomics II 1 / 122 Growth with Overlapping Generations Section 1 Growth with Overlapping Generations
Overlapping Generation Models Ömer Özak SMU Macroeconomics II Ömer Özak (SMU) Economic Growth Macroeconomics II 1 / 122 Growth with Overlapping Generations Section 1 Growth with Overlapping Generations
Advanced Economic Growth: Lecture 2, Review of Endogenous Growth: Expanding Variety Models
 Advanced Economic Growth: Lecture 2, Review of Endogenous Growth: Expanding Variety Models Daron Acemoglu MIT September 10, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 2 September 10, 2007 1 / 56
Advanced Economic Growth: Lecture 2, Review of Endogenous Growth: Expanding Variety Models Daron Acemoglu MIT September 10, 2007 Daron Acemoglu (MIT) Advanced Growth Lecture 2 September 10, 2007 1 / 56
