Chapter 5. Mass and Energy Analysis of Control Volumes. by Asst. Prof. Dr.Woranee Paengjuntuek and Asst. Prof. Dr.Worarattana Pattaraprakorn
|
|
|
- Reynard Lyons
- 6 years ago
- Views:
Transcription
1 Chapter 5 Mass and Energy Analysis of Control Volumes by Asst. Prof. Dr.Woranee Paengjuntuek and Asst. Prof. Dr.Worarattana Pattaraprakorn Reference: Cengel, Yunus A. and Michael A. Boles, Thermodynamics: An Engineering Approach, 5th ed., New York, McGraw-Hill:
2 Conservation of Energy for Control volumes The conservation of mass and the conservation of energy principles for open systems or control volumes apply to systems having mass crossing the system boundary or control surface. In addition to the heat transfer and work crossing the system boundaries, mass carries energy with it as it crosses the system boundaries. Thus, the mass and energy content of the open system may change when mass enters or leaves the control volume. Thermodynamic processes involving control volumes can be considered in two groups: steady-flow processes and unsteady-flow processes. During a steady-flow process, the fluid flows through the control volume steadily, experiencing no change with time at a fixed position. 2
3 Let s review the concepts of mass flow rate and energy transport by mass. Mass Flow Rate Mass flow through a cross-sectional area per unit time is called the mass flow rate. Note the dot over the mass symbol indicates a time rate of change. It is expressed as m where V n is the velocity normal to the cross-sectional flow area. 3
4 If the fluid density and velocity are constant over the flow cross-sectional area, the mass flow rate is m V A ave V ave v A where is the density, kg/m 3 ( = 1/v), A is the cross-sectional area, m 2 ; and average fluid velocity normal to the area, m/s. V ave is the 4
5 Example 5-1 Refrigerant-134a at 200 kpa, 40% quality, flows through a 1.1-cm inside diameter, d, tube with a velocity of 50 m/s. Find the mass flow rate of the refrigerant-134a. At P = 200 kpa, x = 0.4 we determine the specific volume from 5
6 The fluid volume flowing through a cross-section per unit time is called the volume flow rate V. The volume flow rate is given by integrating the product of the velocity normal to the flow area and the differential flow area over the flow area. If the velocity over the flow area is a constant, the volume flow rate is given by (note we are dropping the ave subscript on the velocity) The mass and volume flow rate are related by V VA 3 ( m / s) m V V v ( kg / s) 6
7 Example 5-2 Air at 100 kpa, 50 o C, flows through a pipe with a volume flow rate of 40 m 3 /min. Find the mass flow rate through the pipe, in kg/s. Assume air to be an ideal gas, so 7
8 Conservation of Mass for General Control Volume The conservation of mass principle for the open system or control volume is expressed as m m m ( kg / s) in out system 8
9 Steady-State, Steady-Flow Processes Most energy conversion devices operate steadily over long periods of time. The rates of heat transfer and work crossing the control surface are constant with time. The states of the mass streams crossing the control surface or boundary are constant with time. Under these conditions the mass and energy content of the control volume are constant with time. dm dt CV m CV 0 9
10 Steady-state, Steady-Flow Conservation of Mass: Since the mass of the control volume is constant with time during the steady-state, steady-flow process, the conservation of mass principle becomes m m ( kg / s) in out 10
11 Special Case: Steady Flow of an Incompressible Fluid The mass flow rate is related to volume flow rate and fluid density by m V For one entrance, one exit steady flow control volume, the mass flow rates are related by m V in out in in out out V in in m V out out V V A V A in in out out (kg/s) incompressible assumption 11
12 Flow work and the energy of a flowing fluid Energy flows into and from the control volume with the mass. The energy required to push the mass into or out of the control volume is known as the flow work or flow energy. The fluid up steam of the control surface acts as a piston to push a unit of mass into or out of the control volume. Consider the unit of mass entering the control volume shown below. As the fluid upstream pushes mass across the control surface, work done on that unit of mass is A Wflow F L F L PV Pmv A Wflow wflow Pv m The term Pv is called the flow work done on the unit of mass as it crosses the control surface. 12
13 The total energy of flowing fluid The total energy carried by a unit of mass as it crosses the control surface is the sum of the internal energy, flow work, potential energy, and kinetic energy. 2 V u Pv 2 2 h V gz 2 gz Here we have used the definition of enthalpy, h = u + Pv. 13
14 Energy transport by mass Amount of energy transport across a control surface: 2 V Emass m mh gz 2 (kj) Rate of energy transport across a control surface: 2 V Emass m mh gz ( kw ) 2 14
15 Conservation of Energy for General Control Volume The conservation of energy principle for the control volume or open system has the same word definition as the first law for the closed system. Expressing the energy transfers on a rate basis, the control volume first law is or E E E in out system ( kw) Rate of net energy transfer by heat, work, and mass Rate change in internal, kinetic, potential, etc., energies Considering that energy flows into and from the control volume with the mass, energy enters because net heat is transferred to the control volume, and energy leaves because the control volume does net work on its surroundings, the open system, or control volume, the first law becomes 15
16 where is the energy per unit mass flowing into or from the control volume. The energy per unit mass,, flowing across the control surface that defines the control volume is composed of four terms: the internal energy, the kinetic energy, the potential energy, and the flow work. The total energy carried by a unit of mass as it crosses the control surface is 2 V u Pv gz 2 2 h V gz 2 Where the time rate change of the energy of the control volume has been written as E CV 16
17 Steady-State, Steady-Flow Processes Most energy conversion devices operate steadily over long periods of time. The rates of heat transfer and work crossing the control surface are constant with time. The states of the mass streams crossing the control surface or boundary are constant with time. Under these conditions the mass and energy content of the control volume are constant with time. dm dt de dt CV CV m E CV CV 0 0 Steady-state, Steady-Flow Conservation of Mass: m m ( kg / s) in out 17
18 Steady-state, steady-flow conservation of energy Since the energy of the control volume is constant with time during the steady-state, steady-flow process, the conservation of energy principle becomes or or 0 E E E in out system ( kw) Rate of net energy transfer by heat, work, and mass Rate change in internal, kinetic, potential, etc., energies 18
19 Considering that energy flows into and from the control volume with the mass, energy enters because heat is transferred to the control volume, and energy leaves because the control volume does work on its surroundings, the steady-state, steady-flow first law becomes Often this result is written as where Q Q Q net in out W W W net out in 19
20 Steady-state, steady-flow for one entrance and one exit A number of thermodynamic devices such as pumps, fans, compressors, turbines, nozzles, diffusers, and heaters operate with one entrance and one exit. The steadystate, steady-flow conservation of mass and first law of thermodynamics for these systems reduce to where the entrance to the control volume is state 1 and the exit is state 2 and mass flow rate through the device. When can we neglect the kinetic and potential energy terms in the first law? m is the 20
21 Consider the kinetic and potential energies per unit mass. For V = 45 m s V = 140 m s ke ke ke 2 V 2 2 ( 45m / s) 1kJ / kg m / s ( 140m / s) 1kJ / kg m / s kj kg 10 kj kg pe gz m 1kJ / kg kj For z 100m pe m s 1000m / s kg m 1kJ / kg kj z 1000m pe m s 1000m / s kg 21
22 When compared to the enthalpy of steam (h 2000 to 3000 kj/kg) and the enthalpy of air (h 200 to 6000 kj/kg), the kinetic and potential energies are often neglected. When the kinetic and potential energies can be neglected, the conservation of energy equation becomes Q W m( h h ) ( kw) 2 1 We often write this last result per unit mass flow as q Q m w W m Where and. q w ( h h ) ( kj / kg)
23 Some Steady-Flow Engineering Devices Below are some engineering devices that operate essentially as steady-state, steadyflow control volumes. 23
24 Nozzles and Diffusers V 1 V V 2 1 V 1 V V 2 1 For flow through nozzles, the heat transfer, work, and potential energy are normally neglected, and nozzles have one entrance and one exit. The conservation of energy becomes 24
25 Solving for V 2 V 2( h h ) V
26 Example 5-4 Steam at 0.4 MPa, 300oC, enters an adiabatic nozzle with a low velocity and leaves at 0.2 MPa with a quality of 90%. Find the exit velocity, in m/s. Control Volume: The nozzle Property Relation: Steam tables Process: Assume adiabatic, steady-flow Conservation Principles: Conservation of mass: For one entrance, one exit, the conservation of mass becomes 26
27 Conservation of energy: According to the sketched control volume, mass crosses the control surface, but no work or heat transfer crosses the control surface. Neglecting the potential energies, we have Neglecting the inlet kinetic energy, the exit velocity is V 2( h h ) Now, we need to find the enthalpies from the steam tables. 27
28 28
29 Turbines If we neglect the changes in kinetic and potential energies as fluid flows through an adiabatic turbine having one entrance and one exit, the conservation of mass and the steady-state, steady-flow first law becomes 29
30 Example 5-5 High pressure air at 1300 K flows into an aircraft gas turbine and undergoes a steady-state, steady-flow, adiabatic process to the turbine exit at 660 K. Calculate the work done per unit mass of air flowing through the turbine when (a) Temperature-dependent data are used. (b) C p,ave at the average temperature is used. (c) C p at 300 K is used. Control Volume: The turbine. Property Relation: Assume air is an ideal gas and use ideal gas relations. Process: Steady-state, steady-flow, adiabatic process Conservation Principles: Conservation of mass: m in m out m m m
31 Conservation of energy: According to the sketched control volume, mass and work cross the control surface. Neglecting kinetic and potential energies and noting the process is adiabatic, we have The work done by the air per unit mass flow is Notice that the work done by a fluid flowing through a turbine is equal to the enthalpy decrease of the fluid. 31
32 (a) Using the air tables, Table A-17 at T 1 = 1300 K, h 1 = kj/kg at T 2 = 660 K, h 2 = kj/kg (b) Using Table A-2(c) at T ave = 980 K, C p, ave = kj/kgk 32
33 (c) Using Table A-2(a) at T = 300 K, Cp = kj/kg K 33
34 Compressors and fans Compressors and fans are essentially the same devices. However, compressors operate over larger pressure ratios than fans. If we neglect the changes in kinetic and potential energies as fluid flows through an adiabatic compressor having one entrance and one exit, the steady-state, steady-flow first law or the conservation of energy equation becomes 34
35 Example 5-6 Nitrogen gas is compressed in a steady-state, steady-flow, adiabatic process from 0.1 MPa, 25 o C. During the compression process the temperature becomes 125 o C. If the mass flow rate is 0.2 kg/s, determine the work done on the nitrogen, in kw. Control Volume: The compressor (see the compressor sketched above) Property Relation: Assume nitrogen is an ideal gas and use ideal gas relations Process: Adiabatic, steady-flow Conservation Principles: Conservation of mass: m m Conservation of energy: in out m m m
36 According to the sketched control volume, mass and work cross the control surface. Neglecting kinetic and potential energies and noting the process is adiabatic, we have for one entrance and one exit The work done on the nitrogen is related to the enthalpy rise of the nitrogen as it flows through the compressor. The work done on the nitrogen per unit mass flow is 36
37 Assuming constant specific heats at 300 K from Table A-2(a), we write the work as 37
38 Throttling devices Consider fluid flowing through a one-entrance, one-exit porous plug. The fluid experiences a pressure drop as it flows through the plug. No net work is done by the fluid. Assume the process is adiabatic and that the kinetic and potential energies are neglected; then the conservation of mass and energy equations become 38
39 This process is called a throttling process. What happens when an ideal gas is throttled? When throttling an ideal gas, the temperature does not change. We will see later in Chapter 11 that the throttling process is an important process in the refrigeration cycle. A throttling device may be used to determine the enthalpy of saturated steam. The steam is throttled from the pressure in the pipe to ambient pressure in the calorimeter. The pressure drop is sufficient to superheat the steam in the calorimeter. Thus, the temperature and pressure in the calorimeter will specify the enthalpy of the steam in the pipe. 39
40 Example 5-7 One way to determine the quality of saturated steam is to throttle the steam to a low enough pressure that it exists as a superheated vapor. Saturated steam at 0.4 MPa is throttled to 0.1 MPa, 100 o C. Determine the quality of the steam at 0.4 MPa. Throttling orifice 1 2 Control Surface Control Volume: The throttle Property Relation: The steam tables Process: Steady-state, steady-flow, no work, no heat transfer, neglect kinetic and potential energies, one entrance, one exit Conservation Principles: Conservation of mass: m in m out m m m
41 Conservation of energy: According to the sketched control volume, mass crosses the control surface. Neglecting kinetic and potential energies and noting the process is adiabatic with no work, we have for one entrance and one exit 41
42 Therefore, 42
43 Mixing chambers The mixing of two fluids occurs frequently in engineering applications. The section where the mixing process takes place is called a mixing chamber. The ordinary shower is an example of a mixing chamber. 43
44 Example 5-8 Steam at 0.2 MPa, 300 o C, enters a mixing chamber and is mixed with cold water at 20 o C, 0.2 MPa, to produce 20 kg/s of saturated liquid water at 0.2 MPa. What are the required steam and cold water flow rates? Steam 1 Cold water 2 Control Volume: The mixing chamber Mixing chamber Saturated water 3 Control surface Property Relation: Steam tables Process: Assume steady-flow, adiabatic mixing, with no work Conservation Principles: Conservation of mass: m in m m m m out m m m
45 Conservation of energy: According to the sketched control volume, mass crosses the control surface. Neglecting kinetic and potential energies and noting the process is adiabatic with no work, we have for two entrances and one exit Now, we use the steam tables to find the enthalpies: 45
46 46
47 Heat exchangers Heat exchangers are normally well-insulated devices that allow energy exchange between hot and cold fluids without mixing the fluids. The pumps, fans, and blowers causing the fluids to flow across the control surface are normally located outside the control surface. 47
48 Example 5-9 Air is heated in a heat exchanger by hot water. The water enters the heat exchanger at 45 o C and experiences a 20 o C drop in temperature. As the air passes through the heat exchanger, its temperature is increased by 25 o C. Determine the ratio of mass flow rate of the air to mass flow rate of the water. 1 Air inlet 1 Water inlet Control surface Control Volume: The heat exchanger 2 Air exit 2 Water exit Property Relation: Air: ideal gas relations Water: steam tables or incompressible liquid results Process: Assume adiabatic, steady-flow 48
49 Conservation Principles: Conservation of mass: m m m ( kg / s) in out system 0(steady) For two entrances, two exits, the conservation of mass becomes m in m out m m m m air, 1 w, 1 air, 2 w, 2 For two fluid streams that exchange energy but do not mix, it is better to conserve the mass for the fluid streams separately. Conservation of energy: According to the sketched control volume, mass crosses the control surface, but no work or heat transfer crosses the control surface. Neglecting the kinetic and potential energies, we have for steady-flo 49
50 E E E in out system ( kw) Rate of net energy transfer by heat, work, and mass 0(steady) Rate change in internal, kinetic, potential, etc., energies We assume that the air has constant specific heats at 300 K, Table A-2(a) (we don't know the actual temperatures, just the temperature difference). Because we know the initial and final temperatures for the water, we can use either the incompressible fluid result or the steam tables for its properties. Using the incompressible fluid approach for the water, Table A-3, C p, w = 4.18 kj/kgk. 50
51 A second solution to this problem is obtained by determining the heat transfer rate from the hot water and noting that this is the heat transfer rate to the air. Considering each fluid separately for steady-flow, one entrance, and one exit, and neglecting the kinetic and potential energies, the first law, or conservation of energy, equations become 51
52 Pipe and duct flow The flow of fluids through pipes and ducts is often a steady-state, steady-flow process. We normally neglect the kinetic and potential energies; however, depending on the flow situation, the work and heat transfer may or may not be zero. Example 5-10 In a simple steam power plant, steam leaves a boiler at 3 MPa, 600 o C, and enters a turbine at 2 MPa, 500 o C. Determine the in-line heat transfer from the steam per kilogram mass flowing in the pipe between the boiler and the turbine. Steam from boiler 1 Steam to turbine 2 Control surface Control Volume: Pipe section in which the heat loss occurs. Property Relation: Steam tables Process: Steady-flow Q out Conservation Principles: 52
53 Conservation of mass: m m m 0(steady) ( kg / s) in out system For one entrance, one exit, the conservation of mass becomes Conservation of energy: m in m out m m m 1 2 According to the sketched control volume, heat transfer and mass cross the control surface, but no work crosses the control surface. Neglecting the kinetic and potential energies, we have for steady-flow E E E ( kw ) in out system 0(steady) Rate of net energy transfer Rate change in internal, kinetic, by heat, work, and mass potential, etc., energies We determine the heat transfer rate per unit mass of flowing steam as m h m h Q Q m ( h h ) q out out 1 2 out Q out h h m
54 We use the steam tables to determine the enthalpies at the two states as 54
55 Example 5-11 Air at 100 o C, 0.15 MPa, 40 m/s, flows through a converging duct with a mass flow rate of 0.2 kg/s. The air leaves the duct at 0.1 MPa, m/s. The exit-to-inlet duct area ratio is 0.5. Find the required rate of heat transfer to the air when no work is done by the air. Q in 1 Air inlet Air exit 2 Control surface 55
56 Control Volume: The converging duct Property Relation: Assume air is an ideal gas and use ideal gas relations Process: Steady-flow Conservation Principles: Conservation of mass: m m m ( kg / s) in out system 0(steady) For one entrance, one exit, the conservation of mass becomes m in m out m m m
57 Conservation of energy: According to the sketched control volume, heat transfer and mass cross the control surface, but no work crosses the control surface. Here keep the kinetic energy and still neglect the potential energies, we have for steady-state, steady-flow process E E E 0(steady) ( kw ) in out system Rate of net energy transfer Rate change in internal, kinetic, by heat, work, and mass potential, etc., energies In the first law equation, the following are known: P 1, T 1 (and h 1 ), V 1, V 2, m, and A 2 /A 1. The unknowns are Q in, and h 2 (or T 2 ). We use the first law and the conservation of mass equation to solve for the two unknowns. 57
58 Solving for T 2 Assuming C p = constant, h 2 - h 1 = C p (T 2 - T 1 ) Looks like we made the wrong assumption for the direction of the heat transfer. The heat is really leaving the flow duct. 58
59 Liquid pumps The work required when pumping an incompressible liquid in an adiabatic steadystate, steady-flow process is given by The enthalpy difference can be written as h h ( u u ) ( Pv) ( Pv)
60 For incompressible liquids we assume that the density and specific volume are constant. The pumping process for an incompressible liquid is essentially isothermal, and the internal energy change is approximately zero (we will see this more clearly after introducing the second law). Thus, the enthalpy difference reduces to the difference in the pressure-specific volume products. Since v 2 = v 1 = v the work input to the pump becomes W is the net work done by the control volume, and it is noted that work is input to the pump; so, W W in, pump. If we neglect the changes in kinetic and potential energies, the pump work becomes ( W ) m v( P P ) ( kw) in, pump W m v( P P ) in, pump We use this result to calculate the work supplied to boiler feedwater pumps in steam power plants. If we apply the above energy balance to a pipe section that has no pump ( obtain. W 0 ), we 60
61 2 2 V2 V 1 W m v( P2 P1 ) g( z2 z1) ( kw ) V2 V 1 0 m v( P2 P1 ) g( z2 z1) 2 1 v P V P V 2g 2g z2 z1 This last equation is the famous Bernoulli s equation for frictionless, incompressible fluid flow through a pipe. Uniform-State, Uniform-Flow Problems During unsteady energy transfer to or from open systems or control volumes, the system may have a change in the stored energy and mass. Several unsteady thermodynamic problems may be treated as uniform-state, uniform-flow problems. The assumptions for uniform-state, uniform-flow are 61
62 The process takes place over a specified time period. The state of the mass within the control volume is uniform at any instant of time but may vary with time. The state of mass crossing the control surface is uniform and steady. The mass flow may be different at different control surface locations. To find the amount of mass crossing the control surface at a given location, we integrate the mass flow rate over the time period. The change in mass of the control volume in the time period is The uniform-state, uniform-flow conservation of mass becomes m m ( m2 m1 ) i e CV The change in internal energy for the control volume during the time period is 62
63 The energy crossing the control surface with the mass in the time period is where j =i, for inlets e, for exits The first law for uniform-state, uniform-flow becomes When the kinetic and potential energy changes associated with the control volume and the fluid streams are negligible, it simplifies to 63
64 Example 5-12 Consider an evacuated, insulated, rigid tank connected through a closed valve to a high-pressure line. The valve is opened and the tank is filled with the fluid in the line. If the fluid is an ideal gas, determine the final temperature in the tank when the tank pressure equals that of the line. Control Volume: The tank Property Relation: Ideal gas relations Process: Assume uniform-state, uniform-flow 64
65 Conservation Principles: Conservation of mass: m m ( m2 m1 ) i e CV Or, for one entrance, no exit, and initial mass of zero, this becomes Conservation of energy: m i ( m ) For an insulated tank Q is zero and for a rigid tank with no shaft work W is zero. For a one-inlet mass stream and no-exit mass stream and neglecting changes in kinetic and potential energies, the uniform-state, uniform-flow conservation of energy reduces to 2 CV 65
66 or If the fluid is air, k = 1.4 and the absolute temperature in the tank at the final state is 40 percent higher than the fluid absolute temperature in the supply line. The internal energy in the full tank differs from the internal energy of the supply line by the amount of flow work done to push the fluid from the line into the tank. 66
67 Homework 1. Air enters a 28-cm diameter pipe steadily at 200 kpa and 20 C with a velocity of 5 m/s. Air is heated as it flows, and leaves the pipe at 180 kpa and 40 C. Determine (a) the volume flow rate of air at the inlet, (b) the mass flow rate of air, (c) the velocity and volume flow rate at the exit. 2. Consider a 300-L storage tank of a solar water heating system initially filled with warm water at 45 C. Warm water is withdrawn from the tank through a 2 cm diameter hose at an average velocity of 0.5 m/s while cold water enters the tank at 20 C at a rate of 5 L/min. Determine the amount of water in the tank after a 20-minute period. Assume the pressure in the tank remains constant at 1 atm. 67
68 3. A house is maintained at 1 atm and 24 C, and warm air inside a house is forced to leave the house at a rate of 150 m3/h as a result of outdoor air at 5 C infiltrating into the house through the cracks. Determine the rate of net energy loss of the house due to mass transfer. 4. Air flows steadily in a pipe at 300 kpa, 77 C, and 25 m/s at a rate of 18 kg/min. Determine (a) the diameter of the pipe, (b) the rate of flow energy, (c) the rate of energy transport by mass (d) the error involved in part (c) if the kinetic energy is neglected. 68
Chapter 5. Mass and Energy Analysis of Control Volumes
 Chapter 5 Mass and Energy Analysis of Control Volumes Conservation Principles for Control volumes The conservation of mass and the conservation of energy principles for open systems (or control volumes)
Chapter 5 Mass and Energy Analysis of Control Volumes Conservation Principles for Control volumes The conservation of mass and the conservation of energy principles for open systems (or control volumes)
CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES
 Thermodynamics: An Engineering Approach 8th Edition in SI Units Yunus A. Çengel, Michael A. Boles McGraw-Hill, 2015 CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES Lecture slides by Dr. Fawzi Elfghi
Thermodynamics: An Engineering Approach 8th Edition in SI Units Yunus A. Çengel, Michael A. Boles McGraw-Hill, 2015 CHAPTER 5 MASS AND ENERGY ANALYSIS OF CONTROL VOLUMES Lecture slides by Dr. Fawzi Elfghi
ENT 254: Applied Thermodynamics
 ENT 54: Applied Thermodynamics Mr. Azizul bin Mohamad Mechanical Engineering Program School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) azizul@unimap.edu.my 019-4747351 04-9798679 Chapter
ENT 54: Applied Thermodynamics Mr. Azizul bin Mohamad Mechanical Engineering Program School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) azizul@unimap.edu.my 019-4747351 04-9798679 Chapter
The First Law of Thermodynamics. By: Yidnekachew Messele
 The First Law of Thermodynamics By: Yidnekachew Messele It is the law that relates the various forms of energies for system of different types. It is simply the expression of the conservation of energy
The First Law of Thermodynamics By: Yidnekachew Messele It is the law that relates the various forms of energies for system of different types. It is simply the expression of the conservation of energy
Chapter 7. Entropy. by Asst.Prof. Dr.Woranee Paengjuntuek and Asst. Prof. Dr.Worarattana Pattaraprakorn
 Chapter 7 Entropy by Asst.Prof. Dr.Woranee Paengjuntuek and Asst. Prof. Dr.Worarattana Pattaraprakorn Reference: Cengel, Yunus A. and Michael A. Boles, Thermodynamics: An Engineering Approach, 5th ed.,
Chapter 7 Entropy by Asst.Prof. Dr.Woranee Paengjuntuek and Asst. Prof. Dr.Worarattana Pattaraprakorn Reference: Cengel, Yunus A. and Michael A. Boles, Thermodynamics: An Engineering Approach, 5th ed.,
1 st Law Analysis of Control Volume (open system) Chapter 6
 1 st Law Analysis of Control Volume (open system) Chapter 6 In chapter 5, we did 1st law analysis for a control mass (closed system). In this chapter the analysis of the 1st law will be on a control volume
1 st Law Analysis of Control Volume (open system) Chapter 6 In chapter 5, we did 1st law analysis for a control mass (closed system). In this chapter the analysis of the 1st law will be on a control volume
Week 8. Steady Flow Engineering Devices. GENESYS Laboratory
 Week 8. Steady Flow Engineering Devices Objectives 1. Solve energy balance problems for common steady-flow devices such as nozzles, compressors, turbines, throttling valves, mixers, heaters, and heat exchangers
Week 8. Steady Flow Engineering Devices Objectives 1. Solve energy balance problems for common steady-flow devices such as nozzles, compressors, turbines, throttling valves, mixers, heaters, and heat exchangers
THE FIRST LAW APPLIED TO STEADY FLOW PROCESSES
 Chapter 10 THE FIRST LAW APPLIED TO STEADY FLOW PROCESSES It is not the sun to overtake the moon, nor doth the night outstrip theday.theyfloateachinanorbit. The Holy Qur-ān In many engineering applications,
Chapter 10 THE FIRST LAW APPLIED TO STEADY FLOW PROCESSES It is not the sun to overtake the moon, nor doth the night outstrip theday.theyfloateachinanorbit. The Holy Qur-ān In many engineering applications,
I. (20%) Answer the following True (T) or False (F). If false, explain why for full credit.
 I. (20%) Answer the following True (T) or False (F). If false, explain why for full credit. Both the Kelvin and Fahrenheit scales are absolute temperature scales. Specific volume, v, is an intensive property,
I. (20%) Answer the following True (T) or False (F). If false, explain why for full credit. Both the Kelvin and Fahrenheit scales are absolute temperature scales. Specific volume, v, is an intensive property,
Thermodynamics ENGR360-MEP112 LECTURE 7
 Thermodynamics ENGR360-MEP11 LECTURE 7 Thermodynamics ENGR360/MEP11 Objectives: 1. Conservation of mass principle.. Conservation of energy principle applied to control volumes (first law of thermodynamics).
Thermodynamics ENGR360-MEP11 LECTURE 7 Thermodynamics ENGR360/MEP11 Objectives: 1. Conservation of mass principle.. Conservation of energy principle applied to control volumes (first law of thermodynamics).
first law of ThermodyNamics
 first law of ThermodyNamics First law of thermodynamics - Principle of conservation of energy - Energy can be neither created nor destroyed Basic statement When any closed system is taken through a cycle,
first law of ThermodyNamics First law of thermodynamics - Principle of conservation of energy - Energy can be neither created nor destroyed Basic statement When any closed system is taken through a cycle,
Chapter 5: The First Law of Thermodynamics: Closed Systems
 Chapter 5: The First Law of Thermodynamics: Closed Systems The first law of thermodynamics can be simply stated as follows: during an interaction between a system and its surroundings, the amount of energy
Chapter 5: The First Law of Thermodynamics: Closed Systems The first law of thermodynamics can be simply stated as follows: during an interaction between a system and its surroundings, the amount of energy
Where F1 is the force and dl1 is the infinitesimal displacement, but F1 = p1a1
 In order to force the fluid to flow across the boundary of the system against a pressure p1, work is done on the boundary of the system. The amount of work done is dw = - F1.dl1, Where F1 is the force
In order to force the fluid to flow across the boundary of the system against a pressure p1, work is done on the boundary of the system. The amount of work done is dw = - F1.dl1, Where F1 is the force
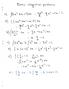 CHAPTER INTRODUCTION AND BASIC PRINCIPLES. (Tutorial). Determine if the following properties of the system are intensive or extensive properties: Property Intensive Extensive Volume Density Conductivity
CHAPTER INTRODUCTION AND BASIC PRINCIPLES. (Tutorial). Determine if the following properties of the system are intensive or extensive properties: Property Intensive Extensive Volume Density Conductivity
ME 2322 Thermodynamics I PRE-LECTURE Lesson 23 Complete the items below Name:
 Lesson 23 1. (10 pt) Write the equation for the thermal efficiency of a Carnot heat engine below: T η = T 1 L H 2. (10 pt) Can the thermal efficiency of an actual engine ever exceed that of an equivalent
Lesson 23 1. (10 pt) Write the equation for the thermal efficiency of a Carnot heat engine below: T η = T 1 L H 2. (10 pt) Can the thermal efficiency of an actual engine ever exceed that of an equivalent
Two mark questions and answers UNIT I BASIC CONCEPT AND FIRST LAW SVCET
 Two mark questions and answers UNIT I BASIC CONCEPT AND FIRST LAW 1. What do you understand by pure substance? A pure substance is defined as one that is homogeneous and invariable in chemical composition
Two mark questions and answers UNIT I BASIC CONCEPT AND FIRST LAW 1. What do you understand by pure substance? A pure substance is defined as one that is homogeneous and invariable in chemical composition
5/6/ :41 PM. Chapter 6. Using Entropy. Dr. Mohammad Abuhaiba, PE
 Chapter 6 Using Entropy 1 2 Chapter Objective Means are introduced for analyzing systems from the 2 nd law perspective as they undergo processes that are not necessarily cycles. Objective: introduce entropy
Chapter 6 Using Entropy 1 2 Chapter Objective Means are introduced for analyzing systems from the 2 nd law perspective as they undergo processes that are not necessarily cycles. Objective: introduce entropy
KNOWN: Pressure, temperature, and velocity of steam entering a 1.6-cm-diameter pipe.
 4.3 Steam enters a.6-cm-diameter pipe at 80 bar and 600 o C with a velocity of 50 m/s. Determine the mass flow rate, in kg/s. KNOWN: Pressure, temperature, and velocity of steam entering a.6-cm-diameter
4.3 Steam enters a.6-cm-diameter pipe at 80 bar and 600 o C with a velocity of 50 m/s. Determine the mass flow rate, in kg/s. KNOWN: Pressure, temperature, and velocity of steam entering a.6-cm-diameter
Thermal Energy Final Exam Fall 2002
 16.050 Thermal Energy Final Exam Fall 2002 Do all eight problems. All problems count the same. 1. A system undergoes a reversible cycle while exchanging heat with three thermal reservoirs, as shown below.
16.050 Thermal Energy Final Exam Fall 2002 Do all eight problems. All problems count the same. 1. A system undergoes a reversible cycle while exchanging heat with three thermal reservoirs, as shown below.
Dishwasher. Heater. Homework Solutions ME Thermodynamics I Spring HW-1 (25 points)
 HW-1 (25 points) (a) Given: 1 for writing given, find, EFD, etc., Schematic of a household piping system Find: Identify system and location on the system boundary where the system interacts with the environment
HW-1 (25 points) (a) Given: 1 for writing given, find, EFD, etc., Schematic of a household piping system Find: Identify system and location on the system boundary where the system interacts with the environment
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA
 Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
THERMODYNAMICS, FLUID AND PLANT PROCESSES. The tutorials are drawn from other subjects so the solutions are identified by the appropriate tutorial.
 THERMODYNAMICS, FLUID AND PLANT PROCESSES The tutorials are drawn from other subjects so the solutions are identified by the appropriate tutorial. THERMODYNAMICS TUTORIAL 2 THERMODYNAMIC PRINCIPLES SAE
THERMODYNAMICS, FLUID AND PLANT PROCESSES The tutorials are drawn from other subjects so the solutions are identified by the appropriate tutorial. THERMODYNAMICS TUTORIAL 2 THERMODYNAMIC PRINCIPLES SAE
c Dr. Md. Zahurul Haq (BUET) Thermodynamic Processes & Efficiency ME 6101 (2017) 2 / 25 T145 = Q + W cv + i h 2 = h (V2 1 V 2 2)
 Thermodynamic Processes & Isentropic Efficiency Dr. Md. Zahurul Haq Professor Department of Mechanical Engineering Bangladesh University of Engineering & Technology (BUET Dhaka-1000, Bangladesh zahurul@me.buet.ac.bd
Thermodynamic Processes & Isentropic Efficiency Dr. Md. Zahurul Haq Professor Department of Mechanical Engineering Bangladesh University of Engineering & Technology (BUET Dhaka-1000, Bangladesh zahurul@me.buet.ac.bd
First Law of Thermodynamics Closed Systems
 First Law of Thermodynamics Closed Systems Content The First Law of Thermodynamics Energy Balance Energy Change of a System Mechanisms of Energy Transfer First Law of Thermodynamics in Closed Systems Moving
First Law of Thermodynamics Closed Systems Content The First Law of Thermodynamics Energy Balance Energy Change of a System Mechanisms of Energy Transfer First Law of Thermodynamics in Closed Systems Moving
ME Thermodynamics I. Lecture Notes and Example Problems
 ME 227.3 Thermodynamics I Lecture Notes and Example Problems James D. Bugg September 2018 Department of Mechanical Engineering Introduction Part I: Lecture Notes This part contains handout versions of
ME 227.3 Thermodynamics I Lecture Notes and Example Problems James D. Bugg September 2018 Department of Mechanical Engineering Introduction Part I: Lecture Notes This part contains handout versions of
Chapter 7. Entropy: A Measure of Disorder
 Chapter 7 Entropy: A Measure of Disorder Entropy and the Clausius Inequality The second law of thermodynamics leads to the definition of a new property called entropy, a quantitative measure of microscopic
Chapter 7 Entropy: A Measure of Disorder Entropy and the Clausius Inequality The second law of thermodynamics leads to the definition of a new property called entropy, a quantitative measure of microscopic
Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No - 03 First Law of Thermodynamics (Open System) Good afternoon,
Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No - 03 First Law of Thermodynamics (Open System) Good afternoon,
ME Thermodynamics I
 Homework - Week 01 HW-01 (25 points) Given: 5 Schematic of the solar cell/solar panel Find: 5 Identify the system and the heat/work interactions associated with it. Show the direction of the interactions.
Homework - Week 01 HW-01 (25 points) Given: 5 Schematic of the solar cell/solar panel Find: 5 Identify the system and the heat/work interactions associated with it. Show the direction of the interactions.
R13 SET - 1 '' ''' '' ' '''' Code No RT21033
 SET - 1 II B. Tech I Semester Supplementary Examinations, June - 2015 THERMODYNAMICS (Com. to ME, AE, AME) Time: 3 hours Max. Marks: 70 Note: 1. Question Paper consists of two parts (Part-A and Part-B)
SET - 1 II B. Tech I Semester Supplementary Examinations, June - 2015 THERMODYNAMICS (Com. to ME, AE, AME) Time: 3 hours Max. Marks: 70 Note: 1. Question Paper consists of two parts (Part-A and Part-B)
Introduction to Engineering thermodynamics 2 nd Edition, Sonntag and Borgnakke. Solution manual
 Introduction to Engineering thermodynamics 2 nd Edition, Sonntag and Borgnakke Solution manual Chapter 6 Claus Borgnakke The picture is a false color thermal image of the space shuttle s main engine. The
Introduction to Engineering thermodynamics 2 nd Edition, Sonntag and Borgnakke Solution manual Chapter 6 Claus Borgnakke The picture is a false color thermal image of the space shuttle s main engine. The
CHAPTER 7 ENTROPY. Copyright Hany A. Al-Ansary and S. I. Abdel-Khalik (2014) 1
 CHAPTER 7 ENTROPY S. I. Abdel-Khalik (2014) 1 ENTROPY The Clausius Inequality The Clausius inequality states that for for all cycles, reversible or irreversible, engines or refrigerators: For internally-reversible
CHAPTER 7 ENTROPY S. I. Abdel-Khalik (2014) 1 ENTROPY The Clausius Inequality The Clausius inequality states that for for all cycles, reversible or irreversible, engines or refrigerators: For internally-reversible
Chapter Four fluid flow mass, energy, Bernoulli and momentum
 4-1Conservation of Mass Principle Consider a control volume of arbitrary shape, as shown in Fig (4-1). Figure (4-1): the differential control volume and differential control volume (Total mass entering
4-1Conservation of Mass Principle Consider a control volume of arbitrary shape, as shown in Fig (4-1). Figure (4-1): the differential control volume and differential control volume (Total mass entering
EVALUATION OF THE BEHAVIOUR OF STEAM EXPANDED IN A SET OF NOZZLES, IN A GIVEN TEMPERATURE
 Equatorial Journal of Engineering (2018) 9-13 Journal Homepage: www.erjournals.com ISSN: 0184-7937 EVALUATION OF THE BEHAVIOUR OF STEAM EXPANDED IN A SET OF NOZZLES, IN A GIVEN TEMPERATURE Kingsley Ejikeme
Equatorial Journal of Engineering (2018) 9-13 Journal Homepage: www.erjournals.com ISSN: 0184-7937 EVALUATION OF THE BEHAVIOUR OF STEAM EXPANDED IN A SET OF NOZZLES, IN A GIVEN TEMPERATURE Kingsley Ejikeme
Chapter 1: Basic Definitions, Terminologies and Concepts
 Chapter : Basic Definitions, Terminologies and Concepts ---------------------------------------. UThermodynamics:U It is a basic science that deals with: -. Energy transformation from one form to another..
Chapter : Basic Definitions, Terminologies and Concepts ---------------------------------------. UThermodynamics:U It is a basic science that deals with: -. Energy transformation from one form to another..
MAE 320 HW 7B. 1e. For an isolated system, please circle the parameter which will change with time. (a) Total energy;
 MAE 320 HW 7B his comprehensive homework is due Monday, December 5 th, 206. Each problem is worth the points indicated. Copying of the solution from another is not acceptable. Multi-choice, multi-answer
MAE 320 HW 7B his comprehensive homework is due Monday, December 5 th, 206. Each problem is worth the points indicated. Copying of the solution from another is not acceptable. Multi-choice, multi-answer
ME 300 Thermodynamics II
 ME 300 Thermodynamics II Prof. S. H. Frankel Fall 2006 ME 300 Thermodynamics II 1 Week 1 Introduction/Motivation Review Unsteady analysis NEW! ME 300 Thermodynamics II 2 Today s Outline Introductions/motivations
ME 300 Thermodynamics II Prof. S. H. Frankel Fall 2006 ME 300 Thermodynamics II 1 Week 1 Introduction/Motivation Review Unsteady analysis NEW! ME 300 Thermodynamics II 2 Today s Outline Introductions/motivations
FINAL EXAM. ME 200 Thermodynamics I, Spring 2013 CIRCLE YOUR LECTURE BELOW:
 ME 200 Thermodynamics I, Spring 2013 CIRCLE YOUR LECTURE BELOW: Div. 5 7:30 am Div. 2 10:30 am Div. 4 12:30 am Prof. Naik Prof. Braun Prof. Bae Div. 3 2:30 pm Div. 1 4:30 pm Div. 6 4:30 pm Prof. Chen Prof.
ME 200 Thermodynamics I, Spring 2013 CIRCLE YOUR LECTURE BELOW: Div. 5 7:30 am Div. 2 10:30 am Div. 4 12:30 am Prof. Naik Prof. Braun Prof. Bae Div. 3 2:30 pm Div. 1 4:30 pm Div. 6 4:30 pm Prof. Chen Prof.
CLASS Fourth Units (Second part)
 CLASS Fourth Units (Second part) Energy analysis of closed systems Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. MOVING BOUNDARY WORK Moving boundary work (P
CLASS Fourth Units (Second part) Energy analysis of closed systems Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. MOVING BOUNDARY WORK Moving boundary work (P
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA
 Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
Thermodynamics I Spring 1432/1433H (2011/2012H) Saturday, Wednesday 8:00am - 10:00am & Monday 8:00am - 9:00am MEP 261 Class ZA Dr. Walid A. Aissa Associate Professor, Mech. Engg. Dept. Faculty of Engineering
First Law of Thermodynamics
 CH2303 Chemical Engineering Thermodynamics I Unit II First Law of Thermodynamics Dr. M. Subramanian 07-July-2011 Associate Professor Department of Chemical Engineering Sri Sivasubramaniya Nadar College
CH2303 Chemical Engineering Thermodynamics I Unit II First Law of Thermodynamics Dr. M. Subramanian 07-July-2011 Associate Professor Department of Chemical Engineering Sri Sivasubramaniya Nadar College
(1)5. Which of the following equations is always valid for a fixed mass system undergoing an irreversible or reversible process:
 Last Name First Name ME 300 Engineering Thermodynamics Exam #2 Spring 2008 March 28, 2008 Form A Note : (i) (ii) (iii) (iv) Closed book, closed notes; one 8.5 x 11 sheet allowed. 60 points total; 60 minutes;
Last Name First Name ME 300 Engineering Thermodynamics Exam #2 Spring 2008 March 28, 2008 Form A Note : (i) (ii) (iii) (iv) Closed book, closed notes; one 8.5 x 11 sheet allowed. 60 points total; 60 minutes;
Thermodynamics: An Engineering Approach Seventh Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, Chapter 7 ENTROPY
 Thermodynamics: An Engineering Approach Seventh Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Chapter 7 ENTROPY Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach Seventh Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Chapter 7 ENTROPY Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
ME 201 Thermodynamics
 ME 0 Thermodynamics Solutions First Law Practice Problems. Consider a balloon that has been blown up inside a building and has been allowed to come to equilibrium with the inside temperature of 5 C and
ME 0 Thermodynamics Solutions First Law Practice Problems. Consider a balloon that has been blown up inside a building and has been allowed to come to equilibrium with the inside temperature of 5 C and
ESO201A: Thermodynamics
 ESO201A: Thermodynamics First Semester 2015-2016 Mid-Semester Examination Instructor: Sameer Khandekar Time: 120 mins Marks: 250 Solve sub-parts of a question serially. Question #1 (60 marks): One kmol
ESO201A: Thermodynamics First Semester 2015-2016 Mid-Semester Examination Instructor: Sameer Khandekar Time: 120 mins Marks: 250 Solve sub-parts of a question serially. Question #1 (60 marks): One kmol
Chapter 4. Energy Analysis of Closed Systems
 Chapter 4 Energy Analysis of Closed Systems The first law of thermodynamics is an expression of the conservation of energy principle. Energy can cross the boundaries of a closed system in the form of heat
Chapter 4 Energy Analysis of Closed Systems The first law of thermodynamics is an expression of the conservation of energy principle. Energy can cross the boundaries of a closed system in the form of heat
Chapter 7. Dr Ali Jawarneh. Department of Mechanical Engineering Hashemite University
 Chapter 7 ENTROPY Dr Ali Jawarneh Department of Mechanical Engineering Hashemite University Objectives Apply the second law of thermodynamics to processes. Define a new property called entropy to quantify
Chapter 7 ENTROPY Dr Ali Jawarneh Department of Mechanical Engineering Hashemite University Objectives Apply the second law of thermodynamics to processes. Define a new property called entropy to quantify
ESO 201A Thermodynamics
 ESO 201A Thermodynamics Instructor: Sameer Khandekar Tutorial 9 [7-27] A completely reversible heat pump produces heat at arate of 300 kw to warm a house maintained at 24 C. Theexterior air, which is at
ESO 201A Thermodynamics Instructor: Sameer Khandekar Tutorial 9 [7-27] A completely reversible heat pump produces heat at arate of 300 kw to warm a house maintained at 24 C. Theexterior air, which is at
Energy and Energy Balances
 Energy and Energy Balances help us account for the total energy required for a process to run Minimizing wasted energy is crucial in Energy, like mass, is. This is the Components of Total Energy energy
Energy and Energy Balances help us account for the total energy required for a process to run Minimizing wasted energy is crucial in Energy, like mass, is. This is the Components of Total Energy energy
ENTROPY. Chapter 7. Mehmet Kanoglu. Thermodynamics: An Engineering Approach, 6 th Edition. Yunus A. Cengel, Michael A. Boles.
 Thermodynamics: An Engineering Approach, 6 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2008 Chapter 7 ENTROPY Mehmet Kanoglu Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 6 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2008 Chapter 7 ENTROPY Mehmet Kanoglu Copyright The McGraw-Hill Companies, Inc. Permission required
2-21. for gage pressure, the high and low pressures are expressed as. Noting that 1 psi = kpa,
 - -58E The systolic and diastolic pressures of a healthy person are given in mmhg. These pressures are to be expressed in kpa, psi, and meter water column. Assumptions Both mercury and water are incompressible
- -58E The systolic and diastolic pressures of a healthy person are given in mmhg. These pressures are to be expressed in kpa, psi, and meter water column. Assumptions Both mercury and water are incompressible
BME-A PREVIOUS YEAR QUESTIONS
 BME-A PREVIOUS YEAR QUESTIONS CREDITS CHANGE ACCHA HAI TEAM UNIT-1 Introduction: Introduction to Thermodynamics, Concepts of systems, control volume, state, properties, equilibrium, quasi-static process,
BME-A PREVIOUS YEAR QUESTIONS CREDITS CHANGE ACCHA HAI TEAM UNIT-1 Introduction: Introduction to Thermodynamics, Concepts of systems, control volume, state, properties, equilibrium, quasi-static process,
Readings for this homework assignment and upcoming lectures
 Homework #3 (group) Tuesday, February 13 by 4:00 pm 5290 exercises (individual) Thursday, February 15 by 4:00 pm extra credit (individual) Thursday, February 15 by 4:00 pm Readings for this homework assignment
Homework #3 (group) Tuesday, February 13 by 4:00 pm 5290 exercises (individual) Thursday, February 15 by 4:00 pm extra credit (individual) Thursday, February 15 by 4:00 pm Readings for this homework assignment
Thermodynamics: An Engineering Approach Seventh Edition in SI Units Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011.
 Thermodynamics: An Engineering Approach Seventh Edition in SI Units Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Chapter 7 ENTROPY Mehmet Kanoglu University of Gaziantep Copyright The McGraw-Hill
Thermodynamics: An Engineering Approach Seventh Edition in SI Units Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Chapter 7 ENTROPY Mehmet Kanoglu University of Gaziantep Copyright The McGraw-Hill
MAHALAKSHMI ENGINEERING COLLEGE
 MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPALLI-621213. Department: Mechanical Subject Code: ME2202 U N IT - 1 Semester: III Subject Name: ENGG. THERMODYNAMICS 1. 1 kg of gas at 1.1 bar, 27 o C is compressed
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPALLI-621213. Department: Mechanical Subject Code: ME2202 U N IT - 1 Semester: III Subject Name: ENGG. THERMODYNAMICS 1. 1 kg of gas at 1.1 bar, 27 o C is compressed
Lecture 44: Review Thermodynamics I
 ME 00 Thermodynamics I Lecture 44: Review Thermodynamics I Yong Li Shanghai Jiao Tong University Institute of Refrigeration and Cryogenics 800 Dong Chuan Road Shanghai, 0040, P. R. China Email : liyo@sjtu.edu.cn
ME 00 Thermodynamics I Lecture 44: Review Thermodynamics I Yong Li Shanghai Jiao Tong University Institute of Refrigeration and Cryogenics 800 Dong Chuan Road Shanghai, 0040, P. R. China Email : liyo@sjtu.edu.cn
Find: a) Mass of the air, in kg, b) final temperature of the air, in K, and c) amount of entropy produced, in kj/k.
 PROBLEM 6.25 Three m 3 of air in a rigid, insulated container fitted with a paddle wheel is initially at 295 K, 200 kpa. The air receives 1546 kj of work from the paddle wheel. Assuming the ideal gas model,
PROBLEM 6.25 Three m 3 of air in a rigid, insulated container fitted with a paddle wheel is initially at 295 K, 200 kpa. The air receives 1546 kj of work from the paddle wheel. Assuming the ideal gas model,
QUESTION BANK UNIT-1 INTRODUCTION. 2. State zeroth law of thermodynamics? Write its importance in thermodynamics.
 QUESTION BANK UNIT-1 INTRODUCTION 1. What do you mean by thermodynamic equilibrium? How does it differ from thermal equilibrium? [05 Marks, June-2015] 2. State zeroth law of thermodynamics? Write its importance
QUESTION BANK UNIT-1 INTRODUCTION 1. What do you mean by thermodynamic equilibrium? How does it differ from thermal equilibrium? [05 Marks, June-2015] 2. State zeroth law of thermodynamics? Write its importance
Objectives. Conservation of mass principle: Mass Equation The Bernoulli equation Conservation of energy principle: Energy equation
 Objectives Conservation of mass principle: Mass Equation The Bernoulli equation Conservation of energy principle: Energy equation Conservation of Mass Conservation of Mass Mass, like energy, is a conserved
Objectives Conservation of mass principle: Mass Equation The Bernoulli equation Conservation of energy principle: Energy equation Conservation of Mass Conservation of Mass Mass, like energy, is a conserved
Topics to be covered. Fundamental Concepts & Definitions: Thermodynamics; definition and scope. Microscopic
 time Class No Text/ Reference page Topics to be covered Fundamental Concepts & Definitions: Thermodynamics; definition and scope. Microscopic 1 and Macroscopic approaches. Engineering Thermodynamics Definition,,
time Class No Text/ Reference page Topics to be covered Fundamental Concepts & Definitions: Thermodynamics; definition and scope. Microscopic 1 and Macroscopic approaches. Engineering Thermodynamics Definition,,
Exergy and the Dead State
 EXERGY The energy content of the universe is constant, just as its mass content is. Yet at times of crisis we are bombarded with speeches and articles on how to conserve energy. As engineers, we know that
EXERGY The energy content of the universe is constant, just as its mass content is. Yet at times of crisis we are bombarded with speeches and articles on how to conserve energy. As engineers, we know that
ECE309 THERMODYNAMICS & HEAT TRANSFER MIDTERM EXAMINATION. Instructor: R. Culham. Name: Student ID Number:
 ECE309 THERMODYNAMICS & HEAT TRANSFER MIDTERM EXAMINATION June 19, 2015 2:30 pm - 4:30 pm Instructor: R. Culham Name: Student ID Number: Instructions 1. This is a 2 hour, closed-book examination. 2. Permitted
ECE309 THERMODYNAMICS & HEAT TRANSFER MIDTERM EXAMINATION June 19, 2015 2:30 pm - 4:30 pm Instructor: R. Culham Name: Student ID Number: Instructions 1. This is a 2 hour, closed-book examination. 2. Permitted
20 m neon m propane. g 20. Problems with solutions:
 Problems with solutions:. A -m tank is filled with a gas at room temperature 0 C and pressure 00 Kpa. How much mass is there if the gas is a) Air b) Neon, or c) Propane? Given: T7K; P00KPa; M air 9; M
Problems with solutions:. A -m tank is filled with a gas at room temperature 0 C and pressure 00 Kpa. How much mass is there if the gas is a) Air b) Neon, or c) Propane? Given: T7K; P00KPa; M air 9; M
ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER. 13 June 2007
 ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER 13 June 2007 Midterm Examination R. Culham This is a 2 hour, open-book examination. You are permitted to use: course text book calculator There are
ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER 13 June 2007 Midterm Examination R. Culham This is a 2 hour, open-book examination. You are permitted to use: course text book calculator There are
Thermodynamics II. Week 9
 hermodynamics II Week 9 Example Oxygen gas in a piston cylinder at 300K, 00 kpa with volume o. m 3 is compressed in a reversible adiabatic process to a final temperature of 700K. Find the final pressure
hermodynamics II Week 9 Example Oxygen gas in a piston cylinder at 300K, 00 kpa with volume o. m 3 is compressed in a reversible adiabatic process to a final temperature of 700K. Find the final pressure
Today lecture. 1. Entropy change in an isolated system 2. Exergy
 Today lecture 1. Entropy change in an isolated system. Exergy - What is exergy? - Reversible Work & Irreversibility - Second-Law Efficiency - Exergy change of a system For a fixed mass For a flow stream
Today lecture 1. Entropy change in an isolated system. Exergy - What is exergy? - Reversible Work & Irreversibility - Second-Law Efficiency - Exergy change of a system For a fixed mass For a flow stream
III. Evaluating Properties. III. Evaluating Properties
 F. Property Tables 1. What s in the tables and why specific volumes, v (m /kg) (as v, v i, v f, v g ) pressure, P (kpa) temperature, T (C) internal energy, u (kj/kg) (as u, u i, u f, u g, u ig, u fg )
F. Property Tables 1. What s in the tables and why specific volumes, v (m /kg) (as v, v i, v f, v g ) pressure, P (kpa) temperature, T (C) internal energy, u (kj/kg) (as u, u i, u f, u g, u ig, u fg )
As Per New GTU Syllabus
 As Per New GTU Syllabus Prepared by: Mr. Bhavin J. Vegada (M.Tech Thermal Engg.) Mr. Ketan C. Agola (M.Tech. Thermal Engg.) Darshan Institute of Engineering &Technology BRIEF CONTENTS Chapter No. Title
As Per New GTU Syllabus Prepared by: Mr. Bhavin J. Vegada (M.Tech Thermal Engg.) Mr. Ketan C. Agola (M.Tech. Thermal Engg.) Darshan Institute of Engineering &Technology BRIEF CONTENTS Chapter No. Title
MAE 11. Homework 8: Solutions 11/30/2018
 MAE 11 Homework 8: Solutions 11/30/2018 MAE 11 Fall 2018 HW #8 Due: Friday, November 30 (beginning of class at 12:00p) Requirements:: Include T s diagram for all cycles. Also include p v diagrams for Ch
MAE 11 Homework 8: Solutions 11/30/2018 MAE 11 Fall 2018 HW #8 Due: Friday, November 30 (beginning of class at 12:00p) Requirements:: Include T s diagram for all cycles. Also include p v diagrams for Ch
Introduction to Chemical Engineering Thermodynamics. Chapter 7. KFUPM Housam Binous CHE 303
 Introduction to Chemical Engineering Thermodynamics Chapter 7 1 Thermodynamics of flow is based on mass, energy and entropy balances Fluid mechanics encompasses the above balances and conservation of momentum
Introduction to Chemical Engineering Thermodynamics Chapter 7 1 Thermodynamics of flow is based on mass, energy and entropy balances Fluid mechanics encompasses the above balances and conservation of momentum
Thermodynamics Introduction and Basic Concepts
 Thermodynamics Introduction and Basic Concepts by Asst. Prof. Channarong Asavatesanupap Mechanical Engineering Department Faculty of Engineering Thammasat University 2 What is Thermodynamics? Thermodynamics
Thermodynamics Introduction and Basic Concepts by Asst. Prof. Channarong Asavatesanupap Mechanical Engineering Department Faculty of Engineering Thammasat University 2 What is Thermodynamics? Thermodynamics
Classification following properties of the system in Intensive and Extensive
 Unit I Classification following properties of the system in Intensive and Extensive Extensive : mass, weight, volume, potential energy, Kinetic energy, Internal energy, entropy, exergy, energy, magnetization
Unit I Classification following properties of the system in Intensive and Extensive Extensive : mass, weight, volume, potential energy, Kinetic energy, Internal energy, entropy, exergy, energy, magnetization
T098. c Dr. Md. Zahurul Haq (BUET) First Law of Thermodynamics ME 201 (2012) 2 / 26
 Conservation of Energy for a Closed System Dr. Md. Zahurul Haq Professor Department of Mechanical Engineering Bangladesh University of Engineering & Technology (BUET Dhaka-, Bangladesh zahurul@me.buet.ac.bd
Conservation of Energy for a Closed System Dr. Md. Zahurul Haq Professor Department of Mechanical Engineering Bangladesh University of Engineering & Technology (BUET Dhaka-, Bangladesh zahurul@me.buet.ac.bd
In the next lecture...
 16 1 In the next lecture... Solve problems from Entropy Carnot cycle Exergy Second law efficiency 2 Problem 1 A heat engine receives reversibly 420 kj/cycle of heat from a source at 327 o C and rejects
16 1 In the next lecture... Solve problems from Entropy Carnot cycle Exergy Second law efficiency 2 Problem 1 A heat engine receives reversibly 420 kj/cycle of heat from a source at 327 o C and rejects
Course: MECH-341 Thermodynamics II Semester: Fall 2006
 FINAL EXAM Date: Thursday, December 21, 2006, 9 am 12 am Examiner: Prof. E. Timofeev Associate Examiner: Prof. D. Frost READ CAREFULLY BEFORE YOU PROCEED: Course: MECH-341 Thermodynamics II Semester: Fall
FINAL EXAM Date: Thursday, December 21, 2006, 9 am 12 am Examiner: Prof. E. Timofeev Associate Examiner: Prof. D. Frost READ CAREFULLY BEFORE YOU PROCEED: Course: MECH-341 Thermodynamics II Semester: Fall
ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER. 20 June 2005
 ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER 20 June 2005 Midterm Examination R. Culham & M. Bahrami This is a 90 minute, closed-book examination. You are permitted to use one 8.5 in. 11 in. crib
ECE309 INTRODUCTION TO THERMODYNAMICS & HEAT TRANSFER 20 June 2005 Midterm Examination R. Culham & M. Bahrami This is a 90 minute, closed-book examination. You are permitted to use one 8.5 in. 11 in. crib
UNIT I Basic concepts and Work & Heat Transfer
 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road 517583 QUESTION BANK (DESCRIPTIVE) Subject with Code: Engineering Thermodynamics (16ME307) Year & Sem: II-B. Tech & II-Sem
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road 517583 QUESTION BANK (DESCRIPTIVE) Subject with Code: Engineering Thermodynamics (16ME307) Year & Sem: II-B. Tech & II-Sem
ME 354 THERMODYNAMICS 2 MIDTERM EXAMINATION. Instructor: R. Culham. Name: Student ID Number: Instructions
 ME 354 THERMODYNAMICS 2 MIDTERM EXAMINATION February 14, 2011 5:30 pm - 7:30 pm Instructor: R. Culham Name: Student ID Number: Instructions 1. This is a 2 hour, closed-book examination. 2. Answer all questions
ME 354 THERMODYNAMICS 2 MIDTERM EXAMINATION February 14, 2011 5:30 pm - 7:30 pm Instructor: R. Culham Name: Student ID Number: Instructions 1. This is a 2 hour, closed-book examination. 2. Answer all questions
Previous lecture. Today lecture
 Previous lecture ds relations (derive from steady energy balance) Gibb s equations Entropy change in liquid and solid Equations of & v, & P, and P & for steady isentropic process of ideal gas Isentropic
Previous lecture ds relations (derive from steady energy balance) Gibb s equations Entropy change in liquid and solid Equations of & v, & P, and P & for steady isentropic process of ideal gas Isentropic
PTT 277/3 APPLIED THERMODYNAMICS SEM 1 (2013/2014)
 PTT 77/3 APPLIED THERMODYNAMICS SEM 1 (013/014) 1 Energy can exist in numerous forms: Thermal Mechanical Kinetic Potential Electric Magnetic Chemical Nuclear The total energy of a system on a unit mass:
PTT 77/3 APPLIED THERMODYNAMICS SEM 1 (013/014) 1 Energy can exist in numerous forms: Thermal Mechanical Kinetic Potential Electric Magnetic Chemical Nuclear The total energy of a system on a unit mass:
+ m B1 = 1. u A1. u B1. - m B1 = V A. /v A = , u B1 + V B. = 5.5 kg => = V tot. Table B.1.
 5.6 A rigid tank is divided into two rooms by a membrane, both containing water, shown in Fig. P5.6. Room A is at 200 kpa, v = 0.5 m3/kg, VA = m3, and room B contains 3.5 kg at 0.5 MPa, 400 C. The membrane
5.6 A rigid tank is divided into two rooms by a membrane, both containing water, shown in Fig. P5.6. Room A is at 200 kpa, v = 0.5 m3/kg, VA = m3, and room B contains 3.5 kg at 0.5 MPa, 400 C. The membrane
ME 2322 Thermodynamics I PRE-LECTURE Lesson 23 Complete the items below Name:
 Lesson 23 1. (10 pt) Write the equation for the thermal efficiency of a Carnot heat engine below: 1 L H 2. (10 pt) Can the thermal efficiency of an actual engine ever exceed that of an equivalent Carnot
Lesson 23 1. (10 pt) Write the equation for the thermal efficiency of a Carnot heat engine below: 1 L H 2. (10 pt) Can the thermal efficiency of an actual engine ever exceed that of an equivalent Carnot
Unit B-1: List of Subjects
 ES31 Energy Transfer Fundamentals Unit B: The First Law of Thermodynamics ROAD MAP... B-1: The Concept of Energy B-: Work Interactions B-3: First Law of Thermodynamics B-4: Heat Transfer Fundamentals Unit
ES31 Energy Transfer Fundamentals Unit B: The First Law of Thermodynamics ROAD MAP... B-1: The Concept of Energy B-: Work Interactions B-3: First Law of Thermodynamics B-4: Heat Transfer Fundamentals Unit
ME 200 Final Exam December 14, :00 a.m. to 10:00 a.m.
 CIRCLE YOUR LECTURE BELOW: First Name Last Name 7:30 a.m. 8:30 a.m. 10:30 a.m. 11:30 a.m. Boregowda Boregowda Braun Bae 2:30 p.m. 3:30 p.m. 4:30 p.m. Meyer Naik Hess ME 200 Final Exam December 14, 2015
CIRCLE YOUR LECTURE BELOW: First Name Last Name 7:30 a.m. 8:30 a.m. 10:30 a.m. 11:30 a.m. Boregowda Boregowda Braun Bae 2:30 p.m. 3:30 p.m. 4:30 p.m. Meyer Naik Hess ME 200 Final Exam December 14, 2015
Lecture 35: Vapor power systems, Rankine cycle
 ME 00 Thermodynamics I Spring 015 Lecture 35: Vapor power systems, Rankine cycle Yong Li Shanghai Jiao Tong University Institute of Refrigeration and Cryogenics 800 Dong Chuan Road Shanghai, 0040, P. R.
ME 00 Thermodynamics I Spring 015 Lecture 35: Vapor power systems, Rankine cycle Yong Li Shanghai Jiao Tong University Institute of Refrigeration and Cryogenics 800 Dong Chuan Road Shanghai, 0040, P. R.
1. (10) Calorically perfect ideal air at 300 K, 100 kpa, 1000 m/s, is brought to rest isentropically. Determine its final temperature.
 AME 5053 Intermediate Thermodynamics Examination Prof J M Powers 30 September 0 0 Calorically perfect ideal air at 300 K, 00 kpa, 000 m/s, is brought to rest isentropically Determine its final temperature
AME 5053 Intermediate Thermodynamics Examination Prof J M Powers 30 September 0 0 Calorically perfect ideal air at 300 K, 00 kpa, 000 m/s, is brought to rest isentropically Determine its final temperature
Engineering Thermodynamics
 David Ng Summer 2017 Contents 1 July 5, 2017 3 1.1 Thermodynamics................................ 3 2 July 7, 2017 3 2.1 Properties.................................... 3 3 July 10, 2017 4 3.1 Systems.....................................
David Ng Summer 2017 Contents 1 July 5, 2017 3 1.1 Thermodynamics................................ 3 2 July 7, 2017 3 2.1 Properties.................................... 3 3 July 10, 2017 4 3.1 Systems.....................................
To receive full credit all work must be clearly provided. Please use units in all answers.
 Exam is Open Textbook, Open Class Notes, Computers can be used (Computer limited to class notes, lectures, homework, book material, calculator, conversion utilities, etc. No searching for similar problems
Exam is Open Textbook, Open Class Notes, Computers can be used (Computer limited to class notes, lectures, homework, book material, calculator, conversion utilities, etc. No searching for similar problems
 Two mark questions and answers UNIT II SECOND LAW 1. Define Clausius statement. It is impossible for a self-acting machine working in a cyclic process, to transfer heat from a body at lower temperature
Two mark questions and answers UNIT II SECOND LAW 1. Define Clausius statement. It is impossible for a self-acting machine working in a cyclic process, to transfer heat from a body at lower temperature
Department of Mechanical Engineering Indian Institute of Technology New Delhi II Semester MEL 140 ENGINEERING THERMODYNAMICS
 PROBLEM SET 1: Review of Basics Problem 1: Define Work. Explain how the force is generated in an automobile. Problem 2: Define and classify Energy and explain the relation between a body and energy. Problem
PROBLEM SET 1: Review of Basics Problem 1: Define Work. Explain how the force is generated in an automobile. Problem 2: Define and classify Energy and explain the relation between a body and energy. Problem
MASS, MOMENTUM, AND ENERGY EQUATIONS
 MASS, MOMENTUM, AND ENERGY EQUATIONS This chapter deals with four equations commonly used in fluid mechanics: the mass, Bernoulli, Momentum and energy equations. The mass equation is an expression of the
MASS, MOMENTUM, AND ENERGY EQUATIONS This chapter deals with four equations commonly used in fluid mechanics: the mass, Bernoulli, Momentum and energy equations. The mass equation is an expression of the
UBMCC11 - THERMODYNAMICS. B.E (Marine Engineering) B 16 BASIC CONCEPTS AND FIRST LAW PART- A
 UBMCC11 - THERMODYNAMICS B.E (Marine Engineering) B 16 UNIT I BASIC CONCEPTS AND FIRST LAW PART- A 1. What do you understand by pure substance? 2. Define thermodynamic system. 3. Name the different types
UBMCC11 - THERMODYNAMICS B.E (Marine Engineering) B 16 UNIT I BASIC CONCEPTS AND FIRST LAW PART- A 1. What do you understand by pure substance? 2. Define thermodynamic system. 3. Name the different types
CONCEPTS AND DEFINITIONS. Prepared by Engr. John Paul Timola
 CONCEPTS AND DEFINITIONS Prepared by Engr. John Paul Timola ENGINEERING THERMODYNAMICS Science that involves design and analysis of devices and systems for energy conversion Deals with heat and work and
CONCEPTS AND DEFINITIONS Prepared by Engr. John Paul Timola ENGINEERING THERMODYNAMICS Science that involves design and analysis of devices and systems for energy conversion Deals with heat and work and
Please welcome for any correction or misprint in the entire manuscript and your valuable suggestions kindly mail us
 Problems of Practices Of Fluid Mechanics Compressible Fluid Flow Prepared By Brij Bhooshan Asst. Professor B. S. A. College of Engg. And Technology Mathura, Uttar Pradesh, (India) Supported By: Purvi Bhooshan
Problems of Practices Of Fluid Mechanics Compressible Fluid Flow Prepared By Brij Bhooshan Asst. Professor B. S. A. College of Engg. And Technology Mathura, Uttar Pradesh, (India) Supported By: Purvi Bhooshan
Chapter 6. Using Entropy
 Chapter 6 Using Entropy Learning Outcomes Demonstrate understanding of key concepts related to entropy and the second law... including entropy transfer, entropy production, and the increase in entropy
Chapter 6 Using Entropy Learning Outcomes Demonstrate understanding of key concepts related to entropy and the second law... including entropy transfer, entropy production, and the increase in entropy
Thermodynamics of solids 5. Unary systems. Kwangheon Park Kyung Hee University Department of Nuclear Engineering
 Thermodynamics of solids 5. Unary systems Kwangheon ark Kyung Hee University Department of Nuclear Engineering 5.1. Unary heterogeneous system definition Unary system: one component system. Unary heterogeneous
Thermodynamics of solids 5. Unary systems Kwangheon ark Kyung Hee University Department of Nuclear Engineering 5.1. Unary heterogeneous system definition Unary system: one component system. Unary heterogeneous
Content. Entropy and principle of increasing entropy. Change of entropy in an ideal gas.
 Entropy Content Entropy and principle of increasing entropy. Change of entropy in an ideal gas. Entropy Entropy can be viewed as a measure of molecular disorder, or molecular randomness. As a system becomes
Entropy Content Entropy and principle of increasing entropy. Change of entropy in an ideal gas. Entropy Entropy can be viewed as a measure of molecular disorder, or molecular randomness. As a system becomes
MAE 110A. Homework 3: Solutions 10/20/2017
 MAE 110A Homework 3: Solutions 10/20/2017 3.10: For H 2O, determine the specified property at the indicated state. Locate the state on a sketch of the T-v diagram. Given a) T 140 C, v 0.5 m 3 kg b) p 30MPa,
MAE 110A Homework 3: Solutions 10/20/2017 3.10: For H 2O, determine the specified property at the indicated state. Locate the state on a sketch of the T-v diagram. Given a) T 140 C, v 0.5 m 3 kg b) p 30MPa,
SEM-2017(03HI MECHANICAL ENGINEERING. Paper II. Please read each of the following instructions carefully before attempting questions.
 We RoU No. 700095 Candidate should write his/her Roll No. here. Total No. of Questions : 7 No. of Printed Pages : 7 SEM-2017(03HI MECHANICAL ENGINEERING Paper II Time ; 3 Hours ] [ Total Marks : 0 Instructions
We RoU No. 700095 Candidate should write his/her Roll No. here. Total No. of Questions : 7 No. of Printed Pages : 7 SEM-2017(03HI MECHANICAL ENGINEERING Paper II Time ; 3 Hours ] [ Total Marks : 0 Instructions
THERMODYNAMICS (Date of document: 8 th March 2016)
 THERMODYNAMICS (Date of document: 8 th March 2016) Course Code : MEHD214 Course Status : Core Level : Diploma Semester Taught : 3 Credit : 4 Pre-requisites : None Assessments : Computerized homework 20
THERMODYNAMICS (Date of document: 8 th March 2016) Course Code : MEHD214 Course Status : Core Level : Diploma Semester Taught : 3 Credit : 4 Pre-requisites : None Assessments : Computerized homework 20
Chapter 8. The increased awareness that the world s energy EXERGY: A MEASURE OF WORK POTENTIAL. Objectives
 Chapter 8 EXERGY: A MEASURE OF WORK POTENTIAL The increased awareness that the world s energy resources are limited has caused many countries to reexamine their energy policies and take drastic measures
Chapter 8 EXERGY: A MEASURE OF WORK POTENTIAL The increased awareness that the world s energy resources are limited has caused many countries to reexamine their energy policies and take drastic measures
