Namely, for regular languages L1. Concatenation. Regular Languages. Star operation L 1. Complement. For regular language L the complement L is regular
|
|
|
- Aubrey Palmer
- 6 years ago
- Views:
Transcription
1 CD5560 FABER For guges, Autot d Modes of Coputtio eture 5 Märde Uiversit 2003 Cotet More Properties of Regur guges (R) Stdrd Represettios of R Eeetr Questios out R No-Regur guges The Pigeohoe Priipe The Pupig e Appitios of the Pupig e More Properties of Regur guges We hve prove Regur guges re osed uder Uio Cotetio Str opertio Ne, for regur guges 1 d 2 : Uio Cotetio Str opertio Regur guges We i prove Regur guges re so osed uder Copeet Itersetio Reverse Reverse R Ne, for regur guges 1 d 2 : Copeet Itersetio Regur guges Theore Copeet For regur guge the opeet is regur Te tht epts d hge: ofi sttes fi sttes (o-eptig sttes eptig sttes) Epe = ( * ),, q0 q1 q2 = ( + ( + )( + ), ) Resutig epts, q0 q1 q
2 Itersetio 1, 2 regur Theore For regur guges 1 d 2 the itersetio 1 2 is regur App DeMorg s : = , regur regur regur regur Stdrd Represettios of Regur guges Stdrd Represettios of Regur guges Meership Questio Regur guges Regur Epressios s NFAs Regur Grrs 13 Eeetr Questios out Regur guges 14 Questio: Aser: Give regur guge d strig ho e he if? Te the tht epts d he if is epted 15 Questio: Give regur guge ho e he if is ept:? ( = ) Aser: Te the tht epts Che if there is pth fro the iiti stte to fi stte =
3 Questio: Give regur guge ho e he if is fiite? is ifiite Questio: Give regur guges 1 d 2 ho e he if 1 = 2? Aser: Te the tht epts Che if there is ith e fro the iiti stte to fi stte is fiite Aser: Fid if ( ) ( ) = ( ) ( ) = ( ) ( ) = d 1 2 = or No-Regur guges 1 = No-regur guges Regur guges??? * * + + ( + )* et... Ho e prove tht guge is ot regur? Prove tht there is o tht epts Proe: this is ot es to prove Soutio: the Pupig e! The Pigeohoe Priipe
4 4 pigeos A pigeohoe ust oti t est to pigeos The Pigeohoe Priipe (Postfpriipe eer Brevduvepriipe?) 3 Pigeohoes (eer postf) The Pigeohoe Priipe pigeos pigeos pigeohoes... > pigeohoes > There is pigeohoe ith t est 2 pigeos The Pigeohoe Priipe d s ith 4 sttes I s of strigs: o stte is repeted I s of strigs:... stte is repeted q 1 q 2 q3 q 4 q 1 q 2 q3 q 4 q 1 q 2 q3 q
5 4 If the of strig hs egth the stte is repeted q 1 q 2 q 3 q 4 Pigeohoe priipe for : If i of strig trsitios sttes of the stte is repeted I other ords for strig trsitios re pigeos q sttes re pigeohoes I geer A strig hs egth uer of sttes A stte q ust e repeted i the of of The Pupig e for Regur guges Te ifiite regur guge tht epts sttes Te strig ith = + 1 If strig hs egth ( uer of sttes) the, fro the pigeohoe priipe: Write = There is ith e stte q is repeted i the
6 egths: (fro pigeo priipe, s q is the first repetitio i sequee) 1 (there is i the grph) Oservtio The strig is epted Oservtio The strig is epted Oservtio The strig is epted Geer The strig i = 0,1, 2,... i is epted The Pupig e Give ifiite regur guge there eists iteger for strig ith egth e rite = 1 ith d suh tht: i i = 0,1, 2, Appitios of the Pupig e Theore The guge = { : 0} is ot regur Use the Pupig e! = { : 0} Assue for otrditio tht is regur guge Sie is ifiite e pp the Pupig e
7 = { : 0} et e the iteger i the Pupig e Pi strig suh tht: e.g. pi egth = Write: = Fro the Pupig e it ust e tht: egth =, 1, 1 = We hve: = Fro the Pupig e: We hoose = i = 0 =, 1 i i = 0,1, 2, CONTRADICTION! 57 Our ssuptio tht is regur guge is ot true No-regur guges { : 0} Theore The guge R = { : Σ*} Σ = {, } Cousio is ot regur guge Regur guges * * + + ( + )* et... is ot regur Use the Pupig e! END OF PROOF R = { : Σ*} Assue for otrditio tht is regur guge Sie is ifiite e pp the Pupig e et e the iteger i the Pupig e Pi strig suh tht: egth pi = { : Σ*} = R Write it ust e tht egth Fro the Pupig e =, 1 =, 1 =
8 =, 1 = We hoose i = 0 So e get s o the eft, hie is o the right CONTRADICTION! 64 Our ssuptio tht is regur guge is ot true Cousio is ot regur guge No-regur guges { : 0} { R : Σ*} Regur guges * * + + ( + )* et... END OF PROOF Theore The guge + = { :, 0} + = { :, 0} + = { :, 0} is ot regur Use the Pupig e Assue for otrditio tht is regur guge Sie is ifiite e pp the Pupig e et e the iteger i the Pupig e Pi strig suh tht: pi egth = Write 2 it ust e tht egth 2 Fro the Pupig e =, 1 =, 1 2 = We hve: Fro the Pupig e Thus: 0 i i = 0,1, 2,... 0 = = = 2 =, 1 2 BUT: CONTRADICTION! = { :, 0}
9 Our ssuptio tht is regur guge is ot true Cousio is ot regur guge No-regur guges { R : Σ*} { : 0 } + { :, 0} Regur guges Theore The guge = {! : 0} is ot regur! = 1 2 ( 1) Use the Pupig e END OF PROOF = {! : 0} Assue for otrditio tht is regur guge Sie is ifiite e pp the Pupig e et e the iteger i the Pupig e Pi strig suh tht: pi = {! : 0} egth! = Write! = Fro the Pupig e it ust e tht egth, 1! = =, 1! We hve: =! =, 1 Fro the Pupig e: Ad sie:!+ 1 = {! : 0} Hoever for > 1! +!+!+! <! +! =! ( + 1) = ( +1)! i i = 0,1, 2,... Thus: 2 2 = =!+ There is p! + = p! 1! + < ( + 1)!! + p! for p
10 BUT:!+ = {! : 0} d 1 Our ssuptio tht is regur guge is ot true + No-regur guges { R : Σ*} { : 0} { :, 0} {! : 0}!+ Cousio is ot regur guge Regur guges CONTRADICTION! END OF PROOF Theore The guge i = { : i prie} is ot regur Use the Pupig e 85 i = { : i prie} Assue for otrditio tht is regur guge Sie is ifiite e pp the Pupig e 86 Fro the Pupig e it ust e tht egth, 1 Fro the Pupig e: i i = 0,1, 2,... The egth of egth + 1 = ust e prie for eh > strig of. 87 But egth( + 1 ) = egth( = egth( ) + egth( hih is ot prie! ) ) = = + ( egth( )) = (1 + egth( )) Our ssuptio tht is regur guge is ot true Cousio is ot regur guge + No-regur guges { R : Σ*} { : 0} { :, 0} {! : 0} Regur guges Thus: CONTRADICTION! 88 END OF PROOF 89 i = { : i prie} 90
Applications of Regular Closure
 Applictios of Regulr Closure 1 The itersectio of cotext-free lguge d regulr lguge is cotext-free lguge L1 L2 cotext free regulr Regulr Closure L1 L 2 cotext-free 2 Liz 6 th, sectio 8.2, exple 8.7, pge
Applictios of Regulr Closure 1 The itersectio of cotext-free lguge d regulr lguge is cotext-free lguge L1 L2 cotext free regulr Regulr Closure L1 L 2 cotext-free 2 Liz 6 th, sectio 8.2, exple 8.7, pge
CD5080 AUBER RECAPITULATION. Context-Free Languages. Models of Computation, Languages and Automata. S asb. S bsb
 CD5080 AUBR RCAPIULAION Models of Coputtio, Lguges d Autot Leture 1 Cotext-ree Lguges, CL Pushdow Autot, PDA Pupig Le for CL eleted CL Proles Cotext-ree Lguges Mälrdle Uiversity 00 1 3 Cotext-ree Lguges
CD5080 AUBR RCAPIULAION Models of Coputtio, Lguges d Autot Leture 1 Cotext-ree Lguges, CL Pushdow Autot, PDA Pupig Le for CL eleted CL Proles Cotext-ree Lguges Mälrdle Uiversity 00 1 3 Cotext-ree Lguges
Formal Languages The Pumping Lemma for CFLs
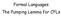 Forl Lguges The Pupig Le for CFLs Review: pupig le for regulr lguges Tke ifiite cotext-free lguge Geertes ifiite uer of differet strigs Exple: 3 I derivtio of log strig, vriles re repeted derivtio: 4 Derivtio
Forl Lguges The Pupig Le for CFLs Review: pupig le for regulr lguges Tke ifiite cotext-free lguge Geertes ifiite uer of differet strigs Exple: 3 I derivtio of log strig, vriles re repeted derivtio: 4 Derivtio
Content. Languages, Alphabets and Strings. Operations on Strings. a ab abba baba. aaabbbaaba b 5. Languages. A language is a set of strings
 CD5560 FABER Forml guges, Automt d Models of Computtio ecture Mälrdle Uiversity 006 Cotet guges, Alphets d Strigs Strigs & Strig Opertios guges & guge Opertios Regulr Expressios Fiite Automt, FA Determiistic
CD5560 FABER Forml guges, Automt d Models of Computtio ecture Mälrdle Uiversity 006 Cotet guges, Alphets d Strigs Strigs & Strig Opertios guges & guge Opertios Regulr Expressios Fiite Automt, FA Determiistic
Positive Properties of Context-Free languages
 CS 30 - Leture 8 Properties of Cotext Free Graars Fall 008 Review Laguages ad Graars Alphabets, strigs, laguages Regular Laguages Deteriisti Fiite ad Nodeteriisti Autoata Equivalee of NFA ad DFA Regular
CS 30 - Leture 8 Properties of Cotext Free Graars Fall 008 Review Laguages ad Graars Alphabets, strigs, laguages Regular Laguages Deteriisti Fiite ad Nodeteriisti Autoata Equivalee of NFA ad DFA Regular
If a is any non zero real or imaginary number and m is the positive integer, then a...
 Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Name: Period: Date: 2.1 Rules of Exponents
 SM NOTES Ne: Period: Dte:.1 Rules of Epoets The followig properties re true for ll rel ubers d b d ll itegers d, provided tht o deoitors re 0 d tht 0 0 is ot cosidered. 1 s epoet: 1 1 1 = e.g.) 7 = 7,
SM NOTES Ne: Period: Dte:.1 Rules of Epoets The followig properties re true for ll rel ubers d b d ll itegers d, provided tht o deoitors re 0 d tht 0 0 is ot cosidered. 1 s epoet: 1 1 1 = e.g.) 7 = 7,
ALGEBRA II CHAPTER 7 NOTES. Name
 ALGEBRA II CHAPTER 7 NOTES Ne Algebr II 7. th Roots d Rtiol Expoets Tody I evlutig th roots of rel ubers usig both rdicl d rtiol expoet ottio. I successful tody whe I c evlute th roots. It is iportt for
ALGEBRA II CHAPTER 7 NOTES Ne Algebr II 7. th Roots d Rtiol Expoets Tody I evlutig th roots of rel ubers usig both rdicl d rtiol expoet ottio. I successful tody whe I c evlute th roots. It is iportt for
Hypergeometric Functions and Lucas Numbers
 IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
IOSR Jourl of Mthetis (IOSR-JM) ISSN: 78-78. Volue Issue (Sep-Ot. ) PP - Hypergeoetri utios d us Nuers P. Rjhow At Kur Bor Deprtet of Mthetis Guhti Uiversity Guwhti-78Idi Astrt: The i purpose of this pper
EXPONENTS AND LOGARITHMS
 978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
978--07-6- Mthemtis Stdrd Level for IB Diplom Eerpt EXPONENTS AND LOGARITHMS WHAT YOU NEED TO KNOW The rules of epoets: m = m+ m = m ( m ) = m m m = = () = The reltioship etwee epoets d rithms: = g where
( ) 2 3 ( ) I. Order of operations II. Scientific Notation. Simplify. Write answers in scientific notation. III.
 Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Assessmet Ceter Elemetry Alger Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Northwest High School s Algebra 2
 Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
Northwest High School s Algebr Summer Review Pcket 0 DUE August 8, 0 Studet Nme This pcket hs bee desiged to help ou review vrious mthemticl topics tht will be ecessr for our success i Algebr. Istructios:
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
Thomas Whitham Sixth Form
 Thoms Whithm ith Form Pure Mthemtis Uit lger Trigoometr Geometr lulus lger equees The ifiite sequee of umers U U U... U... is si to e () overget if U L fiite limit s () iverget to if U s Emple The sequee...
Thoms Whithm ith Form Pure Mthemtis Uit lger Trigoometr Geometr lulus lger equees The ifiite sequee of umers U U U... U... is si to e () overget if U L fiite limit s () iverget to if U s Emple The sequee...
Course Material. CS Lecture 1 Deterministic Finite Automata. Grading and Policies. Workload. Website:http://www.cs.colostate.
 Course Mteril CS 301 - Lecture 1 Determiistic Fiite Automt Fll 2008 Wesite:http://www.cs.colostte.edu/~cs301 Syllus, Outlie, Grdig Policies Homework d Slides Istructor: D Mssey Office hours: 2-3pm Tues
Course Mteril CS 301 - Lecture 1 Determiistic Fiite Automt Fll 2008 Wesite:http://www.cs.colostte.edu/~cs301 Syllus, Outlie, Grdig Policies Homework d Slides Istructor: D Mssey Office hours: 2-3pm Tues
Introduction to Matrix Algebra
 Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Itrodutio to Mtri Alger George H Olso, Ph D Dotorl Progrm i Edutiol Ledership Applhi Stte Uiversit Septemer Wht is mtri? Dimesios d order of mtri A p q dimesioed mtri is p (rows) q (olums) rr of umers,
Accuplacer Elementary Algebra Study Guide
 Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
Testig Ceter Studet Suess Ceter Aupler Elemetry Alger Study Guide The followig smple questios re similr to the formt d otet of questios o the Aupler Elemetry Alger test. Reviewig these smples will give
* power rule: * fraction raised to negative exponent: * expanded power rule:
 Mth 15 Iteredite Alger Stud Guide for E 3 (Chpters 7, 8, d 9) You use 3 5 ote crd (oth sides) d scietific clcultor. You re epected to kow (or hve writte o our ote crd) foruls ou eed. Thik out rules d procedures
Mth 15 Iteredite Alger Stud Guide for E 3 (Chpters 7, 8, d 9) You use 3 5 ote crd (oth sides) d scietific clcultor. You re epected to kow (or hve writte o our ote crd) foruls ou eed. Thik out rules d procedures
Discrete Mathematics I Tutorial 12
 Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece
1 Tangent Line Problem
 October 9, 018 MAT18 Week Justi Ko 1 Tget Lie Problem Questio: Give the grph of fuctio f, wht is the slope of the curve t the poit, f? Our strteg is to pproimte the slope b limit of sect lies betwee poits,
October 9, 018 MAT18 Week Justi Ko 1 Tget Lie Problem Questio: Give the grph of fuctio f, wht is the slope of the curve t the poit, f? Our strteg is to pproimte the slope b limit of sect lies betwee poits,
M098 Carson Elementary and Intermediate Algebra 3e Section 10.2
 M09 Crso Eleetry d Iteredite Alger e Sectio 0. Ojectives. Evlute rtiol epoets.. Write rdicls s epressios rised to rtiol epoets.. Siplify epressios with rtiol uer epoets usig the rules of epoets.. Use rtiol
M09 Crso Eleetry d Iteredite Alger e Sectio 0. Ojectives. Evlute rtiol epoets.. Write rdicls s epressios rised to rtiol epoets.. Siplify epressios with rtiol uer epoets usig the rules of epoets.. Use rtiol
Taylor series expansion of nonlinear integrodifferential equations
 AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
Westchester Community College Elementary Algebra Study Guide for the ACCUPLACER
 Westchester Commuity College Elemetry Alger Study Guide for the ACCUPLACER Courtesy of Aims Commuity College The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry
Westchester Commuity College Elemetry Alger Study Guide for the ACCUPLACER Courtesy of Aims Commuity College The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry
Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral
![Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral Definition Integral. over[ ab, ] the sum of the form. 2. Definite Integral](/thumbs/83/87856510.jpg) Defiite Itegrl Defiitio Itegrl. Riem Sum Let f e futio efie over the lose itervl with = < < < = e ritrr prtitio i suitervl. We lle the Riem Sum of the futio f over[, ] the sum of the form ( ξ ) S = f Δ
Defiite Itegrl Defiitio Itegrl. Riem Sum Let f e futio efie over the lose itervl with = < < < = e ritrr prtitio i suitervl. We lle the Riem Sum of the futio f over[, ] the sum of the form ( ξ ) S = f Δ
Infinite Series Sequences: terms nth term Listing Terms of a Sequence 2 n recursively defined n+1 Pattern Recognition for Sequences Ex:
 Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
Ifiite Series Sequeces: A sequece i defied s fuctio whose domi is the set of positive itegers. Usully it s esier to deote sequece i subscript form rther th fuctio ottio.,, 3, re the terms of the sequece
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
 07 - SEQUENCES AND SERIES Page ( Aswers at he ed of all questios ) ( ) If = a, y = b, z = c, where a, b, c are i A.P. ad = 0 = 0 = 0 l a l
07 - SEQUENCES AND SERIES Page ( Aswers at he ed of all questios ) ( ) If = a, y = b, z = c, where a, b, c are i A.P. ad = 0 = 0 = 0 l a l
Connectivity in Graphs. CS311H: Discrete Mathematics. Graph Theory II. Example. Paths. Connectedness. Example
 Connetiit in Grphs CSH: Disrete Mthemtis Grph Theor II Instrtor: Işıl Dillig Tpil qestion: Is it possile to get from some noe to nother noe? Emple: Trin netork if there is pth from to, possile to tke trin
Connetiit in Grphs CSH: Disrete Mthemtis Grph Theor II Instrtor: Işıl Dillig Tpil qestion: Is it possile to get from some noe to nother noe? Emple: Trin netork if there is pth from to, possile to tke trin
Limits and an Introduction to Calculus
 Nme Chpter Limits d Itroductio to Clculus Sectio. Itroductio to Limits Objective: I this lesso ou lered how to estimte limits d use properties d opertios of limits. I. The Limit Cocept d Defiitio of Limit
Nme Chpter Limits d Itroductio to Clculus Sectio. Itroductio to Limits Objective: I this lesso ou lered how to estimte limits d use properties d opertios of limits. I. The Limit Cocept d Defiitio of Limit
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 10 SOLUTIONS. f m. and. f m = 0. and x i = a + i. a + i. a + n 2. n(n + 1) = a(b a) +
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 0 SOLUTIONS Throughout this problem set, B[, b] will deote the set of ll rel-vlued futios bouded o [, b], C[, b] the set of ll rel-vlued futios
82A Engineering Mathematics
 Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Assessment Center Elementary Algebra Study Guide for the ACCUPLACER (CPT)
 Assessmet Ceter Elemetr Alger Stud Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetr Alger test. Reviewig these smples will give
Assessmet Ceter Elemetr Alger Stud Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetr Alger test. Reviewig these smples will give
CH 45 INTRO TO FRACTIONS
 CH INTRO TO FRACTIONS Itrotio W e re ot to erk o st of frtios. If o ve erstoo ritheti frtios efore, o ll fi tht lgeri frtios follo the se set of rles. If frtios re still ster, let s ke this the seester
CH INTRO TO FRACTIONS Itrotio W e re ot to erk o st of frtios. If o ve erstoo ritheti frtios efore, o ll fi tht lgeri frtios follo the se set of rles. If frtios re still ster, let s ke this the seester
ON n-fold FILTERS IN BL-ALGEBRAS
 Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
Jourl of Alger Numer Theor: Adves d Applitios Volume 2 Numer 29 Pges 27-42 ON -FOLD FILTERS IN BL-ALGEBRAS M. SHIRVANI-GHADIKOLAI A. MOUSSAVI A. KORDI 2 d A. AHMADI 2 Deprtmet of Mthemtis Trit Modres Uiversit
Section The Precise Definition Of A Limit
 Section 2.4 - The Precise Definition Of A imit Introduction So fr we hve tken n intuitive pproch to the concept of limit. In this section we will stte the forml definition nd use this definition to prove
Section 2.4 - The Precise Definition Of A imit Introduction So fr we hve tken n intuitive pproch to the concept of limit. In this section we will stte the forml definition nd use this definition to prove
Chapter 5. Integration
 Chpter 5 Itegrtio Itrodutio The term "itegrtio" hs severl meigs It is usully met s the reverse proess to differetitio, ie fidig ti-derivtive to futio A ti-derivtive of futio f is futio F suh tht its derivtive
Chpter 5 Itegrtio Itrodutio The term "itegrtio" hs severl meigs It is usully met s the reverse proess to differetitio, ie fidig ti-derivtive to futio A ti-derivtive of futio f is futio F suh tht its derivtive
Math 201 (Introduction to Analysis) Fall
 Mth (Itrodutio to Alysis) Fll 4-5 Istrutor: Dr. Ki Y. Li Offie: Room 47 Offie Phoe: 58 74 e-mil ddress: myli@ust.h Offie Hours: Tu. :pm - 4:pm (or y ppoitmets) Prerequisite: A-level Mth or Oe Vrile Clulus
Mth (Itrodutio to Alysis) Fll 4-5 Istrutor: Dr. Ki Y. Li Offie: Room 47 Offie Phoe: 58 74 e-mil ddress: myli@ust.h Offie Hours: Tu. :pm - 4:pm (or y ppoitmets) Prerequisite: A-level Mth or Oe Vrile Clulus
12.2 The Definite Integrals (5.2)
 Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
Course: Aelerted Egieerig Clulus I Istrutor: Mihel Medvisky. The Defiite Itegrls 5. Def: Let fx e defied o itervl [,]. Divide [,] ito suitervls of equl width Δx, so x, x + Δx, x + jδx, x. Let x j j e ritrry
RULES FOR MANIPULATING SURDS b. This is the addition law of surds with the same radicals. (ii)
 SURDS Defiitio : Ay umer which c e expressed s quotiet m of two itegers ( 0 ), is clled rtiol umer. Ay rel umer which is ot rtiol is clled irrtiol. Irrtiol umers which re i the form of roots re clled surds.
SURDS Defiitio : Ay umer which c e expressed s quotiet m of two itegers ( 0 ), is clled rtiol umer. Ay rel umer which is ot rtiol is clled irrtiol. Irrtiol umers which re i the form of roots re clled surds.
Unit 1. Extending the Number System. 2 Jordan School District
 Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
Uit Etedig the Number System Jord School District Uit Cluster (N.RN. & N.RN.): Etedig Properties of Epoets Cluster : Etedig properties of epoets.. Defie rtiol epoets d eted the properties of iteger epoets
Math 153: Lecture Notes For Chapter 1
 Mth : Lecture Notes For Chpter Sectio.: Rel Nubers Additio d subtrctios : Se Sigs: Add Eples: = - - = - Diff. Sigs: Subtrct d put the sig of the uber with lrger bsolute vlue Eples: - = - = - Multiplictio
Mth : Lecture Notes For Chpter Sectio.: Rel Nubers Additio d subtrctios : Se Sigs: Add Eples: = - - = - Diff. Sigs: Subtrct d put the sig of the uber with lrger bsolute vlue Eples: - = - = - Multiplictio
Intermediate Arithmetic
 Git Lerig Guides Iteredite Arithetic Nuer Syste, Surds d Idices Author: Rghu M.D. NUMBER SYSTEM Nuer syste: Nuer systes re clssified s Nturl, Whole, Itegers, Rtiol d Irrtiol uers. The syste hs ee digrticlly
Git Lerig Guides Iteredite Arithetic Nuer Syste, Surds d Idices Author: Rghu M.D. NUMBER SYSTEM Nuer syste: Nuer systes re clssified s Nturl, Whole, Itegers, Rtiol d Irrtiol uers. The syste hs ee digrticlly
Modified Farey Trees and Pythagorean Triples
 Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Orthogonality, orthogonalization, least squares
 ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
ier Alger for Wireless Commuictios ecture: 3 Orthogolit, orthogoliztio, lest squres Ier products d Cosies he gle etee o-zero vectors d is cosθθ he l of Cosies: + cosθ If the gle etee to vectors is π/ (90º),
a f(x)dx is divergent.
 Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Mth 250 Exm 2 review. Thursdy Mrh 5. Brig TI 30 lultor but NO NOTES. Emphsis o setios 5.5, 6., 6.2, 6.3, 3.7, 6.6, 8., 8.2, 8.3, prt of 8.4; HW- 2; Q-. Kow for trig futios tht 0.707 2/2 d 0.866 3/2. From
Running an NFA & the subset algorithm (NFA->DFA) CS 350 Fall 2018 gilray.org/classes/fall2018/cs350/
 Running n NFA & the suset lgorithm (NFA->DFA) CS 350 Fll 2018 gilry.org/lsses/fll2018/s350/ 1 NFAs operte y simultneously exploring ll pths nd epting if ny pth termintes t n ept stte.!2 Try n exmple: L
Running n NFA & the suset lgorithm (NFA->DFA) CS 350 Fll 2018 gilry.org/lsses/fll2018/s350/ 1 NFAs operte y simultneously exploring ll pths nd epting if ny pth termintes t n ept stte.!2 Try n exmple: L
Graphing Review Part 3: Polynomials
 Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
Grphig Review Prt : Polomils Prbols Recll, tht the grph of f ( ) is prbol. It is eve fuctio, hece it is smmetric bout the bout the -is. This mes tht f ( ) f ( ). Its grph is show below. The poit ( 0,0)
FREE Download Study Package from website: &
 FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
FREE Dolod Study Pkge from esite:.tekolsses.om &.MthsBySuhg.om Get Solutio of These Pkges & Ler y Video Tutorils o.mthsbysuhg.om SHORT REVISION. Defiitio : Retgulr rry of m umers. Ulike determits it hs
PhysicsAndMathsTutor.com
 PhysicsAdMthsTutor.com PhysicsAdMthsTutor.com Jue 009 4. Give tht y rsih ( ), > 0, () fid d y d, givig your swer s simplified frctio. () Leve lk () Hece, or otherwise, fid 4 d, 4 [ ( )] givig your swer
PhysicsAdMthsTutor.com PhysicsAdMthsTutor.com Jue 009 4. Give tht y rsih ( ), > 0, () fid d y d, givig your swer s simplified frctio. () Leve lk () Hece, or otherwise, fid 4 d, 4 [ ( )] givig your swer
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Addendum. Addendum. Vector Review. Department of Computer Science and Engineering 1-1
 Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Addedum Addedum Vetor Review Deprtmet of Computer Siee d Egieerig - Coordite Systems Right hded oordite system Addedum y z Deprtmet of Computer Siee d Egieerig - -3 Deprtmet of Computer Siee d Egieerig
Mathematical Induction (selected questions)
 Mtheticl Iductio (selected questios). () Let P() e the propositio : For P(), L.H.S. R.H.S., P() is true. Assue P() is true for soe turl uer, tht is, () For P( ),, y () By the Priciple of Mtheticl Iductio,
Mtheticl Iductio (selected questios). () Let P() e the propositio : For P(), L.H.S. R.H.S., P() is true. Assue P() is true for soe turl uer, tht is, () For P( ),, y () By the Priciple of Mtheticl Iductio,
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
LAWS OF INDICES M.K. HOME TUITION. Mathematics Revision Guides Level: GCSE Higher Tier
 Mthetics Revisio Guides Lws of Idices Pge of 7 Author: Mrk Kudlowski M.K. HOME TUITION Mthetics Revisio Guides Level: GCSE Higher Tier LAWS OF INDICES Versio:. Dte: 0--0 Mthetics Revisio Guides Lws of
Mthetics Revisio Guides Lws of Idices Pge of 7 Author: Mrk Kudlowski M.K. HOME TUITION Mthetics Revisio Guides Level: GCSE Higher Tier LAWS OF INDICES Versio:. Dte: 0--0 Mthetics Revisio Guides Lws of
, we would have a series, designated as + j 1
 Clculus sectio 9. Ifiite Series otes by Ti Pilchowski A sequece { } cosists of ordered set of ubers. If we were to begi ddig the ubers of sequece together s we would hve series desigted s. Ech iteredite
Clculus sectio 9. Ifiite Series otes by Ti Pilchowski A sequece { } cosists of ordered set of ubers. If we were to begi ddig the ubers of sequece together s we would hve series desigted s. Ech iteredite
Société de Calcul Mathématique SA Mathematical Modelling Company, Corp.
 oiété de Calul Mathéatique A Matheatial Modellig Copay, Corp. Deisio-aig tools, sie 995 iple Rado Wals Part V Khihi's Law of the Iterated Logarith: Quatitative versios by Berard Beauzay August 8 I this
oiété de Calul Mathéatique A Matheatial Modellig Copay, Corp. Deisio-aig tools, sie 995 iple Rado Wals Part V Khihi's Law of the Iterated Logarith: Quatitative versios by Berard Beauzay August 8 I this
Section 2.2. Matrix Multiplication
 Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
Mtri Alger Mtri Multiplitio Setio.. Mtri Multiplitio Mtri multiplitio is little more omplite th mtri itio or slr multiplitio. If A is the prout A of A is the ompute s follow: m mtri, the is k mtri, 9 m
National Quali cations AHEXEMPLAR PAPER ONLY
 Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Worksheet #2 Math 285 Name: 1. Solve the following systems of linear equations. The prove that the solutions forms a subspace of
 Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
Approximate Integration
 Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
Study Sheet (7.7) Approimte Itegrtio I this sectio, we will ler: How to fid pproimte vlues of defiite itegrls. There re two situtios i which it is impossile to fid the ect vlue of defiite itegrl. Situtio:
Student Success Center Elementary Algebra Study Guide for the ACCUPLACER (CPT)
 Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
Studet Success Ceter Elemetry Algebr Study Guide for the ACCUPLACER (CPT) The followig smple questios re similr to the formt d cotet of questios o the Accuplcer Elemetry Algebr test. Reviewig these smples
19 Fourier Series and Practical Harmonic Analysis
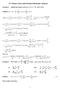 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Viscosity Solutions with Asymptotic Behavior of Hessian Quotient Equations. Limei Dai +
 Itertio oferee o ompter d Atomtio Egieerig IAE IPIT vo 44 IAIT Pre igpore OI: 776/IPIT44 ioit otio ith Amptoti ehvior of Hei Qotiet Eqtio Limei i hoo of Mthemti d Iformtio iee Weifg Uiverit Weifg 66 The
Itertio oferee o ompter d Atomtio Egieerig IAE IPIT vo 44 IAIT Pre igpore OI: 776/IPIT44 ioit otio ith Amptoti ehvior of Hei Qotiet Eqtio Limei i hoo of Mthemti d Iformtio iee Weifg Uiverit Weifg 66 The
a) Read over steps (1)- (4) below and sketch the path of the cycle on a P V plot on the graph below. Label all appropriate points.
 Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
INMO-2018 problems and solutions
 Pioeer Educatio The Best Way To Success INMO-018 proles ad solutios NTSE Olypiad AIPMT JEE - Mais & Advaced 1. Let ABC e a o-equilateral triagle with iteger sides. Let D ad E e respectively the id-poits
Pioeer Educatio The Best Way To Success INMO-018 proles ad solutios NTSE Olypiad AIPMT JEE - Mais & Advaced 1. Let ABC e a o-equilateral triagle with iteger sides. Let D ad E e respectively the id-poits
Here are some examples of algebras: F α = A(G). Also, if A, B A(G) then A, B F α. F α = A(G). In other words, A(G)
 MATH 529 Probability Axioms Here we shall use the geeral axioms of a probability measure to derive several importat results ivolvig probabilities of uios ad itersectios. Some more advaced results will
MATH 529 Probability Axioms Here we shall use the geeral axioms of a probability measure to derive several importat results ivolvig probabilities of uios ad itersectios. Some more advaced results will
Kp for a Wall with Friction with Exact Slip Surface
 K for W ith Frictio ith Ect Si Surfce Frid A. Chouer, P.E., S.E. 7 Frid Chouer rights reserved Revised 7--6 Itroductio: We ko from efore ( htt://.fcsstems.com/si.df ) the est curve for K ith o frictio
K for W ith Frictio ith Ect Si Surfce Frid A. Chouer, P.E., S.E. 7 Frid Chouer rights reserved Revised 7--6 Itroductio: We ko from efore ( htt://.fcsstems.com/si.df ) the est curve for K ith o frictio
Algebra 2 Readiness Summer Packet El Segundo High School
 Algebr Rediess Suer Pcket El Segudo High School This pcket is desiged for those who hve copleted Geoetry d will be erolled i Algebr (CP or H) i the upcoig fll seester. Suer Pcket Algebr II Welcoe to Algebr
Algebr Rediess Suer Pcket El Segudo High School This pcket is desiged for those who hve copleted Geoetry d will be erolled i Algebr (CP or H) i the upcoig fll seester. Suer Pcket Algebr II Welcoe to Algebr
( ) dx ; f ( x ) is height and Δx is
 Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
Mth : 6.3 Defiite Itegrls from Riem Sums We just sw tht the exct re ouded y cotiuous fuctio f d the x xis o the itervl x, ws give s A = lim A exct RAM, where is the umer of rectgles i the Rectgulr Approximtio
SCHOOL OF MATHEMATICS AND STATISTICS. Mathematics II (Materials)
 Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
Math 152 Intermediate Algebra
 Mth 15 Iteredite Alger Stud Guide for the Fil E You use 46 otecrd (oth sides) d scietific clcultor. You re epected to kow (or hve writte o our ote crd) foruls ou eed. Thik out rules d procedures ou eeded
Mth 15 Iteredite Alger Stud Guide for the Fil E You use 46 otecrd (oth sides) d scietific clcultor. You re epected to kow (or hve writte o our ote crd) foruls ou eed. Thik out rules d procedures ou eeded
Geometric Sequences. Geometric Sequence. Geometric sequences have a common ratio.
 s A geometric sequece is sequece such tht ech successive term is obtied from the previous term by multiplyig by fixed umber clled commo rtio. Exmples, 6, 8,, 6,..., 0, 0, 0, 80,... Geometric sequeces hve
s A geometric sequece is sequece such tht ech successive term is obtied from the previous term by multiplyig by fixed umber clled commo rtio. Exmples, 6, 8,, 6,..., 0, 0, 0, 80,... Geometric sequeces hve
Dynamics of Structures
 UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
UNION Dymis of Strutures Prt Zbigiew Wójii Je Grosel Projet o-fied by Europe Uio withi Europe Soil Fud UNION Mtries Defiitio of mtri mtri is set of umbers or lgebri epressios rrged i retgulr form with
degree non-homogeneous Diophantine equation in six unknowns represented by x y 2z
 Scholrs Jourl of Egieerig d Techology (SJET Sch. J. Eg. Tech., ; (A:97- Scholrs Acdeic d Scietific Pulisher (A Itertiol Pulisher for Acdeic d Scietific Resources www.sspulisher.co ISSN -X (Olie ISSN 7-9
Scholrs Jourl of Egieerig d Techology (SJET Sch. J. Eg. Tech., ; (A:97- Scholrs Acdeic d Scietific Pulisher (A Itertiol Pulisher for Acdeic d Scietific Resources www.sspulisher.co ISSN -X (Olie ISSN 7-9
NOP 10 * * * * + NOP NOP + < TIME 1 TIME 2 TIME 3 TIME 4 NOP
 Outlie SCHEDULING The schedulig problem. cgiovi De Micheli Schedulig without costrits. Stford Uiversity Schedulig uder timig costrits. { Reltive schedulig. Schedulig uder resource costrits. { The ILP model.
Outlie SCHEDULING The schedulig problem. cgiovi De Micheli Schedulig without costrits. Stford Uiversity Schedulig uder timig costrits. { Reltive schedulig. Schedulig uder resource costrits. { The ILP model.
AP Calculus AB AP Review
 AP Clulus AB Chpters. Re limit vlues from grphsleft-h Limits Right H Limits Uerst tht f() vlues eist ut tht the limit t oes ot hve to.. Be le to ietify lel isotiuities from grphs. Do t forget out the 3-step
AP Clulus AB Chpters. Re limit vlues from grphsleft-h Limits Right H Limits Uerst tht f() vlues eist ut tht the limit t oes ot hve to.. Be le to ietify lel isotiuities from grphs. Do t forget out the 3-step
The Definite Riemann Integral
 These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
These otes closely follow the presettio of the mteril give i Jmes Stewrt s textook Clculus, Cocepts d Cotexts (d editio). These otes re iteded primrily for i-clss presettio d should ot e regrded s sustitute
MTH 146 Class 16 Notes
 MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si
Chapter 2. LOGARITHMS
 Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
Chpter. LOGARITHMS Dte: - 009 A. INTRODUCTION At the lst hpter, you hve studied bout Idies d Surds. Now you re omig to Logrithms. Logrithm is ivers of idies form. So Logrithms, Idies, d Surds hve strog
10.5 Power Series. In this section, we are going to start talking about power series. A power series is a series of the form
 0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully
Summer Math Requirement Algebra II Review For students entering Pre- Calculus Theory or Pre- Calculus Honors
 Suer Mth Requireet Algebr II Review For studets eterig Pre- Clculus Theory or Pre- Clculus Hoors The purpose of this pcket is to esure tht studets re prepred for the quick pce of Pre- Clculus. The Topics
Suer Mth Requireet Algebr II Review For studets eterig Pre- Clculus Theory or Pre- Clculus Hoors The purpose of this pcket is to esure tht studets re prepred for the quick pce of Pre- Clculus. The Topics
Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best
 Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =
Algebra 2 Important Things to Know Chapters bx c can be factored into... y x 5x. 2 8x. x = a then the solutions to the equation are given by
 Alger Iportt Thigs to Kow Chpters 8. Chpter - Qudrtic fuctios: The stdrd for of qudrtic fuctio is f ( ) c, where 0. c This c lso e writte s (if did equl zero, we would e left with The grph of qudrtic fuctio
Alger Iportt Thigs to Kow Chpters 8. Chpter - Qudrtic fuctios: The stdrd for of qudrtic fuctio is f ( ) c, where 0. c This c lso e writte s (if did equl zero, we would e left with The grph of qudrtic fuctio
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 ypothesis testig Covers (most of) the followig material from hapter 8: Setio 8. Setios 8.. ad 8..3 Setio 8.3. Setio 8.3. (util defiitio 8.3.6) Ørulf Borga Departmet of Mathematis Uiversity
STK4 ad STK9 Autum 6 ypothesis testig Covers (most of) the followig material from hapter 8: Setio 8. Setios 8.. ad 8..3 Setio 8.3. Setio 8.3. (util defiitio 8.3.6) Ørulf Borga Departmet of Mathematis Uiversity
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
Lincoln Land Community College Placement and Testing Office
 Licol Ld Commuity College Plcemet d Testig Office Elemetry Algebr Study Guide for the ACCUPLACER (CPT) A totl of questios re dmiistered i this test. The first type ivolves opertios with itegers d rtiol
Licol Ld Commuity College Plcemet d Testig Office Elemetry Algebr Study Guide for the ACCUPLACER (CPT) A totl of questios re dmiistered i this test. The first type ivolves opertios with itegers d rtiol
Jacobi symbols. p 1. Note: The Jacobi symbol does not necessarily distinguish between quadratic residues and nonresidues. That is, we could have ( a
 Jacobi sybols efiitio Let be a odd positive iteger If 1, the Jacobi sybol : Z C is the costat fuctio 1 1 If > 1, it has a decopositio ( as ) a product of (ot ecessarily distict) pries p 1 p r The Jacobi
Jacobi sybols efiitio Let be a odd positive iteger If 1, the Jacobi sybol : Z C is the costat fuctio 1 1 If > 1, it has a decopositio ( as ) a product of (ot ecessarily distict) pries p 1 p r The Jacobi
Advanced Calculus Test File Spring Test 1
 Advced Clculus Test File Sprig 009 Test Defiitios - Defie the followig terms.) Crtesi product of A d B.) The set, A, is coutble.) The set, A, is ucoutble 4.) The set, A, is ifiite 5.) The sets A d B re
Advced Clculus Test File Sprig 009 Test Defiitios - Defie the followig terms.) Crtesi product of A d B.) The set, A, is coutble.) The set, A, is ucoutble 4.) The set, A, is ifiite 5.) The sets A d B re
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Deriving Euler s identity and Kummer s series of Gauss s hypergeometric functions using the symmetries of Wigner d-matrix
 Derivig Euler s ietity Kuer s series of Guss s hypergeoetri futios usig the syetries of Wiger -trix Mehi Hge Hss To ite this versio: Mehi Hge Hss. Derivig Euler s ietity Kuer s series of Guss s hypergeoetri
Derivig Euler s ietity Kuer s series of Guss s hypergeoetri futios usig the syetries of Wiger -trix Mehi Hge Hss To ite this versio: Mehi Hge Hss. Derivig Euler s ietity Kuer s series of Guss s hypergeoetri
Solutions to RSPL/1. log 3. When x = 1, t = 0 and when x = 3, t = log 3 = sin(log 3) 4. Given planes are 2x + y + 2z 8 = 0, i.e.
 olutios to RPL/. < F < F< Applig C C + C, we get F < 5 F < F< F, $. f() *, < f( h) f( ) h Lf () lim lim lim h h " h h " h h " f( + h) f( ) h Rf () lim lim lim h h " h h " h h " Lf () Rf (). Hee, differetile
olutios to RPL/. < F < F< Applig C C + C, we get F < 5 F < F< F, $. f() *, < f( h) f( ) h Lf () lim lim lim h h " h h " h h " f( + h) f( ) h Rf () lim lim lim h h " h h " h h " Lf () Rf (). Hee, differetile
Some Properties of Brzozowski Derivatives of Regular Expressions
 Itertiol Jourl of Computer Treds d Techology (IJCTT) volume 13 umber 1 Jul 014 Some Properties of Brzozoski erivtives of Regulr Expressios NMuruges #1, OVShmug Sudrm * #1 Assistt Professor, ept of Mthemtics,
Itertiol Jourl of Computer Treds d Techology (IJCTT) volume 13 umber 1 Jul 014 Some Properties of Brzozoski erivtives of Regulr Expressios NMuruges #1, OVShmug Sudrm * #1 Assistt Professor, ept of Mthemtics,
Let. Then. k n. And. Φ npq. npq. ε 2. Φ npq npq. npq. = ε. k will be very close to p. If n is large enough, the ratio n
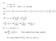 Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
Let The m ( ) ( + ) where > very smll { } { ( ) ( + ) } Ad + + { } Φ Φ Φ Φ Φ Let, the Φ( ) lim This is lled thelw of lrge umbers If is lrge eough, the rtio will be very lose to. Exmle -Tossig oi times.
,... are the terms of the sequence. If the domain consists of the first n positive integers only, the sequence is a finite sequence.
 Chpter 9 & 0 FITZGERALD MAT 50/5 SECTION 9. Sequece Defiitio A ifiite sequece is fuctio whose domi is the set of positive itegers. The fuctio vlues,,, 4,...,,... re the terms of the sequece. If the domi
Chpter 9 & 0 FITZGERALD MAT 50/5 SECTION 9. Sequece Defiitio A ifiite sequece is fuctio whose domi is the set of positive itegers. The fuctio vlues,,, 4,...,,... re the terms of the sequece. If the domi
Introduction of Fourier Series to First Year Undergraduate Engineering Students
 Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
Itertiol Jourl of Adved Reserh i Computer Egieerig & Tehology (IJARCET) Volume 3 Issue 4, April 4 Itrodutio of Fourier Series to First Yer Udergrdute Egieerig Studets Pwr Tejkumr Dtttry, Hiremth Suresh
4. When is the particle speeding up? Why? 5. When is the particle slowing down? Why?
 AB CALCULUS: 5.3 Positio vs Distce Velocity vs. Speed Accelertio All the questios which follow refer to the grph t the right.. Whe is the prticle movig t costt speed?. Whe is the prticle movig to the right?
AB CALCULUS: 5.3 Positio vs Distce Velocity vs. Speed Accelertio All the questios which follow refer to the grph t the right.. Whe is the prticle movig t costt speed?. Whe is the prticle movig to the right?
Prefix-Free Regular-Expression Matching
 Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
THE INTEGRAL TEST AND ESTIMATES OF SUMS
 THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
SM2H. Unit 2 Polynomials, Exponents, Radicals & Complex Numbers Notes. 3.1 Number Theory
 SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
SMH Uit Polyomils, Epoets, Rdicls & Comple Numbers Notes.1 Number Theory .1 Addig, Subtrctig, d Multiplyig Polyomils Notes Moomil: A epressio tht is umber, vrible, or umbers d vribles multiplied together.
18.S34 (FALL, 2007) GREATEST INTEGER PROBLEMS. n + n + 1 = 4n + 2.
 18.S34 (FALL, 007) GREATEST INTEGER PROBLEMS Note: We use the otatio x for the greatest iteger x, eve if the origial source used the older otatio [x]. 1. (48P) If is a positive iteger, prove that + + 1
18.S34 (FALL, 007) GREATEST INTEGER PROBLEMS Note: We use the otatio x for the greatest iteger x, eve if the origial source used the older otatio [x]. 1. (48P) If is a positive iteger, prove that + + 1
Fourier Series and Applications
 9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
