1 are perpendicular to each other then, find. Q06. If the lines x 1 z 3 and x 2 y 5 z
|
|
|
- Anissa Turner
- 6 years ago
- Views:
Transcription
1 Useful for CBSE Board Examination of Math (XII) for 6 For more stuffs on Maths, please visit : Time Allowed : 8 Minutes Max. Marks : SECTION A 3 Q. Evaluate : sin cos 5. Q. State the reason for the following Binar Operation *, defined on the set Z of integers, to be not commutative : a*b = ab 3. Q3. Give an example of a skew smmetric matrix of order 3. Q4. Using derivatives, find the approximate percentage increase in the area of a circle if its radius is increased b %. tan x Q5. Find the derivative of f (e ) w.r.t. x at x. It is given that f () 5. Q6. If the lines x 4 z 3 and x 5 z are perpendicular to each other then, find 3p 4 4p 7 the value of p. SECTION B n, if n is odd Q7. Let f : W W be defined as f (n). Then show that f is invertible. Also find n, if n is even the inverse of f. OR Show that the relation R in the set N N defined b (a, b)r(c,d) iff a d b c a, b,c,d N, is an equivalence relation. x 3 Q8. Prove that tan, where x. 4 Q9. Let A 3 4. Then verif A(adjA) (adja)a A I, where I is the identit matrix of order. p p q Q. Using properties of determinants, prove that OR 3 4 3p 4p 3q p 7p 4q Without expanding the determinant at an stage, prove that Q. Let A and B 4. Then compute AB. Hence, solve the following sstem of equations : x 4, 3x. Q. If the following function is differentiable at x =, then find the value of a and b : x, if x f (x). ax b, if x x x Q3. Let (log x) x. Then find d. OR If x a sin pt and, b cos pt. Then find Q4. Evaluate : d at t.. OR Evaluate : sin x sin x sin d sin cos 3. 5//8
2 x( sin x) Q5. Evaluate the definite integral :. d x Q6. Solve :, x. Q7. Solve : ( ) (tan x)d. x x Q8. Find the shortest distance between the following pair of skew lines : x z and x 3 z Q9. A problem in Mathematics is given to 4 students A, B, C and D. Their chances of solving the problems respectivel are /3, /4, /5 and /3. What is the probabilit that (i) the problem will be solved? (ii) at most one of them will solve the problem? SECTION C Q. Find the intervals in which the following function is strictl increasing or strictl decreasing. Also 3 find the points of local maximum and local minimum, if an : f (x) (x ) (x ). Q. If a, b and c are unit vectors such that a.b a.c and the angle between b and c is, then 6 prove that (i) a (b c) (ii) a b b c c a. Q. Using integration, find the area bounded b the tangent to the curve 4 x at the point (, ) and the lines whose equations are x and x 3 3. Q3. Find the distance of the point 3i ˆ j ˆ kˆ from the plane 3x z measured parallel to the x z. Also find the foot of perpendicular from the given point upon the given plane. 3 OR Find the equation of the plane passing through the line of intersection of the planes r.(i ˆ 3j ˆ k) ˆ and r.(i ˆ ˆj k) ˆ and passing through the point (3,, ). Also find the angle between the two given planes. Q4. A Bag I contains 5 red and 4 white balls and a Bag II contains 3 red and 3 white balls. Two balls are transferred from the Bag I to the Bag II and then one ball is drawn from the Bag II. If the ball drawn from the Bag II is red, then find the probabilit that one red ball and one white ball are transferred from Bag I to the Bag II. OR Find the mean, the variance and the standard deviation of the number of doublets in three throws of a pair of dice. Q5. A farmer wants to construct a circular garden and a square garden in his field. He wants to keep the sum of their perimeters 6m. Prove that the sum of their areas is the least, when the side of the square garden is double the radius of the circular garden. Do ou think that a good planning can save energ, time and mone? Q6. A manufacturing compan makes two models A and B of a product. Each piece of model A requires 9 hours of labour for fabricating and hour for finishing. Each piece of model B requires hours of labour for fabricating and 3 hours for finishing. The maximum number of labour hours, available for fabricating and for finishing are 8 and 3 respectivel. The compan makes a profit of `8 and ` on each piece of model A and B respectivel. How man pieces of each model should be manufactured to get maximum profit? Also, find the maximum profit. A Compilation B : O. P. Gupta [Call or ] 5//8
3 Marking Scheme Of Sample Question Paper SECTION A 4 Q Q. Note that * 8 but * * where, Z. So * isn t commutative. Q Q4. 4%. Q5. 5. Q SECTION B Q7. Here fof : W W fof (n) f f (n) f (n ) n n and if n is is such that if n is odd, even, fof (n) f f (n) f (n ) n n. + Hence fof = I. This implies that f is invertible and f = f. OR Let (a, b) N N. Then as a b b a (a, b)r(a, b). So, R is reflexive. Let (a, b), (c,d) N N be s.t. (a, b)r(c,d). Then as a d b c c b d a (c, d)r(a, b). So R is smmetric. Let (a, b), (c,d), (e,f ) N N be s.t. (a,b)r(c,d) and (c,d)r(e,f ). Then as a d b c and c f d e a d c f b c d e a f b e (a, b)r(e,f ). So R is transitive. Since R is reflexive, smmetric as well as transitive so, R is an equivalence relation. x x cos sin Q8. LHS : tan tan x x cos sin x x cos sin x x 3 x 3 cos sin tan x 4 tan x x cos sin x x cos sin x II quad. x tan x x tan tan tan RHS x. tan Q9. We ve A 3 4 adj.a 3 4 A(adjA) (i) 4 (adja)a (ii) Also, A (iii) 3 4 B (i), (ii) & (iii), A(adjA) (adja)a A I is verified. T 5//8 3
4 Q. LHS : p p q 3 4 3p 4p 3q 4 7 4p 7p 4q p p q p 3 3p p p q B R R 3R, R3 R3 4R B R3 R3 3R p Expanding along C, ( ) RHS. OR LHS: Let Interchanging Rows & Columns, 3 ( )( )( ) RHS Q. Here A and B 4 AB I 4 A B I A B...(i) The given sstem of equations x 4, 3x can be written as x 4 PX C where, P, X and C 3 P PX P C I X P C T T X P C [Note that P A P (A ) x 7 Therefore, X 6 4 X B equalit of matrices, we get : x 7,. Q. As the function f is differentiable at x =, so it is continuous at x = as well. lim f (x) lim f (x) f () lim x lim ax b () 4 a b (i) + x x x x Also, f is differentiable at x = Lf () Rf () f (x) f () f (x) f () i.e., lim lim x x x x x 4 (ax b) 4 (ax b) 4 lim lim lim (x ) lim x x x x x x x b (i), b 4 a (ax 4 a) 4 (x )a 4 lim 4 lim lim a x x x x x a 4 + Replacing value of a in (i), we get : b 4. x x Q3. We have (log x) x. Let Now d du dv...(i) x log u log(log x) log u x log(log x) x xcosx u v where u (log x), v x x u (log x) du du x x log(log x) (log x) log(log x) u log x x log x x x And, v x log v log(x) log v x log x 5//8 4
5 dv dv x log x x sin x x x log x x sin x v x d x x B (i), (log x) log(log x) x ( log x) x sin x log x log x d OR We have x a sin pt and, b cos pt ap cos pt and, bp sin pt dt dt d d dt d bsin pt b tan pt + dt a cos pt a d bp dt bp b 3 sec pt sec pt sec pt + a a ap cos pt a Therefore, d b 3 b sec a a at t. + sin x Q4. Let I I sin x sin x I sin x( ) ( )( )( ) dt Put t sin x dt I ( t)( t)( t) A B C Consider ( t)( t)( t) t t t A( t)( t) B( t)( t) C( t)( t) 4 On equating the coefficients of like terms, we get : A, B, C dt dt 4 dt So, I 6 ( t) ( t) 3 ( t) I log t log t log t C 6 3 I log log log C sin sin OR Let I d I d sin cos 3 cos cos 3 Q5. sin I d Put cos t sin dt 4 cos cos I dt 4 t t t I sin C 5 x sin x Let I dt I + ( 5) (t ) cos I sin C. 5 x x sin x I x x Consider f (x) f ( x) f (x) x sin x ( x)sin( x) x sin x and, g(x) g( x) g(x) cos ( x) Clearl, f (x) is an odd function whereas g (x) is an even function. x sin x x sin x So, I I 4...(i) 5//8 5
6 ( x) sin( x) cos ( x) I 4 ( x)sin x I 4 (ii) x sin x ( x)sin x On adding (i) & (ii), we get : I 4 4 sin x sin x I 4 I sin x sin( x) sin x Consier f (x) f ( x) f (x) cos ( x) a a f x, if f a x f x B using f x, if f a x f x / sin x We have I Put t sin x dt dt When x t & when x t I t I 4 dt t I 4 tan t I 4 tan tan 4 4. Q6. We have d x, x...(i) x x x Consider f (x, ). Put x x, x x x x f ( x, ) f (x, ). So, f is homogeneous. x x x x d dv Let vx v x in (i) dv vx x v x v x x x dv v x x log log Cx x Q7. Given that ( ) (tan x)d The differential equation is in the form So, dv x v log v v log x log C x C x is the required solution. d tan tan x d x tan d tan P()x Q() where P() and Q() d Integration factor, (I.F.) e e + tan solution is given as : x e e d C tan t Put tan t d dt. xe e tdt C tan tan 5//8 6
7 tan t d t xe t e dt (t) e dt C dt tan tan xe e (tan ) C or, tan t t xe te e C x tan Ce Q8. The lines in vector form can be written as : ˆ ˆ ˆ ˆ ˆ ˆ r i j k (i 3j 4k), r iˆ 3j ˆ ( ˆi ˆj 3k) ˆ ˆ ˆ ˆ ˆ ˆ ˆ a i j k, b i 3j 4k, a iˆ 3j, ˆ b ˆi ˆj 3kˆ ˆi ˆj kˆ a a 3i ˆ ˆj k, ˆ b b 3 4 7i ˆ ˆj kˆ tan is the required solution. 3 (a a ).b b Shortest distance between skew lines b b ( 3iˆ ˆj k).( ˆ 7i ˆ ˆj k) ˆ 4 units Q9. Let A, B, C and D denote the events that A, B, C and D solves the problem in Mathematics respectivel. 3 4 P(A), P(B), P(C) and P(D) P(A), P(B), P(C) and P(D) (i) P(the problem will be solved) P(A B C D) P(A B C D) P(A) P(B) P(C) P(D) (ii) P(at most one of them will solve the problem) P(A B C D) P(A B C D) P(A B C D) P(A B C D) P(A B C D) SECTION C 3 Q. Given f (x) (x ) (x ) f (x) (x ) (x )(5x 4) For critical points, f (x) (x ) (x )(5x 4) x,, 5 Interval Sign of f (x) f (x) is (, ) Positive Strictl increasing 4 Negative Strictl decreasing, 5 4 Positive Strictl increasing, 5 (, ) Positive Strictl increasing 4 Hence f (x) is strictl increasing in (, ) and, 5 & strictl decreasing in 4, 5. Also in the left neighbourhood of, f (x) is positive and in right neighbourhood of, f (x) is negative and f ( ). Therefore b the first derivative test, x = is a point of local maximum. Also f (x) changes its sign from negative to positive as x passes through 4/5 so, x = 4/5 is a point of local minimum. + Q. Given that a.b a.c which implies, a is perpendicular to both b and c (since these three vectors are unit vectors). That is, a b c a (b c) + 4 5//8 7
8 a b c b c sin 6 Therefore, a (b c). Hence (i) is proved. Also, a b b c c a (a b) (b c).(c a) a b a c bb bc.(c a) a b a c b c.(c a) a b.c a c.c b c.c a b.a a c.a b c.a [a b c] [b c a] [a b c] a.(b c) [a b c] [b c a] [a b c] + a. a a. Hence (ii) is proved. d d x d Q. The given curve is 4 x 4 x mt at (,) Equation of tangent at (, ) is : (x ) x...(i) Also given lines are x...(ii) and x (iii). Required area 3 6 x x 3 x (x ) x x x 6x x x Mark for 9 9 Labeled-graph sketching 3 sq.unit. 4 4 Q3. The equation of line through 3i ˆ j ˆ kˆ i.e., P(3,, ) and parallel to the given line having d.r. s as (, 3, ), is x 3 z. 3 The coordinates of an random point on this line is : A( 3, 3, ) If A lies on the plane 3x z, then 3( 3) ( 3 ) ( ) 4 Therefore, A( 5,, 3). + Hence, the required distance is, AP (3 5) ( ) ( 3) 4 4 units. Now, the equation of line passing through P(3,, ) and perpendicular to the given equation of plane 3x z is, x 3 z. 3 The coordinates of an random point on this line is : B(3 3,, ) If B lies on the plane 3x z, then 3(3 3) ( ) ( ) Therefore, the required foot of perpendicular is,,. + OR An plane passing through the line of intersection of given planes is r.(i ˆ 3j ˆ k) ˆ r.(i ˆ ˆj k) ˆ i.e., r. (i ˆ 3j ˆ k) ˆ (i ˆ ˆj k) ˆ...(i) If plane (i) contains (3,, ) then, (3iˆ j ˆ k). ˆ (i ˆ 3j ˆ k) ˆ (i ˆ ˆj k) ˆ 6 6 (3 ) 3 5//8 8
9 Replacing value of in (i), we get r. (i ˆ 3j ˆ k) ˆ (i ˆ ˆj k) ˆ 3 3 i.e., r.(4i ˆ 7j ˆ k) ˆ 3. Let be the angle between normals of the given planes (as angle between the planes and their normals remains the same). (i ˆ 3j ˆ k).(i ˆ ˆ ˆj k) ˆ 7 7 So, cos cos Q4. Let E : white balls are transferred from Bag I to the Bag II, E : red balls are transferred from Bag I to the Bag II, E 3 : red and white balls are transferred from Bag I to the Bag II, E : the ball drawn from Bag II is red. / C C C C 4 P(E ), P(E 9 ),P(E 9 3) 9 C 7 C 7 C and, P(E E ), P(E E ), P(E E 3) P(E 3)P(E E 3) B Baes Theorem, P(E 3 E) P(E )P(E E ) P(E )P(E E ) P(E 3)P(E E 3) OR Let X : number of doublets in three throws of a pair of dice. X,,, Here n = 3. Let p be the probabilit of success p, q p r n r n r Therefore b using, P(X r) Crp q 3 5 we have : P(X r) Cr 6 X P( X ) X P(X) X P(X) Mean X P(X) X P(X) 5// X P(X) 3 5 3, Var (X) X P(X) X P(X) 5 5 Also, standard deviation Var X. 6 Q5. Let the radius of circular garden be r (in metres) and the side of the square garden be x (in metres). 6 r Then, 6 r 4x x (i) 4 The sum of the areas, S r x ds 4 r 6 r 4r 3 r dr 6 6 r S r 4 +
10 ds For local points of maxima and/or minima, 4r 3 r dr r 3 4r 3 r metres. 4 Also d S d S 4 4 S is least. dr dr 3 at r 4 B (i), 6 r 4x 6 6 8r 4x x r. Therefore, when the side of the square garden is double the radius of the circular garden, the sum of their areas is least. To achieve an goal, there is ever possibilit that energ, time and mone are required to be invested. One must plan in such a manner that least energ, time and mone are spent. A good planning and execution, therefore, is essentiall needed. Q6. Let the number of pieces of model A and model B respectivel be x and. To maximize : Z ` (8x ) Subject to the constraints : 9x 8, x 3 3, x, That is, 3x 4 6, x 3 3, x, Mark for Graph work on the actual graph paper Corner points Value of Z (in `) O (, ) C (, ) 6 B (, 6) 68 A (, ) Mark for table The number of pieces of model A and model B are and 6 respectivel. Also maximum profit is of `68. # This paper has been issued b CBSE, New Delhi for 6 Board Exams of XII. We ve re-tped the same and done the necessar corrections (as the original paper had some errors). On other hand, if ou still find an error which could have gone un-noticed, please do inform us via or us : theopgupta@gmail.com 5//8
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII:
 SAMPLE QUESTION PAPER MATHEMATICS CLASS XII: 05-6 Question numbers to 6 carry mark each. SAMPLE PAPER II Section A Q. Evaluate: - 3 sin(cos (- )). 5 Q. State the reason for the following Binary Operation
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII: 05-6 Question numbers to 6 carry mark each. SAMPLE PAPER II Section A Q. Evaluate: - 3 sin(cos (- )). 5 Q. State the reason for the following Binary Operation
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII :
 SAMPLE QUESTION PAPER MATHEMATICS CLASS XII : 05-6 TYPOLOGY VSA ( M) L A I (4M) L A II (6M) MARKS %WEIGHTAGE Remembering 3, 6, 8, 9, 5 0 0% Understanding, 9, 0 4, 6 % Applications 4 3, 5, 6, 7, 0 9 9%
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII : 05-6 TYPOLOGY VSA ( M) L A I (4M) L A II (6M) MARKS %WEIGHTAGE Remembering 3, 6, 8, 9, 5 0 0% Understanding, 9, 0 4, 6 % Applications 4 3, 5, 6, 7, 0 9 9%
Series SC/SP Code No. SP-16. Mathematics. Time Allowed: 3 hours Maximum : 100
 Sample Paper (CBSE) Series SC/SP Code No. SP-16 Mathematics Time Allowed: 3 hours Maximum : 100 General Instructions: (i) (ii) (iii) (iv) (v) (vi) There are 26 questions in all. All questions are compulsory.
Sample Paper (CBSE) Series SC/SP Code No. SP-16 Mathematics Time Allowed: 3 hours Maximum : 100 General Instructions: (i) (ii) (iii) (iv) (v) (vi) There are 26 questions in all. All questions are compulsory.
Marking Scheme (Mathematics XII )
 Sr. No. Marking Scheme (Mathematics XII 07-8) Answer Section A., (, ) A A: (, ) A A: (,),(,) Mark(s). -5. a iˆ, b ˆj. (or an other correct answer). 6 6 ( ), () ( ) ( ). Hence, is not associative. Section
Sr. No. Marking Scheme (Mathematics XII 07-8) Answer Section A., (, ) A A: (, ) A A: (,),(,) Mark(s). -5. a iˆ, b ˆj. (or an other correct answer). 6 6 ( ), () ( ) ( ). Hence, is not associative. Section
MATHEMATICS (SET -3) Labour cost Z 300x 400y (to be minimized) The constraints are: SECTION - A 1. f (x) is continuous at x 3 f (3) lim f (x)
 8 Class th (SET -) BD PPER -7 M T H E M T I C S () SECTION -. f () is continuous at f () lim f () ( ) 6 k lim ( )( 6) k lim ( ) k. adj I 8 I 8 I 8I 8. P : z 5 5 P : 5 5z z 8 Distance between P & P sin
8 Class th (SET -) BD PPER -7 M T H E M T I C S () SECTION -. f () is continuous at f () lim f () ( ) 6 k lim ( )( 6) k lim ( ) k. adj I 8 I 8 I 8I 8. P : z 5 5 P : 5 5z z 8 Distance between P & P sin
MATHEMATICS (SET -1)
 8 Class th (SET ) BD PPER -7 M T H E M T I C S (). adj 8 I 8 I 8I 8 SECTION - I. f () is continuous at f () lim f () ( ) 6 k lim ( )( 6) k lim ( ) k sin cos d tan cot d sin cos ln sec ln sin C.. P : z
8 Class th (SET ) BD PPER -7 M T H E M T I C S (). adj 8 I 8 I 8I 8 SECTION - I. f () is continuous at f () lim f () ( ) 6 k lim ( )( 6) k lim ( ) k sin cos d tan cot d sin cos ln sec ln sin C.. P : z
CBSE 2018 ANNUAL EXAMINATION DELHI
 CBSE 08 ANNUAL EXAMINATION DELHI (Series SGN Code No 65/ : Delhi Region) Ma Marks : 00 Time Allowed : Hours SECTION A Q0 Find the value of tan cot ( ) Sol 5 5 tan cot ( ) tan tan cot cot 6 6 6 0 a Q0 If
CBSE 08 ANNUAL EXAMINATION DELHI (Series SGN Code No 65/ : Delhi Region) Ma Marks : 00 Time Allowed : Hours SECTION A Q0 Find the value of tan cot ( ) Sol 5 5 tan cot ( ) tan tan cot cot 6 6 6 0 a Q0 If
SOLUTION CLASS-XII / (CBSE)
 CBSE XII EXAMINATION-6 SOLUTION--6 CBSE th Board MATHEMATICS SET- CLASS-XII / CBSE Corporate Office : CG Tower, A-6 &, IPIA, Near Cit Mall, Jhalawar Road, Kota Raj.- PCCP Head Office: J-, Jawahar Nagar,
CBSE XII EXAMINATION-6 SOLUTION--6 CBSE th Board MATHEMATICS SET- CLASS-XII / CBSE Corporate Office : CG Tower, A-6 &, IPIA, Near Cit Mall, Jhalawar Road, Kota Raj.- PCCP Head Office: J-, Jawahar Nagar,
QUESTION PAPER CODE 65/2/2/F EXPECTED ANSWER/VALUE POINTS
 QUESTION PAPER CODE EXPECTED ANSWER/VALUE POINTS SECTION A. P 6 (A A ) P 6 9. (a b c) (a b c) 0 a b c (a b b c c a) 0 a b b c c a. a b sin θ a b cos θ 400 b 4 4. x z 5 or x z 5 mark for dc's of normal
QUESTION PAPER CODE EXPECTED ANSWER/VALUE POINTS SECTION A. P 6 (A A ) P 6 9. (a b c) (a b c) 0 a b c (a b b c c a) 0 a b b c c a. a b sin θ a b cos θ 400 b 4 4. x z 5 or x z 5 mark for dc's of normal
CBSE Examination Paper, Foreign-2014
 CBSE Eamination Paper, Foreign-4 Time allowed: hours Maimum marks: General Instructions: As per given in CBSE Eamination Paper Delhi-4. SET I SECTION A Question numbers to carr mark each.. Let R = {(a,
CBSE Eamination Paper, Foreign-4 Time allowed: hours Maimum marks: General Instructions: As per given in CBSE Eamination Paper Delhi-4. SET I SECTION A Question numbers to carr mark each.. Let R = {(a,
Rao IIT Academy/ 2015/ XII - CBSE - Board Mathematics Code(65 /2 /MT) Set-2 / Solutions XII - CBSE BOARD CODE (65/2/MT) SET - 2
 Rao IIT Academ/ 5/ XII - CBSE - Board Mathematics Code(65 / /MT) Set- / Solutions XII - CBSE BOARD CODE (65//MT) SET - Date: 8.3.5 MATHEMATICS - SOLUTIONS. Let a iˆ 3iˆ kˆ b iˆ ˆj and a b 3 5, b a b Projection
Rao IIT Academ/ 5/ XII - CBSE - Board Mathematics Code(65 / /MT) Set- / Solutions XII - CBSE BOARD CODE (65//MT) SET - Date: 8.3.5 MATHEMATICS - SOLUTIONS. Let a iˆ 3iˆ kˆ b iˆ ˆj and a b 3 5, b a b Projection
SET-I SECTION A SECTION B. General Instructions. Time : 3 hours Max. Marks : 100
 General Instructions. All questions are compulsor.. This question paper contains 9 questions.. Questions - in Section A are ver short answer tpe questions carring mark each.. Questions 5- in Section B
General Instructions. All questions are compulsor.. This question paper contains 9 questions.. Questions - in Section A are ver short answer tpe questions carring mark each.. Questions 5- in Section B
MATHEMATICS Paper & Solutions
 CBSE-XII-8 EXAMINATION Series SGN MATHEMATICS Paper & Solutions SET- Code : 6/ Time : Hrs. Ma. Marks : General Instruction : (i) All questions are compulsor. (ii) The question paper consists of 9 questions
CBSE-XII-8 EXAMINATION Series SGN MATHEMATICS Paper & Solutions SET- Code : 6/ Time : Hrs. Ma. Marks : General Instruction : (i) All questions are compulsor. (ii) The question paper consists of 9 questions
CBSE Mathematics 2016 Solved paper for Class XII(10+2) Section - A. Q. 1 For what value of k, the system of linear equations.
 A ONE INSTITUTE A SYNONYM TO SUCCESS, OFFICE SCO, SECTOR 40 D, CHANDIGARH CBSE Mathematics 06 Solved paper for Class XII(0+) Section - A Q. For what value of k, the system of linear equations. y z y z
A ONE INSTITUTE A SYNONYM TO SUCCESS, OFFICE SCO, SECTOR 40 D, CHANDIGARH CBSE Mathematics 06 Solved paper for Class XII(0+) Section - A Q. For what value of k, the system of linear equations. y z y z
MATHEMATICS SOLUTION
 MATHEMATICS SOLUTION MHT-CET 6 (MATHEMATICS). (A) 5 0 55 5 9 6 5 9. (A) If the school bus does not come) (I will not go to school) ( I shall meet my friend) (I shall go out for a movie) ~ p ~ q r s ~ p
MATHEMATICS SOLUTION MHT-CET 6 (MATHEMATICS). (A) 5 0 55 5 9 6 5 9. (A) If the school bus does not come) (I will not go to school) ( I shall meet my friend) (I shall go out for a movie) ~ p ~ q r s ~ p
MATHEMATICS. Time allowed : 3 hours Maximum Marks: 100
 MATHEMATICS Time allowed : 3 hours Maimum Marks: 00 General Instructions:. All questions are compulsory.. This question paper contains 9 questions. 3. Questions 4 in Section A are very short-answer type
MATHEMATICS Time allowed : 3 hours Maimum Marks: 00 General Instructions:. All questions are compulsory.. This question paper contains 9 questions. 3. Questions 4 in Section A are very short-answer type
Class XII_All India_Mathematics_Set-2 SECTION C. Question numbers 23 to 29 carry 6 marks each.
 SECTION C Question numbers 3 to 9 carr 6 marks each. 3. Find the equation of the plane passing through the line of intersection of the planes r ˆi 3j ˆ 6 0 r 3i ˆ ˆ j k ˆ 0, whose perpendicular distance
SECTION C Question numbers 3 to 9 carr 6 marks each. 3. Find the equation of the plane passing through the line of intersection of the planes r ˆi 3j ˆ 6 0 r 3i ˆ ˆ j k ˆ 0, whose perpendicular distance
Marking Scheme. Section A 3. 2 [1] l m n 1 n 1 cos [1] Direction ratios of the given line are 2, 1, 2.
![Marking Scheme. Section A 3. 2 [1] l m n 1 n 1 cos [1] Direction ratios of the given line are 2, 1, 2. Marking Scheme. Section A 3. 2 [1] l m n 1 n 1 cos [1] Direction ratios of the given line are 2, 1, 2.](/thumbs/91/106056849.jpg) Marking Scheme Section A. B. AB 6 A B 6. sin( ) cos( ) or sin( ). 4. l m n n cos 45 or 6 4 OR Direction ratios of the given line are,,. [/] Hence, direction cosines of the line are:,, or,, [/] Section
Marking Scheme Section A. B. AB 6 A B 6. sin( ) cos( ) or sin( ). 4. l m n n cos 45 or 6 4 OR Direction ratios of the given line are,,. [/] Hence, direction cosines of the line are:,, or,, [/] Section
SECTION A 1. Find the vector equation of a plane which is at a distance of 5 units from the origin and its normal vector is 2iˆ
 Session: 01-17 Subject: Mathematics Class XII Duration: 3 hr. M.M: 100 General Instructions: (i) All questions are compulsor. (ii) This question paper contains 9 questions. (iii) Question 1 in Section
Session: 01-17 Subject: Mathematics Class XII Duration: 3 hr. M.M: 100 General Instructions: (i) All questions are compulsor. (ii) This question paper contains 9 questions. (iii) Question 1 in Section
All Rights Reserved Wiley India Pvt. Ltd. 1
 Question numbers to carry mark each. CBSE MATHEMATICS SECTION A. If R = {(, y) : + y = 8} is a relation of N, write the range of R. R = {(, y)! + y = 8} a relation of N. y = 8 y must be Integer So Can
Question numbers to carry mark each. CBSE MATHEMATICS SECTION A. If R = {(, y) : + y = 8} is a relation of N, write the range of R. R = {(, y)! + y = 8} a relation of N. y = 8 y must be Integer So Can
Rao IIT Academy/ ISC - Board 2018_Std XII_Mathematics_QP + Solutions JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS. XII - ISC Board
 Rao IIT Academy/ ISC - Board 8_Std XII_Mathematics_QP + Solutions JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS XII - ISC Board MATHEMATICS - QP + SOLUTIONS Date: 6..8 Ma. Marks : Question SECTION - A (8 Marks)
Rao IIT Academy/ ISC - Board 8_Std XII_Mathematics_QP + Solutions JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS XII - ISC Board MATHEMATICS - QP + SOLUTIONS Date: 6..8 Ma. Marks : Question SECTION - A (8 Marks)
BLUE PRINT: CLASS XII MATHS
 BLUE PRINT: CLASS XII MATHS CHAPTER S NAME MARK 4 MARKS 6 MARKS TOTAL. RELATIONS AND FUNCTIONS 5. INVERSE TRIGONOMETRIC 5 FUNCTIONS 3. MATRICES 7 4. DETERMINANTS 6 5. 8 DIFFERENTIATION 6 APPLICATION OF
BLUE PRINT: CLASS XII MATHS CHAPTER S NAME MARK 4 MARKS 6 MARKS TOTAL. RELATIONS AND FUNCTIONS 5. INVERSE TRIGONOMETRIC 5 FUNCTIONS 3. MATRICES 7 4. DETERMINANTS 6 5. 8 DIFFERENTIATION 6 APPLICATION OF
Board Answer Paper: MARCH 2014
 Board Answer Paper: MARCH 04 and Statistics SECTION I Q.. (A) Select and write the correct answer from the given alternatives in each of the following: i. (C) Let l 0, m 3, n be the direction cosines of
Board Answer Paper: MARCH 04 and Statistics SECTION I Q.. (A) Select and write the correct answer from the given alternatives in each of the following: i. (C) Let l 0, m 3, n be the direction cosines of
MATHEMATICS Class: XII Mock Paper 1 Solutions
 MATHEMATICS Class: XII Mock Paper Solutions Section A. If A { a, b, c } and B {,, } and a function f : A B is given by f { (a, ), ( b, ), ( c, ) } Every element of set A is mapped to the unique element
MATHEMATICS Class: XII Mock Paper Solutions Section A. If A { a, b, c } and B {,, } and a function f : A B is given by f { (a, ), ( b, ), ( c, ) } Every element of set A is mapped to the unique element
ANNUAL EXAMINATION - ANSWER KEY II PUC - MATHEMATICS PART - A
 . LCM of and 6 8. -cosec ( ) -. π a a A a a. A A A A 8 8 6 5. 6. sin d ANNUAL EXAMINATION - ANSWER KEY -7 + d + + C II PUC - MATHEMATICS PART - A 7. or more vectors are said to be collinear vectors if
. LCM of and 6 8. -cosec ( ) -. π a a A a a. A A A A 8 8 6 5. 6. sin d ANNUAL EXAMINATION - ANSWER KEY -7 + d + + C II PUC - MATHEMATICS PART - A 7. or more vectors are said to be collinear vectors if
Design of Question Paper Mathematics - Class XII
 Design of Question Paper Mathematics - Class XII Time : 3 hours Max. Marks : 100 Weightage of marks over different dimensions of the question paper shall be as follows : A. Weightage to different topics/content
Design of Question Paper Mathematics - Class XII Time : 3 hours Max. Marks : 100 Weightage of marks over different dimensions of the question paper shall be as follows : A. Weightage to different topics/content
STD. XII ISC - BOARD MATHEMATICS - SOLUTIONS
 Rao IIT Academ/XII-ISC-Board -05_Mathematics_SOLUTIONS Date: 6.0.05 Question STD. XII ISC - BOARD MATHEMATICS - SOLUTIONS SECTION A (i) 4 6 M 6 4 9 5 8 M 8 km k k k k M km I 0 5 8 k k 0 0 0 8 k k 0 0 0
Rao IIT Academ/XII-ISC-Board -05_Mathematics_SOLUTIONS Date: 6.0.05 Question STD. XII ISC - BOARD MATHEMATICS - SOLUTIONS SECTION A (i) 4 6 M 6 4 9 5 8 M 8 km k k k k M km I 0 5 8 k k 0 0 0 8 k k 0 0 0
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII ( ) BLUE PRINT. Unit VSA (1) SA (4) LA (6) Total. I. Relations and Functions 1 (1) 4 (1) 5 (2)
 SAMPLE QUESTION PAPER MATHEMATICS CLASS XII (2013-14) BLUE PRINT Unit VSA (1) SA (4) LA (6) Total I. Relations and Functions 1 (1) 4 (1) 5 (2) Inverse Trigonometric Functions 1 (1) *4 (1) 5 (2) II. Matrices
SAMPLE QUESTION PAPER MATHEMATICS CLASS XII (2013-14) BLUE PRINT Unit VSA (1) SA (4) LA (6) Total I. Relations and Functions 1 (1) 4 (1) 5 (2) Inverse Trigonometric Functions 1 (1) *4 (1) 5 (2) II. Matrices
Sec 4 Maths SET D PAPER 2
 S4MA Set D Paper Sec 4 Maths Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e Answer all questions. Write your answers and working on the separate Answer Paper provided.
S4MA Set D Paper Sec 4 Maths Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e Answer all questions. Write your answers and working on the separate Answer Paper provided.
Mathematics. Section B. CBSE XII Mathematics 2012 Solution (SET 2) General Instructions:
 CBSE XII Mathematics 0 Solution (SET ) General Instructions: Mathematics (i) (ii) (iii) (iv) (v) All questions are compulsor. The question paper consists of 9 questions divided into three Sections A, B
CBSE XII Mathematics 0 Solution (SET ) General Instructions: Mathematics (i) (ii) (iii) (iv) (v) All questions are compulsor. The question paper consists of 9 questions divided into three Sections A, B
Operating C 1 C 1 C 2 and C 2 C 2 C 3, we get = 0, as R 1 and R 3 are identical. Ans: 0
 Q. Write the value of MATHEMATICS y y z z z y y y z z z y Operating R R + R, we get y z y z z y z y ( y z) z y Operating C C C and C C C, we get 0 0 0 0 ( y z) z y y ( y z)( ) z y y 0 0 0 0 = 0, as R and
Q. Write the value of MATHEMATICS y y z z z y y y z z z y Operating R R + R, we get y z y z z y z y ( y z) z y Operating C C C and C C C, we get 0 0 0 0 ( y z) z y y ( y z)( ) z y y 0 0 0 0 = 0, as R and
Time allowed : 3 hours Maximum Marks : 100
 CBSE XII EXAMINATION-8 Series SGN SET- Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains printed pages. Code number given on the right
CBSE XII EXAMINATION-8 Series SGN SET- Roll No. Candiates must write code on the title page of the answer book Please check that this question paper contains printed pages. Code number given on the right
MATHEMATICS. Time allowed : 3 hours Maximum Marks : 100
 MATHEMATICS Time allowed : hours Maimum Marks : General Instructions:. All questions are compulsory.. The question paper consists of 9 questions divided into three sections, A, B and C. Section A comprises
MATHEMATICS Time allowed : hours Maimum Marks : General Instructions:. All questions are compulsory.. The question paper consists of 9 questions divided into three sections, A, B and C. Section A comprises
SAMPLE QUESTION PAPER MATHEMATICS (041) CLASS XII Time allowed : 3 Hours MAX.MARKS 100 Blue Print. Applicatoin.
 Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation
Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation Knowledge Understanding Applicatoin HOTS Evaluation
Multiple Choice. 1.(6 pts) Find symmetric equations of the line L passing through the point (2, 5, 1) and perpendicular to the plane x + 3y z = 9.
 Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
Saturday, March 27, :59 PM Annexure 'F' Unfiled Notes Page 1
 Annexure 'F' CLASS-XII SAMPLE QUESTION PAPER MATHEMATICS CLASS XII (2013-14) BLUE PRINT Unit VSA (1) SA (4) LA (6) Total I. Relations and Functions 1 (1) 4 (1) 5 (2) Inverse Trigonometric Functions
Annexure 'F' CLASS-XII SAMPLE QUESTION PAPER MATHEMATICS CLASS XII (2013-14) BLUE PRINT Unit VSA (1) SA (4) LA (6) Total I. Relations and Functions 1 (1) 4 (1) 5 (2) Inverse Trigonometric Functions
KENDRIYA VIDYALAYA SANGATHAN, CHENNAI REGION CLASS XII-COMMON PRE-BOARD EXAMINATION. Answer key (Mathematics) Section A
 KENDRIYA VIDYALAYA SANGATHAN, CHENNAI REGION CLASS XII-COMMON PRE-BOARD EXAMINATION Answer key (Mathematics) Section A. x =. x + y = 6. degree =. π 5. 6. 7. 5 8. x + y + z = 9.. 66 Section B. Proving Reflexive
KENDRIYA VIDYALAYA SANGATHAN, CHENNAI REGION CLASS XII-COMMON PRE-BOARD EXAMINATION Answer key (Mathematics) Section A. x =. x + y = 6. degree =. π 5. 6. 7. 5 8. x + y + z = 9.. 66 Section B. Proving Reflexive
EINSTEIN CLASSES. C B S E XIIth Board PRACTICE ASSIGNMENT
 EINSTEIN CLASSES P R E S E N T S C B S E XIIth Board PRACTICE ASSIGNMENT MATHEMATICS NOTE THE FOLLOWING POINTS : Einstein Classes is primarily concerned with the preparation of JEE-ADVANCE /JEE-MAIN/BITS/PMT/AIIMS
EINSTEIN CLASSES P R E S E N T S C B S E XIIth Board PRACTICE ASSIGNMENT MATHEMATICS NOTE THE FOLLOWING POINTS : Einstein Classes is primarily concerned with the preparation of JEE-ADVANCE /JEE-MAIN/BITS/PMT/AIIMS
ANSWERS, HINTS & SOLUTIONS
 AIITS-PT-IV-PCM(SOL)-JEE(Main)/6 FIITJEE Students From All Programs have bagged in Top 00, 77 in Top 00 and 05 in Top 500 All India Ranks. FIITJEE Performance in JEE (Advanced), 05: 455 FIITJEE Students
AIITS-PT-IV-PCM(SOL)-JEE(Main)/6 FIITJEE Students From All Programs have bagged in Top 00, 77 in Top 00 and 05 in Top 500 All India Ranks. FIITJEE Performance in JEE (Advanced), 05: 455 FIITJEE Students
MODEL PAPER - I MATHEMATICS. Time allowed : 3 hours Maximum marks : 100
 MODEL PAPER - I MATHEMATICS Time allowed : 3 hours Maimum marks : General Instructions. All questions are compulsy.. The question paper consists of 9 questions divided into three sections A, B and C. Section
MODEL PAPER - I MATHEMATICS Time allowed : 3 hours Maimum marks : General Instructions. All questions are compulsy.. The question paper consists of 9 questions divided into three sections A, B and C. Section
Name: AK-Nummer: Ergänzungsprüfung January 29, 2016
 INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
INSTRUCTIONS: The test has a total of 32 pages including this title page and 9 questions which are marked out of 10 points; ensure that you do not omit a page by mistake. Please write your name and AK-Nummer
Objective Mathematics
 Chapter No - ( Area Bounded by Curves ). Normal at (, ) is given by : y y. f ( ) or f ( ). Area d ()() 7 Square units. Area (8)() 6 dy. ( ) d y c or f ( ) c f () c f ( ) As shown in figure, point P is
Chapter No - ( Area Bounded by Curves ). Normal at (, ) is given by : y y. f ( ) or f ( ). Area d ()() 7 Square units. Area (8)() 6 dy. ( ) d y c or f ( ) c f () c f ( ) As shown in figure, point P is
Sample Paper-05 Mathematics Class XII. Time allowed: 3 hours Answers Maximum Marks: 100. Section A. Section B
 Sample Paper-05 Mathematics Class XII Time allowed: hours Answers Maimum Marks: 00. No. (, ) R but (, ) R r. a () + ( ) + ( 5) 8 5 l, m, n 8 8 8. [0, ]. A A ( 8) 8 ( 6) A 8 Hence Prove tan cos sin sin
Sample Paper-05 Mathematics Class XII Time allowed: hours Answers Maimum Marks: 00. No. (, ) R but (, ) R r. a () + ( ) + ( 5) 8 5 l, m, n 8 8 8. [0, ]. A A ( 8) 8 ( 6) A 8 Hence Prove tan cos sin sin
CBSE Board Paper Class-XII. Time allowed : 3 hours Maximum Marks : 100
 L.K.Gupta (Mathematic Classes) www.poineermathematics.com. MOBILE: 98155771, 461771 CBSE Board Paper -011 Class-XII (SET-1) Time allowed : hours Maimum Marks : 100 General Instructions: (i) All questions
L.K.Gupta (Mathematic Classes) www.poineermathematics.com. MOBILE: 98155771, 461771 CBSE Board Paper -011 Class-XII (SET-1) Time allowed : hours Maimum Marks : 100 General Instructions: (i) All questions
C.B.S.E Class XII Delhi & Outside Delhi Sets
 SOLVED PAPER With CBSE Marking Scheme C.B.S.E. 8 Class XII Delhi & Outside Delhi Sets Mathematics Time : Hours Ma. Marks : General Instructions : (i) All questions are compulsory. (ii) The question paper
SOLVED PAPER With CBSE Marking Scheme C.B.S.E. 8 Class XII Delhi & Outside Delhi Sets Mathematics Time : Hours Ma. Marks : General Instructions : (i) All questions are compulsory. (ii) The question paper
SAMPLE QUESTION PAPER MATHEMATICS (041) CLASS XII
 SAMPLE QUESTION PAPER MATHEMATICS (01) CLASS XII 017-18 Time allowed: hours Maimum Marks: 100 General Instructions: (i) All questions are compulsory. (ii) This question paper contains 9 questions. (iii)
SAMPLE QUESTION PAPER MATHEMATICS (01) CLASS XII 017-18 Time allowed: hours Maimum Marks: 100 General Instructions: (i) All questions are compulsory. (ii) This question paper contains 9 questions. (iii)
CBSE Examination Papers
 CBSE Eamination Papers (Foreign 0) Time allowed: hours Maimum marks: 00 General Instructions: As given in CBSE Sample Question Paper. Set I SECTION A Question numbers to 0 carry mark each.. Write the principal
CBSE Eamination Papers (Foreign 0) Time allowed: hours Maimum marks: 00 General Instructions: As given in CBSE Sample Question Paper. Set I SECTION A Question numbers to 0 carry mark each.. Write the principal
Free Response Questions Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom
 Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
MINIMUM PROGRAMME FOR AISSCE
 KENDRIYA VIDYALAYA DANAPUR CANTT MINIMUM PROGRAMME FOR AISSCE 8 SUBJECT : MATHEMATICS (CLASS XII) Prepared By : K. N. P. Singh Vice-Principal K.V. Danapur Cantt () MATRIX. Find X and Y if 7 y & y 7 8 X,,
KENDRIYA VIDYALAYA DANAPUR CANTT MINIMUM PROGRAMME FOR AISSCE 8 SUBJECT : MATHEMATICS (CLASS XII) Prepared By : K. N. P. Singh Vice-Principal K.V. Danapur Cantt () MATRIX. Find X and Y if 7 y & y 7 8 X,,
MATHEMATICS. IMPORTANT FORMULAE AND CONCEPTS for. Final Revision CLASS XII CHAPTER WISE CONCEPTS, FORMULAS FOR QUICK REVISION.
 MATHEMATICS IMPORTANT FORMULAE AND CONCEPTS for Final Revision CLASS XII 2016 17 CHAPTER WISE CONCEPTS, FORMULAS FOR QUICK REVISION Prepared by M. S. KUMARSWAMY, TGT(MATHS) M. Sc. Gold Medallist (Elect.),
MATHEMATICS IMPORTANT FORMULAE AND CONCEPTS for Final Revision CLASS XII 2016 17 CHAPTER WISE CONCEPTS, FORMULAS FOR QUICK REVISION Prepared by M. S. KUMARSWAMY, TGT(MATHS) M. Sc. Gold Medallist (Elect.),
12 th Class Mathematics Paper
 th Class Mathematics Paper Maimum Time: hours Maimum Marks: 00 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 9 questions divided into four sections A, B, C
th Class Mathematics Paper Maimum Time: hours Maimum Marks: 00 General Instructions: (i) All questions are compulsory. (ii) The question paper consists of 9 questions divided into four sections A, B, C
( ) 2 + ( 2 x ) 12 = 0, and explain why there is only one
 IB Math SL Practice Problems - Algebra Alei - Desert Academy 0- SL Practice Problems Algebra Name: Date: Block: Paper No Calculator. Consider the arithmetic sequence, 5, 8,,. (a) Find u0. (b) Find the
IB Math SL Practice Problems - Algebra Alei - Desert Academy 0- SL Practice Problems Algebra Name: Date: Block: Paper No Calculator. Consider the arithmetic sequence, 5, 8,,. (a) Find u0. (b) Find the
PRADEEP SHARMA INSTITUTE OF COMPETITIVE STUDIES PRADEEP SHARMA. PRADEEP SHARMA INSTITUTE OF COMPETITIVE STUDIES Page 1
 PRADEEP SHARMA PRADEEP SHARMA INSTITUTE OF COMPETITIVE STUDIES Page Chapter Relation and Functions Mark Questions A relation R in a Set A is called..., if each element of A is related to every element
PRADEEP SHARMA PRADEEP SHARMA INSTITUTE OF COMPETITIVE STUDIES Page Chapter Relation and Functions Mark Questions A relation R in a Set A is called..., if each element of A is related to every element
HIGHER SCHOOL CERTIFICATE EXAMINATION MATHEMATICS 3 UNIT (ADDITIONAL) AND 3/4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time)
 HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
HIGHER SCHOOL CERTIFICATE EXAMINATION 000 MATHEMATICS UNIT (ADDITIONAL) AND /4 UNIT (COMMON) Time allowed Two hours (Plus 5 minutes reading time) DIRECTIONS TO CANDIDATES Attempt ALL questions. ALL questions
1. SETS AND FUNCTIONS
 . SETS AND FUNCTIONS. For two sets A and B, A, B A if and only if B A A B A! B A + B z. If A B, then A + B is B A\ B A B\ A. For any two sets Pand Q, P + Q is " x : x! P or x! Q, " x : x! P and x b Q,
. SETS AND FUNCTIONS. For two sets A and B, A, B A if and only if B A A B A! B A + B z. If A B, then A + B is B A\ B A B\ A. For any two sets Pand Q, P + Q is " x : x! P or x! Q, " x : x! P and x b Q,
SOLUTIONS TO CONCEPTS CHAPTER 2
 SOLUTIONS TO CONCPTS CHAPTR 1. As shown in the figure, The angle between A and B = 11 = 9 A = and B = 4m Resultant R = A B ABcos = 5 m Let be the angle between R and A 4 sin9 = tan 1 = tan 1 (4/) = 5 4cos9
SOLUTIONS TO CONCPTS CHAPTR 1. As shown in the figure, The angle between A and B = 11 = 9 A = and B = 4m Resultant R = A B ABcos = 5 m Let be the angle between R and A 4 sin9 = tan 1 = tan 1 (4/) = 5 4cos9
MOST IMPORTANT QUESTIONS
 PART - Centurion Assignment By OP GUPTA INDIRA AWARD WINNER CLASS XII MATHEMATICS MOST IMPORTANT QUESTIONS Without Mathematics, there s nothing you can do Everything around you is Mathematics Everything
PART - Centurion Assignment By OP GUPTA INDIRA AWARD WINNER CLASS XII MATHEMATICS MOST IMPORTANT QUESTIONS Without Mathematics, there s nothing you can do Everything around you is Mathematics Everything
College of Sciences PHYS 101 General Physics 1 F a l l S e m e s t e r Midterm1 Exam October 26, 2015 Monday, 19:00-21:00. Please read.
 Name: Surname: Number: K O Ç U N I V E R S I T Y College of Sciences PHYS 101 General Phsics 1 F a l l S e m e s t e r 0 1 5 Midterm1 Exam October 6, 015 Monda, 19:00-1:00 Please read. Count to make sure
Name: Surname: Number: K O Ç U N I V E R S I T Y College of Sciences PHYS 101 General Phsics 1 F a l l S e m e s t e r 0 1 5 Midterm1 Exam October 6, 015 Monda, 19:00-1:00 Please read. Count to make sure
H2 MATHS SET D PAPER 1
 H Maths Set D Paper H MATHS Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e b The curve y ax c x 3 points, and, H Maths Set D Paper has a stationary point at x 3. It also
H Maths Set D Paper H MATHS Exam papers with worked solutions SET D PAPER Compiled by THE MATHS CAFE P a g e b The curve y ax c x 3 points, and, H Maths Set D Paper has a stationary point at x 3. It also
GOVERNMENT OF KARNATAKA KARNATAKA STATE PRE-UNIVERSITY EDUCATION EXAMINATION BOARD SCHEME OF VALUATION. Subject : MATHEMATICS Subject Code : 35
 GOVERNMENT OF KARNATAKA KARNATAKA STATE PRE-UNIVERSITY EDUCATION EXAMINATION BOARD II YEAR PUC EXAMINATION MARCH APRIL 0 SCHEME OF VALUATION Subject : MATHEMATICS Subject Code : 5 PART A Write the prime
GOVERNMENT OF KARNATAKA KARNATAKA STATE PRE-UNIVERSITY EDUCATION EXAMINATION BOARD II YEAR PUC EXAMINATION MARCH APRIL 0 SCHEME OF VALUATION Subject : MATHEMATICS Subject Code : 5 PART A Write the prime
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
WBJEEM Answer Keys by Aakash Institute, Kolkata Centre MATHEMATICS
 WBJEEM - 05 Answer Keys by, Kolkata Centre MATHEMATICS Q.No. μ β γ δ 0 B A A D 0 B A C A 0 B C A * 04 C B B C 05 D D B A 06 A A B C 07 A * C A 08 D C D A 09 C C A * 0 C B D D B C A A D A A B A C A B 4
WBJEEM - 05 Answer Keys by, Kolkata Centre MATHEMATICS Q.No. μ β γ δ 0 B A A D 0 B A C A 0 B C A * 04 C B B C 05 D D B A 06 A A B C 07 A * C A 08 D C D A 09 C C A * 0 C B D D B C A A D A A B A C A B 4
Transweb Educational Services Pvt. Ltd Tel:
 . An aeroplane flying at a constant speed, parallel to the horizontal ground, km above it, is observed at an elevation of 6º from a point on the ground. If, after five seconds, its elevation from the same
. An aeroplane flying at a constant speed, parallel to the horizontal ground, km above it, is observed at an elevation of 6º from a point on the ground. If, after five seconds, its elevation from the same
Possible C2 questions from past papers P1 P3
 Possible C2 questions from past papers P1 P3 Source of the original question is given in brackets, e.g. [P1 January 2001 Question 1]; a question which has been edited is indicated with an asterisk, e.g.
Possible C2 questions from past papers P1 P3 Source of the original question is given in brackets, e.g. [P1 January 2001 Question 1]; a question which has been edited is indicated with an asterisk, e.g.
CBSE Class-12 Mathematics Sample Paper (By CBSE)
 CBSE Class-12 Mathematics Sample Paper (By CBSE) General Instructions: All questions are compulsory. This question paper contains 29 questions. Question 1-4 in Section A are very short-answer type questions
CBSE Class-12 Mathematics Sample Paper (By CBSE) General Instructions: All questions are compulsory. This question paper contains 29 questions. Question 1-4 in Section A are very short-answer type questions
HALF SYLLABUS TEST. Topics : Ch 01 to Ch 08
 Ma Marks : Topics : Ch to Ch 8 HALF SYLLABUS TEST Time : Minutes General instructions : (i) All questions are compulsory (ii) Please check that this question paper contains 9 questions (iii) Questions
Ma Marks : Topics : Ch to Ch 8 HALF SYLLABUS TEST Time : Minutes General instructions : (i) All questions are compulsory (ii) Please check that this question paper contains 9 questions (iii) Questions
Mathematics. Class 12th. CBSE Examination Paper 2015 (All India Set) (Detailed Solutions)
 CBSE Eamination Paer (All India Set) (Detailed Solutions) Mathematics Class th z z. We have, z On aling R R R, we get z z z z (/) Taking common ( z) from R common from R, we get ( z)( ) z ( z)( ) [ R R
CBSE Eamination Paer (All India Set) (Detailed Solutions) Mathematics Class th z z. We have, z On aling R R R, we get z z z z (/) Taking common ( z) from R common from R, we get ( z)( ) z ( z)( ) [ R R
38. The total number of carboxylic acid groups in the product P is 38. [2] O C HO 3 O C C O C O C O. Total no. of carboxylic group = 2
![38. The total number of carboxylic acid groups in the product P is 38. [2] O C HO 3 O C C O C O C O. Total no. of carboxylic group = 2 38. The total number of carboxylic acid groups in the product P is 38. [2] O C HO 3 O C C O C O C O. Total no. of carboxylic group = 2](/thumbs/78/77697004.jpg) (6) Vidyalankar : IIT JEE 0 Advanced : Question Paper & Solution 8. The total number of carboxylic acid groups in the product P is 8. [] C.... + H Heat C Total no. of carboxylic group = C C H 9. A tetrapeptide
(6) Vidyalankar : IIT JEE 0 Advanced : Question Paper & Solution 8. The total number of carboxylic acid groups in the product P is 8. [] C.... + H Heat C Total no. of carboxylic group = C C H 9. A tetrapeptide
APPLICATIONS OF DERIVATIVES
 9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
EXERCISE - 01 CHECK YOUR GRASP
 XRCIS - 1 CHCK YOUR GRASP SLCT TH CORRCT ALTRNATIV (ONLY ON CORRCT ANSWR) 1. If A B = 1 5 3 7 and A 3B = 5 7, then matrix B is equal to - 4 5 6 7 (B) 6 3 7 1 3 6 1. If A = cos sin sin cos, then A A is
XRCIS - 1 CHCK YOUR GRASP SLCT TH CORRCT ALTRNATIV (ONLY ON CORRCT ANSWR) 1. If A B = 1 5 3 7 and A 3B = 5 7, then matrix B is equal to - 4 5 6 7 (B) 6 3 7 1 3 6 1. If A = cos sin sin cos, then A A is
Prerna Tower, Road No 2, Contractors Area, Bistupur, Jamshedpur , Tel (0657) , PART III MATHEMATICS
 R Prerna Tower, Road No, Contractors Area, Bistupur, Jamshedpur 8300, Tel (0657)89, www.prernaclasses.com Jee Advance 03 Mathematics Paper I PART III MATHEMATICS SECTION : (Only One Option Correct Type)
R Prerna Tower, Road No, Contractors Area, Bistupur, Jamshedpur 8300, Tel (0657)89, www.prernaclasses.com Jee Advance 03 Mathematics Paper I PART III MATHEMATICS SECTION : (Only One Option Correct Type)
Model Answer Paper 24(24 1) 2 12
 ICSE X SUBJECT : MATHEMATICS Marks : 80 Exam No. : MT/ICSE/Semi Prelim II- Set-B-00 Model Answer Paper Time : ½ hrs. SECTION I (40 Marks) A. (a) Maturity value ` 0,000 No. of months (n) 4 months Rate of
ICSE X SUBJECT : MATHEMATICS Marks : 80 Exam No. : MT/ICSE/Semi Prelim II- Set-B-00 Model Answer Paper Time : ½ hrs. SECTION I (40 Marks) A. (a) Maturity value ` 0,000 No. of months (n) 4 months Rate of
AP Calculus (BC) Summer Assignment (169 points)
 AP Calculus (BC) Summer Assignment (69 points) This packet is a review of some Precalculus topics and some Calculus topics. It is to be done NEATLY and on a SEPARATE sheet of paper. Use your discretion
AP Calculus (BC) Summer Assignment (69 points) This packet is a review of some Precalculus topics and some Calculus topics. It is to be done NEATLY and on a SEPARATE sheet of paper. Use your discretion
is equal to = 3 2 x, if x < 0 f (0) = lim h = 0. Therefore f exists and is continuous at 0.
 Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
Physics for Scientists and Engineers. Chapter 3 Vectors and Coordinate Systems
 Phsics for Scientists and Engineers Chapter 3 Vectors and Coordinate Sstems Spring, 2008 Ho Jung Paik Coordinate Sstems Used to describe the position of a point in space Coordinate sstem consists of a
Phsics for Scientists and Engineers Chapter 3 Vectors and Coordinate Sstems Spring, 2008 Ho Jung Paik Coordinate Sstems Used to describe the position of a point in space Coordinate sstem consists of a
Mathematics Extension 1
 013 HIGHER SCHL CERTIFICATE EXAMINATIN Mathematics Etension 1 General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
013 HIGHER SCHL CERTIFICATE EXAMINATIN Mathematics Etension 1 General Instructions Reading time 5 minutes Working time hours Write using black or blue pen Black pen is preferred Board-approved calculators
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE. To find the length of a line segment joining two points A(x 1, y 1 ) and B(x 2, y 2 ), use
 COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
BLUE PRINT - III MATHEMATICS - XII. (b) Applications of Derivatives (1) 44 (11) (b) 3 - dimensional geometry - 4 (1) 6 (1) 17 (6)
 BLUE PRINT - III MATHEMATICS - XII S.No. Topic VSA SA LA TOTAL 1. (a) Relations and Functions 1 (1) 4 (1) - 10 (4) (b) Inverse trigonometric 1 (1) 4 (1) - Functions. (a) Matrices () - 6 (1) - (b) Determinants
BLUE PRINT - III MATHEMATICS - XII S.No. Topic VSA SA LA TOTAL 1. (a) Relations and Functions 1 (1) 4 (1) - 10 (4) (b) Inverse trigonometric 1 (1) 4 (1) - Functions. (a) Matrices () - 6 (1) - (b) Determinants
MATH College Algebra Review for Test 2
 MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
MATH 34 - College Algebra Review for Test 2 Sections 3. and 3.2. For f (x) = x 2 + 4x + 5, give (a) the x-intercept(s), (b) the -intercept, (c) both coordinates of the vertex, and (d) the equation of the
Sudoku Puzzle A.P. Exam (Part B) Questions are from the 1997 and 1998 A.P. Exams A Puzzle by David Pleacher
 Sudoku Puzzle A.P. Exam (Part B) Questions are from the 1997 and 1998 A.P. Exams A Puzzle by David Pleacher Solve the 4 multiple-choice problems below. A graphing calculator is required for some questions
Sudoku Puzzle A.P. Exam (Part B) Questions are from the 1997 and 1998 A.P. Exams A Puzzle by David Pleacher Solve the 4 multiple-choice problems below. A graphing calculator is required for some questions
Complete Syllabus of Class XI & XII
 Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-0005 Ph.: 0-7656 Fa : 0-767 MM : 0 Sample Paper : Campus Recruitment Test Time : ½ Hr. Mathematics (Engineering) Complete Syllabus of Class XI & XII
Regd. Office : Aakash Tower, 8, Pusa Road, New Delhi-0005 Ph.: 0-7656 Fa : 0-767 MM : 0 Sample Paper : Campus Recruitment Test Time : ½ Hr. Mathematics (Engineering) Complete Syllabus of Class XI & XII
y mx 25m 25 4 circle. Then the perpendicular distance of tangent from the centre (0, 0) is the radius. Since tangent
 Mathematics. The sides AB, BC and CA of ABC have, 4 and 5 interior points respectively on them as shown in the figure. The number of triangles that can be formed using these interior points is () 80 ()
Mathematics. The sides AB, BC and CA of ABC have, 4 and 5 interior points respectively on them as shown in the figure. The number of triangles that can be formed using these interior points is () 80 ()
ADVANCED MATHS TEST - I PRELIMS
 Model Papers Code : 1101 Advanced Math Test I & II ADVANCED MATHS TEST - I PRELIMS Max. Marks : 75 Duration : 75 Mins. General Instructions : 1. Please find the Answer Sheets (OMR) with in the envelop
Model Papers Code : 1101 Advanced Math Test I & II ADVANCED MATHS TEST - I PRELIMS Max. Marks : 75 Duration : 75 Mins. General Instructions : 1. Please find the Answer Sheets (OMR) with in the envelop
MATHEMATICS LEVEL 2 TEST FORM B Continued
 Mathematics Level Test Form B For each of the following problems, decide which is the BEST of the choices given. If the eact numerical value is not one of the choices, select the choice that best approimates
Mathematics Level Test Form B For each of the following problems, decide which is the BEST of the choices given. If the eact numerical value is not one of the choices, select the choice that best approimates
3. Total number of functions from the set A to set B is n. 4. Total number of one-one functions from the set A to set B is n Pm
 ASSIGNMENT CLASS XII RELATIONS AND FUNCTIONS Important Formulas If A and B are finite sets containing m and n elements, then Total number of relations from the set A to set B is mn Total number of relations
ASSIGNMENT CLASS XII RELATIONS AND FUNCTIONS Important Formulas If A and B are finite sets containing m and n elements, then Total number of relations from the set A to set B is mn Total number of relations
MATHEMATICS LEVEL 2. MATHEMATICS LEVEL 2 Continued GO ON TO THE NEXT PAGE USE THIS SPACE FOR SCRATCHWORK. 1. If xy 0 and 3x = 0.
 MATHEMATICS LEVEL For each of the following problems, decide which is the BEST of the choices given. If the eact numerical value is not one of the choices, select the choice that best approimates this
MATHEMATICS LEVEL For each of the following problems, decide which is the BEST of the choices given. If the eact numerical value is not one of the choices, select the choice that best approimates this
MOBILE NO : X_STD MATHS RVS - TRICHY R.VETRIVEL
 10 MOBILE NO : 986545111 ONE MARK - FIRST TEST TIME:10 MINUTES 1. If A B, then A B is a) B b) A/B c) A d) B/A. If the product of the first four consecutive terms of a G.P is 56 and if the common ratio
10 MOBILE NO : 986545111 ONE MARK - FIRST TEST TIME:10 MINUTES 1. If A B, then A B is a) B b) A/B c) A d) B/A. If the product of the first four consecutive terms of a G.P is 56 and if the common ratio
S.S.L.C. - MATHS BOOK BACK ONE MARK STUDY MATERIAL
 1 S.S.L.C. - MATHS BOOK BACK ONE MARK STUDY MATERIAL DEAR STUDENTS, I have rearranged MATHS-one mark book questions in the order based on value of the answer so that, you can understand easily Totally
1 S.S.L.C. - MATHS BOOK BACK ONE MARK STUDY MATERIAL DEAR STUDENTS, I have rearranged MATHS-one mark book questions in the order based on value of the answer so that, you can understand easily Totally
AP Calculus Free-Response Questions 1969-present AB
 AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
MATHEMATICS Compulsory Part
 07/8-ME MATH CP PAPER HK YAU CLUB HNG KNG MCK EXAMINATIN 07/8 MATHEMATICS Compulsor Part PAPER 00 nn - 5 pm (¼ hours) INSTRUCTINS Read carefull the instructions on the Answer Sheet After the announcement
07/8-ME MATH CP PAPER HK YAU CLUB HNG KNG MCK EXAMINATIN 07/8 MATHEMATICS Compulsor Part PAPER 00 nn - 5 pm (¼ hours) INSTRUCTINS Read carefull the instructions on the Answer Sheet After the announcement
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
MATHEMATICS. r Statement I Statement II p q ~p ~q ~p q q p ~(p ~q) F F T T F F T F T T F T T F T F F T T T F T T F F F T T
 MATHEMATICS Directions : Questions number to 5 are Assertion-Reason type questions. Each of these questions contains two statements : Statement- (Assertion) and Statement- (Reason). Each of these questions
MATHEMATICS Directions : Questions number to 5 are Assertion-Reason type questions. Each of these questions contains two statements : Statement- (Assertion) and Statement- (Reason). Each of these questions
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 32
 KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 32 SAMPLE PAPER 05 (2018-19) SUBJECT: MATHEMATICS(041) BLUE PRINT : CLASS X Unit Chapter VSA (1 mark) SA I (2 marks) SA II (3 marks) LA (4 marks) Total Unit
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 32 SAMPLE PAPER 05 (2018-19) SUBJECT: MATHEMATICS(041) BLUE PRINT : CLASS X Unit Chapter VSA (1 mark) SA I (2 marks) SA II (3 marks) LA (4 marks) Total Unit
Fundamentals of Engineering (FE) Exam Mathematics Review
 Fundamentals of Engineering (FE) Exam Mathematics Review Dr. Garey Fox Professor and Buchanan Endowed Chair Biosystems and Agricultural Engineering October 16, 2014 Reference Material from FE Review Instructor
Fundamentals of Engineering (FE) Exam Mathematics Review Dr. Garey Fox Professor and Buchanan Endowed Chair Biosystems and Agricultural Engineering October 16, 2014 Reference Material from FE Review Instructor
CLASS XII MATHEMATICS. Weightage (Marks) (i) Relations and Functions 10. Type of Questions Weightage of Number of Total Marks each question questions
 CLASS XII MATHEMATICS Units Weightage (Marks) (i) Relations and Functions 0 (ii) Algebra (Matrices and Determinants) (iii) Calculus 44 (iv) Vector and Three dimensional Geometry 7 (v) Linear Programming
CLASS XII MATHEMATICS Units Weightage (Marks) (i) Relations and Functions 0 (ii) Algebra (Matrices and Determinants) (iii) Calculus 44 (iv) Vector and Three dimensional Geometry 7 (v) Linear Programming
MA304 Differential Geometry
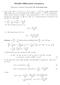 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
Mathematics. Guess Paper: 2014 Class: XII. Time Allowed: 3Hours Maximum Marks: 70. Section A
 Mathematics Guess Paper: 04 Class: XII Time llowed: Hours Maimum Marks: 70 General Instructions:. The question paper consists of 9 questions divided into three sections, B and C.. Section comprises of
Mathematics Guess Paper: 04 Class: XII Time llowed: Hours Maimum Marks: 70 General Instructions:. The question paper consists of 9 questions divided into three sections, B and C.. Section comprises of
PADASALAI CENTUM COACHING TEAM 10 TH MATHS FULL PORTION ONE MARKS ONLY
 PADASALAI CENTUM COACHING TEAM 10 TH MATHS FULL PORTION ONE MARKS ONLY CHOOSE THE CORRECT ANSWER 100 X 1 = 100 1. If ACB, then A is (a) B (b) A \ B (c) A (d) B \ A 2. If n(a) = 20, n(b) = 30 and n(aub)
PADASALAI CENTUM COACHING TEAM 10 TH MATHS FULL PORTION ONE MARKS ONLY CHOOSE THE CORRECT ANSWER 100 X 1 = 100 1. If ACB, then A is (a) B (b) A \ B (c) A (d) B \ A 2. If n(a) = 20, n(b) = 30 and n(aub)
Mathematics Class XII
 Mathematics Class XII Time: hour Total Marks: 00. All questions are compulsory.. The question paper consist of 9 questions divided into three sections A, B, C and D. Section A comprises of 4 questions
Mathematics Class XII Time: hour Total Marks: 00. All questions are compulsory.. The question paper consist of 9 questions divided into three sections A, B, C and D. Section A comprises of 4 questions
