3 More applications of derivatives
|
|
|
- Abigayle McCarthy
- 6 years ago
- Views:
Transcription
1 3 More alications of derivatives 3.1 Eact & ineact differentials in thermodynamics So far we have been discussing total or eact differentials ( ( u u du = d + dy, (1 but we could imagine a more general situation If the differential is eact, M = ( u y du = M(, yd + N(, ydy. (2 ( y and N =. By the identity of mied artial derivatives, we have ( ( M 2 ( u N = = y E: Ideal gas V = R (for 1 mole, take V = V (,, so ( ( dv = d + d = R R d d (4 2 Now the work done in changing the volume of a gas is dw = dv = Rd R u (3 d. (5 Let s calculate the total change in volume and work done in changing the system between two oints A and C in, sace, along aths AC or ABC. 1. Path AC: d d = & 1 = 1 so d = d (6 1 = ( 1 (7 so (8 dv = R dw d R 2[ 1 + ( 1]d = R 2( 1 1d (9 = R ( 1 1d (10 1
2 ( 2, 2 C (, ( 1, 1 A B Figure 1: Path in, lane for thermodynamic rocess. Now we can calculate the change in volume and the work done in the rocess: V 2 V 1 = W 1 W 2 = AC AC dv = R( = R ( dv = R( ln = R ln 2 ( Path ABC: Note along AB d = 0, while along BC d = 0. V 2 V 1 = = W 2 W 1 = ABC ( ( d + 2 R R 1 d ( 1 d d = 2 1 ( 2 ( d + d 1 d = R ( ( R d = R 1 ln 2 + R( 2 1 V 1 Note the change in V is indeendent of the ath the volume is characteristic of a oint (, in equilibrium but the work done in the rocess is not! What s the difference? In the system with, as indeendent variables, dv is an eact differential, while dw is not. How can you see the difference? Go back and eamine the forms we had for dv and dw in (4 and (5. In the case of dv, we had dv = Md + Nd, with M = R M = R 2 2 and N = R 2 (14 N = R 2, (15
3 which is indeed eact, whereas dw = M d + N d M = R ; N = R (16 M = 0 N = R, (17 is not. his is a demonstration (we won t use the word roof that for a for a thermodynamic rocess involving changes in the lane, the volume of the system is a state variable, i.e. (for 1 mole of gas it simly deends on what and are; if you have secified,, you know the volume of the system. he change in volume between two oints will therefore always be V 2 V 1 indeendent of which ath is chosen. he work done in the same rocess is however not indeendent of the ath of integration. 3.2 Maima/minima roblems with constraints (Lagrange multiliers I m going to make a mathematical detour before coming back to thermodynamics, in order to give you some tools you need to solve homework roblems. In hysics we often need to find the etrema of a function of several variables subject to a constraint of some kind. In math, a simle eamle would be the distance function in 3-sace, d = 2 + y 2 + z 2. Of course the minimum of this function over all 3-sace is just 0, achieved at = y = z = 0. But suose we were to look for the minimum of d over the constrained set of oints defined by the lane 2y 2z = 3? he usual way to roceed is often the simlest, if it works: eress y = y(, then set dy/d = 0 and solve. But sometimes one can t solve for y( elicitly, so one can try the method of imlicit differentials (see Boas ch. 4, or use an elegant technique called the method of Lagrange multiliers (Joseh Lagrange ( was a French mathematical hysicist. he idea is, if you can eress the roblem in terms of the minimization of a function f(, y,..., together with a constraint g(, y,... = 0, to imagine you are solving the unconstrained roblem of finding the minimum of F (, y,... ; λ = f(, y,... + λg(, y,.... hen you can simly treat λ as an additional variable, and minimize with resect to it as well. In the rocess of solving the roblem, you eliminate λ from the solution. E: Coming back to our roblem with the lane, let s first make our life a bit easier by recalling that if we minimize d = 2 + y 2 + z 2, the square root will also 3
4 be a minimum. So define and set all the derivatives equal to zero: F = 2 + y 2 + z 2 + λ( 2y 2z 3 (18 z λ = 2 + λ = 0 (19 = 2y 2λ = 0 (20 = 2z 2λ = 0 (21 = 2y 2z 3 = 0. (22 Note the equation / λ = 0 is always just the constraint equation itself. Now we have a roblem with 4 equations and 4 unknowns, and it can be solved. he usual idea is to eliminate the constraint as quickly as ossible. he first eqn. tells us that λ = 2, so 2y + 4 = 0 (23 2z + 4 = 0 (24 2y 2z 3 = 0, (25 which we can solve to find (, y, z = (1/3, 2/3, 2/ Differentiation of integrals Leibnitz rule for differentiating integrals: d d v( u( f(, tdt = f(, v dv f(, udu d d + v( u( ( f dt. (26 E : 2 e t I = dt (27 t di e 2 e 2 d = e t dt (28 = 2 (e22 e 2 (29 4
5 3.4 Laws of thermodynamics Let s come back to the idea of eact and ineact differentials in thermodynamics. Here s another eamle of an ineact differential: dq = c }{{}}{{} d + Λ d, (30 }{{} heat absorbed heat caacity const. latent heat. (31 We showed already that the work done is also not an eact differential, however the combination of the two is: du dq dw (32 [ ( ] [ ( ] = c d + Λ d (33 his is called the internal energy, and this equation is sometimes referred to as the 1st law of thermodynamics, eressing energy conservation, i.e. the change in internal energy of a gas in a thermodynamic cycle goes either into heating the system (dq is the infinitesimal heat absorbed by the system is the or into doing work (done by the system. Another eact differential is ds = dq/. Remark 1: sometimes you will see the notation dq and dw for infinitesimal heat absorbed and work done. his is just a more careful notation to remind you that they are ineact differentials. Remark 2: since the work done in a thermodynamic rocess deends on the ath, it is really nonsense what I wrote above W 2 W 1. You are to think of this as the work erformed by the system in the rocess of going 1 2, but W 2 and W 1 have no indeendent meaning, since they are not characteristic of a macrostate. 3.5 Legendre transformation If for a function f(, y we have the differential df = d + qdy, where and q are equal to f/ and f/, resectively, we might ask the question, how do we make a simle change of variables to a new function g(, q with q one of the the indeendent variables? We simly make use of the fact that d(f qy = df dq y q dy = d + q dy dq y q dy = d y dq. (34 his function is by definition associated with an eact differential dg. You elored this on the HW for various thermodynamic quantities. 5
I have not proofread these notes; so please watch out for typos, anything misleading or just plain wrong.
 hermodynamics I have not roofread these notes; so lease watch out for tyos, anything misleading or just lain wrong. Please read ages 227 246 in Chater 8 of Kittel and Kroemer and ay attention to the first
hermodynamics I have not roofread these notes; so lease watch out for tyos, anything misleading or just lain wrong. Please read ages 227 246 in Chater 8 of Kittel and Kroemer and ay attention to the first
8.7 Associated and Non-associated Flow Rules
 8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
8.7 Associated and Non-associated Flow Rules Recall the Levy-Mises flow rule, Eqn. 8.4., d ds (8.7.) The lastic multilier can be determined from the hardening rule. Given the hardening rule one can more
Practice Midterm Solutions
 Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
Lecture 7: Thermodynamic Potentials
 Lecture 7: Thermodynamic Potentials Chater II. Thermodynamic Quantities A.G. Petukhov, PHY 743 etember 27, 2017 Chater II. Thermodynamic Quantities Lecture 7: Thermodynamic Potentials A.G. Petukhov, etember
Lecture 7: Thermodynamic Potentials Chater II. Thermodynamic Quantities A.G. Petukhov, PHY 743 etember 27, 2017 Chater II. Thermodynamic Quantities Lecture 7: Thermodynamic Potentials A.G. Petukhov, etember
δq T = nr ln(v B/V A )
 hysical Chemistry 007 Homework assignment, solutions roblem 1: An ideal gas undergoes the following reversible, cyclic rocess It first exands isothermally from state A to state B It is then comressed adiabatically
hysical Chemistry 007 Homework assignment, solutions roblem 1: An ideal gas undergoes the following reversible, cyclic rocess It first exands isothermally from state A to state B It is then comressed adiabatically
Phase transition. Asaf Pe er Background
 Phase transition Asaf Pe er 1 November 18, 2013 1. Background A hase is a region of sace, throughout which all hysical roerties (density, magnetization, etc.) of a material (or thermodynamic system) are
Phase transition Asaf Pe er 1 November 18, 2013 1. Background A hase is a region of sace, throughout which all hysical roerties (density, magnetization, etc.) of a material (or thermodynamic system) are
Chapter-6: Entropy. 1 Clausius Inequality. 2 Entropy - A Property
 hater-6: Entroy When the first law of thermodynamics was stated, the existence of roerty, the internal energy, was found. imilarly, econd law also leads to definition of another roerty, known as entroy.
hater-6: Entroy When the first law of thermodynamics was stated, the existence of roerty, the internal energy, was found. imilarly, econd law also leads to definition of another roerty, known as entroy.
The Second Law: The Machinery
 The Second Law: The Machinery Chater 5 of Atkins: The Second Law: The Concets Sections 3.7-3.9 8th Ed, 3.3 9th Ed; 3.4 10 Ed.; 3E 11th Ed. Combining First and Second Laws Proerties of the Internal Energy
The Second Law: The Machinery Chater 5 of Atkins: The Second Law: The Concets Sections 3.7-3.9 8th Ed, 3.3 9th Ed; 3.4 10 Ed.; 3E 11th Ed. Combining First and Second Laws Proerties of the Internal Energy
Chemistry 163B Winter 2013 notes for lecture 4
 Chemistry 163B Lecture 4 Winter 013 Challenged enmanship Notes 1 st Law recapitulation U internal energy du = dq + dw + dn sys sys sys sys sys surr du du energy conserved (n=number of moles; dn=0 for closed
Chemistry 163B Lecture 4 Winter 013 Challenged enmanship Notes 1 st Law recapitulation U internal energy du = dq + dw + dn sys sys sys sys sys surr du du energy conserved (n=number of moles; dn=0 for closed
Engineering Mathematics (E35 317) Exam 3 November 7, 2007
 Engineering Mathematics (E35 317) Exam 3 November 7, 2007 This exam contains four multile-choice roblems worth two oints each, twelve true-false roblems worth one oint each, and four free-resonse roblems
Engineering Mathematics (E35 317) Exam 3 November 7, 2007 This exam contains four multile-choice roblems worth two oints each, twelve true-false roblems worth one oint each, and four free-resonse roblems
1 Entropy 1. 3 Extensivity 4. 5 Convexity 5
 Contents CONEX FUNCIONS AND HERMODYNAMIC POENIALS 1 Entroy 1 2 Energy Reresentation 2 3 Etensivity 4 4 Fundamental Equations 4 5 Conveity 5 6 Legendre transforms 6 7 Reservoirs and Legendre transforms
Contents CONEX FUNCIONS AND HERMODYNAMIC POENIALS 1 Entroy 1 2 Energy Reresentation 2 3 Etensivity 4 4 Fundamental Equations 4 5 Conveity 5 6 Legendre transforms 6 7 Reservoirs and Legendre transforms
Lecture Thermodynamics 9. Entropy form of the 1 st law. Let us start with the differential form of the 1 st law: du = d Q + d W
 Lecture hermodnamics 9 Entro form of the st law Let us start with the differential form of the st law: du = d Q + d W Consider a hdrostatic sstem. o know the required d Q and d W between two nearb states,
Lecture hermodnamics 9 Entro form of the st law Let us start with the differential form of the st law: du = d Q + d W Consider a hdrostatic sstem. o know the required d Q and d W between two nearb states,
As in the book. Each of the other thermopotentials yield similar and useful relations. Let s just do the Legendre Transformations and list them all:
 hysics 430 Solutions to roblem Set 9 1. Schroeder roblem 5.1. Mixed derivatives are fun and useful. One of the most important things that we have yet to see is that thermodynamics INSISS that certain things,
hysics 430 Solutions to roblem Set 9 1. Schroeder roblem 5.1. Mixed derivatives are fun and useful. One of the most important things that we have yet to see is that thermodynamics INSISS that certain things,
Short Solutions to Practice Material for Test #2 MATH 2421
 Short Solutions to Practice Material for Test # MATH 4 Kawai (#) Describe recisely the D surfaces listed here (a) + y + z z = Shere ( ) + (y ) + (z ) = 4 = The center is located at C (; ; ) and the radius
Short Solutions to Practice Material for Test # MATH 4 Kawai (#) Describe recisely the D surfaces listed here (a) + y + z z = Shere ( ) + (y ) + (z ) = 4 = The center is located at C (; ; ) and the radius
0.1 Practical Guide - Surface Integrals. C (0,0,c) A (0,b,0) A (a,0,0)
 . Practical Guide - urface Integrals urface integral,means to integrate over a surface. We begin with the stud of surfaces. The easiest wa is to give as man familiar eamles as ossible ) a lane surface
. Practical Guide - urface Integrals urface integral,means to integrate over a surface. We begin with the stud of surfaces. The easiest wa is to give as man familiar eamles as ossible ) a lane surface
whether a process will be spontaneous, it is necessary to know the entropy change in both the
 93 Lecture 16 he entroy is a lovely function because it is all we need to know in order to redict whether a rocess will be sontaneous. However, it is often inconvenient to use, because to redict whether
93 Lecture 16 he entroy is a lovely function because it is all we need to know in order to redict whether a rocess will be sontaneous. However, it is often inconvenient to use, because to redict whether
Statics and dynamics: some elementary concepts
 1 Statics and dynamics: some elementary concets Dynamics is the study of the movement through time of variables such as heartbeat, temerature, secies oulation, voltage, roduction, emloyment, rices and
1 Statics and dynamics: some elementary concets Dynamics is the study of the movement through time of variables such as heartbeat, temerature, secies oulation, voltage, roduction, emloyment, rices and
dn i where we have used the Gibbs equation for the Gibbs energy and the definition of chemical potential
 Chem 467 Sulement to Lectures 33 Phase Equilibrium Chemical Potential Revisited We introduced the chemical otential as the conjugate variable to amount. Briefly reviewing, the total Gibbs energy of a system
Chem 467 Sulement to Lectures 33 Phase Equilibrium Chemical Potential Revisited We introduced the chemical otential as the conjugate variable to amount. Briefly reviewing, the total Gibbs energy of a system
MATH 2710: NOTES FOR ANALYSIS
 MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
Solutions to Homework #05 MATH ln z 2 + x 2 1 = 2x2 z 2 + x 2 + ln z2 + x 2. = x. ln z 2 + x 2 2z z 2 + x 2 = 2xz
 Solutions to Homeork #05 MATH Kaai Section. (I) Exercise #. g x and g z : Product Rule: g x = x @ ln z + x + ln z + x @ [x] = x x z + x + ln z + x = x z + x + ln z + x x is eld constant. g z = x @ ln z
Solutions to Homeork #05 MATH Kaai Section. (I) Exercise #. g x and g z : Product Rule: g x = x @ ln z + x + ln z + x @ [x] = x x z + x + ln z + x = x z + x + ln z + x x is eld constant. g z = x @ ln z
Spring 2011 solutions. We solve this via integration by parts with u = x 2 du = 2xdx. This is another integration by parts with u = x du = dx and
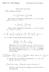 Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Homework #11. (Due December 5 at the beginning of the class.) Numerical Method Series #6: Engineering applications of Newton-Raphson Method to
 Homework #11 (Due December 5 at the beginning of the class.) Numerical Method Series #6: Engineering alications of Newton-Rahson Method to solving systems of nonlinear equations Goals: 1. Understanding
Homework #11 (Due December 5 at the beginning of the class.) Numerical Method Series #6: Engineering alications of Newton-Rahson Method to solving systems of nonlinear equations Goals: 1. Understanding
3. Show that if there are 23 people in a room, the probability is less than one half that no two of them share the same birthday.
 N12c Natural Sciences Part IA Dr M. G. Worster Mathematics course B Examles Sheet 1 Lent erm 2005 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damt.cam.ac.uk. Note that there
N12c Natural Sciences Part IA Dr M. G. Worster Mathematics course B Examles Sheet 1 Lent erm 2005 Please communicate any errors in this sheet to Dr Worster at M.G.Worster@damt.cam.ac.uk. Note that there
Multivariable Calculus
 Multivariable Calculus In thermodynamics, we will frequently deal with functions of more than one variable e.g., P PT, V, n, U UT, V, n, U UT, P, n U = energy n = # moles etensive variable: depends on
Multivariable Calculus In thermodynamics, we will frequently deal with functions of more than one variable e.g., P PT, V, n, U UT, V, n, U UT, P, n U = energy n = # moles etensive variable: depends on
On the Field of a Stationary Charged Spherical Source
 Volume PRORESS IN PHYSICS Aril, 009 On the Field of a Stationary Charged Sherical Source Nikias Stavroulakis Solomou 35, 533 Chalandri, reece E-mail: nikias.stavroulakis@yahoo.fr The equations of gravitation
Volume PRORESS IN PHYSICS Aril, 009 On the Field of a Stationary Charged Sherical Source Nikias Stavroulakis Solomou 35, 533 Chalandri, reece E-mail: nikias.stavroulakis@yahoo.fr The equations of gravitation
Simplifications to Conservation Equations
 Chater 5 Simlifications to Conservation Equations 5.1 Steady Flow If fluid roerties at a oint in a field do not change with time, then they are a function of sace only. They are reresented by: ϕ = ϕq 1,
Chater 5 Simlifications to Conservation Equations 5.1 Steady Flow If fluid roerties at a oint in a field do not change with time, then they are a function of sace only. They are reresented by: ϕ = ϕq 1,
Series Handout A. 1. Determine which of the following sums are geometric. If the sum is geometric, express the sum in closed form.
 Series Handout A. Determine which of the following sums are geometric. If the sum is geometric, exress the sum in closed form. 70 a) k= ( k ) b) 50 k= ( k )2 c) 60 k= ( k )k d) 60 k= (.0)k/3 2. Find the
Series Handout A. Determine which of the following sums are geometric. If the sum is geometric, exress the sum in closed form. 70 a) k= ( k ) b) 50 k= ( k )2 c) 60 k= ( k )k d) 60 k= (.0)k/3 2. Find the
Lecture 8: The First Fundamental Form Table of contents
 Math 38 Fall 2016 Lecture 8: The First Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this
Math 38 Fall 2016 Lecture 8: The First Fundamental Form Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this
Chemistry 163B. Lecture 5 Winter Challenged Penmanship. Notes
 Chemistry 163B Lecture 5 Winter 2014 Challenged enmanship Notes 1 total differential (math handout #4; E&R ch. 3) infinitesimal change in value of state function (well behaved function) total change in
Chemistry 163B Lecture 5 Winter 2014 Challenged enmanship Notes 1 total differential (math handout #4; E&R ch. 3) infinitesimal change in value of state function (well behaved function) total change in
THE FIRST LAW OF THERMODYNAMICS
 THE FIRST LA OF THERMODYNAMIS 9 9 (a) IDENTIFY and SET UP: The ressure is constant and the volume increases (b) = d Figure 9 Since is constant, = d = ( ) The -diagram is sketched in Figure 9 The roblem
THE FIRST LA OF THERMODYNAMIS 9 9 (a) IDENTIFY and SET UP: The ressure is constant and the volume increases (b) = d Figure 9 Since is constant, = d = ( ) The -diagram is sketched in Figure 9 The roblem
Multivariate Calculus Solution 1
 Math Camp Multivariate Calculus Solution Hessian Matrices Math Camp In st semester micro, you will solve general equilibrium models. Sometimes when solving these models it is useful to see if utility functions
Math Camp Multivariate Calculus Solution Hessian Matrices Math Camp In st semester micro, you will solve general equilibrium models. Sometimes when solving these models it is useful to see if utility functions
PHYS 301 HOMEWORK #9-- SOLUTIONS
 PHYS 0 HOMEWORK #9-- SOLUTIONS. We are asked to use Dirichlet' s theorem to determine the value of f (x) as defined below at x = 0, ± /, ± f(x) = 0, - < x
PHYS 0 HOMEWORK #9-- SOLUTIONS. We are asked to use Dirichlet' s theorem to determine the value of f (x) as defined below at x = 0, ± /, ± f(x) = 0, - < x
Lecture 13 Heat Engines
 Lecture 3 Heat Engines hermodynamic rocesses and entroy hermodynamic cycles Extracting work from heat - How do we define engine efficiency? - Carnot cycle: the best ossible efficiency Reading for this
Lecture 3 Heat Engines hermodynamic rocesses and entroy hermodynamic cycles Extracting work from heat - How do we define engine efficiency? - Carnot cycle: the best ossible efficiency Reading for this
Radial Basis Function Networks: Algorithms
 Radial Basis Function Networks: Algorithms Introduction to Neural Networks : Lecture 13 John A. Bullinaria, 2004 1. The RBF Maing 2. The RBF Network Architecture 3. Comutational Power of RBF Networks 4.
Radial Basis Function Networks: Algorithms Introduction to Neural Networks : Lecture 13 John A. Bullinaria, 2004 1. The RBF Maing 2. The RBF Network Architecture 3. Comutational Power of RBF Networks 4.
ATMOS Lecture 7. The First Law and Its Consequences Pressure-Volume Work Internal Energy Heat Capacity Special Cases of the First Law
 TMOS 5130 Lecture 7 The First Law and Its Consequences Pressure-Volume Work Internal Energy Heat Caacity Secial Cases of the First Law Pressure-Volume Work Exanding Volume Pressure δw = f & dx δw = F ds
TMOS 5130 Lecture 7 The First Law and Its Consequences Pressure-Volume Work Internal Energy Heat Caacity Secial Cases of the First Law Pressure-Volume Work Exanding Volume Pressure δw = f & dx δw = F ds
PHYSICS 214A Midterm Exam February 10, 2009
 Clearly Print LAS NAME: FIRS NAME: SIGNAURE: I.D. # PHYSICS 2A Midterm Exam February 0, 2009. Do not open the exam until instructed to do so. 2. Write your answers in the spaces provided for each part
Clearly Print LAS NAME: FIRS NAME: SIGNAURE: I.D. # PHYSICS 2A Midterm Exam February 0, 2009. Do not open the exam until instructed to do so. 2. Write your answers in the spaces provided for each part
Solutions to Test #2 (Kawai) MATH 2421
 Solutions to Test # (Kawai) MATH 4 (#) Each vector eld deicted below is a characterization of F (; ) hm; Ni : The directions of all eld vectors are correct, but the magnitudes are scaled for ease of grahing.
Solutions to Test # (Kawai) MATH 4 (#) Each vector eld deicted below is a characterization of F (; ) hm; Ni : The directions of all eld vectors are correct, but the magnitudes are scaled for ease of grahing.
HEAT, WORK, AND THE FIRST LAW OF THERMODYNAMICS
 HET, ORK, ND THE FIRST L OF THERMODYNMIS 8 EXERISES Section 8. The First Law of Thermodynamics 5. INTERPRET e identify the system as the water in the insulated container. The roblem involves calculating
HET, ORK, ND THE FIRST L OF THERMODYNMIS 8 EXERISES Section 8. The First Law of Thermodynamics 5. INTERPRET e identify the system as the water in the insulated container. The roblem involves calculating
Week 8 lectures. ρ t +u ρ+ρ u = 0. where µ and λ are viscosity and second viscosity coefficients, respectively and S is the strain tensor:
 Week 8 lectures. Equations for motion of fluid without incomressible assumtions Recall from week notes, the equations for conservation of mass and momentum, derived generally without any incomressibility
Week 8 lectures. Equations for motion of fluid without incomressible assumtions Recall from week notes, the equations for conservation of mass and momentum, derived generally without any incomressibility
Chapter 10. Supplemental Text Material
 Chater 1. Sulemental Tet Material S1-1. The Covariance Matri of the Regression Coefficients In Section 1-3 of the tetbook, we show that the least squares estimator of β in the linear regression model y=
Chater 1. Sulemental Tet Material S1-1. The Covariance Matri of the Regression Coefficients In Section 1-3 of the tetbook, we show that the least squares estimator of β in the linear regression model y=
1. Read the section on stability in Wallace and Hobbs. W&H 3.53
 Assignment 2 Due Set 5. Questions marked? are otential candidates for resentation 1. Read the section on stability in Wallace and Hobbs. W&H 3.53 2.? Within the context of the Figure, and the 1st law of
Assignment 2 Due Set 5. Questions marked? are otential candidates for resentation 1. Read the section on stability in Wallace and Hobbs. W&H 3.53 2.? Within the context of the Figure, and the 1st law of
Curves I: Curvature and Torsion. Table of contents
 Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture
Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture
ECE 534 Information Theory - Midterm 2
 ECE 534 Information Theory - Midterm Nov.4, 009. 3:30-4:45 in LH03. You will be given the full class time: 75 minutes. Use it wisely! Many of the roblems have short answers; try to find shortcuts. You
ECE 534 Information Theory - Midterm Nov.4, 009. 3:30-4:45 in LH03. You will be given the full class time: 75 minutes. Use it wisely! Many of the roblems have short answers; try to find shortcuts. You
The Dominating Graph DG bcd (G) of a Graph G
 The Dominating Grah (G) of a Grah G M. Bhanumathi 1, J. John Flavia 2 1 Associate Professor, Government Arts College for Women, Pudukkottai, TN, India 2 Research Scholar, Government Arts College for Women,
The Dominating Grah (G) of a Grah G M. Bhanumathi 1, J. John Flavia 2 1 Associate Professor, Government Arts College for Women, Pudukkottai, TN, India 2 Research Scholar, Government Arts College for Women,
D. Dimitrijević, G. S. Djordjević and Lj. Nešić. Abstract
 Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: htt://www.mf.ni.ac.yu/filomat Filomat 21:2 2007), 251 260 ON GREEN FUNCTION FOR THE FREE PARTICLE D. Dimitrijević, G. S. Djordjević
Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: htt://www.mf.ni.ac.yu/filomat Filomat 21:2 2007), 251 260 ON GREEN FUNCTION FOR THE FREE PARTICLE D. Dimitrijević, G. S. Djordjević
John Weatherwax. Analysis of Parallel Depth First Search Algorithms
 Sulementary Discussions and Solutions to Selected Problems in: Introduction to Parallel Comuting by Viin Kumar, Ananth Grama, Anshul Guta, & George Karyis John Weatherwax Chater 8 Analysis of Parallel
Sulementary Discussions and Solutions to Selected Problems in: Introduction to Parallel Comuting by Viin Kumar, Ananth Grama, Anshul Guta, & George Karyis John Weatherwax Chater 8 Analysis of Parallel
ESCI 341 Atmospheric Thermodynamics Lesson 12 The Energy Minimum Principle
 ESCI 341 Atmospheric Thermodynamics Lesson 12 The Energy Minimum Principle References: Thermodynamics and an Introduction to Thermostatistics, Callen Physical Chemistry, Levine THE ENTROPY MAXIMUM PRINCIPLE
ESCI 341 Atmospheric Thermodynamics Lesson 12 The Energy Minimum Principle References: Thermodynamics and an Introduction to Thermostatistics, Callen Physical Chemistry, Levine THE ENTROPY MAXIMUM PRINCIPLE
Lecture 13. Heat Engines. Thermodynamic processes and entropy Thermodynamic cycles Extracting work from heat
 Lecture 3 Heat Engines hermodynamic rocesses and entroy hermodynamic cycles Extracting work from heat - How do we define engine efficiency? - Carnot cycle: the best ossible efficiency Reading for this
Lecture 3 Heat Engines hermodynamic rocesses and entroy hermodynamic cycles Extracting work from heat - How do we define engine efficiency? - Carnot cycle: the best ossible efficiency Reading for this
Topic 7: Using identity types
 Toic 7: Using identity tyes June 10, 2014 Now we would like to learn how to use identity tyes and how to do some actual mathematics with them. By now we have essentially introduced all inference rules
Toic 7: Using identity tyes June 10, 2014 Now we would like to learn how to use identity tyes and how to do some actual mathematics with them. By now we have essentially introduced all inference rules
Lecture 9 Overview (Ch. 1-3)
 Lecture 9 Overview (Ch. -) Format of the first midterm: four problems with multiple questions. he Ideal Gas Law, calculation of δw, δq and ds for various ideal gas processes. Einstein solid and two-state
Lecture 9 Overview (Ch. -) Format of the first midterm: four problems with multiple questions. he Ideal Gas Law, calculation of δw, δq and ds for various ideal gas processes. Einstein solid and two-state
NOTES. Hyperplane Sections of the n-dimensional Cube
 NOTES Edited by Sergei Tabachnikov Hyerlane Sections of the n-dimensional Cube Rolfdieter Frank and Harald Riede Abstract. We deduce an elementary formula for the volume of arbitrary hyerlane sections
NOTES Edited by Sergei Tabachnikov Hyerlane Sections of the n-dimensional Cube Rolfdieter Frank and Harald Riede Abstract. We deduce an elementary formula for the volume of arbitrary hyerlane sections
Lecture 1.2 Units, Dimensions, Estimations 1. Units To measure a quantity in physics means to compare it with a standard. Since there are many
 Lecture. Units, Dimensions, Estimations. Units To measure a quantity in hysics means to comare it with a standard. Since there are many different quantities in nature, it should be many standards for those
Lecture. Units, Dimensions, Estimations. Units To measure a quantity in hysics means to comare it with a standard. Since there are many different quantities in nature, it should be many standards for those
CALCULUS I. Practice Problems Integrals. Paul Dawkins
 CALCULUS I Practice Problems Integrals Paul Dawkins Table of Contents Preface... Integrals... Introduction... Indefinite Integrals... Comuting Indefinite Integrals... Substitution Rule for Indefinite Integrals...
CALCULUS I Practice Problems Integrals Paul Dawkins Table of Contents Preface... Integrals... Introduction... Indefinite Integrals... Comuting Indefinite Integrals... Substitution Rule for Indefinite Integrals...
Principles of Computed Tomography (CT)
 Page 298 Princiles of Comuted Tomograhy (CT) The theoretical foundation of CT dates back to Johann Radon, a mathematician from Vienna who derived a method in 1907 for rojecting a 2-D object along arallel
Page 298 Princiles of Comuted Tomograhy (CT) The theoretical foundation of CT dates back to Johann Radon, a mathematician from Vienna who derived a method in 1907 for rojecting a 2-D object along arallel
Feedback-error control
 Chater 4 Feedback-error control 4.1 Introduction This chater exlains the feedback-error (FBE) control scheme originally described by Kawato [, 87, 8]. FBE is a widely used neural network based controller
Chater 4 Feedback-error control 4.1 Introduction This chater exlains the feedback-error (FBE) control scheme originally described by Kawato [, 87, 8]. FBE is a widely used neural network based controller
NENG 301 Week 8 Unary Heterogeneous Systems (DeHoff, Chap. 7, Chap )
 NENG 301 Week 8 Unary Heterogeneous Systems (DeHoff, Chap. 7, Chap. 5.3-5.4) Learning objectives for Chapter 7 At the end of this chapter you will be able to: Understand the general features of a unary
NENG 301 Week 8 Unary Heterogeneous Systems (DeHoff, Chap. 7, Chap. 5.3-5.4) Learning objectives for Chapter 7 At the end of this chapter you will be able to: Understand the general features of a unary
Homework Set #3 Rates definitions, Channel Coding, Source-Channel coding
 Homework Set # Rates definitions, Channel Coding, Source-Channel coding. Rates (a) Channels coding Rate: Assuming you are sending 4 different messages using usages of a channel. What is the rate (in bits
Homework Set # Rates definitions, Channel Coding, Source-Channel coding. Rates (a) Channels coding Rate: Assuming you are sending 4 different messages using usages of a channel. What is the rate (in bits
Thermodynamics of phase transitions
 Thermodynamics of phase transitions Katarzyna Sznajd-Weron Department of Theoretical of Physics Wroc law University of Science and Technology, Poland March 12, 2017 Katarzyna Sznajd-Weron (WUST) Thermodynamics
Thermodynamics of phase transitions Katarzyna Sznajd-Weron Department of Theoretical of Physics Wroc law University of Science and Technology, Poland March 12, 2017 Katarzyna Sznajd-Weron (WUST) Thermodynamics
8.044 Lecture Notes Chapter 5: Thermodynamcs, Part 2
 8.044 Lecture Notes Chapter 5: hermodynamcs, Part 2 Lecturer: McGreevy 5.1 Entropy is a state function............................ 5-2 5.2 Efficiency of heat engines............................. 5-6 5.3
8.044 Lecture Notes Chapter 5: hermodynamcs, Part 2 Lecturer: McGreevy 5.1 Entropy is a state function............................ 5-2 5.2 Efficiency of heat engines............................. 5-6 5.3
4. Score normalization technical details We now discuss the technical details of the score normalization method.
 SMT SCORING SYSTEM This document describes the scoring system for the Stanford Math Tournament We begin by giving an overview of the changes to scoring and a non-technical descrition of the scoring rules
SMT SCORING SYSTEM This document describes the scoring system for the Stanford Math Tournament We begin by giving an overview of the changes to scoring and a non-technical descrition of the scoring rules
Magnetospheric Physics - Homework, 4/04/2014
 Magnetosheric hysics - Homework, // 7. Fast wave, fast shock, erendicular shock, entroy, jum relation. Consider the fast erendicular shock. a) Determine the ositive root of the solution for the comression
Magnetosheric hysics - Homework, // 7. Fast wave, fast shock, erendicular shock, entroy, jum relation. Consider the fast erendicular shock. a) Determine the ositive root of the solution for the comression
A Numerical Method for Critical Buckling Load for a Beam Supported on Elastic Foundation
 A Numerical Method for Critical Buckling Load for a Beam Suorted on Elastic Foundation Guo-ing Xia Institute of Bridge Engineering, Dalian University of Technology, Dalian, Liaoning Province, P. R. China
A Numerical Method for Critical Buckling Load for a Beam Suorted on Elastic Foundation Guo-ing Xia Institute of Bridge Engineering, Dalian University of Technology, Dalian, Liaoning Province, P. R. China
Internal Energy in terms of Properties
 Lecture #3 Internal Energy in terms of roerties Internal energy is a state function. A change in the state of the system causes a change in its roerties. So, we exress the change in internal energy in
Lecture #3 Internal Energy in terms of roerties Internal energy is a state function. A change in the state of the system causes a change in its roerties. So, we exress the change in internal energy in
Problem: Calculate the entropy change that results from mixing 54.0 g of water at 280 K with 27.0 g of water at 360 K in a vessel whose walls are
 Problem: Calculate the entropy change that results from mixing 54.0 g of water at 280 K with 27.0 g of water at 360 K in a vessel whose walls are perfectly insulated from the surroundings. Is this a spontaneous
Problem: Calculate the entropy change that results from mixing 54.0 g of water at 280 K with 27.0 g of water at 360 K in a vessel whose walls are perfectly insulated from the surroundings. Is this a spontaneous
First law of thermodynamics (Jan 12, 2016) page 1/7. Here are some comments on the material in Thompkins Chapter 1
 First law of thermodynamics (Jan 12, 2016) age 1/7 Here are some comments on the material in Thomkins Chater 1 1) Conservation of energy Adrian Thomkins (eq. 1.9) writes the first law as: du = d q d w
First law of thermodynamics (Jan 12, 2016) age 1/7 Here are some comments on the material in Thomkins Chater 1 1) Conservation of energy Adrian Thomkins (eq. 1.9) writes the first law as: du = d q d w
Principal Components Analysis and Unsupervised Hebbian Learning
 Princial Comonents Analysis and Unsuervised Hebbian Learning Robert Jacobs Deartment of Brain & Cognitive Sciences University of Rochester Rochester, NY 1467, USA August 8, 008 Reference: Much of the material
Princial Comonents Analysis and Unsuervised Hebbian Learning Robert Jacobs Deartment of Brain & Cognitive Sciences University of Rochester Rochester, NY 1467, USA August 8, 008 Reference: Much of the material
Lecture 21: Quantum Communication
 CS 880: Quantum Information Processing 0/6/00 Lecture : Quantum Communication Instructor: Dieter van Melkebeek Scribe: Mark Wellons Last lecture, we introduced the EPR airs which we will use in this lecture
CS 880: Quantum Information Processing 0/6/00 Lecture : Quantum Communication Instructor: Dieter van Melkebeek Scribe: Mark Wellons Last lecture, we introduced the EPR airs which we will use in this lecture
Chapter 3- Answers to selected exercises
 Chater 3- Anwer to elected exercie. he chemical otential of a imle uid of a ingle comonent i gien by the exreion o ( ) + k B ln o ( ) ; where i the temerature, i the reure, k B i the Boltzmann contant,
Chater 3- Anwer to elected exercie. he chemical otential of a imle uid of a ingle comonent i gien by the exreion o ( ) + k B ln o ( ) ; where i the temerature, i the reure, k B i the Boltzmann contant,
[S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B
![[S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B [S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B](/thumbs/72/67524544.jpg) Canonical ensemble (Two derivations) Determine the probability that a system S in contact with a reservoir 1 R to be in one particular microstate s with energy ɛ s. (If there is degeneracy we are picking
Canonical ensemble (Two derivations) Determine the probability that a system S in contact with a reservoir 1 R to be in one particular microstate s with energy ɛ s. (If there is degeneracy we are picking
The Fekete Szegő theorem with splitting conditions: Part I
 ACTA ARITHMETICA XCIII.2 (2000) The Fekete Szegő theorem with slitting conditions: Part I by Robert Rumely (Athens, GA) A classical theorem of Fekete and Szegő [4] says that if E is a comact set in the
ACTA ARITHMETICA XCIII.2 (2000) The Fekete Szegő theorem with slitting conditions: Part I by Robert Rumely (Athens, GA) A classical theorem of Fekete and Szegő [4] says that if E is a comact set in the
Topic 30 Notes Jeremy Orloff
 Toic 30 Notes Jeremy Orloff 30 Alications to oulation biology 30.1 Modeling examles 30.1.1 Volterra redator-rey model The Volterra redator-rey system models the oulations of two secies with a redatorrey
Toic 30 Notes Jeremy Orloff 30 Alications to oulation biology 30.1 Modeling examles 30.1.1 Volterra redator-rey model The Volterra redator-rey system models the oulations of two secies with a redatorrey
Applied Fitting Theory VI. Formulas for Kinematic Fitting
 Alied Fitting heory VI Paul Avery CBX 98 37 June 9, 1998 Ar. 17, 1999 (rev.) I Introduction Formulas for Kinematic Fitting I intend for this note and the one following it to serve as mathematical references,
Alied Fitting heory VI Paul Avery CBX 98 37 June 9, 1998 Ar. 17, 1999 (rev.) I Introduction Formulas for Kinematic Fitting I intend for this note and the one following it to serve as mathematical references,
Improved Capacity Bounds for the Binary Energy Harvesting Channel
 Imroved Caacity Bounds for the Binary Energy Harvesting Channel Kaya Tutuncuoglu 1, Omur Ozel 2, Aylin Yener 1, and Sennur Ulukus 2 1 Deartment of Electrical Engineering, The Pennsylvania State University,
Imroved Caacity Bounds for the Binary Energy Harvesting Channel Kaya Tutuncuoglu 1, Omur Ozel 2, Aylin Yener 1, and Sennur Ulukus 2 1 Deartment of Electrical Engineering, The Pennsylvania State University,
Foundations of thermodynamics Fundamental thermodynamical concepts
 Foundations of thermodynamics Fundamental thermodynamical concets System is the macrohysical entity under consideration Surrounding is the wld outside of the system Oen system can exchange matter heat
Foundations of thermodynamics Fundamental thermodynamical concets System is the macrohysical entity under consideration Surrounding is the wld outside of the system Oen system can exchange matter heat
Liquid water static energy page 1/8
 Liquid water static energy age 1/8 1) Thermodynamics It s a good idea to work with thermodynamic variables that are conserved under a known set of conditions, since they can act as assive tracers and rovide
Liquid water static energy age 1/8 1) Thermodynamics It s a good idea to work with thermodynamic variables that are conserved under a known set of conditions, since they can act as assive tracers and rovide
Section 7.4 #1, 5, 6, 8, 12, 13, 44, 53; Section 7.5 #7, 10, 11, 20, 22; Section 7.7 #1, 4, 10, 15, 22, 44
 Math B Prof. Audrey Terras HW #4 Solutions Due Tuesday, Oct. 9 Section 7.4 #, 5, 6, 8,, 3, 44, 53; Section 7.5 #7,,,, ; Section 7.7 #, 4,, 5,, 44 7.4. Since 5 = 5 )5 + ), start with So, 5 = A 5 + B 5 +.
Math B Prof. Audrey Terras HW #4 Solutions Due Tuesday, Oct. 9 Section 7.4 #, 5, 6, 8,, 3, 44, 53; Section 7.5 #7,,,, ; Section 7.7 #, 4,, 5,, 44 7.4. Since 5 = 5 )5 + ), start with So, 5 = A 5 + B 5 +.
1 Gambler s Ruin Problem
 Coyright c 2017 by Karl Sigman 1 Gambler s Ruin Problem Let N 2 be an integer and let 1 i N 1. Consider a gambler who starts with an initial fortune of $i and then on each successive gamble either wins
Coyright c 2017 by Karl Sigman 1 Gambler s Ruin Problem Let N 2 be an integer and let 1 i N 1. Consider a gambler who starts with an initial fortune of $i and then on each successive gamble either wins
Chemical Kinetics and Equilibrium - An Overview - Key
 Chemical Kinetics and Equilibrium - An Overview - Key The following questions are designed to give you an overview of the toics of chemical kinetics and chemical equilibrium. Although not comrehensive,
Chemical Kinetics and Equilibrium - An Overview - Key The following questions are designed to give you an overview of the toics of chemical kinetics and chemical equilibrium. Although not comrehensive,
Differential equations
 Differential equations First order differential equation Imlicit F(, y, y ) = or Elicit y = f ( y, ) In general = hysical laws involving a rate of change (with time) of an event = function Solution of
Differential equations First order differential equation Imlicit F(, y, y ) = or Elicit y = f ( y, ) In general = hysical laws involving a rate of change (with time) of an event = function Solution of
8 STOCHASTIC PROCESSES
 8 STOCHASTIC PROCESSES The word stochastic is derived from the Greek στoχαστικoς, meaning to aim at a target. Stochastic rocesses involve state which changes in a random way. A Markov rocess is a articular
8 STOCHASTIC PROCESSES The word stochastic is derived from the Greek στoχαστικoς, meaning to aim at a target. Stochastic rocesses involve state which changes in a random way. A Markov rocess is a articular
Convex Optimization methods for Computing Channel Capacity
 Convex Otimization methods for Comuting Channel Caacity Abhishek Sinha Laboratory for Information and Decision Systems (LIDS), MIT sinhaa@mit.edu May 15, 2014 We consider a classical comutational roblem
Convex Otimization methods for Comuting Channel Caacity Abhishek Sinha Laboratory for Information and Decision Systems (LIDS), MIT sinhaa@mit.edu May 15, 2014 We consider a classical comutational roblem
Distinguish between. and non-thermal energy sources.
 Distinguish between System & Surroundings We also distinguish between thermal We also distinguish between thermal and non-thermal energy sources. P Work The gas in the cylinder is the system How much work
Distinguish between System & Surroundings We also distinguish between thermal We also distinguish between thermal and non-thermal energy sources. P Work The gas in the cylinder is the system How much work
Linear diophantine equations for discrete tomography
 Journal of X-Ray Science and Technology 10 001 59 66 59 IOS Press Linear diohantine euations for discrete tomograhy Yangbo Ye a,gewang b and Jiehua Zhu a a Deartment of Mathematics, The University of Iowa,
Journal of X-Ray Science and Technology 10 001 59 66 59 IOS Press Linear diohantine euations for discrete tomograhy Yangbo Ye a,gewang b and Jiehua Zhu a a Deartment of Mathematics, The University of Iowa,
Basic statistical models
 Basic statistical models Valery Pokrovsky March 27, 2012 Part I Ising model 1 Definition and the basic roerties The Ising model (IM) was invented by Lenz. His student Ising has found the artition function
Basic statistical models Valery Pokrovsky March 27, 2012 Part I Ising model 1 Definition and the basic roerties The Ising model (IM) was invented by Lenz. His student Ising has found the artition function
f(x) p(x) =p(b)... d. A function can have two different horizontal asymptotes...
 Math Final Eam, Fall. ( ts.) Mark each statement as either true [T] or false [F]. f() a. If lim f() =and lim g() =, then lim does not eist......................!5!5!5 g() b. If is a olynomial, then lim!b
Math Final Eam, Fall. ( ts.) Mark each statement as either true [T] or false [F]. f() a. If lim f() =and lim g() =, then lim does not eist......................!5!5!5 g() b. If is a olynomial, then lim!b
PY2005: Thermodynamics
 ome Multivariate Calculus Y2005: hermodynamics Notes by Chris Blair hese notes cover the enior Freshman course given by Dr. Graham Cross in Michaelmas erm 2007, except for lecture 12 on phase changes.
ome Multivariate Calculus Y2005: hermodynamics Notes by Chris Blair hese notes cover the enior Freshman course given by Dr. Graham Cross in Michaelmas erm 2007, except for lecture 12 on phase changes.
Homework Solution 4 for APPM4/5560 Markov Processes
 Homework Solution 4 for APPM4/556 Markov Processes 9.Reflecting random walk on the line. Consider the oints,,, 4 to be marked on a straight line. Let X n be a Markov chain that moves to the right with
Homework Solution 4 for APPM4/556 Markov Processes 9.Reflecting random walk on the line. Consider the oints,,, 4 to be marked on a straight line. Let X n be a Markov chain that moves to the right with
You may not start to read the questions printed on the subsequent pages until instructed to do so by the Invigilator.
 NAURAL SCIENCES RIPOS Part IA Wednesday 5 June 2005 9 to 2 MAHEMAICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions. All questions carry the
NAURAL SCIENCES RIPOS Part IA Wednesday 5 June 2005 9 to 2 MAHEMAICS (2) Before you begin read these instructions carefully: You may submit answers to no more than six questions. All questions carry the
Math 120: Examples. Green s theorem. x 2 + y 2 dx + x. x 2 + y 2 dy. y x 2 + y 2, Q = x. x 2 + y 2
 Math 12: Examples Green s theorem Example 1. onsider the integral Evaluate it when (a) is the circle x 2 + y 2 = 1. (b) is the ellipse x 2 + y2 4 = 1. y x 2 + y 2 dx + Solution. (a) We did this in class.
Math 12: Examples Green s theorem Example 1. onsider the integral Evaluate it when (a) is the circle x 2 + y 2 = 1. (b) is the ellipse x 2 + y2 4 = 1. y x 2 + y 2 dx + Solution. (a) We did this in class.
More Thermodynamics. Specific Specific Heats of a Gas Equipartition of Energy Reversible and Irreversible Processes
 More Thermodynamics Specific Specific Heats of a Gas Equipartition of Energy Reversible and Irreversible Processes Carnot Cycle Efficiency of Engines Entropy More Thermodynamics 1 Specific Heat of Gases
More Thermodynamics Specific Specific Heats of a Gas Equipartition of Energy Reversible and Irreversible Processes Carnot Cycle Efficiency of Engines Entropy More Thermodynamics 1 Specific Heat of Gases
PHYS1001 PHYSICS 1 REGULAR Module 2 Thermal Physics Chapter 17 First Law of Thermodynamics
 PHYS1001 PHYSICS 1 REGULAR Module Thermal Physics Chater 17 First Law of Thermodynamics References: 17.1 to 17.9 Examles: 17.1 to 17.7 Checklist Thermodynamic system collection of objects and fields. If
PHYS1001 PHYSICS 1 REGULAR Module Thermal Physics Chater 17 First Law of Thermodynamics References: 17.1 to 17.9 Examles: 17.1 to 17.7 Checklist Thermodynamic system collection of objects and fields. If
Basic Thermodynamic Relations
 Basic herodynaic Relations Isolated syste: this is a syste that does not exchange energy with the surrounding edia. First Postulate (equilibriu theore) : Isolated syste always reaches the equilibriu state
Basic herodynaic Relations Isolated syste: this is a syste that does not exchange energy with the surrounding edia. First Postulate (equilibriu theore) : Isolated syste always reaches the equilibriu state
MTH234 Chapter 15 - Multiple Integrals Michigan State University
 MTH24 Chater 15 - Multile Integrals Michigan State University 6 Surface Area Just as arc length is an alication of a single integral, surface area is an alication of double integrals. In 15.6 we comute
MTH24 Chater 15 - Multile Integrals Michigan State University 6 Surface Area Just as arc length is an alication of a single integral, surface area is an alication of double integrals. In 15.6 we comute
Solution Week 75 (2/16/04) Hanging chain
 Catenary Catenary is idealized shae of chain or cable hanging under its weight with the fixed end oints. The chain (cable) curve is catenary that minimizes the otential energy PHY 322, Sring 208 Solution
Catenary Catenary is idealized shae of chain or cable hanging under its weight with the fixed end oints. The chain (cable) curve is catenary that minimizes the otential energy PHY 322, Sring 208 Solution
EXACT EQUATIONS AND INTEGRATING FACTORS
 MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
Exam Question 10: Differential Equations. June 19, Applied Mathematics: Lecture 6. Brendan Williamson. Introduction.
 Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Rigorous bounds on scaling laws in fluid dynamics
 Rigorous bounds on scaling laws in fluid dynamics Felix Otto Notes written by Steffen Pottel Contents Main Result on Thermal Convection Derivation of the Model. A Stability Criterion........................
Rigorous bounds on scaling laws in fluid dynamics Felix Otto Notes written by Steffen Pottel Contents Main Result on Thermal Convection Derivation of the Model. A Stability Criterion........................
Real Analysis 1 Fall Homework 3. a n.
 eal Analysis Fall 06 Homework 3. Let and consider the measure sace N, P, µ, where µ is counting measure. That is, if N, then µ equals the number of elements in if is finite; µ = otherwise. One usually
eal Analysis Fall 06 Homework 3. Let and consider the measure sace N, P, µ, where µ is counting measure. That is, if N, then µ equals the number of elements in if is finite; µ = otherwise. One usually
