Procedure used to solve equations of the form
|
|
|
- Cornelius Hunter
- 6 years ago
- Views:
Transcription
1 Equations of the form a d 2 y dx 2 + bdy dx + cy = 0 (5) Procedure used to solve equations of the form a d 2 y dx 2 + b dy dx 1. rewrite the given differential equation + cy = 0 (1) a d 2 y dx 2 + b dy + cy = 0 dx (2) (ad 2 + bd + c)y = 0 (3) 2. Substitute m for D and solve the auxillary equation (am 2 + bm + c)y = 0 (4)
2 3 different types of solutions 1. Roots of auxillary equation are REAL and DIFFERENT say m = α and m = β, then the general solution is y = Ae αx + Be βx (6) 2. If the roots of the auxillary equation are real and equal, say m = α twice then, the general solution is y = (Ax + B)e αx (7) 3. if the roots of the auxiliary equation are complex, say m = α ± jβ then the general solution is y = e αx (Ccosβx + Dsinβx) (8)
3 Equations of the form d 2 y dx 2 ± n2 y = 0 1. d 2 y dx 2 +n2 y = 0 m 2 +n 2 = 0 m 2 = n 2 m = ±jn (9) This is a special case of C above α = 0 and β = n.
4 Solution y = e 0x (Ccosβx + Dsinβx) (10) y = (Ccosβx + Dsinβx) (11) d 2 y dx 2 n2 y = 0 m 2 n 2 = 0 m 2 = n 2 m = ±n (12) This is a special case of 1 above. y = Ae αx + Be βx (13)
5 If the particular solution of a differential equation is required then substitute the given boundary conditions to find the unknown constants.
6 Example 1 Find the general solution of 6 d 2 y dx 2 + 5dy dx 4y = 0 (14) and then find the particular solution given that when x=0, y=11 and dy dx =0
7 Solution 1. In D operator form (6D 2 + 5D 4)y = 0 (15) where D = d dx 2. The auxiliary equation is factorising gives 6m 2 + 5m 4 = 0 (16) (3m + 4)(2m 1) = 0 (17) That is m = 4 3 or m = 1 2
8 Since both roots are real and different the general solution is y = Ae 4 3 x + Be 1 2 x (18) When x=0, y=11 then 11 = Ae Be (19) 11 = A + B (20)
9 The other condition we have is that when x=0 dy dx =0 since y = Ae 4 3 x + Be 1 2 x (21) dy dx = 4 3 Ae 4 3 x Be 1 2 x (22)
10 Thus 0 = 4 3 A B (23) 2 0 = 8 3 A + B (24) so B = 8 3A Sub in above A=3 and B=8 11 = A A = 11 3 A (25) y = 3e 4 3 x + 8e 1 2 x (26)
11 Exercise 1 Determine the general solution of 4 d 2 y dt 2 12dy + 9y = 0 (27) dt and then find the particular solution given that when t=0, y=2 and dy dt =4
12 Solution 1. Write in D operator form (4D 2 12D + 9)y = 0 (28) where 2. The Auxiliary equation is D = d dt (29) (4m 2 12m + 9)y = 0 (30) (2m 3)(2m 3) = 0 (31) so m 3 2 twice
13 Since the two roots are real and equal the general solution is y = (At + B)e 3 2 t (32) To find the particular solution when y=2, t=0 2 = (A0 + B)e 3 2 t (33) B=2
14 When dy dt = 4, t = 0 Thus dy dt = (At + B)3 2 e 3 2 t + e 3 2 t (A) (34) 4 = () + B) 3 2 e e (A) (35) So A=1 The particular solution is 4 = 3 2 B + A (36) y = (t + 2)e 3 2 t (37)
15 Exercise 2 Determine the general solution of the DE d 2 y dx 2 + 2dy dx + 5y = 0 (38) and find the particular solution given that when x=0, y=1 and dy dx = 5
16 Solution y = e x (cos2x + 3sin2x) (39)
17 Exercise 3 Determine the general solution of the DE Solution d 2 y 16y = 0 (40) dx 2 y = Ae 4x + Be 4x (41)
18 Exercise 4 Determine the general solution of the DE Solution d 2 y + 49y = 0 (42) dx 2 y = Acos7x + Bsin7x (43)
19 Equations of the Form a d 2 y dx 2 + bdy dx + cy = f (x) (45) The DE a d 2 y dx 2 + b dy + cy = f (x) (44) dx where a,b,c are constants, is a linear, second oreder differential equation with constant coefficients. In order to solve this type of equation a substitution is made.
20 Let y=u+v a d 2 dx 2 (u + v) + b d (u + v) + c(u + v) = f (x) (46) dx (a d 2 u dx 2 + b du dx + cu) + (ad 2 v dx 2 + b dv dx + cv) = f (x) (47)
21 Let v be any solution such that a d 2 v dx 2 + b dv dx + cv = f (x) (48) This means that (a d 2 u dx 2 + b du + cu) = 0 (49) dx We learned how to solve this in the last section
22 The final solution y = u + v (50) The function u is called the Complementary Function(C.F) The function v is called the particular integral(p.i) y = u + v = C.F + P.I (51)
23 Example 1: f(x)= a constant If f(x) is a constant then first try v=k, where k is a constant. Solve d 2 y dx 2 + 4dy dx + 3y = 6 (52)
24 Solution (a d 2 u dx 2 + b du 2 dx + cu) + (ad v dx 2 + b dv + cv) = f (x) (53) dx The complementary function u is obtained as in the previous section (a d 2 u dx 2 + b du + cu) = 0 (54) dx
25 The auxilliary eqn is m 2 + 4m + 3 = 0 (55) (m + 3)(m + 1) = 0 (56) so m=-3 and m=-1
26 2 roots are real and different so the complementary function u = Ae 3x + Be x (57)
27 To get the particular integral we let v=k (a d 2 v dx 2 + b dv dx (a d 2 k dx 2 + b dk dx + cv) = 6 (58) + ck) = 6 (59) (D 2 + 4D + 3)k = 6 (60)
28 D 2 k = 0, D(k) = 0, then 3k = 6, and = 2 (61) Hence the particular integral v=2
29 The general solution is given by y=u+v y = Ae 3x + Be x + 2 (62)
30 Exercise 1: f(x)= a constant If f(x) is a constant then first try v=k, where k is a constant. Solve d 2 y dx 2 5dy + 4y = 20 (63) dx
31 Solution (a d 2 u dx 2 + b du 2 dx + cu) + (ad v dx 2 + b dv + cv) = f (x) (64) dx The complementary function u is obtained as in the previous section
32 The auxilliary eqn is so m=4 and m=1 (a d 2 u dx 2 + b du + cu) = 0 (65) dx m 2 5m + 4 = 0 (66) (m 4)(m 1) = 0 (67)
33 2 roots are real and different so the complementary function u = Ae 4x + Be x (68)
34 To get the particular integral we let v=k (a d 2 v dx 2 + b dv dx (a d 2 k dx 2 + b dk dx + cv) = 20 (69) + ck) = 20 (70) (D 2 5D + 4)k = 20 (71)
35 D 2 k = 0, D(k) = 0, then 4k = 20, and k = 5 (72) Hence the particular integral v=5 The general solution is given by y=u+v y = Ae 4x + Be x + 5 (73)
36 Special Case Find the general solution of d 2 y dx 2 + 4dy dx = 6 (74) and then find the particular solution given that when x=0, y=0 and dy dx = 0.
37 Solution First we find the complementary function u In D operator form the DE is (D 2 + 4D)y = 6 (75) The auxilliary eqn is m 2 + 4m = 0 (76) m(m + 4) = 0 (77)
38 Hence m=0 or -4 We have 2 real roots which are different so u = Ae 0x + Be 4x (78) u = A + Be 4x (79)
39 we must find the particular integral so we assume v=k we obtain which gives us (D 2 + 4D)k = 6 (80) 0 = 6 (81) which is impossible. This occurs because the CF already includes a constant
40 Instead we let v=kx (D 2 + 4D)kx = 6 (82) 4k = 6 (83) k = 3 2 (84) Hence the particular integral v = 3 2 x
41 So the general solution y = u + v = A + Be 4x x (85)
42 Now to find the particular solution When x=0,y=0 and since y = A + Be 4x x (86) 0 = A + Be (87) 0 = A + B (88)
43 dy dx = 0 4Be 4x dy dx = 0, x = 0, 0 = 4B + 3 2, B = 3 8 A = 3 8 (89) (90) (91) Hence the particular solution is y = u + v = e 4x x (92)
44 Exercise 2 Find the general solution of d 2 y dx 2 2dy dx = 4 (93) and then find the particular solution given that when x=0, y=0 and dy dx = 0
45 Solution First we find the complementary function u In D operator form the DE is (D 2 2D)y = 4 (94) The auxilliary eqn is m 2 2m = 0 (95) m(m 2) = 0 (96)
46 Hence m=0 or 2 We have 2 real roots which are different so y = Ae 0x + Be 2x (97) y = A + Be 2x (98)
47 we must find the particular integral so we assume v=k we obtain which gives us (D 2 2D)k = 4 (99) 0 = 4 (100) which is impossible. This occurs because the CF already includes a constant
48 Instead we let v=kx (D 2 2D)kx = 4 (101) 2k = 4 (102) k = 2 (103) Hence the particular integral v = 2x
49 So the general solution y = u + v = A + Be 2x 2x (104)
50 Now to find the particular solution When x=0,y=0 and since y = A + Be 2x 2x (105) 0 = A + Be (0) (106) 0 = A + B (107)
51 dy dx Hence the particular solution is dy dx = 0 + 2Be2x 2 (108) = 0, x = 0, 0 = 2B 2, B = 1 (109) A = 1 (110) y = u + v = 1 + 1e 2x 2x (111)
52 Applications Typical examples of the equation solved above are the equations for the charge q in a series-connected electrical circuit L dq2 dt + R dq dt + 1 C q = E (112) and the force equation for a mass, spring, damped mechanical system m dq2 dt + adq + ks = F (113) dt
JUST THE MATHS UNIT NUMBER ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 15.4 ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) by A.J.Hobson 15.4.1 Introduction 15.4.2 Second order homogeneous equations 15.4.3 Special cases of the auxiliary
JUST THE MATHS UNIT NUMBER 15.4 ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) by A.J.Hobson 15.4.1 Introduction 15.4.2 Second order homogeneous equations 15.4.3 Special cases of the auxiliary
JUST THE MATHS SLIDES NUMBER ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) A.J.Hobson
 JUST THE MATHS SLIDES NUMBER 15.4 ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) by A.J.Hobson 15.4.1 Introduction 15.4.2 Second order homogeneous equations 15.4.3 Special cases of the
JUST THE MATHS SLIDES NUMBER 15.4 ORDINARY DIFFERENTIAL EQUATIONS 4 (Second order equations (A)) by A.J.Hobson 15.4.1 Introduction 15.4.2 Second order homogeneous equations 15.4.3 Special cases of the
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
Ma 221. The material below was covered during the lecture given last Wed. (1/29/14). Homogeneous Linear Equations with Constant Coefficients
 Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
dx n a 1(x) dy
 HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
HIGHER ORDER DIFFERENTIAL EQUATIONS Theory of linear equations Initial-value and boundary-value problem nth-order initial value problem is Solve: a n (x) dn y dx n + a n 1(x) dn 1 y dx n 1 +... + a 1(x)
MATH 312 Section 4.3: Homogeneous Linear Equations with Constant Coefficients
 MATH 312 Section 4.3: Homogeneous Linear Equations with Constant Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Getting Started 2 Second Order Equations Two Real
MATH 312 Section 4.3: Homogeneous Linear Equations with Constant Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Getting Started 2 Second Order Equations Two Real
17.2 Nonhomogeneous Linear Equations. 27 September 2007
 17.2 Nonhomogeneous Linear Equations 27 September 2007 Nonhomogeneous Linear Equations The differential equation to be studied is of the form ay (x) + by (x) + cy(x) = G(x) (1) where a 0, b, c are given
17.2 Nonhomogeneous Linear Equations 27 September 2007 Nonhomogeneous Linear Equations The differential equation to be studied is of the form ay (x) + by (x) + cy(x) = G(x) (1) where a 0, b, c are given
Calculus I Announcements
 Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
ENGI 4430 PDEs - d Alembert Solutions Page 11.01
 ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
6 Second Order Linear Differential Equations
 6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
4.2 Homogeneous Linear Equations
 4.2 Homogeneous Linear Equations Homogeneous Linear Equations with Constant Coefficients Consider the first-order linear differential equation with constant coefficients a 0 and b. If f(t) = 0 then this
4.2 Homogeneous Linear Equations Homogeneous Linear Equations with Constant Coefficients Consider the first-order linear differential equation with constant coefficients a 0 and b. If f(t) = 0 then this
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Math 106 Fall 2014 Exam 2.1 October 31, ln(x) x 3 dx = 1. 2 x 2 ln(x) + = 1 2 x 2 ln(x) + 1. = 1 2 x 2 ln(x) 1 4 x 2 + C
 Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
Math 6 Fall 4 Exam. October 3, 4. The following questions have to do with the integral (a) Evaluate dx. Use integration by parts (x 3 dx = ) ( dx = ) x3 x dx = x x () dx = x + x x dx = x + x 3 dx dx =
The particular integral :
 Second order linear equation with constant coefficients The particular integral : d f df Lf = a + a + af = h( x) Solutions with combinations of driving functions d f df Lf = a + a + af = h( x) + h( x)
Second order linear equation with constant coefficients The particular integral : d f df Lf = a + a + af = h( x) Solutions with combinations of driving functions d f df Lf = a + a + af = h( x) + h( x)
Review for Ma 221 Final Exam
 Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
REFERENCE: CROFT & DAVISON CHAPTER 20 BLOCKS 1-3
 IV ORDINARY DIFFERENTIAL EQUATIONS REFERENCE: CROFT & DAVISON CHAPTER 0 BLOCKS 1-3 INTRODUCTION AND TERMINOLOGY INTRODUCTION A differential equation (d.e.) e) is an equation involving an unknown function
IV ORDINARY DIFFERENTIAL EQUATIONS REFERENCE: CROFT & DAVISON CHAPTER 0 BLOCKS 1-3 INTRODUCTION AND TERMINOLOGY INTRODUCTION A differential equation (d.e.) e) is an equation involving an unknown function
Math 4B Notes. Written by Victoria Kala SH 6432u Office Hours: T 12:45 1:45pm Last updated 7/24/2016
 Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 4B Notes Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: T 2:45 :45pm Last updated 7/24/206 Classification of Differential Equations The order of a differential equation is the
Math 226 Calculus Spring 2016 Practice Exam 1. (1) (10 Points) Let the differentiable function y = f(x) have inverse function x = f 1 (y).
 Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Math 6 Calculus Spring 016 Practice Exam 1 1) 10 Points) Let the differentiable function y = fx) have inverse function x = f 1 y). a) Write down the formula relating the derivatives f x) and f 1 ) y).
Substitutions and by Parts, Area Between Curves. Goals: The Method of Substitution Areas Integration by Parts
 Week #7: Substitutions and by Parts, Area Between Curves Goals: The Method of Substitution Areas Integration by Parts 1 Week 7 The Indefinite Integral The Fundamental Theorem of Calculus, b a f(x) dx =
Week #7: Substitutions and by Parts, Area Between Curves Goals: The Method of Substitution Areas Integration by Parts 1 Week 7 The Indefinite Integral The Fundamental Theorem of Calculus, b a f(x) dx =
I. Impulse Response and Convolution
 I. Impulse Response and Convolution 1. Impulse response. Imagine a mass m at rest on a frictionless track, then given a sharp kick at time t =. We model the kick as a constant force F applied to the mass
I. Impulse Response and Convolution 1. Impulse response. Imagine a mass m at rest on a frictionless track, then given a sharp kick at time t =. We model the kick as a constant force F applied to the mass
Title: Solving Ordinary Differential Equations (ODE s)
 ... Mathematics Support Centre Title: Solving Ordinary Differential Equations (ODE s) Target: On completion of this workbook you should be able to recognise and apply the appropriate method for solving
... Mathematics Support Centre Title: Solving Ordinary Differential Equations (ODE s) Target: On completion of this workbook you should be able to recognise and apply the appropriate method for solving
Solutions to Exam 2, Math 10560
 Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Indefinite Integration
 Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, pm-9pm. Make sure you show your work!
 PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, 2013 7pm-9pm Make sure you show your work! Problem 1 - Current and Resistivity (20 pts) a) A cable of diameter d carries a current
PHYSICS 7B, Section 1 Fall 2013 Midterm 2, C. Bordel Monday, November 4, 2013 7pm-9pm Make sure you show your work! Problem 1 - Current and Resistivity (20 pts) a) A cable of diameter d carries a current
4 Differential Equations
 Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Integration by Parts
 Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Higher-order ordinary differential equations
 Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
3 DIFFERENTIATION RULES DIFFERENTIATION RULES We have: Seen how to interpret derivatives as slopes and rates of change Seen how to estimate derivatives of functions given by tables of values Learned how
y = x 3 and y = 2x 2 x. 2x 2 x = x 3 x 3 2x 2 + x = 0 x(x 2 2x + 1) = 0 x(x 1) 2 = 0 x = 0 and x = (x 3 (2x 2 x)) dx
 Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Chapter 3. Reading assignment: In this chapter we will cover Sections dx 1 + a 0(x)y(x) = g(x). (1)
 Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
June 2011 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations
 June 20 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations The topics covered in this exam can be found in An introduction to differential equations
June 20 PURDUE UNIVERSITY Study Guide for the Credit Exam in (MA 262) Linear Algebra and Differential Equations The topics covered in this exam can be found in An introduction to differential equations
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
TAM3B DIFFERENTIAL EQUATIONS Unit : I to V
 TAM3B DIFFERENTIAL EQUATIONS Unit : I to V Unit I -Syllabus Homogeneous Functions and examples Homogeneous Differential Equations Exact Equations First Order Linear Differential Equations Reduction of
TAM3B DIFFERENTIAL EQUATIONS Unit : I to V Unit I -Syllabus Homogeneous Functions and examples Homogeneous Differential Equations Exact Equations First Order Linear Differential Equations Reduction of
MAT187H1F Lec0101 Burbulla
 Spring 2017 Second Order Linear Homogeneous Differential Equation DE: A(x) d 2 y dx 2 + B(x)dy dx + C(x)y = 0 This equation is called second order because it includes the second derivative of y; it is
Spring 2017 Second Order Linear Homogeneous Differential Equation DE: A(x) d 2 y dx 2 + B(x)dy dx + C(x)y = 0 This equation is called second order because it includes the second derivative of y; it is
Section 11.1 What is a Differential Equation?
 1 Section 11.1 What is a Differential Equation? Example 1 Suppose a ball is dropped from the top of a building of height 50 meters. Let h(t) denote the height of the ball after t seconds, then it is known
1 Section 11.1 What is a Differential Equation? Example 1 Suppose a ball is dropped from the top of a building of height 50 meters. Let h(t) denote the height of the ball after t seconds, then it is known
Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
UNIVERSITY OF SOUTHAMPTON. A foreign language dictionary (paper version) is permitted provided it contains no notes, additions or annotations.
 UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
Ordinary differential equations
 CP3 REVISION LECTURE ON Ordinary differential equations 1 First order linear equations First order nonlinear equations 3 Second order linear equations with constant coefficients 4 Systems of linear ordinary
CP3 REVISION LECTURE ON Ordinary differential equations 1 First order linear equations First order nonlinear equations 3 Second order linear equations with constant coefficients 4 Systems of linear ordinary
Calculus II Practice Test 1 Problems: , 6.5, Page 1 of 10
 Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II)
 McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
Fourier transforms. c n e inπx. f (x) = Write same thing in an equivalent form, using n = 1, f (x) = l π
 Fourier transforms We can imagine our periodic function having periodicity taken to the limits ± In this case, the function f (x) is not necessarily periodic, but we can still use Fourier transforms (related
Fourier transforms We can imagine our periodic function having periodicity taken to the limits ± In this case, the function f (x) is not necessarily periodic, but we can still use Fourier transforms (related
About the HELM Project HELM (Helping Engineers Learn Mathematics) materials were the outcome of a three-year curriculum development project
 About the HELM Project HELM (Helping Engineers Learn Mathematics) materials were the outcome of a three-year curriculum development project undertaken by a consortium of five English universities led by
About the HELM Project HELM (Helping Engineers Learn Mathematics) materials were the outcome of a three-year curriculum development project undertaken by a consortium of five English universities led by
6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS
 6.0 Introduction to Differential Equations Contemporary Calculus 1 6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS This chapter is an introduction to differential equations, a major field in applied and theoretical
6.0 Introduction to Differential Equations Contemporary Calculus 1 6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS This chapter is an introduction to differential equations, a major field in applied and theoretical
2. Which of the following is an equation of the line tangent to the graph of f(x) = x 4 + 2x 2 at the point where
 AP Review Chapter Name: Date: Per: 1. The radius of a circle is decreasing at a constant rate of 0.1 centimeter per second. In terms of the circumference C, what is the rate of change of the area of the
AP Review Chapter Name: Date: Per: 1. The radius of a circle is decreasing at a constant rate of 0.1 centimeter per second. In terms of the circumference C, what is the rate of change of the area of the
2015 Mathematics. Advanced Higher. Finalised Marking Instructions
 015 Mathematics Advanced Higher Finalised ing Instructions Scottish Qualifications Authority 015 The information in this publication may be reproduced to support SQA qualifications only on a noncommercial
015 Mathematics Advanced Higher Finalised ing Instructions Scottish Qualifications Authority 015 The information in this publication may be reproduced to support SQA qualifications only on a noncommercial
Methods in differential equations 7B
 Methods in differential equations 7B a The auxiliary equation is m +5m+6= (m+)(m+)= m= or y=ae x +Be x d y dy The auxiliary equation of a b cy + + = is am + bm + c=. If αandβ are real roots of this quadratic
Methods in differential equations 7B a The auxiliary equation is m +5m+6= (m+)(m+)= m= or y=ae x +Be x d y dy The auxiliary equation of a b cy + + = is am + bm + c=. If αandβ are real roots of this quadratic
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
APPLIED MATHEMATICS. Part 1: Ordinary Differential Equations. Wu-ting Tsai
 APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
2003 Mathematics. Advanced Higher. Finalised Marking Instructions
 2003 Mathematics Advanced Higher Finalised Marking Instructions 2003 Mathematics Advanced Higher Section A Finalised Marking Instructions Advanced Higher 2003: Section A Solutions and marks A. (a) Given
2003 Mathematics Advanced Higher Finalised Marking Instructions 2003 Mathematics Advanced Higher Section A Finalised Marking Instructions Advanced Higher 2003: Section A Solutions and marks A. (a) Given
Ordinary Differential Equations
 Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 10 Undetermined coefficients-annihilator
Ordinary Differential Equations (MA102 Mathematics II) Shyamashree Upadhyay IIT Guwahati Shyamashree Upadhyay ( IIT Guwahati ) Ordinary Differential Equations 1 / 10 Undetermined coefficients-annihilator
x+ y = 50 Dividing both sides by 2 : ( ) dx By (7.2), x = 25m gives maximum area. Substituting this value into (*):
 Solutions 7(b 1 Complete solutions to Exercise 7(b 1. Since the perimeter 100 we have x+ y 100 [ ] ( x+ y 50 ividing both sides by : y 50 x * The area A xy, substituting y 50 x gives: A x( 50 x A 50x x
Solutions 7(b 1 Complete solutions to Exercise 7(b 1. Since the perimeter 100 we have x+ y 100 [ ] ( x+ y 50 ividing both sides by : y 50 x * The area A xy, substituting y 50 x gives: A x( 50 x A 50x x
Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1
 Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1 Questions Example Differentiate the function y = ae v + b v + c v 2. Example Differentiate the function y = A + B x
Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1 Questions Example Differentiate the function y = ae v + b v + c v 2. Example Differentiate the function y = A + B x
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
3. Riley 12.9: The equation sin x dy +2ycos x 1 dx can be reduced to a quadrature by the standard integrating factor,» Z x f(x) exp 2 dt cos t exp (2
 PHYS 725 HW #4. Due 15 November 21 1. Riley 12.3: R dq dt + q C V (t); The solution is obtained with the integrating factor exp (t/rc), giving q(t) e t/rc 1 R dsv (s) e s/rc + q() With q() and V (t) V
PHYS 725 HW #4. Due 15 November 21 1. Riley 12.3: R dq dt + q C V (t); The solution is obtained with the integrating factor exp (t/rc), giving q(t) e t/rc 1 R dsv (s) e s/rc + q() With q() and V (t) V
SECOND-ORDER LINEAR ODEs. Generalities. Structure of general solution. Equations with constant coefficients
 SECOND-ORDER LINEAR ODEs f +p(x)f +q(x)f = h(x) Generalities Structure of general solution Equations with constant coefficients Second order linear equations General form : d f df + p( x) + q( x) f = h(
SECOND-ORDER LINEAR ODEs f +p(x)f +q(x)f = h(x) Generalities Structure of general solution Equations with constant coefficients Second order linear equations General form : d f df + p( x) + q( x) f = h(
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3. The Product and Quotient Rules In this section, we will learn about: Formulas that enable us to differentiate new functions formed from old functions by
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3. The Product and Quotient Rules In this section, we will learn about: Formulas that enable us to differentiate new functions formed from old functions by
Jim Lambers MAT 285 Spring Semester Practice Exam 2 Solution. y(t) = 5 2 e t 1 2 e 3t.
 . Solve the initial value problem which factors into Jim Lambers MAT 85 Spring Semester 06-7 Practice Exam Solution y + 4y + 3y = 0, y(0) =, y (0) =. λ + 4λ + 3 = 0, (λ + )(λ + 3) = 0. Therefore, the roots
. Solve the initial value problem which factors into Jim Lambers MAT 85 Spring Semester 06-7 Practice Exam Solution y + 4y + 3y = 0, y(0) =, y (0) =. λ + 4λ + 3 = 0, (λ + )(λ + 3) = 0. Therefore, the roots
Differential Equations Class Notes
 Differential Equations Class Notes Dan Wysocki Spring 213 Contents 1 Introduction 2 2 Classification of Differential Equations 6 2.1 Linear vs. Non-Linear.................................. 7 2.2 Seperable
Differential Equations Class Notes Dan Wysocki Spring 213 Contents 1 Introduction 2 2 Classification of Differential Equations 6 2.1 Linear vs. Non-Linear.................................. 7 2.2 Seperable
Spring 2015 Sample Final Exam
 Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
2t t dt.. So the distance is (t2 +6) 3/2
 Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
ENGINEERING MATH 1 Fall 2009 VECTOR SPACES
 ENGINEERING MATH 1 Fall 2009 VECTOR SPACES A vector space, more specifically, a real vector space (as opposed to a complex one or some even stranger ones) is any set that is closed under an operation of
ENGINEERING MATH 1 Fall 2009 VECTOR SPACES A vector space, more specifically, a real vector space (as opposed to a complex one or some even stranger ones) is any set that is closed under an operation of
Problem set 5, Real Analysis I, Spring, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, 1 x (log 1/ x ) 2 dx 1
 Problem set 5, Real Analysis I, Spring, 25. (5) Consider the function on R defined by f(x) { x (log / x ) 2 if x /2, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, R f /2
Problem set 5, Real Analysis I, Spring, 25. (5) Consider the function on R defined by f(x) { x (log / x ) 2 if x /2, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, R f /2
NATIONAL ACADEMY DHARMAPURI TRB MATHEMATICS DIFFERENTAL EQUATIONS. Material Available with Question papers CONTACT ,
 NATIONAL ACADEMY DHARMAPURI TRB MATHEMATICS DIFFERENTAL EQUATIONS Material Available with Question papers CONTACT 8486 17507, 70108 65319 TEST BACTH SATURDAY & SUNDAY NATIONAL ACADEMY DHARMAPURI http://www.trbtnpsc.com/013/07/trb-questions-and-stu-materials.html
NATIONAL ACADEMY DHARMAPURI TRB MATHEMATICS DIFFERENTAL EQUATIONS Material Available with Question papers CONTACT 8486 17507, 70108 65319 TEST BACTH SATURDAY & SUNDAY NATIONAL ACADEMY DHARMAPURI http://www.trbtnpsc.com/013/07/trb-questions-and-stu-materials.html
Section 3.4. Second Order Nonhomogeneous. The corresponding homogeneous equation. is called the reduced equation of (N).
 Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Section 3.4. Second Order Nonhomogeneous Equations y + p(x)y + q(x)y = f(x) (N) The corresponding homogeneous equation y + p(x)y + q(x)y = 0 (H) is called the reduced equation of (N). 1 General Results
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
ENGI Second Order Linear ODEs Page Second Order Linear Ordinary Differential Equations
 ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
ENGI 344 - Second Order Linear ODEs age -01. Second Order Linear Ordinary Differential Equations The general second order linear ordinary differential equation is of the form d y dy x Q x y Rx dx dx Of
2.2 Separable Equations
 2.2 Separable Equations Definition A first-order differential equation that can be written in the form Is said to be separable. Note: the variables of a separable equation can be written as Examples Solve
2.2 Separable Equations Definition A first-order differential equation that can be written in the form Is said to be separable. Note: the variables of a separable equation can be written as Examples Solve
Monday, 6 th October 2008
 MA211 Lecture 9: 2nd order differential eqns Monday, 6 th October 2008 MA211 Lecture 9: 2nd order differential eqns 1/19 Class test next week... MA211 Lecture 9: 2nd order differential eqns 2/19 This morning
MA211 Lecture 9: 2nd order differential eqns Monday, 6 th October 2008 MA211 Lecture 9: 2nd order differential eqns 1/19 Class test next week... MA211 Lecture 9: 2nd order differential eqns 2/19 This morning
First and Second Order ODEs
 Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
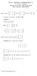 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
JUST THE MATHS UNIT NUMBER 6.1. COMPLEX NUMBERS 1 (Definitions and algebra) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 6.1 COMPLEX NUMBERS 1 (Definitions and algebra) by A.J.Hobson 6.1.1 The definition of a complex number 6.1.2 The algebra of complex numbers 6.1.3 Exercises 6.1.4 Answers to exercises
JUST THE MATHS UNIT NUMBER 6.1 COMPLEX NUMBERS 1 (Definitions and algebra) by A.J.Hobson 6.1.1 The definition of a complex number 6.1.2 The algebra of complex numbers 6.1.3 Exercises 6.1.4 Answers to exercises
Math 2250 Lab 08 Lab Section: Class ID: Name/uNID: Due Date: 3/23/2017
 Math 2250 Lab 08 Lab Section: Class ID: Name/uNID: Due Date: 3/23/2017 TA: Instructions: Unless stated otherwise, please show all your work and explain your reasoning when necessary, as partial credit
Math 2250 Lab 08 Lab Section: Class ID: Name/uNID: Due Date: 3/23/2017 TA: Instructions: Unless stated otherwise, please show all your work and explain your reasoning when necessary, as partial credit
Introductory Differential Equations
 Introductory Differential Equations Lecture Notes June 3, 208 Contents Introduction Terminology and Examples 2 Classification of Differential Equations 4 2 First Order ODEs 5 2 Separable ODEs 5 22 First
Introductory Differential Equations Lecture Notes June 3, 208 Contents Introduction Terminology and Examples 2 Classification of Differential Equations 4 2 First Order ODEs 5 2 Separable ODEs 5 22 First
Math 308 Week 8 Solutions
 Math 38 Week 8 Solutions There is a solution manual to Chapter 4 online: www.pearsoncustom.com/tamu math/. This online solutions manual contains solutions to some of the suggested problems. Here are solutions
Math 38 Week 8 Solutions There is a solution manual to Chapter 4 online: www.pearsoncustom.com/tamu math/. This online solutions manual contains solutions to some of the suggested problems. Here are solutions
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
2005 Mathematics. Advanced Higher. Finalised Marking Instructions
 2005 Mathematics Advanced Higher Finalised Marking Instructions These Marking Instructions have been prepared by Examination Teams for use by SQA Appointed Markers when marking External Course Assessments.
2005 Mathematics Advanced Higher Finalised Marking Instructions These Marking Instructions have been prepared by Examination Teams for use by SQA Appointed Markers when marking External Course Assessments.
18.02 Multivariable Calculus Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 3. Double Integrals 3A. Double
MIT OpenCourseWare http://ocw.mit.edu 18.02 Multivariable Calculus Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 3. Double Integrals 3A. Double
Homework Solutions: , plus Substitutions
 Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Lecture 2. Introduction to Differential Equations. Roman Kitsela. October 1, Roman Kitsela Lecture 2 October 1, / 25
 Lecture 2 Introduction to Differential Equations Roman Kitsela October 1, 2018 Roman Kitsela Lecture 2 October 1, 2018 1 / 25 Quick announcements URL for the class website: http://www.math.ucsd.edu/~rkitsela/20d/
Lecture 2 Introduction to Differential Equations Roman Kitsela October 1, 2018 Roman Kitsela Lecture 2 October 1, 2018 1 / 25 Quick announcements URL for the class website: http://www.math.ucsd.edu/~rkitsela/20d/
2. Determine whether the following pair of functions are linearly dependent, or linearly independent:
 Topics to be covered on the exam include: Recognizing, and verifying solutions to homogeneous second-order linear differential equations, and their corresponding Initial Value Problems Recognizing and
Topics to be covered on the exam include: Recognizing, and verifying solutions to homogeneous second-order linear differential equations, and their corresponding Initial Value Problems Recognizing and
Direct Proof Rational Numbers
 Direct Proof Rational Numbers Lecture 14 Section 4.2 Robb T. Koether Hampden-Sydney College Thu, Feb 7, 2013 Robb T. Koether (Hampden-Sydney College) Direct Proof Rational Numbers Thu, Feb 7, 2013 1 /
Direct Proof Rational Numbers Lecture 14 Section 4.2 Robb T. Koether Hampden-Sydney College Thu, Feb 7, 2013 Robb T. Koether (Hampden-Sydney College) Direct Proof Rational Numbers Thu, Feb 7, 2013 1 /
Math 212-Lecture 8. The chain rule with one independent variable
 Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Lesson 3: Linear differential equations of the first order Solve each of the following differential equations by two methods.
 Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Introduction to Differentials
 Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Department of Aerospace Engineering AE602 Mathematics for Aerospace Engineers Assignment No. 6
 Department of Aerospace Engineering AE Mathematics for Aerospace Engineers Assignment No.. Find the best least squares solution x to x, x 5. What error E is minimized? heck that the error vector ( x, 5
Department of Aerospace Engineering AE Mathematics for Aerospace Engineers Assignment No.. Find the best least squares solution x to x, x 5. What error E is minimized? heck that the error vector ( x, 5
Problem 1 In each of the following problems find the general solution of the given differential
 VI Problem 1 dt + 2dy 3y = 0; dt 9dy + 9y = 0. Problem 2 dt + dy 2y = 0, y(0) = 1, y (0) = 1; dt 2 y = 0, y( 2) = 1, y ( 2) = Problem 3 Find the solution of the initial value problem 2 d2 y dt 2 3dy dt
VI Problem 1 dt + 2dy 3y = 0; dt 9dy + 9y = 0. Problem 2 dt + dy 2y = 0, y(0) = 1, y (0) = 1; dt 2 y = 0, y( 2) = 1, y ( 2) = Problem 3 Find the solution of the initial value problem 2 d2 y dt 2 3dy dt
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Tangent Planes, Linear Approximations and Differentiability
 Jim Lambers MAT 80 Spring Semester 009-10 Lecture 5 Notes These notes correspond to Section 114 in Stewart and Section 3 in Marsden and Tromba Tangent Planes, Linear Approximations and Differentiability
Jim Lambers MAT 80 Spring Semester 009-10 Lecture 5 Notes These notes correspond to Section 114 in Stewart and Section 3 in Marsden and Tromba Tangent Planes, Linear Approximations and Differentiability
Exam Question 10: Differential Equations. June 19, Applied Mathematics: Lecture 6. Brendan Williamson. Introduction.
 Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Exam Question 10: June 19, 2016 In this lecture we will study differential equations, which pertains to Q. 10 of the Higher Level paper. It s arguably more theoretical than other topics on the syllabus,
Calculus II Practice Test Problems for Chapter 7 Page 1 of 6
 Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
13 Implicit Differentiation
 - 13 Implicit Differentiation This sections highlights the difference between explicit and implicit expressions, and focuses on the differentiation of the latter, which can be a very useful tool in mathematics.
- 13 Implicit Differentiation This sections highlights the difference between explicit and implicit expressions, and focuses on the differentiation of the latter, which can be a very useful tool in mathematics.
4r 2 12r + 9 = 0. r = 24 ± y = e 3x. y = xe 3x. r 2 6r + 25 = 0. y(0) = c 1 = 3 y (0) = 3c 1 + 4c 2 = c 2 = 1
 Mathematics MATB44, Assignment 2 Solutions to Selected Problems Question. Solve 4y 2y + 9y = 0 Soln: The characteristic equation is The solutions are (repeated root) So the solutions are and Question 2
Mathematics MATB44, Assignment 2 Solutions to Selected Problems Question. Solve 4y 2y + 9y = 0 Soln: The characteristic equation is The solutions are (repeated root) So the solutions are and Question 2
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
1.4 Techniques of Integration
 .4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
.4 Techniques of Integration Recall the following strategy for evaluating definite integrals, which arose from the Fundamental Theorem of Calculus (see Section.3). To calculate b a f(x) dx. Find a function
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
Modeling with Differential Equations: Introduction to the Issues
 Modeling with Differential Equations: Introduction to the Issues Warm-up Do you know a function...... whose first derivative is the same as the function itself, i.e. d f (x) = f (x)?... whose first derivative
Modeling with Differential Equations: Introduction to the Issues Warm-up Do you know a function...... whose first derivative is the same as the function itself, i.e. d f (x) = f (x)?... whose first derivative
=================~ NONHOMOGENEOUS LINEAR EQUATIONS. rn y" - y' - 6y = 0. lid y" + 2y' + 2y = 0, y(o) = 2, y'(0) = I
 ~ EXERCISES rn y" - y' - 6y = 0 3. 4y" + y = 0 5. 9y" - 12y' + 4y = 0 2. y" + 4 y' + 4 y = 0 4. y" - 8y' + 12y = 0 6. 25y" + 9y = 0 dy 8. dt2-6 d1 + 4y = 0 00 y" - 4y' + By = 0 10. y" + 3y' = 0 [ITJ2-+2--y=0
~ EXERCISES rn y" - y' - 6y = 0 3. 4y" + y = 0 5. 9y" - 12y' + 4y = 0 2. y" + 4 y' + 4 y = 0 4. y" - 8y' + 12y = 0 6. 25y" + 9y = 0 dy 8. dt2-6 d1 + 4y = 0 00 y" - 4y' + By = 0 10. y" + 3y' = 0 [ITJ2-+2--y=0
Partial Derivatives for Math 229. Our puropose here is to explain how one computes partial derivatives. We will not attempt
 Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Partial Derivatives for Math 229 Our puropose here is to explain how one computes partial derivatives. We will not attempt to explain how they arise or why one would use them; that is left to other courses
Coordinate systems and vectors in three spatial dimensions
 PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
PHYS2796 Introduction to Modern Physics (Spring 2015) Notes on Mathematics Prerequisites Jim Napolitano, Department of Physics, Temple University January 7, 2015 This is a brief summary of material on
