Friction may well be nature s most useful phenomenon.
|
|
|
- Eustace Hicks
- 6 years ago
- Views:
Transcription
1 Modeling and Measuring Friction Effects AVRAHAM HARNOY, BERNARD FRIEDLAND, and SIMON COHN PHYSICS, APPARATUS, AND EXPERIMENTS Friction may well be nature s most useful phenomenon. Without friction we would hae no belt dries, no clutches, no wheels, and no brakes. Walking, and een standing upright on a moderately inclined surface, would be impossible. In machinery in which it is not the driing force, howeer, friction is an undesirable parasitic phenomenon, generating heat and wasting energy. Large sums are spent each year on lubricants to eliminate as much friction as possible in mechanical deices. On the other hand, when friction is the source of traction and braking, it is important to keep friction at a high leel. To achiee this end, much effort and funding are expended on projects such as improing tires and antilock brakes. In traction applications, the process starts with the ehicle at rest, whereas in braking applications, the process ends with the ehicle at rest. In both applications, the behaior of friction when the elocity of the ehicle crosses zero is of little interest. In motion-control applications, howeer, the elocity of the controlled object typically crosses zero, often seeral times, during operation. Hence, in such applications, it is necessary to understand the behaior of friction in the icinity of zero elocity. Experiments [1] show that friction in the icinity of zero elocity is a dynamic phenomenon that static models fail to adequately describe. The goals of this article are first to reiew some of the physical characteristics of friction, especially the need for state-space dynamic models; then to describe apparatus for measuring friction effects and Digital Object Identifier 1.119/MCS to present the results achieed using this apparatus; and, finally, to discuss some of the issues relating to measurement of friction effects. PHYSICAL MODELS OF FRICTION PHOTODISC Static Friction Models Friction effects can be imagined as resulting from two mountainous surfaces, one inerted aboe the other, as 82 IEEE CONTROL SYSTEMS MAGAZINE» DECEMBER X/8/$25. 28IEEE
2 illustrated in Figure 1. The motion of one surface relatie to the other causes the friction force. The height and sharpness of the mountains (asperities) represent the roughness of the surfaces. The lower mountains support the normal force (load) pressing down on the upper surface. The larger the load, the more deeply the upper surface penetrates into the lower, making it more difficult for the surfaces to moe apart. This effect helps explain why the friction force depends on the load F. The simplest friction model is the Coulomb model, in which the force of friction is gien by f = μfsgn(), (1) where F is the normal force, μ <1 is the coefficient of friction, and is the elocity of one surface relatie to the other. Note that the Coulomb model (1) has a discontinuity at zero relatie elocity. This discontinuity implies that a friction force f, with f μf, can be present een when there is no relatie motion. This phenomenon, which is sometimes called starting friction, helps explain why an object can remain motionless on an inclined plane. Static friction also explains the idealization of rolling without slipping in which the translational elocity of the center of the wheel equals the angular elocity of the wheel multiplied by the wheel radius. The discontinuity at zero elocity presents mathematical and computational difficulties [2]. These difficulties may possibly be alleiated by smoothing the discontinuity, thus replacing the model of (1) by In many situations the leel of starting friction is greater than the leel of friction at nonzero elocity, and there is a rapid transition from starting friction to sliding friction, as shown in Figure 2. When linear iscous damping, that is, a force proportional to elocity, is included in the friction model, the cure may increase with increasing positie elocity as shown by the broken line. The phenomenon of friction decreasing and then increasing with elocity is known as the Stribeck effect. The Coulomb friction model, including the Stribeck effect shown in Figure 2, is often adequate for representing the effects of friction in practical systems. In some applications, howeer, the Coulomb model fails to proide a satisfactory description of system behaior. In one such application, a precision line-of-sight stabilization system [1], a limit cycle predicted by the Coulomb model is absent in the test results. Dynamic Friction Models The upper object in Figure 1 can t moe unless the asperities either break off (the phenomenon of polishing) or bend. Bending of the asperities implies energy storage, which introduces dynamics into the model of friction. Friction Force f Normal Force F FIGURE 1 Rubbing surfaces without lubrication. The mountains, which are called asperities, impede motion and result in friction force. The normal force F is supported by the asperities. The drawing is similar to a figure in [1] Velocity f = φ() = μnsgn()s(, a), (2) where the smoothing function s(, a) is a continuous, een function of, but, depending on a, rapidly rises to one as departs from zero. Candidates for the smoothing function include f μf and s(, a) = 1 e 2 /a 2 s(, a) = e a2 / 2. f μf FIGURE 2 Conentional friction representations. The idealized Coulomb friction cure shows larger starting friction than moing friction. The friction force is represented as a smooth function for >. The broken line shows the Stribeck effect when linear damping is included in the friction model. DECEMBER 28 «IEEE CONTROL SYSTEMS MAGAZINE 83
3 One conception of energy storage is the electrical analogy shown in Figure 3, with oltage analogous to elocity and current analogous to friction force. In this circuit, the pair of back-to-back Zener diodes represents static Coulomb friction. The storage of energy in this analogy is represented by a capacitor in parallel with the diodes accounts for energy storage. Owing to the presence of this capacitor, the circuit is now a firstorder dynamic system, goerned by d/dt = (1/C)(i ψ()), (3) where ψ is the inerse of the nonlinear function φ defined in (2). Another conception of the effect of flexible asperities is the bristle model, in which the lower surface of the moing object is regarded as a brush moing oer an inerted brush that represents the fixed surface. The relatie motion of the two surfaces causes the bristles of the brushes to bend and thereby store energy [1]. A more detailed ersion of the bristle model is gien in [3]. The bristle model accounts for the physics of dynamic friction, but the number of bristles required for erisimilitude may preclude efficient simulation. The LuGre model [5], [6], widely used in the control system literature, captures the effect of the bristles as the output of a system goerned by a first-order system in which the friction force is gien by with where f = σ z + σ 1 ż + α 2, (4) ż = σ z, (5) g() g() = α + α 1 e (/ ) 2. As shown in [7], the LuGre model, with the appropriate selection of the parameters α i,σ i, subsumes seeral of the earlier dynamic friction models. A more general first-order model represents the friction force f as the output of a dynamic system in which the input is the relatie elocity. This model takes the form f = f (z, ), (6) ż = g(z, ). (7) The nature of the functions f and g determines the behaior of the friction force [4] Hydrodynamic Model In dry (unlubricated) friction, the asperities of the rubbing surfaces are in direct contact. As shown in Figure 4, the effect of introducing a lubricant between the surfaces is to create a band of separation between the upper surface and the lower one. This band reduces the depth of penetration of the upper surface into the lower one, thereby reducing the coefficient of friction. The LuGre model can cope with the effects of lubrication but is not based on the hydrodynamics of lubrication. Under the assumption that the mass of the lubricant is negligible, hydrodynamic theory [8] leads to a second-order model for the friction force in a lubricated journal bearing. In the resulting model, the friction force is gien by c 2 f = c 1 κ(ε)(ε ε T ) sgn() +, (8) (1 ε 2 ) 1 2 with J 11 (ε)ε ϕ + J 12 ε = c 3 Fsin ϕ + c 4 J 11 (ε), (9) J 12 (ε)ε ϕ + J 22 ε = c 3 Fcos ϕ + c 4 J 12 (ε), (1) in which ε and ϕ are dimensionless ariables proportional to the eccentricity of the shaft and the angular position of i i + 1/c 1/s Normal Force F ϕ () C Friction Force f Velocity FIGURE 3 An electric circuit that proides an analogue of friction. The back-to-back Zener diodes in parallel with a small capacitor comprise a possible electrical analogue of friction. The capacitor stores energy, which leads to a dynamic model. This block diagram represents the circuit of. FIGURE 4 Rubbing surfaces with lubrication. The lubrication has the effect of separating the surfaces. Hence the asperities are farther apart and impede motion less, resulting in a lower friction force than in Figure IEEE CONTROL SYSTEMS MAGAZINE» DECEMBER 28
4 the point on the shaft nearest to the bearing wall, respectiely; J ij are integrals relating to the ariable film thickness around the bearing; and c i are constants related to the geometry of the shaft and journal bearing. The quantity ε T is the eccentricity at which the friction achiees its minimum alue, and { 1, for ε>ε = T,, for ε ε T, by a calibrated, full strain-gauge bridge bonded to the elastic ring. The total friction torque of all four bearings is measured by a calibrated rigid piezoelectric load cell, which preents rotation of the outer bearing housing K. This torque is and κ(ε) is an asperity stiffness function gien, for example, by κ(ε) = κ (ε ε ) n. The first term in (8) represents the friction component due to the asperities; the second term represents the contribution due to the hydrodynamics [8]. APPARATUS FOR MEASURING FRICTION COEFFICIENTS Friction in a Journal Bearing When the purpose of measuring the force of friction is simply to estimate the energy loss due to friction at a constant elocity, only a rudimentary apparatus is required for measuring the static friction characteristic. Measuring the friction force when the relatie elocity is time arying and crosses through zero, howeer, is more complicated. First, it is necessary to generate and apply periodic or nonperiodic elocities of the magnitudes necessary to elicit the friction effect that is being inestigated. Second, it is necessary to isolate the friction force from all other forces in the system. (Since forces other than the friction force may be present in the system, these forces must not be allowed to corrupt the measurement.) Finally, it is necessary to measure the elocity of one of the rubbing surfaces relatie to the other. To achiee these requirements, the apparatus shown in Figure 5 is designed to measure the friction force in a journal bearing. This apparatus comprises an actuated shaft that can oscillate within a journal bearing housed in a structure designed to measure the friction force between the shaft and the bearing. The components of the apparatus are identified in Table 1. The apparatus measures the aerage dynamic friction force of four identical sleee bearings in isolation from all other sources of friction in the system, for example, friction in the ball bearings supporting the shaft. The apparatus is rigid enough to minimize errors [9]. The design concept is based on applying an internal load (action and reaction) between the inner housing N and the outer housing K by tightening the nut P on the bolt R, and preloading the elastic steel ring E. The apparatus contains the four sleee bearings H, with two bearings inside each of the inner and outer housings. All four test bearings thus hae equal radial load, but in opposite direction for each pair of bearings, due to the preload in the elastic ring. The load on the bearings is measured D A B C K FIGURE 5 Apparatus for measuring friction effect in a journal bearing. This apparatus is designed to minimize all forces on the shaft except the force due to friction. The photograph shows the apparatus in use. The cross-sectional iew shows the basic components as described in Table 1 and the text. TABLE 1 Components of the friction-measuring apparatus. The deice is illustrated in Figure 5. Component Description/function A Ball-bearing support for rotating shaft B Apparatus frame C Rotating shaft D Belt drie pulley E Elastic steel ring F, K Outer housing G Oil retainer disk H Sleee bearings (four) N Inner housing P Tightening nut R Tightening bolt P R N E F G H DECEMBER 28 «IEEE CONTROL SYSTEMS MAGAZINE 85
5 transferred to the load cell by a radial arm attached to the external housing as shown in Figure 5. Thus the measured friction torque of the four bearings is isolated from all other sources of friction. Oil is fed into the four bearings through four segments of flexible tubing and is drained from the bearings through a hole in the external housing into a collecting essel. The shaft is actuated by a position sero designed to track a ariety of reference signals. The apparatus is designed so that it can operate dry or with arious lubricants. I P Friction in a Line Contact The apparatus shown in Figure 6 is designed to measure the friction force in a sliding line contact at ery low elocity. This apparatus comprises a linear motion sliding table, drien by a seromotor and a ball screw drie. The apparatus is designed on the concept of a ball-screw-drien linear positioning table in which backlash is eliminated by preloading the screw drie. Low elocity is achieed by speed reduction of a screw drie. In addition, the speed of the motor is reduced by a set of pulleys and a timing belt. Closed-loop controlled motion is generated by a computer-controlled dc seromotor. The line contact is created between a short, finely ground, cylindrical shaft K and the flat friction surface N. The shaft K is clamped in the housing assembly I, J, and H, which is designed to hold arious shaft diameters. The normal load, which is centered aboe the line contact, is supplied by a rod P, which has weights attached to it that are not shown in the figure. When the friction test surface moes, the friction force is transmitted through the housing assembly to a piezoelectric load cell. The load cell generates a oltage signal, proportional to the friction force magnitude, which is fed to a dataacquisition system. Another concept of measurement of effects of friction at low elocities is presented in Another Concept. N L M O FIGURE 6 Apparatus for measuring friction force in a line contact. This diagram shows the completed apparatus. The cross-sectional iew shows the basic components described in the text. TABLE 2 Conditions for friction measurement experiments. The apparatus shown in Figure 5 is used in the experiment. Bearing diameter Bearing length Bearing material Clearance between bearing and shaft Journal mass Lubricant 2.54 cm 1.9 cm Brass.5 mm 2.27 kg SAE 1W-4 oil RESULTS OF FRICTION- COEFFICIENT MEASUREMENT in a Lubricated Journal Bearing The apparatus of Figure 5 is deployed in a series of measurements to examine the alidity of the hydrodynamic model (8) (1). The experimental conditions gien in Table 2 are established. All the experiments are performed with the shaft subjected to a controlled sinusoidal elocity with frequency ω rad/s, calibrated to impart a tangential elocity (t) of the shaft surface gien by (t) = r θ =.127 sin ωt m/s (11) where r is the shaft radius, and θ is the shaft angular elocity. 86 IEEE CONTROL SYSTEMS MAGAZINE» DECEMBER 28
6 Static In principle, the static friction-coefficient cure of Figure 2 can be obtained by establishing a series of constant elocity settings of the shaft relatie to the bearing and, at each setting, measuring the friction force. To expedite the experiment, howeer, the apparatus is run at an extremely low oscillation frequency ω in (11), namely,.55 rad/s (around 2 cycles/min). The results of this measurement are gien in Figure 7, which reeals a pronounced Stribeck effect. Also notice that the measured friction cure for increasing elocity is not identical to that for decreasing elocity, in the range of.2.5 m/s. This result may be due to not using a sufficiently low input frequency or to a hysteresis effect, as discussed in [1]. Dynamic To inestigate the dynamic effects of friction in the lubricated journal bearing, the apparatus is operated at f FIGURE 7 Measured static friction in a lubricated journal bearing. The input elocity is sinusoidal at the ery low frequency of.55 rad/s (about 2 cycles/min). The load is 14 N; the shaft is steel, 2.5 cm in diameter; the sleee is brass; the lubricant is SAE 1W-4 automotie oil. The Stribeck effect is eident..3 Another Concept An apparatus for measuring friction effects often comprises a massie fixed base and a relatiely light object, such as a machine shaft, that is actuated to moe at a prescribed elocity relatie to the base. This configuration is necessary for friction measurements at substantial elocities, since it may be impractical to moe the base adequately. But keeping the base fixed leads to a problem associated with measuring dynamic friction, namely ensuring that the friction is the only force on the object subjected to friction. In control applications, low elocities and elocity reersals can occur. For measuring friction effects in such applications, an alternatie configuration, shown schematically in Figure S1, might be more appropriate. In this configuration, the object that is actuated is the base. A relatiely light test object of mass m rests on the base. The only force that makes the test object stick to the base is friction, since, if friction were absent, the test mass would remain stationary in inertial space while the base would moe under it. It can be shown that the friction acceleration f/m on the test mass is equal to μg, where μ is the coefficient of friction. For the Coulomb friction model, the test mass remains stationary in inertial space if the base acceleration is greater than μg but remains fixed to the base if the acceleration is less than μg. (Remember the familiar tablecloth trick: if the acceleration of the tablecloth is large enough, the objects on it remain stationary as the tablecloth is pulled from under them.) We are interested in determining what happens when the relatie elocity is close to zero, which occurs when the frictional acceleration, which is the only acceleration on the test mass, is around μg, and μ is the quantity to be determined. Since friction is the only horizontal force on the test mass, it can be measured by means of an accelerometer mounted as shown in Figure S1. To measure the elocity of the test mass relatie to the moing base, a noncontacting sensor is used. The sensor can be optical, acoustic, inductie, capacitie, or based on the Hall effect. Motion can be imparted to the base by means of a sero actuator designed to track the reference elocity. The same principle can be used to measure rotational friction. The base is a hollow bearing housing actuated to proide the desired motion. The shaft within the bearing, being completely free, moes only because of friction between it and the housing. The elocity of the shaft relatie the housing can be measured without contact by means of a shaft encoder. Instruments for direct measurement of angular acceleration are uncommon, but the inertial elocity of the shaft is readily measured by means of a gyro. If the noise in the gyro is low enough, it might be feasible to differentiate the inertial angular elocity signal to estimate the inertial angular acceleration. Noncontacting Velocity Sensor Test Mass m Reciprocating Base (t ) Accelerometer FIGURE S1 Conceptual representation of an apparatus for measuring translational friction at low elocity. Friction is the only force acting on the upper object. This force is measured by the accelerometer. f (Friction Force) Actuation DECEMBER 28 «IEEE CONTROL SYSTEMS MAGAZINE 87
7 seeral angular elocities and at two leels of normal force. Figure 8 shows the friction coefficient f/f ersus elocity for three frequencies with a normal force of (c) FIGURE 8 Measured dynamic friction in a lubricated journal bearing. The shaft is steel, and the sleee is brass. These results show that the friction coefficient depends on frequency. The normal force is 14 N; the input elocity is sinusoidal. Three frequencies are used for the input elocity: ω =.1 rad/s, ω =.25 rad/s, and (c) ω = 1 rad/s. The solid cures are experimental data; the dashed cures are fit to the hydrodynamic model. N. Figure 9 shows the behaior at three frequencies for a normal force of 84 N. The solid lines show the experimental results, and the dashed lines show the results predicted by the hydrodynamic model of (8) (1). In this model, the parameters c 1, c 2, and ε T are fitted to the static friction cure Figure 7, and the other coefficients are determined theoretically from the bearing dimensions and the iscosity of the lubricant (c) FIGURE 9 Measured dynamic friction in a lubricated journal bearing. The shaft is steel, and the sleee is brass. These results show that the friction coefficient depends on the frequency of oscillation of the input elocity. The normal force is 84 N; the input elocity is sinusoidal at three frequencies: ω =.45 rad/s, ω =.25 rad/s, and (c) ω =.5 rad/s. The solid cures are experimental data; the dashed cures are fit to the hydrodynamic model. 88 IEEE CONTROL SYSTEMS MAGAZINE» DECEMBER 28
8 In machinery in which it is not the driing force, friction is an undesirable parasitic phenomenon, generating heat and wasting energy. Both sets of cures form a loop, enclosing a nonzero area, typical of dynamic friction. The loops enclose more area as the frequency increases, as would be expected with a dynamic model such as discussed in (6) and (7). The upper portion of the cure shows the behaior for increasing elocity, while the lower portion shows the behaior for decreasing elocity. This phenomenon is often erroneously referred to as hysteresis, since the phenomenon may be a consequence of the dynamics of the process rather than of the nonlinearity. Een in a linear dynamic system, the cure is a loop; in fact, for sinusoidal inputs, it is an ellipse, which is a special case of a Lissajous figure. Note also that the coefficient of friction, namely, the ratio of the friction force to the normal force, depends somewhat on the magnitude of the normal force. The Coulomb model does not predict this dependence. Another property of these characteristics is that they appear to lie entirely in the first and third quadrants, implying that energy is dissipated by friction, not only on the aerage but at eery instant of time. Careful examination of the experimental cures, howeer, reeals a slight penetration into the second and fourth quadrants, as is the case with a stable linear electric circuit. (In an electric circuit, the ellipse of oltage ersus current, for sinusoidal input current, has its major axis in the first and third quadrant, but with the instantaneous alue sometimes in the second and fourth quadrants, representing time instants in which the circuit is returning stored energy to the external system.) Operation of the experiment at lower maximum elocity would likely reeal this characteristic in more detail. The experimental cures exhibit the characteristic loops and approximately the same maximum and minimum alues as the theoretical cures; they also show similar frequency dependence. But the experimental cures are not as smooth and not always symmetric. These discrepancies could be due to effects not included in the model or to imperfections in the apparatus. The need for more inestigation is eident. Dry Measurements The coefficient of friction for an unlubricated (dry) bearing is studied using the same apparatus. Figures 1 and 11 show the results for two different sleee treatments. The cure of the friction coefficient for an uncoated steel shaft 2.5 cm in diameter is shown in Figure 1. The cure of the same sleee, coated with ultra-high molecular FIGURE 1 Measured static friction in a dry journal bearing with a steel, uncoated shaft, 2.5 cm in diameter. The input elocity is sinusoidal at a frequency of.5 rad/s. The load is 14 N. The sleee is uncoated brass FIGURE 11 Measured friction in a dry journal bearing with a steel sleee coated with ultra-high molecular weight polyethylene, 2.5 cm in diameter. The input elocity is sinusoidal with a frequency of.25 rad/s. The load is 14 N; the shaft is steel. Note that the lower and upper cures are separated and that the coefficient of friction increases with elocity..5 DECEMBER 28 «IEEE CONTROL SYSTEMS MAGAZINE 89
9 Friction effects can be imagined as resulting from two mountainous surfaces, one inerted aboe the other. Friction (kg-m Torque) Friction (kg-m Torque) Velocity (rad/s) FIGURE 12 Estimated and measured friction force in a friction-compensation experiment. The estimated friction force is determined by the friction-compensation algorithm. The measured friction force is determined using the experimental apparatus shown in Figure 5. Note that the measurements show a calibration bias. Neertheless, the estimate of friction force tracks the measurement. The largest discrepancy is near zero elocity. weight polyethylene, is shown in Figure 11. In the former case, the cure exhibits the typical Stribeck effect, namely the reduction of friction coefficient magnitude with increasing elocity. For the coated sleee, howeer, the cure exhibits a negatie Stribeck effect, in which the friction coefficient magnitude increases with elocity. Both results show a separation between the cure for increasing elocity and the cure for decreasing elocity, which suggests either that the frequency is not sufficiently low or that pure hysteresis is present. The angular elocity of the coated sleee is fie times higher than it is for the uncoated sleee; neertheless, the separation between the cures in this case is not significantly greater than it is for the uncoated sleee. The effect of the coating is eident. For the uncoated shaft, the starting friction coefficient is about.4, which decreases to about.2 as the elocity increases, owing to the Stribeck effect. For the coated sleee, the starting friction coefficient is about.2 and does not rise as high as.4 as the elocity is increased. All the cures in the figures 7 11 are obtained using a sinusoidal input elocity. It can be demonstrated by simulation that the cures corresponding to the force-ersuselocity cures for other input waeforms are generally not the same as those for sinusoidal inputs [1]. Online Friction Force Estimation If the source of friction in a system can be isolated for measurement, it may be possible to determine the parameters of a friction model with accuracy sufficient for control system design and performance simulation. If the source of friction cannot be isolated, howeer, an online friction estimation algorithm might be effectie for this purpose. The adaptie friction compensation algorithm described in [11] is an example of such an algorithm. Based on the static Coulomb friction model, this algorithm is designed to determine the maximum friction force leel μf and thereby deelop a control force to cancel it. Although the algorithm is based on the static Coulomb friction model (1), the friction force estimate that it produces is time arying and tracks the experimentally measured friction force, as shown in Figure 12. The experimental results [12], obtained using the apparatus of Figure 5, show that the online-estimated friction force and the directly measured friction force both exhibit the characteristic loops and are approximately the same magnitude. The discrepancy between the online estimate and the direct measurement is greatest in the lowelocity range, where the Coulomb friction model is least accurate, because the cures for increasing elocity and for decreasing elocity differ most at low elocities. Another experimental inestigation of this technique is reported in [13]. CONCLUSIONS Much progress has been made during the past two decades in understanding and modeling the physical characteristics of friction and its effects in motion-control systems. The recognition that friction is a dynamic phenomenon that can be represented by state-space models is a significant deelopment that is still ongoing. The nature of the elocity input is part of a larger question of the goal or goals of measuring dynamic friction effects. From the scientific iewpoint, the goal is to determine which of seeral friction models best represents the obsered measurements and to determine the parameters of the model that best fit the data. The choice of input elocity is part of the goal. In the case of a linear system, the only issue is the order of the model and the alues of the parameters therein. 9 IEEE CONTROL SYSTEMS MAGAZINE» DECEMBER 28
10 The bristle model accounts for the physics of dynamic friction, but the number of bristles required for erisimilitude may preclude efficient simulation. Identification techniques are aailable to determine the appropriate order of the model and the parameter alues. For nonlinear systems, howeer, similar identification techniques are not readily aailable. The proper inputs to use and the means to discriminate between contending models remain as open questions. The deelopment of effectie means for compensating friction effects in control systems is another research area that continues to receie attention. Experimental inestigations lag behind the deelopment of theory. In particular, control algorithms for systems in which friction is important are typically demonstrated by simulations in which the friction model, not experimentally alidated, is the same as the model used in the deelopment of the algorithm. Notwithstanding the alue of such simulations, it must be recognized that these are only first steps toward practical designs. To merit serious consideration in practice, the algorithms must ultimately be demonstrated experimentally. REFERENCES [1] D.A. Haessig, Jr., and B. Friedland, On the modeling and simulation of friction, Trans. ASME, J. Dyn. Syst. Meas. Contr., ol. 113, pp , Sept [2] J. Cortes, Discontinuous dynamic systems, IEEE Control Syst. Mag., ol. 28, no. 3, pp , June 28. [3] Y. Guo, Y. Braiman, Z. Zhang, and J. Barben, Nanotribology and nanoscale friction control, IEEE Control Syst. Mag., ol. 28, no. 6, pp. 92 1, 28. [4] B.S.R. Amstrong and Q. Chen, The Z-Properties chart, IEEE Control Syst. Mag., ol. 28, no. 5, pp , 28. [5] C. Canudas de Wit, H. Olsson, K.J. Åstrom, and P. Lischinsky, A new model for control systems with friction, IEEE Trans. Automa. Contr., ol 4, no. 3, pp , Mar [6] H. Olsson, K.J. Åstrom, C. Canudas de Wit, M. Gäfert, and P. Lischinsky, Friction models and friction compensation, Euro. J. Contr., ol. 4, pp , [7] H. Olsson, Control systems with friction, Ph.D. dissertation, Dept. Automatic Control, Uniersity of Lund, Sweden, [8] A. Harnoy and B. Friedland, Dynamic friction model of lubricatioed surfaces for precise motion control, Tribology Trans., ol. 37, no. 3, pp , [9] A. Harnoy, B. Friedland, R. Semenock, H. Rachoor, and A. Aly, Apparatus for empirical determination of dynamic friction, in Proc. American Control Conf., Baltimore, MD, 1994, pp [1] A.K. Padthe, J. Oh, D.S. Bernstein, D.D. Rizos, and S.D. Fassois, Duhem modeling of friction-induced hysteresis, IEEE Control Syst. Mag., ol. 28, no. 5, pp. 9 17, 28. [11] B. Friedland and Y.-J. Park, On adaptie friction compensation, IEEE Trans. Automat. Contr., ol. 37, no. 1, pp , Oct [12] J. Amin, B. Friedland, and A. Harnoy, Implementation of a friction estimation and compensation technique, IEEE Control Syst. Mag., ol. 17, no. 4, pp , Aug [13] S. Tafazoli, C.W. de Sila, and P.D. Lawrence, Tracking control of an electrohydraulic manipulator in the presence of friction, IEEE Trans. Contr. Syst. Technol., ol. 6, no. 3, pp , May AUTHOR INFORMATION Araham Harnoy is a professor in the Department of Mechanical Engineering at New Jersey Institute of Technology where he has taught since He has been engaged in teaching and directing the mechanical laboratories and has been inoled in research in tribology, bearings and lubrication, fluid mechanics, heat transfer, and rheology. He has many years of diersified industrial and academic experience in seeral countries. He holds the B.S. and M.S. degrees in mechanical engineering and a doctor of science in mechanics, all from the Technion Israel Institute of Technology. He is the author of the textbook, Bearing Design in Machinery, Engineering Tribology and Lubrication (Marcel Dekker, 23). Bernard Friedland (bf@njit.edu) is a distinguished professor in the Department of Electrical and Computer Engineering at the New Jersey Institute of Technology (NJIT), which he joined in 199. He was a Lady Dais isiting professor at the Technion Israel Institute of Technology and has held appointments as an adjunct professor of electrical engineering at the Polytechnic Uniersity, New York Uniersity, and Columbia Uniersity. He was educated in New York City and receied the B.S., M.S., and Ph.D. degrees from Columbia Uniersity. He is the author of two textbooks on automatic control and coauthor of two other textbooks, one on circuit theory and the other on linear systems theory. He is the author or coauthor of oer 1 technical papers on control theory and its applications. For 27 years prior to joining NJIT, he was manager of systems research in the Kearfott Guidance and Naigation Corporation. While at Kearfott, he was awarded 12 patents in the field of naigation, instrumentation, and control systems. He is a fellow of the ASME, which awarded him the 1982 Oldenberger Medal. He is a Fellow of the IEEE and has receied the the IEEE Third Millennium Medal and the Control Systems Society s Distinguished Member Award. He can be contacted at the Department of Electrical and Computer Engineering, New Jersey Institute of Technology, Newark, NJ 712. Simon Cohn receied the B.S. degree in mechanical engineering from Boston Uniersity and the M.S. degree from the New Jersey Institute of Technology with a thesis on the measurement of dynamic friction. He is a principal engineer with Ethicon, Inc., a diision of Johnson and Johnson, deeloping surgical instruments. He holds ten patents in surgical instrumentation. DECEMBER 28 «IEEE CONTROL SYSTEMS MAGAZINE 91
Friction. Modeling, Identification, & Analysis
 Friction Modeling, Identification, & Analysis Objectives Understand the friction phenomenon as it relates to motion systems. Develop a control-oriented model with appropriate simplifying assumptions for
Friction Modeling, Identification, & Analysis Objectives Understand the friction phenomenon as it relates to motion systems. Develop a control-oriented model with appropriate simplifying assumptions for
Reversal in time order of interactive events: Collision of inclined rods
 Reersal in time order of interactie eents: Collision of inclined rods Published in The European Journal of Physics Eur. J. Phys. 27 819-824 http://www.iop.org/ej/abstract/0143-0807/27/4/013 Chandru Iyer
Reersal in time order of interactie eents: Collision of inclined rods Published in The European Journal of Physics Eur. J. Phys. 27 819-824 http://www.iop.org/ej/abstract/0143-0807/27/4/013 Chandru Iyer
MODELING AND SIMULATION OF HYDRAULIC ACTUATOR WITH VISCOUS FRICTION
 MODELING AND SIMULATION OF HYDRAULIC ACTUATOR WITH VISCOUS FRICTION Jitendra Yadav 1, Dr. Geeta Agnihotri 1 Assistant professor, Mechanical Engineering Department, University of petroleum and energy studies,
MODELING AND SIMULATION OF HYDRAULIC ACTUATOR WITH VISCOUS FRICTION Jitendra Yadav 1, Dr. Geeta Agnihotri 1 Assistant professor, Mechanical Engineering Department, University of petroleum and energy studies,
Purpose of the experiment
 Impulse and Momentum PES 116 Adanced Physics Lab I Purpose of the experiment Measure a cart s momentum change and compare to the impulse it receies. Compare aerage and peak forces in impulses. To put the
Impulse and Momentum PES 116 Adanced Physics Lab I Purpose of the experiment Measure a cart s momentum change and compare to the impulse it receies. Compare aerage and peak forces in impulses. To put the
Chapter 1: Kinematics of Particles
 Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS
 SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
Transmission lines using a distributed equivalent circuit
 Cambridge Uniersity Press 978-1-107-02600-1 - Transmission Lines Equialent Circuits, Electromagnetic Theory, and Photons Part 1 Transmission lines using a distributed equialent circuit in this web serice
Cambridge Uniersity Press 978-1-107-02600-1 - Transmission Lines Equialent Circuits, Electromagnetic Theory, and Photons Part 1 Transmission lines using a distributed equialent circuit in this web serice
LABORATORY VI. ROTATIONAL DYNAMICS
 LABORATORY VI. ROTATIONAL DYNAMICS So far this semester, you hae been asked to think of objects as point particles rather than extended bodies. This assumption is useful and sometimes good enough. Howeer,
LABORATORY VI. ROTATIONAL DYNAMICS So far this semester, you hae been asked to think of objects as point particles rather than extended bodies. This assumption is useful and sometimes good enough. Howeer,
On my honor, I have neither given nor received unauthorized aid on this examination.
 Instructor(s): Field/Furic PHYSICS DEPARTENT PHY 2053 Exam 1 October 5, 2011 Name (print, last first): Signature: On my honor, I hae neither gien nor receied unauthorized aid on this examination. YOUR
Instructor(s): Field/Furic PHYSICS DEPARTENT PHY 2053 Exam 1 October 5, 2011 Name (print, last first): Signature: On my honor, I hae neither gien nor receied unauthorized aid on this examination. YOUR
CHAPTER 6 FRICTION AND WEAR ANALYSIS FOR BUSHING
 CHAPTER 6 FRICTION AND WEAR ANALYSIS FOR BUSHING 6.1 TEST RIG SETUP FOR THE FRICTION AND WEAR ANALYSIS Knowing the frictional coefficient is important for the determination of wear loss and power loss
CHAPTER 6 FRICTION AND WEAR ANALYSIS FOR BUSHING 6.1 TEST RIG SETUP FOR THE FRICTION AND WEAR ANALYSIS Knowing the frictional coefficient is important for the determination of wear loss and power loss
Two Phase Pressure Drop of CO2, Ammonia, and R245fa in Multiport Aluminum Microchannel Tubes
 Purdue Uniersity Purdue e-pubs International Refrigeration and Air Conditioning Conference School of Mechanical Engineering 6 Two Phase Pressure Drop of CO, Ammonia, and R45fa in Multiport Aluminum Microchannel
Purdue Uniersity Purdue e-pubs International Refrigeration and Air Conditioning Conference School of Mechanical Engineering 6 Two Phase Pressure Drop of CO, Ammonia, and R45fa in Multiport Aluminum Microchannel
Purpose of the experiment
 Centripetal Force PES 116 Adanced Physics Lab I Purpose of the experiment Determine the dependence of mass, radius and angular elocity on Centripetal force. FYI FYI Hershey s Kisses are called that because
Centripetal Force PES 116 Adanced Physics Lab I Purpose of the experiment Determine the dependence of mass, radius and angular elocity on Centripetal force. FYI FYI Hershey s Kisses are called that because
Tools for Investigation of Dynamics of DC-DC Converters within Matlab/Simulink
 Tools for Inestigation of Dynamics of DD onerters within Matlab/Simulink Riga Technical Uniersity, Riga, Latia Email: pikulin03@inbox.l Dmitry Pikulin Abstract: In this paper the study of complex phenomenon
Tools for Inestigation of Dynamics of DD onerters within Matlab/Simulink Riga Technical Uniersity, Riga, Latia Email: pikulin03@inbox.l Dmitry Pikulin Abstract: In this paper the study of complex phenomenon
Position in the xy plane y position x position
 Robust Control of an Underactuated Surface Vessel with Thruster Dynamics K. Y. Pettersen and O. Egeland Department of Engineering Cybernetics Norwegian Uniersity of Science and Technology N- Trondheim,
Robust Control of an Underactuated Surface Vessel with Thruster Dynamics K. Y. Pettersen and O. Egeland Department of Engineering Cybernetics Norwegian Uniersity of Science and Technology N- Trondheim,
Last Time: Start Rotational Motion (now thru mid Nov) Basics: Angular Speed, Angular Acceleration
 Last Time: Start Rotational Motion (now thru mid No) Basics: Angular Speed, Angular Acceleration Today: Reiew, Centripetal Acceleration, Newtonian Graitation i HW #6 due Tuesday, Oct 19, 11:59 p.m. Exam
Last Time: Start Rotational Motion (now thru mid No) Basics: Angular Speed, Angular Acceleration Today: Reiew, Centripetal Acceleration, Newtonian Graitation i HW #6 due Tuesday, Oct 19, 11:59 p.m. Exam
6. Find the net torque on the wheel in Figure about the axle through O if a = 10.0 cm and b = 25.0 cm.
 1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
1. During a certain period of time, the angular position of a swinging door is described by θ = 5.00 + 10.0t + 2.00t 2, where θ is in radians and t is in seconds. Determine the angular position, angular
DYNAMICS ME HOMEWORK PROBLEM SETS
 DYNAMICS ME 34010 HOMEWORK PROBLEM SETS Mahmoud M. Safadi 1, M.B. Rubin 2 1 safadi@technion.ac.il, 2 mbrubin@technion.ac.il Faculty of Mechanical Engineering Technion Israel Institute of Technology Spring
DYNAMICS ME 34010 HOMEWORK PROBLEM SETS Mahmoud M. Safadi 1, M.B. Rubin 2 1 safadi@technion.ac.il, 2 mbrubin@technion.ac.il Faculty of Mechanical Engineering Technion Israel Institute of Technology Spring
Lecture 12! Center of mass! Uniform circular motion!
 Lecture 1 Center of mass Uniform circular motion Today s Topics: Center of mass Uniform circular motion Centripetal acceleration and force Banked cures Define the center of mass The center of mass is a
Lecture 1 Center of mass Uniform circular motion Today s Topics: Center of mass Uniform circular motion Centripetal acceleration and force Banked cures Define the center of mass The center of mass is a
Modification of the Leuven Integrated Friction Model Structure
 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 47, NO. 4, APRIL 2002 683 Modification of the Leuven Integrated Friction Model Structure Vincent Lampaert, Jan Swevers, and Farid Al-Bender Abstract This note
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 47, NO. 4, APRIL 2002 683 Modification of the Leuven Integrated Friction Model Structure Vincent Lampaert, Jan Swevers, and Farid Al-Bender Abstract This note
On the LuGre Model and Friction-Induced Hysteresis
 Proceedings of the 6 American Control Conference Minneapolis, Minnesota, USA, June 4-6, 6 ThB3.4 On the LuGre Model and Friction-nduced Hysteresis Ashwani K. Padthe, JinHyoung Oh, and Dennis S. Bernstein
Proceedings of the 6 American Control Conference Minneapolis, Minnesota, USA, June 4-6, 6 ThB3.4 On the LuGre Model and Friction-nduced Hysteresis Ashwani K. Padthe, JinHyoung Oh, and Dennis S. Bernstein
Plane Motion of Rigid Bodies: Forces and Accelerations
 Plane Motion of Rigid Bodies: Forces and Accelerations Reference: Beer, Ferdinand P. et al, Vector Mechanics for Engineers : Dynamics, 8 th Edition, Mc GrawHill Hibbeler R.C., Engineering Mechanics: Dynamics,
Plane Motion of Rigid Bodies: Forces and Accelerations Reference: Beer, Ferdinand P. et al, Vector Mechanics for Engineers : Dynamics, 8 th Edition, Mc GrawHill Hibbeler R.C., Engineering Mechanics: Dynamics,
The Kinetic Theory of Gases
 978-1-107-1788-3 Classical and Quantum Thermal Physics The Kinetic Theory of Gases CHAPTER 1 1.0 Kinetic Theory, Classical and Quantum Thermodynamics Two important components of the unierse are: the matter
978-1-107-1788-3 Classical and Quantum Thermal Physics The Kinetic Theory of Gases CHAPTER 1 1.0 Kinetic Theory, Classical and Quantum Thermodynamics Two important components of the unierse are: the matter
A. unchanged increased B. unchanged unchanged C. increased increased D. increased unchanged
 IB PHYSICS Name: DEVIL PHYSICS Period: Date: BADDEST CLASS ON CAMPUS CHAPTER B TEST REVIEW. A rocket is fired ertically. At its highest point, it explodes. Which one of the following describes what happens
IB PHYSICS Name: DEVIL PHYSICS Period: Date: BADDEST CLASS ON CAMPUS CHAPTER B TEST REVIEW. A rocket is fired ertically. At its highest point, it explodes. Which one of the following describes what happens
Frequency Domain Identification of Dynamic Friction Model Parameters
 IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, VOL. 10, NO. 2, MARCH 2002 191 Frequency Domain Identification of Dynamic Friction Model Parameters Ron H. A. Hensen, Marinus (René) J. G. van de Molengraft,
IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, VOL. 10, NO. 2, MARCH 2002 191 Frequency Domain Identification of Dynamic Friction Model Parameters Ron H. A. Hensen, Marinus (René) J. G. van de Molengraft,
MOTION OF FALLING OBJECTS WITH RESISTANCE
 DOING PHYSICS WIH MALAB MECHANICS MOION OF FALLING OBJECS WIH RESISANCE Ian Cooper School of Physics, Uniersity of Sydney ian.cooper@sydney.edu.au DOWNLOAD DIRECORY FOR MALAB SCRIPS mec_fr_mg_b.m Computation
DOING PHYSICS WIH MALAB MECHANICS MOION OF FALLING OBJECS WIH RESISANCE Ian Cooper School of Physics, Uniersity of Sydney ian.cooper@sydney.edu.au DOWNLOAD DIRECORY FOR MALAB SCRIPS mec_fr_mg_b.m Computation
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
Precision Ball Screw/Spline
 58-2E Models BNS-A, BNS, NS-A and NS Seal Outer ring Shim plate Seal Spline nut Seal Collar Shim plate Seal End cap Ball Outer ring Ball screw nut Outer ring Ball Retainer Retainer Outer ring Point of
58-2E Models BNS-A, BNS, NS-A and NS Seal Outer ring Shim plate Seal Spline nut Seal Collar Shim plate Seal End cap Ball Outer ring Ball screw nut Outer ring Ball Retainer Retainer Outer ring Point of
Space Probe and Relative Motion of Orbiting Bodies
 Space robe and Relatie Motion of Orbiting Bodies Eugene I. Butiko Saint etersburg State Uniersity, Saint etersburg, Russia E-mail: e.butiko@phys.spbu.ru bstract. Seeral possibilities to launch a space
Space robe and Relatie Motion of Orbiting Bodies Eugene I. Butiko Saint etersburg State Uniersity, Saint etersburg, Russia E-mail: e.butiko@phys.spbu.ru bstract. Seeral possibilities to launch a space
Lecture #8-6 Waves and Sound 1. Mechanical Waves We have already considered simple harmonic motion, which is an example of periodic motion in time.
 Lecture #8-6 Waes and Sound 1. Mechanical Waes We hae already considered simple harmonic motion, which is an example of periodic motion in time. The position of the body is changing with time as a sinusoidal
Lecture #8-6 Waes and Sound 1. Mechanical Waes We hae already considered simple harmonic motion, which is an example of periodic motion in time. The position of the body is changing with time as a sinusoidal
End-of-Chapter Exercises
 End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
Realization of Hull Stability Control System for Continuous Track Vehicle with the Robot Arm
 Adanced Science and Technology Letters Vol.86 (Ubiquitous Science and Engineering 05), pp.96-0 http://dx.doi.org/0.457/astl.05.86.0 Realization of Hull Stability Control System for Continuous Track Vehicle
Adanced Science and Technology Letters Vol.86 (Ubiquitous Science and Engineering 05), pp.96-0 http://dx.doi.org/0.457/astl.05.86.0 Realization of Hull Stability Control System for Continuous Track Vehicle
An Introduction to Three-Dimensional, Rigid Body Dynamics. James W. Kamman, PhD. Volume II: Kinetics. Unit 3
 Summary An Introduction to hree-dimensional, igid ody Dynamics James W. Kamman, PhD Volume II: Kinetics Unit Degrees of Freedom, Partial Velocities and Generalized Forces his unit defines the concepts
Summary An Introduction to hree-dimensional, igid ody Dynamics James W. Kamman, PhD Volume II: Kinetics Unit Degrees of Freedom, Partial Velocities and Generalized Forces his unit defines the concepts
DYNAMICS. Kinematics of Particles Engineering Dynamics Lecture Note VECTOR MECHANICS FOR ENGINEERS: Eighth Edition CHAPTER
 27 The McGraw-Hill Companies, Inc. All rights resered. Eighth E CHAPTER 11 VECTOR MECHANICS FOR ENGINEERS: DYNAMICS Ferdinand P. Beer E. Russell Johnston, Jr. Kinematics of Particles Lecture Notes: J.
27 The McGraw-Hill Companies, Inc. All rights resered. Eighth E CHAPTER 11 VECTOR MECHANICS FOR ENGINEERS: DYNAMICS Ferdinand P. Beer E. Russell Johnston, Jr. Kinematics of Particles Lecture Notes: J.
متلب سایت MatlabSite.com
 Vehicle Velocity Estimation based on Data fusion by Kalman Filtering for ABS Melika Amiri Graduate student in electrical engineering, Islamic Azad uniersity, Science and Research ehran, Iran Melika_64@yahoo.com
Vehicle Velocity Estimation based on Data fusion by Kalman Filtering for ABS Melika Amiri Graduate student in electrical engineering, Islamic Azad uniersity, Science and Research ehran, Iran Melika_64@yahoo.com
The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72.
![The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72. The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72.](/thumbs/96/127505807.jpg) ADVANCED GCE UNIT 76/ MATHEMATICS (MEI Mechanics MONDAY MAY 7 Additional materials: Answer booklet (8 pages Graph paper MEI Examination Formulae and Tables (MF Morning Time: hour minutes INSTRUCTIONS TO
ADVANCED GCE UNIT 76/ MATHEMATICS (MEI Mechanics MONDAY MAY 7 Additional materials: Answer booklet (8 pages Graph paper MEI Examination Formulae and Tables (MF Morning Time: hour minutes INSTRUCTIONS TO
STATICS. Friction VECTOR MECHANICS FOR ENGINEERS: Eighth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 Eighth E 8 Friction CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University Contents Introduction Laws of Dry Friction.
Eighth E 8 Friction CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University Contents Introduction Laws of Dry Friction.
Introduction to Thermodynamic Cycles Part 1 1 st Law of Thermodynamics and Gas Power Cycles
 Introduction to Thermodynamic Cycles Part 1 1 st Law of Thermodynamics and Gas Power Cycles by James Doane, PhD, PE Contents 1.0 Course Oeriew... 4.0 Basic Concepts of Thermodynamics... 4.1 Temperature
Introduction to Thermodynamic Cycles Part 1 1 st Law of Thermodynamics and Gas Power Cycles by James Doane, PhD, PE Contents 1.0 Course Oeriew... 4.0 Basic Concepts of Thermodynamics... 4.1 Temperature
State-space Modelling of Hysteresis-based Control Schemes
 European Control Conference (ECC) July 7-9,, Zürich, Switzerland. State-space Modelling of Hysteresis-based Control Schemes Soumya Kundu Ian A. Hiskens Abstract The paper deelops a state-space model for
European Control Conference (ECC) July 7-9,, Zürich, Switzerland. State-space Modelling of Hysteresis-based Control Schemes Soumya Kundu Ian A. Hiskens Abstract The paper deelops a state-space model for
Section 6: PRISMATIC BEAMS. Beam Theory
 Beam Theory There are two types of beam theory aailable to craft beam element formulations from. They are Bernoulli-Euler beam theory Timoshenko beam theory One learns the details of Bernoulli-Euler beam
Beam Theory There are two types of beam theory aailable to craft beam element formulations from. They are Bernoulli-Euler beam theory Timoshenko beam theory One learns the details of Bernoulli-Euler beam
Physics 12. Unit 5 Circular Motion and Gravitation Part 1
 Physics 12 Unit 5 Circular Motion and Gravitation Part 1 1. Nonlinear motions According to the Newton s first law, an object remains its tendency of motion as long as there is no external force acting
Physics 12 Unit 5 Circular Motion and Gravitation Part 1 1. Nonlinear motions According to the Newton s first law, an object remains its tendency of motion as long as there is no external force acting
PHYSICS LAB Experiment 9 Fall 2004 THE TORSION PENDULUM
 PHYSICS 83 - LAB Experiment 9 Fall 004 THE TORSION PENDULUM In this experiment we will study the torsion constants of three different rods, a brass rod, a thin steel rod and a thick steel rod. We will
PHYSICS 83 - LAB Experiment 9 Fall 004 THE TORSION PENDULUM In this experiment we will study the torsion constants of three different rods, a brass rod, a thin steel rod and a thick steel rod. We will
Centripetal force. Objectives. Assessment. Assessment. Equations. Physics terms 5/13/14
 Centripetal force Objecties Describe and analyze the motion of objects moing in circular motion. Apply Newton s second law to circular motion problems. Interpret free-body force diagrams. 1. A race car
Centripetal force Objecties Describe and analyze the motion of objects moing in circular motion. Apply Newton s second law to circular motion problems. Interpret free-body force diagrams. 1. A race car
Why does Saturn have many tiny rings?
 2004 Thierry De Mees hy does Saturn hae many tiny rings? or Cassini-Huygens Mission: New eidence for the Graitational Theory with Dual Vector Field T. De Mees - thierrydemees @ pandora.be Abstract This
2004 Thierry De Mees hy does Saturn hae many tiny rings? or Cassini-Huygens Mission: New eidence for the Graitational Theory with Dual Vector Field T. De Mees - thierrydemees @ pandora.be Abstract This
Investigation on Ring Valve Motion and Impact Stress in Reciprocating Compressors
 Purdue Uniersity Purdue e-pubs International Compressor Engineering Conference School of Mechanical Engineering 2010 Inestigation on Ring Vale Motion and Impact Stress in Reciprocating Compressors Yu Wang
Purdue Uniersity Purdue e-pubs International Compressor Engineering Conference School of Mechanical Engineering 2010 Inestigation on Ring Vale Motion and Impact Stress in Reciprocating Compressors Yu Wang
PROBLEM Copyright McGraw-Hill Education. Permission required for reproduction or display. SOLUTION. ω = 29.6 rad/s. ω = = 36 3.
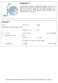 PROLEM 15.1 The brake drum is attached to a larger flywheel that is not shown. The motion of the brake drum is defined by the relation θ = 36t 1.6 t, where θ is expressed in radians and t in seconds. Determine
PROLEM 15.1 The brake drum is attached to a larger flywheel that is not shown. The motion of the brake drum is defined by the relation θ = 36t 1.6 t, where θ is expressed in radians and t in seconds. Determine
Simulations of Space Probes and their Motions Relative to the Host Orbital Station
 Simulations of Space robes and their Motions Relatie to the Host Orbital Station Eugene I. Butiko St. etersburg State Uniersity, St. etersburg, Russia Abstract Launching a space probe from an orbiting
Simulations of Space robes and their Motions Relatie to the Host Orbital Station Eugene I. Butiko St. etersburg State Uniersity, St. etersburg, Russia Abstract Launching a space probe from an orbiting
Physics 4C Spring 2016 Test 3
 Physics 4C Spring 016 Test 3 Name: June 1, 016 Please show your work! Answers are not complete without clear reasoning. When asked for an expression, you must gie your answer in terms of the ariables gien
Physics 4C Spring 016 Test 3 Name: June 1, 016 Please show your work! Answers are not complete without clear reasoning. When asked for an expression, you must gie your answer in terms of the ariables gien
The student will be able to: 1 Determine the torque of an applied force and solve related problems.
 Honors Physics Assignment Rotational Mechanics Reading Chapters 10 and 11 Objectives/HW The student will be able to: HW: 1 Determine the torque of an applied force and solve related problems. (t = rx r
Honors Physics Assignment Rotational Mechanics Reading Chapters 10 and 11 Objectives/HW The student will be able to: HW: 1 Determine the torque of an applied force and solve related problems. (t = rx r
Sliding Bearings. Fig.(1) (a) Full-journal bearing and (b) partial-journal bearing
 Sliding Bearings The goal of a bearing is to provide relative positioning and rotational freedom while transmitting a load between two parts, commonly a shaft and its housing. The object of lubrication
Sliding Bearings The goal of a bearing is to provide relative positioning and rotational freedom while transmitting a load between two parts, commonly a shaft and its housing. The object of lubrication
FLOW-FORCE COMPENSATION IN A HYDRAULIC VALVE
 FLOW-FORCE COMPENSATION IN A HYDRAULIC VALVE Jan Lugowski Purdue Uniersity West Lafayette, IN, USA lugowskj@purdue.edu ABSTRACT Flow-reaction forces acting in hydraulic ales hae been studied for many decades.
FLOW-FORCE COMPENSATION IN A HYDRAULIC VALVE Jan Lugowski Purdue Uniersity West Lafayette, IN, USA lugowskj@purdue.edu ABSTRACT Flow-reaction forces acting in hydraulic ales hae been studied for many decades.
Agricultural Science 1B Principles & Processes in Agriculture. Mike Wheatland
 Agricultural Science 1B Principles & Processes in Agriculture Mike Wheatland (m.wheatland@physics.usyd.edu.au) Outline - Lectures weeks 9-12 Chapter 6: Balance in nature - description of energy balance
Agricultural Science 1B Principles & Processes in Agriculture Mike Wheatland (m.wheatland@physics.usyd.edu.au) Outline - Lectures weeks 9-12 Chapter 6: Balance in nature - description of energy balance
Observer Based Friction Cancellation in Mechanical Systems
 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014) Oct. 22 25, 2014 in KINTEX, Gyeonggi-do, Korea Observer Based Friction Cancellation in Mechanical Systems Caner Odabaş
2014 14th International Conference on Control, Automation and Systems (ICCAS 2014) Oct. 22 25, 2014 in KINTEX, Gyeonggi-do, Korea Observer Based Friction Cancellation in Mechanical Systems Caner Odabaş
Friction Modeling and Compensation for Haptic Interfaces
 Friction Modeling and Compensation for Haptic Interfaces Nicholas L. Bernstein * Dale A. Lawrence * Lucy Y. Pao (*) University of Colorado, Aerospace Engineering, USA ( ) University of Colorado, Electrical
Friction Modeling and Compensation for Haptic Interfaces Nicholas L. Bernstein * Dale A. Lawrence * Lucy Y. Pao (*) University of Colorado, Aerospace Engineering, USA ( ) University of Colorado, Electrical
Name: Date: Period: AP Physics C Rotational Motion HO19
 1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
The student will be able to: the torque of an applied force and solve related problems.
 Honors Physics Assignment Rotational Mechanics Reading Chapters 10 and 11 Objectives/HW: Assignment #1 M: Assignment #2 M: Assignment #3 M: Assignment #4 M: 1 2 3 #1-5 #6-10 #14, 15, 17, 18, 20-23 #24,
Honors Physics Assignment Rotational Mechanics Reading Chapters 10 and 11 Objectives/HW: Assignment #1 M: Assignment #2 M: Assignment #3 M: Assignment #4 M: 1 2 3 #1-5 #6-10 #14, 15, 17, 18, 20-23 #24,
Lubrication and Journal Bearings
 UNIVERSITY OF HAIL College of Engineering Department of Mechanical Engineering Chapter 12 Lubrication and Journal Bearings Text Book : Mechanical Engineering Design, 9th Edition Dr. Badreddine AYADI 2016
UNIVERSITY OF HAIL College of Engineering Department of Mechanical Engineering Chapter 12 Lubrication and Journal Bearings Text Book : Mechanical Engineering Design, 9th Edition Dr. Badreddine AYADI 2016
Magnetic braking: Finding the effective length over which the eddy currents form
 Magnetic braking: Finding the effectie length oer which the eddy currents form Scott B. Hughes Physics Department, The College of Wooster, Wooster, Ohio 44691 May 5, 2000 This experiment uses a square
Magnetic braking: Finding the effectie length oer which the eddy currents form Scott B. Hughes Physics Department, The College of Wooster, Wooster, Ohio 44691 May 5, 2000 This experiment uses a square
VISUAL PHYSICS ONLINE RECTLINEAR MOTION: UNIFORM ACCELERATION
 VISUAL PHYSICS ONLINE RECTLINEAR MOTION: UNIFORM ACCELERATION Predict Obsere Explain Exercise 1 Take an A4 sheet of paper and a heay object (cricket ball, basketball, brick, book, etc). Predict what will
VISUAL PHYSICS ONLINE RECTLINEAR MOTION: UNIFORM ACCELERATION Predict Obsere Explain Exercise 1 Take an A4 sheet of paper and a heay object (cricket ball, basketball, brick, book, etc). Predict what will
TutorBreeze.com 7. ROTATIONAL MOTION. 3. If the angular velocity of a spinning body points out of the page, then describe how is the body spinning?
 1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
CFD PREDICTIONS OF DRILLING FLUID VELOCITY AND PRESSURE PROFILES IN LAMINAR HELICAL FLOW
 Brazilian Journal of Chemical Engineering ISSN 4-66 Printed in Brazil www.abeq.org.br/bjche Vol. 4, No. 4, pp. 587-595, October - December, 7 CFD PREDICTIONS OF DRILLING FLUID VELOCITY AND PRESSURE PROFILES
Brazilian Journal of Chemical Engineering ISSN 4-66 Printed in Brazil www.abeq.org.br/bjche Vol. 4, No. 4, pp. 587-595, October - December, 7 CFD PREDICTIONS OF DRILLING FLUID VELOCITY AND PRESSURE PROFILES
Engineering Mechanics. Friction in Action
 Engineering Mechanics Friction in Action What is friction? Friction is a retarding force that opposes motion. Friction types: Static friction Kinetic friction Fluid friction Sources of dry friction Dry
Engineering Mechanics Friction in Action What is friction? Friction is a retarding force that opposes motion. Friction types: Static friction Kinetic friction Fluid friction Sources of dry friction Dry
Chapter 15 Magnetism and Electromagnetic Induction 15.1 Magnetic Force on a Current-Carrying Wire Homework # 125
 Magnetism and Electromagnetic nduction 15.1 Magnetic Force on a Current-Carrying Wire Homework # 125 01. A wire carrying a 2.45-A current wire passes through a 1.60-T magnetic field. What is the force
Magnetism and Electromagnetic nduction 15.1 Magnetic Force on a Current-Carrying Wire Homework # 125 01. A wire carrying a 2.45-A current wire passes through a 1.60-T magnetic field. What is the force
KNIFE EDGE FLAT ROLLER
 EXPERIMENT N0. 1 To Determine jumping speed of cam Equipment: Cam Analysis Machine Aim: To determine jumping speed of Cam Formulae used: Upward inertial force = Wvω 2 /g Downward force = W + Ks For good
EXPERIMENT N0. 1 To Determine jumping speed of cam Equipment: Cam Analysis Machine Aim: To determine jumping speed of Cam Formulae used: Upward inertial force = Wvω 2 /g Downward force = W + Ks For good
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
DEVELOPMENT OF DROP WEIGHT IMPACT TEST MACHINE
 CHAPTER-8 DEVELOPMENT OF DROP WEIGHT IMPACT TEST MACHINE 8.1 Introduction The behavior of materials is different when they are subjected to dynamic loading [9]. The testing of materials under dynamic conditions
CHAPTER-8 DEVELOPMENT OF DROP WEIGHT IMPACT TEST MACHINE 8.1 Introduction The behavior of materials is different when they are subjected to dynamic loading [9]. The testing of materials under dynamic conditions
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
Conditions for Capacitor Voltage Regulation in a Five-Level Cascade Multilevel Inverter: Application to Voltage-Boost in a PM Drive
 Conditions for Capacitor oltage Regulation in a FieLeel Cascade Multileel Inerter: Application to oltageboost in a PM Drie John Chiasson, Burak Özpineci, Zhong Du 3 and Leon M. Tolbert 4 Abstract A cascade
Conditions for Capacitor oltage Regulation in a FieLeel Cascade Multileel Inerter: Application to oltageboost in a PM Drie John Chiasson, Burak Özpineci, Zhong Du 3 and Leon M. Tolbert 4 Abstract A cascade
SIMULATIONS OF CHARACTERISTICS OF TUNED LIQUID COLUMN DAMPER USING AN ELLIPTICAL FLOW PATH ESTIMATION METHOD
 October -7, 008, Beijing, China SIMULATIONS OF CHARACTERISTICS OF TUNED LIQUID COLUMN DAMPER USING AN ELLIPTICAL FLOW PATH ESTIMATION METHOD P. Chaiiriyawong, S. Limkatanyu and T. Pinkaew 3 Lecturer, Dept.
October -7, 008, Beijing, China SIMULATIONS OF CHARACTERISTICS OF TUNED LIQUID COLUMN DAMPER USING AN ELLIPTICAL FLOW PATH ESTIMATION METHOD P. Chaiiriyawong, S. Limkatanyu and T. Pinkaew 3 Lecturer, Dept.
A study of jacking force for a curved pipejacking
 Journal of Rock Mechanics and Geotechnical Engineering. 200, 2 (4): 298 304 A study of jacking force for a cured pipejacking K. J. Shou, J. M. Jiang Department of Ciil Engineering, National Chung Hsing
Journal of Rock Mechanics and Geotechnical Engineering. 200, 2 (4): 298 304 A study of jacking force for a cured pipejacking K. J. Shou, J. M. Jiang Department of Ciil Engineering, National Chung Hsing
SLIP MODEL PERFORMANCE FOR MICRO-SCALE GAS FLOWS
 3th AIAA Thermophysics Conference 3- June 3, Orlando, Florida AIAA 3-5 SLIP MODEL PERFORMANCE FOR MICRO-SCALE GAS FLOWS Matthew J. McNenly* Department of Aerospace Engineering Uniersity of Michigan, Ann
3th AIAA Thermophysics Conference 3- June 3, Orlando, Florida AIAA 3-5 SLIP MODEL PERFORMANCE FOR MICRO-SCALE GAS FLOWS Matthew J. McNenly* Department of Aerospace Engineering Uniersity of Michigan, Ann
Generalized d-q Model of n-phase Induction Motor Drive
 Generalized d-q Model of n-phase Induction Motor Drie G. Renukadei, K. Rajambal Abstract This paper presents a generalized d-q model of n- phase induction motor drie. Multi -phase (n-phase) induction motor
Generalized d-q Model of n-phase Induction Motor Drie G. Renukadei, K. Rajambal Abstract This paper presents a generalized d-q model of n- phase induction motor drie. Multi -phase (n-phase) induction motor
Doppler shifts in astronomy
 7.4 Doppler shift 253 Diide the transformation (3.4) by as follows: = g 1 bck. (Lorentz transformation) (7.43) Eliminate in the right-hand term with (41) and then inoke (42) to yield = g (1 b cos u). (7.44)
7.4 Doppler shift 253 Diide the transformation (3.4) by as follows: = g 1 bck. (Lorentz transformation) (7.43) Eliminate in the right-hand term with (41) and then inoke (42) to yield = g (1 b cos u). (7.44)
Product description. Compact Modules. Characteristic features. Further highlights
 4 Compact Modules Product description Characteristic features Five fine-tuned sizes based on a compact precision aluminum profile with two integrated pre-tensioned ball rail systems Identical external
4 Compact Modules Product description Characteristic features Five fine-tuned sizes based on a compact precision aluminum profile with two integrated pre-tensioned ball rail systems Identical external
D : SOLID MECHANICS. Q. 1 Q. 9 carry one mark each.
 GTE 2016 Q. 1 Q. 9 carry one mark each. D : SOLID MECHNICS Q.1 single degree of freedom vibrating system has mass of 5 kg, stiffness of 500 N/m and damping coefficient of 100 N-s/m. To make the system
GTE 2016 Q. 1 Q. 9 carry one mark each. D : SOLID MECHNICS Q.1 single degree of freedom vibrating system has mass of 5 kg, stiffness of 500 N/m and damping coefficient of 100 N-s/m. To make the system
An Elastic Contact Problem with Normal Compliance and Memory Term
 Machine Dynamics Research 2012, Vol. 36, No 1, 15 25 Abstract An Elastic Contact Problem with Normal Compliance and Memory Term Mikäel Barboteu, Ahmad Ramadan, Mircea Sofonea Uniersité de Perpignan, France
Machine Dynamics Research 2012, Vol. 36, No 1, 15 25 Abstract An Elastic Contact Problem with Normal Compliance and Memory Term Mikäel Barboteu, Ahmad Ramadan, Mircea Sofonea Uniersité de Perpignan, France
Adaptive Control of Mass-Spring Systems with Unknown Hysteretic Contact Friction
 26 American Control Conference (ACC) Boston arriott Copley Place July 6-8, 26. Boston, A, USA Adaptive Control of ass-spring Systems with Unknown Hysteretic Contact Friction ohammad Al Janaideh and Dennis
26 American Control Conference (ACC) Boston arriott Copley Place July 6-8, 26. Boston, A, USA Adaptive Control of ass-spring Systems with Unknown Hysteretic Contact Friction ohammad Al Janaideh and Dennis
MATHEMATICAL MODELLING AND IDENTIFICATION OF THE FLOW DYNAMICS IN
 MATHEMATICAL MOELLING AN IENTIFICATION OF THE FLOW YNAMICS IN MOLTEN GLASS FURNACES Jan Studzinski Systems Research Institute of Polish Academy of Sciences Newelska 6-447 Warsaw, Poland E-mail: studzins@ibspan.waw.pl
MATHEMATICAL MOELLING AN IENTIFICATION OF THE FLOW YNAMICS IN MOLTEN GLASS FURNACES Jan Studzinski Systems Research Institute of Polish Academy of Sciences Newelska 6-447 Warsaw, Poland E-mail: studzins@ibspan.waw.pl
Chapter 6: Operational Amplifiers
 Chapter 6: Operational Amplifiers Circuit symbol and nomenclature: An op amp is a circuit element that behaes as a VCVS: The controlling oltage is in = and the controlled oltage is such that 5 5 A where
Chapter 6: Operational Amplifiers Circuit symbol and nomenclature: An op amp is a circuit element that behaes as a VCVS: The controlling oltage is in = and the controlled oltage is such that 5 5 A where
Centripetal acceleration ac = to2r Kinetic energy of rotation KE, = \lto2. Moment of inertia. / = mr2 Newton's second law for rotational motion t = la
 The Language of Physics Angular displacement The angle that a body rotates through while in rotational motion (p. 241). Angular velocity The change in the angular displacement of a rotating body about
The Language of Physics Angular displacement The angle that a body rotates through while in rotational motion (p. 241). Angular velocity The change in the angular displacement of a rotating body about
Force and Motion. Thought Experiment
 Team Force and Motion In previous labs, you used a motion sensor to measure the position, velocity, and acceleration of moving objects. You were not concerned about the mechanism that caused the object
Team Force and Motion In previous labs, you used a motion sensor to measure the position, velocity, and acceleration of moving objects. You were not concerned about the mechanism that caused the object
Trajectory Estimation for Tactical Ballistic Missiles in Terminal Phase Using On-line Input Estimator
 Proc. Natl. Sci. Counc. ROC(A) Vol. 23, No. 5, 1999. pp. 644-653 Trajectory Estimation for Tactical Ballistic Missiles in Terminal Phase Using On-line Input Estimator SOU-CHEN LEE, YU-CHAO HUANG, AND CHENG-YU
Proc. Natl. Sci. Counc. ROC(A) Vol. 23, No. 5, 1999. pp. 644-653 Trajectory Estimation for Tactical Ballistic Missiles in Terminal Phase Using On-line Input Estimator SOU-CHEN LEE, YU-CHAO HUANG, AND CHENG-YU
Final Exam April 30, 2013
 Final Exam Instructions: You have 120 minutes to complete this exam. This is a closed-book, closed-notes exam. You are allowed to use a calculator during the exam. Usage of mobile phones and other electronic
Final Exam Instructions: You have 120 minutes to complete this exam. This is a closed-book, closed-notes exam. You are allowed to use a calculator during the exam. Usage of mobile phones and other electronic
PHYSICS (B) v 2 r. v r
 PHYSICS 1. If Q be the amount of liquid (iscosity ) flowing per second through a capillary tube of radius r and length l under a pressure difference P, then which of the following relation is correct?
PHYSICS 1. If Q be the amount of liquid (iscosity ) flowing per second through a capillary tube of radius r and length l under a pressure difference P, then which of the following relation is correct?
LECTURE NOTE THERMODYNAMICS (GEC 221)
 LETURE NOTE ON THERMODYNAMIS (GE ) Thermodynamics is the branch of science that treats the arious phenomena of energy and related properties of matter especially the relationship between heat, work and
LETURE NOTE ON THERMODYNAMIS (GE ) Thermodynamics is the branch of science that treats the arious phenomena of energy and related properties of matter especially the relationship between heat, work and
1 MR SAMPLE EXAM 3 FALL 2013
 SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
SAMPLE EXAM 3 FALL 013 1. A merry-go-round rotates from rest with an angular acceleration of 1.56 rad/s. How long does it take to rotate through the first rev? A) s B) 4 s C) 6 s D) 8 s E) 10 s. A wheel,
Step 1: Mathematical Modeling
 083 Mechanical Vibrations Lesson Vibration Analysis Procedure The analysis of a vibrating system usually involves four steps: mathematical modeling derivation of the governing uations solution of the uations
083 Mechanical Vibrations Lesson Vibration Analysis Procedure The analysis of a vibrating system usually involves four steps: mathematical modeling derivation of the governing uations solution of the uations
HELICAL BUCKLING OF DRILL-STRINGS
 HELICAL BUCKLING OF DRILL-STRINGS Marcin Kapitaniak 1,, Vahid Vaziri 1,, and Marian Wiercigroch 1 1 Centre for Applied Dynamics Research, School of Engineering, University of Aberdeen, Aberdeen, AB24 3UE,
HELICAL BUCKLING OF DRILL-STRINGS Marcin Kapitaniak 1,, Vahid Vaziri 1,, and Marian Wiercigroch 1 1 Centre for Applied Dynamics Research, School of Engineering, University of Aberdeen, Aberdeen, AB24 3UE,
Unit 8 Notetaking Guide Torque and Rotational Motion
 Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Key words: Polymeric Composite Bearing, Clearance, FEM
 A study on the effect of the clearance on the contact stresses and kinematics of polymeric composite journal bearings under reciprocating sliding conditions Abstract The effect of the clearance on the
A study on the effect of the clearance on the contact stresses and kinematics of polymeric composite journal bearings under reciprocating sliding conditions Abstract The effect of the clearance on the
ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D225 TUTORIAL 3 CENTRIPETAL FORCE
 ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D5 TUTORIAL CENTRIPETAL FORCE This tutorial examines the relationship between inertia and acceleration. On completion of this tutorial you should be able
ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D5 TUTORIAL CENTRIPETAL FORCE This tutorial examines the relationship between inertia and acceleration. On completion of this tutorial you should be able
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
5. Plane Kinetics of Rigid Bodies
 5. Plane Kinetics of Rigid Bodies 5.1 Mass moments of inertia 5.2 General equations of motion 5.3 Translation 5.4 Fixed axis rotation 5.5 General plane motion 5.6 Work and energy relations 5.7 Impulse
5. Plane Kinetics of Rigid Bodies 5.1 Mass moments of inertia 5.2 General equations of motion 5.3 Translation 5.4 Fixed axis rotation 5.5 General plane motion 5.6 Work and energy relations 5.7 Impulse
The Effect of the Static Striebeck Friction in the Robust VS/Sliding Mode Control of a Ball-Beam System
 The Effect of the Static Striebeck Friction in the Robust VS/Sliding Mode Control of a -Beam System József K. Tar, János F. Bitó Institute of Intelligent Engineering Systems, Budapest Tech Bécsi út 96/B,
The Effect of the Static Striebeck Friction in the Robust VS/Sliding Mode Control of a -Beam System József K. Tar, János F. Bitó Institute of Intelligent Engineering Systems, Budapest Tech Bécsi út 96/B,
Received 21 April 2008; accepted 6 January 2009
 Indian Journal of Engineering & Materials Sciences Vol. 16, February 2009, pp. 7-13 Inestigation on the characteristics of a new high frequency three-way proportional pressure reducing ale in ariable ale
Indian Journal of Engineering & Materials Sciences Vol. 16, February 2009, pp. 7-13 Inestigation on the characteristics of a new high frequency three-way proportional pressure reducing ale in ariable ale
4 Fundamentals of Continuum Thermomechanics
 4 Fundamentals of Continuum Thermomechanics In this Chapter, the laws of thermodynamics are reiewed and formulated for a continuum. The classical theory of thermodynamics, which is concerned with simple
4 Fundamentals of Continuum Thermomechanics In this Chapter, the laws of thermodynamics are reiewed and formulated for a continuum. The classical theory of thermodynamics, which is concerned with simple
Physics for Scientist and Engineers third edition Rotational Motion About a Fixed Axis Problems
 A particular bird s eye can just distinguish objects that subtend an angle no smaller than about 3 E -4 rad, A) How many degrees is this B) How small an object can the bird just distinguish when flying
A particular bird s eye can just distinguish objects that subtend an angle no smaller than about 3 E -4 rad, A) How many degrees is this B) How small an object can the bird just distinguish when flying
Here is what you will be able to do when you complete each objective: 1. State the general laws of static and kinetic friction.
 Friction I Learning Outcome When you complete this module you will be able to: Describe and solve problems involving friction. Learning Objectives Here is what you will be able to do when you complete
Friction I Learning Outcome When you complete this module you will be able to: Describe and solve problems involving friction. Learning Objectives Here is what you will be able to do when you complete
A Nonlinear Disturbance Observer for Robotic Manipulators
 932 IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 47, NO. 4, AUGUST 2000 A Nonlinear Disturbance Observer for Robotic Manipulators Wen-Hua Chen, Member, IEEE, Donald J. Ballance, Member, IEEE, Peter
932 IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 47, NO. 4, AUGUST 2000 A Nonlinear Disturbance Observer for Robotic Manipulators Wen-Hua Chen, Member, IEEE, Donald J. Ballance, Member, IEEE, Peter
AP Physics C: Work, Energy, and Power Practice
 AP Physics C: Work, Energy, and Power Practice 1981M2. A swing seat of mass M is connected to a fixed point P by a massless cord of length L. A child also of mass M sits on the seat and begins to swing
AP Physics C: Work, Energy, and Power Practice 1981M2. A swing seat of mass M is connected to a fixed point P by a massless cord of length L. A child also of mass M sits on the seat and begins to swing
Lesson 6: Apparent weight, Radial acceleration (sections 4:9-5.2)
 Beore we start the new material we will do another Newton s second law problem. A bloc is being pulled by a rope as shown in the picture. The coeicient o static riction is 0.7 and the coeicient o inetic
Beore we start the new material we will do another Newton s second law problem. A bloc is being pulled by a rope as shown in the picture. The coeicient o static riction is 0.7 and the coeicient o inetic
