A Construction for Steiner 3-Designs
|
|
|
- Mavis O’Neal’
- 6 years ago
- Views:
Transcription
1 JOURNAL OF COMBINATORIAL THEORY, Series A 71, (1995) A Construction for Steiner 3-Designs JOHN L. BLANCHARD * California Institute of Technology, Pasadena, California Communicated by the Managing Editors Received May 12, 1994 Let q be a prime power. For every v satisfying necessary arithmetic conditions we construct a Steiner 3-design S(3, q + 1; v. qn+ 1) for every n sufficiently large. Starting with a Steiner 2-design S(2, q;v), this is extended to a 3-design S;~(3, q + 1; v + 1), with index 2= qd for some d, such that the derived design is 2 copies of the Steiner 2-design. The 3-design is used, by a generalization of a construction of Wilson, to form a group-divisible 3-design GD(3, {q, q + 1}, vy) with index one. The structure of the derived design allows a circle geometry S(3, q+ 1; qd+ 1) to be combined with the group-divisible design to form, via a method of Hanani, the desired Steiner 3-design S(3, q + 1; vq ~ + 1), for all n/> no Academic Press, Inc. 1. STEINER 3-DESIGNS For any positive s let I~ = { 1, 2... s}. A set is called an s-set when it is of size s. Given t ~<k~< v 2, a t-design, written Sx(t, k; v), is a family of k-subsets of Iv, called blocks, such that every t-subset of I v is contained in exactly 2 blocks. A given k-set can occur as a block with any non-negative multiplicity. When 2 = 1 we write S(t, k; v); such a design is called a Steiner system [ 1 ]. For a Sx(t, k; v) to exist the following arithmetic conditions [1, p. 78] are necessary : 2(v-a) -- 0, rood (~52), for all a, O<~a<~t. (1) t--a Let q be a prime power. When there exists a S(3, q + 1; v. q~+ 1), for some n >/0, it is shown below that v satisfies the congruences v - 1-0, mod(q - 1), (2) v(v 2-1) -0, mod(q 2-1). (3) * address: jblanch@cco.caltech.edu /95 $12.00 Copyright 1995 by Academic Press, Inc. All rights of reproduction in any form reserved. 60
2 STEINER 3-DESIGNS 61 Hanani [ 5, p. 7 ] gives the following recursive construction for 3-designs. THEOREM 1. Let q be a prime power. If there is a Sx(3, q + 1; v + 1) then there is a S~(3, q + 1 ; q~. v + 1 ) for all n >~ O. The next theorem is a generalization of Hanani's construction for 2 = 1. THEOREM 2. Let q be a prime power. If there is a Steiner system S(2, q; v) with v ~ vo( q ) v satisfies the necessary condition (3), then there is a Steiner 3-design S(3, q + 1 ; v. q" + 1 ), for all n >~ no(q, v ). The function vo(q) is a degree 7 polynomial in q. Whereas Theorem 1 constructs a S(3, q+ 1; q.v+ 1) when a S(3, q+ 1; v+ 1) is available as starting material, Theorem 2 only requires the existence of a S(2, q; v). By a theorem of Wilson [6, p. 72; 1, p. 559], Steiner 2-designs S(2, q; v) exist for all sufficiently large v satisfying the necessary arithmetic conditions; we use this to prove our main theorem. THEOREM 3. Let q be a prime power. If v satisfies the necessary conditions (2) (3), then there is a Steiner 3-design S(3, q + 1; v. qn + 1), for all n >~ nl(q, v). Some classical Steiner 3-designs are constructed by Witt [7]. TrIEOREM 4. n>.l. For any prime power q, there is a S(3, q + 1; qn + 1) for all The following structure theorem is needed in the following. Let Xn + i = Iq x Iq, u { oo }. For each i ~ Iq call the subset { i} x Iqo w { oo } a level of X,+ 1 (that is, a row union the point or). THEOREM 5. Let q be a prime power. For each n>~ 1, there is a S(3, q+ 1; qn+l+ 1) over the set X~+I such that on each level there is a sub-s(3, q + 1; q"+ 1) over that level. The case of n = 1 is mentioned by Hanani [ 5, p. 7 ]. 2. DESIGN EXTENSIONS If ~ is a family of blocks from Iv, define the derived family ~d as the set of blocks
3 62 JOHN L. BLANCHARD that is, the blocks of ~ that contain v with v deleted. We call ~ an extension Define the residual family ~r as namely, the blocks of N avoiding v. Given a S(2, k; v), if for some 2 there is a S;(3, k+ 1; v + 1) with derived design 2-S(2, k; v), that is, 2 copies of S(2, k; v), a necessary condition [1, pp. 78, 114] is 2 (V3 1)-0, mod (k3 1). (4) The following extension theorem is given by Blanchard [2] is used in the proof of Theorem 2. THEOREM 6. Given a Steiner system S(2, k; v), with v >>. vo(k ) any 2>~20(k, v) satisfying the necessary condition (4), there is a S;(3, k+ 1; v + 1), call it 9, such that ~a = 2- S(2, k; v); that is, the derived design is 2 copies of the Steiner system. 3. TRANSVERSAL DESIGNS AND RELATED DESIGNS Define a transversal 3-design [1, p. 51;5], written TD(3, k;g), as a family of blocks (k-sets) over the set J(=Ikxlg with the following properties: (i) (ii) each block intersects each of the k rows of X in exactly one point. each 3-set of points from distinct rows is in exactly one block. We need the following fact. THEOREM 7. For any prime power p, there is a transversal design TD(3, k; p) for all k, 3 <<.k<.p + 1. This is given by Bose Bush [4] (in the form of orthogonal arrays) by Hanani [ 5 ]. Let ~ be a family of k-sets (with possible multiplicities) from the set Iv let Y be an family of 3-sets of Iv. We say ~ is a partial design, written P;(3, k; v), that covers the 3-sets 3- if (i) each 3-set in 3- is in exactly 2 blocks of N, counting multiplicities, (ii) each 3-set not in 3- is not in any block of ~.
4 STEINER 3-DESIGNS 63 Given a prime power qd a 3-set T= {tl, t2, t3} c Iv, following families of 3-sets from Iv x I d define the T@Iqd= {{(tl, "1), (t2, U2), (t3, U3)} :/A1, 2, U3EIq'} j i#= U T~.7 That is, J Iq~ consists of all 3-sets in Iv x I d whose projection into Iv is a 3-set in Y. THEOREM 8. Given v, let q be a prime power satisfying q >>, 3v. Let J- be a family of3-sets of I~. If there is apartial design Pq(3, k; v) that covers the 3-sets ~-, then there is partial design P(3, k; v. qd) that covers the 3-sets.Y- I#, for all d> (~). Theorem 8 is given by Blanchard [3] is a generalization of a construction of Wilson [6, p. 74; 1, p. 551] for the case of 2-sets. 4. PROOFS Proof of Theorem 2. Let q be a prime power. If there is a S(3, q+ 1; v. q" + 1), for some n ~> 0, then, from (1), vq" - 1 =- O, mod(q- 1) since q - 1, mod(q - 1), v-l~0, mod(q - 1 ). This shows that condition (2) is necessary. Also from (1), Since q is coprime to q2_ 1, vq"(v2q 2n - 1) - 0, mod(q(q 2-1)). further V(v2q 2n -- 1 ) = 0, mod(q 2-1), V(V2-- 1) ~- 0, mod(q2-- 1). 582a/71/1-5
5 64 JOHN L. BLANCHARD This proves (3). For any m >~ 1 we have qm (V+ 1 3 )=0, m d (q+ 3 1) " Assume there is a Steiner system S(2, q; v) with v ~> c0(q), where Vo(q) is as in Theorem 6. By Theorem 6, for any m o with qmo ~>20(q ' v) there is a Sq,,o(3, q + 1; v + 1), call it ~, such that ~d= qmo. S(2 ' q; v). We can choose mo large enough to satisfy qmo ~ 3V. Let ~- be the family of 3-sets that are contained in the blocks Because the derived design of ~ is qmo copies of the Steiner system, any 3-set in a block of the derived design is covered by that block of the derived design (that is, the 3-set is contained the complete number qmo times). So the 3-sets covered by the derived design are complementary to the family Y-. It follows that ~r, which is a 2-design, is a partial design Pq,%(3, q + 1; v) that covers the 3-sets ~-. Set no = mo. (~) X= ~ Iq,o u { oo }. Now we construct the blocks of a Steiner 3-design S(3, q + 1; v. qno + 1 ) over the set X. Both ~r ~d are over the set Iv. From the blocks of Y we obtain, by Theorem 8 (with power qmo d=(~)), a partial design P(3, q+ 1; u.q " ) that covers the 3-sets ~- Iq o. These blocks cover (exactly once) all 3-sets of X\{ ~ } whose projection onto I, is a 3-set not covered by the Steiner system S(2, q; v). For each block A of the Steiner system S(2, q;v), form a S(3, q+l; qno ) on the set A x Iq, o w { co }, where on each level there is a sub-design S(3, q + 1; qno + 1 ), as in Theorem 5. Each level is indexed by many blocks of the Steiner system, so on each level we take only one copy of a sub-design S(3, q + 1; qno + 1 ). Let T be a 3-set of X. If ~ T the projection of Tonto Iv (which is not necessarily a 3-set) is in a block A of the Steiner system, then T is in A Iq%w {or} is therefore covered by the S(3, q+ 1; q,o+l + 1) constructed there. If ~ e T, then T\{~} intersects one or two levels of X\{ ~ }. If two, then these levels are indexed by two points oflo these are in a unique block A of the Steiner system. So, as above, T is in A Iq,,o w { ~ } is covered by the S(3, q + 1; q,o + ~ + 1 ) constructed there. Finally, if T is in a single level, it is covered by the sub-design S(3, q + 1; q'o + 1) placed there. This shows the blocks constructed form a Steiner 3-design S(3, q+ 1; v.qn + 1) on the set X. From Theorem 1, there is a S(3, q+ 1; v.q"+ 1) for each n >~ no. The proof is complete. Proof of Theorem 3. Assume v satisfies (2) (3). Since q-1, mod(q-1), we have, for any e>~ 1, vq e o, mod(q - 1 ) (5) vqe(vq e - 1 ) -~ 0, mod(q(q - 1 )). (6)
6 From (3) we have, similarly, STEINER 3-DESIGNS 65 vq~((vqe) 2-1) - 0, mod(q(q 2-1)) (7) for any e~> 1. Relations (5) (6) are the arithmetic conditions for a S(2, q; vqe). From Wilson's theorem [6, p. 72] there is a function vl(k) such that for any u >~ va(k) there exists a S(2, k; u) if u satisfies the conditions (1). We can choose e~>l large enough so that vq~>>.va(q) vqe>>-vo(q), where vo(q) is from Theorem 2; it follows that there is a S(2, q; vq~). From relation (7), the conditions of Theorem 2 are satisfied we conclude there exists a S(3, q+ 1; v.q"+ 1) for each n>~nl(q, v), where nl(q, v) = no(q, vq~). The theorem is proved. Proof of Theorem 5. We use induction on n. When n= 1, a sub- S(3, q+ 1; q+ 1) on each level means that each level is a block. Just such a S(3, q+ 1; qzq_ 1) is given by Hanani [5, p. 7]. Another way to see this is as follows: the design S(3, q+ 1; qzq_ 1) has derived design S(2, q; q2), which is an affine plane is resolvable. A parallel class of blocks from S(2, q; q2) corresponds to a set of blocks in S(3, q + 1; q2+ 1) that form a complete set of levels. When n>~2, be a S(3, q+ 1; qn+ 1) over the set Xn on each level of Xn assume there is a sub-s(3, q + 1; qn-1 + 1) call it ~n-1. We use a variant of a construction of Hanani [5, pp. 7, 12] to construct a S(3, q + 1; qn+l+ 1) with the desired properties. Write X,,+I = Iq x Iq~ w { co } = Iq2 x Iq, ~ w { oo }. On the set Iq2 w { y}, for some extra point y, take a design ~ which is a S(3, q+ 1; q2+ 1) also satisfies the induction hypothesis; that is, the derived design ~a (with respect to the point y) contains q blocks that partition Iq~. For each block A' in ~a, form a ~n over the set A' x [q._~ ~3 { oo } such that each level carries as assumed by the induction. Many blocks of ~a will index the same level so take only one copy of ~,_ 1 per level. For each block A in ~r, form a transversal 3-design TD(3, q+ 1; qn-1) on the set A x Iqo 1. It is easy to check that the blocks so formed constitute a S(3, q + 1; qn ). As mentioned above, there are q blocks A'I,..., A'q in ~d that partition Iq2. From each of these blocks a ~n was formed over the sets A; x Iq,_~ u {oo}, the pairwise intersection of these sets is oo. Taking these sets as the levels of Xn + 1 shows that N, + 1 has the desired structure. REFERENCES 1. T. BETH, D. JUNGNICKEL, AND H. LENZ, "Design Theory," Bibliographisches Institut, Mannheim, J. L. BLANCHARD, An extension theorem for Steiner systems, Discrete Math., to appear.
7 66 JOHN L. BLANCHARD 3. J. L. BLANCHARD, A construction for orthogonal arrays of strength t ~> 3, Discrete Math. 137 (1995), R. C. BOSE AND K. A. BUSH, Orthogonal arrays of strength two three, Ann. Math. Statist. 23 (1952), H. HANM,a, A class of 3-designs, J. Combin. Theory Ser. A 26 (1979), R. M. WtLSON, An existence theory for pairwise balanced designs, III, J. Combin. Theory Ser. A 18 (1975), E. WITT, Uber Steinersche Systeme, Abh. Math. Sere. Univ. Hamburg 12 (1938),
New infinite families of Candelabra Systems with block size 6 and stem size 2
 New infinite families of Candelabra Systems with block size 6 and stem size 2 Niranjan Balachandran Department of Mathematics The Ohio State University Columbus OH USA 4210 email:niranj@math.ohio-state.edu
New infinite families of Candelabra Systems with block size 6 and stem size 2 Niranjan Balachandran Department of Mathematics The Ohio State University Columbus OH USA 4210 email:niranj@math.ohio-state.edu
THE MAXIMUM SIZE OF A PARTIAL 3-SPREAD IN A FINITE VECTOR SPACE OVER GF (2)
 THE MAXIMUM SIZE OF A PARTIAL 3-SPREAD IN A FINITE VECTOR SPACE OVER GF (2) S. EL-ZANATI, H. JORDON, G. SEELINGER, P. SISSOKHO, AND L. SPENCE 4520 MATHEMATICS DEPARTMENT ILLINOIS STATE UNIVERSITY NORMAL,
THE MAXIMUM SIZE OF A PARTIAL 3-SPREAD IN A FINITE VECTOR SPACE OVER GF (2) S. EL-ZANATI, H. JORDON, G. SEELINGER, P. SISSOKHO, AND L. SPENCE 4520 MATHEMATICS DEPARTMENT ILLINOIS STATE UNIVERSITY NORMAL,
Affine designs and linear orthogonal arrays
 Affine designs and linear orthogonal arrays Vladimir D. Tonchev Department of Mathematical Sciences, Michigan Technological University, Houghton, Michigan 49931, USA, tonchev@mtu.edu Abstract It is proved
Affine designs and linear orthogonal arrays Vladimir D. Tonchev Department of Mathematical Sciences, Michigan Technological University, Houghton, Michigan 49931, USA, tonchev@mtu.edu Abstract It is proved
A Design and a Code Invariant
 JOURNAL OF COMBINATORIAL THEORY, Series A 62, 225-233 (1993) A Design and a Code Invariant under the Simple Group Co3 WILLEM H. HAEMERS Department of Economics, Tilburg University, P.O. Box 90153, 5000
JOURNAL OF COMBINATORIAL THEORY, Series A 62, 225-233 (1993) A Design and a Code Invariant under the Simple Group Co3 WILLEM H. HAEMERS Department of Economics, Tilburg University, P.O. Box 90153, 5000
Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs
 Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs Colleen M. Swanson Computer Science & Engineering Division University of Michigan Ann Arbor, MI 48109,
Additional Constructions to Solve the Generalized Russian Cards Problem using Combinatorial Designs Colleen M. Swanson Computer Science & Engineering Division University of Michigan Ann Arbor, MI 48109,
A three-factor product construction for mutually orthogonal latin squares
 A three-factor product construction for mutually orthogonal latin squares Peter J. Dukes (joint work with Alan C.H. Ling, UVM) June 17, 2014 Introduction Latin squares and MOLS Product construction Main
A three-factor product construction for mutually orthogonal latin squares Peter J. Dukes (joint work with Alan C.H. Ling, UVM) June 17, 2014 Introduction Latin squares and MOLS Product construction Main
FRACTIONAL FACTORIAL DESIGNS OF STRENGTH 3 AND SMALL RUN SIZES
 FRACTIONAL FACTORIAL DESIGNS OF STRENGTH 3 AND SMALL RUN SIZES ANDRIES E. BROUWER, ARJEH M. COHEN, MAN V.M. NGUYEN Abstract. All mixed (or asymmetric) orthogonal arrays of strength 3 with run size at most
FRACTIONAL FACTORIAL DESIGNS OF STRENGTH 3 AND SMALL RUN SIZES ANDRIES E. BROUWER, ARJEH M. COHEN, MAN V.M. NGUYEN Abstract. All mixed (or asymmetric) orthogonal arrays of strength 3 with run size at most
Mathematical Department, University of Bayreuth, D Bayreuth
 ,, {6 () c Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. A Steiner 5-Design on 36 Points ANTON BETTEN anton.betten@uni-bayreuth.de REINHARD LAUE reinhard.laue@uni-bayreuth.de ALFRED
,, {6 () c Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. A Steiner 5-Design on 36 Points ANTON BETTEN anton.betten@uni-bayreuth.de REINHARD LAUE reinhard.laue@uni-bayreuth.de ALFRED
Transversal Designs in Classical Planes and Spaces. Aiden A. Bruen and Charles J. Colbourn. Computer Science. University of Vermont
 Transversal Designs in Classical Planes and Spaces Aiden A. Bruen and Charles J. Colbourn Computer Science University of Vermont Burlington, VT 05405 U.S.A. Abstract Possible embeddings of transversal
Transversal Designs in Classical Planes and Spaces Aiden A. Bruen and Charles J. Colbourn Computer Science University of Vermont Burlington, VT 05405 U.S.A. Abstract Possible embeddings of transversal
ORTHOGONAL ARRAYS OF STRENGTH 3 AND SMALL RUN SIZES
 ORTHOGONAL ARRAYS OF STRENGTH 3 AND SMALL RUN SIZES ANDRIES E. BROUWER, ARJEH M. COHEN, MAN V.M. NGUYEN Abstract. All mixed (or asymmetric) orthogonal arrays of strength 3 with run size at most 64 are
ORTHOGONAL ARRAYS OF STRENGTH 3 AND SMALL RUN SIZES ANDRIES E. BROUWER, ARJEH M. COHEN, MAN V.M. NGUYEN Abstract. All mixed (or asymmetric) orthogonal arrays of strength 3 with run size at most 64 are
Square 2-designs/1. 1 Definition
 Square 2-designs Square 2-designs are variously known as symmetric designs, symmetric BIBDs, and projective designs. The definition does not imply any symmetry of the design, and the term projective designs,
Square 2-designs Square 2-designs are variously known as symmetric designs, symmetric BIBDs, and projective designs. The definition does not imply any symmetry of the design, and the term projective designs,
Extending MDS Codes. T. L. Alderson
 Extending MDS Codes T. L. Alderson Abstract A q-ary (n,k)-mds code, linear or not, satisfies n q + k 1. A code meeting this bound is said to have maximum length. Using purely combinatorial methods we show
Extending MDS Codes T. L. Alderson Abstract A q-ary (n,k)-mds code, linear or not, satisfies n q + k 1. A code meeting this bound is said to have maximum length. Using purely combinatorial methods we show
A Construction for Authentication/ secrecy Codes from 3-homogeneous Permutation Groups
 Europ. J. Combinatorics (1990) 11, 73-79 A Construction for Authentication/ secrecy Codes from 3-homogeneous Permutation Groups D. R. STINSON AND L. TEIRLINCK In this paper, we construct codes which provide
Europ. J. Combinatorics (1990) 11, 73-79 A Construction for Authentication/ secrecy Codes from 3-homogeneous Permutation Groups D. R. STINSON AND L. TEIRLINCK In this paper, we construct codes which provide
Blocking Sets in Designs with Block Size 4
 Europ. J. Combinatorics (1990) 11,451-457 Blocking Sets in Designs with Block Size 4 D. G. HOFFMAN, C. C. LINDNER AND K. T. PHELPS We construct A-fold block designs with block size 4 and A E {1, 2} of
Europ. J. Combinatorics (1990) 11,451-457 Blocking Sets in Designs with Block Size 4 D. G. HOFFMAN, C. C. LINDNER AND K. T. PHELPS We construct A-fold block designs with block size 4 and A E {1, 2} of
PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES
 PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES S.I. EL-ZANATI, G.F. SEELINGER, P.A. SISSOKHO, L.E. SPENCE, AND C. VANDEN EYNDEN Abstract. Let V n (q) denote a vector space of dimension n over the field
PARTITIONS OF FINITE VECTOR SPACES INTO SUBSPACES S.I. EL-ZANATI, G.F. SEELINGER, P.A. SISSOKHO, L.E. SPENCE, AND C. VANDEN EYNDEN Abstract. Let V n (q) denote a vector space of dimension n over the field
NOTE. On a Problem of Erdo s and Sa rko zy
 Journal of Combinatorial Theory, Series A 94, 191195 (2001) doi10.1006jcta.2000.3142, available online at httpwww.idealibrary.com on NOTE On a Problem of Erdo s and Sa rko zy Tomasz Schoen Mathematisches
Journal of Combinatorial Theory, Series A 94, 191195 (2001) doi10.1006jcta.2000.3142, available online at httpwww.idealibrary.com on NOTE On a Problem of Erdo s and Sa rko zy Tomasz Schoen Mathematisches
Orthogonal arrays obtained by repeating-column difference matrices
 Discrete Mathematics 307 (2007) 246 261 www.elsevier.com/locate/disc Orthogonal arrays obtained by repeating-column difference matrices Yingshan Zhang Department of Statistics, East China Normal University,
Discrete Mathematics 307 (2007) 246 261 www.elsevier.com/locate/disc Orthogonal arrays obtained by repeating-column difference matrices Yingshan Zhang Department of Statistics, East China Normal University,
ax b mod m. has a solution if and only if d b. In this case, there is one solution, call it x 0, to the equation and there are d solutions x m d
 10. Linear congruences In general we are going to be interested in the problem of solving polynomial equations modulo an integer m. Following Gauss, we can work in the ring Z m and find all solutions to
10. Linear congruences In general we are going to be interested in the problem of solving polynomial equations modulo an integer m. Following Gauss, we can work in the ring Z m and find all solutions to
arxiv: v1 [math.co] 13 Apr 2018
![arxiv: v1 [math.co] 13 Apr 2018 arxiv: v1 [math.co] 13 Apr 2018](/thumbs/79/80102791.jpg) Constructions of Augmented Orthogonal Arrays Lijun Ji 1, Yun Li 1 and Miao Liang 2 1 Department of Mathematics, Soochow University, Suzhou 215006, China arxiv:180405137v1 [mathco] 13 Apr 2018 E-mail: jilijun@sudaeducn
Constructions of Augmented Orthogonal Arrays Lijun Ji 1, Yun Li 1 and Miao Liang 2 1 Department of Mathematics, Soochow University, Suzhou 215006, China arxiv:180405137v1 [mathco] 13 Apr 2018 E-mail: jilijun@sudaeducn
Problems for Putnam Training
 Problems for Putnam Training 1 Number theory Problem 1.1. Prove that for each positive integer n, the number is not prime. 10 1010n + 10 10n + 10 n 1 Problem 1.2. Show that for any positive integer n,
Problems for Putnam Training 1 Number theory Problem 1.1. Prove that for each positive integer n, the number is not prime. 10 1010n + 10 10n + 10 n 1 Problem 1.2. Show that for any positive integer n,
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
Small Group Divisible Steiner Quadruple Systems
 Small Group Divisible Steiner Quadruple Systems Artem A. Zhuravlev, Melissa S. Keranen, Donald L. Kreher Department of Mathematical Sciences, Michigan Technological University Houghton, MI 49913-0402,
Small Group Divisible Steiner Quadruple Systems Artem A. Zhuravlev, Melissa S. Keranen, Donald L. Kreher Department of Mathematical Sciences, Michigan Technological University Houghton, MI 49913-0402,
Part IA. Numbers and Sets. Year
 Part IA Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2017 19 Paper 4, Section I 1D (a) Show that for all positive integers z and n, either z 2n 0 (mod 3) or
Part IA Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2017 19 Paper 4, Section I 1D (a) Show that for all positive integers z and n, either z 2n 0 (mod 3) or
E-SYMMETRIC NUMBERS (PUBLISHED: COLLOQ. MATH., 103(2005), NO. 1, )
 E-SYMMETRIC UMBERS PUBLISHED: COLLOQ. MATH., 032005), O., 7 25.) GAG YU Abstract A positive integer n is called E-symmetric if there exists a positive integer m such that m n = φm), φn)). n is called E-asymmetric
E-SYMMETRIC UMBERS PUBLISHED: COLLOQ. MATH., 032005), O., 7 25.) GAG YU Abstract A positive integer n is called E-symmetric if there exists a positive integer m such that m n = φm), φn)). n is called E-asymmetric
Fermat's Little Theorem
 Fermat's Little Theorem CS 2800: Discrete Structures, Spring 2015 Sid Chaudhuri Not to be confused with... Fermat's Last Theorem: x n + y n = z n has no integer solution for n > 2 Recap: Modular Arithmetic
Fermat's Little Theorem CS 2800: Discrete Structures, Spring 2015 Sid Chaudhuri Not to be confused with... Fermat's Last Theorem: x n + y n = z n has no integer solution for n > 2 Recap: Modular Arithmetic
Latin Squares and Orthogonal Arrays
 School of Electrical Engineering and Computer Science University of Ottawa lucia@eecs.uottawa.ca Winter 2017 Latin squares Definition A Latin square of order n is an n n array, with symbols in {1,...,
School of Electrical Engineering and Computer Science University of Ottawa lucia@eecs.uottawa.ca Winter 2017 Latin squares Definition A Latin square of order n is an n n array, with symbols in {1,...,
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Math 319 Problem Set #2 Solution 14 February 2002
 Math 39 Problem Set # Solution 4 February 00. (.3, problem 8) Let n be a positive integer, and let r be the integer obtained by removing the last digit from n and then subtracting two times the digit ust
Math 39 Problem Set # Solution 4 February 00. (.3, problem 8) Let n be a positive integer, and let r be the integer obtained by removing the last digit from n and then subtracting two times the digit ust
Mutually Orthogonal Latin Squares: Covering and Packing Analogues
 Squares: Covering 1 1 School of Computing, Informatics, and Decision Systems Engineering Arizona State University Mile High Conference, 15 August 2013 Latin Squares Definition A latin square of side n
Squares: Covering 1 1 School of Computing, Informatics, and Decision Systems Engineering Arizona State University Mile High Conference, 15 August 2013 Latin Squares Definition A latin square of side n
Sums of Squares. Bianca Homberg and Minna Liu
 Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
An Asymptotic Bound on the Composition Number of Integer Sums of Squares Formulas
 Canad. Math. Bull. Vol. 56 (1), 2013 pp. 70 79 http://dx.doi.org/10.4153/cmb-2011-143-x c Canadian Mathematical Society 2011 An Asymptotic Bound on the Composition Number of Integer Sums of Squares Formulas
Canad. Math. Bull. Vol. 56 (1), 2013 pp. 70 79 http://dx.doi.org/10.4153/cmb-2011-143-x c Canadian Mathematical Society 2011 An Asymptotic Bound on the Composition Number of Integer Sums of Squares Formulas
Maximum Distance Separable Symbol-Pair Codes
 2012 IEEE International Symposium on Information Theory Proceedings Maximum Distance Separable Symbol-Pair Codes Yeow Meng Chee, Han Mao Kiah, and Chengmin Wang School of Physical and Mathematical Sciences,
2012 IEEE International Symposium on Information Theory Proceedings Maximum Distance Separable Symbol-Pair Codes Yeow Meng Chee, Han Mao Kiah, and Chengmin Wang School of Physical and Mathematical Sciences,
Math 261 Spring 2014 Final Exam May 5, 2014
 Math 261 Spring 2014 Final Exam May 5, 2014 1. Give a statement or the definition for ONE of the following in each category. Circle the letter next to the one you want graded. For an extra good final impression,
Math 261 Spring 2014 Final Exam May 5, 2014 1. Give a statement or the definition for ONE of the following in each category. Circle the letter next to the one you want graded. For an extra good final impression,
Pencils of Quadratic Forms over Finite Fields
 Southern Illinois University Carbondale OpenSIUC Articles and Preprints Department of Mathematics 2004 Pencils of Quadratic Forms over Finite Fields Robert W. Fitzgerald Southern Illinois University Carbondale,
Southern Illinois University Carbondale OpenSIUC Articles and Preprints Department of Mathematics 2004 Pencils of Quadratic Forms over Finite Fields Robert W. Fitzgerald Southern Illinois University Carbondale,
Mutually embeddable graphs and the tree alternative conjecture
 Journal of Combinatorial Theory, Series B 96 (2006) 874 880 www.elsevier.com/locate/jctb Mutually embeddable graphs and the tree alternative conjecture Anthony Bonato a, Claude Tardif b a Department of
Journal of Combinatorial Theory, Series B 96 (2006) 874 880 www.elsevier.com/locate/jctb Mutually embeddable graphs and the tree alternative conjecture Anthony Bonato a, Claude Tardif b a Department of
Simple 3-(q + 1, 5, 3) designs admitting an automorphism group PSL(2, q) with q 1 (mod 4)
 Simple -(q + 5 ) designs admitting an automorphism group PSL( q) with q (mod 4) Weixia Li School of Mathematical Sciences Qingdao University Qingdao 667 China Dameng Deng Department of Mathematics Shanghai
Simple -(q + 5 ) designs admitting an automorphism group PSL( q) with q (mod 4) Weixia Li School of Mathematical Sciences Qingdao University Qingdao 667 China Dameng Deng Department of Mathematics Shanghai
Sequences of height 1 primes in Z[X]
![Sequences of height 1 primes in Z[X] Sequences of height 1 primes in Z[X]](/thumbs/87/96347391.jpg) Sequences of height 1 primes in Z[X] Stephen McAdam Department of Mathematics University of Texas Austin TX 78712 mcadam@math.utexas.edu Abstract: For each partition J K of {1, 2,, n} (n 2) with J 2, let
Sequences of height 1 primes in Z[X] Stephen McAdam Department of Mathematics University of Texas Austin TX 78712 mcadam@math.utexas.edu Abstract: For each partition J K of {1, 2,, n} (n 2) with J 2, let
1 Take-home exam and final exam study guide
 Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Journal of Combinatorial Theory, Series A
 Journal of Combinatorial Theory, Series A 118 (2011) 623 633 Contents lists available at ScienceDirect Journal of Combinatorial Theory, Series A www.elsevier.com/locate/jcta Characterizing geometric designs,
Journal of Combinatorial Theory, Series A 118 (2011) 623 633 Contents lists available at ScienceDirect Journal of Combinatorial Theory, Series A www.elsevier.com/locate/jcta Characterizing geometric designs,
DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS
 DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS JEREMY LOVEJOY Abstract. We study the generating function for (n), the number of partitions of a natural number n into distinct parts. Using
DIVISIBILITY AND DISTRIBUTION OF PARTITIONS INTO DISTINCT PARTS JEREMY LOVEJOY Abstract. We study the generating function for (n), the number of partitions of a natural number n into distinct parts. Using
Fall 2014 CMSC250/250H Midterm II
 Fall 2014 CMSC250/250H Midterm II Circle Your Section! 0101 (10am: 3120, Ladan) 0102 (11am: 3120, Ladan) 0103 (Noon: 3120, Peter) 0201 (2pm: 3120, Yi) 0202 (10am: 1121, Vikas) 0203 (11am: 1121, Vikas)
Fall 2014 CMSC250/250H Midterm II Circle Your Section! 0101 (10am: 3120, Ladan) 0102 (11am: 3120, Ladan) 0103 (Noon: 3120, Peter) 0201 (2pm: 3120, Yi) 0202 (10am: 1121, Vikas) 0203 (11am: 1121, Vikas)
The Witt designs, Golay codes and Mathieu groups
 The Witt designs, Golay codes and Mathieu groups 1 The Golay codes Let V be a vector space over F q with fixed basis e 1,..., e n. A code C is a subset of V. A linear code is a subspace of V. The vector
The Witt designs, Golay codes and Mathieu groups 1 The Golay codes Let V be a vector space over F q with fixed basis e 1,..., e n. A code C is a subset of V. A linear code is a subspace of V. The vector
MATH 433 Applied Algebra Lecture 4: Modular arithmetic (continued). Linear congruences.
 MATH 433 Applied Algebra Lecture 4: Modular arithmetic (continued). Linear congruences. Congruences Let n be a postive integer. The integers a and b are called congruent modulo n if they have the same
MATH 433 Applied Algebra Lecture 4: Modular arithmetic (continued). Linear congruences. Congruences Let n be a postive integer. The integers a and b are called congruent modulo n if they have the same
A new look at an old construction: constructing (simple) 3-designs from resolvable 2-designs
 A new look at an old construction: constructing (simple) 3-designs from resolvable 2-designs Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, N2L
A new look at an old construction: constructing (simple) 3-designs from resolvable 2-designs Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo Waterloo, Ontario, N2L
A second infinite family of Steiner triple systems without almost parallel classes
 A second infinite family of Steiner triple systems without almost parallel classes Darryn Bryant The University of Queensland Department of Mathematics Qld 4072, Australia Daniel Horsley School of Mathematical
A second infinite family of Steiner triple systems without almost parallel classes Darryn Bryant The University of Queensland Department of Mathematics Qld 4072, Australia Daniel Horsley School of Mathematical
MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM
 MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM Basic Questions 1. Compute the factor group Z 3 Z 9 / (1, 6). The subgroup generated by (1, 6) is
MATH 3030, Abstract Algebra FALL 2012 Toby Kenney Midyear Examination Friday 7th December: 7:00-10:00 PM Basic Questions 1. Compute the factor group Z 3 Z 9 / (1, 6). The subgroup generated by (1, 6) is
VARGA S THEOREM IN NUMBER FIELDS
 VARGA S THEOREM IN NUMBER FIELDS PETE L. CLARK AND LORI D. WATSON Abstract. We give a number field version of a recent result of Varga on solutions of polynomial equations with binary input variables and
VARGA S THEOREM IN NUMBER FIELDS PETE L. CLARK AND LORI D. WATSON Abstract. We give a number field version of a recent result of Varga on solutions of polynomial equations with binary input variables and
PALINDROMIC AND SŪDOKU QUASIGROUPS
 PALINDROMIC AND SŪDOKU QUASIGROUPS JONATHAN D. H. SMITH Abstract. Two quasigroup identities of importance in combinatorics, Schroeder s Second Law and Stein s Third Law, share many common features that
PALINDROMIC AND SŪDOKU QUASIGROUPS JONATHAN D. H. SMITH Abstract. Two quasigroup identities of importance in combinatorics, Schroeder s Second Law and Stein s Third Law, share many common features that
A Block Negacyclic Bush-Type Hadamard Matrix and Two Strongly Regular Graphs
 Journal of Combinatorial Theory, Series A 98, 118 126 (2002) doi:10.1006/jcta.2001.3231, available online at http://www.idealibrary.com on A Block Negacyclic Bush-Type Hadamard Matrix and Two Strongly
Journal of Combinatorial Theory, Series A 98, 118 126 (2002) doi:10.1006/jcta.2001.3231, available online at http://www.idealibrary.com on A Block Negacyclic Bush-Type Hadamard Matrix and Two Strongly
arxiv: v1 [math.co] 27 Jul 2015
![arxiv: v1 [math.co] 27 Jul 2015 arxiv: v1 [math.co] 27 Jul 2015](/thumbs/87/95098250.jpg) Perfect Graeco-Latin balanced incomplete block designs and related designs arxiv:1507.07336v1 [math.co] 27 Jul 2015 Sunanda Bagchi Theoretical Statistics and Mathematics Unit Indian Statistical Institute
Perfect Graeco-Latin balanced incomplete block designs and related designs arxiv:1507.07336v1 [math.co] 27 Jul 2015 Sunanda Bagchi Theoretical Statistics and Mathematics Unit Indian Statistical Institute
University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics
 University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics Examiners: D. Burbulla, P. Glynn-Adey, S. Homayouni Time: 7-10
University of Toronto Faculty of Arts and Science Solutions to Final Examination, April 2017 MAT246H1S - Concepts in Abstract Mathematics Examiners: D. Burbulla, P. Glynn-Adey, S. Homayouni Time: 7-10
On zero-sum partitions and anti-magic trees
 Discrete Mathematics 09 (009) 010 014 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: wwwelseviercom/locate/disc On zero-sum partitions and anti-magic trees Gil Kaplan,
Discrete Mathematics 09 (009) 010 014 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: wwwelseviercom/locate/disc On zero-sum partitions and anti-magic trees Gil Kaplan,
Part IA Numbers and Sets
 Part IA Numbers and Sets Definitions Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IA Numbers and Sets Definitions Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
CS 5319 Advanced Discrete Structure. Lecture 9: Introduction to Number Theory II
 CS 5319 Advanced Discrete Structure Lecture 9: Introduction to Number Theory II Divisibility Outline Greatest Common Divisor Fundamental Theorem of Arithmetic Modular Arithmetic Euler Phi Function RSA
CS 5319 Advanced Discrete Structure Lecture 9: Introduction to Number Theory II Divisibility Outline Greatest Common Divisor Fundamental Theorem of Arithmetic Modular Arithmetic Euler Phi Function RSA
Congruences. September 16, 2006
 Congruences September 16, 2006 1 Congruences If m is a given positive integer, then we can de ne an equivalence relation on Z (the set of all integers) by requiring that an integer a is related to an integer
Congruences September 16, 2006 1 Congruences If m is a given positive integer, then we can de ne an equivalence relation on Z (the set of all integers) by requiring that an integer a is related to an integer
Homework #2 solutions Due: June 15, 2012
 All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
All of the following exercises are based on the material in the handout on integers found on the class website. 1. Find d = gcd(475, 385) and express it as a linear combination of 475 and 385. That is
Chapter 1 : The language of mathematics.
 MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
An Analytic Approach to the Problem of Matroid Representibility: Summer REU 2015
 An Analytic Approach to the Problem of Matroid Representibility: Summer REU 2015 D. Capodilupo 1, S. Freedman 1, M. Hua 1, and J. Sun 1 1 Department of Mathematics, University of Michigan Abstract A central
An Analytic Approach to the Problem of Matroid Representibility: Summer REU 2015 D. Capodilupo 1, S. Freedman 1, M. Hua 1, and J. Sun 1 1 Department of Mathematics, University of Michigan Abstract A central
Spanning Paths in Infinite Planar Graphs
 Spanning Paths in Infinite Planar Graphs Nathaniel Dean AT&T, ROOM 2C-415 600 MOUNTAIN AVENUE MURRAY HILL, NEW JERSEY 07974-0636, USA Robin Thomas* Xingxing Yu SCHOOL OF MATHEMATICS GEORGIA INSTITUTE OF
Spanning Paths in Infinite Planar Graphs Nathaniel Dean AT&T, ROOM 2C-415 600 MOUNTAIN AVENUE MURRAY HILL, NEW JERSEY 07974-0636, USA Robin Thomas* Xingxing Yu SCHOOL OF MATHEMATICS GEORGIA INSTITUTE OF
arxiv: v2 [math.co] 17 May 2017
![arxiv: v2 [math.co] 17 May 2017 arxiv: v2 [math.co] 17 May 2017](/thumbs/72/66706399.jpg) New nonbinary code bounds based on divisibility arguments Sven Polak 1 arxiv:1606.05144v [math.co] 17 May 017 Abstract. For q, n, d N, let A q (n, d) be the maximum size of a code C [q] n with minimum
New nonbinary code bounds based on divisibility arguments Sven Polak 1 arxiv:1606.05144v [math.co] 17 May 017 Abstract. For q, n, d N, let A q (n, d) be the maximum size of a code C [q] n with minimum
RATIONAL POLYNOMIALS OF SIMPLE TYPE: A COMBINATORIAL PROOF
 RATIONAL POLYNOMIALS OF SIMPLE TYPE: A COMBINATORIAL PROOF PIERRETTE CASSOU-NOGUÈS AND DANIEL DAIGLE Abstract. We determine the Newton trees of the rational polynomials of simple type, thus filling a gap
RATIONAL POLYNOMIALS OF SIMPLE TYPE: A COMBINATORIAL PROOF PIERRETTE CASSOU-NOGUÈS AND DANIEL DAIGLE Abstract. We determine the Newton trees of the rational polynomials of simple type, thus filling a gap
Frobenius and His Density Theorem for Primes
 Frobenius and His Density Theorem for Primes Introduction B Sury Our sta.rting point is the following problem which appea.red in the recent IMO (International Mathematical Olympiad) : If p is a prime number,
Frobenius and His Density Theorem for Primes Introduction B Sury Our sta.rting point is the following problem which appea.red in the recent IMO (International Mathematical Olympiad) : If p is a prime number,
Algorithms CMSC Homework set #1 due January 14, 2015
 Algorithms CMSC-27200 http://alg15.cs.uchicago.edu Homework set #1 due January 14, 2015 Read the homework instructions on the website. The instructions that follow here are only an incomplete summary.
Algorithms CMSC-27200 http://alg15.cs.uchicago.edu Homework set #1 due January 14, 2015 Read the homework instructions on the website. The instructions that follow here are only an incomplete summary.
Some V(12,t) vectors and designs from difference and quasi-difference matrices
 AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 4 (28), Pages 69 85 Some V(12,t) vectors and designs from difference and quasi-difference matrices R Julian R Abel School of Mathematics and Statistics University
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 4 (28), Pages 69 85 Some V(12,t) vectors and designs from difference and quasi-difference matrices R Julian R Abel School of Mathematics and Statistics University
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography
 Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
Course 2BA1: Trinity 2006 Section 9: Introduction to Number Theory and Cryptography David R. Wilkins Copyright c David R. Wilkins 2006 Contents 9 Introduction to Number Theory and Cryptography 1 9.1 Subgroups
Quasimultiples of Geometric Designs
 Quasimultiples of Geometric Designs G. L. Ebert Department of Mathematical Sciences University of Delaware Newark, DE 19716 ebert@math.udel.edu Dedicated to Curt Lindner on the occasion of his 65th birthday
Quasimultiples of Geometric Designs G. L. Ebert Department of Mathematical Sciences University of Delaware Newark, DE 19716 ebert@math.udel.edu Dedicated to Curt Lindner on the occasion of his 65th birthday
2 ERDOS AND NATHANSON k > 2. Then there is a partition of the set of positive kth powers In k I n > } = A, u A Z such that Waring's problem holds inde
 JOURNAL OF NUMBER THEORY 2, - ( 88) Partitions of Bases into Disjoint Unions of Bases* PAUL ERDÓS Mathematical Institute of the Hungarian Academy of Sciences, Budapest, Hungary AND MELVYN B. NATHANSON
JOURNAL OF NUMBER THEORY 2, - ( 88) Partitions of Bases into Disjoint Unions of Bases* PAUL ERDÓS Mathematical Institute of the Hungarian Academy of Sciences, Budapest, Hungary AND MELVYN B. NATHANSON
download instant at
 2 CRYPTOGRAPHY AND NUMBER THEORY 2.1 CRYPTOGRAPHY AND MODULAR ARITHMETIC Pages 54 to 56 Problem 1 Problem 2 Problem 3 Problem 4 14 mod 9 = 5; 1 mod 9 = 8; 11 mod 9 = 7. KHUH LV D PHVVDJH. EBOB FP X JBPPXDB.
2 CRYPTOGRAPHY AND NUMBER THEORY 2.1 CRYPTOGRAPHY AND MODULAR ARITHMETIC Pages 54 to 56 Problem 1 Problem 2 Problem 3 Problem 4 14 mod 9 = 5; 1 mod 9 = 8; 11 mod 9 = 7. KHUH LV D PHVVDJH. EBOB FP X JBPPXDB.
Modern Algebra I. Circle the correct answer; no explanation is required. Each problem in this section counts 5 points.
 1 2 3 style total Math 415 Please print your name: Answer Key 1 True/false Circle the correct answer; no explanation is required. Each problem in this section counts 5 points. 1. Every group of order 6
1 2 3 style total Math 415 Please print your name: Answer Key 1 True/false Circle the correct answer; no explanation is required. Each problem in this section counts 5 points. 1. Every group of order 6
Note. On the Upper Bound of the Size of the r-cover-free Families*
 JOURNAL OF COMBINATORIAL THEORY, Series A 66, 302-310 (1994) Note On the Upper Bound of the Size of the r-cover-free Families* MIKL6S RUSZlNK6* Research Group for Informatics and Electronics, Hungarian
JOURNAL OF COMBINATORIAL THEORY, Series A 66, 302-310 (1994) Note On the Upper Bound of the Size of the r-cover-free Families* MIKL6S RUSZlNK6* Research Group for Informatics and Electronics, Hungarian
The decomposability of simple orthogonal arrays on 3 symbols having t + 1 rows and strength t
 The decomposability of simple orthogonal arrays on 3 symbols having t + 1 rows and strength t Wiebke S. Diestelkamp Department of Mathematics University of Dayton Dayton, OH 45469-2316 USA wiebke@udayton.edu
The decomposability of simple orthogonal arrays on 3 symbols having t + 1 rows and strength t Wiebke S. Diestelkamp Department of Mathematics University of Dayton Dayton, OH 45469-2316 USA wiebke@udayton.edu
ON LINEAR CODES WHOSE WEIGHTS AND LENGTH HAVE A COMMON DIVISOR. 1. Introduction
 ON LINEAR CODES WHOSE WEIGHTS AND LENGTH HAVE A COMMON DIVISOR SIMEON BALL, AART BLOKHUIS, ANDRÁS GÁCS, PETER SZIKLAI, AND ZSUZSA WEINER Abstract. In this paper we prove that a set of points (in a projective
ON LINEAR CODES WHOSE WEIGHTS AND LENGTH HAVE A COMMON DIVISOR SIMEON BALL, AART BLOKHUIS, ANDRÁS GÁCS, PETER SZIKLAI, AND ZSUZSA WEINER Abstract. In this paper we prove that a set of points (in a projective
Steiner triple and quadruple systems of low 2-rank
 Steiner triple and quadruple systems of low 2-rank Vladimir D. Tonchev Department of Mathematical Sciences Michigan Technological University Houghton, MI 49931, USA tonchev@mtu.edu, www.math.mtu.edu/ tonchev
Steiner triple and quadruple systems of low 2-rank Vladimir D. Tonchev Department of Mathematical Sciences Michigan Technological University Houghton, MI 49931, USA tonchev@mtu.edu, www.math.mtu.edu/ tonchev
NEW SPHERE PACKINGS IN DIMENSIONS 9-15 BY JOHN LEECH AND N. J. A. SLOANE
 EW SPHERE PACKIGS I DIMESIOS 9-15 Y JOH LEECH AD. J. A. SLOAE Communicated by H. S. M. Coxeter, March 13, 1970 ew sphere packings in Euclidean spaces E 9 to E u are constructed using nonlinear error-correcting
EW SPHERE PACKIGS I DIMESIOS 9-15 Y JOH LEECH AD. J. A. SLOAE Communicated by H. S. M. Coxeter, March 13, 1970 ew sphere packings in Euclidean spaces E 9 to E u are constructed using nonlinear error-correcting
Mutually orthogonal latin squares (MOLS) and Orthogonal arrays (OA)
 and Orthogonal arrays (OA) Bimal Roy Indian Statistical Institute, Kolkata. Bimal Roy, Indian Statistical Institute, Kolkata. and Orthogonal arrays (O Outline of the talk 1 Latin squares 2 3 Bimal Roy,
and Orthogonal arrays (OA) Bimal Roy Indian Statistical Institute, Kolkata. Bimal Roy, Indian Statistical Institute, Kolkata. and Orthogonal arrays (O Outline of the talk 1 Latin squares 2 3 Bimal Roy,
Sidon sets and C 4 -saturated graphs
 Sidon sets and C 4 -saturated graphs arxiv:1810.056v1 [math.co] 11 Oct 018 David F. Daza Carlos A. Trujillo Universidad del Cauca, A.A. 755, Colombia. davidaza@unicauca.edu.co - trujillo@unicauca.edu.co
Sidon sets and C 4 -saturated graphs arxiv:1810.056v1 [math.co] 11 Oct 018 David F. Daza Carlos A. Trujillo Universidad del Cauca, A.A. 755, Colombia. davidaza@unicauca.edu.co - trujillo@unicauca.edu.co
The embedding problem for partial Steiner triple systems
 Late last year several news-items appeared announcing the solution of the 30 year old Lindner s conjecture by UoQ Graduate student Daniel Horsley and his supervisor Darryn Bryant, see e.g., http://www.uq.edu.au/news/?article=8359,
Late last year several news-items appeared announcing the solution of the 30 year old Lindner s conjecture by UoQ Graduate student Daniel Horsley and his supervisor Darryn Bryant, see e.g., http://www.uq.edu.au/news/?article=8359,
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST
 MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
MATH 115, SUMMER 2012 LECTURE 4 THURSDAY, JUNE 21ST JAMES MCIVOR Today we enter Chapter 2, which is the heart of this subject. Before starting, recall that last time we saw the integers have unique factorization
A UNIVERSAL SEQUENCE OF CONTINUOUS FUNCTIONS
 A UNIVERSAL SEQUENCE OF CONTINUOUS FUNCTIONS STEVO TODORCEVIC Abstract. We show that for each positive integer k there is a sequence F n : R k R of continuous functions which represents via point-wise
A UNIVERSAL SEQUENCE OF CONTINUOUS FUNCTIONS STEVO TODORCEVIC Abstract. We show that for each positive integer k there is a sequence F n : R k R of continuous functions which represents via point-wise
An Exponential Number of Generalized Kerdock Codes
 INFORMATION AND CONTROL 53, 74--80 (1982) An Exponential Number of Generalized Kerdock Codes WILLIAM M. KANTOR* Department of Mathematics, University of Oregon, Eugene, Oregon 97403 If n- 1 is an odd composite
INFORMATION AND CONTROL 53, 74--80 (1982) An Exponential Number of Generalized Kerdock Codes WILLIAM M. KANTOR* Department of Mathematics, University of Oregon, Eugene, Oregon 97403 If n- 1 is an odd composite
Resolvable partially pairwise balanced designs and their applications in computer experiments
 Resolvable partially pairwise balanced designs and their applications in computer experiments Kai-Tai Fang Department of Mathematics, Hong Kong Baptist University Yu Tang, Jianxing Yin Department of Mathematics,
Resolvable partially pairwise balanced designs and their applications in computer experiments Kai-Tai Fang Department of Mathematics, Hong Kong Baptist University Yu Tang, Jianxing Yin Department of Mathematics,
On the Frobenius Numbers of Symmetric Groups
 Journal of Algebra 221, 551 561 1999 Article ID jabr.1999.7992, available online at http://www.idealibrary.com on On the Frobenius Numbers of Symmetric Groups Yugen Takegahara Muroran Institute of Technology,
Journal of Algebra 221, 551 561 1999 Article ID jabr.1999.7992, available online at http://www.idealibrary.com on On the Frobenius Numbers of Symmetric Groups Yugen Takegahara Muroran Institute of Technology,
CSE 20 DISCRETE MATH. Winter
 CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Today's learning goals Define and use the congruence modulo m equivalence relation Perform computations using modular arithmetic
CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Today's learning goals Define and use the congruence modulo m equivalence relation Perform computations using modular arithmetic
Codegree problems for projective geometries
 Codegree problems for projective geometries Peter Keevash Yi Zhao Abstract The codegree density γ(f ) of an r-graph F is the largest number γ such that there are F -free r-graphs G on n vertices such that
Codegree problems for projective geometries Peter Keevash Yi Zhao Abstract The codegree density γ(f ) of an r-graph F is the largest number γ such that there are F -free r-graphs G on n vertices such that
INITIAL COMPLEX ASSOCIATED TO A JET SCHEME OF A DETERMINANTAL VARIETY. the affine space of dimension k over F. By a variety in A k F
 INITIAL COMPLEX ASSOCIATED TO A JET SCHEME OF A DETERMINANTAL VARIETY BOYAN JONOV Abstract. We show in this paper that the principal component of the first order jet scheme over the classical determinantal
INITIAL COMPLEX ASSOCIATED TO A JET SCHEME OF A DETERMINANTAL VARIETY BOYAN JONOV Abstract. We show in this paper that the principal component of the first order jet scheme over the classical determinantal
HSOLSSOM(hn) * Research supported in part by NSERC grant A-5320 for the flrst author, and NSFC grant for the second.
 on HSOLSSOM(hn) Bennett )p.n,qrt'rrlp.1nt of Mathematics Mount Saint Vincent University Halifax, Nova Scotia B3M 2J6, Canada L.Zhu lp'l"\
on HSOLSSOM(hn) Bennett )p.n,qrt'rrlp.1nt of Mathematics Mount Saint Vincent University Halifax, Nova Scotia B3M 2J6, Canada L.Zhu lp'l"\
A CONGRUENTIAL IDENTITY AND THE 2-ADIC ORDER OF LACUNARY SUMS OF BINOMIAL COEFFICIENTS
 A CONGRUENTIAL IDENTITY AND THE 2-ADIC ORDER OF LACUNARY SUMS OF BINOMIAL COEFFICIENTS Gregory Tollisen Department of Mathematics, Occidental College, 1600 Campus Road, Los Angeles, USA tollisen@oxy.edu
A CONGRUENTIAL IDENTITY AND THE 2-ADIC ORDER OF LACUNARY SUMS OF BINOMIAL COEFFICIENTS Gregory Tollisen Department of Mathematics, Occidental College, 1600 Campus Road, Los Angeles, USA tollisen@oxy.edu
Mutually embeddable graphs and the Tree Alternative conjecture
 Mutually embeddable graphs and the Tree Alternative conjecture Anthony Bonato a a Department of Mathematics Wilfrid Laurier University Waterloo, ON Canada, N2L 3C5 Claude Tardif b b Department of Mathematics
Mutually embeddable graphs and the Tree Alternative conjecture Anthony Bonato a a Department of Mathematics Wilfrid Laurier University Waterloo, ON Canada, N2L 3C5 Claude Tardif b b Department of Mathematics
Construction of some new families of nested orthogonal arrays
 isid/ms/2017/01 April 7, 2017 http://www.isid.ac.in/ statmath/index.php?module=preprint Construction of some new families of nested orthogonal arrays Tian-fang Zhang, Guobin Wu and Aloke Dey Indian Statistical
isid/ms/2017/01 April 7, 2017 http://www.isid.ac.in/ statmath/index.php?module=preprint Construction of some new families of nested orthogonal arrays Tian-fang Zhang, Guobin Wu and Aloke Dey Indian Statistical
Overview of some Combinatorial Designs
 Bimal Roy Indian Statistical Institute, Kolkata. Outline of the talk 1 Introduction 2 3 4 5 6 7 Outline of the talk 1 Introduction 2 3 4 5 6 7 Introduction Design theory: Study of combinatorial objects
Bimal Roy Indian Statistical Institute, Kolkata. Outline of the talk 1 Introduction 2 3 4 5 6 7 Outline of the talk 1 Introduction 2 3 4 5 6 7 Introduction Design theory: Study of combinatorial objects
3-Class Association Schemes and Hadamard Matrices of a Certain Block Form
 Europ J Combinatorics (1998) 19, 943 951 Article No ej980251 3-Class Association Schemes and Hadamard Matrices of a Certain Block Form R W GOLDBACH AND H L CLAASEN We describe 3-class association schemes
Europ J Combinatorics (1998) 19, 943 951 Article No ej980251 3-Class Association Schemes and Hadamard Matrices of a Certain Block Form R W GOLDBACH AND H L CLAASEN We describe 3-class association schemes
Steiner Triple Systems Intersecting in Pairwise Disjoint Blocks
 Steiner Triple Systems Intersecting in Pairwise Disjoint Blocks Yeow Meng Chee Netorics Pte Ltd 130 Joo Seng Road #05-02 Olivine Building Singapore 368357 ymchee@alumni.uwaterloo.ca Submitted: Feb 18,
Steiner Triple Systems Intersecting in Pairwise Disjoint Blocks Yeow Meng Chee Netorics Pte Ltd 130 Joo Seng Road #05-02 Olivine Building Singapore 368357 ymchee@alumni.uwaterloo.ca Submitted: Feb 18,
CONSTRUCTION OF SLICED SPACE-FILLING DESIGNS BASED ON BALANCED SLICED ORTHOGONAL ARRAYS
 Statistica Sinica 24 (2014), 1685-1702 doi:http://dx.doi.org/10.5705/ss.2013.239 CONSTRUCTION OF SLICED SPACE-FILLING DESIGNS BASED ON BALANCED SLICED ORTHOGONAL ARRAYS Mingyao Ai 1, Bochuan Jiang 1,2
Statistica Sinica 24 (2014), 1685-1702 doi:http://dx.doi.org/10.5705/ss.2013.239 CONSTRUCTION OF SLICED SPACE-FILLING DESIGNS BASED ON BALANCED SLICED ORTHOGONAL ARRAYS Mingyao Ai 1, Bochuan Jiang 1,2
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
 Bull. Aust. Math. Soc. 9 2016, 400 409 doi:10.1017/s000497271500167 CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS M. S. MAHADEVA NAIKA, B. HEMANTHKUMAR H. S. SUMANTH BHARADWAJ Received 9 August
Bull. Aust. Math. Soc. 9 2016, 400 409 doi:10.1017/s000497271500167 CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS M. S. MAHADEVA NAIKA, B. HEMANTHKUMAR H. S. SUMANTH BHARADWAJ Received 9 August
k-subsets of V: Finding a collection which forms a t-design is equivalent to the problem of solving a system of diophantine equations, as mentioned ab
 Simple 6- and 7-designs on 19 to 33 points Anton Betten 1, Reinhard Laue, Alfred Wassermann Universitat Bayreuth, Lehrstuhl II fur Mathematik, Lehrstuhl fur Mathematik und ihre Didaktik, D-95440 Bayreuth
Simple 6- and 7-designs on 19 to 33 points Anton Betten 1, Reinhard Laue, Alfred Wassermann Universitat Bayreuth, Lehrstuhl II fur Mathematik, Lehrstuhl fur Mathematik und ihre Didaktik, D-95440 Bayreuth
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
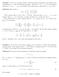 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Putnam Greedy Algorithms Cody Johnson. Greedy Algorithms. May 30, 2016 Cody Johnson.
 1 Introduction Greedy Algorithms May 0, 2016 Cody Johnson ctj@math.cmu.edu A greedy algorithm is an algorithm that chooses the optimal choice in the short run. 2 Examples 1. Prove that every nonnegative
1 Introduction Greedy Algorithms May 0, 2016 Cody Johnson ctj@math.cmu.edu A greedy algorithm is an algorithm that chooses the optimal choice in the short run. 2 Examples 1. Prove that every nonnegative
Part IA Numbers and Sets
 Part IA Numbers and Sets Theorems Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IA Numbers and Sets Theorems Based on lectures by A. G. Thomason Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Independent Dominating Sets and a Second Hamiltonian Cycle in Regular Graphs
 Journal of Combinatorial Theory, Series B 72, 104109 (1998) Article No. TB971794 Independent Dominating Sets and a Second Hamiltonian Cycle in Regular Graphs Carsten Thomassen Department of Mathematics,
Journal of Combinatorial Theory, Series B 72, 104109 (1998) Article No. TB971794 Independent Dominating Sets and a Second Hamiltonian Cycle in Regular Graphs Carsten Thomassen Department of Mathematics,
Balanced Nested Designs and Balanced n-ary Designs
 Balanced Nested Designs and Balanced n-ary Designs Ryoh Fuji-Hara a, Shinji Kuriki b, Ying Miao a and Satoshi Shinohara c a Institute of Policy and Planning Sciences, University of Tsukuba, Tsukuba, Ibaraki
Balanced Nested Designs and Balanced n-ary Designs Ryoh Fuji-Hara a, Shinji Kuriki b, Ying Miao a and Satoshi Shinohara c a Institute of Policy and Planning Sciences, University of Tsukuba, Tsukuba, Ibaraki
