Rolle s Theorem and the Mean Value Theorem. Rolle s Theorem
|
|
|
- Bruno Russell
- 6 years ago
- Views:
Transcription
1 0_00qd //0 0:50 AM Page 7 7 CHAPTER Applications o Dierentiation Section ROLLE S THEOREM French mathematician Michel Rolle irst published the theorem that bears his name in 9 Beore this time, however, Rolle was one o the most vocal critics o calculus, stating that it gave erroneous results and was based on unsound reasoning Later in lie, Rolle came to see the useulness o calculus Rolle s Theorem and the Mean Value Theorem Understand and use Rolle s Theorem Understand and use the Mean Value Theorem Rolle s Theorem The Etreme Value Theorem (Section ) states that a continuous unction on a closed interval a, b must have both a minimum and a maimum on the interval Both o these values, however, can occur at the endpoints Rolle s Theorem, named ater the French mathematician Michel Rolle (5 79), gives conditions that guarantee the eistence o an etreme value in the interior o a closed interval EXPLORATION Etreme Values in a Closed Interval Sketch a rectangular coordinate plane on a piece o paper Label the points, and 5, Using a pencil or pen, draw the graph o a dierentiable unction that starts at, and ends at 5, Is there at least one point on the graph or which the derivative is zero? Would it be possible to draw the graph so that there isn t a point or which the derivative is zero? Eplain our reasoning Relative maimum THEOREM Rolle s Theorem Let be continuous on the closed interval a, b and dierentiable on the open interval a, b I a b then there is at least one number c in a, b such that c 0 d a c (a) is continuous on a, b and dierentiable on a, b Relative maimum b Proo Let a d b Case : I d or all in a, b, is constant on the interval and, b Theorem, 0 or all in a, b Case : Suppose > d or some in a, b B the Etreme Value Theorem, ou know that has a maimum at some c in the interval Moreover, because c > d, this maimum does not occur at either endpoint So, has a maimum in the open interval a, b This implies that c is a relative maimum and, b Theorem, c is a critical number o Finall, because is dierentiable at c, ou can conclude that c 0 Case : I < d or some in a, b, ou can use an argument similar to that in Case, but involving the minimum instead o the maimum d a c b (b) is continuous on a, b Figure 8 From Rolle s Theorem, ou can see that i a unction is continuous on a, b and dierentiable on a, b, and i a b, there must be at least one -value between a and b at which the graph o has a horizontal tangent, as shown in Figure 8(a) I the dierentiabilit requirement is dropped rom Rolle s Theorem, will still have a critical number in a, b, but it ma not ield a horizontal tangent Such a case is shown in Figure 8(b)
2 0_00qd //0 0:50 AM Page 7 SECTION Rolle s Theorem and the Mean Value Theorem 7 EXAMPLE Illustrating Rolle s Theorem () = + (, 0) (, 0) ( ) = 0 Horizontal tangent The -value or which 0 is between the two -intercepts Figure 9 Find the two -intercepts o and show that ) 0 at some point between the two -intercepts Solution Note that is dierentiable on the entire real line Setting equal to 0 produces 0 0 Set equal to 0 Factor So, 0, and rom Rolle s Theorem ou know that there eists at least one c in the interval, such that c 0 To ind such a c, ou can solve the equation 0 Set equal to 0 and determine that 0 when Note that the -value lies in the open interval,, as shown in Figure 9 Rolle s Theorem states that i satisies the conditions o the theorem, there must be at least one point between a and b at which the derivative is 0 There ma o course be more than one such point, as shown in the net eample ( ) = 8 8 () = (0) = 0 ( ) = 0 () = 0 () = 8 0 or more than one -value in the interval, Figure 0 EXAMPLE Illustrating Rolle s Theorem Let Find all values o c in the interval, such that c 0 Solution To begin, note that the unction satisies the conditions o Rolle s Theorem That is, is continuous on the interval, and dierentiable on the interval, Moreover, because 8, ou can conclude that there eists at least one c in, such that c 0 Setting the derivative equal to 0 produces 0 Set equal to 0 0 0,, Factor -values or which 0 So, in the interval,, the derivative is zero at three dierent values o, as shown in Figure 0 Figure TECHNOLOGY PITFALL A graphing utilit can be used to indicate whether the points on the graphs in Eamples and are relative minima or relative maima o the unctions When using a graphing utilit, however, ou should keep in mind that it can give misleading pictures o graphs For eample, use a graphing utilit to graph With most viewing windows, it appears that the unction has a maimum o when (see Figure ) B evaluating the unction at, however, ou can see that 0 To determine the behavior o this unction near, ou need to eamine the graph analticall to get the complete picture
3 0_00qd //0 0:50 AM Page 7 7 CHAPTER Applications o Dierentiation The Mean Value Theorem Rolle s Theorem can be used to prove another theorem the Mean Value Theorem Slope o tangent line = (c) THEOREM The Mean Value Theorem I is continuous on the closed interval a, b and dierentiable on the open interval a, b, then there eists a number c in a, b such that c b a b a Figure Mar Evans Picture Librar (a, (a)) a c b Tangent line Secant line (b, (b)) JOSEPH-LOUIS LAGRANGE (7 8) The Mean Value Theorem was irst proved b the amous mathematician Joseph-Louis Lagrange Born in Ital, Lagrange held a position in the court o Frederick the Great in Berlin or 0 ears Aterward, he moved to France, where he met emperor Napoleon Bonaparte, who is quoted as saing, Lagrange is the lot pramid o the mathematical sciences Proo Reer to Figure The equation o the secant line containing the points a, a and b, b is b a b a a a Let g be the dierence between and Then g B evaluating g at a and b, ou can see that ga 0 gb Because is continuous on a, b it ollows that g is also continuous on a, b Furthermore, because is dierentiable, g is also dierentiable, and ou can appl Rolle s Theorem to the unction g So, there eists a number c in a, b such that gc 0, which implies that 0 gc c So, there eists a number c in a, b such that c b a b a b a b a b a b a a a NOTE The mean in the Mean Value Theorem reers to the mean (or average) rate o change o in the interval a, b Although the Mean Value Theorem can be used directl in problem solving, it is used more oten to prove other theorems In act, some people consider this to be the most important theorem in calculus it is closel related to the Fundamental Theorem o Calculus discussed in Chapter For now, ou can get an idea o the versatilit o this theorem b looking at the results stated in Eercises in this section The Mean Value Theorem has implications or both basic interpretations o the derivative Geometricall, the theorem guarantees the eistence o a tangent line that is parallel to the secant line through the points a, a and b, b, as shown in Figure Eample illustrates this geometric interpretation o the Mean Value Theorem In terms o rates o change, the Mean Value Theorem implies that there must be a point in the open interval a, b at which the instantaneous rate o change is equal to the average rate o change over the interval a, b This is illustrated in Eample
4 0_00qd //0 0:50 AM Page 75 SECTION Rolle s Theorem and the Mean Value Theorem 75 EXAMPLE Finding a Tangent Line Tangent line (, ) (, ) Secant line () = 5 (, ) The tangent line at, is parallel to the secant line through, and, Figure Given 5, ind all values o c in the open interval, such that c Solution The slope o the secant line through, and, is Because satisies the conditions o the Mean Value Theorem, there eists at least one number c in, such that c Solving the equation ields which implies that ± So, in the interval,, ou can conclude that c, as shown in Figure EXAMPLE Finding an Instantaneous Rate o Change 5 miles t = minutes t = 0 Not drawn to scale At some time t, the instantaneous velocit is equal to the average velocit over minutes Figure Two stationar patrol cars equipped with radar are 5 miles apart on a highwa, as shown in Figure As a truck passes the irst patrol car, its speed is clocked at 55 miles per hour Four minutes later, when the truck passes the second patrol car, its speed is clocked at 50 miles per hour Prove that the truck must have eceeded the speed limit (o 55 miles per hour) at some time during the minutes Solution Let t 0 be the time (in hours) when the truck passes the irst patrol car The time when the truck passes the second patrol car is t 0 5 hour B letting st represent the distance (in miles) traveled b the truck, ou have s0 0 and s5 5 So, the average velocit o the truck over the ive-mile stretch o highwa is s5 s0 Average velocit miles per hour 5 Assuming that the position unction is dierentiable, ou can appl the Mean Value Theorem to conclude that the truck must have been traveling at a rate o 75 miles per hour sometime during the minutes A useul alternative orm o the Mean Value Theorem is as ollows: I is continuous on a, b and dierentiable on a, b, then there eists a number c in a, b such that b a b ac Alternative orm o Mean Value Theorem NOTE When doing the eercises or this section, keep in mind that polnomial unctions, rational unctions, and trigonometric unctions are dierentiable at all points in their domains
5 0_00qd //0 0:50 AM Page 7 7 CHAPTER Applications o Dierentiation Eercises or Section In Eercises, eplain wh Rolle s Theorem does not appl to the unction even though there eist a and b such that a b (0, 0),, (, 0) In Eercises 5 8, ind the two -intercepts o the unction and show that 0 at some point between the two -intercepts Rolle s Theorem In Eercises 9 and 0, the graph o is shown Appl Rolle s Theorem and ind all values o c such that c 0 at some point between the labeled intercepts 9 0 () = + (, 0) (, 0) cot (0, 0) (, 0) (, 0),, () = sin (, 0 ) See wwwcalcchatcom or worked-out solutions to odd-numbered eercises In Eercises 5 8, use a graphing utilit to graph the unction on the closed interval [a, b] Determine whether Rolle s Theorem can be applied to on the interval and, i so, ind all values o c in the open interval a, b such that c 0 5,,, 0, 7 tan,, 8 sin,, 0 9 Vertical Motion The height o a ball t seconds ater it is thrown upward rom a height o eet and with an initial velocit o 8 eet per second is t t 8t (a) Veri that (b) According to Rolle s Theorem, what must be the velocit at some time in the interval,? Find that time 0 Reorder Costs The ordering and transportation cost C or components used in a manuacturing process is approimated b C 0 where C is measured in thousands, o dollars and is the order size in hundreds (a) Veri that C C (b) According to Rolle s Theorem, the rate o change o the cost must be 0 or some order size in the interval, Find that order size In Eercises and, cop the graph and sketch the secant line to the graph through the points a, a and b, b Then sketch an tangent lines to the graph or each value o c guaranteed b the Mean Value Theorem To print an enlarged cop o the graph, go to the website wwwmathgraphscom In Eercises, determine whether Rolle s Theorem can be applied to on the closed interval [a, b] I Rolle s Theorem can be applied, ind all values o c in the open interval a, b such that c 0, 0, 5,,,,,, 5, 8, 8, 0, 7, 8,,, 9 sin, 0, 0 cos, 0, sin, 0, cos,, tan, 0, sec,, Writing In Eercises, eplain wh the Mean Value Theorem does not appl to the unction on the interval [0, ] 5 a 5 b 5 5 a 5 b
6 0_00qd //0 0:50 AM Page 77 SECTION Rolle s Theorem and the Mean Value Theorem 77 7 Mean Value Theorem Consider the graph o the unction (a) Find the equation o the secant line joining the points, and, 5 (b) Use the Mean Value Theorem to determine a point c in the interval, such that the tangent line at c is parallel to the secant line (c) Find the equation o the tangent line through c (d) Then use a graphing utilit to graph, the secant line, and the tangent line Figure or 7 Figure or 8 8 Mean Value Theorem Consider the graph o the unction (a) Find the equation o the secant line joining the points, and, 0 (b) Use the Mean Value Theorem to determine a point c in the interval, such that the tangent line at c is parallel to the secant line (c) Find the equation o the tangent line through c (d) Then use a graphing utilit to graph, the secant line, and the tangent line In Eercises 9, determine whether the Mean Value Theorem can be applied to on the closed interval [a, b] I the Mean Value Theorem can be applied, ind all values o c in the b a open interval a, b such that c b a 9,, 0,,, 0,,, 7,, 5 sin, 0, sin sin, 0, In Eercises 7 50, use a graphing utilit to (a) graph the unction on the given interval, (b) ind and graph the secant line through points on the graph o at the endpoints o the given interval, and (c) ind and graph an tangent lines to the graph o that are parallel to the secant line 7 8 sin,,, 9,, , 0, 5 (, ) 5 () = +, (, 5) () = + (, ) 0, (, 0), 5 Vertical Motion The height o an object t seconds ater it is dropped rom a height o 500 meters is st 9t 500 (a) Find the average velocit o the object during the irst seconds (b) Use the Mean Value Theorem to veri that at some time during the irst seconds o all the instantaneous velocit equals the average velocit Find that time 5 Sales A compan introduces a new product or which the number o units sold S is St t where t is the time in months (a) Find the average value o St during the irst ear (b) During what month does St equal the average value during the irst ear? Writing About Concepts 5 Let be continuous on a, b and dierentiable on a, b I there eists c in a, b such that c 0, does it ollow that a b? Eplain 5 Let be continuous on the closed interval a, b and dierentiable on the open interval a, b Also, suppose that a b and that c is a real number in the interval such that c 0 Find an interval or the unction g over which Rolle s Theorem can be applied, and ind the corresponding critical number o g ( k is a constant) (a) g k (b) g k (c) g k 55 The unction 0,, 0 0 < is dierentiable on 0, and satisies 0 However, its derivative is never zero on 0, Does this contradict Rolle s Theorem? Eplain 5 Can ou ind a unction such that,, and < or all Wh or wh not? 57 Speed A plane begins its takeo at :00 PM on a 500-mile light The plane arrives at its destination at 7:0 PM Eplain wh there are at least two times during the light when the speed o the plane is 00 miles per hour 58 Temperature When an object is removed rom a urnace and placed in an environment with a constant temperature o 90F, its core temperature is 500F Five hours later the core temperature is 90F Eplain wh there must eist a time in the interval when the temperature is decreasing at a rate o F per hour 59 Velocit Two bicclists begin a race at 8:00 AM The both inish the race hours and 5 minutes later Prove that at some time during the race, the bicclists are traveling at the same velocit 0 Acceleration At 9: AM, a sports car is traveling 5 miles per hour Two minutes later, the car is traveling 85 miles per hour Prove that at some time during this two-minute interval, the car s acceleration is eactl 500 miles per hour squared
7 0_00qd //0 0:50 AM Page CHAPTER Applications o Dierentiation Graphical Reasoning The igure shows two parts o the graph o a continuous dierentiable unction on 0, The derivative is also continuous To print an enlarged cop o the graph, go to the website wwwmathgraphscom (a) Eplain wh must have at least one zero in 0, (b) Eplain wh must also have at least one zero in the interval 0, What are these zeros called? (c) Make a possible sketch o the unction with one zero o on the interval 0, (d) Make a possible sketch o the unction with two zeros o on the interval 0, (e) Were the conditions o continuit o and necessar to do parts (a) through (d)? Eplain Consider the unction (a) Use a graphing utilit to graph and (b) Is a continuous unction? Is a continuous unction? (c) Does Rolle s Theorem appl on the interval,? Does it appl on the interval,? Eplain (d) Evaluate, i possible, lim and lim Think About It In Eercises and, sketch the graph o an arbitrar unction that satisies the given condition but does not satis the conditions o the Mean Value Theorem on the interval [5, 5] is continuous on 5, 5 is not continuous on 5, 5 In Eercises 5 and, use the Intermediate Value Theorem and Rolle s Theorem to prove that the equation has eactl one real solution cos 0 7 Determine the values a, b, and c such that the unction satisies the hpotheses o the Mean Value Theorem on the interval 0,, a b, c, cos 0 0 < < 8 Determine the values a, b, c, and d so that the unction satisies the hpotheses o the Mean Value Theorem on the interval, a,, b c, d, Dierential Equations In Eercises 9 7, ind a unction that has the derivative and whose graph passes through the given point Eplain our reasoning 9 0,, 5 70, 0, 7,, 0 7,, 0 True or False? In Eercises 7 7, determine whether the statement is true or alse I it is alse, eplain wh or give an eample that shows it is alse 7 The Mean Value Theorem can be applied to on the interval, 7 I the graph o a unction has three -intercepts, then it must have at least two points at which its tangent line is horizontal 75 I the graph o a polnomial unction has three -intercepts, then it must have at least two points at which its tangent line is horizontal 7 I 0 or all in the domain o, then is a constant unction 77 Prove that i a > 0 and n is an positive integer, then the polnomial unction p n a b cannot have two real roots 78 Prove that i 0 or all in an interval a, b, then is constant on a, b 79 Let p A B C Prove that or an interval a, b, the value c guaranteed b the Mean Value Theorem is the midpoint o the interval 80 (a) Let and g Then g and g Show that there is at least one value c in the interval, where the tangent line to at c, c is parallel to the tangent line to g at c, gc Identi c (b) Let and g be dierentiable unctions on a, b where a ga and b gb Show that there is at least one value c in the interval a, b where the tangent line to at c, c is parallel to the tangent line to g at c, gc 8 Prove that i is dierentiable on, and < or all real numbers, then has at most one ied point A ied point o a unction is a real number c such that c c 8 Use the result o Eercise 8 to show that cos has at most one ied point 8 Prove that cos a cos b a b or all a and b 8 Prove that sin a sin b a b or all a and b 85 Let 0 < a < b Use the Mean Value Theorem to show that b a < b a a < 0 0 < <
Increasing and Decreasing Functions and the First Derivative Test. Increasing and Decreasing Functions. Video
 SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
SECTION and Decreasing Functions and the First Derivative Test 79 Section and Decreasing Functions and the First Derivative Test Determine intervals on which a unction is increasing or decreasing Appl
Tangent Line Approximations
 60_009.qd //0 :8 PM Page SECTION.9 Dierentials Section.9 EXPLORATION Tangent Line Approimation Use a graphing utilit to graph. In the same viewing window, graph the tangent line to the graph o at the point,.
60_009.qd //0 :8 PM Page SECTION.9 Dierentials Section.9 EXPLORATION Tangent Line Approimation Use a graphing utilit to graph. In the same viewing window, graph the tangent line to the graph o at the point,.
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
Product and Quotient Rules and Higher-Order Derivatives. The Product Rule
 330_003.q 11/3/0 :3 PM Page 119 SECTION.3 Prouct an Quotient Rules an Higher-Orer Derivatives 119 Section.3 Prouct an Quotient Rules an Higher-Orer Derivatives Fin the erivative o a unction using the Prouct
330_003.q 11/3/0 :3 PM Page 119 SECTION.3 Prouct an Quotient Rules an Higher-Orer Derivatives 119 Section.3 Prouct an Quotient Rules an Higher-Orer Derivatives Fin the erivative o a unction using the Prouct
0,0 B 5,0 C 0, 4 3,5. y x. Recitation Worksheet 1A. 1. Plot these points in the xy plane: A
 Math 13 Recitation Worksheet 1A 1 Plot these points in the y plane: A 0,0 B 5,0 C 0, 4 D 3,5 Without using a calculator, sketch a graph o each o these in the y plane: A y B 3 Consider the unction a Evaluate
Math 13 Recitation Worksheet 1A 1 Plot these points in the y plane: A 0,0 B 5,0 C 0, 4 D 3,5 Without using a calculator, sketch a graph o each o these in the y plane: A y B 3 Consider the unction a Evaluate
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
4.2 Mean Value Theorem Calculus
 4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
4. MEAN VALUE THEOREM The Mean Value Theorem is considered b some to be the most important theorem in all of calculus. It is used to prove man of the theorems in calculus that we use in this course as
Quick Review 4.1 (For help, go to Sections 1.2, 2.1, 3.5, and 3.6.)
 Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
Rolle s Theorem. THEOREM 3 Rolle s Theorem. x x. then there is at least one number c in (a, b) at which ƒ scd = 0.
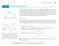 4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
This is only a list of questions use a separate sheet to work out the problems. 1. (1.2 and 1.4) Use the given graph to answer each question.
 Mth Calculus Practice Eam Questions NOTE: These questions should not be taken as a complete list o possible problems. The are merel intended to be eamples o the diicult level o the regular eam questions.
Mth Calculus Practice Eam Questions NOTE: These questions should not be taken as a complete list o possible problems. The are merel intended to be eamples o the diicult level o the regular eam questions.
Finding Limits Graphically and Numerically. An Introduction to Limits
 60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
Properties of Limits
 33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
Homework Assignments Math /02 Spring 2015
 Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
5.5 Worksheet - Linearization
 AP Calculus 4.5 Worksheet 5.5 Worksheet - Linearization All work must be shown in this course for full credit. Unsupported answers ma receive NO credit. 1. Consider the function = sin. a) Find the equation
AP Calculus 4.5 Worksheet 5.5 Worksheet - Linearization All work must be shown in this course for full credit. Unsupported answers ma receive NO credit. 1. Consider the function = sin. a) Find the equation
Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 119 Mark Sparks 2012
 Unit # Understanding the Derivative Homework Packet f ( h) f ( Find lim for each of the functions below. Then, find the equation of the tangent line to h 0 h the graph of f( at the given value of. 1. f
Unit # Understanding the Derivative Homework Packet f ( h) f ( Find lim for each of the functions below. Then, find the equation of the tangent line to h 0 h the graph of f( at the given value of. 1. f
+ 2 on the interval [-1,3]
![+ 2 on the interval [-1,3] + 2 on the interval [-1,3]](/thumbs/89/98527152.jpg) Section.1 Etrema on an Interval 1. Understand the definition of etrema of a function on an interval.. Understand the definition of relative etrema of a function on an open interval.. Find etrema on a closed
Section.1 Etrema on an Interval 1. Understand the definition of etrema of a function on an interval.. Understand the definition of relative etrema of a function on an open interval.. Find etrema on a closed
Lesson Goals. Unit 2 Functions Analyzing Graphs of Functions (Unit 2.2) Graph of a Function. Lesson Goals
 Unit Functions Analzing Graphs of Functions (Unit.) William (Bill) Finch Mathematics Department Denton High School Lesson Goals When ou have completed this lesson ou will: Find the domain and range of
Unit Functions Analzing Graphs of Functions (Unit.) William (Bill) Finch Mathematics Department Denton High School Lesson Goals When ou have completed this lesson ou will: Find the domain and range of
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Finding Limits Graphically and Numerically. An Introduction to Limits
 8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
8 CHAPTER Limits and Their Properties Section Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach Learn different was that a it can fail to eist Stud and use
Applications of Derivatives
 58_Ch04_pp86-60.qd /3/06 :35 PM Page 86 Chapter 4 Applications of Derivatives A n automobile s gas mileage is a function of man variables, including road surface, tire tpe, velocit, fuel octane rating,
58_Ch04_pp86-60.qd /3/06 :35 PM Page 86 Chapter 4 Applications of Derivatives A n automobile s gas mileage is a function of man variables, including road surface, tire tpe, velocit, fuel octane rating,
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment As Advanced placement students, our irst assignment or the 07-08 school ear is to come to class the ver irst da in top mathematical orm. Calculus is a world o change. While
AP Calculus AB Summer Assignment As Advanced placement students, our irst assignment or the 07-08 school ear is to come to class the ver irst da in top mathematical orm. Calculus is a world o change. While
Basic Differentiation Rules and Rates of Change. The Constant Rule
 460_00.q //04 4:04 PM Page 07 SECTION. Basic Differentiation Rules an Rates of Change 07 Section. The slope of a horizontal line is 0. Basic Differentiation Rules an Rates of Change Fin the erivative of
460_00.q //04 4:04 PM Page 07 SECTION. Basic Differentiation Rules an Rates of Change 07 Section. The slope of a horizontal line is 0. Basic Differentiation Rules an Rates of Change Fin the erivative of
Inverse of a Function
 . Inverse o a Function Essential Question How can ou sketch the graph o the inverse o a unction? Graphing Functions and Their Inverses CONSTRUCTING VIABLE ARGUMENTS To be proicient in math, ou need to
. Inverse o a Function Essential Question How can ou sketch the graph o the inverse o a unction? Graphing Functions and Their Inverses CONSTRUCTING VIABLE ARGUMENTS To be proicient in math, ou need to
AP Calculus AB Ch. 2 Derivatives (Part I) Intro to Derivatives: Definition of the Derivative and the Tangent Line 9/15/14
 AP Calculus AB Ch. Derivatives (Part I) Name Intro to Derivatives: Deinition o the Derivative an the Tangent Line 9/15/1 A linear unction has the same slope at all o its points, but non-linear equations
AP Calculus AB Ch. Derivatives (Part I) Name Intro to Derivatives: Deinition o the Derivative an the Tangent Line 9/15/1 A linear unction has the same slope at all o its points, but non-linear equations
New Functions from Old Functions
 .3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
.3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
One of the most common applications of Calculus involves determining maximum or minimum values.
 8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
SEE and DISCUSS the pictures on pages in your text. Key picture:
 Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
Extreme Values of Functions
 Extreme Values o Functions When we are using mathematics to model the physical world in which we live, we oten express observed physical quantities in terms o variables. Then, unctions are used to describe
Extreme Values o Functions When we are using mathematics to model the physical world in which we live, we oten express observed physical quantities in terms o variables. Then, unctions are used to describe
Chapter 6 Overview: Applications of Derivatives
 Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
x c x c This suggests the following definition.
 110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
MATH section 3.4 Curve Sketching Page 1 of 29
 MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
MATH section. Curve Sketching Page of 9 The step by step procedure below is for regular rational and polynomial functions. If a function contains radical or trigonometric term, then proceed carefully because
4.3 Mean-Value Theorem and Monotonicity
 .3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
.3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
2.4 Library of Functions; Piecewise-defined Functions. 1 Graph the Functions Listed in the Library of Functions
 80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
Find the following limits. For each one, if it does not exist, tell why not. Show all necessary work.
 Calculus I Eam File Spring 008 Test #1 Find the following its. For each one, if it does not eist, tell why not. Show all necessary work. 1.) 4.) + 4 0 1.) 0 tan 5.) 1 1 1 1 cos 0 sin 3.) 4 16 3 1 6.) For
Calculus I Eam File Spring 008 Test #1 Find the following its. For each one, if it does not eist, tell why not. Show all necessary work. 1.) 4.) + 4 0 1.) 0 tan 5.) 1 1 1 1 cos 0 sin 3.) 4 16 3 1 6.) For
4.1 & 4.2 Student Notes Using the First and Second Derivatives. for all x in D, where D is the domain of f. The number f()
 4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
4.1 & 4. Student Notes Using the First and Second Derivatives Deinition A unction has an absolute maimum (or global maimum) at c i ( c) ( ) or all in D, where D is the domain o. The number () c is called
Pre-Calculus Module 4
 Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
Pre-Calculus Module 4 4 th Nine Weeks Table of Contents Precalculus Module 4 Unit 9 Rational Functions Rational Functions with Removable Discontinuities (1 5) End Behavior of Rational Functions (6) Rational
Partial Fractions. dx dx x sec tan d 1 4 tan 2. 2 csc d. csc cot C. 2x 5. 2 ln. 2 x 2 5x 6 C. 2 ln. 2 ln x
 460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
2.3 Product and Quotient Rules and Higher-Order Derivatives
 Chapter Dierentiation. Prouct an Quotient Rules an Higher-Orer Derivatives Fin the erivative o a unction using the Prouct Rule. Fin the erivative o a unction using the Quotient Rule. Fin the erivative
Chapter Dierentiation. Prouct an Quotient Rules an Higher-Orer Derivatives Fin the erivative o a unction using the Prouct Rule. Fin the erivative o a unction using the Quotient Rule. Fin the erivative
Fitting Integrands to Basic Rules
 6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
Review Exercises for Chapter 3. Review Exercises for Chapter r v 0 2. v ft sec. x 1 2 x dx f x x 99.4.
 Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
1.7 Inverse Functions
 71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
AP Calculus Notes: Unit 1 Limits & Continuity. Syllabus Objective: 1.1 The student will calculate limits using the basic limit theorems.
 Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
Syllabus Objective:. The student will calculate its using the basic it theorems. LIMITS how the outputs o a unction behave as the inputs approach some value Finding a Limit Notation: The it as approaches
PACKET Unit 4 Honors ICM Functions and Limits 1
 PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
Mat 267 Engineering Calculus III Updated on 9/19/2010
 Chapter 11 Partial Derivatives Section 11.1 Functions o Several Variables Deinition: A unction o two variables is a rule that assigns to each ordered pair o real numbers (, ) in a set D a unique real number
Chapter 11 Partial Derivatives Section 11.1 Functions o Several Variables Deinition: A unction o two variables is a rule that assigns to each ordered pair o real numbers (, ) in a set D a unique real number
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
1. The cost (in dollars) of producing x units of a certain commodity is C(x) = x x 2.
 APPM 1350 Review #2 Summer 2014 1. The cost (in dollars) of producing units of a certain commodity is C() 5000 + 10 + 0.05 2. (a) Find the average rate of change of C with respect to when the production
APPM 1350 Review #2 Summer 2014 1. The cost (in dollars) of producing units of a certain commodity is C() 5000 + 10 + 0.05 2. (a) Find the average rate of change of C with respect to when the production
Limits and Their Properties
 Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Differentiation and applications
 FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
Antiderivatives and Indefinite Integration
 60_00.q //0 : PM Page 8 8 CHAPTER Integration Section. EXPLORATION Fining Antierivatives For each erivative, escribe the original function F. a. F b. F c. F. F e. F f. F cos What strateg i ou use to fin
60_00.q //0 : PM Page 8 8 CHAPTER Integration Section. EXPLORATION Fining Antierivatives For each erivative, escribe the original function F. a. F b. F c. F. F e. F f. F cos What strateg i ou use to fin
Math 2412 Activity 1(Due by EOC Sep. 17)
 Math 4 Activity (Due by EOC Sep. 7) Determine whether each relation is a unction.(indicate why or why not.) Find the domain and range o each relation.. 4,5, 6,7, 8,8. 5,6, 5,7, 6,6, 6,7 Determine whether
Math 4 Activity (Due by EOC Sep. 7) Determine whether each relation is a unction.(indicate why or why not.) Find the domain and range o each relation.. 4,5, 6,7, 8,8. 5,6, 5,7, 6,6, 6,7 Determine whether
Roberto s Notes on Differential Calculus Chapter 8: Graphical analysis Section 1. Extreme points
 Roberto s Notes on Dierential Calculus Chapter 8: Graphical analysis Section 1 Extreme points What you need to know already: How to solve basic algebraic and trigonometric equations. All basic techniques
Roberto s Notes on Dierential Calculus Chapter 8: Graphical analysis Section 1 Extreme points What you need to know already: How to solve basic algebraic and trigonometric equations. All basic techniques
All work must be shown in this course for full credit. Unsupported answers may receive NO credit.
 AP Calculus.1 Worksheet Day 1 All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. The only way to guarantee the eistence of a it is to algebraically prove
AP Calculus.1 Worksheet Day 1 All work must be shown in this course for full credit. Unsupported answers may receive NO credit. 1. The only way to guarantee the eistence of a it is to algebraically prove
In everyday speech, a continuous. Limits and Continuity. Critical Thinking Exercises
 062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
Representation of Functions by Power Series. Geometric Power Series
 60_0909.qd //0 :09 PM Page 669 SECTION 9.9 Representation of Functions b Power Series 669 The Granger Collection Section 9.9 JOSEPH FOURIER (768 80) Some of the earl work in representing functions b power
60_0909.qd //0 :09 PM Page 669 SECTION 9.9 Representation of Functions b Power Series 669 The Granger Collection Section 9.9 JOSEPH FOURIER (768 80) Some of the earl work in representing functions b power
Derivatives of Multivariable Functions
 Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Slopes and Rates of Change
 Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
Slopes and Rates of Change If a particle is moving in a straight line at a constant velocity, then the graph of the function of distance versus time is as follows s s = f(t) t s s t t = average velocity
Tangent Line Approximations. y f c f c x c. y f c f c x c. Find the tangent line approximation of. f x 1 sin x
 SECTION 9 Differentials 5 Section 9 EXPLORATION Tangent Line Approimation Use a graphing utilit to graph f In the same viewing window, graph the tangent line to the graph of f at the point, Zoom in twice
SECTION 9 Differentials 5 Section 9 EXPLORATION Tangent Line Approimation Use a graphing utilit to graph f In the same viewing window, graph the tangent line to the graph of f at the point, Zoom in twice
Mathematical Preliminaries. Developed for the Members of Azera Global By: Joseph D. Fournier B.Sc.E.E., M.Sc.E.E.
 Mathematical Preliminaries Developed or the Members o Azera Global B: Joseph D. Fournier B.Sc.E.E., M.Sc.E.E. Outline Chapter One, Sets: Slides: 3-27 Chapter Two, Introduction to unctions: Slides: 28-36
Mathematical Preliminaries Developed or the Members o Azera Global B: Joseph D. Fournier B.Sc.E.E., M.Sc.E.E. Outline Chapter One, Sets: Slides: 3-27 Chapter Two, Introduction to unctions: Slides: 28-36
Math Review and Lessons in Calculus
 Math Review and Lessons in Calculus Agenda Rules o Eponents Functions Inverses Limits Calculus Rules o Eponents 0 Zero Eponent Rule a * b ab Product Rule * 3 5 a / b a-b Quotient Rule 5 / 3 -a / a Negative
Math Review and Lessons in Calculus Agenda Rules o Eponents Functions Inverses Limits Calculus Rules o Eponents 0 Zero Eponent Rule a * b ab Product Rule * 3 5 a / b a-b Quotient Rule 5 / 3 -a / a Negative
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
In #1-5, find the indicated limits. For each one, if it does not exist, tell why not. Show all necessary work.
 Calculus I Eam File Fall 7 Test # In #-5, find the indicated limits. For each one, if it does not eist, tell why not. Show all necessary work. lim sin.) lim.) 3.) lim 3 3-5 4 cos 4.) lim 5.) lim sin 6.)
Calculus I Eam File Fall 7 Test # In #-5, find the indicated limits. For each one, if it does not eist, tell why not. Show all necessary work. lim sin.) lim.) 3.) lim 3 3-5 4 cos 4.) lim 5.) lim sin 6.)
CHAPTER P Preparation for Calculus
 PART II CHAPTER P Preparation for Calculus Section P. Graphs and Models..................... 8 Section P. Linear Models and Rates of Change............ 87 Section P. Functions and Their Graphs................
PART II CHAPTER P Preparation for Calculus Section P. Graphs and Models..................... 8 Section P. Linear Models and Rates of Change............ 87 Section P. Functions and Their Graphs................
Math 180, Final Exam, Spring 2008 Problem 1 Solution. 1. For each of the following limits, determine whether the limit exists and, if so, evaluate it.
 Math 80, Final Eam, Spring 008 Problem Solution. For each of the following limits, determine whether the limit eists and, if so, evaluate it. + (a) lim 0 (b) lim ( ) 3 (c) lim Solution: (a) Upon substituting
Math 80, Final Eam, Spring 008 Problem Solution. For each of the following limits, determine whether the limit eists and, if so, evaluate it. + (a) lim 0 (b) lim ( ) 3 (c) lim Solution: (a) Upon substituting
Applications of Derivatives
 Applications of Derivatives Extrema on an Interval Objective: Understand the definition of extrema of a function on an interval. Understand the definition of relative extrema of a function on an open interval.
Applications of Derivatives Extrema on an Interval Objective: Understand the definition of extrema of a function on an interval. Understand the definition of relative extrema of a function on an open interval.
The concept of limit
 Roberto s Notes on Dierential Calculus Chapter 1: Limits and continuity Section 1 The concept o limit What you need to know already: All basic concepts about unctions. What you can learn here: What limits
Roberto s Notes on Dierential Calculus Chapter 1: Limits and continuity Section 1 The concept o limit What you need to know already: All basic concepts about unctions. What you can learn here: What limits
Lesson 59 Rolle s Theorem and the Mean Value Theorem
 Lesson 59 Rolle s Theorem and the Mean Value Theorem HL Math - Calculus After this lesson, you should be able to: Understand and use Rolle s Theorem Understand and use the Mean Value Theorem 1 Rolle s
Lesson 59 Rolle s Theorem and the Mean Value Theorem HL Math - Calculus After this lesson, you should be able to: Understand and use Rolle s Theorem Understand and use the Mean Value Theorem 1 Rolle s
(b) Find the difference quotient. Interpret your result. 3. Find the average rate of change of ƒ(x) = x 2-3x from
 6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
Higher. Differentiation 28
 Higher Mathematics UNIT OUTCOME Differentiation Contents Differentiation 8 Introduction to Differentiation 8 Finding the Derivative 9 Differentiating with Respect to Other Variables 4 Rates of Change 4
Higher Mathematics UNIT OUTCOME Differentiation Contents Differentiation 8 Introduction to Differentiation 8 Finding the Derivative 9 Differentiating with Respect to Other Variables 4 Rates of Change 4
Technical Calculus I Homework. Instructions
 Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
FIRST- AND SECOND-ORDER IVPS The problem given in (1) is also called an nth-order initial-value problem. For example, Solve: Solve:
 .2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
.2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
4.3 Exercises. local maximum or minimum. The second derivative is. e 1 x 2x 1. f x x 2 e 1 x 1 x 2 e 1 x 2x x 4
 SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Chapter Practice Dicsclaimer: The actual eam is different. On the actual eam ou must show the correct reasoning to receive credit for the question. SHORT ANSWER. Write the word or phrase that best completes
Chapter Practice Dicsclaimer: The actual eam is different. On the actual eam ou must show the correct reasoning to receive credit for the question. SHORT ANSWER. Write the word or phrase that best completes
( x) f = where P and Q are polynomials.
 9.8 Graphing Rational Functions Lets begin with a deinition. Deinition: Rational Function A rational unction is a unction o the orm ( ) ( ) ( ) P where P and Q are polynomials. Q An eample o a simple rational
9.8 Graphing Rational Functions Lets begin with a deinition. Deinition: Rational Function A rational unction is a unction o the orm ( ) ( ) ( ) P where P and Q are polynomials. Q An eample o a simple rational
Limits and Their Properties
 Limits and Their Properties The it of a function is the primar concept that distinguishes calculus from algebra and analtic geometr. The notion of a it is fundamental to the stud of calculus. Thus, it
Limits and Their Properties The it of a function is the primar concept that distinguishes calculus from algebra and analtic geometr. The notion of a it is fundamental to the stud of calculus. Thus, it
2Polynomial and. Rational Functions
 Polnomial and Rational Functions A ballista was used in ancient times as a portable rock-throwing machine. Its primar function was to destro the siege weaponr of opposing forces. Skilled artiller men aimed
Polnomial and Rational Functions A ballista was used in ancient times as a portable rock-throwing machine. Its primar function was to destro the siege weaponr of opposing forces. Skilled artiller men aimed
Introduction Direct Variation Rates of Change Scatter Plots. Introduction. EXAMPLE 1 A Mathematical Model
 APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
APPENDIX B Mathematical Modeling B1 Appendi B Mathematical Modeling B.1 Modeling Data with Linear Functions Introduction Direct Variation Rates of Change Scatter Plots Introduction The primar objective
Exact Differential Equations. The general solution of the equation is f x, y C. If f has continuous second partials, then M y 2 f
 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
Derivatives of Multivariable Functions
 Chapter 10 Derivatives of Multivariable Functions 10.1 Limits Motivating Questions What do we mean b the limit of a function f of two variables at a point (a, b)? What techniques can we use to show that
Chapter 10 Derivatives of Multivariable Functions 10.1 Limits Motivating Questions What do we mean b the limit of a function f of two variables at a point (a, b)? What techniques can we use to show that
Review Exercises. lim 5 x. lim. x x 9 x. lim. 4 x. sin 2. ln cos. x sin x
 MATHEMATICS 0-0-RE Dierential Calculus Martin Huard Winter 08 Review Eercises. Find the ollowing its. (Do not use l Hôpital s Rul. a) b) 0 6 6 g) j) m) sin 0 9 9 h) k) n) cos 0 sin. Find the ollowing its.
MATHEMATICS 0-0-RE Dierential Calculus Martin Huard Winter 08 Review Eercises. Find the ollowing its. (Do not use l Hôpital s Rul. a) b) 0 6 6 g) j) m) sin 0 9 9 h) k) n) cos 0 sin. Find the ollowing its.
and ( x, y) in a domain D R a unique real number denoted x y and b) = x y = {(, ) + 36} that is all points inside and on
 Mat 7 Calculus III Updated on 10/4/07 Dr. Firoz Chapter 14 Partial Derivatives Section 14.1 Functions o Several Variables Deinition: A unction o two variables is a rule that assigns to each ordered pair
Mat 7 Calculus III Updated on 10/4/07 Dr. Firoz Chapter 14 Partial Derivatives Section 14.1 Functions o Several Variables Deinition: A unction o two variables is a rule that assigns to each ordered pair
CHAPTER 1 Limits and Their Properties
 CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
MEAN VALUE THEOREM. Section 3.2 Calculus AP/Dual, Revised /30/2018 1:16 AM 3.2: Mean Value Theorem 1
 MEAN VALUE THEOREM Section 3. Calculus AP/Dual, Revised 017 viet.dang@humbleisd.net 7/30/018 1:16 AM 3.: Mean Value Theorem 1 ACTIVITY A. Draw a curve (x) on a separate sheet o paper within a deined closed
MEAN VALUE THEOREM Section 3. Calculus AP/Dual, Revised 017 viet.dang@humbleisd.net 7/30/018 1:16 AM 3.: Mean Value Theorem 1 ACTIVITY A. Draw a curve (x) on a separate sheet o paper within a deined closed
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Exam. Name. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. For the given epression (), sketch the general shape of the graph of = f(). [Hint: it ma
Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. For the given epression (), sketch the general shape of the graph of = f(). [Hint: it ma
AP Calculus AB/IB Math SL2 Unit 1: Limits and Continuity. Name:
 AP Calculus AB/IB Math SL Unit : Limits and Continuity Name: Block: Date:. A bungee jumper dives from a tower at time t = 0. Her height h (in feet) at time t (in seconds) is given by the graph below. In
AP Calculus AB/IB Math SL Unit : Limits and Continuity Name: Block: Date:. A bungee jumper dives from a tower at time t = 0. Her height h (in feet) at time t (in seconds) is given by the graph below. In
Answer Key-Math 11- Optional Review Homework For Exam 2
 Answer Key-Math - Optional Review Homework For Eam 2. Compute the derivative or each o the ollowing unctions: Please do not simpliy your derivatives here. I simliied some, only in the case that you want
Answer Key-Math - Optional Review Homework For Eam 2. Compute the derivative or each o the ollowing unctions: Please do not simpliy your derivatives here. I simliied some, only in the case that you want
CHAPTER P Preparation for Calculus
 CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
CHAPTER P Preparation for Calculus Section P. Graphs and Models...................... Section P. Linear Models and Rates of Change............ Section P. Functions and Their Graphs................. Section
November 13, 2018 MAT186 Week 8 Justin Ko
 1 Mean Value Theorem Theorem 1 (Mean Value Theorem). Let f be a continuous on [a, b] and differentiable on (a, b). There eists a c (a, b) such that f f(b) f(a) (c) =. b a Eample 1: The Mean Value Theorem
1 Mean Value Theorem Theorem 1 (Mean Value Theorem). Let f be a continuous on [a, b] and differentiable on (a, b). There eists a c (a, b) such that f f(b) f(a) (c) =. b a Eample 1: The Mean Value Theorem
Objectives. By the time the student is finished with this section of the workbook, he/she should be able
 FUNCTIONS Quadratic Functions......8 Absolute Value Functions.....48 Translations o Functions..57 Radical Functions...61 Eponential Functions...7 Logarithmic Functions......8 Cubic Functions......91 Piece-Wise
FUNCTIONS Quadratic Functions......8 Absolute Value Functions.....48 Translations o Functions..57 Radical Functions...61 Eponential Functions...7 Logarithmic Functions......8 Cubic Functions......91 Piece-Wise
Quadratic Functions and Models
 Quadratic Functions and Models What ou should learn Analze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Use quadratic functions
Quadratic Functions and Models What ou should learn Analze graphs of quadratic functions. Write quadratic functions in standard form and use the results to sketch graphs of functions. Use quadratic functions
Applications of Derivatives
 Chapter Applications of Derivatives. Etrema of Functions on Intervals Maimum and Minimum Values of a Function Relative Etrema and Critical Numbers Finding the Etrema on a Closed Interval Maimum and Minimum
Chapter Applications of Derivatives. Etrema of Functions on Intervals Maimum and Minimum Values of a Function Relative Etrema and Critical Numbers Finding the Etrema on a Closed Interval Maimum and Minimum
Additional Topics in Differential Equations
 0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
lim 2 x lim lim sin 3 (9) l)
 MAC FINAL EXAM REVIEW. Find each of the following its if it eists, a) ( 5). (7) b). c). ( 5 ) d). () (/) e) (/) f) (-) sin g) () h) 5 5 5. DNE i) (/) j) (-/) 7 8 k) m) ( ) (9) l) n) sin sin( ) 7 o) DNE
MAC FINAL EXAM REVIEW. Find each of the following its if it eists, a) ( 5). (7) b). c). ( 5 ) d). () (/) e) (/) f) (-) sin g) () h) 5 5 5. DNE i) (/) j) (-/) 7 8 k) m) ( ) (9) l) n) sin sin( ) 7 o) DNE
2.1 Rates of Change and Limits AP Calculus
 . Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
. Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
