arxiv:hep-ph/ v2 7 Mar 2006
|
|
|
- Joshua Chambers
- 6 years ago
- Views:
Transcription
1 Small- QCD effects in forward-jet and Mueller-Navelet jet production C. Marquet Service de physique théorique, CEA/Saclay, 99 Gif-sur-Yvette cede, France URA 36, unité de recherche associée au CNRS C. Royon DAPNIA/Service de physique des particules, CEA/Saclay, 99 Gif-sur-Yvette cede, France and Fermi National Accelerator Laboratory, Batavia, Illinois 65, USA We investigate small QCD effects in forward-jet production in deep inelastic scattering in the kinematic regime where the virtuality of the photon and the transverse momentum of the jet are two hard scales of about the same magnitude. We show that the data from HERA published by the H and ZEUS collaborations are well described by leading-logarithmic BFKL predictions. Parametrizations containing saturation effects epected to be relevant at higher energies also compare well to the present data. We etend our analysis to Mueller-Navelet jets at the LHC and discuss to what etent this observable could test these small effects and help distinguishing between the different descriptions. arxiv:hep-ph/566v 7 Mar 6 I. INTRODUCTION The Regge limit of perturbative QCD comes about when the centre-of-mass energy in a collision is much bigger than the fied hard scales of the problem. In this limit usually called the small regime, parton densities inside the projectiles grow with increasing energy, leading to the growth of the scattering amplitudes. As long as the densities are not too high, this growth is described by the Balitsky-Fadin-Kuraev-Lipatov (BFKL) equation [] that resums the leading logarithms. As the parton density becomes higher and the scattering amplitudes approach the unitarity limit, one enters a regime called saturation [, 3, 4, 5] where the BFKL evolution breaks down and parton densities saturate. In the past years, as colliders started to eplore the small regime, proposals were made to test the relevance of the BFKL equation at the available energies. In this paper we concentrate on two of the proposed measurements: forward jets [6] in deep inelastic scattering (DIS) and Mueller-Navelet jets [7] in hadron-hadron collisions. Forward-jet production is a process in which the virtual photon interacts with the proton and a jet is detected in the forward direction of the proton. The virtuality of the photon and the squared transverse momentum of the jet are hard scales of about the same magnitude. In the case of Mueller-Navelet jets, a proton interacts with another proton or antiproton and a jet is detected in each of the two forward directions; the transverse momenta of the jets are as well hard scales of about the same magnitude. If the total energy in the photon-proton (for forward jets) or proton-proton (for Mueller-Navelet jets) collision is large enough, these processes feature the kinematics corresponding to the Regge limit. The description of forward jets with fied-order perturbative QCD in the Bjorken limit amounts in the following. Large logarithms coming from the strong ordering between the soft proton scale and the hard forward-jet scale are resummed using the Dokshitzer-Gribov-Lipatov-Altarelli-Parisi (DGLAP) evolution equation [8] and the hard crosssection is computed at fied order in the coupling constant. In the small regime, due to the etra ordering between the total energy and the hard scales, other large logarithms arise and should be resummed within the hard cross-section itself. In other words, the inclusion of small effects aims at improving QCD predictions by replacing fied-order hard cross-sections with resummed hard cross-section, using the BFKL equation or, at even higher energies, using resummations that include saturation effects. To study different observables in this small regime, a convenient approach is to formulate the cross-sections in terms of scattering amplitudes for colorless combinations of partons. The simplest of those is the q q dipole, a quarkantiquark pair in the color singlet state; it describes for instance the interaction of a virtual photon. Any colorless gg, q qg,... multiplets can a priori be involved, for instance the gluon-gluon (gg) dipole is what describes gluon emissions. To compute the evolution of those scattering amplitudes with energy, the QCD dipole model [9] has been developed. This formalism constructs the light-cone wavefunction of a q q dipole in the leading logarithmic approimation. As Electronic address: marquet@spht.saclay.cea.fr Electronic address: royon@hep.saclay.cea.fr
2 the energy increases, the original dipole evolves and the wavefunction of this evolved dipole is described as a system of elementary q q dipoles. When this system of dipoles scatters on a target, the scattering amplitude has been shown to obey the BFKL equation. Interestingly enough, the dipole formalism was shown to be also well-suited to include density effects and non-linearities that lead to saturation and unitarization of the scattering amplitudes [, ]. This is why the dipole picture is suitable for investigating the small regime of QCD, it allows to study both BFKL and saturation effects within the same theoretical framework. The formulation of the forward-jet and Mueller-Navelet jet processes in terms of dipole amplitudes has been addressed in []. In both cases the problem is similar to the one of onium-onium scattering: the growth with energy of the total cross-section due to BFKL evolution is damped by saturation effects which arise purely perturbatively. For instance in the large N c limit, that involves multiple Pomeron echanges. In our study, we consider both the BFKL energy regime and saturation effects. We shall implement saturation in a very simple way, using a phenomenological parametrization inspired by the Golec-Biernat and Wüsthoff (GBW) approach [3] which gave a good description of the proton structure functions with a very few parameters. First comparisons of small predictions with forward-jet data from HERA were quite successful: the first sets of data published by the H [4] and ZEUS [5] collaborations are well described by the leading-logarithmic (LL) BFKL predictions [6] and also show compatibility with saturation parametrizations [7, 8]. In both cases, the DGLAP resummation associated accounted for leading logarithms. Very recently, new forward-jet eperimental results have been published [9, ]. They involve a broader range of observables with several differential cross-sections and go to smaller values of than the previous measurements. As QCD at net-to-leading order (NLO) is not sufficient to describe the small data, we shall address the following issues: whether the BFKL-LL predictions keep being in good agreement and whether saturation parametrizations still show compatibility. The first part of the present work is devoted to those questions. In the second part of the paper, we deal with Mueller-Navelet jets. We display BFKL-LL predictions in the LHC energy range for different differential cross-sections. We compare them with saturation predictions obtained from our parametrizations of saturation effects constrained by the forward-jet data. We propose different measurements and discuss their potential for identifying BFKL and saturation behaviors. The paper will be organized as follows. In section II, we compute the forward-jet cross-section in the high-energy regime and epress it in terms of a dipole-dipole cross-section. We compare the BFKL-LL predictions and the saturation parametrization with the new H and ZEUS data for several differential cross-sections. In section II, we compute the Mueller-Navelet jet cross-section and show the BFKL and saturation predictions for LHC energies and for several differential cross-sections. The final section V is devoted to conclusion and outlook. II. FORWARD-JET PRODUCTION Forward-jet production in a lepton-proton collision is represented in Fig. with the different kinematic variables. We denote s the total energy of the lepton-proton collision and Q the virtuality of the intermediate photon that undergoes the hadronic interaction. We shall use the usual kinematic variables of deep inelastic scattering: =Q /(Q +W ) and y=q /(s) where W is the center-of-mass energy of the photon-proton collision. In addition, k T Λ QCD is the jet transverse momentum and J its longitudinal momentum fraction with respect to the proton. In the following, we compute the forward-jet cross-section in the high-energy limit, recall the BFKL predictions and give our formulation of the saturation model. A. Formulation The QCD cross-section for forward-jet production reads {( d (4) σ ddq d J dkt = α em dσ γ p JX T πq d J dkt + dσγ p JX L d J dkt ) ( y)+ dσγ p JX T d J dkt } y, () where dσ γ p JX T,L /d J dkt is the cross-section for forward-jet production in the collision of the transversely (T) or longitudinally (L) polarized virtual photon with the target proton. We now consider the high-energy regime. In an appropriate frame called the dipole frame, the virtual photon undergoes the hadronic interaction via a fluctuation into a dipole. The dipole then interacts with the target proton
3 s W P J f eff Jet ( k T ) Y= log( / ) J l Q γ* FIG. : Production of a forward jet in a proton-lepton collision. The kinematic variables of the problem are displayed. Q is the virtuality of the photon that undergoes the hadronic interaction. s and W are the total energies squared in the leptonproton and photon-proton collisions respectively. k T is the transverse momentum of the forward jet and J is its longitudinal momentum fraction with respect to the incident proton. Y is the rapidity interval between the two hard probes. and one has the following factorization dσ γ p JX T,L d J dk T = d r dz ψ γ dσ q q T,L (r,z;q) d J dkt (r). () The wavefunctions ψ γ T and ψγ L describe the splitting of the photon on the dipole and dσ q q/d J dkt is the cross-section for forward-jet production in the dipole-proton collision. ψ γ T and ψγ L are given by ψ γ T (r,z;q) = α emn c ( ) π e f (z +( z) )z( z)q K z( z)q r (3) f ψ γ L (r,z;q) = α emn c π ( ) e f 4Q z ( z) K z( z)q r f (4) for a transversely (3) and longitudinally (4) polarized photon where e f is the charge of the quark with flavor f. The integration variable r is the transverse size of the q q pair and z is the longitudinal momentum fraction of the antiquark with respect to the photon. In the leading logarithmic approimation we are interested in, the cross-section dσ q q /d J dkt does not depend on z but only on the dipole size r. This cross-section has been computed in [] where it was shown that the emission of the forward jet can be described through the interaction of an effective gluonic (gg) dipole: dσ q q d J dk T (r) = πn c 6kT f eff ( J,kT) d r J (k T r) r ( r ) r σ (q q)(gg)(r, r,y) with Y =log( J /) the rapidity assumed to be very large. σ (q q)(gg) (r, r,y) is the cross-section in the collision of a q q dipole of size r with a gg dipole of size r with total rapidity Y. f eff ( J,kT ) is the effective parton distribution (5) We consider massless quarks and sum over four flavors in (3) and (4). This is justified considering the rather high values of the photon virtuality (Q >5 GeV ) used for the measurement.
4 function and resums the leading logarithms log(kt /Λ QCD ). It has the following epression f eff ( J,k T) = g( J,k T)+ C F N c ( q(j,k T)+ q( J,k T) ), (6) where g (resp. q, q) is the gluon (resp. quark, antiquark) distribution function in the incident proton. Let us comment formula (5). Since the forward jet measurement involves perturbative values of k T and moderate values of J, it is not surprising that formula (5) features the collinear factorization of f eff ; note also that k T has been chosen as the factorization scale. The remaining hard interaction is between a gg dipole and the incident q q dipole of size r. The gg dipole emerges as the effective degree of freedom for the gluon emission at high energies []. This feature has been pointed out several times []. Formulae ()-(6) epress the forward-jet observable () in terms of the cross-section σ (q q)(gg) which contains the high-energy QCD dynamics: the problem is analogous to the one of onium-onium scattering. In the net subsection (II-B), wedeal with the BFKLenergyregimeforwhich the interactionbetween the q q dipoleand gg dipoleis restricted to a Pomeron echange. In that case of course, our formulation is equivalent to the k T factorization approach. In subsection (II-C), we go beyond k T factorization and investigate the saturation regime in which σ (q q)(gg) a priori contains any number of gluon echanges. B. The BFKL energy regime The BFKL q q-gg dipole-dipole cross-section reads (see for instance []) dγ σ(q q)(gg) BFKL (r, r,y) = πα sr ( r/r) γ ( ) iπ γ ( γ) ep αs N c π χ(γ)y (7) with the comple integral running along the imaginary ais from / i to /+i and with the BFKL kernel given by χ(γ) = ψ() ψ( γ) ψ(γ) (8) where ψ(γ) is the logarithmic derivative of the Gamma function. It comes about when the interaction between the q q dipole and the gg dipole is restricted to a two-gluon echange. Summing the leading-logarithmic contributions of ladders with any number of real gluon emissions, one obtains the BFKL Pomeron and the resulting growth of the cross-section with rapidity. Inserting (7) in (5) and (), one obtains dσ γ p JX T,L d J dk T = π N c α s dγ 4kT f eff( J,kT) Q iπ where we have defined the following Mellin-transforms which are given by ( φ γ T (γ) ) φ γ L (γ) = α emn c π φ γ T,L (γ) = q e q ( Q k T ) γ 4 γ Γ(γ) φ γ T,L (γ) ( ) ( γ) Γ( γ) ep αs N c π χ(γ)y d r(r Q ) γ dz ψ γ T,L (r,z;q) () 4 γ γ Γ (+γ)γ ( γ)γ ( ) ( γ) (+γ)( γ). () Γ( γ)γ(+γ)(3 γ) γ( γ) Inserting formula (9) into () gives the forward-jet cross-section in the BFKL energy regime. One can easily show that the result is identical to the one obtained using k T factorization [6, 3]. The only undetermined parameter is ᾱ α s N c /π (with α s the strong coupling constant kept fied) which appears in the eponential in formula (9). (9) C. The saturation regime Contrary to the BFKL case, the onium-onium cross-section in the saturation regime has not yet been computed from QCD. Studies are being carried out to identify the dominant terms in the multiple gluon echanges [, 4,
5 5, 6] but the cross-section σ(q q)(gg) sat remains unknown. To take into account saturation effects, we are led to use a phenomenological parametrization. We consider the following model introduced in [7] which is inspired by the GBW approach: ( ( σ(q q)(gg) sat (r, r,y) = 4πα s σ ep r eff (r, r) )) 4R (Y). () The dipole-dipole effective radius reff (r, r) is defined through the two-gluon echange: 4πα sr eff(r, r) σ BFKL (q q)(gg) (r, r,) = 4πα smin(r, r ) { +log ma(r, r) min(r, r) }. (3) For the saturation radius we use the parametrization R (Y)=e λ (Y Y) /Q with Q GeV. Let us epress the cross-section in terms of a double Mellin-transform: with ( ) dγ dτ r σ(q q)(gg) sat γ ( ) r τ (r, r,y) = 4πα sσ iπ iπ 4R (Y) 4R (Y) g(γ,τ) (4) g(γ,τ) = du dū u γ 4 ū τ ( e r (u,ū)) Γ(γ τ) eff = +τ γ {Ψ(,3+τ γ,τ)+ψ(,3+τ γ, γ)} < Re(τ), Re(γ), Re(γ τ) < (5) where the confluent hypergeometric function of Tricomi Ψ(, a, b) can be epressed [7] in terms of incomplete Gamma functions. Inserting (4) in (5) and (), one obtains dσ γ p JX T,L d J dk T = π N c α sσ dγ 8Q kt R (Y)f eff( J,kT ) iπ (4Q R (Y))γ φ γ dτ T,L (γ) iπ (4k T R (Y)) τ 4τ τ Γ(τ) Γ( τ) g(γ,τ). (6) Inserting formula (6) into () gives our parametrization of the forward-jet cross-section in the saturation regime. The parameters are λ, Y and the normalization σ. D. Fiing the parameters The first sets of data published by the H [4] and ZEUS [5] collaborations regarded the measurement of dσ/d. In previous studies, we fitted the BFKL-LL [6] and saturation parametrization [7] on those data with the cut <. Despite corresponding different energy regimes, in both cases we obtained good descriptions with χ values of about. The obtained values of the parameters and the χ of the fits are given in Table I. fit parameters /R (Y =) χ (/d.o.f.) BFKL-LL 4ᾱ log() =.43 (/3) strong sat. λ =.4 and Y =.8.8 Gev 6.8 (/) weak sat. λ =.37 and Y = 8.3. Gev 8.3 (/) TABLE I: Results of the BFKL and saturation fits to the first HERA forward-jet data. The saturation fits shows two independent solutions showing either strong or weak saturation parameters (see tet). In the BFKL-LL case, the only parameter is ᾱ and the value obtained was 4ᾱlog()=.43. For the saturation fit, the two relevant parameters are λ and Y and the fit showed two χ minima for (λ=.4,y =.8) and (λ=.37,y =8.3).We shall referto the first (resp. second) solution as astrong(resp. weak)saturationparametrization. Indeed, the first saturation minimum corresponds to strong saturation effects as, for typical values of Y, the saturation scale /R is about 5 Gev which is the value of a typical k T. The second saturation minima corresponds to small saturation effects and rather describes BFKL physics. Along with formulae (9) and (6), the values of the parameters given in Table I completely determine the BFKL-LL predictions and two parametrizations for the saturation model. We are now going to compare these with the very recent data without any adjustment of the parameters. This will provide a strong test of those small effects.
6 d σ / d (nb) 8 H DATA BFKL LL weak saturation strong saturation d σ / d (nb) ZEUS DATA BFKL LL weak sat. 6 NLO QCD 5 strong sat. 4 NLO QCD FIG. : The forward-jet cross-section dσ/d. The points are measurement by the H (left plot) and ZEUS (right plot) collaborations. The lines are comparisons with BFKL-LL predictions (full lines) and the two saturation parametrizations (dotted and dashed lines). In both cases, there is good agreement with the data. For comparison, fied-order QCD predictions at NLO are also displayed. E. Comparison to the 5 HERA data d σ / dq (pb/gev ) BFKL-LL weak sat. strong sat. d σ / dk T (pb/gev) ZEUS DATA BFKL LL weak sat. strong sat. - ZEUS DATA Q (GeV ) k T (GeV) FIG. 3: The forward-jet cross-sections dσ/dq (left plot) and dσ/dk T (right plot). The points are measurement by the ZEUS collaboration. The lines are comparisons with BFKL-LL predictions (full lines) and the two saturation parametrizations (dotted and dashed lines). For the two observables, there is good agreement with the data. We want to compare the cross-section() obtained from the BFKL-LL prediction(9) and the saturation parametrization (6) with the new data coming from measurements performed at HERA [9, ]. On one side, our theoretical
7 d σ/d dk T d Q (nb/gev 4 ) - H DATA 5<Q < (GeV ) <Q < (GeV ) <Q <85 (GeV ).5<k T <35. (GeV ) <k T <95. (GeV ) 95.<k T <4. (GeV ) FIG. 4: The forward-jet cross-section dσ/ddq dk T. The points are measurement by the H collaboration. The lines are comparisons with BFKL-LL predictions (full lines) and the two saturation parametrizations (dotted and dashed lines for strong and weak saturation respectively). In the regime where on epects small effects to be important (r k T/Q ), there is a good description of the data. In the regime where r, the small parametrizations do not reproduce the data as epected from the hierarchy of the hard scales. results are for the cross-section () which is differential with respect to all four kinematic variables, Q, J, and k T. On the other side, HERA data concern observables which are less differential: dσ/d, dσ/dq, dσ/dkt, and dσ/ddq dkt. Therefore, on the top of the Mellin integrations in (9) and (6), one has to carry out a number of integrations over the kinematic variables which have to be done taking into account the kinematic cuts applied by the different eperiments. A detailed description of how we performed those integrations in given in Appendi A and the resulting cross-sections that can be compared to the data are given in Appendi B. The method allows for a direct comparison of the data with theoretical predictions but it does not allow to control the overall normalization. In the following studies, we therefore compare only spectra and will not refer to normalizations anymore. As already mentioned, one does not adjust any of the parameters of Table I. Let us start with the observable dσ/d which has been measured by both the H and ZEUS collaborations and which now features lower values of than the first measurements. The comparison is displayed in Fig., the three small parametrizations describe very well the data. One cannot really distinguish between the three curves, ecept at small values of where one starts to see a difference: the BFKL curve is above the weak-saturation curve which is itself above the strong-saturation curve. However the main conclusion is that the data seem to feature the BFKL growth, when going to small values of. For comparison, the fied-order QCD predictions at NLO computed in [9, ]
8 with the DISENT Monte-Carloprogram [8] are reproduced in Fig.. At the lowest values of, they do not reproduce the data as they are about a factor.5 to.5 below depending on the eperiment and the error bars. Even adding a resolved-photon component to the NLO predictions [] does not pull them within the uncertainties, contrary to what happened for the previous data [9]. This is an interesting difference with the forward-pion case [3] for which it seems that no higher-order effect other than a NLO resolved-photon contribution is needed. In Fig.3 are represented the two other single differential cross-sections that we shall briefly discuss: dσ/dq and dσ/dk T measured by the ZEUS collaboration. One can see again that the three small parametrizations agree well with the data, it is a strong result that one is able to describe the Q and k T spectra without any adjustment of the parameters as they were only fitted to describe the dependence. We shall finally compare our predictions with the triple differential cross-section dσ/ddq dkt measured by the H collaboration. The interesting part of this measurement is that it has been carried out in 9 different bins of r kt /Q from.<r<.8 to 9.5<r <8. This allows to test the limits of our parametrizations which are supposed to be valid only when r as they do not take into account any transverse momentum ordering of the gluons emitted in rapidity between the forward jet and the photon. The comparisons with the data are shown on Fig.4 and one sees the epected trend. The bins which have r are well described by the small parametrizations while the others are not: for the latter, we overshoot the data as the BFKL rise towards small values of is too steep. Interestingly enough, the trend is reversed for QCD predictions at NLO: they describe better the data which feature large values of r. These observations favor the need of the BFKL resummation to describe the r data. The large r bins also ehibit a limitation of the saturation model as one can see that the strong saturation parametrization lies above the weak saturation parametrization. Such a behavior indicates that the model should not be used when kt Q. Let us comment further on the two saturation parametrizations. While the BFKL formula (9) is a QCD prediction as it is computed from Feynman diagrams [], the saturation parametrization (6) is a phenomenological model. The fact that it describes well the data does not call for the same conclusions as in the BFKL case. It only ehibits that, as it is the case for a number of observables, data are compatible with saturation effects even at energies which do not require them. In other words, the forward-jet measurement at the present energies cannot distinguish between saturation and BFKL effects; one would start seeing a significant difference at higher energies. It is the purpose of the net section to look for such differences, by studying another process similar to forward-jets, namely Mueller-Navelet jets, at LHC energies. III. TOWARDS THE LHC: MUELLER-NAVELET JETS Mueller-Navelet jet production in a proton-proton collision is represented in Fig.5 with the different kinematic variables. We denote S the total energy of the collision, k and k the transverse momenta of the two forward jets and and their longitudinal fraction of momentum with respect to the protons as indicated on the figure. In the following, we compute the Mueller-Navelet jet cross-section in the high-energy limit, recall the BFKL predictions and formulate our saturation model. We then display predictions for observables which can be measured at the LHC. A. Formulation As in the original paper [7], we consider the cross-section differential with respect to and and integrated over the transverse momenta of the jets with k >Q and k >Q. Q and Q represent then eperimental k T cuts. Considering the high energy limit, the QCD cross-section for Mueller-Navelet jet production reads [, 3]: dσ pp JXJ d d = π N c 64 f eff(,q )f eff(,q ) dr d r Q J (Q r)q J (Q r) σ (gg)(gg) (r, r,y) (7) with Y =log( S/Q Q ) the rapidity assumed to be very large. σ (gg)(gg) (r, r,y) is the cross-section in the collision of two gg dipoles of size r and r with rapidity total Y. As before f eff is the effective parton distribution function (6). Let us comment formula (7). As before, each forward jet involves perturbative values of transverse momenta and moderate values for and. This eplains the collinear factorization of the two functions f eff ; here we have taken the factorization scales to be Q and Q. The remaining hard interaction is between two gg dipoles: as we have seen in the previous section, each of them describes a gluon emission at high energies. Formula (7) epresses the Mueller-Navelet jet observable in terms of the cross-section σ (gg)(gg) which contains the high-energy QCD dynamics. This is the similarity with the forward-jet case: the problem is also analogous to the one of onium-onium scattering.
9 P f eff Jet ( k > Q ) S Y= log( S/Q Q ) P f eff Jet ( k > Q ) FIG. 5: Mueller-Navelet jet production in a proton-proton collision. The kinematic variables of the problem are displayed. S is the total energy squared, k and k are the transverse momenta of the jets and and are their longitudinal momentum fraction with respect to the incident protons. Y is the rapidity interval between the hard probes. Let us first consider the BFKL energy regime, the gg-gg dipole-dipole cross-section reads σ(gg)(gg) BFKL (r, r,y) = πn cα s dγ r ( r/r) γ ( ) C F iπ γ ( γ) ep αs N c π χ(γ)y (8) which combined with (7) gives dσ BFKL = π3 Nc 3α s d d 8C F Q dγ f eff (,Q )f eff(,q ) (Q /Q ) γ iπ γ( γ) ( ) αs N c ep π χ(γ)y. (9) One can easily show that the result is identical to the one obtains using k T factorization [7]. As in the forward-jet case, the only undetermined parameter is ᾱ which appears in the eponential in formula (9). We shall consider in this study the same value that was used for forward jets, that is ᾱ=.6. For the saturation parametrization, we use the following gg-gg dipole-dipole cross-section: σ(gg)(gg) sat (r, r,y) = 4πN cα ( s σ C F ep ( r eff (r, r) )) 4R (Y). () which up to the normalization is the same as (). The effective radius r eff is defined by formula (3) and the saturation radius by R (Y)=e λ (Y Y) /Q with Q GeV. Inserting () into (7), one obtains [3] dσ sat = π3 Nc 3α s σ f eff (,Q d d 6C )f eff (,Q ) { R (Y)Q Q F ) [ ( ep Q +u Q +log(u) R (Y) du +log(u) I +ep ( Q Q ur (Y) ) +log(u) )]}. () ( Q +u Q +log(u) R (Y) In the following we consider only the strong saturation parametrization to display what could be the maimal epected effects at the LHC. The parameters are λ=.4 and Y =.8. The normalization σ is a priori not determined but we have fied it so that at large momenta and small Y, one obtains the BFKL result.
10 dσ/dy dy (µb) - Q > GeV BFKL LL saturation dσ/dy dy (µb) - Q > 5 GeV y y dσ/dy dy (µb) - - Q > 5 GeV dσ/dy dy (µb) Q > 35 GeV y y FIG. 6: The Mueller-Navelet jet cross-section dσ/dy dy as a function of y for different values of Q. The kinematics of the other jet are fied at Q =3 GeV and y = 4.5. The full lines are BFKL-LL predictions and the dashed lines are the saturation parametrization. B. Phenomenology We are going to study the dependence of the cross-sections (9) and () as a function of the different kinematic variables,, Q, and Q. We want to consider large rapidities Y which implies very forward jets and therefore large values of and. The well-known problem is that the cross-section is then damped by the parton distribution functions which at large become very small. This prevents one to see the BFKL enhancement of the hard part of the cross-section with rapidity. A way out of this problem is to consider the following observables R S/ S : / R S/ S dσpp JXJ dσ pp JXJ (Q,Q,S) (Q,Q, d d d d S), () in other words, cross-section ratios for same jet kinematics and two different values of the total energy squared (S and S). The advantage of such observables is that they are independent of the parton densities and allow to study more quantitatively the influence of small effects [6, 7, 3]. For instance the BFKL-LL prediction is (via a saddle point approimation): ( ) 4ᾱlog() R S/ S. (3) S S The eperimental verification of this at the Tevatron[3] was not conclusive. The data were found above the prediction (3), howeverithasbeen argued[33] thatthe measurementwasbiasedbytheuseofupperk T cuts, the choiceofequal lowerk T cuts, and hadronization corrections. The ratios () also display in a clear way the saturation effects [7, 3]
11 sat./bfkl ratio. Q > 35. GeV Q > 5. GeV Q > 5. GeV Q >. GeV y FIG. 7: Ratio of the saturation and BFKL-LL Mueller-Navelet jet cross-sections dσ/dy dy as a function of y for different values of Q. The kinematics of the other jet are fied at Q =7 GeV and y = 3.5. which lead to ratios that, as a function of Q and Q, go from the value (3) to as the momentum cuts decrease into the saturation region (see Fig.4 in Ref. [7] and Fig.3,4 in Ref. [3]). There is however an important eperimental limitation to carry out the measurement (): it would require to run the LHC at two different center-of-mass energies. If it turns out not to be possible, then one should settle for the cross-section dσ/d d. We shall now ehibit some of its characteristics, fiing the LHC center-of-mass energy at S =4 TeV. Also the absolute normalization is fied to reproduce the Tevatron data at S =.8 TeV published in [3]. These data feature somewhat large error bars which leads to a significant uncertainty on the normalization for the LHC predictions. Let us introduce the rapidities of the two jets: y = log ( S Q ), y = log ( ) S. (4) Q We first considered the case where one of the two jets has fied kinematics Q =3 GeV and y = 4.5. We looked at the dependence of the cross-section dσ/dy dy = dσ/d d as a function of the other jet kinematic variables. In Fig.6, we plotted the results for the BFKL-LL prediction (9) and the saturation parametrization () where the different plots feature the y dependence for different values of Q. As epected, the cross-sections decrease quickly as y gets large which corresponds to getting closer to one. For each value of Q, one cannot really see a difference between the behaviors of the BFKL and saturation curves as a function of y. However the relative normalization between the two curves is quite sensitive to the value of Q. This is better ehibited on Fig.7 where one displays the ratio of the saturation and BFKL results of Fig.6. The ratio goes down to about.3 for Q = GeV which represents a significant difference between the BFKL and saturation predictions. Note that this difference does not appear to be that large on Fig.6 where the cross-sections are plotted. The second case we considered is the symmetric case Q Q =Q and y y = y which allows to go to bigger values of Y. We looked at the dependence of the cross-section dσ/dy dy as a function of Q and y. In Fig.8, we plotted the results for the BFKL prediction (9) and the saturation parametrization () where the different plots feature the Q dependence for different values of y. In this case, the cross-section falls even faster when y gets big as both and get close to. Again, because of that, one does not see on the plot the difference between the BFKL and the saturation curves, yet it is still quite big as shown on Fig.9 where we have displayed the ratio of the saturation and BFKL results of Fig.8. For y=5.5 and Q decreasing down to GeV, the ratio goes down to about.4. We did not include in this study the weak saturation parametrization, the corresponding curves would lie in between
12 dσ/dy dy (µb) y =.5 BFKL LL saturation dσ/dy dy (µb) - y = Q 3 4 Q dσ/dy dy (µb) y = 4.5 dσ/dy dy (µb) Q y = Q FIG. 8: The Mueller-Navelet jet cross-section dσ/dy dy as a function of Q Q =Q for different values of y y = y. The full lines are BFKL-LL predictions and the dashed lines are the saturation parametrization. the BFKL and strong saturation curves which are displayed, and even is closer to the BFKL curve. There is a number of other plots one could study showing other dependences of dσ/dy dy but they are not needed for drawing our conclusions: testing BFKL effects and saturation effects with the observable dσ/dy dy at the LHC will be a major eperimental challenge as one will have to measure cross-sections with a great precision. We insist that this is due to the fact that the parton distribution functions at large really damp the cross-section. Obtaining a high accuracy is not unfeasible because of the high luminosity at the LHC but this will require a very good understanding of the systematics errors. However we would like to emphasize the fact that better tests of small effects could be realized with the measurement of the ratio R S/ S, see formula (). IV. CONCLUSIONS Let us summarize the main results of the paper. The first part of the work was devoted to the study of the forwardjet measurement. We started by computing the QCD cross-section for forward-jet production () in the high-energy (small ) limit. We recalled the BFKL-LL predictions (9) and also formulated the phenomenological model (6) that takes into account saturation effects. We then compared the BFKL and saturation-model predictions to the recent data from HERA for a number of observables: dσ/d, dσ/dq, dσ/dk T, and dσ/ddq dk T. We obtained a very good agreement with the BFKL predictions and saturation parametrizations also show compatibility with the data. Along with the fact that QCD at NLO predictions do not reproduce the small data, this observation leads us to the conclusion that the present forward-jet data display the BFKL enhancement when going to small values of. However, to make a definitive statement, one would have to make comparisons with BFKL predictions at net-toleading-logarithmic (NLL) accuracy. The latter are under investigations and will hopefully be available soon. In the mean time, let us discuss the epected qualitative impact of these BFKL-NLL corrections. Because we are describing
13 sat./bfkl ratio.. y =.5 y =.5 y = 3.5 y = 4.5 y = Q FIG. 9: Ratio of the saturation and BFKL-LL Mueller-Navelet jet cross-sections dσ/dy dy as a function of Q Q =Q for different values of y y = y. a kinematic regime in which k T Q, one can infer that they should be small. For instance, the contribution coming from the running of the coupling between those two scales would be unimportant. By comparison, the BKFL- NNL corrections seem to be very large for the proton structure function measurement [34], in which case one easily understands why: the evolution takes place in a large range, from the soft proton scale up to the hard scale Q. The situation is much different for forward jets. In the second part of the paper, we investigated small effects for Mueller-Navelet jets in the LHC energy range, using the parameters that successfully describe forward-jets at HERA. We compared the BFKL-LL predictions (9) with those of the saturation model () and concluded that the measurement of the simple cross-section will require a great precision to test the different scenarios. We argued that a better option to look for small effects was to measure the ratio of cross-sections () which implies running the LHC at two different energies. On longer time scales, the international linear collider would give the opportunity to measure the virtual photonvirtual photon total cross-section at very high energies. This would also offer great possibilities [35, 36] for testing the BFKL enhancement and the saturation regime of QCD. Acknowledgments The authors would like to thank Robi Peschanski for useful comments and fruitful discussions. Appendi A: on the integration method To compare the forward-jet cross-section () obtained from the BFKL-LL prediction (9) and the saturation parametrization (6) with the data for observables which are less differential (dσ/d, dσ/dq, dσ/dkt, and dσ/ddq dkt ), one has to carry out a number of integrations over the kinematic variables. They have to be done while properly taking into account the kinematic cuts applied by the different eperiments. This Appendi deals with these issues. Let us start from the quadruple differential cross-section dσ/ddq d J dkt, see formula (). First one performs the Mellin integrations of (9) and (6). Then we choose the appropriate variables for the remaining integrations: to avoid numerical problems in the integral calculations, we chose variables which lead to the weakest possible dependence of the differential cross-section. We noticed that the best choice is /Q, /kt, log(/ J), and log(/). Since the
14 eperimental measurements are not differential with respect to J, we carry out the integration d (3) σ J d (4) ( ) σ ddq dkt = ddq d J dkt dlog. J With the BFKL-LL formula(9), the convergence is fast enough so that one can perform all the remaining integrations to obtain any of the four observables mentioned above. With the saturation formula (6), because of the etra Mellin integration and the time it takes to compute the functions Ψ, performing all the remaining integrations would require important numerical work. We chose to use another method to obtain the cross-sections in that case. We shall describe it now with the eample of dσ/d. For a given value of, the first step is to compute the differential cross-section dσ BFKL d = Q 4 kt 4 d (3) σ BFKL ddq dk T ( ) ( ) d Q d kt for the BFKL case. The second step is to compute the bin center (ktc, Q C ) defined as follows: d (3) σ BFKL ddq dkt (Q C,k TC ) dσbfkl /d dq dkt The bin center is thus the point in the (k T,Q ) phase space where the differential cross-section in k T and Q is equal to the integral over the bin divided by the bin size (we will specify the integration limits later on). The third step is to obtain the cross section for the saturation case. We compute the cross-section at the bin center (k TC, Q C ): dσ sat d = d(3) σ sat ddq dkt (Q C,k TC ). dq dk T. This procedure is valid if the bin center does not change much between the BFKL and saturated cross-sections. In other words, it means that the difference between the BFKL and saturated cross-sections is small. We saw in Section II-E that this is indeed the case. The method is easily adapted to the case of dσ/dq for which one finds a bin center ( C,kTC ) for each value of Q and to the case of dσ/dkt with a bin center ( C,Q C ) for each value of k T. For the triple differential cross-section dσ/ddq dkt which is measured as a function of, integrating over J is not enough since one does not know the (Q,kT ) bin-center. Instead, for a given value of, one integrates also over Q and kt and then divide the result by the Q and kt bin sizes to obtain dσ/ddq dkt. This is done for the BFKL case and one uses again the method described above to compute the cross-section in the saturation case. The other difficulty arises when setting the integration limits as one has to take into account the correlations between the kinematic variables (for instance y=q /s<) and the cuts applied by the eperiments (for instance cuts on the forward jet phase space). There are two ways to take these into account: either appropriately set the limits of integration while computing the integrals or evaluate later the phase space correction due to the eperimental cuts. We are going to use both, since it is not possible to include all eperimental cuts while computing the integrals. Table II is a list of the different set of cuts used by the H and ZEUS eperiments to carry out their measurements. For the ZEUS cuts, we only consider what they call the forward-bfkl phase space which corresponds the most to the Regge limit kinematics. Refering to this table, let us enumerate the integration limits which are used for the different integral calculations: dσ/d for H: We integrate over /k T with the limit on k T defined by.5<k T /Q <5 (this is an etra cut that H applies to this measurement only), over /Q with Q <s, and over log(/ J ) with.35< J < dσ/d for ZEUS: We integrate over /k T with the limit on k T defined by.5<k T /Q <, over /Q with Q <s, and over log(/ J ) with <log(/ J )< 3 dσ/dq for ZEUS: We integrate over /k T with the limit on k T defined by.5<k T /Q <, over log(/) with Q /s, and over log(/ J ) between and 3 dσ/dk T for ZEUS: We integrate over log(/) with Q /s, over /Q with the limits on Q defined by.5<k T /Q <, and over log(/ J ) between and 3 dσ/ddq dk T for H: The /k T and /Q limits of the integrals are defined by the bin values measured by the H collaboration with also the kinematic constraint.<y = Q /s<.7. The log(/ J ) limits are obtained taking into account the cuts on the forward-jet angle which leads to.7354<log(/ J )<.794.
15 H ZEUS E e GeV E e GeV. y.7.4 y < Q < 85 GeV Q > 5 GeV k T > 3.5 GeV k T > 6 GeV 7 θ J degrees < η J < 3 J >.35.5 < kt/q < TABLE II: ZEUS ( forward-bfkl phase space ) [9] and H [] cuts to define the forward-jet phase space. E e is the energy of the outgoing electron and η J=log(/ J)= logtan(θ J/). The other kinematic variables have been defined in the tet. The effects of the cuts defined in Table II which are not used above need to be computed using a toy Monte Carlo. They are modeled by bin-per-bin correction factors that multiply the cross-sections obtained as described above. This is how one proceeds: we generate flat distributions in the variables /k T, /Q, log(/ J ), and log(/) using reference intervals which include the whole eperimental phase-space (the azimuthal angle of the jet is not used in the generation since all the cross-section measurements are independent of that angle). In practice, we get the correction factors by counting the numbers of events which fullfil the eperimental cuts for each bin when we compute dσ/d, each Q bin when we compute dσ/dq and so on. The correction factors are obtained by the ratio of the number of events which pass the eperimental cuts and the kinematic constraints to the number of events which fullfil only the kinematic constraints, i.e. the so-called reference bin. Of course the eperimental or kinematic cuts which have been applied already while computing the integrals are not applied in this study to avoid double counting effects. This method allows for a direct comparison of the data with theoretical predictions but it does not allow to control the overall normalization. This would require a full Monte-Carlo. Note that we did not use one in order to avoid any strong model dependence of the correction factors as they are only due to kinematic-cut effects. The derivation of the correction factors is independent of the theoretical input. They are given in Appendi B and they can be used to test any model suitable for the forward-jet cross-section, providing the same integration method as described above is used. Appendi B: tables with correction factors and resulting cross-sections In this section, we list the corrections factors that we obtained for the observables dσ/d (H and ZEUS), dσ/dq (ZEUS), dσ/dkt (ZEUS), and dσ/ddq dkt (H). We also give the resulting cross-sections for the different points that we used to draw the curves on Fig., Fig.3, and Fig.4. factor bfkl-ll weak sat. strong sat factor bfkl-ll weak sat. strong sat TABLE III: Correction factors due to eperimental cuts and the resulting corrected cross-sections for dσ/d in nb for BFKL-LL, weak saturation and strong saturation (see Fig.). Left Table: for H cuts, right Table: for ZEUS cuts.
16 Q (GeV ) factor bfkl-ll weak sat. strong sat k T (GeV) factor bfkl-ll weak sat. strong sat TABLE IV: Correction factors due to eperimental cuts and the resulting corrected cross-sections for BFKL-LL, weak saturation and strong saturation. Left Table: for dσ/dq in pb/gev, right Table: for dσ/dk T in pb/gev (see Fig.3). k T (GeV ) Q (GeV ) factor bfkl-ll weak sat. strong sat..5 < kt < 35 5 < Q < < kt < 35 < Q < e- 9.53e- 9.95e e- 5.7e- 5.34e-..65.e-.e-.5e-.5 < kt < 35 < Q < e- 4.7e- 3.97e e- 3.45e- 3.9e e-.63e-.46e e-.8e-.76e e-.7e-.5e e-3 7.9e-3 7.9e e e-3 5.5e-3 TABLE V: Correction factors due to eperimental cuts and the resulting corrected cross-sections for dσ/ddk TdQ in nb/gev 4 (bins with.5<k T <35 GeV ) for BFKL-LL, weak saturation and strong saturation (see Fig.4). [] L. N. Lipatov, Sov. J. Nucl. Phys. 3 (976) 338; E. A. Kuraev, L. N. Lipatov and V. S. Fadin, Sov. Phys. JETP 45 (977) 99; I. I. Balitsky and L. N. Lipatov, Sov. J. Nucl. Phys. 8 (978) 8. [] L. V. Gribov, E. M. Levin and M. G. Ryskin, Phys. Rep. (983). [3] A. H. Mueller and J. Qiu, Nucl. Phys. B68 (986) 47; E. Levin and J. Bartels, Nucl. Phys. B387 (99) 67. [4] L. McLerran and R. Venugopalan, Phys. Rev. D49 (994) 33; ibid., (994) 335; Phys. Rev. D5 (994) 5; A. Kovner, L. McLerran and H. Weigert, Phys. Rev. D5 (995) 63; ibid., (995) 389; R. Venugopalan, Acta Phys. Polon. B3 (999) 373. [5] E. Iancu, A. Leonidov and L. McLerran, Nucl. Phys. A69 () 583; Phys. Lett. B5 () 33; E. Iancu and L. McLerran, Phys. Lett. B5 () 45; E. Ferreiro, E. Iancu, A. Leonidov and L. McLerran, Nucl. Phys. A73 () 489; H. Weigert, Nucl. Phys. A73 () 83. [6] A. H. Mueller, Nucl. Phys. Proc. Suppl. B8C (99) 5; J. Phys. G7 (99) 443. [7] A. H. Mueller and H. Navelet, Nucl. Phys. B8 (987) 77. [8] G. Altarelli and G. Parisi, Nucl. Phys. B6 8C (977) 98; V. N. Gribov and L. N. Lipatov, Sov. Journ. Nucl. Phys. (97) 438 and 675; Yu. L. Dokshitzer, Sov. Phys. JETP. 46 (977) 64. For a review: Yu. L. Dokshitzer, V. A. Khoze, A. H. Mueller and S. I. Troyan Basics of perturbative QCD (Editions Frontières, J.Tran Thanh Van Ed. 99). [9] A. H. Mueller, Nucl. Phys. B45 (994) 373; A. H. Mueller and B. Patel, Nucl. Phys. B45 (994) 47; A. H. Mueller, Nucl. Phys. B437 (995) 7.
17 k T (GeV ) Q (GeV ) factor bfkl-ll weak sat. strong sat. 35 < kt < 95 5 < Q < e- 6.7e- 7.58e- 35 < kt < 95 < Q < e- 7.8e- 8.79e e- 4.5e- 5.4e e-.4e-.68e-...8e-.e-.e- 35 < kt < 95 < Q < e-.44e-.55e e-.8e-.9e-...4e-.38e-.46e e e-3.e e e e e e e e-3 3.4e-3 3.3e-3 TABLE VI: Correction factors due to eperimental cuts and the resulting corrected cross-sections for dσ/ddk TdQ in nb/gev 4 (bins with 35<k T <95 GeV ) for BFKL-LL, weak saturation and strong saturation (see Fig.4). [] I. Balitsky, Nucl. Phys. B463 (996) 99; Y. V. Kovchegov, Phys. Rev. D6 (999) 348; Phys. Rev. D6 () 748. [] E. Iancu and A. H. Mueller, Nucl. Phys. A73 (4) 46; ibid., (4) 494. [] C. Marquet, Nucl. Phys. B75 (5) 39; Nucl. Phys. A755 (5) 63c. [3] K. Golec-Biernat and M. Wüsthoff, Phys. Rev. D59 (999) 47; Phys. Rev. D6 (999) 43. [4] H Collaboration, Phys.Lett. B356 (995) 8; H Collaboration, C. Adloff et al, Nucl. Phys. B538 (999) 3. [5] ZEUS Collaboration, J. Breitweg et al, Eur. Phys. J. C6 (999) 39; ZEUS Collaboration, Phys.Lett. B474 () 3. [6] J. G. Contreras, R. Peschanski and C. Royon, Phys. Rev. D6 () 346; R. Peschanski and C. Royon, Pomeron intercepts at colliders, Workshop on physics at LHC, hep-ph/57. [7] C. Marquet, R. Peschanski and C. Royon, Phys. Lett. B599 (4) 36. [8] C. Marquet, Small- effects in forward-jet production at HERA, hep-ph/578. [9] ZEUS Collaboration, S. Chekanov et al., Forward jet production in deep inelastic ep scattering and low parton dynamics at HERA, hep-e/59. [] H Collaboration, A. Aktas et al., Forward jet production in deep inelastic scattering at HERA, hep-e/5855. [] B. Z. Kopeliovich, A. V. Tarasov and A. Schafer, Phys. Rev. C59 (999) 69; A. Kovner and U. Wiedemann, Phys. Rev. D64 () 4; Y. V. Kovchegov and K. Tuchin, Phys. Rev. D65 () 746. [] H. Navelet and S. Wallon, Nucl. Phys. B5 (998) 37. [3] J. Bartels, A. De Roeck and M. Loewe, Zeit. für Phys. C54 (99) 635; W-K. Tang, Phys. lett. B78 (99) 363; J. Kwiecinski, A. D. Martin, P. J. Sutton, Phys. Rev. D46 (99) 9. [4] E. Iancu and D. N. Triantafyllopoulos, Nucl. Phys. A756 (5) 49; Phys. Lett. B6 (5) 53; J. P. Blaizot, E. Iancu, K. Itakura and D. N. Triantafyllopoulos, Phys. Lett. B65 (5) ; Y. Hatta, E. Iancu, L. McLerran and A. Stasto, Color dipoles from bremsstrahlung in QCD evolution at high energy, hep-ph/5535. [5] A. Kovner and M. Lublinsky, Phys. Rev. D7 (5) 854; JHEP 53 (5) ; Phys. Rev. Lett. 94 (5) 863; Dense - dilute duality at work: Dipoles of the target, hep-ph/5355. [6] A. H. Mueller, A. I. Shoshi and S. M. H. Wong, Nucl. Phys. B75 (5) 44; C. Marquet, A. H. Mueller, A. I. Shoshi and S. M. H. Wong, On the projectile-target duality of the color glass condensate in the dipole picture, hep-ph/559. [7] A. Prudnikov, Y. Brychkov, and O. Marichev, Integrals and Series (Gordon and Breach Science Publishers, 986). [8] S. Catani and M. H. Seymour, Nucl. Phys. B485 (997) 9; erratum-ibid. B5 (997) 53. [9] H. Jung, L. Jönsson and H. Küster, Eur. Phys. J. C9 (999) 383. [3] P. Aurenche, R. Basu, M. Fontannaz and R. M. Godbole, Eur. Phys. J. C34 (4) 77; Eur. Phys. J. C4 (5) 43. [3] C. Marquet and R. Peschanski, Phys. Lett. B587 (4) ; C. Marquet, Strbske Pleso 4, Deep Inelastic Scattering 35, hep-ph/46. [3] D Collaboration, B. Abbott et al, Phys. Rev. Lett. 84 () 57.
PoS(DIS2015)084. Saturation and geometrical scaling from small x deep inelastic ep scattering to high energy proton-proton and heavy ion collisions
 Saturation and geometrical scaling from small x deep inelastic ep scattering to high energy proton-proton and heavy ion collisions M. Smoluchowski Institute of Physics, Jagiellonian University, ul. S.
Saturation and geometrical scaling from small x deep inelastic ep scattering to high energy proton-proton and heavy ion collisions M. Smoluchowski Institute of Physics, Jagiellonian University, ul. S.
On the singular behaviour of structure functions at low x. F Gif-sur-Yvette Cedex, FRANCE ABSTRACT
 On the singular behaviour of structure functions at low by H. Navelet, R. Peschanski, S. Wallon Service de Physique Theorique, CEA-Saclay F-99 Gif-sur-Yvette Cede, FRANCE ABSTRACT We discuss the phenomenological
On the singular behaviour of structure functions at low by H. Navelet, R. Peschanski, S. Wallon Service de Physique Theorique, CEA-Saclay F-99 Gif-sur-Yvette Cede, FRANCE ABSTRACT We discuss the phenomenological
Measurements of Proton Structure at Low Q 2 at HERA
 Measurements of Proton Structure at Low Q 2 at HERA Victor Lendermann Kirchhoff-Institut für Physik, Universität Heidelberg Im Neuenheimer Feld 227, 69120 Heidelberg Germany Abstract. Inclusive ep scattering
Measurements of Proton Structure at Low Q 2 at HERA Victor Lendermann Kirchhoff-Institut für Physik, Universität Heidelberg Im Neuenheimer Feld 227, 69120 Heidelberg Germany Abstract. Inclusive ep scattering
arxiv:hep-ph/ v1 15 Jul 1998
 The DLLA limit of BFKL in the Dipole Picture arxiv:hep-ph/9807389v1 15 Jul 1998 M. B. Gay Ducati and V. P. Gonçalves Instituto de Física, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970
The DLLA limit of BFKL in the Dipole Picture arxiv:hep-ph/9807389v1 15 Jul 1998 M. B. Gay Ducati and V. P. Gonçalves Instituto de Física, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970
Pomeron intercepts at colliders
 Pomeron intercepts at colliders arxiv:hep-ph/000395v 20 Mar 2000 R. Peschanski (SPhT) Ch. Royon (DAPNIA/SPP) Commissariat à l Energie Atomique, Saclay, F-99 Gif-sur-Yvette Cedex France June 5, 208 Abstract
Pomeron intercepts at colliders arxiv:hep-ph/000395v 20 Mar 2000 R. Peschanski (SPhT) Ch. Royon (DAPNIA/SPP) Commissariat à l Energie Atomique, Saclay, F-99 Gif-sur-Yvette Cedex France June 5, 208 Abstract
arxiv: v1 [hep-ph] 28 May 2012
![arxiv: v1 [hep-ph] 28 May 2012 arxiv: v1 [hep-ph] 28 May 2012](/thumbs/92/109864099.jpg) Evidence for the higher twists effects in diffractive DIS at HERA M. Sadzikowski, L. Motyka, W. S lomiński Smoluchowski Institute of Physics, Jagiellonian University, Reymonta 4, 3-59 Kraków, Poland We
Evidence for the higher twists effects in diffractive DIS at HERA M. Sadzikowski, L. Motyka, W. S lomiński Smoluchowski Institute of Physics, Jagiellonian University, Reymonta 4, 3-59 Kraków, Poland We
Matching collinear and small x factorization calculations for inclusive hadron production in pa collisions
 Matching collinear and small x factorization calculations for inclusive hadron production in pa collisions The Pennsylvania State University, Physics Department, University Park, PA 16802 H. Niewodniczański
Matching collinear and small x factorization calculations for inclusive hadron production in pa collisions The Pennsylvania State University, Physics Department, University Park, PA 16802 H. Niewodniczański
arxiv:hep-ph/ v1 22 Dec 1999
 DTP/99/4 DAMTP-999-79 Cavendish-HEP-99/9 BFKL Dynamics at Hadron Colliders arxiv:hep-ph/992469v 22 Dec 999 Carlo Ewerz a,b,, Lynne H. Orr c,2, W. James Stirling d,e,3 and Bryan R. Webber a,f,4 a Cavendish
DTP/99/4 DAMTP-999-79 Cavendish-HEP-99/9 BFKL Dynamics at Hadron Colliders arxiv:hep-ph/992469v 22 Dec 999 Carlo Ewerz a,b,, Lynne H. Orr c,2, W. James Stirling d,e,3 and Bryan R. Webber a,f,4 a Cavendish
Multi-jet production and jet correlations at CMS
 Multi-jet production and jet correlations at Gábor I. Veres on behalf of the Collaboration CERN E-mail: gabor.veres@cern.ch Hadronic jet production at the LHC is an excellent testing ground for QCD. Essential
Multi-jet production and jet correlations at Gábor I. Veres on behalf of the Collaboration CERN E-mail: gabor.veres@cern.ch Hadronic jet production at the LHC is an excellent testing ground for QCD. Essential
Mueller Navelet jets at LHC: a clean test of QCD resummation effects at high energy?
 Mueller Navelet jets at LHC: a clean test of QCD resummation effects at high energy? LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr Lech Szymanowski National
Mueller Navelet jets at LHC: a clean test of QCD resummation effects at high energy? LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr Lech Szymanowski National
arxiv: v1 [hep-ph] 27 Dec 2018
![arxiv: v1 [hep-ph] 27 Dec 2018 arxiv: v1 [hep-ph] 27 Dec 2018](/thumbs/93/111212246.jpg) Rare fluctuations of the S-matrix at NLO in QCD arxiv:8.739v hep-ph] 7 Dec 8 Wenchang Xiang,,, Yanbing Cai,, Mengliang Wang,, and Daicui Zhou 3, Guizhou Key Laboratory in Physics and Related Areas, Guizhou
Rare fluctuations of the S-matrix at NLO in QCD arxiv:8.739v hep-ph] 7 Dec 8 Wenchang Xiang,,, Yanbing Cai,, Mengliang Wang,, and Daicui Zhou 3, Guizhou Key Laboratory in Physics and Related Areas, Guizhou
Resumming large collinear logarithms in the non-linear QCD evolution at high energy
 Resumming large collinear logarithms in the non-linear QCD evolution at high energy Institut de physique théorique, Université Paris Saclay, CNRS, CEA, F-91191 Gif-sur-Yvette, France E-mail: edmond.iancu@cea.fr
Resumming large collinear logarithms in the non-linear QCD evolution at high energy Institut de physique théorique, Université Paris Saclay, CNRS, CEA, F-91191 Gif-sur-Yvette, France E-mail: edmond.iancu@cea.fr
Opportunities with diffraction
 Opportunities with diffraction Krzysztof Golec-Biernat Institute of Nuclear Physics in Kraków IWHSS17, Cortona, 2 5 April 2017 Krzysztof Golec-Biernat Opportunities with diffraction 1 / 29 Plan Diffraction
Opportunities with diffraction Krzysztof Golec-Biernat Institute of Nuclear Physics in Kraków IWHSS17, Cortona, 2 5 April 2017 Krzysztof Golec-Biernat Opportunities with diffraction 1 / 29 Plan Diffraction
Jet Photoproduction at THERA
 DESY 0 03 ISSN 048 9833 hep ph/00309 March 200 Jet Photoproduction at THERA arxiv:hep-ph/00309v 9 Mar 200 M. Klasen II. Institut für Theoretische Physik, Universität Hamburg, Luruper Chaussee 49, 2276
DESY 0 03 ISSN 048 9833 hep ph/00309 March 200 Jet Photoproduction at THERA arxiv:hep-ph/00309v 9 Mar 200 M. Klasen II. Institut für Theoretische Physik, Universität Hamburg, Luruper Chaussee 49, 2276
Mueller-Navelet jets at LHC: an observable to reveal high energy resummation effects?
 Mueller-Navelet jets at LHC: an observable to reveal high energy resummation effects? LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr Lech Szymanowski National
Mueller-Navelet jets at LHC: an observable to reveal high energy resummation effects? LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr Lech Szymanowski National
Institut fur Theoretische Teilchenphysik, Universitat Karlsruhe, D Karlsruhe, Germany
 University of Wisconsin - Madison TTP96-24 MADPH-96-946 QCD Corrections to Jet Cross Sections in DIS June 1996 Erwin Mirkes a and Dieter Zeppenfeld b a Institut fur Theoretische Teilchenphysik, Universitat
University of Wisconsin - Madison TTP96-24 MADPH-96-946 QCD Corrections to Jet Cross Sections in DIS June 1996 Erwin Mirkes a and Dieter Zeppenfeld b a Institut fur Theoretische Teilchenphysik, Universitat
Introduction to Saturation Physics
 Introduction to Saturation Physics Introduction to Saturation Physics April 4th, 2016 1 / 32 Bibliography F. Gelis, E. Iancu, J. Jalilian-Marian and R. Venugopalan, Ann. Rev. Nucl. Part. Sci. 60, 463 (2010)
Introduction to Saturation Physics Introduction to Saturation Physics April 4th, 2016 1 / 32 Bibliography F. Gelis, E. Iancu, J. Jalilian-Marian and R. Venugopalan, Ann. Rev. Nucl. Part. Sci. 60, 463 (2010)
arxiv:hep-ph/ v1 2 Oct 2001
 DESY 01-136 LUNFD6/(NFFL 7203) 2001 October 2001 Heavy Quark production at the TEVATRON and HERA using k t - factorization with CCFM evolution arxiv:hep-ph/0110034v1 2 Oct 2001 H. Jung Physics Department,
DESY 01-136 LUNFD6/(NFFL 7203) 2001 October 2001 Heavy Quark production at the TEVATRON and HERA using k t - factorization with CCFM evolution arxiv:hep-ph/0110034v1 2 Oct 2001 H. Jung Physics Department,
Constraining the pomeron structure using LHC data
 CEA Saclay - Irfu/SPP E-mail: matthias.saimpert@cea.fr Cyrille Marquet Centre de physique théorique, École Polytechnique, CNRS, 9118 Palaiseau, France E-mail: cyrille.marquet@cern.ch Christophe Royon CEA
CEA Saclay - Irfu/SPP E-mail: matthias.saimpert@cea.fr Cyrille Marquet Centre de physique théorique, École Polytechnique, CNRS, 9118 Palaiseau, France E-mail: cyrille.marquet@cern.ch Christophe Royon CEA
Proton Structure Function Measurements from HERA
 Proton Structure Function Measurements from HERA Jörg Gayler DESY, Notkestrasse 85, 2263 Hamburg, Germany E-mail: gayler@mail.desy.de Abstract. Measurements of proton structure functions made in neutral
Proton Structure Function Measurements from HERA Jörg Gayler DESY, Notkestrasse 85, 2263 Hamburg, Germany E-mail: gayler@mail.desy.de Abstract. Measurements of proton structure functions made in neutral
Calculation of the Gluon Distribution Function Using Alternative Method for the Proton Structure Function
 Commun. Theor. Phys. (Beijing, China 40 (2003 pp. 551 557 c International Academic Publishers Vol. 40, No. 5, November 15, 2003 Calculation of the Gluon Distribution Function Using Alternative Method for
Commun. Theor. Phys. (Beijing, China 40 (2003 pp. 551 557 c International Academic Publishers Vol. 40, No. 5, November 15, 2003 Calculation of the Gluon Distribution Function Using Alternative Method for
arxiv:hep-ph/ v1 31 Aug 1999
 The AGL Equation from the Dipole Picture arxiv:hep-ph/9908528v1 31 Aug 1999 M. B. Gay Ducati and V. P. Gonçalves Instituto de Física, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970 Porto
The AGL Equation from the Dipole Picture arxiv:hep-ph/9908528v1 31 Aug 1999 M. B. Gay Ducati and V. P. Gonçalves Instituto de Física, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970 Porto
arxiv:hep-ph/ v4 24 Feb 1999
 NUC-MN-99/-T TPI-MINN-99/5 Small x F Structure Function of a Nucleus Including Multiple Pomeron Exchanges arxiv:hep-ph/998v4 4 Feb 999 Yuri V. Kovchegov School of Physics and stronomy, University of Minnesota,
NUC-MN-99/-T TPI-MINN-99/5 Small x F Structure Function of a Nucleus Including Multiple Pomeron Exchanges arxiv:hep-ph/998v4 4 Feb 999 Yuri V. Kovchegov School of Physics and stronomy, University of Minnesota,
Azimuthal angle decorrelation of Mueller Navelet jets at NLO
 Azimuthal angle decorrelation of Mueller Navelet jets at NLO Physics Department, Theory Division, CERN, CH- Geneva 3, Switzerland E-mail: Agustin.Sabio.Vera@cern.ch F. Schwennsen II. Institut für Theoretische
Azimuthal angle decorrelation of Mueller Navelet jets at NLO Physics Department, Theory Division, CERN, CH- Geneva 3, Switzerland E-mail: Agustin.Sabio.Vera@cern.ch F. Schwennsen II. Institut für Theoretische
On the Projectile-Target Duality of the Color Glass Condensate in the Dipole Picture. Abstract
 CU-TP-1129 On the Projectile-Target Duality of the Color Glass Condensate in the Dipole Picture C. Marquet 1 a, A.H. Mueller 2 b, A.I. Shoshi 2 c, S.M.H. Wong 2 d 1 Service de Physique Théorique, CEA/Saclay,
CU-TP-1129 On the Projectile-Target Duality of the Color Glass Condensate in the Dipole Picture C. Marquet 1 a, A.H. Mueller 2 b, A.I. Shoshi 2 c, S.M.H. Wong 2 d 1 Service de Physique Théorique, CEA/Saclay,
Analytical properties of NLL-BK equation
 Guillaume Beuf Brookhaven National Laboratory Institute for Nuclear Theory, Seattle, September 28, 2010 Outline 1 Introduction 2 Traveling wave solutions of BK with fixed coupling 3 Asymptotic behavior
Guillaume Beuf Brookhaven National Laboratory Institute for Nuclear Theory, Seattle, September 28, 2010 Outline 1 Introduction 2 Traveling wave solutions of BK with fixed coupling 3 Asymptotic behavior
arxiv: v2 [hep-ph] 18 Feb 2009
![arxiv: v2 [hep-ph] 18 Feb 2009 arxiv: v2 [hep-ph] 18 Feb 2009](/thumbs/72/67476418.jpg) Quantum chromodynamics at high energy and statistical physics S. Munier arxiv:0901.2823v2 [hep-ph] 18 Feb 2009 Centre de physique théorique, École Polytechnique, CNRS, Palaiseau, France Abstract When hadrons
Quantum chromodynamics at high energy and statistical physics S. Munier arxiv:0901.2823v2 [hep-ph] 18 Feb 2009 Centre de physique théorique, École Polytechnique, CNRS, Palaiseau, France Abstract When hadrons
QCD saturation predictions in momentum space: heavy quarks at HERA
 QCD saturation predictions in momentum space: heavy quarks at HERA J. T. S. Amaral, E. A. F. Basso and M. B. Gay Ducati thiago.amaral@ufrgs.br, andre.basso@if.ufrgs.br, beatriz.gay@ufrgs.br High Energy
QCD saturation predictions in momentum space: heavy quarks at HERA J. T. S. Amaral, E. A. F. Basso and M. B. Gay Ducati thiago.amaral@ufrgs.br, andre.basso@if.ufrgs.br, beatriz.gay@ufrgs.br High Energy
arxiv: v1 [hep-ph] 7 Jul 2015
![arxiv: v1 [hep-ph] 7 Jul 2015 arxiv: v1 [hep-ph] 7 Jul 2015](/thumbs/72/67518689.jpg) arxiv:1507.01916v1 [hep-ph] 7 Jul 2015 Department of Physics and Astronomy, Iowa State University, Ames, Iowa, 50011, USA E-mail: tuchin@iastate.edu An essential part of experimental program at the future
arxiv:1507.01916v1 [hep-ph] 7 Jul 2015 Department of Physics and Astronomy, Iowa State University, Ames, Iowa, 50011, USA E-mail: tuchin@iastate.edu An essential part of experimental program at the future
Diffusive scaling and the high energy limit of DDIS
 RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, NY 11973, USA E-mail: hatta@quark.phy.bnl.gov After reviewing the recent developments on the high energy evolution equation beyond the
RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, NY 11973, USA E-mail: hatta@quark.phy.bnl.gov After reviewing the recent developments on the high energy evolution equation beyond the
Mueller-Navelet jets at LHC: the first complete NLL BFKL study
 Mueller-Navelet jets at LHC: the first complete NLL BFKL study B. Ducloué LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr L. Szymanowski National Center for Nuclear
Mueller-Navelet jets at LHC: the first complete NLL BFKL study B. Ducloué LPT, Université Paris-Sud, CNRS, 945, Orsay, France E-mail: Bertrand.Ducloue@th.u-psud.fr L. Szymanowski National Center for Nuclear
arxiv: v3 [hep-ph] 29 Sep 2017
![arxiv: v3 [hep-ph] 29 Sep 2017 arxiv: v3 [hep-ph] 29 Sep 2017](/thumbs/93/113489687.jpg) arxiv:79.28v3 [hep-ph] 29 Sep 27 Inclusive charged light di-hadron production at 7 and 3 TeV LHC in the full NLA BFKL approach F.G. Celiberto,2, D.u. Ivanov 3,4, B. Murdaca 2 and A. Papa,2 Dipartimento
arxiv:79.28v3 [hep-ph] 29 Sep 27 Inclusive charged light di-hadron production at 7 and 3 TeV LHC in the full NLA BFKL approach F.G. Celiberto,2, D.u. Ivanov 3,4, B. Murdaca 2 and A. Papa,2 Dipartimento
PoS(DIS 2010)071. Diffractive electroproduction of ρ and φ mesons at H1. Xavier Janssen Universiteit Antwerpen
 Diffractive electroproduction of ρ and φ mesons at Universiteit Antwerpen E-mail: xavier.janssen@ua.ac.be Diffractive electroproduction of ρ and φ mesons is measured at HERA with the detector in the elastic
Diffractive electroproduction of ρ and φ mesons at Universiteit Antwerpen E-mail: xavier.janssen@ua.ac.be Diffractive electroproduction of ρ and φ mesons is measured at HERA with the detector in the elastic
PICTURE OF BFKL DYNAMICS a. Ch. ROYON. DAPNIA-SPP, Centre d'etudes de Saclay, F Gif-sur-Yvette Cedex, France
 PROTON STRUCTURE FUNCTIONS IN THE DIPOLE PICTURE OF BFKL DYNAMICS a Ch. ROYON DAPNIA-SPP, Centre d'etudes de Saclay, F-9 9 Gif-sur-Yvette Cedex, France The F, F G, R = F L =F T proton structure functions
PROTON STRUCTURE FUNCTIONS IN THE DIPOLE PICTURE OF BFKL DYNAMICS a Ch. ROYON DAPNIA-SPP, Centre d'etudes de Saclay, F-9 9 Gif-sur-Yvette Cedex, France The F, F G, R = F L =F T proton structure functions
arxiv: v1 [nucl-ex] 7 Nov 2009
![arxiv: v1 [nucl-ex] 7 Nov 2009 arxiv: v1 [nucl-ex] 7 Nov 2009](/thumbs/81/84737718.jpg) Low-x QCD at the LHC with the ALICE detector Magdalena Malek for the ALICE Collaboration arxiv:0911.1458v1 [nucl-ex] 7 Nov 2009 Institut de Physique Nucléaire d Orsay (IPNO) - France CNRS: UMR8608 - IN2P3
Low-x QCD at the LHC with the ALICE detector Magdalena Malek for the ALICE Collaboration arxiv:0911.1458v1 [nucl-ex] 7 Nov 2009 Institut de Physique Nucléaire d Orsay (IPNO) - France CNRS: UMR8608 - IN2P3
Initial-state splitting
 QCD lecture (p. 14) 1st order analysis For initial state splitting, hard process occurs after splitting, and momentum entering hard process is modified: p zp. σ g+h (p) σ h (zp) α sc F π dz dkt 1 z kt
QCD lecture (p. 14) 1st order analysis For initial state splitting, hard process occurs after splitting, and momentum entering hard process is modified: p zp. σ g+h (p) σ h (zp) α sc F π dz dkt 1 z kt
Color dipoles: from HERA to EIC
 Université de Moncton INT workshop: Gluons and the quark sea at high energies,distributions, polarisation, tomography September 29, 2010 based on work done with J. R. Forshaw, G.Shaw and B. E. Cox (Manchester
Université de Moncton INT workshop: Gluons and the quark sea at high energies,distributions, polarisation, tomography September 29, 2010 based on work done with J. R. Forshaw, G.Shaw and B. E. Cox (Manchester
arxiv:hep-ph/ v2 22 Oct 2001
 DESY 01-136 LUNFD6/(NFFL 7203) 2001 hep-ph/0110034 October 2001 arxiv:hep-ph/0110034v2 22 Oct 2001 Heavy Quark production at the TEVATRON and HERA using k t - factorization with CCFM evolution H. Jung
DESY 01-136 LUNFD6/(NFFL 7203) 2001 hep-ph/0110034 October 2001 arxiv:hep-ph/0110034v2 22 Oct 2001 Heavy Quark production at the TEVATRON and HERA using k t - factorization with CCFM evolution H. Jung
arxiv: v2 [hep-ph] 19 Feb 2016
![arxiv: v2 [hep-ph] 19 Feb 2016 arxiv: v2 [hep-ph] 19 Feb 2016](/thumbs/94/118270241.jpg) TWIST EXPANSION OF FORWARD DRE YAN PROCESS Tomasz Stebel, eszek Motyka, Mariusz Sadzikowski arxiv:1602.01762v2 [hep-ph] 19 Feb 2016 The Marian Smoluchowski Institute of Physics, Jagiellonian University
TWIST EXPANSION OF FORWARD DRE YAN PROCESS Tomasz Stebel, eszek Motyka, Mariusz Sadzikowski arxiv:1602.01762v2 [hep-ph] 19 Feb 2016 The Marian Smoluchowski Institute of Physics, Jagiellonian University
arxiv: v3 [hep-ph] 14 Apr 2016
![arxiv: v3 [hep-ph] 14 Apr 2016 arxiv: v3 [hep-ph] 14 Apr 2016](/thumbs/93/111501447.jpg) Prompt photon production in double-pomeron-exchange events at the LHC A.K. Kohara 1, 2, and C. Marquet 1, 1 Centre de Physique Théorique, École Polytechnique, CNRS, Université Paris-Saclay, F-91128 Palaiseau,
Prompt photon production in double-pomeron-exchange events at the LHC A.K. Kohara 1, 2, and C. Marquet 1, 1 Centre de Physique Théorique, École Polytechnique, CNRS, Université Paris-Saclay, F-91128 Palaiseau,
High Energy Physics. Lecture 9. Deep Inelastic Scattering Scaling Violation. HEP Lecture 9 1
 High Energy Physics Lecture 9 Deep Inelastic Scattering Scaling Violation HEP Lecture 9 1 Deep Inelastic Scattering: The reaction equation of DIS is written e+ p e+ X where X is a system of outgoing hadrons
High Energy Physics Lecture 9 Deep Inelastic Scattering Scaling Violation HEP Lecture 9 1 Deep Inelastic Scattering: The reaction equation of DIS is written e+ p e+ X where X is a system of outgoing hadrons
Measurements of charm and beauty proton structure functions F2 c c and F2 b b at HERA
 Measurements of charm and beauty proton structure functions F c c and F b b at HERA Vladimir Chekelian MPI for Physics, Germany E-mail: shekeln@mail.desy.de Inclusive charm and beauty production is studied
Measurements of charm and beauty proton structure functions F c c and F b b at HERA Vladimir Chekelian MPI for Physics, Germany E-mail: shekeln@mail.desy.de Inclusive charm and beauty production is studied
arxiv:hep-ph/ v1 23 Apr 2002
 DESY 01-116 LUNFD6/(NFFL 70) 001 hep-ph/0069 arxiv:hep-ph/0069v1 3 Apr 00 Massive c cg - Calculation in Diffractive DIS and Diffractive D - Production at HERA J. Bartels 1, H. Jung, A. Kyrieleis 1 1 II.
DESY 01-116 LUNFD6/(NFFL 70) 001 hep-ph/0069 arxiv:hep-ph/0069v1 3 Apr 00 Massive c cg - Calculation in Diffractive DIS and Diffractive D - Production at HERA J. Bartels 1, H. Jung, A. Kyrieleis 1 1 II.
PoS(DIS2014)064. Forward-Central Jet Correlations. Pedro Miguel RIBEIRO CIPRIANO, on behalf of CMS. DESY - CMS
 DESY - CMS E-mail: pedro.cipriano@desy.de The azimuthal correlation between forward and central jets has been measured in proton proton collisions at the LHC, at the centre-of-mass energy of 7 TeV. The
DESY - CMS E-mail: pedro.cipriano@desy.de The azimuthal correlation between forward and central jets has been measured in proton proton collisions at the LHC, at the centre-of-mass energy of 7 TeV. The
arxiv:hep-ph/ v1 13 Nov 2003
 Unintegrated parton distributions and particle production in hadronic collisions arxiv:hep-ph/0311175v1 13 Nov 2003 Antoni Szczurek Institute of Nuclear Physics PL-31-342 Cracow, Poland Rzeszów University
Unintegrated parton distributions and particle production in hadronic collisions arxiv:hep-ph/0311175v1 13 Nov 2003 Antoni Szczurek Institute of Nuclear Physics PL-31-342 Cracow, Poland Rzeszów University
PoS(LHC07)034. Dijet correlations in pp collisions at RHIC
 Institute of Nuclear Physics, PL-31-342 Cracow, Poland and University of Rzeszów, PL-35-959 Rzeszów, Poland E-mail: Antoni.Szczurek@ifj.edu.pl Anna Rybarska Institute of Nuclear Physics, PL-31-342 Cracow,
Institute of Nuclear Physics, PL-31-342 Cracow, Poland and University of Rzeszów, PL-35-959 Rzeszów, Poland E-mail: Antoni.Szczurek@ifj.edu.pl Anna Rybarska Institute of Nuclear Physics, PL-31-342 Cracow,
Di-hadron Angular Correlations as a Probe of Saturation Dynamics
 Di-hadron Angular Correlations as a Probe of Saturation Dynamics Jamal Jalilian-Marian Baruch College Hard Probes 2012, Cagliari, Italy Many-body dynamics of universal gluonic matter How does this happen?
Di-hadron Angular Correlations as a Probe of Saturation Dynamics Jamal Jalilian-Marian Baruch College Hard Probes 2012, Cagliari, Italy Many-body dynamics of universal gluonic matter How does this happen?
arxiv:hep-ph/ v2 13 Jan 2006
 Infrared instability from nonlinear QCD evolution R. Enberg Theoretical Physics Group, Lawrence Bereley National Laboratory, Bereley, CA 94720, USA R. Peschansi Service de Physique Théorique, CEA/Saclay,
Infrared instability from nonlinear QCD evolution R. Enberg Theoretical Physics Group, Lawrence Bereley National Laboratory, Bereley, CA 94720, USA R. Peschansi Service de Physique Théorique, CEA/Saclay,
PoS(Photon 2013)004. Proton structure and PDFs at HERA. Vladimir Chekelian MPI for Physics, Munich
 MPI for Physics, Munich E-mail: shekeln@mail.desy.de The neutral and charged current deep-inelastic ep scattering cross sections are measured in the H and ZEUS eperiments at HERA (99-7), with an electron
MPI for Physics, Munich E-mail: shekeln@mail.desy.de The neutral and charged current deep-inelastic ep scattering cross sections are measured in the H and ZEUS eperiments at HERA (99-7), with an electron
The growth with energy of vector meson photo-production cross-sections and low x evolution
 The growth with energy of vector meson photo-production cross-sections and low x evolution Departamento de Actuaria, Física y Matemáticas, Universidad de las Américas Puebla, Santa Catarina Martir, 78,
The growth with energy of vector meson photo-production cross-sections and low x evolution Departamento de Actuaria, Física y Matemáticas, Universidad de las Américas Puebla, Santa Catarina Martir, 78,
Improving the kinematics in BK/BFKL to resum the dominant part of higher orders
 Improving the kinematics in BK/BFKL to resum the dominant part of higher orders Guillaume Beuf Brookhaven National Laboratory QCD Evolution Workshop: from collinear to non collinear case Jefferson Lab,
Improving the kinematics in BK/BFKL to resum the dominant part of higher orders Guillaume Beuf Brookhaven National Laboratory QCD Evolution Workshop: from collinear to non collinear case Jefferson Lab,
Jets and Diffraction Results from HERA
 Jets and Diffraction Results from HERA A. Buniatyan DESY, Notkestrasse 5, 7 Hamburg, Germany for the H and ZEUS Collaborations he latest results on precision measurements of jet and diffractive cross sections
Jets and Diffraction Results from HERA A. Buniatyan DESY, Notkestrasse 5, 7 Hamburg, Germany for the H and ZEUS Collaborations he latest results on precision measurements of jet and diffractive cross sections
Lecture 3 Cross Section Measurements. Ingredients to a Cross Section
 Lecture 3 Cross Section Measurements Ingredients to a Cross Section Prerequisites and Reminders... Natural Units Four-Vector Kinematics Lorentz Transformation Lorentz Boost Lorentz Invariance Rapidity
Lecture 3 Cross Section Measurements Ingredients to a Cross Section Prerequisites and Reminders... Natural Units Four-Vector Kinematics Lorentz Transformation Lorentz Boost Lorentz Invariance Rapidity
Gluon density and gluon saturation
 Gluon density and gluon saturation Narodowe Centrum Nauki Krzysztof Kutak Supported by NCN with Sonata BIS grant Based on: Small-x dynamics in forward-central dijet decorrelations at the LHC A. van Hameren,
Gluon density and gluon saturation Narodowe Centrum Nauki Krzysztof Kutak Supported by NCN with Sonata BIS grant Based on: Small-x dynamics in forward-central dijet decorrelations at the LHC A. van Hameren,
QCD at hadron colliders Lecture 3: Parton Distribution Functions
 QCD at hadron colliders Lecture : Parton Distribution Functions Gavin Salam CERN, Princeton & LPTHE/CNRS (Paris) Maria Laach Herbtschule für Hochenenergiephysik September, Germany QCD lecture (p. ) PDF
QCD at hadron colliders Lecture : Parton Distribution Functions Gavin Salam CERN, Princeton & LPTHE/CNRS (Paris) Maria Laach Herbtschule für Hochenenergiephysik September, Germany QCD lecture (p. ) PDF
Measurement of Charged Particle Spectra in Deep-Inelastic ep Scattering at HERA
 Measurement of Charged Particle Spectra in Deep-Inelastic ep Scattering at HERA Alexander BYLINKIN ( Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia) E-mail: alexander.bylinkin@gmail.com
Measurement of Charged Particle Spectra in Deep-Inelastic ep Scattering at HERA Alexander BYLINKIN ( Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia) E-mail: alexander.bylinkin@gmail.com
DIFFRACTIVE DIJET PHOTOPRODUCTION AND THE OFF-DIAGONAL GLUON DISTRIBUTION a
 DIFFRACTIVE DIJET PHOTOPRODUCTION AND THE OFF-DIAGONAL GLUON DISTRIBUTION a K. GOLEC BIERNAT,,J.KWIECIŃSKI, A.D.MARTIN Department of Physics, University of Durham, Durham DH LE, England H. Niewodniczański
DIFFRACTIVE DIJET PHOTOPRODUCTION AND THE OFF-DIAGONAL GLUON DISTRIBUTION a K. GOLEC BIERNAT,,J.KWIECIŃSKI, A.D.MARTIN Department of Physics, University of Durham, Durham DH LE, England H. Niewodniczański
Seeking the Shadowing in ea Processes. M. B. Gay Ducati. V. P. Gonçalves
 Seeking the Shadowing in ea Processes M. B. Gay Ducati and V. P. Gonçalves InstitutodeFísica, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970 Porto Alegre, RS, BRAZIL Abstract: We consider
Seeking the Shadowing in ea Processes M. B. Gay Ducati and V. P. Gonçalves InstitutodeFísica, Univ. Federal do Rio Grande do Sul Caixa Postal 15051, 91501-970 Porto Alegre, RS, BRAZIL Abstract: We consider
PoS(DIFF2006)005. Inclusive diffraction in DIS H1 Results. Paul Laycock
 University of Liverpool Oliver Lodge Laboratory, Department of Physics, Oxford St. Liverpool L69 7ZE, United Kingdom E-mail: laycock@mail.desy.de Results are presented of three analyses on the diffractive
University of Liverpool Oliver Lodge Laboratory, Department of Physics, Oxford St. Liverpool L69 7ZE, United Kingdom E-mail: laycock@mail.desy.de Results are presented of three analyses on the diffractive
Kinematical correlations: from RHIC to LHC
 : from RHIC to LHC Institute of Nuclear Physics, PL-31-342 Cracow, Poland and Univeristy of Rzeszów, PL-35-959 Cracow, Poland E-mail: Antoni.Szczurek@ifj.edu.pl Kinematical correlations between outgoing
: from RHIC to LHC Institute of Nuclear Physics, PL-31-342 Cracow, Poland and Univeristy of Rzeszów, PL-35-959 Cracow, Poland E-mail: Antoni.Szczurek@ifj.edu.pl Kinematical correlations between outgoing
Opportunities in low x physics at a future Electron-Ion Collider (EIC) facility
 1 Opportunities in low x physics at a future Electron-Ion Collider (EIC) facility Motivation Quantum Chromo Dynamics Proton=uud Visible Universe Galaxies, stars, people, Silent Partners: Protons & Neutrons
1 Opportunities in low x physics at a future Electron-Ion Collider (EIC) facility Motivation Quantum Chromo Dynamics Proton=uud Visible Universe Galaxies, stars, people, Silent Partners: Protons & Neutrons
New Unified Evolution Equation
 CHINESE JOURNAL OF PHYSICS VOL. 38, NO. 4 AUGUST 000 New Unified Evolution Equation Jyh-Liong Lim 1 and Hsiang-nan Li 1 Department of Electrophysics, National Chiao-Tung University, Hsinchu, Taiwan 300,
CHINESE JOURNAL OF PHYSICS VOL. 38, NO. 4 AUGUST 000 New Unified Evolution Equation Jyh-Liong Lim 1 and Hsiang-nan Li 1 Department of Electrophysics, National Chiao-Tung University, Hsinchu, Taiwan 300,
Coherent and incoherent diffractive hadron production in pa collisions and gluon saturation
 Physics and Astronomy Publications Physics and Astronomy 009 Coherent and incoherent diffractive hadron production in pa collisions and gluon saturation Kirill Tuchin Iowa State University, tuchin@iastate.edu
Physics and Astronomy Publications Physics and Astronomy 009 Coherent and incoherent diffractive hadron production in pa collisions and gluon saturation Kirill Tuchin Iowa State University, tuchin@iastate.edu
arxiv:hep-ex/ v1 14 Sep 1999
 ANL-HEP-CP-99-99 September, 1999 Short-Range and Long-Range Correlations in DIS at HERA 1 arxiv:hep-ex/99926v1 14 Sep 1999 S.V. Chekanov Argonne National Laboratory, 97 S.Cass Avenue, Argonne, IL 6439
ANL-HEP-CP-99-99 September, 1999 Short-Range and Long-Range Correlations in DIS at HERA 1 arxiv:hep-ex/99926v1 14 Sep 1999 S.V. Chekanov Argonne National Laboratory, 97 S.Cass Avenue, Argonne, IL 6439
QCD Measurements at HERA
 QCD Measurements at HERA Armen Bunyatyan, Max-Planck-Institut für Kernphysik, Heidelberg, Germany Yerevan Physics Institute, Armenia November, 7 Abstract A review is presented of recent results in QCD
QCD Measurements at HERA Armen Bunyatyan, Max-Planck-Institut für Kernphysik, Heidelberg, Germany Yerevan Physics Institute, Armenia November, 7 Abstract A review is presented of recent results in QCD
PoS(Baldin ISHEPP XXI)032
 Prompt photon and associated heavy quark production in the k T -factorization approach A.V. Lipatov, and N.P. Zotov Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University Moscow, Russia
Prompt photon and associated heavy quark production in the k T -factorization approach A.V. Lipatov, and N.P. Zotov Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University Moscow, Russia
ZEUS 1995 F ZEUS BPC95 ZEUS SVX95 ZEUS94 E665 H1 SVX95 ZEUSREGGE ZEUSQCD
 MEASUREMENT AND PHENOMENOLOGY OF THE PROTON STRUCTURE FUNCTION F FROM ZEUS AT HERA A. Quadt Department of Physics, Particle Physics, Keble Road, Oford OX 3RH, England E-mail: quadt@mail.desy.de Measurements
MEASUREMENT AND PHENOMENOLOGY OF THE PROTON STRUCTURE FUNCTION F FROM ZEUS AT HERA A. Quadt Department of Physics, Particle Physics, Keble Road, Oford OX 3RH, England E-mail: quadt@mail.desy.de Measurements
arxiv:hep-ph/ v1 13 Jan 2003
 Preprint typeset in JHEP style - HYPER VERSION Cavendish HEP 2002 21 DAMTP 2002 154 IPPP/02/80 DCPT/02/160 arxiv:hep-ph/0301081v1 13 Jan 2003 Energy Consumption and Jet Multiplicity from the Leading Log
Preprint typeset in JHEP style - HYPER VERSION Cavendish HEP 2002 21 DAMTP 2002 154 IPPP/02/80 DCPT/02/160 arxiv:hep-ph/0301081v1 13 Jan 2003 Energy Consumption and Jet Multiplicity from the Leading Log
Physique des Particules Avancées 2
 Physique des Particules Avancées Interactions Fortes et Interactions Faibles Leçon 6 Les collisions p p (http://dpnc.unige.ch/~bravar/ppa/l6) enseignant Alessandro Bravar Alessandro.Bravar@unige.ch tél.:
Physique des Particules Avancées Interactions Fortes et Interactions Faibles Leçon 6 Les collisions p p (http://dpnc.unige.ch/~bravar/ppa/l6) enseignant Alessandro Bravar Alessandro.Bravar@unige.ch tél.:
arxiv: v1 [nucl-th] 25 Sep 2017
![arxiv: v1 [nucl-th] 25 Sep 2017 arxiv: v1 [nucl-th] 25 Sep 2017](/thumbs/72/67416435.jpg) Nuclear Physics A (217) 1 1 Sub-leading correction of two-gluon rapidity correlations of strong colour field Ye-Yin Zhao, Ming-Mei Xu, Heng-Ying Zhang and Yuan-Fang Wu Key Laboratory of Quark and Lepton
Nuclear Physics A (217) 1 1 Sub-leading correction of two-gluon rapidity correlations of strong colour field Ye-Yin Zhao, Ming-Mei Xu, Heng-Ying Zhang and Yuan-Fang Wu Key Laboratory of Quark and Lepton
arxiv:hep-ph/ v1 25 Apr 2002
 Unitarity Corrections and Structure Functions M.B. Gay Ducati, M.V.T. Machado arxiv:hep-ph/0204298v1 25 Apr 2002 Abstract Instituto de Física, Universidade Federal do Rio Grande do Sul Caixa Postal 15051,
Unitarity Corrections and Structure Functions M.B. Gay Ducati, M.V.T. Machado arxiv:hep-ph/0204298v1 25 Apr 2002 Abstract Instituto de Física, Universidade Federal do Rio Grande do Sul Caixa Postal 15051,
2. HEAVY QUARK PRODUCTION
 2. HEAVY QUARK PRODUCTION In this chapter a brief overview of the theoretical and experimental knowledge of heavy quark production is given. In particular the production of open beauty and J/ψ in hadronic
2. HEAVY QUARK PRODUCTION In this chapter a brief overview of the theoretical and experimental knowledge of heavy quark production is given. In particular the production of open beauty and J/ψ in hadronic
arxiv:hep-ph/ v1 4 Feb 1997
 DOUBLE SPIN TRANSVERSE ASYMMETRIES IN DRELL YAN PROCESSES V. Barone a,b, T. Calarco c and A. Drago c a Dipartimento di Fisica Teorica, Università di Torino and INFN, Sezione di Torino, 10125 Torino, Italy
DOUBLE SPIN TRANSVERSE ASYMMETRIES IN DRELL YAN PROCESSES V. Barone a,b, T. Calarco c and A. Drago c a Dipartimento di Fisica Teorica, Università di Torino and INFN, Sezione di Torino, 10125 Torino, Italy
Electromagnetic emission from the CGC at early stages of heavy ion collisions
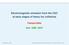 Electromagnetic emission from the CGC at early stages of heavy ion collisions François Gelis CEA / DSM / SPhT François Gelis 2005 Electromagnetic Probes of Hot and Dense Matter, ECT*, Trento, June 2005
Electromagnetic emission from the CGC at early stages of heavy ion collisions François Gelis CEA / DSM / SPhT François Gelis 2005 Electromagnetic Probes of Hot and Dense Matter, ECT*, Trento, June 2005
arxiv:hep-ph/ v2 29 Jan 2001
 SELF-ORGANIZED CRITICALITY IN GLUON SYSTEMS AND ITS CONSEQUENCES K. TABELOW Institut für Theoretische Physik, FU Berlin, Arnimallee 14, 14195 Berlin,Germany E-mail: karsten.tabelow@physik.fu-berlin.de
SELF-ORGANIZED CRITICALITY IN GLUON SYSTEMS AND ITS CONSEQUENCES K. TABELOW Institut für Theoretische Physik, FU Berlin, Arnimallee 14, 14195 Berlin,Germany E-mail: karsten.tabelow@physik.fu-berlin.de
QCD, Colliders & Jets - HW II Solutions. x, x
 QCD, Colliders & Jets - HW II Solutions. As discussed in the Lecture the parton distributions do not scale as in the naïve parton model but rather are epected to ehibit the scaling violation predicted
QCD, Colliders & Jets - HW II Solutions. As discussed in the Lecture the parton distributions do not scale as in the naïve parton model but rather are epected to ehibit the scaling violation predicted
Single inclusive jet production at very forward rapidity in proton-proton collisions with s = 7 and 13 TeV
 production at very forward rapidity in proton-proton collisions with s = 7 and ev Instytut izyki Jadrowej, Radzikowskiego, - Krakow, Poland E-mail: krzysztof.kutak@ifj.edu.pl Hans Van Haevermaet Particle
production at very forward rapidity in proton-proton collisions with s = 7 and ev Instytut izyki Jadrowej, Radzikowskiego, - Krakow, Poland E-mail: krzysztof.kutak@ifj.edu.pl Hans Van Haevermaet Particle
Soft gluon resummation
 Soft gluon resummation Simone Marzani University of Manchester Institute on Parton Shower and Resummation DESY Hamburg, Germany May 2009 In collaboration with Jeff Forshaw and James Keates arxiv:0905.1350
Soft gluon resummation Simone Marzani University of Manchester Institute on Parton Shower and Resummation DESY Hamburg, Germany May 2009 In collaboration with Jeff Forshaw and James Keates arxiv:0905.1350
Results on the proton structure from HERA
 Results on the proton structure from HERA Shima Shimizu (Univ. of Tokyo) Introduction HERA physics Proton structure The world only e-p collider: HERA electron proton A unique collider at DESY, Hamburg
Results on the proton structure from HERA Shima Shimizu (Univ. of Tokyo) Introduction HERA physics Proton structure The world only e-p collider: HERA electron proton A unique collider at DESY, Hamburg
Beauty contribution to the proton structure function and charm results
 and charm results Istituto Nazionale di Fisica Nucleare, Laboratori Nazionali di Frascati E-mail: andrea.longhin@lnf.infn.it Recent heavy quark production results in deep inelastic scattering and photoproduction
and charm results Istituto Nazionale di Fisica Nucleare, Laboratori Nazionali di Frascati E-mail: andrea.longhin@lnf.infn.it Recent heavy quark production results in deep inelastic scattering and photoproduction
Diffractive parton distributions from the HERA data
 Diffractive parton distributions from the HER data Michael Groys a, haron Levy a and lexander Proskuryakov b a Raymond and Beverly Sackler Faculty of Exact Sciences, School of Physics and stronomy, Tel
Diffractive parton distributions from the HER data Michael Groys a, haron Levy a and lexander Proskuryakov b a Raymond and Beverly Sackler Faculty of Exact Sciences, School of Physics and stronomy, Tel
High Energy QCD and Pomeron Loops
 High Energy QCD and Pomeron Loops Dionysis Triantafyllopoulos Saclay (CEA/SPhT) Based on : E. Iancu, D.N.T., Nucl. Phys. A 756 (2005) 419, Phys. Lett. B 610 (2005) 253 J.-P. Blaizot, E. Iancu, K. Itakura,
High Energy QCD and Pomeron Loops Dionysis Triantafyllopoulos Saclay (CEA/SPhT) Based on : E. Iancu, D.N.T., Nucl. Phys. A 756 (2005) 419, Phys. Lett. B 610 (2005) 253 J.-P. Blaizot, E. Iancu, K. Itakura,
Forward Jets with the CAL
 Forward Jets with the CAL Sabine Lammers Juan Terron March 4, 004 ZEUS Collaboration Meeting Motivation Event Selection Monte Carlo Programs Forward Jet Measurements Summary and Plans Parton Evolution
Forward Jets with the CAL Sabine Lammers Juan Terron March 4, 004 ZEUS Collaboration Meeting Motivation Event Selection Monte Carlo Programs Forward Jet Measurements Summary and Plans Parton Evolution
Azimuthal-angle Observables in Inclusive Three-jet Production
 Azimuthal-angle Observables in Inclusive Three-jet Production & Universidad Autónoma de Madrid, E-89 Madrid, Spain. E-mail: chachamis@gmail.com F. Caporale & Universidad Autónoma de Madrid, E-89 Madrid,
Azimuthal-angle Observables in Inclusive Three-jet Production & Universidad Autónoma de Madrid, E-89 Madrid, Spain. E-mail: chachamis@gmail.com F. Caporale & Universidad Autónoma de Madrid, E-89 Madrid,
arxiv:hep-ph/ v1 4 Mar 2002
 DESY -7 LUNFD6/(NFFL 79) hep-ph/35 arxiv:hep-ph/35v Mar A phenomenological interpretation of open charm production at HERA in terms of the semi-hard approach S.P. Baranov Lebedev Institute of Physics,
DESY -7 LUNFD6/(NFFL 79) hep-ph/35 arxiv:hep-ph/35v Mar A phenomenological interpretation of open charm production at HERA in terms of the semi-hard approach S.P. Baranov Lebedev Institute of Physics,
Soft Colour Exchanges and the Hadronic Final State 1 A. Edin a, G. Ingelman ab, J. Rathsman c
 TSL/ISV-99-0215 ISSN 0284-2769 August 1999 Soft Colour Exchanges and the Hadronic Final State 1 A. Edin a, G. Ingelman ab, J. Rathsman c a Deutsches Elektronen-Synchrotron DESY, Notkestrasse 85, D-22603
TSL/ISV-99-0215 ISSN 0284-2769 August 1999 Soft Colour Exchanges and the Hadronic Final State 1 A. Edin a, G. Ingelman ab, J. Rathsman c a Deutsches Elektronen-Synchrotron DESY, Notkestrasse 85, D-22603
Nonlinear GLR-MQ evolution equation and Q 2 -evolution of gluon distribution function
 Eur. Phys. J. C (2014) 74:2751 DOI 10.1140/epjc/s10052-014-2751-4 Regular Article - Theoretical Physics Nonlinear GLR-MQ evolution equation and Q 2 -evolution of gluon distribution function Mayuri Devee
Eur. Phys. J. C (2014) 74:2751 DOI 10.1140/epjc/s10052-014-2751-4 Regular Article - Theoretical Physics Nonlinear GLR-MQ evolution equation and Q 2 -evolution of gluon distribution function Mayuri Devee
Inclusive and Exclusive Processes with a Leading Neutron in ep and pp collisions
 Inclusive and Exclusive Processes with a Leading Neutron in ep and pp collisions Victor P. Goncalves High and Medium Energy Group UFPel Brazil Based on PLB 572(2016) 76, PRD93 (2016) 054025 and PRD94 (2016)
Inclusive and Exclusive Processes with a Leading Neutron in ep and pp collisions Victor P. Goncalves High and Medium Energy Group UFPel Brazil Based on PLB 572(2016) 76, PRD93 (2016) 054025 and PRD94 (2016)
Forward physics with proton tagging at the LHC
 Forward physics with proton tagging at the LHC Christophe Royon University of Kansas, Lawrence, USA LHC Forward Physics Workshop, March 0-3, Madrid, Spain QCD: structure of pomeron, jet gap jet Photon
Forward physics with proton tagging at the LHC Christophe Royon University of Kansas, Lawrence, USA LHC Forward Physics Workshop, March 0-3, Madrid, Spain QCD: structure of pomeron, jet gap jet Photon
Structure Functions at Very High Q 2 From HERA
 Structure Functions at Very High Q 2 From HERA Christopher M. Cormack For the H1 and ZEUS Collaborations Rutherford Appleton Laboratory, Chilton, Didcot, Oxford, OX11 0QX, United Kingdom Abstract. Measurements
Structure Functions at Very High Q 2 From HERA Christopher M. Cormack For the H1 and ZEUS Collaborations Rutherford Appleton Laboratory, Chilton, Didcot, Oxford, OX11 0QX, United Kingdom Abstract. Measurements
Superleading logarithms in QCD
 Superleading logarithms in QCD Soft gluons in QCD: an introduction. Gaps between jets I: the old way (
Superleading logarithms in QCD Soft gluons in QCD: an introduction. Gaps between jets I: the old way (
Diffractive production of isolated photons with the ZEUS detector at HERA
 Diffractive production of isolated photons with the ZEUS detector at HERA On behalf of the ZEUS Collaboration Tel Aviv University, Tel Aviv, Israel levyaron@post.tau.ac.il The photoproduction of isolated
Diffractive production of isolated photons with the ZEUS detector at HERA On behalf of the ZEUS Collaboration Tel Aviv University, Tel Aviv, Israel levyaron@post.tau.ac.il The photoproduction of isolated
arxiv:hep-ph/ v1 29 Oct 2005
 1 Electroproduction of two light vector mesons in next-to-leading BFKL D.Yu. Ivanov 1 and A. Papa arxiv:hep-ph/0510397v1 9 Oct 005 1 Sobolev Institute of Mathematics, 630090 Novosibirsk, Russia Dipartimento
1 Electroproduction of two light vector mesons in next-to-leading BFKL D.Yu. Ivanov 1 and A. Papa arxiv:hep-ph/0510397v1 9 Oct 005 1 Sobolev Institute of Mathematics, 630090 Novosibirsk, Russia Dipartimento
Factorization in high energy nucleus-nucleus collisions
 Factorization in high energy nucleus-nucleus collisions ISMD, Kielce, September 2012 François Gelis IPhT, Saclay 1 / 30 Outline 1 Color Glass Condensate 2 Factorization in Deep Inelastic Scattering 3 Factorization
Factorization in high energy nucleus-nucleus collisions ISMD, Kielce, September 2012 François Gelis IPhT, Saclay 1 / 30 Outline 1 Color Glass Condensate 2 Factorization in Deep Inelastic Scattering 3 Factorization
hep-ex/ Jun 1995
 Department of Physics & Astronomy Experimental Particle Physics Group Kelvin Building, University of Glasgow, Glasgow, G 8QQ, Scotland Telephone: +44 ()4 9 8855 Fax: +44 ()4 4 99 GLAS{PPE/95{ 9 th June
Department of Physics & Astronomy Experimental Particle Physics Group Kelvin Building, University of Glasgow, Glasgow, G 8QQ, Scotland Telephone: +44 ()4 9 8855 Fax: +44 ()4 4 99 GLAS{PPE/95{ 9 th June
Nonperturbative QCD in pp scattering at the LHC
 Nonperturbative QCD in pp scattering at the LHC IX Simpósio Latino Americano de Física de Altas Energias SILAFAE Jochen Bartels, Hamburg University and Universidad Tecnica Federico Santa Maria Introduction:
Nonperturbative QCD in pp scattering at the LHC IX Simpósio Latino Americano de Física de Altas Energias SILAFAE Jochen Bartels, Hamburg University and Universidad Tecnica Federico Santa Maria Introduction:
Pomeron-Odderon interference in production of
 LPT-ORSAY 08-86 CPHT-PC 08.1008 Pomeron-Odderon interference in production of π + π pairs in ultraperipheral collisions arxiv:08155v1 [hep-ph] 3 Nov 008 B. Pire, F. Schwennsen,, L. Szymanowski and S. Wallon
LPT-ORSAY 08-86 CPHT-PC 08.1008 Pomeron-Odderon interference in production of π + π pairs in ultraperipheral collisions arxiv:08155v1 [hep-ph] 3 Nov 008 B. Pire, F. Schwennsen,, L. Szymanowski and S. Wallon
Parton saturation and diffractive processes
 Parton saturation and diffractive processes Krzysztof Golec-Biernat Institute of Nuclear Physics PAN, Kraków Institute of Physics, University of Rzeszów Diffractive and electromagnetic processes at high
Parton saturation and diffractive processes Krzysztof Golec-Biernat Institute of Nuclear Physics PAN, Kraków Institute of Physics, University of Rzeszów Diffractive and electromagnetic processes at high
The photon PDF from high-mass Drell Yan data at the LHC
 The photon PDF from high-mass Drell Yan data at the LHC University of Oford E-mail: francesco.giuli@cern.ch In this contribution, we review the results of [1], where a determination of the photon PDF from
The photon PDF from high-mass Drell Yan data at the LHC University of Oford E-mail: francesco.giuli@cern.ch In this contribution, we review the results of [1], where a determination of the photon PDF from
arxiv: v1 [hep-ph] 29 Dec 2017
![arxiv: v1 [hep-ph] 29 Dec 2017 arxiv: v1 [hep-ph] 29 Dec 2017](/thumbs/82/85347302.jpg) F. Caporale & Universidad Autónoma de Madrid, E-89 Madrid, Spain. E-mail: francesco.caporale@uam.es arxiv:181.1v1 [hep-ph] 9 Dec 17 F. G. Celiberto & Universidad Autónoma de Madrid, E-89 Madrid, Spain.
F. Caporale & Universidad Autónoma de Madrid, E-89 Madrid, Spain. E-mail: francesco.caporale@uam.es arxiv:181.1v1 [hep-ph] 9 Dec 17 F. G. Celiberto & Universidad Autónoma de Madrid, E-89 Madrid, Spain.
