PHYSICS - CLUTCH CH 14: ANGULAR MOMENTUM.
|
|
|
- Drusilla Gilbert
- 5 years ago
- Views:
Transcription
1 !!
2 EXAMPLE: HOLDING WEIGHTS ON A SPINNING STOOL EXAMPLE: You stand on a stool that is free to rotate about an axis perpendicular to itself and through its center. Suppose that your combined moment of inertia (you + stool) around this axis is 8 kg m 2, and that it is the same whether you have your arms stretched open, or pressed against your body (not true, but simpler). You stand on the stool with arms wide open, holding one 10 kg small weight on each hand, at a distance of 80 cm from the central axis. (a) Calculate the system s total (you + stool + 2 weights) moment of inertia about its central axis. (b) Suppose the system spins with 60 RPM. Calculate its angular moment about its central axis. (c) You bring the weights to your chest, so they lie on the axis of rotation. Calculate the system s new moment of inertia. (d) You bring the weights to your chest, so they lie on the axis of rotation. How fast, in RPM, will the system rotate now? Page 2
3 PRACTICE: CLOSING YOUR ARMS ON A SPINNING STOOL PRACTICE: You stand on a stool that is free to rotate about an axis perpendicular to itself and through its center. The stool s moment of inertia around its central axis is 1.50 kg m 2. Suppose you can model your body as a vertical solid cylinder (height = 1.80 m, radius = 20 cm, mass = 80 kg) with two horizontal thin rods as your arms (each: length = 80 cm, mass = 3 kg) that rotate at their ends, about the same axis, as shown. Suppose that your arms contribution to the total moment of inertia is negligible if you have them pressed against your body, but significant if you have them wide open. If you initially spin at 5 rad/s with your arms against your body, how fast will you spin once you stretch them wide open? (Note: The system has 4 objects (stool + body + 2 arms), but initially only stool + body contribute to its moment of inertia) Page 3
4 CONSERVATION OF ANGULAR MOMENTUM Remember: The most important part about LINEAR Momentum was that it is. - The same is true for ANGULAR Momentum. Most Angular Momentum problems are about. LINEAR MOMENTUM ( p = ) ANGULAR MOMENTUM ( L = ) - Conserved if no external. - Or better yet, if Σ. - MOST problems involve TWO objects. - Conservation:. - Conserved if no external. - Or better yet, if Σ. - MANY problems involve just ONE object. - Conservation:. - TWO Objects: Push-Away; Collision - Add/remove mass (collision/push-away) - ONE Object: Objects:. EXAMPLE: For each of the following, indicate whether the angular speed will increase or decrease: (a) An ice skater spins on frictionless ice. What happens to her angular speed if she closes her arm? (b) A large horizontal disc spins around itself. What happens to the disc s angular speed if you land on it? (c) An object tied to a point via a string spins horizontally around it. What happens if you shorten the string? (d) A star (like the Sun) spins around itself. What happens if it collapses and loses half its mass and half its radius? Page 4
5 EXAMPLE: ICE SKATER CLOSES HER ARMS EXAMPLE: Suppose an ice skater has moment of inertia of 6 kg m 2 while spinning with arms wide open, and 4 kg m 2 if she closes her arms. If she spins at 120 RPM with arms open, what RPM will she have as a result of closing her arms? Page 5
6 PRACTICE: DIVER CHANGING ANGULAR SPEED PRACTICE: Suppose a diver spins at 8 rad/s while falling with a moment of inertia about an axis through himself of 3 kg m 2. What moment of inertia would the diver need to have to spin at 4 rad/s? BONUS: How could he accomplish this? Page 6
7 EXAMPLE: ANGULAR SPEED OF STAR AFTER COLLAPSE EXAMPLE: When a star exhausts all its stellar energy, it dies, at which point a gravitational collapse happens, causing its radius and mass to decrease substantially. Our Sun spins around itself, at its equator, every 24.5 days. If our Sun were to collapse and shrink 90% in mass and 90% in radius, how long would its new period of rotation take, in days? Page 7
8 PRACTICE: TWO ASTRONAUTS SPINNING IN SPACE PRACTICE: Two astronauts, both 80 kg, are connected in space by a light cable. When they are 10 m apart, they spin about their center of mass with 6 rad/s. Calculate the new angular speed they ll have if they pull on the rope to reduce their distance to 5 m. You may treat them as point masses, and assume they continue to spin around their center of mass. Page 8
9 EXAMPLE: MOVING ON A ROTATING DISC EXAMPLE: A 200 kg disc 4 m in radius spins around a perpendicular axis through its center at 2 rad/s. An 80 kg person falls into the disc, with no horizontal speed, at a point 3 m away from the disc s center. Treating the person as a point mass: (a) Calculate the disc s new angular speed. (b) Calculate the person s new tangential speed. (c) The person starts walking towards the disc s center. Calculate the disc s speed once the person reaches it. Page 9
10 ANGULAR MOMENTUM AND NEWTON S SECOND LAW Remember: Newton s Second Law,, can be re-written in terms of Linear Momentum: - The Rotational version,, can also be re-written, in terms of Angular Momentum: EXAMPLE: A small object, 10 kg in mass, spins at 180 RPM in a circular path of radius 5 m. If a constant torque of 80 N m is applied to the object, in trying to stop it, how long will it take for the object to come to a complete stop? Page 10
11 PRACTICE: ANGULAR MOMENTUM / FORCE TO ACCELERATE PRACTICE: A solid disc of mass M = 40 kg and radius R = 2 m is free to rotate about a fixed, frictionless, perpendicular axis through its center. You apply a constant, tangential force on the disc s surface (as shown), to get it to spin. Calculate the magnitude of the force needed to get the disc to 100 rad/s in just one minute. Page 11
12 ANGULAR COLLISIONS Angular Collisions happen when ONE of the TWO objects involved in the collision is rotating OR rotates as a result. - Similar to Linear Collisions: We use the Conversation of Momentum equation, but the version: = = - For a Point Mass in linear motion, we use the linear version of the Angular Momentum equation L =. - Where is the distance between where the linear object collides and the axis of the rotating object. - Note: Adding mass to a rotating disc is an Angular Collision problem; but simple if the mass was at rest. EXAMPLE: A 100 kg solid disc of radius 6 m spins clockwise around a perpendicular axis through its center at 120 RPM. A second solid disc, 50 kg in mass, 3 m in radius, is carefully placed on top of the first disc, as shown, causing the discs to spin together about the same axis. Calculate the new rate, in RPM, that the discs will have, if the second disc was initially: (a) at rest; (b) spinning counter-clockwise with 360 RPM. Page 12
13 EXAMPLE: JUMPING INTO A MOVING DISC EXAMPLE: A 200 kg disc 4 m in radius spins around a perpendicular axis through its center at 2 rad/s counter-clockwise. Find the new speed the disc would have if an 80 kg person (treat as a point mass): (a) Steps into the disc s edge with negligible speed; (b) Jumps into the disc, at its edge, with 9 m/s, directed towards the center; (c) Jumps into the disc s edge with 9 m/s, directed tangentially up, as shown in red; (d) Jumps into the disc s edge with 9 m/s, directed tangentially down (green); Page 13
14 PRACTICE: JUMPING OUT OF A MOVING DISC PRACTICE: A 200 kg disc 2 m in radius spins around a perpendicular axis through its center, with a person on it, at 3 rad/s counter-clockwise. The person has mass 70 kg, is at rest (relative to the disc, that is, spins with it) at the disc s edge, and can be treated as a point mass. If the person jumps tangentially out of the disc with 10 m/s (relative to the floor), as shown by the red arrow, what new angular speed will the disc have as a result? BONUS: If the person steps out into ice with negligible speed of his/her own, what speed would it have upon exiting? Page 14
15 EXAMPLE: SPINNING ON A STRING OF VARIABLE LENGTH EXAMPLE: A small object (red, m1 = 2 kg), is on a smooth table top and attached to a light string that runs through a hole in the table. The other end of the string attaches to a hanging weight (green, m2). When the small object is given some speed, it spins in a circular path around the hole, with the tension from the hanging weight providing the centripetal force that keeps it spinning. Suppose the small object spins at 120 RPM when it is a radial distance of 10 cm from the hole. (a) How fast, in RPM, would it spin if the radial distance was reduced (by pulling on the hanging weight) to 6 cm? (b) At this new RPM, what linear (tangential) speed would the small object have? (c) What mass m2 does the hanging weight need to have to maintain the small object spinning at the RPM found in (b)? Page 15
16 PRACTICE: SPINNING ON A STRING OF VARIABLE LENGTH PRACTICE: A small object (red, m) is on a smooth table top and attached to a light string that runs through a hole in the table. The other end of the spring attaches to a hanging weight (green, M). When the small object is given some speed, it spins in a circular path around the hole, with the tension from the hanging weight providing the centripetal force that keeps it spinning. If the object spins with angular speed ω when it is a distance R from the central role, what new angular speed (in terms of ω) does it have when this distance is halved? BONUS: What new mass does the hanging weight need, in terms of M, to support a circular path at the new speed? Page 16
17 PRACTICE: BIRD COLLIDES AGAINST ROTATING DOORS PRACTICE: Two rotating doors, each 4 kg in mass and 6 m long, are fixed to the same central axis of rotation, as shown above (top view). Suppose a 4 kg bird flying with 30 m/s horizontal collides against the door and stays stuck to it, at a point 50 cm from one end. Calculate the angular speed with which the system (doors + bird) spin together. 50 cm I = 1/3 m A 2 A = side that extends away from axis I = 1/12 m (A 2 + B 2 ) A and B = sides on face of rectangle Page 17
18 INTRO TO ANGULAR MOMENTUM Remember: If you have linear speed ( ), you have Linear Momentum p = m v [ kg * m / s ] - If you have rotational speed ( ), you have Angular Momentum L = [ kg * m 2 / s ] - Difference: Linear Momentum is absolute; Angular Momentum is relative to the Axis of Rotation like Torque! - Do NOT confuse Angular Momentum (L = Iw) with Moment of Inertia (I; angular equivalent of mass). EXAMPLE: A solid cylinder of mass M = 5 kg and radius R = 2 m rotates about a perpendicular axis through its center with 120 RPM. Calculate its angular momentum about its central axis. Page 18
19 PRACTICE: ANGULAR MOMENTUM / FIND MASS PRACTICE: When solid sphere 4 m in diameter spins around its central axis at 120 RPM, it has 1,000 kg m 2 / s in angular momentum. Calculate the sphere s mass. Page 19
20 PRACTICE: ANGULAR MOMENTUM / COMPOSITE DISC PRACTICE: A composite disc is built from a solid disc and a concentric, thick-walled hoop, as shown below. The inner disc has mass 4 kg and radius 2 m. The outer disc (thick-walled) has mass 5 kg, inner radius 2 m, and outer radius 3 m. The two discs spin together and complete one revolution every 3 s. Calculate the system s angular momentum about its central axis. Page 20
21 ANGULAR MOMENTUM OF A POINT MASS A Point Mass in a circular path has rotational speed (w) and a linear equivalent (v,tan), but only ONE type of motion. - Note that Linear Momentum and Rotational Momentum do NOT give you the same number! - This is because Linear Momentum is absolute, and Angular Momentum is relative it depends on the Axis! - So if you calculate Linear and Angular Momenta for a Point Mass, you get different equations and numbers: EXAMPLE: A small 2-kg object spins horizontally around a vertical axis at a rate of 3 rad/s, maintaining a constant distance of 4 m to the axis. Calculate the object s (a) linear momentum, and (b) angular momentum about its central axis. L = is also used for Angular Momentum of an object in LINEAR motion, about an axis of rotation (more soon) Page 21
22 PRACTICE: ANGULAR MOMENTUM / EARTH PRACTICE: The Earth has mass 5.97 x kg, radius 6.37 x 10 6 m. The Earth-Sun distance is 1.5 x m. Calculate its angular momentum as it spins around itself. Treat the Earth as a solid sphere of uniform mass distribution. BONUS 1: Treating the Earth as a point mass, calculate its angular momentum as it spins around the Sun. BONUS 2: Does the Earth have linear momentum as it spins around (i) itself; (ii) the Sun? Page 22
23 PRACTICE: ANGULAR MOMENTUM / ROD WITH MASSES PRACTICE: A system is made of two small, 3 kg masses attached to the ends of a 5 kg, 4 m long, thin rod. The system rotates with 180 RPM about an axis perpendicular to the rod and through one of its ends, as shown. Calculate the system s angular momentum about its axis. Page 23
24 ANGULAR MOMENTUM OF OBJECTS IN LINEAR MOTION In some problems, an object moving in a straight line collides against an object fixed in a rotating axis: - Remember we used Linear Momentum to solve Collision problems! - BUT in this case, we need the first object s Momentum, not its Momentum. - But how do you get the Momentum of an object that is moving in a straight line?!? - An object in a straight line has Angular Momentum relative to unrelated axis of rotation L = - Notice that this is the SAME equation as the Angular Momentum of a. EXAMPLE: Two rotating doors, each 6.0 m long, are fixed to the same central axis of rotation, as shown above (top view). Suppose a 4 kg bird flying with 30 m/s horizontal is about to collide against the door, at a point 50 cm from one end. Calculate the bird s angular momentum about the axis through the center of the door, just before hitting the door. Later we will see how to FULLY solve these types of Rotational Collisions! (For now, contain your excitement, please!) Page 24
Rotation Quiz II, review part A
 Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Rotation Quiz II, review part A 1. A solid disk with a radius R rotates at a constant rate ω. Which of the following points has the greater angular velocity? A. A B. B C. C D. D E. All points have the
Rolling, Torque & Angular Momentum
 PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
PHYS 101 Previous Exam Problems CHAPTER 11 Rolling, Torque & Angular Momentum Rolling motion Torque Angular momentum Conservation of angular momentum 1. A uniform hoop (ring) is rolling smoothly from the
Chapter 8, Rotational Equilibrium and Rotational Dynamics. 3. If a net torque is applied to an object, that object will experience:
 CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
CHAPTER 8 3. If a net torque is applied to an object, that object will experience: a. a constant angular speed b. an angular acceleration c. a constant moment of inertia d. an increasing moment of inertia
Physics 201 Midterm Exam 3
 Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above. Please write and bubble your Name and Student Id number on
Physics 201 Midterm Exam 3
 Name: Date: _ Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above Please write and bubble your Name and Student
Name: Date: _ Physics 201 Midterm Exam 3 Information and Instructions Student ID Number: Section Number: TA Name: Please fill in all the information above Please write and bubble your Name and Student
TutorBreeze.com 7. ROTATIONAL MOTION. 3. If the angular velocity of a spinning body points out of the page, then describe how is the body spinning?
 1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
1. rpm is about rad/s. 7. ROTATIONAL MOTION 2. A wheel rotates with constant angular acceleration of π rad/s 2. During the time interval from t 1 to t 2, its angular displacement is π rad. At time t 2
Suggested Problems. Chapter 1
 Suggested Problems Ch1: 49, 51, 86, 89, 93, 95, 96, 102. Ch2: 9, 18, 20, 44, 51, 74, 75, 93. Ch3: 4, 14, 46, 54, 56, 75, 91, 80, 82, 83. Ch4: 15, 59, 60, 62. Ch5: 14, 52, 54, 65, 67, 83, 87, 88, 91, 93,
Suggested Problems Ch1: 49, 51, 86, 89, 93, 95, 96, 102. Ch2: 9, 18, 20, 44, 51, 74, 75, 93. Ch3: 4, 14, 46, 54, 56, 75, 91, 80, 82, 83. Ch4: 15, 59, 60, 62. Ch5: 14, 52, 54, 65, 67, 83, 87, 88, 91, 93,
Description: Using conservation of energy, find the final velocity of a "yo yo" as it unwinds under the influence of gravity.
 Chapter 10 [ Edit ] Overview Summary View Diagnostics View Print View with Answers Chapter 10 Due: 11:59pm on Sunday, November 6, 2016 To understand how points are awarded, read the Grading Policy for
Chapter 10 [ Edit ] Overview Summary View Diagnostics View Print View with Answers Chapter 10 Due: 11:59pm on Sunday, November 6, 2016 To understand how points are awarded, read the Grading Policy for
On my honor, I have neither given nor received unauthorized aid on this examination.
 Instructor(s): Profs. D. Reitze, H. Chan PHYSICS DEPARTMENT PHY 2053 Exam 2 April 2, 2009 Name (print, last first): Signature: On my honor, I have neither given nor received unauthorized aid on this examination.
Instructor(s): Profs. D. Reitze, H. Chan PHYSICS DEPARTMENT PHY 2053 Exam 2 April 2, 2009 Name (print, last first): Signature: On my honor, I have neither given nor received unauthorized aid on this examination.
Angular Momentum System of Particles Concept Questions
 Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Question 1: Angular Momentum Angular Momentum System of Particles Concept Questions A non-symmetric body rotates with an angular speed ω about the z axis. Relative to the origin 1. L 0 is constant. 2.
Chapter 9-10 Test Review
 Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
Chapter 9-10 Test Review Chapter Summary 9.2. The Second Condition for Equilibrium Explain torque and the factors on which it depends. Describe the role of torque in rotational mechanics. 10.1. Angular
A) 1 gm 2 /s. B) 3 gm 2 /s. C) 6 gm 2 /s. D) 9 gm 2 /s. E) 10 gm 2 /s. A) 0.1 kg. B) 1 kg. C) 2 kg. D) 5 kg. E) 10 kg A) 2:5 B) 4:5 C) 1:1 D) 5:4
 1. A 4 kg object moves in a circle of radius 8 m at a constant speed of 2 m/s. What is the angular momentum of the object with respect to an axis perpendicular to the circle and through its center? A)
1. A 4 kg object moves in a circle of radius 8 m at a constant speed of 2 m/s. What is the angular momentum of the object with respect to an axis perpendicular to the circle and through its center? A)
Chapter 8. Rotational Equilibrium and Rotational Dynamics. 1. Torque. 2. Torque and Equilibrium. 3. Center of Mass and Center of Gravity
 Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Chapter 8 Rotational Equilibrium and Rotational Dynamics 1. Torque 2. Torque and Equilibrium 3. Center of Mass and Center of Gravity 4. Torque and angular acceleration 5. Rotational Kinetic energy 6. Angular
Unit 8 Notetaking Guide Torque and Rotational Motion
 Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
Unit 8 Notetaking Guide Torque and Rotational Motion Rotational Motion Until now, we have been concerned mainly with translational motion. We discussed the kinematics and dynamics of translational motion
PY205N Spring The vectors a, b, and c. are related by c = a b. The diagram below that best illustrates this relationship is (a) I
 PY205N Spring 2013 Final exam, practice version MODIFIED This practice exam is to help students prepare for the final exam to be given at the end of the semester. Please note that while problems on this
PY205N Spring 2013 Final exam, practice version MODIFIED This practice exam is to help students prepare for the final exam to be given at the end of the semester. Please note that while problems on this
Webreview Torque and Rotation Practice Test
 Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
Please do not write on test. ID A Webreview - 8.2 Torque and Rotation Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A 0.30-m-radius automobile
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Physics 201, Practice Midterm Exam 3, Fall 2006
 Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Physics 201, Practice Midterm Exam 3, Fall 2006 1. A figure skater is spinning with arms stretched out. A moment later she rapidly brings her arms close to her body, but maintains her dynamic equilibrium.
Centripetal acceleration ac = to2r Kinetic energy of rotation KE, = \lto2. Moment of inertia. / = mr2 Newton's second law for rotational motion t = la
 The Language of Physics Angular displacement The angle that a body rotates through while in rotational motion (p. 241). Angular velocity The change in the angular displacement of a rotating body about
The Language of Physics Angular displacement The angle that a body rotates through while in rotational motion (p. 241). Angular velocity The change in the angular displacement of a rotating body about
PHYSICS - CLUTCH CH 13: ROTATIONAL EQUILIBRIUM.
 !! www.clutchprep.com EXAMPLE: POSITION OF SECOND KID ON SEESAW EXAMPLE: A 4 m-long seesaw 50 kg in mass and of uniform mass distribution is pivoted on a fulcrum at its middle, as shown. Two kids sit on
!! www.clutchprep.com EXAMPLE: POSITION OF SECOND KID ON SEESAW EXAMPLE: A 4 m-long seesaw 50 kg in mass and of uniform mass distribution is pivoted on a fulcrum at its middle, as shown. Two kids sit on
Rotation. PHYS 101 Previous Exam Problems CHAPTER
 PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
PHYS 101 Previous Exam Problems CHAPTER 10 Rotation Rotational kinematics Rotational inertia (moment of inertia) Kinetic energy Torque Newton s 2 nd law Work, power & energy conservation 1. Assume that
1 The displacement, s in metres, of an object after a time, t in seconds, is given by s = 90t 4 t 2
 CFE Advanced Higher Physics Unit 1 Rotational Motion and Astrophysics Kinematic relationships 1 The displacement, s in metres, of an object after a time, t in seconds, is given by s = 90t 4 t 2 a) Find
CFE Advanced Higher Physics Unit 1 Rotational Motion and Astrophysics Kinematic relationships 1 The displacement, s in metres, of an object after a time, t in seconds, is given by s = 90t 4 t 2 a) Find
CHAPTER 8: ROTATIONAL OF RIGID BODY PHYSICS. 1. Define Torque
 7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
7 1. Define Torque 2. State the conditions for equilibrium of rigid body (Hint: 2 conditions) 3. Define angular displacement 4. Define average angular velocity 5. Define instantaneous angular velocity
Slide 1 / 133. Slide 2 / 133. Slide 3 / How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m?
 1 How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? Slide 1 / 133 2 How many degrees are subtended by a 0.10 m arc of a circle of radius of 0.40 m? Slide 2 / 133 3 A ball rotates
1 How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? Slide 1 / 133 2 How many degrees are subtended by a 0.10 m arc of a circle of radius of 0.40 m? Slide 2 / 133 3 A ball rotates
Slide 2 / 133. Slide 1 / 133. Slide 3 / 133. Slide 4 / 133. Slide 5 / 133. Slide 6 / 133
 Slide 1 / 133 1 How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? Slide 2 / 133 2 How many degrees are subtended by a 0.10 m arc of a circle of radius of 0.40 m? Slide 3 / 133
Slide 1 / 133 1 How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? Slide 2 / 133 2 How many degrees are subtended by a 0.10 m arc of a circle of radius of 0.40 m? Slide 3 / 133
Test 7 wersja angielska
 Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
Test 7 wersja angielska 7.1A One revolution is the same as: A) 1 rad B) 57 rad C) π/2 rad D) π rad E) 2π rad 7.2A. If a wheel turns with constant angular speed then: A) each point on its rim moves with
PHYSICS 221, FALL 2011 EXAM #2 SOLUTIONS WEDNESDAY, NOVEMBER 2, 2011
 PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
PHYSICS 1, FALL 011 EXAM SOLUTIONS WEDNESDAY, NOVEMBER, 011 Note: The unit vectors in the +x, +y, and +z directions of a right-handed Cartesian coordinate system are î, ĵ, and ˆk, respectively. In this
Big Idea 4: Interactions between systems can result in changes in those systems. Essential Knowledge 4.D.1: Torque, angular velocity, angular
 Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
Unit 7: Rotational Motion (angular kinematics, dynamics, momentum & energy) Name: Big Idea 3: The interactions of an object with other objects can be described by forces. Essential Knowledge 3.F.1: Only
PHYSICS - CLUTCH 1E CH 12: TORQUE & ROTATIONAL DYNAMICS.
 !! www.clutchprep.com INTRO TO TORQUE TORQUE is a twist that a Force gives an object around an axis of rotation. - For example, when you push on a door, it rotates around its hinges. - When a Force acts
!! www.clutchprep.com INTRO TO TORQUE TORQUE is a twist that a Force gives an object around an axis of rotation. - For example, when you push on a door, it rotates around its hinges. - When a Force acts
PHYSICS - CLUTCH CH 12: TORQUE & ROTATIONAL DYNAMICS.
 !! www.clutchprep.com TORQUE & ACCELERATION (ROTATIONAL DYNAMICS) When a Force causes rotation, it produces a Torque. Think of TORQUE as the equivalent of FORCE! FORCE (F) TORQUE (τ) - Causes linear acceleration
!! www.clutchprep.com TORQUE & ACCELERATION (ROTATIONAL DYNAMICS) When a Force causes rotation, it produces a Torque. Think of TORQUE as the equivalent of FORCE! FORCE (F) TORQUE (τ) - Causes linear acceleration
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013
 Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Chapter 9: Rotational Dynamics Tuesday, September 17, 2013 10:00 PM The fundamental idea of Newtonian dynamics is that "things happen for a reason;" to be more specific, there is no need to explain rest
Quest Chapter 09. Eliminate the obviously wrong answers. Consider what is changing: speed, velocity, some part of velocity? Choose carefully.
 1 A dragster maintains a speedometer reading of 100 km/h and passes through a curve with a constant radius. Which statement is true? 1. The dragster rounded the curve at a changing speed of 100 km/h. 2.
1 A dragster maintains a speedometer reading of 100 km/h and passes through a curve with a constant radius. Which statement is true? 1. The dragster rounded the curve at a changing speed of 100 km/h. 2.
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics
 UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 115.3 Physics and the Universe FINAL EXAMINATION December 19, 2015 NAME: (Last) Please Print (Given) Time: 3 hours STUDENT
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 115.3 Physics and the Universe FINAL EXAMINATION December 19, 2015 NAME: (Last) Please Print (Given) Time: 3 hours STUDENT
Exam 3 Practice Solutions
 Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
Exam 3 Practice Solutions Multiple Choice 1. A thin hoop, a solid disk, and a solid sphere, each with the same mass and radius, are at rest at the top of an inclined plane. If all three are released at
End-of-Chapter Exercises
 End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
End-of-Chapter Exercises Exercises 1 12 are conceptual questions that are designed to see if you have understood the main concepts of the chapter. 1. Figure 11.21 shows four different cases involving a
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Common Quiz Mistakes / Practice for Final Exam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A ball is thrown directly upward and experiences
Common Quiz Mistakes / Practice for Final Exam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A ball is thrown directly upward and experiences
PHYSICS 221 SPRING EXAM 2: March 30, 2017; 8:15pm 10:15pm
 PHYSICS 221 SPRING 2017 EXAM 2: March 30, 2017; 8:15pm 10:15pm Name (printed): Recitation Instructor: Section # Student ID# INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit
PHYSICS 221 SPRING 2017 EXAM 2: March 30, 2017; 8:15pm 10:15pm Name (printed): Recitation Instructor: Section # Student ID# INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit
 1 of 5 7/13/2015 9:03 AM HW8 due 6 pm Day 18 (Wed. July 15) (7426858) Question 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1. Question Details OSColPhys1 10.P.028.WA. [2611790] The specifications for
1 of 5 7/13/2015 9:03 AM HW8 due 6 pm Day 18 (Wed. July 15) (7426858) Question 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1. Question Details OSColPhys1 10.P.028.WA. [2611790] The specifications for
PHYSICS 221 SPRING 2014
 PHYSICS 221 SPRING 2014 EXAM 2: April 3, 2014 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
PHYSICS 221 SPRING 2014 EXAM 2: April 3, 2014 8:15-10:15pm Name (printed): Recitation Instructor: Section # INSTRUCTIONS: This exam contains 25 multiple-choice questions plus 2 extra credit questions,
1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
 AP Physics B Practice Questions: Rotational Motion Multiple-Choice Questions 1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
AP Physics B Practice Questions: Rotational Motion Multiple-Choice Questions 1. Which of the following is the unit for angular displacement? A. Meters B. Seconds C. Radians D. Radian per second E. Inches
Advanced Higher Physics. Rotational motion
 Wallace Hall Academy Physics Department Advanced Higher Physics Rotational motion Problems AH Physics: Rotational Motion 1 2013 Data Common Physical Quantities QUANTITY SYMBOL VALUE Gravitational acceleration
Wallace Hall Academy Physics Department Advanced Higher Physics Rotational motion Problems AH Physics: Rotational Motion 1 2013 Data Common Physical Quantities QUANTITY SYMBOL VALUE Gravitational acceleration
Rolling, Torque, and Angular Momentum
 AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
AP Physics C Rolling, Torque, and Angular Momentum Introduction: Rolling: In the last unit we studied the rotation of a rigid body about a fixed axis. We will now extend our study to include cases where
It will be most difficult for the ant to adhere to the wheel as it revolves past which of the four points? A) I B) II C) III D) IV
 AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
AP Physics 1 Lesson 16 Homework Newton s First and Second Law of Rotational Motion Outcomes Define rotational inertia, torque, and center of gravity. State and explain Newton s first Law of Motion as it
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion
 PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
PSI AP Physics I Rotational Motion Multiple-Choice questions 1. Which of the following is the unit for angular displacement? A. meters B. seconds C. radians D. radians per second 2. An object moves from
Practice Test 3. Name: Date: ID: A. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
Name: Date: _ Practice Test 3 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A wheel rotates about a fixed axis with an initial angular velocity of 20
Name: Date: Period: AP Physics C Rotational Motion HO19
 1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
1.) A wheel turns with constant acceleration 0.450 rad/s 2. (9-9) Rotational Motion H19 How much time does it take to reach an angular velocity of 8.00 rad/s, starting from rest? Through how many revolutions
Angular Momentum L = I ω
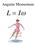 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Fall 2007 RED Barcode Here Physics 105, sections 1 and 2 Please write your CID Colton
 Fall 007 RED Barcode Here Physics 105, sections 1 and Exam 3 Please write your CID Colton -3669 3 hour time limit. One 3 5 handwritten note card permitted (both sides). Calculators permitted. No books.
Fall 007 RED Barcode Here Physics 105, sections 1 and Exam 3 Please write your CID Colton -3669 3 hour time limit. One 3 5 handwritten note card permitted (both sides). Calculators permitted. No books.
Wiley Plus. Final Assignment (5) Is Due Today: Before 11 pm!
 Wiley Plus Final Assignment (5) Is Due Today: Before 11 pm! Final Exam Review December 9, 009 3 What about vector subtraction? Suppose you are given the vector relation A B C RULE: The resultant vector
Wiley Plus Final Assignment (5) Is Due Today: Before 11 pm! Final Exam Review December 9, 009 3 What about vector subtraction? Suppose you are given the vector relation A B C RULE: The resultant vector
Part Two: Earlier Material
 Part Two: Earlier Material Problem 1: (Momentum and Impulse) A superball of m 1 = 0.08kg, starting at rest, is dropped from a height falls h 0 = 3.0m above the ground and bounces back up to a height of
Part Two: Earlier Material Problem 1: (Momentum and Impulse) A superball of m 1 = 0.08kg, starting at rest, is dropped from a height falls h 0 = 3.0m above the ground and bounces back up to a height of
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion. Torque and angular momentum
 Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Angular Momentum L = I ω
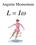 Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
Angular Momentum L = Iω If no NET external Torques act on a system then Angular Momentum is Conserved. Linitial = I ω = L final = Iω Angular Momentum L = Iω Angular Momentum L = I ω A Skater spins with
UNIT HW ROTATION ANSWER KEY
 Conceptual Questions UNIT HW ROTATION ANSWER KEY 1) D_What type of linear acceleration does an object moving with constant linear speed (st) in a circular path experience? A) free fall C) linear acceleration
Conceptual Questions UNIT HW ROTATION ANSWER KEY 1) D_What type of linear acceleration does an object moving with constant linear speed (st) in a circular path experience? A) free fall C) linear acceleration
Concept Question: Normal Force
 Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
Concept Question: Normal Force Consider a person standing in an elevator that is accelerating upward. The upward normal force N exerted by the elevator floor on the person is 1. larger than 2. identical
ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM
 ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM Chapter 11 Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static Equilibrium Center of Mass and Balance Dynamic Applications of Torque
ROTATIONAL DYNAMICS AND STATIC EQUILIBRIUM Chapter 11 Units of Chapter 11 Torque Torque and Angular Acceleration Zero Torque and Static Equilibrium Center of Mass and Balance Dynamic Applications of Torque
Rotational Motion What is the difference between translational and rotational motion? Translational motion.
 Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
Rotational Motion 1 1. What is the difference between translational and rotational motion? Translational motion Rotational motion 2. What is a rigid object? 3. What is rotational motion? 4. Identify and
Mechanics II. Which of the following relations among the forces W, k, N, and F must be true?
 Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Mechanics II 1. By applying a force F on a block, a person pulls a block along a rough surface at constant velocity v (see Figure below; directions, but not necessarily magnitudes, are indicated). Which
Physics 121, Sections 1 and 2, Winter 2011 Instructor: Scott Bergeson Exam #3 April 16 April 21, 2011 RULES FOR THIS TEST:
 Physics 121, Sections 1 and 2, Winter 2011 Instructor: Scott Bergeson Exam #3 April 16 April 21, 2011 RULES FOR THIS TEST: This test is closed book. You may use a dictionary. You may use your own calculator
Physics 121, Sections 1 and 2, Winter 2011 Instructor: Scott Bergeson Exam #3 April 16 April 21, 2011 RULES FOR THIS TEST: This test is closed book. You may use a dictionary. You may use your own calculator
APC PHYSICS CHAPTER 11 Mr. Holl Rotation
 APC PHYSICS CHAPTER 11 Mr. Holl Rotation Student Notes 11-1 Translation and Rotation All of the motion we have studied to this point was linear or translational. Rotational motion is the study of spinning
APC PHYSICS CHAPTER 11 Mr. Holl Rotation Student Notes 11-1 Translation and Rotation All of the motion we have studied to this point was linear or translational. Rotational motion is the study of spinning
AP Physics 1 Rotational Motion Practice Test
 AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
AP Physics 1 Rotational Motion Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A spinning ice skater on extremely smooth ice is able
Physics 131: Lecture 22. Today s Agenda
 Physics 131: Lecture 22 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released
Physics 131: Lecture 22 Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 201: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released
AP Physics 1: Rotational Motion & Dynamics: Problem Set
 AP Physics 1: Rotational Motion & Dynamics: Problem Set I. Axis of Rotation and Angular Properties 1. How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? 2. How many degrees are
AP Physics 1: Rotational Motion & Dynamics: Problem Set I. Axis of Rotation and Angular Properties 1. How many radians are subtended by a 0.10 m arc of a circle of radius 0.40 m? 2. How many degrees are
PHYSICS I RESOURCE SHEET
 PHYSICS I RESOURCE SHEET Cautions and Notes Kinematic Equations These are to be used in regions with constant acceleration only You must keep regions with different accelerations separate (for example,
PHYSICS I RESOURCE SHEET Cautions and Notes Kinematic Equations These are to be used in regions with constant acceleration only You must keep regions with different accelerations separate (for example,
PHYS 1303 Final Exam Example Questions
 PHYS 1303 Final Exam Example Questions 1.Which quantity can be converted from the English system to the metric system by the conversion factor 5280 mi f 12 f in 2.54 cm 1 in 1 m 100 cm 1 3600 h? s a. feet
PHYS 1303 Final Exam Example Questions 1.Which quantity can be converted from the English system to the metric system by the conversion factor 5280 mi f 12 f in 2.54 cm 1 in 1 m 100 cm 1 3600 h? s a. feet
Review PHYS114 Chapters 4-7
 Review PHYS114 Chapters 4-7 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A 27 kg object is accelerated at a rate of 1.7 m/s 2. What force does
Review PHYS114 Chapters 4-7 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) A 27 kg object is accelerated at a rate of 1.7 m/s 2. What force does
Preview. Circular Motion and Gravitation Section 1. Section 1 Circular Motion. Section 2 Newton s Law of Universal Gravitation
 Circular Motion and Gravitation Section 1 Preview Section 1 Circular Motion Section 2 Newton s Law of Universal Gravitation Section 3 Motion in Space Section 4 Torque and Simple Machines Circular Motion
Circular Motion and Gravitation Section 1 Preview Section 1 Circular Motion Section 2 Newton s Law of Universal Gravitation Section 3 Motion in Space Section 4 Torque and Simple Machines Circular Motion
Chapter 8 - Rotational Dynamics and Equilibrium REVIEW
 Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
Pagpalain ka! (Good luck, in Filipino) Date Chapter 8 - Rotational Dynamics and Equilibrium REVIEW TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body
PS 11 GeneralPhysics I for the Life Sciences
 PS 11 GeneralPhysics I for the Life Sciences ROTATIONAL MOTION D R. B E N J A M I N C H A N A S S O C I A T E P R O F E S S O R P H Y S I C S D E P A R T M E N T F E B R U A R Y 0 1 4 Questions and Problems
PS 11 GeneralPhysics I for the Life Sciences ROTATIONAL MOTION D R. B E N J A M I N C H A N A S S O C I A T E P R O F E S S O R P H Y S I C S D E P A R T M E N T F E B R U A R Y 0 1 4 Questions and Problems
TOPIC D: ROTATION EXAMPLES SPRING 2018
 TOPIC D: ROTATION EXAMPLES SPRING 018 Q1. A car accelerates uniformly from rest to 80 km hr 1 in 6 s. The wheels have a radius of 30 cm. What is the angular acceleration of the wheels? Q. The University
TOPIC D: ROTATION EXAMPLES SPRING 018 Q1. A car accelerates uniformly from rest to 80 km hr 1 in 6 s. The wheels have a radius of 30 cm. What is the angular acceleration of the wheels? Q. The University
= o + t = ot + ½ t 2 = o + 2
 Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
Chapters 8-9 Rotational Kinematics and Dynamics Rotational motion Rotational motion refers to the motion of an object or system that spins about an axis. The axis of rotation is the line about which the
NAME. (2) Choose the graph below that represents the velocity vs. time for constant, nonzero acceleration in one dimension.
 (1) The figure shows a lever (which is a uniform bar, length d and mass M), hinged at the bottom and supported steadily by a rope. The rope is attached a distance d/4 from the hinge. The two angles are
(1) The figure shows a lever (which is a uniform bar, length d and mass M), hinged at the bottom and supported steadily by a rope. The rope is attached a distance d/4 from the hinge. The two angles are
11. (7 points: Choose up to 3 answers) What is the tension,!, in the string? a.! = 0.10 N b.! = 0.21 N c.! = 0.29 N d.! = N e.! = 0.
 A harmonic wave propagates horizontally along a taut string of length! = 8.0 m and mass! = 0.23 kg. The vertical displacement of the string along its length is given by!!,! = 0.1!m cos 1.5!!! +!0.8!!,
A harmonic wave propagates horizontally along a taut string of length! = 8.0 m and mass! = 0.23 kg. The vertical displacement of the string along its length is given by!!,! = 0.1!m cos 1.5!!! +!0.8!!,
. d. v A v B. e. none of these.
 General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
General Physics I Exam 3 - Chs. 7,8,9 - Momentum, Rotation, Equilibrium Oct. 28, 2009 Name Rec. Instr. Rec. Time For full credit, make your work clear to the grader. Show the formulas you use, the essential
Rotational Motion. 1 Purpose. 2 Theory 2.1 Equation of Motion for a Rotating Rigid Body
 Rotational Motion Equipment: Capstone, rotary motion sensor mounted on 80 cm rod and heavy duty bench clamp (PASCO ME-9472), string with loop at one end and small white bead at the other end (125 cm bead
Rotational Motion Equipment: Capstone, rotary motion sensor mounted on 80 cm rod and heavy duty bench clamp (PASCO ME-9472), string with loop at one end and small white bead at the other end (125 cm bead
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics
 UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 5.3 FINAL EXAMINATION NAME: (Last) Please Print (Given) Time: 80 minutes STUDENT NO.: LECTURE SECTION (please check): 0
UNIVERSITY OF SASKATCHEWAN Department of Physics and Engineering Physics Physics 5.3 FINAL EXAMINATION NAME: (Last) Please Print (Given) Time: 80 minutes STUDENT NO.: LECTURE SECTION (please check): 0
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
General Physics Physics 101 Test #2 Spring 2017 Wednesday 3/1/17 Prof. Bob Ekey
 General Physics Physics 101 Test #2 Spring 2017 Wednesday 3/1/17 Prof. Bob Ekey Name (print): I hereby declare upon my word of honor that I have neither given nor received unauthorized help on this work.
General Physics Physics 101 Test #2 Spring 2017 Wednesday 3/1/17 Prof. Bob Ekey Name (print): I hereby declare upon my word of honor that I have neither given nor received unauthorized help on this work.
Physics A - PHY 2048C
 Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Physics A - PHY 2048C and 11/15/2017 My Office Hours: Thursday 2:00-3:00 PM 212 Keen Building Warm-up Questions 1 Did you read Chapter 12 in the textbook on? 2 Must an object be rotating to have a moment
Problem Set x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology. 1. Moment of Inertia: Disc and Washer
 8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
Chapter Rotational Motion
 26 Chapter Rotational Motion 1. Initial angular velocity of a circular disc of mass M is ω 1. Then two small spheres of mass m are attached gently to diametrically opposite points on the edge of the disc.
26 Chapter Rotational Motion 1. Initial angular velocity of a circular disc of mass M is ω 1. Then two small spheres of mass m are attached gently to diametrically opposite points on the edge of the disc.
Name: Date: 5. A 5.0-kg ball and a 10.0-kg ball approach each other with equal speeds of 20 m/s. If
 Name: Date: 1. For this question, assume that all velocities are horizontal and that there is no friction. Two skaters A and B are on an ice surface. A and B have the same mass M = 90.5 kg. A throws a
Name: Date: 1. For this question, assume that all velocities are horizontal and that there is no friction. Two skaters A and B are on an ice surface. A and B have the same mass M = 90.5 kg. A throws a
1301W.600 Lecture 16. November 6, 2017
 1301W.600 Lecture 16 November 6, 2017 You are Cordially Invited to the Physics Open House Friday, November 17 th, 2017 4:30-8:00 PM Tate Hall, Room B20 Time to apply for a major? Consider Physics!! Program
1301W.600 Lecture 16 November 6, 2017 You are Cordially Invited to the Physics Open House Friday, November 17 th, 2017 4:30-8:00 PM Tate Hall, Room B20 Time to apply for a major? Consider Physics!! Program
Physics 131: Lecture 22. Today s Agenda
 Physics 131: Lecture Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released at
Physics 131: Lecture Today s Agenda Rotational dynamics Torque = I Angular Momentum Physics 01: Lecture 10, Pg 1 An Unfair Race A frictionless block and a rolling (without slipping) disk are released at
Chapter 9. Rotational Dynamics
 Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Chapter 9 Rotational Dynamics In pure translational motion, all points on an object travel on parallel paths. The most general motion is a combination of translation and rotation. 1) Torque Produces angular
Physics 23 Exam 3 April 2, 2009
 1. A string is tied to a doorknob 0.79 m from the hinge as shown in the figure. At the instant shown, the force applied to the string is 5.0 N. What is the torque on the door? A) 3.3 N m B) 2.2 N m C)
1. A string is tied to a doorknob 0.79 m from the hinge as shown in the figure. At the instant shown, the force applied to the string is 5.0 N. What is the torque on the door? A) 3.3 N m B) 2.2 N m C)
PHYSICS 221 Fall 2016 EXAM 2: November 02, :15pm 10:15pm. Name (printed): Recitation Instructor: Section #:
 PHYSICS 221 Fall 2016 EXAM 2: November 02, 2016 8:15pm 10:15pm Name (printed): Recitation Instructor: Section #: INSTRUCTIONS: This exam contains 25 multiple-choice questions, plus 2 extra-credit questions,
PHYSICS 221 Fall 2016 EXAM 2: November 02, 2016 8:15pm 10:15pm Name (printed): Recitation Instructor: Section #: INSTRUCTIONS: This exam contains 25 multiple-choice questions, plus 2 extra-credit questions,
Chapter 10: Dynamics of Rotational Motion
 Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Chapter 10: Dynamics of Rotational Motion What causes an angular acceleration? The effectiveness of a force at causing a rotation is called torque. QuickCheck 12.5 The four forces shown have the same strength.
Physics 8, Fall 2017, Homework #6. Due at start of class on Friday, October 20, 2017
 Physics 8, Fall 2017, Homework #6. Due at start of class on Friday, October 20, 2017 Problems marked with (*) must include your own drawing or graph representing the problem and at least one complete sentence
Physics 8, Fall 2017, Homework #6. Due at start of class on Friday, October 20, 2017 Problems marked with (*) must include your own drawing or graph representing the problem and at least one complete sentence
3) When a rigid body rotates about a fixed axis all the points in the body have the same centripetal acceleration. FALSE
 PHYSICS 1401 Exam 3 Review Name TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body rotates about a fixed axis all the points in the body have the same
PHYSICS 1401 Exam 3 Review Name TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1) When a rigid body rotates about a fixed axis all the points in the body have the same
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Phys 106 Practice Problems Common Quiz 1 Spring 2003
 Phys 106 Practice Problems Common Quiz 1 Spring 2003 1. For a wheel spinning with constant angular acceleration on an axis through its center, the ratio of the speed of a point on the rim to the speed
Phys 106 Practice Problems Common Quiz 1 Spring 2003 1. For a wheel spinning with constant angular acceleration on an axis through its center, the ratio of the speed of a point on the rim to the speed
Phys101 Second Major-173 Zero Version Coordinator: Dr. M. Al-Kuhaili Thursday, August 02, 2018 Page: 1. = 159 kw
 Coordinator: Dr. M. Al-Kuhaili Thursday, August 2, 218 Page: 1 Q1. A car, of mass 23 kg, reaches a speed of 29. m/s in 6.1 s starting from rest. What is the average power used by the engine during the
Coordinator: Dr. M. Al-Kuhaili Thursday, August 2, 218 Page: 1 Q1. A car, of mass 23 kg, reaches a speed of 29. m/s in 6.1 s starting from rest. What is the average power used by the engine during the
A) 4.0 m/s B) 5.0 m/s C) 0 m/s D) 3.0 m/s E) 2.0 m/s. Ans: Q2.
 Coordinator: Dr. W. Al-Basheer Thursday, July 30, 2015 Page: 1 Q1. A constant force F ( 7.0ˆ i 2.0 ˆj ) N acts on a 2.0 kg block, initially at rest, on a frictionless horizontal surface. If the force causes
Coordinator: Dr. W. Al-Basheer Thursday, July 30, 2015 Page: 1 Q1. A constant force F ( 7.0ˆ i 2.0 ˆj ) N acts on a 2.0 kg block, initially at rest, on a frictionless horizontal surface. If the force causes
Preview. Circular Motion and Gravitation Section 1. Section 1 Circular Motion. Section 2 Newton s Law of Universal Gravitation
 Circular Motion and Gravitation Section 1 Preview Section 1 Circular Motion Section 2 Newton s Law of Universal Gravitation Section 3 Motion in Space Section 4 Torque and Simple Machines Circular Motion
Circular Motion and Gravitation Section 1 Preview Section 1 Circular Motion Section 2 Newton s Law of Universal Gravitation Section 3 Motion in Space Section 4 Torque and Simple Machines Circular Motion
Chapter 8 Rotational Motion and Equilibrium. 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction
 Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
Chapter 8 Rotational Motion and Equilibrium Name 1. Give explanation of torque in own words after doing balance-the-torques lab as an inquiry introduction 1. The distance between a turning axis and the
University of Houston Mathematics Contest: Physics Exam 2017
 Unless otherwise specified, please use g as the acceleration due to gravity at the surface of the earth. Vectors x, y, and z are unit vectors along x, y, and z, respectively. Let G be the universal gravitational
Unless otherwise specified, please use g as the acceleration due to gravity at the surface of the earth. Vectors x, y, and z are unit vectors along x, y, and z, respectively. Let G be the universal gravitational
Circular Motion Dynamics Concept Questions
 Circular Motion Dynamics Concept Questions Problem 1: A puck of mass m is moving in a circle at constant speed on a frictionless table as shown above. The puck is connected by a string to a suspended bob,
Circular Motion Dynamics Concept Questions Problem 1: A puck of mass m is moving in a circle at constant speed on a frictionless table as shown above. The puck is connected by a string to a suspended bob,
Physics 111. Tuesday, November 2, Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy
 ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
ics Tuesday, ember 2, 2002 Ch 11: Rotational Dynamics Torque Angular Momentum Rotational Kinetic Energy Announcements Wednesday, 8-9 pm in NSC 118/119 Sunday, 6:30-8 pm in CCLIR 468 Announcements This
Exercise Torque Magnitude Ranking Task. Part A
 Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
Exercise 10.2 Calculate the net torque about point O for the two forces applied as in the figure. The rod and both forces are in the plane of the page. Take positive torques to be counterclockwise. τ 28.0
