Introduction (1) A. Beckwith 1, F.Y. Li 2, N. Yang 3, J. Dickau 4, G. Stephenson 5, L. Glinka 6, R. Baker 7
|
|
|
- Cameron Wheeler
- 5 years ago
- Views:
Transcription
1 ompeing osmology Models. n enropy producion help flsify cyclic models of cosmology, or vrins long he lines discussed by Roger Penrose he IG conference in Penn Se, 7? A. Beckwih, F.Y. Li, N. Yng, J. Dicku, G. Sephenson 5, L. Glink 6, R. Bker 7 ) beckwih@uh.edu, hongquing Universiy deprmen of physics; Insiue of heoreicl Physics; Beckwih@iibep.org, Americn Insiue of Bemed Energy Propulsion ( ibep.org); Seculine onsuling, USA ) cqufngyuli@homil.com, hongquing Universiy deprmen of Physics, Insiue of heoreicl Physics ) cqunnyng@homil.com, hongquing Universiy deprmen of Physics, Universiy of exs Brownsville ) gry.sephenson@gmil.com, Seculine onsuling, USA 5) jondu@oponline.ne, Independen Science resercher, dvisory bord of Prespceime Journl 6) lglink@gmil.com, Seculine onsuling, USA 7) drroberbker@grvwve.com,grvwve LL nd rnsporion Science orporion, 8 uscny Avenue, Ply d Rey, A 99, USA Absrc: In he inugurl IG meeing, on Augus, 7 Penn Se, Roger Penrose[] gve presenion bou n lernive o cyclic cosmologicl models, which needs experimenl ess for flsifibiy. As discussed by Beckwih, in EJP [], Penrose brough up how De Alberin wve equion, s simplified in fl spce could led o rising vcuum nucleion field which would engender he pop up behvior s sough in mos emergen field models of grviy. he sclr field pop up wih cerin qulificions is no so srling in iself. Now for he rdicl exension Penrose brough o ber. Penrose ssered in his IG lecure h here ws good chnce h here ws no collpse in fuure evens, bu h mer would be evenully sucked up by millions of blck holes, creing clen up of mos inersellr mer. he issue o be brough up is how o come up wih mpping for re combinion of he blck hole colleced meril, for big bng. A opic which ws no solved by Penrose. We lso discuss crieri for firs order phse rnsiion which would be feed ino new universe, which wis experimenl confirmion. Inroducion Penrose ssered h he millions of blck holes would evenully undergo Hwking s evporion [], i.e. h in some fshion h here would be relese of he mer- energy For hose who wish o look i up, Hwking s evporion of blck holes, involves suble qunum rgumens nd ries o reconcile blck hole physics wih known hermodynmics.,eg. As n exmple he nd lw of Blck hole dynmics. rschen[] ses he bsic ssumpions involved, while Hwkings [] sed evporion s o wys which my ie in wih ypicl enropy / re clculions s given by Bernsein nd oher wriers. he esies concepul sring poin is o use he equivlence beween number of operions which Lloyd [5] used in his model, nd ol unis of enropy s he uhor referenced from rroll [6], nd oher heoriss. he key equion Seh Lloyd [5] wroe is s follows, ssuming low enropy vlue in he beginning 5 6 [# operions] / ~ Sol ~ k B ln () Seh Lloyd[5] is mking direc reference o linkge beween he number of operions qunum compuer model of how he Universe evolves is responsible for, in he onse of big bng picure, nd enropy. Needless o se hough, Eq () bove, nd he issue of if or no here is well defined hreshold bulk elecric nd mgneic chrge conribuion o energy. If here is, indeed n evporion effec of blck
2 hole physics, wh juncure does one hve collpse of hreshold effec for clculions bou he minimum enropy bsed upon blck hole models involving elecric nd mgneic chrges? Assuming hen, h he relevn Blck holes evpore, Penrose [] nex presened he quesion of n undeermined mpping of he evpored Hwking rdiion bck o he nexus poin for new big bng. he uhor, Beckwih, sked Penrose repeedly he IG bou he nure of he mpping of relesed Hwking rdiion bck o new big bng. Penrose hrew he quesion bck o Beckwih, s Beckwih s reserch problem, no his..assume, if one will h here re N number of universes under going Penrose syle expnsion nd hen blck hole clen up of mer- energy s hese N universes expnd. Ech universe conins roughly 88 enropy unis of compuionl informion s embedded in sy spirl 9 glxies. If ech spirl glxy hs n enropy reding of bou enropy unis, his leds o n over 88 hng of bou enropy unis, s opposed o n observble enropy unis for he universe s cn be ccessed by insrumenion. Which leds sking wh is he significnce of h enropy gp? Secondly, nd mos imporn o his discussion, here is srnge rcor suck up of bis of informion from ech of he N expnding universes, nd he Hwking rdiion is, wihin meg srucure mpped bck o he locus poin of noher sen of N big bngs vi ypicl phse spce srnge rcor dynmics. How o verify his wild supposiion experimenlly? See he conclusion of his ricle for Beckwih s guess s o wh o ry o do experimenlly o indirecly infer he exisence of his meg srucure nd of srnge rcor collpse of Hwkings rdiion bck o N locus poins for N number of big bngs. Wh is needed o be experimenlly flsified: relic grvion producion involves HFGWs, indiced by rpid drop off of grvion creion fer he onse of he big bng We should firs look he key ssumpion of he Ng [7],[8] pproch o enropy : he wvelengh of he pricles conribuing o enropy re ulr-long, i.e., here is n order of mgniude difference beween he cube of he wvelenghs of he pricles nd of he conining volume of spce, V, which is nlyzed o obin he enropy figure Ng [7],[8] uses o ge his infinie qunum sisics.he sme mehodology of compring he cube of wvelenghs wih he expeced spceime volume is used o ge Ng s [7,[8]infinie qunum sisics, ssuming h relic grvion producion involves HFGWs. hen one nlyzes enropy producion wh Ng did wih DM nd wvelenghs, nd he volume of spce V,. Bu insed of DM, his involves grvions, wih n ulr-shor wvelengh, necessiing smll volume of spce in he beginning of grvion producion. So he sme infinie qunum sisics procedure Ng used for DM cn be used for grvions, excep h he grvions re produced in he very beginning of he inflionry er. So he creion of grvions is enhnced in he beginning of cosmologicl nucleion by he requiremen of oneo-one relionship beween shorwve lenghs of HFGW nd smll spce ime volume for relic grvion creion.hen i s likely h he d ses observed in he Li-Bker deecor could indice rpid drop off of grvion creion fer he onse of he big bng. his should be invesiged by flsifible experimenl procedures. Predicion: relively nrrow rnge of GW frequencies for relic grvion producion Appendix exmines his ssumpion nd compres i direcly wih noher ssumpion mde by Giovnnini[9], which is reformuled o sser h if ll frequency rnges for GW rdiion were 9 permissible, one would see ol vlue of enropy of nerly. his is done while no ssuming s we did HFGW condiions. herefore, Giovnnini s (99) predicion s wrien up in 8 [9] is ssumed o be indefensible, nd h
3 relively nrrow rnge of GW frequencies for relic grvion producion is wh should be looked for vi eiher he Li-Bker HFGW deecor or by he sellie mission. Implicion: How n inflon could rise nd fll from herml inpus from prior universe Here re some ddiionl possible spinoffs of hese sors of ides, if hey re experimenlly verified. Appendix D bsed upon Beckwih s work, [9] shows o-he-poin presenion of how n inflon could rise nd fll from herml inpus from prior universe. hese re noes dped from presenion by Dr. Penrose regrding his lernives o ypicl cyclic-universe cosmologies []. We elbore upon Penrose s srling conclusions, bu his firs pr of his presenion is useful, since i fis very closely wih he uhor s mehodologies for herml inpus from prior universe. Are irregulriies in he MBR specr reled o enropy producion? If his cn be verified experimenlly, he bigges pyoff would be o ddress n issue h he uhor discussed wih Srkr of Oxford[]. Appendix A gives he bsic ide: re he irregulriies in he MBR specr, due o non-sndrd physics, which re n exension of he sndrd inflon model, used o jusify enropy producion? We hink h here is meri o his ide nd h i should be invesiged. A he minimum, undersnding enropy producion would llow us o nlyze if he srucure formion mehodology experimenlly presened by Ruu, e l. [] ies in wih models of enropy producion, nd if no, wh bou verifying he sndrd model for MBR producion, s G. Hingsw [] nd ohers promoe? Or wh if Srkr [] is righ? A summry of wh A.W. Beckwih [] hinks of hese issues my be found in presenion mde IDM 8 Srucure formion from enropy generion Sring wih wh Beckwih used in 8 [], nd lso in Renconres De Blois [] /' 5 [ ] / N S ~ k ln # operions N log logv log E ~ inf B ol Iniil cond () Aiding in he developmen of confirming/flsifying Eqn. () bove re srucure formion quesions h we leve s open quesions o be ddressed by he MBR/srophysics communiy: his would be ligned wih he quesion of how srucure formion could rise s resul of enropy generion. Srkr [] nd ohers, wih heir rce rck models of inflion, hve done useful pioneering work in defining coupled fields undergoing symmery breking h re coupled o he inflon. he uhor, A.W. Beckwih, hinks h such supposiions need experimenl verificion, nd h he boos of ol enropy by he relic grvion vlue given in ΔS grvion producion 5 in ime inervl could led o ddiionl insighs ino wheher or no Srkr [] (8) or Hingsw [] is righ bou he origins of irregulriies in he MBR specr. Srkr {} ses h he irregulriies mens physics beyond he sndrd cosmologicl model ssumed for WMAP, while Hingsw[] ses h he irregulriies re merely sisicl nomlies. How iniilly huge vcuum energy nd is rpid collpse in spce-ime o much smller cosmologicl consn vlue ids in he brekup nd reformulion of enropy producion???? he uhor, A.W. Beckwih, wishes o close wih wh will be fuure projecs o ddress some of he bove issues. As discussed wih chrkin,[5]bremen, Augus 9 h, 8, he uhor wishes o deermine if or no he dichoomy beween n iniilly huge vcuum energy, s specified bove in his mnuscrip, nd is rpid collpse in spce-ime o much smller cosmologicl consn vlue, ids in he brekup nd reformulion of enropy producion. he uhor s supposiion is h i is relevn o wo res. Firs, he
4 uhor ssume h here is brekup of he iniil insnon srucure from prior universe. Since he uhor lso views grvions s kink-nikink srucure, he supposiion is h iniilly, from prior o presen universe, here would be similr phenomenon: iniil lck of numericl densiy of grvions jus before second-order phse rnsiion, which is discussed in pr in Appendix. Secondly if, fer second-order phse rnsiion we see evidence of srophysicl d supporing he rebirh of boh enropy nd grvion producion, we should ke his hypohesis seriously. Should he cosmologicl consn/vcuum energy linkge be proved o be consisen wih he brekup nd hen reformulion of grvion producion in phse rnsiion, hen he uhor, A.W. Beckwih, hinks h reserchers could be on rck for new experimenlly flsifible crieri, o be developed for MBR physics. Finlly, Relic grvion produced enropy he onse of he big bng. Why sring enropy would be so smll while MBR enropy would be so lrge As closing remrk, Beckwih wishes o sugges soluion o Penrose s implied quesion bou enropy s rised in Edingborough, Scolnd [6] conference proceedings. Penrose lks bou he nd lw, nd is implied requiremens s o he smll iniil vlue of erly universe enropy, nd hen ses h grviionl enropy would no be so mjor, wheres MBR mer conribued enropy would be much lrger. Beckwih is convinced h relic grvion producion he onse of he big bng, i.e. before he 5 conribuion of enropy from mer iself would be necessry o boos enropy from is smll vlue he onse of he big bng, o much higher level, nd h enropy would be iniilly drmiclly boosed by h process. I.e. he uniformiy requiremen Penrose lks bou in srucure would be cully s of up o he Elecro wek rnsiion, nd fr fer he iniil onse of inflion iself. A new ide exending Penrose s suggesion of cyclic universes, blck hole evporion, nd he embedding srucure our universe is conined wihin Beckwih srongly suspecs h here re no fewer hn N ( lrge number) of universes under going Penrose infinie expnsion nd ll hese re conined wihin meg universe srucure. Furhermore, h ech of he N universes hs blck hole evporion commencing, wih he Hwking rdiion from decying blck holes. Ξ i i i N If ech of he N universes is definble by priion funcion, we cn cll { }, hen here exis n 7 informion minimum ensemble of mixed minimum informion roughly correled s bou i bis of informion per ech priion funcion in he se { } conserved beween se of priion funcions per ech universe i i N before Ξ, so minimum informion is 8 i i { } { Ξ } i i N i i N before fer Ξ () Ξ i i. i N However, h here is non uniqueness of informion pu ino ech priion funcion { } Furhermore h wihin he meg srucure, h Hwking rdiion from he blck holes is colled vi srnge rcor collecion in he meg universe srucure o form new big bng for ech of he N
5 Ξ i i i N universes s represened by { }. Verificion of his meg srucure compression nd expnsion of informion wih non unique venue of informion plced in ech of he N universes would srongly fvor Ergodic mixing remens of iniil vlues for ech of he N universes expnding from qusi singulriy beginning.if his ide is in ny wy confirmble, i would lend credence s o he formion of he drk flow hypohesis, nd of how nhrmonic perurbive conribuions o iniil inflionry expnsion my occur, wihin prilly rndom ergoic bckground. Beckwih clims h such process would inherenly fvor 7 he smll bis of informion per ech priion funcion represening he sr of expnsion of new universe. Hopefully, in doing so, one cn explin, evenully, he problems wih enropy modeling presened in Appendix below. his hs similriy wih consrucion done by Beckwih [8], nmely looking he following expression of energy flux being re formuled for ech universe. I.e. sr wih he Alcubierre s formlism bou energy flux, ssuming h here is solid ngle for energy disribuion Ω for he energy flux o rvel hrough. [8] de d r 6π ' = [ lim r ] Ψd dω () he expression Ψ is Weyl sclr which we will wrie in he form of Ψ i x x x [ h h h ] [ h h h ] = r r r r () Our ssumpions re simple, h if he energy flux expression is o be evlued properly, before he elecro x x wek phse rnsiion, h ime dependence of boh h nd h is miniscule nd h iniilly h h, so s o iniie re wrie of Eq. () bove s Ψ [ h ] ( i) r (5) he upsho, is h he iniil energy flux bou he inflionry regime would led o looking Ψ d ' [ r ] h ( n~ ) (6) his will led o n iniil energy flux he onse of inflion which will be presened s de d r = 6π [ n~ ] Ω r h (7) If we re lking bou n iniil energy flux, we hen cn pproxime he bove s E iniil flux Inpus ino boh he expression r h our conclusions. he derived vlue of r 6π r h [ n~ ] Ωeffecive, s well s Ω effecive will comprise he res of his documen, plus Ω effecive s well s Einiil flux will be ied ino wy o presen (8)
6 energy per grvion, s wy of obining n f. he n f vlue so obined, will be used o mke S ~ n. We sser h relionship, using Y. J. Ng s enropy [7,8] couning lgorihm of roughly enropy f in order o obin S enropy ~ n f from iniil grvion producion, s wy o qunify n f, h smll mss of he grvion cn be ssumed. How o ie in his energy expression, s given in Eq. (8) will be o look he formion of non rivil grviionl mesure which we cn se s new big bng for ech of he N universes s represened by [9] nd n( Ei ) he densiy of ses given energy E i for priion funcion defined by i N N Ei i de i i n Ei e ( ). (9) i i { Ξ } Ech of he erms N universes E i would be idenified wih Eq.(8) bove, wih he following ierion given, nmely for N N Ξ j= j jbeforenucleionregime Ξ vcuumnucleionrnfer i i fixed fernucleionregime () For N number of universes, wih ech Ξ for j = o N being he priion funcion j jbeforenucleionregime of ech universe jus before he blend ino he RHS of Eq. () bove for our presen universe. Also, ech of he independen universes given by Ξ would be consruced by he bsorion of j jbeforenucleionregime sy one million blck holes sucking in energy. I.e. in he end Ξ j jbeforenucleionregime Mx k = ~ Ξ k blck holes jhuniverse () One cn re Eq. () s de fco Ergoic mixing of prior universes o presen universe, wih he priion funcion of ech of he universes defined by Eq (9) bove. Filling in he impus ino Eq. (9) o Eq. () is wh will be done in he monhs ghed. r h will be he one o fill in, vi considering [] plus oher models. Doing so will begin o llow us o form more precise evluions of Eq. (9) o Eq. () For he ske of convenience, one cn wrie [, ] So, hen r h ~ k h () For our purposes, we shll cll E r ~ l iniil flux [ h ] [ n~ ] Ω effecive r ~ k () 6π cm, ~ sec, Ω effecive n effecive cross secionl re s o he emission of grvions, nd k defined s physicl wve vecor. L. rowell
7 sed h GW would undergo mssive red shifing []. Needless o se, he vlue of k o consider would be for he GHz bnd of GW [,] d ( k kgw ) >> () dη 9 Also, for he frequences of [,] Hz, hen h ~ h rms ~ (5) hen he numericl coun fcor cn eiher be of wo imes, eiher s bi coun, or jus s srigh For primordil blck hole. Nmely, if ne ccelerion is such h ccel = π B h s menioned by Verlinde [], [] s n Unruh resul, nd h he number of bis is * ΔS c (.66) g c nbi = (6) Δx π k B [ Δx l p ] π k B his Eq. (6) hs emperure dependence for informion bis, s opposed o [5] Should he Δx l p k [ g ~.66 ] n f c S ~ ~ (7) order of mgniude minimum grid size hold, hen conceivbly when ~ 9 GeV[] n Bi (.66) g [ Δx l ] p * c π k B / / l ~ [.66 g~ ] he siuion for which one hs [], [5] Δ x l wih l wheres n Bi if Δx l / l / >> l Here, we mke hs ssumpion h eiher ~n ~. n Bi or ~n ~ l ~ corresponds o n Bi (8) n Bi per uni volume of phse spce wih he emperure vrying from low vlue o up o Kelvin ( emperure scle). All hese scling prmeers would be plced in Eq. () bove, wih Eq. () hen pu in discreized version of Eq. (9), Eq. (), nd Eq. (). We shll nex lk bou if his nlysis of bis nd he like cn be reled o Sephn-Bolzmnn nd simir remens of qunum flucuions. Looking generl relion beween herml nd qunum flucuions in relivisic field heories From considering sclr field remen of energy densiy nd pressure for non inercing gses, nd hen rele he nlysis o how domin wll brek down would led o GW generion, we shll consider how GW my be inroduced in he presen universe. o begin wih, go o he [6, 7, 8] consrucion given in ble below which compres he vlues s given by ble Sefn Bolzmnn smir ε = π 5 π P = [ ] 5 L
8 p = π π [ ] 5 ε = 5 L he concep of qunum phse rnsiion involving he geomery of spil box of lengh L wih criicl emperure is sed s [6, 7, 8] by prmeers for qunum phse rdiion [9] Depending upon he geomery of L = (9) Qunum phse rnsiion, se by wih differen vlues of L Δx l / / l If one picks he vlue of corresponds o L Δx l / / l, where if / / Δ x l l wih l ~ l n Bi nd he vlue of n Bi corresponding o Δx l / l / >> l will hen ell us how he bsolue mgniude of energy densiy in smir ple remen of n iniil energy densiy would scle s n Bi. o ge o he ide, we would mke he nex ble, nmely L Δx ~ l n Bi [ Δx l ] when l ~ l ble L Δx >> l n Bi [ Δx >> l ] he number of bis goes highes when number of bis when L Δx >> l L Δx ~ l n Bi n Bi low. high, nd he lower he min poin is h hving high criicl emperure [ Δx l ] is no he sring heory picure, nd corresponds o more rdiionl picure of dimensionl universe. Hivng [ Δx >> l ] is nmore consisen wih regrds o sring heory nd is congruen wih [,,] L Δx >> l When he bis drop is when, i.e. he sring heory version minimum unceriny mens h one hs less number of pek bis, wheres L Δx ~ l mens much higher pek vlue of bis my be possible. his cn,be ied ino model of he universe where we ge mximum chnge in he flux of bis from so clled cold universe model. I.e. wh if here ws nerly zero degrees Kelvin sring poin for he increse in ermperure? Assessing wh would hppen in he brne heory cse would be, for GW equivlen o,
9 Figure, he mpliude nd frequency of he HFGWs expeced by he brne oscillion models in he submillimere-size exr dimensions. he figure is ken from [], where l is he curvure sclr of he bulk, d is he disnce beween he "visible" brne nd he "shdow" brne If one hs high frequency Grviionl wves, wih regrds o brne heory, hen his figure bove would hve o be reconciled o he vlue of Eq. (8) bove, wih, up o poin he iniil energy defined vi looking Fig. () bove, wih Eq. (8) se s proporionl o. Einiil Energy flux ~ hω () GrviyWve he iner relionship beween Eq. () nd n bsolue vlue of energy densiy for, sy relic pricles i.e. grvions s informion crriers ε π = 5 π [ L ] 5 () 5 π E [ ] his would hve o be esblished, i.e. how iniilenergyflux L = ε () he ide which we hve is h he deils of filling in he seps of Eq. () bove, nd reconciling i o Eq. () nd Eq. (8) will llow us o sr o esime he number of bis rnsferred from prior o he presen universe, in erms of when he precise vlue of L is obined, h we re looking poin where he qunum effecs, nd firs order phse rnsiion hve occurred.. hen, s n exmple, he precise vlue of ~ Δx being reched, vi build up of emperure, is defined by. phse rnsiion delineed L wih he rise of emperure going from low vlue up o reching [ Δx >> l ] We cn close wih his consrucion by sying h reching up o criicl emperure is phse rnsiion, wih subsequen decy of domin wll occurring ferwrds, in order o void he well
10 known dum h if domin wlls did no decy rpidly, h he MBR specrum would be drmiclly differen from wh is observed ody. [] onclusion, orgnizing inpus ino finding he mpping for Eq. (), from blck Holes Job one will be in deermining if ~n ~ n Bi or ~n ~ n Bi per uni volume of phse spce wih he emperure vrying from low vlue o up o Kelvin ( emperure scle). Once his would be esblished, hen coming up wih deils of Eq. () mpping would be fesible. he uhor views his s wy o esblish if here is n ergoic mixing proocol, of millions of blck holes from differen universes. he deils of his mpping, s specified s n invesigive proocol, where discreizion of Eq.(9) would be necessrily pr of he physics reserch work. Also, i would necessie mking linkge o wh Beckwih e l pu up s fr s numericl coun for mssive grvion couns in per uni phse spce volume of GW deecor which cn be wrien s [,5] J effecive ncoun mdgrvion () ~ 65 m grms As sed by Beckwih, in [5], DGrvion n, while coun is he number of grvions which my be in he deecor smple. Geing Eq. () srigh for deecor while undersnding he iner n relionship of coun o ~n ~ n Bi or ~n ~ n Bi per uni volume of phse spce iniilly is wh we should be doing.[6]. In ddiion, our ble resuls should be reconciled o Eq. ()., i.e. wh o do wih he mximum energy densiy. h will require lo of work. Noe h he iniil GW emerging from inflion would be defined by some equivlen srucure s defined in [7] wih regrds o n iner relionship beween enropy, bis of informion, nd inflon physics, deils which we expec would be seled if nd when GW sronomy becomes n iompericl science. Wh we would like o see, would be o ge he mppings described by Eq. () rigorously defined. Doing so would enble use o mke connecion wih wh ws done by Beckwih i.e. mking connecion beween Eq. () nd hen he increse in he degrees of freedom problem Beckwih wroe bou s follows. he formul E herml k B emperure ~ β is feed ino ω g provided h we pick ime ime, nd lso by seing up he E ~ herml k Bemperure β. In oher words, for relic GW/ grvion producion, opologicl rnsformion nd inerrelionship beween he componens ~ α nd Eherml k Bemperure ~ β in he iniil increse in he degrees of freedom problem denoed by [] ~ ~ x i = exp α x [ ] β i () Appendix A: Vriions in he MBR specr nd wh hey imply for enropy producion Our guess is s follows: he mer-energy flux implied by he exisence of wormhole ccouns for 7 perhps bis of informion. hese could be rnsferred vi wormhole soluion from prior universe
11 o our presen, nd here could be perhps 7 minus bis of informion emporrily suppressed during he iniil bozonificion phse of mer righ he onse of he big bng iself. hen we predic h here is drmic drop in he degrees of freedom during he beginning of he descen of emperure from bou Kelvin o les hree orders of mgniude less. he drop in degrees 5 of freedom hppens s we move ou in ime from n iniil red shif, z, o somehing lower, which is when he emperure drops from bou Kelvin o significnly lower vlue of [7] h H εv 8 Kelvin ~ Hwkings π k iniil B Which model we cn come up wih h does his is he one we need o follow, experimenlly. And i gives us hope of confirming wheher or no we cn evenully nlyze he growh of srucure in he iniil phses of qunum nucleion of emergen spce-ime. We lso need o consider he dum so referenced for he irregulriies of he cooling-down phse of inflion, s menioned by Skr [8] in n e mil o he uhor, Beckwih,. Qusi-DeSier spce-ime during inflion hs no "lumpiness" -- i is necessrily very smooh. Neverheless one cn genere srucure in he specrum of qunum flucuions origining from inflion by disurbing he slow-roll of he inflon -- in our model his hppens becuse oher fields o which he inflon couples hrough grviy undergo symmery breking phse rnsiions s he universe cools during inflion. he rce rck models, fer he inflon begins o decline, would be idel in obining he necessry couplings beween he inflon, nd fields which undergo symmery breking rnsformion. We will refer o his opic in fuure publicion. We cn mke few observions hough bou he ssumed coupling. Firs, here is quesion of wheher here is finie or infinie fifh dimension. Sring heoriss hve rgued for brne world wih wrped, infinie exr dimension, llowing for he inflon o decy ino he bulk so h fer inflion, he effecive drk energy disppers from our brne. his is chieved by shifing wy he decy producs ino he infiniy of he 5h dimension. Nice hypohesis, bu i presumes MB densiy perurbions could hve heir origin in he decy of MSSM fl direcion. I would reduce he dynmics of he inflon if here were seprion beween Dp brne nd Dp nibrne vi moduli rgumen. h if we do no hve n infinie fifh dimension? Wh if i is compced only? We hen hve o chnge our nlysis. Anoher hing. We plce limis on inflionry models; for exmple, minimlly coupled λ is disfvored more hn σ. Resul? Forge quric inflionry fields, s hs been shown by. Peiris, Hingshw e l. [9] We cn relisiclly hope h WMAP will be ble o prse hrough he rce rck models o disinguish beween he differen cndides. So fr, Firs-Yer Wilkinson Microwve Anisoropy Probe (WMAP) Observions: Implicions For Inflion is giving choic inflion run for is money. (A)
12 Figure by Srkr shows he gliches h need o be ddressed in order o mke MBR d se congruen wih n exension of he sndrd model of cosmology. Pssed o he uhor, Februry 8 [8, ], nd brough up in IDM 8 [] Appendix B: Formulion of crieri for second-order phse rnsiion he onse of nucleion of new universe Le us firs review orrieri s nd Mushunin s [] conribuion o sbiliy nlysis of wve funcionl remen of QD bulk viscosiy-over-enropy consn-rio se equion. he ide is h we hve iniilly super ho plsm reching pek vlue of viscosiy for given emperure, which is less hn or equl o criicl emperure, reflecing he QD plsm hving pek vlue for viscosiy. For hose who wish o undersnd how his my work ou, we cn refer o pper by Askw e l [6] which specified sheer bulk viscosiy pproximed by viscosiy vlue wih d f O(), which wekly depends upon he number of qurk flvors n f in he qurk-gluon plsm [ g ln ] η = g (B) d f Here, g is fixed by he number of degrees of freedom of he sysem. Askw e l.[] lso specify h in qurk-gluon plsm, frequenly here is n ddiionl nomlous conribuion o viscosiy, η A cused by urbulen fields wihin he qurk-gluon plsm. Askw e l. [] concluded in heir documen h frequenly we hve η (B) = ol = η η A
13 Frequenly we lso hve for exremely high emperures o good firs pproximion, s Densiy π g 5 = Where For high emperures, if g is he ne degrees of freedom of he plsm gs h we cn model s n ulr-relivisic fluid. g is on he order of, i.e., reflecing mny iniil degrees of freedom, [ ] η cons ~ π s Densiy ol (B) Wih clssicl fluid models, even for qurk-gluon plsms, his ssumes we re working wih η A s no very srong conribuing fcor o Eq (B), leding o lmos infinie viscosiy if we hve viscosiy lmos enirely dependen upon emperure, s he emperure climbs.. Wih he model of enropy so offered bove, we hve if he emperure is no eleved nd he wo erms in Eq. (B) conribue, rouble in obining sble vlue for Eq. (B) bove s consn. I so hppens h orrieri s nd Mushunin s [] ide is o incorpore modificion of he Bjorken equion for cosmology pplicions, τ [ τ s] d s = dτ Rτ where τ is conforml ime, nd R is he Reynolds number, nd s is enropy densiy. his Eq. (B5) is well bove he complexiy level of wh one expecs from he simple linerized models, where we look, sy, if y represens spce ime lengh, ec., wih s ( τ ) s ( τ ) δ s( y) exp[ iky] = (B6) τ, And velociy sbiliy nlysis we hve is v x / so h evenully we look x = δ s s nd x y y spce ime (B) (B5). So he x τ x A A A x x τ (B7) A his is when we hve high emperures mjor simplificion of he Aij erms in he mrix in he righ hnd side of Eq. (B7).his simplificion of he righ hnd side of Eq. (7) hppens when we wrie η nd s. We obin wih his simplificion of enropy nd viscosiy relively consn Reynolds number R, nd relively consn speed of sound in he viscous medi c s. he resuling simplificion nd drop ou of erms in he evoluion equion llows us o wrie [,] A = cs R (B8) nd A = k ( R ) (B9) nd A = kcs R /( R (B) ( ) )
14 nd A ( c ) c R c R ( R ) k R ]/( ) = [ s s s R (B) In his limi we hve sbiliy nlysis performed for he eigenvlues of A A (B) Where we re using (B) re such h, if A A A A, nd wih he summrized resuls h for { min,λ mx } A λ of Eq λ we lwys hve insbiliy (B) λ we lwys hve sbiliy (B) > min mx < λ <, λ, we some imes hve sbiliy, (B5) min mx > nd someimes we do no hve sbiliy. he forms of Eq (B) o Eq (B5) remin he sme, bu we sser h if we devie from sric dherence o η nd s due o mrked iniil condiions, i.e., unusul conribuions due o he nhrmonic conribuion o viscosiy η A we will hve incresingly involved crieri for forming he mrix for Eqn. (B) nd Eq. (B7) o Eqn. (). We re looking ino wh hese crieri should be for very unsble iniil GU crieri, wih he proviso h we re no ble o use simple linerizion in GU iniil condiions, bu h he rio of ηol s Densiy ~ [ π ] holds.[,]. Appendix : ompring implemenion of Jck Ng s Δ S ΔN for wvelenghs cubed, of he order of mgniude of n enropy genering volume of spce, wih Giovnnini s clculion of enropy for ll permissible rnges of frequencies. As sed bove, our implemenion of he Δ S ΔN rule for HFGW [7,8] ssumes we re ble o mke direc comprison beween he wvelengh of HFGWs nd he region of spce in which hey re evlued. his comprison yields n inerpreion of growh of enropy due o n infusion of vcuum energy he onse of inflion, which we hink needs o be flsified experimenlly. I.e., h in he 7 beginning of qunum nucleion, here were perhps bis of informion presen. h he producion of relic grvions in HFGW erly universe nucleion environmen perhps dded up o bis of informion in 5 seconds -- perhps closer o n order of mgniude of seconds in he boos effecs of enropy from informion rnsferred from prior universe o our presen universe. he nlysis for how his could hppen depends upon he verificion of supposiion h HFGWs hve wvelengh whose vlue cubed would be wihin n order of mgniude of he iniil volume of spce-ime in which he HFGW re nucleed in relic inflionry condiions. Sying his hough leds us o consider: do ll frequencies conribue o he generion of grviionl wves eqully? (his hs implicions for he generion of enropy, for resons we will ge o nex.) On he fce of i, his quesion is nonsense. LISA nd LIGO, wo very well engineered deecors, re superb deecors of low frequency grviionl wves, s ws given by he Amldi 5 meeing. In ddiion, he being is h llegedly h signl/noise issues will mke deecion of HFGWs, especilly from relic condiions, excepionlly difficul. he Li-Bker design effor, wih is emphsis on sic mgneic field h cn be impinged upon by HFGWs hs redy nswer o his lleged difficuly. However, he sheer number of conribuions o enropy if ll rnges of frequencies conribue o GW producion in he universe should be considered.[]
15 Forunely, here is clculion uhored by Giovnnini [9] nd ohers h does coun o enropy generion in ol from he enire specrum of GW genered, wih srling conclusion: h he presen high level of enropy ody cn be effecively genered by GW producion! his clculion reds s 8 follows. If we se V s he spce-ime volume, hen look v ~ Hz, nd v ( ) / ~ H M P ~ Hz s n upper bound, ssuming no relionship like he GW wvelengh cubed, s proporionl o erly universe volume, which leds o r( ν ) ln ngrvions, where n grvions refers o he number of produced grvions over very wide specrl rnge of frequencies. his ssumes h we re working wih S H M v gw = V r P ν P ( ) v dv ( ) ( H M ) / ν () ΔN ~ his should be compred wih HFGW producion in relic condiions righ relichfgw fer he onse of nucleion of new universe. I.e. here is hve relic grviionl producion, s occurring fer he nd order iniil phse rnsiion referenced in Appendix B, for GU, wih informion/enropy 7 5 for universe which Dr. Smoo pegs s less hn or equl o informion / enropy 88 informion / enropy in our presen universe, which will be nd order phsernsiion explined more fully in fuure publicions. his should be compred wih he resul h Sen rroll [6] cme up wih: h for he universe s whole 88 S ol ~ () his Eq.() should be compred wih he even odder resul h he uhor discussed in quesion nd nswer period in he Bd Honnef perspecives in qunum grviy [] meeing, April 8 o reconcile Eq. () wih he odd predicion given in Eq. () nmely, s presened by rroll, [6] ΔS BlckHole 9 M ~ 6 M SolrMss S () I.e. he blck hole in he cener of our glxy my hve purporedly more enropy hn he enropy of he enire KNOWN universe. Our hierrchy of how o genere enropy from iniil condiions presen in he iniil cosmologicl evoluion is n emp o mke sense of he inheren weirdness presen in Eq. (), Eq. (), nd Eq. (). he hree equions ogeher do no fi s consisen whole. We sser h here is no wy h we cn meningfully jusify he conclusions of Eq. (). And while we view grvion producion s crucilly imporn for he rise in enropy, s oulined by Dr. Smoo [5], grvion producion is mos likely o be concenred s nrrow relic grvion producion s n onse o enropy generion. We hope h he ricles following his mnuscrip will enble us o hndle he frnkly physiclly bsurd implicions inheren in ll hree of he bsic equions wrien in his documen nd permi us o develop n experimenlly flsifible se of experimenl procedures o resonbly invesige enropy creion from firs principles.
16 Appendix D: Emergen inflon field due o herml inpu from prior universe (he D Albemberin operion in n equion of moion for emergen sclr fields) his ws presened he IUAA meeing in Indi by he uhor, Beckwih, in December 7[6] nd Beckwih [ ] We begin wih he D Alberin operor s pr of n equion of moion for n emergen sclr field. We refer o he Penrose poenil ( wih n iniil ssumpion of Euclidin fl spce for compuionl simpliciy) o ccoun for, in high emperure regime, n emergen non-zero vlue for he sclr field due o zero effecive mss high emperures. When he mss pproches fr lower vlues is when non-zero sclr field reppers. Le us now begin o model he Penrose quinessence sclr field evoluion equion. Look he fl spce version of he evoluion equion = V & & (D) In he Friedmn-Wlker meric, his uses he following s poenil sysem o work wih, nmely: ( ) ( ) ( ) () R ~ 6 ~ 6 ~ κ M M V (D) his ssumes ±, κ, nd curvure signure compible wih n open universe. h mens, = κ s possibiliies. So we will look he, = κ vlues, beginning wih () ( ) ( ) c e M c V r exp 6 ~ = = α κ α & & (D) We find he following bsic phenomen, nmely () ( ) ( ) 6 ~ ) ~ ( = ε κ α high M M c (D) () ( ) ( ) 6 ~ ) ~ ( = ε κ α Low M M c (D5)
17 he difference is due o he behvior of M ( ). We use M ( ) ~ xion mss m ( ) in sympoic limis wih Kolb s [7]. m.m = ( Λ / ) (6D) ( ) ( ) 7 QD Bibliogrphy [] Penrose, Roger, onforml yclic osmology, Drk Mer, nd Blck Hole Evporion, Augus, 7,IG Inugurl onference. Se ollege, PA. Penn Se Universiy... Augus 7 Augus, 7 [] Beckwih, A.W. Penrose Model poenil, compred wih olemn-weinberg Poenil for erly universe sclr evoluion, Elecron.J.heor.Phys.5N7:95-6,8. [] rschen, Jennie, An inroducion o Blck Hole Evporion, hp://rxiv.org/bs/gr-qc/55, pges, lex. Published in Mhemicl Mehods of Physics, proceedings of he 999 Londrin Winer School, ediors A. Bysenko nd F. Willims, World Scienific () [] Hwking, S.W., Evporion of wo-dimensionl blck holes, Phys. Rev. Le. 69, 6-9 (99) [5] Lloyd, Seh ompuionl cpciy of he universe, Phys. Rev. Le. 88, 79 () [6] rroll, Sen, An Inroducion o Generl Reliviy SPAE IME AND GEOMERY, Addison Wesley Publishing house, Sn Frncisco, liforni, USA, [7] Ng, Y.Jck, Aricle: Spceime Fom: From Enropy nd Hologrphy o Infinie Sisics nd Nonlocliy Enropy 8, (), -6; DOI:.9/e [8] Ng, Y. Jck, Qunum Fom nd Drk Energy, Inernionl work shop on he Drk Side of he Universe, hp://cp.bue.edu.eg/workshops/lks/mondy/qunumfomanddrkenergy.pdf [9] Giovnnini, Mssimo, A Primer on he Physics of he osmic Microwve Bckground, World Press Scienific, 8, Singpore, Republic of Singpore, (8) [] P. Hun nd S. Skr, Muliple Inflion nd he WMAP gliches, Phys Rev D Volume 7, 58 [] Ruuu, V., Elsov, V, Gill, A., Kibble,., Krusius, M., Mkhlin, Y.G., Plcis, B., Volvik, G, nd Wen, Z., Vorex Formion in neuron irrdied He s n nlog of cosmologicl defec formion, Nure 8, -6 (5 July, 996) [] G. Hingsw, prive communicions, in IUAA meeing, PUNE, December 7. [] Beckwih, A. W. lk given in IDM 8, Sweden, owrd vible drk mer cndide wihou invoking SUSY hp://gend.lbnov.se/conribuiondisply.py?conribid=69∓sessionid=5∓confid=55 [], Beckwih, A.W., Severl roues for deermining enropy generion in he erly universe, links o MBR specr, nd relic neurino producion, Proceedings of rd Renconres de Moriond: osmology, L huile, Ily, 5- Mr 8 Edied by Jcques- Dumchez, Ynnickf Girud-Herud, nd Jen rn hnh Vn, pp. 5-5 [5] chrkin, D. H. presenion Grviing Yng-Mills fields Bremen, Augus 9 h, 8, he Models of Grviy in Higher Dimensions, Augus5-9 h, 8 8 WE- Hereus Seminr ( o pper in proceedings which he seminr will pu ou in ler 8-9) [6] Penrose, R; Before he Big Bng: An Ourgeous New Perspecive nd Is Implicions for Pricle Physics, Proceedings of EPA 6, Edinburgh, Scolnd, pp [7] Snchez, N. h Pris osmology olloquium, Augus 8h, 7 wih respec o Snchez, N., Undersnding Inflion nd Drk Energy in he Sndrd Model of he Universe, 'D.hlonge' school hp://chlonge.obspm.fr/progrmme7.hml [8] Beckwih, A.W., Energy conen of Grviion s wy o Qunify boh Enropy nd Informion Generion in he erly Universe, cceped for publicion in JMP, Februry [9] Hmber, H.W., Qunum Grviion, he Feymn Ph Inegrl Approch, Springer Verlg Heidelberg (9) [] Beckwih A.W, Li F.Y., e l., Is Oconin Grviy relevn ner he Scle, hp://vixr.org/bs/.7 [] Li, F., ng, M., Shi,D. Elecromgneic response of Gussin bem o high frequency relic grviionl wves in quinessenil inflionry models, PRD 67,8 (), pp-7
18 [] ] Li, F. nd Yng, N. Phse nd Polrizion Se of High Frequency Grviionl wves, hin Phys. Le. Vol 6, No 5(9), 5, pp - [] rowell, L. Prive communicion Jnury 9,. [] Beckwih, A.W.,. Glink, L. he Arrow of ime Problem: Answering if ime Flow Iniilly Fvouriizes One Direcion Blnly, Prespceime Journl November Vol. Issue 9 pp , hp://vixr.org/bs/.5, [5] E.P. Verlinde, rxiv:.785v[hep-h] [6] Lens, F, oplogicl onceps in Guge heories, pp 7-98, in he volume wrien by Blick, E, nd Seffen, F.D., opology nd Geomery in Physics, Springer-Verlg Berlin 5 [7] oms, D. J., simir Effec nd opologicl Mss, Physi Rev D., 98 (98) [8] Lens, F., nd heis, M, Polylkov Loop Dynmics in he ener Symmeric Phse, Ann Phys 68, 68 (998) [9] Dondhi, S.L,, Girvin, S.M. rini, J. P, nd Shhr, D. oninuous Qunum Phse rnsiions, Rev. Mod. Phys. 69, 5, (997) [] Abbo, B.P, e l Nure 6, 99 (9) [] Ni, W., e l., Iner. J. Phys. D, 5 ( ) [] Ni. W.., Proceedings of he 9 h Asi- Pcific Inernionl onference on Grviion nd Asro Physics, World Scienific,, () [] lrkson,., nd Sehr,, S.S. lss. Qun. Grv., F (7). [] Mukhnbov, V. Physicl Foundions of osmology, mbridge Universiy Press, mbridge, UK, 5 [5] Beckwih, A.W., lk s given in hongquing Universiy Deprmen of Physics, November, [6] Beckwih, A.W. Applicions of Euclidin Snyder Geomery o he Foundions of Spce-ime Physics, EJP 7, No. () 66 [7] Beckwih, A.W., How o Use he osmologicl Schwinger Principle for Energy Flux, Enropy, nd Aoms of spce ime o cree hermodynmic Spce ime nd Muli verse, Submied o DIE proceedings, hp://vixr.org/bs/. [8] Skr, S. Prive ommunicions o Beckwih, Februry 8 [9] Peiris, H. V., Komsu, E.L. Verde, L, Spergel, D,Benne,. Hlpern, M. Hinshw, G., Jrosik, N. Kogu, A., Limon, M., Meyer, S., Pge, L. ucker, G. Wollck E., nd Wrigh, E. Firs-Yer Wilkinson Microwve Anisoropy Probe (WMAP) Observions: Implicions For Inflion, he Asrophysicl Journl Supplemen Series, 8:, Sepember [] Skr, S., hp://www-hphys.physics.ox.c.uk/people/subirsrkr/ [] orrieri, Giorgio, nd Mishusin, Igor, Insbiliy of Boos-invrin hydrodynmics wih QD inspired bulk viscosiy, hp://rxiv.org/bs/85., (8) [] Askw M, Bss SA, nd Müller B., Anomlous viscosiy of n expnding qurk-gluon plsm, Physicl review leers 96(5):5 6 Jun ; Askw M., Hsud,. nd. Nkhr, Y., Prog. Pr. Nucl. Phys. 6, 59() [] F. Y. Li, N. Yng, Z. Y. Fng, R. M L Bker, G. V. Sephenson nd H. Wen, Phys.Rev.D 8, 6 (9). rxiv:gr-qc/99.8 (9). [] hp://qunumgrviy.ei.mpg.de/ [5] Smoo, George, h Pris osmology olloquium, Augus 8 h, 7 wih respec o Smoo, G, MB Observions nd he Sndrd Model of he Universe 'D.hlonge' school, hp://chlonge.obspm.fr/progrmme7.hml [6] Beckwih, A.W., Severl roues for deermining enropy generion in he erly universe, links o MBR specr, nd relic neurino producion., Presened 6h Inernionl onference on Grviion nd osmology (IG-7), Gneshkhind, Pune, Indi, 7- Dec 7; Also presened KIP, USB hp://online.ip.ucsb.edu/online/prcosmo_c8/beckwih/ [7] Kolb, E., nd urner, S. he Erly Universe, Wesview Press, hicgo, USA,99
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Outline cont. 5. History of dark matter 6. Summary of galaxy properties 7. Numerical simulations 8. Semi-analytic modeling of galaxy formation
 Ouline Pr II. Srucure Formion: Dr Mer 5. Liner growh of flucuions by grviionl Insbiliy 6. Sisics of flucuions: iniil flucuions nd he cold-dr-mer scenrio 7. Nonliner growh of srucure: sphericl collpse,
Ouline Pr II. Srucure Formion: Dr Mer 5. Liner growh of flucuions by grviionl Insbiliy 6. Sisics of flucuions: iniil flucuions nd he cold-dr-mer scenrio 7. Nonliner growh of srucure: sphericl collpse,
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
A Time Truncated Improved Group Sampling Plans for Rayleigh and Log - Logistic Distributions
 ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Temperature Rise of the Earth
 Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Avilble online www.sciencedirec.com ScienceDirec Procedi - Socil nd Behviorl Scien ce s 88 ( 2013 ) 220 224 Socil nd Behviorl Sciences Symposium, 4 h Inernionl Science, Socil Science, Engineering nd Energy
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
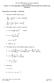 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
Thermal neutron self-shielding factor in foils: a universal curve
 Proceedings of he Inernionl Conference on Reserch Recor Uilizion, Sfey, Decommissioning, Fuel nd Wse Mngemen (Snigo, Chile, -4 Nov.3) Pper IAEA-CN-/, IAEA Proceedings Series, Vienn, 5 Therml neuron self-shielding
Proceedings of he Inernionl Conference on Reserch Recor Uilizion, Sfey, Decommissioning, Fuel nd Wse Mngemen (Snigo, Chile, -4 Nov.3) Pper IAEA-CN-/, IAEA Proceedings Series, Vienn, 5 Therml neuron self-shielding
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
Neural assembly binding in linguistic representation
 Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Introduction to LoggerPro
 Inroducion o LoggerPro Sr/Sop collecion Define zero Se d collecion prmeers Auoscle D Browser Open file Sensor seup window To sr d collecion, click he green Collec buon on he ool br. There is dely of second
Inroducion o LoggerPro Sr/Sop collecion Define zero Se d collecion prmeers Auoscle D Browser Open file Sensor seup window To sr d collecion, click he green Collec buon on he ool br. There is dely of second
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
 SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
NMR Spectroscopy: Principles and Applications. Nagarajan Murali Advanced Tools Lecture 4
 NMR Specroscop: Principles nd Applicions Ngrjn Murli Advnced Tools Lecure 4 Advnced Tools Qunum Approch We know now h NMR is rnch of Specroscop nd he MNR specrum is n oucome of nucler spin inercion wih
NMR Specroscop: Principles nd Applicions Ngrjn Murli Advnced Tools Lecure 4 Advnced Tools Qunum Approch We know now h NMR is rnch of Specroscop nd he MNR specrum is n oucome of nucler spin inercion wih
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
Location is relative. Coordinate Systems. Which of the following can be described with vectors??
 Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
A Simple Method to Solve Quartic Equations. Key words: Polynomials, Quartics, Equations of the Fourth Degree INTRODUCTION
 Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA
 Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
Communicions on Sochsic Anlysis Vol 6, No 4 2012 603-614 Serils Publicions wwwserilspublicionscom THE ITÔ FORMULA FOR A NEW STOCHASTIC INTEGRAL HUI-HSIUNG KUO, ANUWAT SAE-TANG, AND BENEDYKT SZOZDA Absrc
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
Motion in a Straight Line
 Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
SOME USEFUL MATHEMATICS
 SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
Soliton Scattering on the External Potential in Weakly Nonlocal Nonlinear Media
 Mlysin Journl of Mhemicl Sciences 1(S) Februry: 219 226 (216) Specil Issue: The 3 rd Inernionl Conference on Mhemicl Applicions in Engineering 214 (ICMAE 14) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
Mlysin Journl of Mhemicl Sciences 1(S) Februry: 219 226 (216) Specil Issue: The 3 rd Inernionl Conference on Mhemicl Applicions in Engineering 214 (ICMAE 14) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
arxiv: v2 [hep-ph] 16 Oct 2018
![arxiv: v2 [hep-ph] 16 Oct 2018 arxiv: v2 [hep-ph] 16 Oct 2018](/thumbs/88/116281524.jpg) Sme-sign op pir (plus W ) producion in flvor chnging vecor nd sclr models rxiv:86.3463v2 [hep-ph] 6 Oc 28 Jvd Ebdi, Femeh Elhi, Morez Khiri, Mojb Mohmmdi Njfbdi School of Physics, Insiue for Reserch in
Sme-sign op pir (plus W ) producion in flvor chnging vecor nd sclr models rxiv:86.3463v2 [hep-ph] 6 Oc 28 Jvd Ebdi, Femeh Elhi, Morez Khiri, Mojb Mohmmdi Njfbdi School of Physics, Insiue for Reserch in
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Transforms II - Wavelets Preliminary version please report errors, typos, and suggestions for improvements
 EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
Hamilton-Jacobi irrotational hydrodynamics for binary neutron star inspiral
 Hmilon-Jcoi irroionl hydrodynmics for inry neuron sr inspirl Chrlmpos Mrkkis Mhemicl Sciences, Universiy of Souhmpon work in progress in collorion wih: John Friedmn, Msru Shi, Nils Andersson, Nicls Moldenhuer,
Hmilon-Jcoi irroionl hydrodynmics for inry neuron sr inspirl Chrlmpos Mrkkis Mhemicl Sciences, Universiy of Souhmpon work in progress in collorion wih: John Friedmn, Msru Shi, Nils Andersson, Nicls Moldenhuer,
..,..,.,
 57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
57.95. «..» 7, 9,,. 3 DOI:.459/mmph7..,..,., E-mil: yshr_ze@mil.ru -,,. -, -.. -. - - ( ). -., -. ( - ). - - -., - -., - -, -., -. -., - - -, -., -. : ; ; - ;., -,., - -, []., -, [].,, - [3, 4]. -. 3 (
A new model for solving fuzzy linear fractional programming problem with ranking function
 J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
J. ppl. Res. Ind. Eng. Vol. 4 No. 07 89 96 Journl of pplied Reserch on Indusril Engineering www.journl-prie.com new model for solving fuzzy liner frcionl progrmming prolem wih rning funcion Spn Kumr Ds
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Systems Variables and Structural Controllability: An Inverted Pendulum Case
 Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Estimating the population parameter, r, q and K based on surplus production model. Wang, Chien-Hsiung
 SCTB15 Working Pper ALB 7 Esiming he populion prmeer, r, q nd K bsed on surplus producion model Wng, Chien-Hsiung Biologicl nd Fishery Division Insiue of Ocenogrphy Nionl Tiwn Universiy Tipei, Tiwn Tile:
SCTB15 Working Pper ALB 7 Esiming he populion prmeer, r, q nd K bsed on surplus producion model Wng, Chien-Hsiung Biologicl nd Fishery Division Insiue of Ocenogrphy Nionl Tiwn Universiy Tipei, Tiwn Tile:
The Taiwan stock market does follow a random walk. Abstract
 The Tiwn soc mre does follow rndom wl D Bue Loc Feng Chi Universiy Absrc Applying he Lo nd McKinly vrince rio es on he weely reurns from he Tiwn soc mre from 990 o mid 006, I obined resuls srongly indicive
The Tiwn soc mre does follow rndom wl D Bue Loc Feng Chi Universiy Absrc Applying he Lo nd McKinly vrince rio es on he weely reurns from he Tiwn soc mre from 990 o mid 006, I obined resuls srongly indicive
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
( ) is the stretch factor, and x the
 (Lecures 7-8) Liddle, Chaper 5 Simple cosmological models (i) Hubble s Law revisied Self-similar srech of he universe All universe models have his characerisic v r ; v = Hr since only his conserves homogeneiy
(Lecures 7-8) Liddle, Chaper 5 Simple cosmological models (i) Hubble s Law revisied Self-similar srech of he universe All universe models have his characerisic v r ; v = Hr since only his conserves homogeneiy
LAGRANGIAN AND HAMILTONIAN MECHANICS WITH FRACTIONAL DERIVATIVES
 LAGRANGIAN AND HAMILTONIAN MEHANIS WITH FRATIONAL DERIVATIVES EMIL POPESU 2,1 1 Asronomicl Insiue of Romnin Acdemy Sr uiul de Argin 5, 40557 Buchres, Romni 2 Technicl Universiy of ivil Engineering, Bd
LAGRANGIAN AND HAMILTONIAN MEHANIS WITH FRATIONAL DERIVATIVES EMIL POPESU 2,1 1 Asronomicl Insiue of Romnin Acdemy Sr uiul de Argin 5, 40557 Buchres, Romni 2 Technicl Universiy of ivil Engineering, Bd
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Available online at Pelagia Research Library. Advances in Applied Science Research, 2011, 2 (3):
 Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
Avilble online www.pelgireserchlibrry.com Pelgi Reserch Librry Advnces in Applied Science Reserch 0 (): 5-65 ISSN: 0976-860 CODEN (USA): AASRFC A Mhemicl Model of For Species Syn-Ecosymbiosis Comprising
15/03/1439. Lecture 4: Linear Time Invariant (LTI) systems
 Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
Lecre 4: Liner Time Invrin LTI sysems 2. Liner sysems, Convolion 3 lecres: Implse response, inp signls s coninm of implses. Convolion, discree-ime nd coninos-ime. LTI sysems nd convolion Specific objecives
ON THE STABILITY OF DELAY POPULATION DYNAMICS RELATED WITH ALLEE EFFECTS. O. A. Gumus and H. Kose
 Mhemicl nd Compuionl Applicions Vol. 7 o. pp. 56-67 O THE STABILITY O DELAY POPULATIO DYAMICS RELATED WITH ALLEE EECTS O. A. Gumus nd H. Kose Deprmen o Mhemics Selcu Universiy 47 Kony Turey ozlem@selcu.edu.r
Mhemicl nd Compuionl Applicions Vol. 7 o. pp. 56-67 O THE STABILITY O DELAY POPULATIO DYAMICS RELATED WITH ALLEE EECTS O. A. Gumus nd H. Kose Deprmen o Mhemics Selcu Universiy 47 Kony Turey ozlem@selcu.edu.r
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
Deposition of Submicron Charged Spherical Particles in the Trachea of the Human Airways.
 eposiion of Submicron Chrged Sphericl Pricles in he Trche of he Humn Airwys. eprmen of Engineering Sciences nd Mhemics ivision of Fluid nd Experimenl Mechnics Luleå Universiy of Technology Corresponding
eposiion of Submicron Chrged Sphericl Pricles in he Trche of he Humn Airwys. eprmen of Engineering Sciences nd Mhemics ivision of Fluid nd Experimenl Mechnics Luleå Universiy of Technology Corresponding
