Mathematical PhySΪCS by Springer-Verlag 1978
|
|
|
- Kevin George
- 5 years ago
- Views:
Transcription
1 Commun. math. Phys. 58, (1978) Communications in Mathematical PhySΪCS by Springer-Verlag 1978 N Body Scattering in the Two-Cluster Region^ Barry Simon**" Department of Mathematics, Weizmann Institute of Science, Rehovot, Israel Abstract. We extend Combes' result on completeness of TV-body scattering at energies below the lowest 3-body threshold from potentials with x ~ v ~ ε falloff (v = number of dimensions for each particle) to central potentials with xl" 1 " 8. We also treat the scattering of electrons from neutral atoms in the two cluster region. 1. Introduction This paper is a contribution to our program [2, 8, 3] of using geometric ( = configuration space) methods to study multiparticle non-relativistic quantum mechanical systems. Indeed, it can be viewed as an addendum to Section 3 of [8]. Consider the Hamiltonian of N particles in v-dimensions, i.e., on L 2 (R Nv ). As is traditional, we separate out the center of mass and consider the "reduced" operator, H on L 2 (R (N ~ 1)V ). Corresponding to any decomposition α of {!,..., rc} into two non-trivial subsets C ( \C%\ H decomposes into ) + H(Cf ) + Γ α + I a where I Λ is the interaction between clusters, i.e., and 7^ is the relative kinetic energy of the clusters. One defines and where the operator is viewed as acting on L 2 (R (N 2)v ). Finally, Σ 2 = mm (Σ 2 α ), * Research supported by U.S. N.S.F. Grant MPS ** Permanent address: Departments of Mathematics and Physics, Princeton University, Princeton, New Jersey 08540, USA /78/0058/0205/S01.20
2 206 B. Simon Σ 3 = min( 3 α ). The HVZ theorem (see [5, 6] for general information on TV-body α systems) asserts that the essential spectrum of H is [Σ 2, oo] and implies that Σ 3 is the lowest energy for breakup into three clusters. In the energy range [^2^3]' the only open scattering channels are two cluster channels. The problem is genuinely multichannel since excitations and rearrangements are allowed but as it is "essentially two body" one would hope that two-body methods, especially the elegant Kato-Birman theory (reviewed in [5], XL3) would be applicable. That this is indeed the case was a discovery of Combes [1]. In 3 of [8], we showed how Combes' proof could be streamlined and made quite elementary. Both [1] and [8] require V^x) to (more-or-less) behave at x ~ v ~ ε at infinity ([1] only considers v = 3) which is not surprising since this is well-known to be the restrictions needed for the applicability of the Kato-Birman theory in the two body case. What is not so well-known is the remark of Kuroda [4] that for central potentials where one can make a partial wave expansion, the Kato-Birman theory applicable so long as V is O^^l" 1 " 8 ). Our goal in 2 below will be to combine this remark of Kuroda [4] with [1, 8] to prove completeness of the scattering in the energy range [ 2, 3 ] for central potentials V tj with (Xl*!" 1 " 6 ) falloff. There is one irony in this situation : The study of non-central potentials in the two-body case is often defended on the basis that they will better mock up the TV-body situation where a partial wave expansion is not available. At least in the two cluster region, this argument is discredited by our considerations in 2. To avoid the special value / = f which occurs in the v = 2 partial wave expansion, we will suppose v ^ 3 in 2. It is probably quite easy to accommodate v = 2. In the method of [8], one had to show that an operator Alβ was trace class and there (and also in 2, below) we accomplished this by looking at each AV^B. Doing this prevents the use of any kind of cancellations between the V tj. Such cancellations are expected to be present in the scattering of an electron from a neutral system. We discuss this problem in 3 and prove completeness in the two cluster region by treating Alβ all at once. This is the first completeness result for Coulomb systems with more than two particles. 2. Short Range Potentials with Slow Decay In this section, we will prove : Theorem 1. Let v ^ 3. Let each potential V^ be central (spherically symmetric) and obey: for p = 2(v = 3), > 2(v = 4), v/2(v ^ 5). Then scattering is complete in the energy range [Σ 2,Σ 3 ],i.e, where Ω^ are the usual channel wave operators, and E Ω (E ac ) are spectral projections forh.
3 w tsoαy scattering in tne iwo-lλuster κegιon zυ/ Proof. We begin by recalling some notation and results from [8]. Let P α be the projection onto all states of the form ^(CJ^ίίaW'OU where. is the coordinate internal to cluster Cf\ η a is the coordinate between the center of mass of the clusters and φ ί9 φ 2 are eigenfunctions of H(Cf ] } with energies. obeying E 1 + E 2 < Γ 3. By definition of 3, we can (by replacing Γ 3 by Σ 3 s) suppose each P α is "finite dimensional" in the. coordinates. Let P be the projection onto the span of the P α and let Q = I P. Then, as in [8], (P - P^~ ϊth Eφ and Q(e~ ίth Eφ) -> 0 as t -> oo where E = E ac E [Σ^Σ3Γ The proofs of these facts depended not at all on the x " v ~ ε falloff of V. Thus, as in [8], the proof is reduced to showing the existence of the limits (H Λ = H / α ) Ω ± (H ol,hιp α ) = s - Hme ίth «P Λ e- ίth. ί-* +00 Now let J be the total angular momentum of the particles about their center of mass. We use the symbols <2j^.(resp. Q J=j ) to denote the projection onto all vectors with J 2 ^j(j + l)(resp. J 2 =j(j+ϊ). We are supposing for notational simplicity that v = 3 otherwise more involved notation is needed to label the relevant spherical harmonics and representations. For each α, we can write J = L α 4- S α where S α is the angular momentum of the cluster about their centers of mass and L α is the angular momentum of the two clusters about each other. Notice that J commutes with H, H α,p α and that L α,s α commutes with H α,p α. Moreover for some 5, since P α is "finite dimensional in the ζ. coordinates". Since J commutes with H, the existence of Ω ± (H α,h;p ΰ ) follows from the existence of Ω ± (H 0[,H;P α Q J^j) for each). By Birman's form of the Kato-Birman theorem, we only need that (for [H α, P α β JΐS j] = 0) C = H x (P Λ Qj^ - (P.Qκj)H = - P.Qj^jI.. has the property that Ej(H x )CEj(H) is trace class for each bounded interval. (Mutual subordination is trivial.) As in the proof of Lemma 3.4 of [8], write E I (H α )CE I (H) = ABDE (2) (3) (4) where we have used P^ = P α and the fact that P α and J commutes with P α, T α and I τ? α 2. Now A and E are bounded as in [8]. The proof will be completed if we show that D is bounded and B is trace class. To handle D, decompose I α = ΣV tj and for a given term, write
4 208 B. Simon for a suitable internal coordinate ζ. Then using that is bounded by hypothesis and that is bounded by the exponential falloff of bound states, we conclude that D is bounded. To control B, use (1) and write where we have used the fact that if J 2 =j(j + 1), S 2 = s(s + 1), then L 2 can only have eigenvalue /(/ + 1) with I ^ j + s. Thus, we only need that is trace class for each fixed /. Now, P α is a sum of rank 1 operators in the C's, so we can suppose that P α is rank 1 in the C's. But then the operator in (5) is a finite direct sum of operators unitarily equivalent to on L 2 (0, oo, dr) where h 0>l is the operator with angular momentum barrier, /, i.e.,, d 2 1(1+1) Λ I ~ dr 2 + r 2 ' Let p 2 be the operator d 2 /dr 2 on all of ( oo, oo). Then, (We remove a Dirichlet B.C. in the last step.) By a standard theorem, for ε < \ (which can be assumed without loss). Thus, since ( 1+Γ 2)-l/4-ε (p 2 +1) -l/2-ε (1+r 2 ) -l/4-ε is known to be trace class on L 2 (R) (see e.g. [5] ), we have that is trace class. Using the fact that (1 + ΓJ-^-d + \η, 2 )-^-(l + is bounded, we conclude that B is trace class. Π 3. Scattering from Neutral Coulomb Systems In this section, we want to prove :
5 N Body Scattering in the Two-Cluster Region 209 Theorem 2. Let N = m +2 and v=3. Suppose that V^x) = \x\~ l for i^j ^m + 1 and J^ (x) = m \ x \ ~~ 1 for i < m + lj = m + 2, Then scattering is complete in the region[σ 29 Σ 3 ]. Remarks. 1. We describe a system with a nucleus of charge m and m + 1 electrons. Thus we are talking scattering of an electron off a neutral atom at energies too small to ionize a second electron. 2. Since atoms have an infinity of bound states [9, 7], as Σ 3 is approached, an infinity of channels open. But at no energy that we consider, is the problem genuinely infinite channel. 3. One can allow more than one positive change so long as one cluster is neutral in each allowed two cluster state in the energy range considered. Also, one can add central short range potentials as in 2. Proof. We follow the proof of Theorem 1 including the decomposition (2). A and E are bounded as before and B is trace class. All that is different is the proof that D is bounded. Let/(x) = x^1 (if x ^ 1) and = 1 (if x ^ 1). Let g(x) = jxj- 1 - f(x). Let V tj =f tj -f g tj and let I Λ = I ΛΛ + I Λ 2 corresponding to this decomposition. I Λ 2 is a sum of finite range pieces, so its contribution is bounded as in 2 and [8]. Restricting to a "rank 1" P α and to specific coordinates, we find that it suffices to show that the following operator is bounded : where we have passed to atomic coordinates ^j = r r m+2 and we use Dirac notation for P α. Now, (Vf)(x) < x c - 2 where \x c = \x\(if x ^ 1) and - 1 (if x ^ 1). Thus I/O* - y) -/(x) ^ It follows that we need only prove that is bounded. This is easy; for (1 + a 2 ) [min(α, a - b)~\~ 2 ^ max[(l + α 2 K~ 2,(l + a 2 )(a - b)~ where we used a 2 ^ 2(α - b) 2 + 2b 2. Thus taking ε = \ (without loss) and using Ίm+i ^2x m + ι + 2 C 2? we need only that \ηxη x m (3 + 2x 2 ) is bounded. This is immediate from the exponential falloff of η in the xj(j ^ m) variables. Π Acknowledgement. It is a pleasure to thank Y. Kannai for the hospitality of the Weizmann Institute where this work was completed.
6 210 B. Simon References 1. Combes, J. M.: Nuovo Cimento 64A, 111 (1969) 2. Deift, P., Simon, B.: Commun. Pure Appl. Math., to appear 3. Deift, P., Hunziker, W., Simon, B., Vock, E.: ETH Preprint, in preparation 4. Kuroda, S. : J. Math. Phys. 3, 933 (1962) 5. Reed, M., Simon, B. : Methods of modern mathematical physics, Vol. III. Scattering theory. New York: Academic Press Reed, M., Simon, B. : Methods of modern mathematical physics, Vol. IV. Analysis of Operators. New York: Academic Press Simon, B. : Helv. Phys. Acta 43, 607 (1970) 8. Simon, B. : Commun. math. Phys. 55, 259 (1977) 9. Zhislin, G. M. : Tr. Mosk. Math. Obsc. 9, 82 (1960) Communicated by J. Ginibre Received August 5, 1977
BOOK REVIEWS 165. Square integrable eigenfunctions of the Schrodinger equation decay exponentially.
 BOOK REVIEWS 165 16. A. W. Goodman, Univalent functions, Vols. I, II, Mariner, Tampa, 1983. 17. D. H. Hamilton, Extremal boundary problems for Schlicht functions, preprint, Univ. of Maryland, 1984. 18.
BOOK REVIEWS 165 16. A. W. Goodman, Univalent functions, Vols. I, II, Mariner, Tampa, 1983. 17. D. H. Hamilton, Extremal boundary problems for Schlicht functions, preprint, Univ. of Maryland, 1984. 18.
The Twisting Trick for Double Well Hamiltonians
 Commun. Math. Phys. 85, 471-479 (1982) Communications in Mathematical Physics Springer-Verlag 1982 The Twisting Trick for Double Well Hamiltonians E. B. Davies Department of Mathematics, King's College,
Commun. Math. Phys. 85, 471-479 (1982) Communications in Mathematical Physics Springer-Verlag 1982 The Twisting Trick for Double Well Hamiltonians E. B. Davies Department of Mathematics, King's College,
SELF-ADJOINTNESS OF DIRAC OPERATORS VIA HARDY-DIRAC INEQUALITIES
 SELF-ADJOINTNESS OF DIRAC OPERATORS VIA HARDY-DIRAC INEQUALITIES MARIA J. ESTEBAN 1 AND MICHAEL LOSS Abstract. Distinguished selfadjoint extension of Dirac operators are constructed for a class of potentials
SELF-ADJOINTNESS OF DIRAC OPERATORS VIA HARDY-DIRAC INEQUALITIES MARIA J. ESTEBAN 1 AND MICHAEL LOSS Abstract. Distinguished selfadjoint extension of Dirac operators are constructed for a class of potentials
Summary of Last Time Barrier Potential/Tunneling Case I: E<V 0 Describes alpha-decay (Details are in the lecture note; go over it yourself!!) Case II:
 Quantum Mechanics and Atomic Physics Lecture 8: Scattering & Operators and Expectation Values http://www.physics.rutgers.edu/ugrad/361 Prof. Sean Oh Summary of Last Time Barrier Potential/Tunneling Case
Quantum Mechanics and Atomic Physics Lecture 8: Scattering & Operators and Expectation Values http://www.physics.rutgers.edu/ugrad/361 Prof. Sean Oh Summary of Last Time Barrier Potential/Tunneling Case
Isotropic harmonic oscillator
 Isotropic harmonic oscillator 1 Isotropic harmonic oscillator The hamiltonian of the isotropic harmonic oscillator is H = h m + 1 mω r (1) = [ h d m dρ + 1 ] m ω ρ, () ρ=x,y,z a sum of three one-dimensional
Isotropic harmonic oscillator 1 Isotropic harmonic oscillator The hamiltonian of the isotropic harmonic oscillator is H = h m + 1 mω r (1) = [ h d m dρ + 1 ] m ω ρ, () ρ=x,y,z a sum of three one-dimensional
Simple Harmonic Oscillator
 Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Classical harmonic oscillator Linear force acting on a particle (Hooke s law): F =!kx From Newton s law: F = ma = m d x dt =!kx " d x dt + # x = 0, # = k / m Position and momentum solutions oscillate in
Trace Class Operators and Lidskii s Theorem
 Trace Class Operators and Lidskii s Theorem Tom Phelan Semester 2 2009 1 Introduction The purpose of this paper is to provide the reader with a self-contained derivation of the celebrated Lidskii Trace
Trace Class Operators and Lidskii s Theorem Tom Phelan Semester 2 2009 1 Introduction The purpose of this paper is to provide the reader with a self-contained derivation of the celebrated Lidskii Trace
G : Quantum Mechanics II
 G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
CHAPTER 6 Quantum Mechanics II
 CHAPTER 6 Quantum Mechanics II 6.1 6.2 6.3 6.4 6.5 6.6 6.7 The Schrödinger Wave Equation Expectation Values Infinite Square-Well Potential Finite Square-Well Potential Three-Dimensional Infinite-Potential
CHAPTER 6 Quantum Mechanics II 6.1 6.2 6.3 6.4 6.5 6.6 6.7 The Schrödinger Wave Equation Expectation Values Infinite Square-Well Potential Finite Square-Well Potential Three-Dimensional Infinite-Potential
Potential energy, from Coulomb's law. Potential is spherically symmetric. Therefore, solutions must have form
 Lecture 6 Page 1 Atoms L6.P1 Review of hydrogen atom Heavy proton (put at the origin), charge e and much lighter electron, charge -e. Potential energy, from Coulomb's law Potential is spherically symmetric.
Lecture 6 Page 1 Atoms L6.P1 Review of hydrogen atom Heavy proton (put at the origin), charge e and much lighter electron, charge -e. Potential energy, from Coulomb's law Potential is spherically symmetric.
SCHRÖDINGER OPERATORS WITH PURELY DISCRETE SPECTRUM
 SCHRÖDINGER OPERATORS WITH PURELY DISCRETE SPECTRUM BARRY SIMON Dedicated to A. Ya. Povzner Abstract. We prove +V has purely discrete spectrum if V 0 and, for all M, {x V (x) < M} < and various extensions.
SCHRÖDINGER OPERATORS WITH PURELY DISCRETE SPECTRUM BARRY SIMON Dedicated to A. Ya. Povzner Abstract. We prove +V has purely discrete spectrum if V 0 and, for all M, {x V (x) < M} < and various extensions.
Physics 218 Polarization sum for massless spin-one particles Winter 2016
 Physics 18 Polarization sum for massless spin-one particles Winter 016 We first consider a massless spin-1 particle moving in the z-direction with four-momentum k µ = E(1; 0, 0, 1). The textbook expressions
Physics 18 Polarization sum for massless spin-one particles Winter 016 We first consider a massless spin-1 particle moving in the z-direction with four-momentum k µ = E(1; 0, 0, 1). The textbook expressions
ONE AND MANY ELECTRON ATOMS Chapter 15
 See Week 8 lecture notes. This is exactly the same as the Hamiltonian for nonrigid rotation. In Week 8 lecture notes it was shown that this is the operator for Lˆ 2, the square of the angular momentum.
See Week 8 lecture notes. This is exactly the same as the Hamiltonian for nonrigid rotation. In Week 8 lecture notes it was shown that this is the operator for Lˆ 2, the square of the angular momentum.
General Lower Bounds for Resonances in One Dimension*
 Commun. Math. Phys. 86, 221-225 (1982) Communications in Mathematical Physics Springer-Verlag 1982 General Lower Bounds for Resonances in One Dimension* Evans M. Harrell II Department of Mathematics, The
Commun. Math. Phys. 86, 221-225 (1982) Communications in Mathematical Physics Springer-Verlag 1982 General Lower Bounds for Resonances in One Dimension* Evans M. Harrell II Department of Mathematics, The
Quantum Many Body Systems and Tensor Networks
 Quantum Many Body Systems and Tensor Networks Aditya Jain International Institute of Information Technology, Hyderabad aditya.jain@research.iiit.ac.in July 30, 2015 Aditya Jain (IIIT-H) Quantum Hamiltonian
Quantum Many Body Systems and Tensor Networks Aditya Jain International Institute of Information Technology, Hyderabad aditya.jain@research.iiit.ac.in July 30, 2015 Aditya Jain (IIIT-H) Quantum Hamiltonian
Representations of Sp(6,R) and SU(3) carried by homogeneous polynomials
 Representations of Sp(6,R) and SU(3) carried by homogeneous polynomials Govindan Rangarajan a) Department of Mathematics and Centre for Theoretical Studies, Indian Institute of Science, Bangalore 560 012,
Representations of Sp(6,R) and SU(3) carried by homogeneous polynomials Govindan Rangarajan a) Department of Mathematics and Centre for Theoretical Studies, Indian Institute of Science, Bangalore 560 012,
The spectral zeta function
 The spectral zeta function Bernd Ammann June 4, 215 Abstract In this talk we introduce spectral zeta functions. The spectral zeta function of the Laplace-Beltrami operator was already introduced by Minakshisundaram
The spectral zeta function Bernd Ammann June 4, 215 Abstract In this talk we introduce spectral zeta functions. The spectral zeta function of the Laplace-Beltrami operator was already introduced by Minakshisundaram
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi
 Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 07 Bra-Ket Algebra and Linear Harmonic Oscillator II Lecture No. # 02 Dirac s Bra and
Basic Quantum Mechanics Prof. Ajoy Ghatak Department of Physics Indian Institute of Technology, Delhi Module No. # 07 Bra-Ket Algebra and Linear Harmonic Oscillator II Lecture No. # 02 Dirac s Bra and
Introduction to Spectral Theory
 P.D. Hislop I.M. Sigal Introduction to Spectral Theory With Applications to Schrodinger Operators Springer Introduction and Overview 1 1 The Spectrum of Linear Operators and Hilbert Spaces 9 1.1 TheSpectrum
P.D. Hislop I.M. Sigal Introduction to Spectral Theory With Applications to Schrodinger Operators Springer Introduction and Overview 1 1 The Spectrum of Linear Operators and Hilbert Spaces 9 1.1 TheSpectrum
which implies that we can take solutions which are simultaneous eigen functions of
 Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
Module 1 : Quantum Mechanics Chapter 6 : Quantum mechanics in 3-D Quantum mechanics in 3-D For most physical systems, the dynamics is in 3-D. The solutions to the general 3-d problem are quite complicated,
Research Article A Note on the Discrete Spectrum of Gaussian Wells (I): The Ground State Energy in One Dimension
 Mathematical Physics Volume 016, Article ID 15769, 4 pages http://dx.doi.org/10.1155/016/15769 Research Article A Note on the Discrete Spectrum of Gaussian Wells (I: The Ground State Energy in One Dimension
Mathematical Physics Volume 016, Article ID 15769, 4 pages http://dx.doi.org/10.1155/016/15769 Research Article A Note on the Discrete Spectrum of Gaussian Wells (I: The Ground State Energy in One Dimension
Momentum expectation Momentum expectation value value for for infinite square well
 Quantum Mechanics and Atomic Physics Lecture 9: The Uncertainty Principle and Commutators http://www.physics.rutgers.edu/ugrad/361 Prof. Sean Oh Announcement Quiz in next class (Oct. 5): will cover Reed
Quantum Mechanics and Atomic Physics Lecture 9: The Uncertainty Principle and Commutators http://www.physics.rutgers.edu/ugrad/361 Prof. Sean Oh Announcement Quiz in next class (Oct. 5): will cover Reed
Lecture 6. Fermion Pairing. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Lecture 6 Fermion Pairing WS2010/11: Introduction to Nuclear and Particle Physics Experimental indications for Cooper-Pairing Solid state physics: Pairing of electrons near the Fermi surface with antiparallel
Properties of the Scattering Transform on the Real Line
 Journal of Mathematical Analysis and Applications 58, 3 43 (001 doi:10.1006/jmaa.000.7375, available online at http://www.idealibrary.com on Properties of the Scattering Transform on the Real Line Michael
Journal of Mathematical Analysis and Applications 58, 3 43 (001 doi:10.1006/jmaa.000.7375, available online at http://www.idealibrary.com on Properties of the Scattering Transform on the Real Line Michael
An inverse scattering problem for short-range systems in a time-periodic electric field. François Nicoleau
 An inverse scattering problem for short-range systems in a time-periodic electric field. François Nicoleau Laboratoire Jean Leray UMR CNRS-UN 6629 Département de Mathématiques 2, rue de la Houssinière
An inverse scattering problem for short-range systems in a time-periodic electric field. François Nicoleau Laboratoire Jean Leray UMR CNRS-UN 6629 Département de Mathématiques 2, rue de la Houssinière
arxiv:hep-th/ v2 5 May 1993
 WIS-9/1/Dec-PH arxiv:hep-th/9348v 5 May 1993 NORMALIZATION OF SCATTERING STATES SCATTERING PHASE SHIFTS AND LEVINSON S THEOREM Nathan Poliatzky Department of Physics, The Weizmann Institute of Science,
WIS-9/1/Dec-PH arxiv:hep-th/9348v 5 May 1993 NORMALIZATION OF SCATTERING STATES SCATTERING PHASE SHIFTS AND LEVINSON S THEOREM Nathan Poliatzky Department of Physics, The Weizmann Institute of Science,
The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of hydrogen atom.
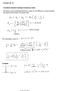 Lecture 20-21 Page 1 Lectures 20-21 Transitions between hydrogen stationary states The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of
Lecture 20-21 Page 1 Lectures 20-21 Transitions between hydrogen stationary states The energy of the emitted light (photons) is given by the difference in energy between the initial and final states of
Addition of Angular Momenta
 Addition of Angular Momenta What we have so far considered to be an exact solution for the many electron problem, should really be called exact non-relativistic solution. A relativistic treatment is needed
Addition of Angular Momenta What we have so far considered to be an exact solution for the many electron problem, should really be called exact non-relativistic solution. A relativistic treatment is needed
arxiv: v3 [math-ph] 19 Oct 2017
![arxiv: v3 [math-ph] 19 Oct 2017 arxiv: v3 [math-ph] 19 Oct 2017](/thumbs/94/118694632.jpg) ABSECE OF A GROUD STATE FOR BOSOIC COULOMB SYSTEMS WITH CRITICAL CHARGE YUKIMI GOTO arxiv:1605.02949v3 [math-ph] 19 Oct 2017 Abstract. We consider bosonic Coulomb systems with -particles and K static nuclei.
ABSECE OF A GROUD STATE FOR BOSOIC COULOMB SYSTEMS WITH CRITICAL CHARGE YUKIMI GOTO arxiv:1605.02949v3 [math-ph] 19 Oct 2017 Abstract. We consider bosonic Coulomb systems with -particles and K static nuclei.
Chemistry 3502/4502. Final Exam Part I. May 14, 2005
 Chemistry 3502/4502 Final Exam Part I May 14, 2005 1. For which of the below systems is = where H is the Hamiltonian operator and T is the kinetic-energy operator? (a) The free particle (e) The
Chemistry 3502/4502 Final Exam Part I May 14, 2005 1. For which of the below systems is = where H is the Hamiltonian operator and T is the kinetic-energy operator? (a) The free particle (e) The
Mathematical Tripos Part IB Michaelmas Term Example Sheet 1. Values of some physical constants are given on the supplementary sheet
 Mathematical Tripos Part IB Michaelmas Term 2015 Quantum Mechanics Dr. J.M. Evans Example Sheet 1 Values of some physical constants are given on the supplementary sheet 1. Whenasampleofpotassiumisilluminatedwithlightofwavelength3
Mathematical Tripos Part IB Michaelmas Term 2015 Quantum Mechanics Dr. J.M. Evans Example Sheet 1 Values of some physical constants are given on the supplementary sheet 1. Whenasampleofpotassiumisilluminatedwithlightofwavelength3
Physics 221A Fall 2017 Notes 27 The Variational Method
 Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Copyright c 2018 by Robert G. Littlejohn Physics 221A Fall 2017 Notes 27 The Variational Method 1. Introduction Very few realistic problems in quantum mechanics are exactly solvable, so approximation methods
Chemistry 3502/4502. Final Exam Part I. May 14, 2005
 Advocacy chit Chemistry 350/450 Final Exam Part I May 4, 005. For which of the below systems is = where H is the Hamiltonian operator and T is the kinetic-energy operator? (a) The free particle
Advocacy chit Chemistry 350/450 Final Exam Part I May 4, 005. For which of the below systems is = where H is the Hamiltonian operator and T is the kinetic-energy operator? (a) The free particle
Total Angular Momentum for Hydrogen
 Physics 4 Lecture 7 Total Angular Momentum for Hydrogen Lecture 7 Physics 4 Quantum Mechanics I Friday, April th, 008 We have the Hydrogen Hamiltonian for central potential φ(r), we can write: H r = p
Physics 4 Lecture 7 Total Angular Momentum for Hydrogen Lecture 7 Physics 4 Quantum Mechanics I Friday, April th, 008 We have the Hydrogen Hamiltonian for central potential φ(r), we can write: H r = p
Angular Momentum Algebra
 Angular Momentum Algebra Chris Clark August 1, 2006 1 Input We will be going through the derivation of the angular momentum operator algebra. The only inputs to this mathematical formalism are the basic
Angular Momentum Algebra Chris Clark August 1, 2006 1 Input We will be going through the derivation of the angular momentum operator algebra. The only inputs to this mathematical formalism are the basic
arxiv: v1 [physics.gen-ph] 6 Jan 2014
![arxiv: v1 [physics.gen-ph] 6 Jan 2014 arxiv: v1 [physics.gen-ph] 6 Jan 2014](/thumbs/88/117915581.jpg) Kinematic relativity of quantum Hamiltonian Gintautas P. Kamuntavičius Department of Physics, Vytautas Magnus University, Vileikos 8, Kaunas 44404, Lithuania arxiv:1401.1098v1 [physics.gen-ph] 6 Jan 2014
Kinematic relativity of quantum Hamiltonian Gintautas P. Kamuntavičius Department of Physics, Vytautas Magnus University, Vileikos 8, Kaunas 44404, Lithuania arxiv:1401.1098v1 [physics.gen-ph] 6 Jan 2014
Lecture Models for heavy-ion collisions (Part III): transport models. SS2016: Dynamical models for relativistic heavy-ion collisions
 Lecture Models for heavy-ion collisions (Part III: transport models SS06: Dynamical models for relativistic heavy-ion collisions Quantum mechanical description of the many-body system Dynamics of heavy-ion
Lecture Models for heavy-ion collisions (Part III: transport models SS06: Dynamical models for relativistic heavy-ion collisions Quantum mechanical description of the many-body system Dynamics of heavy-ion
Quantum Mechanics Solutions. λ i λ j v j v j v i v i.
 Quantum Mechanics Solutions 1. (a) If H has an orthonormal basis consisting of the eigenvectors { v i } of A with eigenvalues λ i C, then A can be written in terms of its spectral decomposition as A =
Quantum Mechanics Solutions 1. (a) If H has an orthonormal basis consisting of the eigenvectors { v i } of A with eigenvalues λ i C, then A can be written in terms of its spectral decomposition as A =
Time dependent perturbation theory 1 D. E. Soper 2 University of Oregon 11 May 2012
 Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
Time dependent perturbation theory D. E. Soper University of Oregon May 0 offer here some background for Chapter 5 of J. J. Sakurai, Modern Quantum Mechanics. The problem Let the hamiltonian for a system
SHABNAM AKHTARI AND JEFFREY D. VAALER
 ON THE HEIGHT OF SOLUTIONS TO NORM FORM EQUATIONS arxiv:1709.02485v2 [math.nt] 18 Feb 2018 SHABNAM AKHTARI AND JEFFREY D. VAALER Abstract. Let k be a number field. We consider norm form equations associated
ON THE HEIGHT OF SOLUTIONS TO NORM FORM EQUATIONS arxiv:1709.02485v2 [math.nt] 18 Feb 2018 SHABNAM AKHTARI AND JEFFREY D. VAALER Abstract. Let k be a number field. We consider norm form equations associated
Lecture #1. Review. Postulates of quantum mechanics (1-3) Postulate 1
 L1.P1 Lecture #1 Review Postulates of quantum mechanics (1-3) Postulate 1 The state of a system at any instant of time may be represented by a wave function which is continuous and differentiable. Specifically,
L1.P1 Lecture #1 Review Postulates of quantum mechanics (1-3) Postulate 1 The state of a system at any instant of time may be represented by a wave function which is continuous and differentiable. Specifically,
C/CS/Phys C191 Particle-in-a-box, Spin 10/02/08 Fall 2008 Lecture 11
 C/CS/Phys C191 Particle-in-a-box, Spin 10/0/08 Fall 008 Lecture 11 Last time we saw that the time dependent Schr. eqn. can be decomposed into two equations, one in time (t) and one in space (x): space
C/CS/Phys C191 Particle-in-a-box, Spin 10/0/08 Fall 008 Lecture 11 Last time we saw that the time dependent Schr. eqn. can be decomposed into two equations, one in time (t) and one in space (x): space
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 22, March 20, 2006
 Chem 350/450 Physical Chemistry II Quantum Mechanics 3 Credits Spring Semester 006 Christopher J. Cramer Lecture, March 0, 006 Some material in this lecture has been adapted from Cramer, C. J. Essentials
Chem 350/450 Physical Chemistry II Quantum Mechanics 3 Credits Spring Semester 006 Christopher J. Cramer Lecture, March 0, 006 Some material in this lecture has been adapted from Cramer, C. J. Essentials
On compact operators
 On compact operators Alen Aleanderian * Abstract In this basic note, we consider some basic properties of compact operators. We also consider the spectrum of compact operators on Hilbert spaces. A basic
On compact operators Alen Aleanderian * Abstract In this basic note, we consider some basic properties of compact operators. We also consider the spectrum of compact operators on Hilbert spaces. A basic
AN ELEMENTARY PROOF OF THE GROUP LAW FOR ELLIPTIC CURVES
 AN ELEMENTARY PROOF OF THE GROUP LAW FOR ELLIPTIC CURVES Abstract. We give a proof of the group law for elliptic curves using explicit formulas. 1. Introduction In the following K will denote an algebraically
AN ELEMENTARY PROOF OF THE GROUP LAW FOR ELLIPTIC CURVES Abstract. We give a proof of the group law for elliptic curves using explicit formulas. 1. Introduction In the following K will denote an algebraically
Fermionic coherent states in infinite dimensions
 Fermionic coherent states in infinite dimensions Robert Oeckl Centro de Ciencias Matemáticas Universidad Nacional Autónoma de México Morelia, Mexico Coherent States and their Applications CIRM, Marseille,
Fermionic coherent states in infinite dimensions Robert Oeckl Centro de Ciencias Matemáticas Universidad Nacional Autónoma de México Morelia, Mexico Coherent States and their Applications CIRM, Marseille,
Lecture 5. Hartree-Fock Theory. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Lecture 5 Hartree-Fock Theory WS2010/11: Introduction to Nuclear and Particle Physics Particle-number representation: General formalism The simplest starting point for a many-body state is a system of
Harmonic Oscillator I
 Physics 34 Lecture 7 Harmonic Oscillator I Lecture 7 Physics 34 Quantum Mechanics I Monday, February th, 008 We can manipulate operators, to a certain extent, as we would algebraic expressions. By considering
Physics 34 Lecture 7 Harmonic Oscillator I Lecture 7 Physics 34 Quantum Mechanics I Monday, February th, 008 We can manipulate operators, to a certain extent, as we would algebraic expressions. By considering
One-electron Atom. (in spherical coordinates), where Y lm. are spherical harmonics, we arrive at the following Schrödinger equation:
 One-electron Atom The atomic orbitals of hydrogen-like atoms are solutions to the Schrödinger equation in a spherically symmetric potential. In this case, the potential term is the potential given by Coulomb's
One-electron Atom The atomic orbitals of hydrogen-like atoms are solutions to the Schrödinger equation in a spherically symmetric potential. In this case, the potential term is the potential given by Coulomb's
Mathematical Analysis of a Generalized Chiral Quark Soliton Model
 Symmetry, Integrability and Geometry: Methods and Applications Vol. 2 (2006), Paper 018, 12 pages Mathematical Analysis of a Generalized Chiral Quark Soliton Model Asao ARAI Department of Mathematics,
Symmetry, Integrability and Geometry: Methods and Applications Vol. 2 (2006), Paper 018, 12 pages Mathematical Analysis of a Generalized Chiral Quark Soliton Model Asao ARAI Department of Mathematics,
Does Møller Plesset perturbation theory converge? A look at two electron systems
 Does Møller Plesset perturbation theory converge? A look at two electron systems Mark S. Herman George A. Hagedorn Department of Mathematics and Center for Statistical Mechanics, Mathematical Physics,
Does Møller Plesset perturbation theory converge? A look at two electron systems Mark S. Herman George A. Hagedorn Department of Mathematics and Center for Statistical Mechanics, Mathematical Physics,
Linear Algebra in Hilbert Space
 Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Physics 342 Lecture 16 Linear Algebra in Hilbert Space Lecture 16 Physics 342 Quantum Mechanics I Monday, March 1st, 2010 We have seen the importance of the plane wave solutions to the potentialfree Schrödinger
Quantum Mechanics (Draft 2010 Nov.)
 Quantum Mechanics (Draft 00 Nov) For a -dimensional simple harmonic quantum oscillator, V (x) = mω x, it is more convenient to describe the dynamics by dimensionless position parameter ρ = x/a (a = h )
Quantum Mechanics (Draft 00 Nov) For a -dimensional simple harmonic quantum oscillator, V (x) = mω x, it is more convenient to describe the dynamics by dimensionless position parameter ρ = x/a (a = h )
Section 3 Electronic Configurations, Term Symbols, and States
 Section 3 Electronic Configurations, Term Symbols, and States Introductory Remarks- The Orbital, Configuration, and State Pictures of Electronic Structure One of the goals of quantum chemistry is to allow
Section 3 Electronic Configurations, Term Symbols, and States Introductory Remarks- The Orbital, Configuration, and State Pictures of Electronic Structure One of the goals of quantum chemistry is to allow
d 3 r d 3 vf( r, v) = N (2) = CV C = n where n N/V is the total number of molecules per unit volume. Hence e βmv2 /2 d 3 rd 3 v (5)
 LECTURE 12 Maxwell Velocity Distribution Suppose we have a dilute gas of molecules, each with mass m. If the gas is dilute enough, we can ignore the interactions between the molecules and the energy will
LECTURE 12 Maxwell Velocity Distribution Suppose we have a dilute gas of molecules, each with mass m. If the gas is dilute enough, we can ignore the interactions between the molecules and the energy will
CHAPTER 6 Quantum Mechanics II
 CHAPTER 6 Quantum Mechanics II 6.1 The Schrödinger Wave Equation 6.2 Expectation Values 6.3 Infinite Square-Well Potential 6.4 Finite Square-Well Potential 6.5 Three-Dimensional Infinite-Potential Well
CHAPTER 6 Quantum Mechanics II 6.1 The Schrödinger Wave Equation 6.2 Expectation Values 6.3 Infinite Square-Well Potential 6.4 Finite Square-Well Potential 6.5 Three-Dimensional Infinite-Potential Well
. α β γ δ ε ζ η θ ι κ λ μ Aμ ν(x) ξ ο π ρ ς σ τ υ φ χ ψ ω. Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω. Friday April 1 ± ǁ
 . α β γ δ ε ζ η θ ι κ λ μ Aμ ν(x) ξ ο π ρ ς σ τ υ φ χ ψ ω. Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω Friday April 1 ± ǁ 1 Chapter 5. Photons: Covariant Theory 5.1. The classical fields 5.2. Covariant
. α β γ δ ε ζ η θ ι κ λ μ Aμ ν(x) ξ ο π ρ ς σ τ υ φ χ ψ ω. Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω Friday April 1 ± ǁ 1 Chapter 5. Photons: Covariant Theory 5.1. The classical fields 5.2. Covariant
Systematics of the α-decay fine structure in even-even nuclei
 Systematics of the α-decay fine structure in even-even nuclei A. Dumitrescu 1,4, D. S. Delion 1,2,3 1 Department of Theoretical Physics, NIPNE-HH 2 Academy of Romanian Scientists 3 Bioterra University
Systematics of the α-decay fine structure in even-even nuclei A. Dumitrescu 1,4, D. S. Delion 1,2,3 1 Department of Theoretical Physics, NIPNE-HH 2 Academy of Romanian Scientists 3 Bioterra University
Elements of linear algebra
 Elements of linear algebra Elements of linear algebra A vector space S is a set (numbers, vectors, functions) which has addition and scalar multiplication defined, so that the linear combination c 1 v
Elements of linear algebra Elements of linear algebra A vector space S is a set (numbers, vectors, functions) which has addition and scalar multiplication defined, so that the linear combination c 1 v
3.024 Electrical, Optical, and Magnetic Properties of Materials Spring 2012 Recitation 3 Notes
 3.024 Electrical, Optical, and Magnetic Properties of Materials Spring 2012 Outline 1. Schr dinger: Eigenfunction Problems & Operator Properties 2. Piecewise Function/Continuity Review -Scattering from
3.024 Electrical, Optical, and Magnetic Properties of Materials Spring 2012 Outline 1. Schr dinger: Eigenfunction Problems & Operator Properties 2. Piecewise Function/Continuity Review -Scattering from
ACCUMULATION OF DISCRETE EIGENVALUES OF THE RADIAL DIRAC OPERATOR
 ACCUMULATION OF DISCRETE EIGENVALUES OF THE RADIAL DIRAC OPERATOR MARCEL GRIESEMER AND JOSEPH LUTGEN Abstract. For bounded potentials which behave like cx γ at infinity we investigate whether discrete
ACCUMULATION OF DISCRETE EIGENVALUES OF THE RADIAL DIRAC OPERATOR MARCEL GRIESEMER AND JOSEPH LUTGEN Abstract. For bounded potentials which behave like cx γ at infinity we investigate whether discrete
1 Math 241A-B Homework Problem List for F2015 and W2016
 1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
Plane wave solutions of the Dirac equation
 Lecture #3 Spherical spinors Hydrogen-like systems again (Relativistic version) irac energy levels Chapter, pages 48-53, Lectures on Atomic Physics Chapter 5, pages 696-76, Bransden & Joachain,, Quantum
Lecture #3 Spherical spinors Hydrogen-like systems again (Relativistic version) irac energy levels Chapter, pages 48-53, Lectures on Atomic Physics Chapter 5, pages 696-76, Bransden & Joachain,, Quantum
MP463 QUANTUM MECHANICS
 MP463 QUANTUM MECHANICS Introduction Quantum theory of angular momentum Quantum theory of a particle in a central potential - Hydrogen atom - Three-dimensional isotropic harmonic oscillator (a model of
MP463 QUANTUM MECHANICS Introduction Quantum theory of angular momentum Quantum theory of a particle in a central potential - Hydrogen atom - Three-dimensional isotropic harmonic oscillator (a model of
BRST and Dirac Cohomology
 BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
Second quantization: where quantization and particles come from?
 110 Phys460.nb 7 Second quantization: where quantization and particles come from? 7.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system? 7.1.1.Lagrangian Lagrangian
110 Phys460.nb 7 Second quantization: where quantization and particles come from? 7.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system? 7.1.1.Lagrangian Lagrangian
Outline Spherical symmetry Free particle Coulomb problem Keywords and References. Central potentials. Sourendu Gupta. TIFR, Mumbai, India
 Central potentials Sourendu Gupta TIFR, Mumbai, India Quantum Mechanics 1 2013 3 October, 2013 Outline 1 Outline 2 Rotationally invariant potentials 3 The free particle 4 The Coulomb problem 5 Keywords
Central potentials Sourendu Gupta TIFR, Mumbai, India Quantum Mechanics 1 2013 3 October, 2013 Outline 1 Outline 2 Rotationally invariant potentials 3 The free particle 4 The Coulomb problem 5 Keywords
Course Description for Real Analysis, Math 156
 Course Description for Real Analysis, Math 156 In this class, we will study elliptic PDE, Fourier analysis, and dispersive PDE. Here is a quick summary of the topics will study study. They re described
Course Description for Real Analysis, Math 156 In this class, we will study elliptic PDE, Fourier analysis, and dispersive PDE. Here is a quick summary of the topics will study study. They re described
Interpolating the arithmetic geometric mean inequality and its operator version
 Linear Algebra and its Applications 413 (006) 355 363 www.elsevier.com/locate/laa Interpolating the arithmetic geometric mean inequality and its operator version Rajendra Bhatia Indian Statistical Institute,
Linear Algebra and its Applications 413 (006) 355 363 www.elsevier.com/locate/laa Interpolating the arithmetic geometric mean inequality and its operator version Rajendra Bhatia Indian Statistical Institute,
Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2
 Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2 arxiv:quant-ph/0410063v1 8 Oct 2004 Nilanjana Datta Statistical Laboratory Centre for Mathematical Sciences University of Cambridge
Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2 arxiv:quant-ph/0410063v1 8 Oct 2004 Nilanjana Datta Statistical Laboratory Centre for Mathematical Sciences University of Cambridge
Summary of free theory: one particle state: vacuum state is annihilated by all a s: then, one particle state has normalization:
 The LSZ reduction formula based on S-5 In order to describe scattering experiments we need to construct appropriate initial and final states and calculate scattering amplitude. Summary of free theory:
The LSZ reduction formula based on S-5 In order to describe scattering experiments we need to construct appropriate initial and final states and calculate scattering amplitude. Summary of free theory:
The Quantum Hall Conductance: A rigorous proof of quantization
 Motivation The Quantum Hall Conductance: A rigorous proof of quantization Spyridon Michalakis Joint work with M. Hastings - Microsoft Research Station Q August 17th, 2010 Spyridon Michalakis (T-4/CNLS
Motivation The Quantum Hall Conductance: A rigorous proof of quantization Spyridon Michalakis Joint work with M. Hastings - Microsoft Research Station Q August 17th, 2010 Spyridon Michalakis (T-4/CNLS
Physical Chemistry Quantum Mechanics, Spectroscopy, and Molecular Interactions. Solutions Manual. by Andrew Cooksy
 Physical Chemistry Quantum Mechanics, Spectroscopy, and Molecular Interactions Solutions Manual by Andrew Cooksy February 4, 2014 Contents Contents i Objectives Review Questions 1 Chapter Problems 11 Notes
Physical Chemistry Quantum Mechanics, Spectroscopy, and Molecular Interactions Solutions Manual by Andrew Cooksy February 4, 2014 Contents Contents i Objectives Review Questions 1 Chapter Problems 11 Notes
Exact Solution of the Dirac Equation with a Central Potential
 Commun. math. Phys. 27, 155 161 (1972) by Springer-Verlag 1972 Exact Solution of the Dirac Equation with a Central Potential E. J. KANELLOPOULOS, TH. V. KANELLOPOULOS, and K. WILDERMUTH Institut fur Theoretische
Commun. math. Phys. 27, 155 161 (1972) by Springer-Verlag 1972 Exact Solution of the Dirac Equation with a Central Potential E. J. KANELLOPOULOS, TH. V. KANELLOPOULOS, and K. WILDERMUTH Institut fur Theoretische
Probability and Normalization
 Probability and Normalization Although we don t know exactly where the particle might be inside the box, we know that it has to be in the box. This means that, ψ ( x) dx = 1 (normalization condition) L
Probability and Normalization Although we don t know exactly where the particle might be inside the box, we know that it has to be in the box. This means that, ψ ( x) dx = 1 (normalization condition) L
A DECOMPOSITION THEOREM FOR FRAMES AND THE FEICHTINGER CONJECTURE
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX)0000-0 A DECOMPOSITION THEOREM FOR FRAMES AND THE FEICHTINGER CONJECTURE PETER G. CASAZZA, GITTA KUTYNIOK,
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX)0000-0 A DECOMPOSITION THEOREM FOR FRAMES AND THE FEICHTINGER CONJECTURE PETER G. CASAZZA, GITTA KUTYNIOK,
The 3 dimensional Schrödinger Equation
 Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Chapter 6 The 3 dimensional Schrödinger Equation 6.1 Angular Momentum To study how angular momentum is represented in quantum mechanics we start by reviewing the classical vector of orbital angular momentum
Boundedly complete weak-cauchy basic sequences in Banach spaces with the PCP
 Journal of Functional Analysis 253 (2007) 772 781 www.elsevier.com/locate/jfa Note Boundedly complete weak-cauchy basic sequences in Banach spaces with the PCP Haskell Rosenthal Department of Mathematics,
Journal of Functional Analysis 253 (2007) 772 781 www.elsevier.com/locate/jfa Note Boundedly complete weak-cauchy basic sequences in Banach spaces with the PCP Haskell Rosenthal Department of Mathematics,
here, this space is in fact infinite-dimensional, so t σ ess. Exercise Let T B(H) be a self-adjoint operator on an infinitedimensional
 15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
15. Perturbations by compact operators In this chapter, we study the stability (or lack thereof) of various spectral properties under small perturbations. Here s the type of situation we have in mind:
16. GAUGE THEORY AND THE CREATION OF PHOTONS
 6. GAUGE THEORY AD THE CREATIO OF PHOTOS In the previous chapter the existence of a gauge theory allowed the electromagnetic field to be described in an invariant manner. Although the existence of this
6. GAUGE THEORY AD THE CREATIO OF PHOTOS In the previous chapter the existence of a gauge theory allowed the electromagnetic field to be described in an invariant manner. Although the existence of this
Molecular Rydberg states
 1 Molecular Rydberg states 1.1 The nature of Rydberg states The nature of atomic Rydberg states is well described by Gallagher, though with less emphasis on theory [1]. Those of molecules are severely
1 Molecular Rydberg states 1.1 The nature of Rydberg states The nature of atomic Rydberg states is well described by Gallagher, though with less emphasis on theory [1]. Those of molecules are severely
THE NUMBER OF ORTHOGONAL CONJUGATIONS
 THE NUMBER OF ORTHOGONAL CONJUGATIONS Armin Uhlmann University of Leipzig, Institute for Theoretical Physics After a short introduction to anti-linearity, bounds for the number of orthogonal (skew) conjugations
THE NUMBER OF ORTHOGONAL CONJUGATIONS Armin Uhlmann University of Leipzig, Institute for Theoretical Physics After a short introduction to anti-linearity, bounds for the number of orthogonal (skew) conjugations
Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world,
 Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world, x p h π If you try to specify/measure the exact position of a particle you
Introduction to Quantum Mechanics (Prelude to Nuclear Shell Model) Heisenberg Uncertainty Principle In the microscopic world, x p h π If you try to specify/measure the exact position of a particle you
The Linear Sampling Method and the MUSIC Algorithm
 CODEN:LUTEDX/(TEAT-7089)/1-6/(2000) The Linear Sampling Method and the MUSIC Algorithm Margaret Cheney Department of Electroscience Electromagnetic Theory Lund Institute of Technology Sweden Margaret Cheney
CODEN:LUTEDX/(TEAT-7089)/1-6/(2000) The Linear Sampling Method and the MUSIC Algorithm Margaret Cheney Department of Electroscience Electromagnetic Theory Lund Institute of Technology Sweden Margaret Cheney
Applications of Quantum Theory to Some Simple Systems
 Applications of Quantum Theory to Some Simple Systems Arbitrariness in the value of total energy. We will use classical mechanics, and for simplicity of the discussion, consider a particle of mass m moving
Applications of Quantum Theory to Some Simple Systems Arbitrariness in the value of total energy. We will use classical mechanics, and for simplicity of the discussion, consider a particle of mass m moving
The Dirac Equation. Topic 3 Spinors, Fermion Fields, Dirac Fields Lecture 13
 The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
Combinatorial Hopf algebras in particle physics I
 Combinatorial Hopf algebras in particle physics I Erik Panzer Scribed by Iain Crump May 25 1 Combinatorial Hopf Algebras Quantum field theory (QFT) describes the interactions of elementary particles. There
Combinatorial Hopf algebras in particle physics I Erik Panzer Scribed by Iain Crump May 25 1 Combinatorial Hopf Algebras Quantum field theory (QFT) describes the interactions of elementary particles. There
Thermodynamic limit for a system of interacting fermions in a random medium. Pieces one-dimensional model
 Thermodynamic limit for a system of interacting fermions in a random medium. Pieces one-dimensional model Nikolaj Veniaminov (in collaboration with Frédéric Klopp) CEREMADE, University of Paris IX Dauphine
Thermodynamic limit for a system of interacting fermions in a random medium. Pieces one-dimensional model Nikolaj Veniaminov (in collaboration with Frédéric Klopp) CEREMADE, University of Paris IX Dauphine
Brief review of Quantum Mechanics (QM)
 Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
Brief review of Quantum Mechanics (QM) Note: This is a collection of several formulae and facts that we will use throughout the course. It is by no means a complete discussion of QM, nor will I attempt
Physics 115C Homework 3
 Physics 115C Homework 3 Problem 1 In this problem, it will be convenient to introduce the Einstein summation convention. Note that we can write S = i S i i where the sum is over i = x,y,z. In the Einstein
Physics 115C Homework 3 Problem 1 In this problem, it will be convenient to introduce the Einstein summation convention. Note that we can write S = i S i i where the sum is over i = x,y,z. In the Einstein
SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS
 C O L L O Q U I U M M A T H E M A T I C U M VOL. LXIII 1992 FASC. 2 SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS BY JACEK D Z I U B A Ń S K I (WROC
C O L L O Q U I U M M A T H E M A T I C U M VOL. LXIII 1992 FASC. 2 SCHWARTZ SPACES ASSOCIATED WITH SOME NON-DIFFERENTIAL CONVOLUTION OPERATORS ON HOMOGENEOUS GROUPS BY JACEK D Z I U B A Ń S K I (WROC
THE MAPPING CLASS GROUP ACTS REDUCIBLY ON SU(n)-CHARACTER VARIETIES
 THE MAPPING CLASS GROUP ACTS REDUCIBLY ON SU(n)-CHARACTER VARIETIES WILLIAM M. GOLDMAN Abstract. When G is a connected compact Lie group, and π is a closed surface group, then Hom(π, G)/G contains an open
THE MAPPING CLASS GROUP ACTS REDUCIBLY ON SU(n)-CHARACTER VARIETIES WILLIAM M. GOLDMAN Abstract. When G is a connected compact Lie group, and π is a closed surface group, then Hom(π, G)/G contains an open
If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle.
 CHEM 2060 Lecture 18: Particle in a Box L18-1 Atomic Orbitals If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle. We can only talk
CHEM 2060 Lecture 18: Particle in a Box L18-1 Atomic Orbitals If electrons moved in simple orbits, p and x could be determined, but this violates the Heisenberg Uncertainty Principle. We can only talk
Recall that any inner product space V has an associated norm defined by
 Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
Hilbert Spaces Recall that any inner product space V has an associated norm defined by v = v v. Thus an inner product space can be viewed as a special kind of normed vector space. In particular every inner
Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction
 Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Lecture 5 Coupling of Angular Momenta Isospin Nucleon-Nucleon Interaction WS0/3: Introduction to Nuclear and Particle Physics,, Part I I. Angular Momentum Operator Rotation R(θ): in polar coordinates the
Problems and Multiple Choice Questions
 Problems and Multiple Choice Questions 1. A momentum operator in one dimension is 2. A position operator in 3 dimensions is 3. A kinetic energy operator in 1 dimension is 4. If two operator commute, a)
Problems and Multiple Choice Questions 1. A momentum operator in one dimension is 2. A position operator in 3 dimensions is 3. A kinetic energy operator in 1 dimension is 4. If two operator commute, a)
Lecture notes for QFT I (662)
 Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Preprint typeset in JHEP style - PAPER VERSION Lecture notes for QFT I (66) Martin Kruczenski Department of Physics, Purdue University, 55 Northwestern Avenue, W. Lafayette, IN 47907-036. E-mail: markru@purdue.edu
Linear Algebra and Dirac Notation, Pt. 3
 Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer. Lecture 9, February 8, 2006
 Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
Chem 3502/4502 Physical Chemistry II (Quantum Mechanics) 3 Credits Spring Semester 2006 Christopher J. Cramer Lecture 9, February 8, 2006 The Harmonic Oscillator Consider a diatomic molecule. Such a molecule
Elementary linear algebra
 Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
Chapter 1 Elementary linear algebra 1.1 Vector spaces Vector spaces owe their importance to the fact that so many models arising in the solutions of specific problems turn out to be vector spaces. The
