Prentice Hall Geometry (c) 2007 correlated to American Diploma Project, High School Math Benchmarks
|
|
|
- Lambert Marsh
- 5 years ago
- Views:
Transcription
1 I1.1. Add, subtract, multiply and divide integers, fractions and decimals. I1.2. Calculate and apply ratios, proportions, rates and percentages to solve problems. I1.3. Use the correct order of operations to evaluate arithmetic expressions, including those containing parentheses. Math Benchmarks - I I. Number Sense and Numerical Operations I1. Compute fluently and accurately with rational numbers without a calculator: Addressed in an applied context throughout the text. Sample citations: SE/TE: 32-34, 62, , , 288, , , , 563, SE/TE: , , , , , 404, , 423, , , , , 574, 580, 581, , , 604, 614, 630, 644, 645, , , 761 SE/TE: 754 I1.4. Explain and apply basic number theory concepts such as prime number, factor, divisibility, least common multiple and greatest common divisor. I1.5. Multiply and divide numbers expressed in scientific notation. I2. Recognize and apply magnitude (absolute value) and ordering of real numbers: I2.1. Locate the position of a number on the number line, know that its distance from the origin is its absolute value and know that the distance between two numbers on the number line is the absolute value of their difference. SE/TE: 757 I2.2. Determine the relative position on the number line of numbers and the relative magnitude of numbers expressed in fractional form, in decimal form, as roots or in scientific notation. I3. Understand that to solve certain problems and equations, number systems need to be extended from whole numbers to the set of all integers (positive, negative and zero), from integers to rational numbers, from rational numbers to real numbers (rational and irrational numbers) and from real numbers to complex numbers; define and give examples of each of these types of numbers. Page 1 of 10
2 I4. Understand the capabilities and the limitations of calculators and computers in solving problems: I4.1. Use calculators appropriately and make SE/TE: 63, estimations without a calculator regularly to detect potential errors. I4.2. Use graphing calculators and computer spreadsheets. SE/TE: 67, 69, 163, 170, , 179, 187, 355, 436, 442, 563, 586, 616, 636, 642, 645, 682, 699 Math Benchmarks - J J. Algebra J1. Perform basic operations on algebraic expressions fluently and accurately: J1.1. Understand the properties of integer exponents and roots and apply these properties to simplify algebraic expressions. J1.2. * Understand the properties of rational exponents and apply these properties to simplify algebraic expressions. J1.3. Add, subtract and multiply polynomials; divide a polynomial by a low-degree polynomial. SE/TE: 754 J1.4. Factor polynomials by removing the greatest common factor; factor quadratic polynomials. J1.5. Add, subtract, multiply, divide and simplify rational expressions. J1.6. Evaluate polynomial and rational expressions and expressions containing radicals and absolute values at specified values of their variables. J1.7. * Derive and use the formulas for the general term and summation of finite arithmetic and geometric series; find the sum of an infinite geometric series whose common ratio, r, is in the interval ( 1, 1). J2. Understand functions, their representations and their properties: J2.1. Recognize whether a relationship given in symbolic or graphical form is a function. J2.2. * Determine the domain of a function represented in either symbolic or graphical form. J2.3. Understand functional notation and evaluate a function at a specified point in its domain. Page 2 of 10
3 J2.4. * Combine functions by composition, as well as by addition, subtraction, multiplication and division. J2.5. * Identify whether a function has an inverse and when functions are inverses of each other; explain why the graph of a function and its inverse are reflections of one another over the line y = x. J2.6. * Know that the inverse of an exponential function is a logarithm, prove basic properties of a logarithm using properties of its inverse and apply those properties to solve problems. J3. Apply basic algebraic operations to solve equations and inequalities: J3.1. Solve linear equations and inequalities in one variable including those involving the absolute value of a linear function. J3.2. Solve an equation involving several variables for one variable in terms of the others. Addressed in an applied context. SE/TE: 30, 32-35, 41-42, 46-48, 59, 72, 74, , , , 119, , 288, , , 404 SE/TE: 607, 759 J3.3. Solve systems of two linear equations in two variables. J3.4. * Solve systems of three linear equations in three variables. SE/TE: 234, 760 J3.5. Solve quadratic equations in one variable. SE/TE: , 372, J4. Graph a variety of equations and inequalities in two variables, demonstrate understanding of the relationships between the algebraic properties of an equation and the geometric properties of its graph, and interpret a graph: J4.1. Graph a linear equation and demonstrate that it has a constant rate of change. SE/TE: , 169, 180, 191 J4.2. Understand the relationship between the coefficients of a linear equation and the slope and x- and y-intercepts of its graph. J4.3. Understand the relationship between a solution of a system of two linear equations in two variables and the graphs of the corresponding lines. J4.4. Graph the solution set of a linear inequality and identify whether the solution set is an open or a closed half-plane; graph the solution set of a system of two or three linear inequalities. SE/TE: , 191 SE/TE: 234, 760 Page 3 of 10
4 J4.5. Graph a quadratic function and understand the relationship between its real zeros and the x- intercepts of its graph. J4.6. * Graph ellipses and hyperbolas whose axes are parallel to the x and y axes and demonstrate understanding of the relationship between their standard algebraic form and their graphical characteristics. J.4.7. Graph exponential functions and identify their key characteristics. J4.8. Read information and draw conclusions from graphs; identify properties of a graph that provide useful information about the original problem. SE/TE: Addressed in Prentice Hall Algebra 1 and Algebra 2. SE/TE: , 751 J5. Solve problems by converting the verbal information given into an appropriate mathematical model involving equations or systems of equations; apply appropriate mathematical techniques to analyze these mathematical models; and interpret the solution obtained in written form using appropriate units of measurement: J5.1. Recognize and solve problems that can be modeled using a linear equation in one variable, such as time/rate/distance problems, percentage increase or decrease problems, and ratio and proportion problems. J5.2. Recognize and solve problems that can be modeled using a system of two equations in two variables, such as mixture problems. SE/TE: , 399, J5.3. Recognize and solve problems that can be modeled using a quadratic equation, such as the motion of an object under the force of gravity. J5.4. Recognize and solve problems that can be modeled using an exponential function, such as compound interest problems. J5.5. * Recognize and solve problems that can be modeled using an exponential function but whose solution requires facility with logarithms, such as exponential growth and decay problems. J5.6. Recognize and solve problems that can be modeled using a finite geometric series, such as home mortgage problems and other compound interest problems. J6. * Understand the binomial theorem and its connections to combinatorics, Pascal's triangle and probability. Page 4 of 10
5 K1.1. Identify, explain the necessity of and give examples of definitions, axioms and theorems. Math Benchmarks - K K. Geometry K1. Understand the different roles played by axioms, definitions and theorems in the logical structure of mathematics, especially in geometry: Addressed throughout the text. Sample citations: SE/TE: 18-19, 21, 31-32, 35, 38, 64, 66 (#40), 89-91, 99, 100 (#7), , 118, 120, 128, 130, , , 147, 149, 154, , 199, , , 228, 235, 260, , , , 306, , , , , 348, , , , 417, 419, , , 516, , , 547, 554, 561, , 576, 610, , , , 638, 640, 647, 662, 664, , , 687, 689, 695 K1.2. State and prove key basic theorems in SE/TE: , , geometry such as the Pythagorean theorem, the sum of the angles of a triangle is 180 degrees, and the line joining the midpoints of two sides of a triangle is parallel to the third side and half its length. K1.3. Recognize that there are geometries, other than Euclidean geometry, in which the parallel postulate is not true. SE/TE: K2. Identify and apply the definitions related to lines and angles and use them to prove theorems in (Euclidean) geometry, solve problems, and perform basic geometric constructions using a straight edge and compass: K2.1. Identify and apply properties of and theorems about parallel lines and use them to prove theorems such as two lines parallel to a third are parallel to each other and to perform constructions such as a line parallel to a given line through a point not on the line. SE/TE: , 145, 147, 153, , , , , K2.2. Identify and apply properties of and theorems about perpendicular lines and use them to prove theorems such as the perpendicular bisectors of line segments are the set of all points equidistant from the two end points and to perform constructions such as the perpendicular bisector of a line segment. SE/TE: 46, , , , , 265 Page 5 of 10
6 K2.3. Identify and apply properties of and theorems about angles and use them to prove theorems such as two lines are parallel exactly when the alternate interior angles they make with a transversal are equal and to perform constructions such as the bisector of an angle. SE/TE: 46-49, 59, 74, , , , 144, , , 171, , , , , , 250, 252, , 286, , , , , K3. Know the basic theorems about congruent and similar triangles and use them to prove additional theorems and solve problems. K4. Know the definitions and basic properties of a circle and use them to prove basic theorems and solve problems. SE/TE: , , , , 233, , , 279, , , 404, SE/TE: 62-63, 65-68, 73-74, 273, 563 (#34), , , , , , , K5. Apply the Pythagorean theorem, its converse and properties of special right triangles to solve problems. SE/TE: , , 443, 459, , K6. Use rigid motions (compositions of reflections, translations and rotations) to determine whether two geometric figures are congruent and to create and analyze geometric designs. SE/TE: 471, 473, 488, , 513, , K7. Know about the similarity of figures and use the scale factor to solve problems. SE/TE: , , , 393, 395, 404, , 410, , , , 564, 590, 592 K8. Know that geometric measurements (length, area, perimeter, volume) depend on the choice of a unit and that measurements made on physical objects are approximations; calculate the measurements of common plane and solid geometric figures: K8.1. Understand that numerical values associated with measurements of physical quantities must be assigned units of measurement or dimensions; apply such units correctly in expressions, equations and problem solutions that involve measurements; and convert a measurement using one unit of measurement to another unit of measurement. Angle measures addressed throughout the text. Other geometric measurements: SE/TE: 31, 34-37, 52, 57-59, 61-69, 73-74, 222, 232, , , , , , 399, , , , 418, , , , , 443, , 453, , , , 526, , , , 568, , , , , 609, , 616, , , , , , 663, , , 682, , , 699, 707, 710, 747, 748 Page 6 of 10
7 K8.2. Determine the perimeter of a polygon and the circumference of a circle; the area of a rectangle, a circle, a triangle and a polygon with more than four sides by decomposing it into triangles; the surface area of a prism, a pyramid, a cone and a sphere; and the volume of a rectangular box, a prism, a pyramid, a cone and a sphere. SE/TE: 62-68, 73-74, , , , , , 587, , , , , , , K8.3. Know that the effect of a scale factor k on length, area and volume is to multiply each by k, k 2 and k 3, respectively. K9. Visualize solids and surfaces in threedimensional space when given twodimensional representations (e.g., nets, multiple views) and create two-dimensional representations for the surfaces of threedimensional objects. SE/TE: , , SE/TE: 10-15, 22, 72, , , 612 (#20), 617, 619, 623, 631, 653, 656 K10. Represent geometric objects and figures algebraically using coordinates; use algebra to solve geometric problems: K10.1. Express the intuitive concept of the "slant" of a line in terms of the precise concept of slope, use the coordinates of two points on a line to define its slope, and use slope to express the parallelism and perpendicularity of lines. SE/TE: , , 186, K10.2. Describe a line by a linear equation. SE/TE: , , K10.3. Find the distance between two points using their coordinates and the Pythagorean theorem. SE/TE: 53-54, 56-59, 68, 73-74, 421 (#34) K10.4. * Find an equation of a circle given its center and radius and, given an equation of a circle, find its center and radius. SE/TE: , 705, K11. Understand basic right-triangle trigonometry and apply it to solve problems: K11.1. Understand how similarity of right triangles allows the trigonometric functions sine, cosine and tangent to be defined as ratios of sides and be able to use these functions to solve problems. K11.2. Apply the trigonometric functions sine, cosine and tangent to solve for an unknown length of a side of a right triangle, given one of the acute angles and the length of another side. SE/TE: , , , , , , , 565, 590, 592 SE/TE: , , , 459, 462, 464 Page 7 of 10
8 K11.3. Use the standard formula for the area of a triangle, A=1/2bh, to explain the area formula, A=1/2absinC where a and b are the lengths of two sides of a triangle and C is the measure of the included angle formed by these two sides, and use it to find the area of a triangle when given the lengths of two of its sides and the included angle. SE/TE: , 590, 592 K12. * Know how the trigonometric functions can be extended to periodic functions on the real line, derive basic formulas involving these functions, and use these functions and formulas to solve problems: K12.1. * Know that the trigonometric functions sine and cosine, and thus all trigonometric functions, can be extended to periodic functions on the real line by defining them as functions on the unit circle, that radian measure of an angle between 0 and 360 degrees is the arc length of the unit circle subtended by that central angle, and that by similarity, the arc length s of a circle of radius r subtended by a central angle of measure t radians is s = rt. K12.2. * Know and use the basic identities, such as sin2 (x) + cos2 (x) = 1 and cos(π/2 - x) = sin(x) and formulas for sine and cosine, such as addition and double angle formulas. K12.3. * Graph sine, cosine and tangent as well as their reciprocals, secant, cosecant and cotangent; identify key characteristics. K12.4. * Know and use the law of cosines and the law of sines to find missing sides and angles of a triangle. SE/TE: 440 SE/TE: 565 Math Benchmarks - L L. Data Interpretation, Statistics and Probability L1. Explain and apply quantitative information: L1.1. Organize and display data using appropriate methods (including spreadsheets) to detect patterns and departures from patterns. SE/TE: 76, , , 645, 742, 751, 752 L1.2. Read and interpret tables, charts and graphs. L1.3. Compute and explain summary statistics for distributions of data including measures of center (mean, median) and spread (range, percentiles, variance, standard deviation). SE/TE: 6 9, 163 (#57), 187, 320, 363, 413, 563 (#34), , 616, 645, , 742, SE/TE: 431, 750 Page 8 of 10
9 L1.4. Compare data sets using graphs and summary statistics. L1.5. Create scatter plots, analyze patterns and describe relationships in paired data. L1.6. Know the characteristics of the Gaussian normal distribution (bell-shaped curve). SE/TE: SE/TE: 742 L2. Explain and critique alternative ways of presenting and using information: L2.1. Evaluate reports based on data published in the media by considering the source of the data, the design of the study, and the way the data are analyzed and displayed. An opportunity to address this standard can be found on: SE/TE: L2.2. Identify and explain misleading uses of data. SE/TE: L2.3. Recognize when arguments based on data confuse correlation with causation. An opportunity to address this standard can be found in Prentice Hall Algebra 1. L3. Explain the use of data and statistical thinking to draw inferences, make predictions and justify conclusions: L3.1. Explain the impact of sampling methods, bias and the phrasing of questions asked during data collection and the conclusions that can rightfully be made. Addressed in Prentice Hall Algebra 1 and Algebra 2. L3.2. Design simple experiments or investigations to collect data to answer questions of interest. Addressed in Prentice Hall Algebra 1 and Algebra 2. L3.3. Explain the differences between randomized experiments and observational studies. L3.4. Construct a scatter plot of a set of paired data and if it demonstrates a linear trend, use a graphing calculator to find the regression line that best fits this data; recognize that the correlation coefficient measures goodness of fit and explain when it is appropriate to use the regression line to make predictions. Addressed in Prentice Hall Algebra 1 and Algebra 2. L4. Explain and apply probability concepts and calculate simple probabilities: L4.1. Explain how probability quantifies the likelihood that an event occurs in terms of numbers. L4.2. Explain how the relative frequency of a specified outcome of an event can be used to estimate the probability of the outcome. SE/TE: 762 An opportunity to address this standard can be found on: SE/TE: 538 (#29), , L4.3. Explain how the law of large numbers can be applied in simple examples. Addressed in Prentice Hall Algebra 1 and Algebra 2. Page 9 of 10
10 L4.4. Apply probability concepts such as conditional probability and independent events to calculate simple probabilities. L4.5. Apply probability concepts to practical situations to make informed decisions. SE/TE: 22, 162 (#45), 218 (#31), , 294, 326 (#26), 459 (#50), 538 (#29), , , 762 SE/TE: Page 10 of 10
Hawai`i Post-Secondary Math Survey -- Content Items
 Hawai`i Post-Secondary Math Survey -- Content Items Section I: Number sense and numerical operations -- Several numerical operations skills are listed below. Please rank each on a scale from 1 (not essential)
Hawai`i Post-Secondary Math Survey -- Content Items Section I: Number sense and numerical operations -- Several numerical operations skills are listed below. Please rank each on a scale from 1 (not essential)
Prentice Hall PreCalculus, 3rd Edition 2007, (Blitzer)
 Prentice Hall PreCalculus, 3rd Edition 2007, (Blitzer) C O R R E L A T E D T O Number Properties and Operations High school students should enter high school with a strong background in rational numbers
Prentice Hall PreCalculus, 3rd Edition 2007, (Blitzer) C O R R E L A T E D T O Number Properties and Operations High school students should enter high school with a strong background in rational numbers
Prentice Hall Intermediate Algebra, 5th Edition 2009 (Martin-Gay)
 Prentice Hall Intermediate Algebra, 5th Edition 2009 (Martin-Gay) C O R R E L A T E D T O Number Properties and Operations High school students should enter high school with a strong background in rational
Prentice Hall Intermediate Algebra, 5th Edition 2009 (Martin-Gay) C O R R E L A T E D T O Number Properties and Operations High school students should enter high school with a strong background in rational
CME Project, Geometry 2009 Correlated to: Kentucky Core Content for Mathematics Assessment 4.1 (High School, Grade 11)
 Number Properties and Operations High school students should enter high school with a strong background in rational numbers and numerical operations and expand this to real numbers. This becomes the foundation
Number Properties and Operations High school students should enter high school with a strong background in rational numbers and numerical operations and expand this to real numbers. This becomes the foundation
ALGEBRA I: State Standards, MPS Objectives and Essential Learnings
 ALGEBRA I: s, s and s MA 12.1 Students will communicate number sense concepts using multiple representations to reason, solve problems, and make connections within mathematics and across disciplines. MA
ALGEBRA I: s, s and s MA 12.1 Students will communicate number sense concepts using multiple representations to reason, solve problems, and make connections within mathematics and across disciplines. MA
Algebra 2 with Trigonometry Correlation of the ALEKS course Algebra 2 with Trigonometry to the Tennessee Algebra II Standards
 Algebra 2 with Trigonometry Correlation of the ALEKS course Algebra 2 with Trigonometry to the Tennessee Algebra II Standards Standard 2 : Number & Operations CLE 3103.2.1: CLE 3103.2.2: CLE 3103.2.3:
Algebra 2 with Trigonometry Correlation of the ALEKS course Algebra 2 with Trigonometry to the Tennessee Algebra II Standards Standard 2 : Number & Operations CLE 3103.2.1: CLE 3103.2.2: CLE 3103.2.3:
Algebra II Crosswalk. Red font indicates a passage that is not addressed in the compared sets of standards.
 The chart below includes the assessed on the Algebra II California Test, the Mathematics ), the the, the Competencies in Mathematics from the Intersegmental Committee of the Academic Senate (ICAS), and
The chart below includes the assessed on the Algebra II California Test, the Mathematics ), the the, the Competencies in Mathematics from the Intersegmental Committee of the Academic Senate (ICAS), and
Common Core Edition Table of Contents
 Common Core Edition Table of Contents ALGEBRA 1 Chapter 1 Foundations for Algebra 1-1 Variables and Expressions 1-2 Order of Operations and Evaluating Expressions 1-3 Real Numbers and the Number Line 1-4
Common Core Edition Table of Contents ALGEBRA 1 Chapter 1 Foundations for Algebra 1-1 Variables and Expressions 1-2 Order of Operations and Evaluating Expressions 1-3 Real Numbers and the Number Line 1-4
Algebra II Learning Targets
 Chapter 0 Preparing for Advanced Algebra LT 0.1 Representing Functions Identify the domain and range of functions LT 0.2 FOIL Use the FOIL method to multiply binomials LT 0.3 Factoring Polynomials Use
Chapter 0 Preparing for Advanced Algebra LT 0.1 Representing Functions Identify the domain and range of functions LT 0.2 FOIL Use the FOIL method to multiply binomials LT 0.3 Factoring Polynomials Use
Right Triangles And Trigonometery
 Big Idea: Number Properties and Operations Academic Expectations 2.7 Students understand number concepts and use numbers appropriately and accurately. 2.8 Students understand various mathematical procedures
Big Idea: Number Properties and Operations Academic Expectations 2.7 Students understand number concepts and use numbers appropriately and accurately. 2.8 Students understand various mathematical procedures
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1
 Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
How well do I know the content? (scale 1 5)
 Page 1 I. Number and Quantity, Algebra, Functions, and Calculus (68%) A. Number and Quantity 1. Understand the properties of exponents of s I will a. perform operations involving exponents, including negative
Page 1 I. Number and Quantity, Algebra, Functions, and Calculus (68%) A. Number and Quantity 1. Understand the properties of exponents of s I will a. perform operations involving exponents, including negative
Prentice Hall Geometry, Foundations Series 2011 Correlated to: Minnesota K-12 Academic Standards in Mathematics, 9/2008, to grade 9, 10, 11
 Algebra Understand the concept of function, and identify important features of functions and other relations using symbolic and graphical methods. 9.2.1.1 Understand the definition of a function. Use functional
Algebra Understand the concept of function, and identify important features of functions and other relations using symbolic and graphical methods. 9.2.1.1 Understand the definition of a function. Use functional
9-12 Mathematics Vertical Alignment ( )
 Algebra I Algebra II Geometry Pre- Calculus U1: translate between words and algebra -add and subtract real numbers -multiply and divide real numbers -evaluate containing exponents -evaluate containing
Algebra I Algebra II Geometry Pre- Calculus U1: translate between words and algebra -add and subtract real numbers -multiply and divide real numbers -evaluate containing exponents -evaluate containing
Standards for Mathematical Practice. Ratio and Proportional Relationships
 North Carolina Standard Course of Study Sixth Grade Mathematics 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique
North Carolina Standard Course of Study Sixth Grade Mathematics 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique
Content Guidelines Overview
 Content Guidelines Overview The Pearson Video Challenge is open to all students, but all video submissions must relate to set of predetermined curriculum areas and topics. In the following pages the selected
Content Guidelines Overview The Pearson Video Challenge is open to all students, but all video submissions must relate to set of predetermined curriculum areas and topics. In the following pages the selected
STEM-Prep Pathway SLOs
 STEM-Prep Pathway SLOs Background: The STEM-Prep subgroup of the MMPT adopts a variation of the student learning outcomes for STEM from the courses Reasoning with Functions I and Reasoning with Functions
STEM-Prep Pathway SLOs Background: The STEM-Prep subgroup of the MMPT adopts a variation of the student learning outcomes for STEM from the courses Reasoning with Functions I and Reasoning with Functions
Region 16 Board of Education. Precalculus Curriculum
 Region 16 Board of Education Precalculus Curriculum 2008 1 Course Description This course offers students an opportunity to explore a variety of concepts designed to prepare them to go on to study calculus.
Region 16 Board of Education Precalculus Curriculum 2008 1 Course Description This course offers students an opportunity to explore a variety of concepts designed to prepare them to go on to study calculus.
Arizona Mathematics Standards Articulated by Grade Level (2008) for College Work Readiness (Grades 11 and 12)
 Strand 1: Number and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, and the relationships among numbers and different number systems. College Work Readiness
Strand 1: Number and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, and the relationships among numbers and different number systems. College Work Readiness
Integrated Mathematics I, II, III 2016 Scope and Sequence
 Mathematics I, II, III 2016 Scope and Sequence I Big Ideas Math 2016 Mathematics I, II, and III Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational
Mathematics I, II, III 2016 Scope and Sequence I Big Ideas Math 2016 Mathematics I, II, and III Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational
Prentice Hall Mathematics, Geometry 2009 Correlated to: Maine Learning Results 2007 Mathematics Grades 9-Diploma
 A. NUMBER: Students use numbers in everyday and mathematical contexts to quantify or describe phenomena, develop concepts of operations with different types of numbers, use the structure and properties
A. NUMBER: Students use numbers in everyday and mathematical contexts to quantify or describe phenomena, develop concepts of operations with different types of numbers, use the structure and properties
STAAR STANDARDS ALGEBRA I ALGEBRA II GEOMETRY
 STANDARDS ALGEBRA I ALGEBRA II GEOMETRY STANDARDS ALGEBRA I TEKS Snapshot Algebra I (New TEKS 2015-16) Mathematical Process Standards A.1 Mathematical process standards. The student uses mathematical processes
STANDARDS ALGEBRA I ALGEBRA II GEOMETRY STANDARDS ALGEBRA I TEKS Snapshot Algebra I (New TEKS 2015-16) Mathematical Process Standards A.1 Mathematical process standards. The student uses mathematical processes
T a b l e o f C o n t e n t s
 T a b l e o f C o n t e n t s C O M P E T E N C Y 1 KNOWLEDGE OF ALGEBRA... 1 SKILL 1.1: Apply the properties of real numbers: closure, commutative, associative, distributive, transitive, identities, and
T a b l e o f C o n t e n t s C O M P E T E N C Y 1 KNOWLEDGE OF ALGEBRA... 1 SKILL 1.1: Apply the properties of real numbers: closure, commutative, associative, distributive, transitive, identities, and
MyMathLab for School Precalculus Graphical, Numerical, Algebraic Common Core Edition 2016
 A Correlation of MyMathLab for School Precalculus Common Core Edition 2016 to the Tennessee Mathematics Standards Approved July 30, 2010 Bid Category 13-090-10 , Standard 1 Mathematical Processes Course
A Correlation of MyMathLab for School Precalculus Common Core Edition 2016 to the Tennessee Mathematics Standards Approved July 30, 2010 Bid Category 13-090-10 , Standard 1 Mathematical Processes Course
Saxon Advanced Mathematics Scope and Sequence
 hmhco.com Saxon Advanced Mathematics Scope and Sequence Foundations Calculator Perform two-variable analysis Use graphing calculators Find roots of equations Solve systems of equations Exponentials and
hmhco.com Saxon Advanced Mathematics Scope and Sequence Foundations Calculator Perform two-variable analysis Use graphing calculators Find roots of equations Solve systems of equations Exponentials and
Mathematics AIMM Scope and Sequence 176 Instructional Days 16 Units
 Mathematics AIMM Scope and Sequence 176 Instructional 16 Units Unit 1: Area and Surface Area Solve real-world and mathematical problems involving area, surface area, and volume. NC.6.G.1 Create geometric
Mathematics AIMM Scope and Sequence 176 Instructional 16 Units Unit 1: Area and Surface Area Solve real-world and mathematical problems involving area, surface area, and volume. NC.6.G.1 Create geometric
Use estimation strategies reasonably and fluently while integrating content from each of the other strands. PO 1. Recognize the limitations of
 for Strand 1: Number and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, and the relationships among numbers and different number systems. PO 1. Solve problems
for Strand 1: Number and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, and the relationships among numbers and different number systems. PO 1. Solve problems
hmhco.com Adaptive. Intuitive. Transformative. AGA Scope and Sequence
 hmhco.com Adaptive. Intuitive. Transformative. AGA Algebra 1 Geometry Algebra 2 Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational exponents Properties
hmhco.com Adaptive. Intuitive. Transformative. AGA Algebra 1 Geometry Algebra 2 Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational exponents Properties
9th and 10th Grade Math Proficiency Objectives Strand One: Number Sense and Operations
 Strand One: Number Sense and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, the relationships among numbers, and different number systems. Justify with examples
Strand One: Number Sense and Operations Concept 1: Number Sense Understand and apply numbers, ways of representing numbers, the relationships among numbers, and different number systems. Justify with examples
Mathematics 6 12 Section 26
 Mathematics 6 12 Section 26 1 Knowledge of algebra 1. Identify graphs of linear inequalities on a number line. 2. Identify graphs of linear equations and inequalities in the coordinate plane. 3. Identify
Mathematics 6 12 Section 26 1 Knowledge of algebra 1. Identify graphs of linear inequalities on a number line. 2. Identify graphs of linear equations and inequalities in the coordinate plane. 3. Identify
Algebra Topic Alignment
 Preliminary Topics Absolute Value 9N2 Compare, order and determine equivalent forms for rational and irrational numbers. Factoring Numbers 9N4 Demonstrate fluency in computations using real numbers. Fractions
Preliminary Topics Absolute Value 9N2 Compare, order and determine equivalent forms for rational and irrational numbers. Factoring Numbers 9N4 Demonstrate fluency in computations using real numbers. Fractions
Copyright 2016 Pearson Education, Inc. or its affiliates. All rights reserved. NES, the NES logo, Pearson, the Pearson logo, and National Evaluation
 Mathematics (304) Copyright 2016 Pearson Education, Inc. or its affiliates. All rights reserved. NES, the NES logo, Pearson, the Pearson logo, and National Evaluation Series are trademarks, in the U.S.
Mathematics (304) Copyright 2016 Pearson Education, Inc. or its affiliates. All rights reserved. NES, the NES logo, Pearson, the Pearson logo, and National Evaluation Series are trademarks, in the U.S.
Mathematics (6-8) Graduation Standards and Essential Outcomes
 Mathematics (6-8) Graduation Standards and Essential Outcomes Mathematics Graduation Standard 1 NUMBER AND QUANTITY: Reason and model quantitatively, using units and number systems to solve problems. Common
Mathematics (6-8) Graduation Standards and Essential Outcomes Mathematics Graduation Standard 1 NUMBER AND QUANTITY: Reason and model quantitatively, using units and number systems to solve problems. Common
Purposeful Design Publications. Intermediate Mathematics Series Scope and Sequence
 Purposeful Design Publications Intermediate Mathematics Series Scope and Sequence All rights reserved, 2004 PO Box 35097 Colorado Springs, CO 80935-3509 800.367.0798 www.purposefuldesign.com I. NUMBER
Purposeful Design Publications Intermediate Mathematics Series Scope and Sequence All rights reserved, 2004 PO Box 35097 Colorado Springs, CO 80935-3509 800.367.0798 www.purposefuldesign.com I. NUMBER
Grade Eight (All Disciplines) Mathematics Standards Map Basic Program
 1 Publisher Instructions. 1. In the header of this document, please fill in the program s identifying information. A basic program in mathematics for grade eight must address the standards for one of the
1 Publisher Instructions. 1. In the header of this document, please fill in the program s identifying information. A basic program in mathematics for grade eight must address the standards for one of the
PreCalculus. Curriculum (447 topics additional topics)
 PreCalculus This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
PreCalculus This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Test at a Glance (formerly known as the Praxis II) Test Breakdown
 * Subject Assessments: Mathematics (5161) Test at a Glance (formerly known as the Praxis II) The following information was retrieved from the ETS website. It includes information regarding material for
* Subject Assessments: Mathematics (5161) Test at a Glance (formerly known as the Praxis II) The following information was retrieved from the ETS website. It includes information regarding material for
6-12 Mathematics Missouri Learning Standards: Grade-Level Expectations
 6- Mathematics Missouri Learning Standards: Grade-Level Expectations Missouri Department of Elementary and Secondary Education Spring 06 Ratios and Proportional Relationships RP Grade 6 Grade 7 Grade 8
6- Mathematics Missouri Learning Standards: Grade-Level Expectations Missouri Department of Elementary and Secondary Education Spring 06 Ratios and Proportional Relationships RP Grade 6 Grade 7 Grade 8
Histogram, cumulative frequency, frequency, 676 Horizontal number line, 6 Hypotenuse, 263, 301, 307
 INDEX A Abscissa, 76 Absolute value, 6 7, 55 Absolute value function, 382 386 transformations of, reflection, 386 scaling, 386 translation, 385 386 Accuracy, 31 Acute angle, 249 Acute triangle, 263 Addition,
INDEX A Abscissa, 76 Absolute value, 6 7, 55 Absolute value function, 382 386 transformations of, reflection, 386 scaling, 386 translation, 385 386 Accuracy, 31 Acute angle, 249 Acute triangle, 263 Addition,
Algebra 2. Curriculum (384 topics additional topics)
 Algebra 2 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Algebra 2 This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
1 ** The performance objectives highlighted in italics have been identified as core to an Algebra II course.
 Strand One: Number Sense and Operations Every student should understand and use all concepts and skills from the pervious grade levels. The standards are designed so that new learning builds on preceding
Strand One: Number Sense and Operations Every student should understand and use all concepts and skills from the pervious grade levels. The standards are designed so that new learning builds on preceding
Math Prep for College Physics
 Math Prep for College Physics This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (190 topics + 52 additional
Math Prep for College Physics This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (190 topics + 52 additional
MATH Spring 2010 Topics per Section
 MATH 101 - Spring 2010 Topics per Section Chapter 1 : These are the topics in ALEKS covered by each Section of the book. Section 1.1 : Section 1.2 : Ordering integers Plotting integers on a number line
MATH 101 - Spring 2010 Topics per Section Chapter 1 : These are the topics in ALEKS covered by each Section of the book. Section 1.1 : Section 1.2 : Ordering integers Plotting integers on a number line
Utah Math Standards for College Prep Mathematics
 A Correlation of 8 th Edition 2016 To the A Correlation of, 8 th Edition to the Resource Title:, 8 th Edition Publisher: Pearson Education publishing as Prentice Hall ISBN: SE: 9780133941753/ 9780133969078/
A Correlation of 8 th Edition 2016 To the A Correlation of, 8 th Edition to the Resource Title:, 8 th Edition Publisher: Pearson Education publishing as Prentice Hall ISBN: SE: 9780133941753/ 9780133969078/
College Algebra with Trigonometry
 College Algebra with Trigonometry This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (556 topics + 614 additional
College Algebra with Trigonometry This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (556 topics + 614 additional
Prentice Hall Mathematics, Algebra Correlated to: Achieve American Diploma Project Algebra II End-of-Course Exam Content Standards
 Core: Operations on Numbers and Expressions Priority: 15% Successful students will be able to perform operations with rational, real, and complex numbers, using both numeric and algebraic expressions,
Core: Operations on Numbers and Expressions Priority: 15% Successful students will be able to perform operations with rational, real, and complex numbers, using both numeric and algebraic expressions,
TEACHER CERTIFICATION EXAM 1.0 KNOWLEDGE OF ALGEBRA Identify graphs of linear inequalities on a number line...1
 TABLE OF CONTENTS COMPETENCY/SKILL PG # 1.0 KNOWLEDGE OF ALGEBRA...1 1.1. Identify graphs of linear inequalities on a number line...1 1.2. Identify graphs of linear equations and inequalities in the coordinate
TABLE OF CONTENTS COMPETENCY/SKILL PG # 1.0 KNOWLEDGE OF ALGEBRA...1 1.1. Identify graphs of linear inequalities on a number line...1 1.2. Identify graphs of linear equations and inequalities in the coordinate
Math Review for AP Calculus
 Math Review for AP Calculus This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Math Review for AP Calculus This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Math Prep for Statics
 Math Prep for Statics This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular
Math Prep for Statics This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular
Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A)
 Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A) Updated 06/05/16 http://www.haesemathematics.com.au/ Note: Exercises in red text indicate material in the 10A textbook
Scope and Sequence: National Curriculum Mathematics from Haese Mathematics (7 10A) Updated 06/05/16 http://www.haesemathematics.com.au/ Note: Exercises in red text indicate material in the 10A textbook
Math 75 Mini-Mod Due Dates Spring 2016
 Mini-Mod 1 Whole Numbers Due: 4/3 1.1 Whole Numbers 1.2 Rounding 1.3 Adding Whole Numbers; Estimation 1.4 Subtracting Whole Numbers 1.5 Basic Problem Solving 1.6 Multiplying Whole Numbers 1.7 Dividing
Mini-Mod 1 Whole Numbers Due: 4/3 1.1 Whole Numbers 1.2 Rounding 1.3 Adding Whole Numbers; Estimation 1.4 Subtracting Whole Numbers 1.5 Basic Problem Solving 1.6 Multiplying Whole Numbers 1.7 Dividing
Mathematics: Essential Learning Expectations: 9 th -12th Grade:
 Mathematics: Essential Learning Expectations: 9 th -12th Grade: Content Standard 1: Number Sense and Operation A student, applying reasoning and problem solving, will use number sense and operations to
Mathematics: Essential Learning Expectations: 9 th -12th Grade: Content Standard 1: Number Sense and Operation A student, applying reasoning and problem solving, will use number sense and operations to
Rational Numbers and Exponents
 Rational and Exponents Math 7 Topic 4 Math 7 Topic 5 Math 8 - Topic 1 4-2: Adding Integers 4-3: Adding Rational 4-4: Subtracting Integers 4-5: Subtracting Rational 4-6: Distance on a Number Line 5-1: Multiplying
Rational and Exponents Math 7 Topic 4 Math 7 Topic 5 Math 8 - Topic 1 4-2: Adding Integers 4-3: Adding Rational 4-4: Subtracting Integers 4-5: Subtracting Rational 4-6: Distance on a Number Line 5-1: Multiplying
Copyright 2018 UC Regents and ALEKS Corporation. ALEKS is a registered trademark of ALEKS Corporation. 2/10
 Prep for Calculus This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (281 topics + 125 additional topics) Real
Prep for Calculus This course covers the topics outlined below. You can customize the scope and sequence of this course to meet your curricular needs. Curriculum (281 topics + 125 additional topics) Real
Pre Algebra. Curriculum (634 topics)
 Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Pre Algebra This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs.
Ohio Department of Education Academic Content Standards Mathematics Detailed Checklist ~Grade 9~
 Ohio Department of Education Academic Content Standards Mathematics Detailed Checklist ~Grade 9~ Number, Number Sense and Operations Standard Students demonstrate number sense, including an understanding
Ohio Department of Education Academic Content Standards Mathematics Detailed Checklist ~Grade 9~ Number, Number Sense and Operations Standard Students demonstrate number sense, including an understanding
MATH 7 HONORS. Unit 1: Rational and Irrational Numbers (Term 1) Unit 2: Using Algebraic Properties to Simplify Expressions - Probability
 MATH 7 HONORS Unit 1: Rational and Irrational Numbers (Term 1) 1. I CAN write an algebraic expression for a given phrase. 2. I CAN define a variable and write an equation given a relationship. 3. I CAN
MATH 7 HONORS Unit 1: Rational and Irrational Numbers (Term 1) 1. I CAN write an algebraic expression for a given phrase. 2. I CAN define a variable and write an equation given a relationship. 3. I CAN
Algebra II/Geometry Curriculum Guide Dunmore School District Dunmore, PA
 Algebra II/Geometry Dunmore School District Dunmore, PA Algebra II/Geometry Prerequisite: Successful completion of Algebra 1 Part 2 K Algebra II/Geometry is intended for students who have successfully
Algebra II/Geometry Dunmore School District Dunmore, PA Algebra II/Geometry Prerequisite: Successful completion of Algebra 1 Part 2 K Algebra II/Geometry is intended for students who have successfully
Mathematics. Pre Algebra
 Mathematics Pre Algebra Tools for Algebra & Geometry Use Problem Solving Strategies Use the Order of Operation to compute real numbers Evaluate expressions containing variables Write algebraic expression
Mathematics Pre Algebra Tools for Algebra & Geometry Use Problem Solving Strategies Use the Order of Operation to compute real numbers Evaluate expressions containing variables Write algebraic expression
Contents. CHAPTER P Prerequisites 1. CHAPTER 1 Functions and Graphs 69. P.1 Real Numbers 1. P.2 Cartesian Coordinate System 14
 CHAPTER P Prerequisites 1 P.1 Real Numbers 1 Representing Real Numbers ~ Order and Interval Notation ~ Basic Properties of Algebra ~ Integer Exponents ~ Scientific Notation P.2 Cartesian Coordinate System
CHAPTER P Prerequisites 1 P.1 Real Numbers 1 Representing Real Numbers ~ Order and Interval Notation ~ Basic Properties of Algebra ~ Integer Exponents ~ Scientific Notation P.2 Cartesian Coordinate System
MATH 8. Unit 1: Rational and Irrational Numbers (Term 1) Unit 2: Using Algebraic Properties to Simplify Expressions - Probability
 MATH 8 Unit 1: Rational and Irrational Numbers (Term 1) 1. I CAN write an algebraic expression for a given phrase. 2. I CAN define a variable and write an equation given a relationship. 3. I CAN use order
MATH 8 Unit 1: Rational and Irrational Numbers (Term 1) 1. I CAN write an algebraic expression for a given phrase. 2. I CAN define a variable and write an equation given a relationship. 3. I CAN use order
Integrated Math 3 Math 3 Course Description:
 Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Prentice Hall Geometry and Algebra 2, North Carolina Editions 2011
 Prentice Hall Geometry and Algebra 2, C O R R E L A T E D T O Number and Operations MBC.N.1 Represent expressions involving rational exponents in various forms. MBC.N.1.1 Translate numbers with rational
Prentice Hall Geometry and Algebra 2, C O R R E L A T E D T O Number and Operations MBC.N.1 Represent expressions involving rational exponents in various forms. MBC.N.1.1 Translate numbers with rational
Mathematics Scope and Sequence Louisburg USD #416 - Revisions Algebra 1 Geometry Algebra 2 Advanced Math/PreCalculus
 Standard 1: Number and Computation Benchmark 1: Number Sense Whole numbers, parts of a whole Whole numbers, parts of a whole Reasonableness of numbers ematics Scope and Sequence 1.1.K.1 Knows, explains,
Standard 1: Number and Computation Benchmark 1: Number Sense Whole numbers, parts of a whole Whole numbers, parts of a whole Reasonableness of numbers ematics Scope and Sequence 1.1.K.1 Knows, explains,
Academic Outcomes Mathematics
 Academic Outcomes Mathematics Mathematic Content Standards Overview: TK/ Kindergarten Counting and Cardinality: Know number names and the count sequence. Count to tell the number of objects. Compare numbers.
Academic Outcomes Mathematics Mathematic Content Standards Overview: TK/ Kindergarten Counting and Cardinality: Know number names and the count sequence. Count to tell the number of objects. Compare numbers.
Honors Integrated Algebra/Geometry 3 Critical Content Mastery Objectives Students will:
 Content Standard 1: Numbers, Number Sense, and Computation Place Value Fractions Comparing and Ordering Counting Facts Estimating and Estimation Strategies Determine an approximate value of radical and
Content Standard 1: Numbers, Number Sense, and Computation Place Value Fractions Comparing and Ordering Counting Facts Estimating and Estimation Strategies Determine an approximate value of radical and
Standard 1: Standard 2: Standard 3: Standard 1: Standard 3: Standard 4: Standard 5: Standard 6: Standard 8: Standard 5: Standard 6: Standard 7:
 6th Grade Math Standards Ratio and Proportional Relationships Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. Understand the concept of
6th Grade Math Standards Ratio and Proportional Relationships Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. Understand the concept of
Pre-Algebra (7) B Mathematics
 Course Overview Students will develop skills in using variables, evaluating algebraic expressions by the use of the order of operations, solving equations and inequalities, graphing linear equations, functions
Course Overview Students will develop skills in using variables, evaluating algebraic expressions by the use of the order of operations, solving equations and inequalities, graphing linear equations, functions
NFC ACADEMY COURSE OVERVIEW
 NFC ACADEMY COURSE OVERVIEW Algebra II Honors is a full-year, high school math course intended for the student who has successfully completed the prerequisite course Algebra I. This course focuses on algebraic
NFC ACADEMY COURSE OVERVIEW Algebra II Honors is a full-year, high school math course intended for the student who has successfully completed the prerequisite course Algebra I. This course focuses on algebraic
Catchup Math and the Common Core Standards. Spring 2011
 Catchup Math and the Common Core Standards Spring 2011 The Catchup Math curriculum addresses nearly all the Common Core Mathematics Standards for Grades 6 8 and High School (including most of the optional
Catchup Math and the Common Core Standards Spring 2011 The Catchup Math curriculum addresses nearly all the Common Core Mathematics Standards for Grades 6 8 and High School (including most of the optional
Secondary 1 - Secondary 3 CCSS Vocabulary Word List Revised Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation
 Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation (optional) absolute value function absolute value inequality (optional) acute angle addition rule algebraic representation alternate exterior angles
Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation (optional) absolute value function absolute value inequality (optional) acute angle addition rule algebraic representation alternate exterior angles
CONSTRUCTION TRADES Monroe High School February, 2007 Michigan Mathematics High School Content Expectations ALGEBRA 1 GEOMETRY
 The following is a list of Mathematics content identified by the CTE instructor as part of the established curriculum. L1.1.3 L1.1.4 L1.2.4 L.2.1.6 A1.1.2 A1.2.8 A2.4.1 A2.4.3 A3.1.3 L1.1.6 L2.1.6 ALGEBRA
The following is a list of Mathematics content identified by the CTE instructor as part of the established curriculum. L1.1.3 L1.1.4 L1.2.4 L.2.1.6 A1.1.2 A1.2.8 A2.4.1 A2.4.3 A3.1.3 L1.1.6 L2.1.6 ALGEBRA
Algebra and Trigonometry
 Algebra and Trigonometry 978-1-63545-098-9 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable) OpenStax Jay Abramson, Arizona State
Algebra and Trigonometry 978-1-63545-098-9 To learn more about all our offerings Visit Knewtonalta.com Source Author(s) (Text or Video) Title(s) Link (where applicable) OpenStax Jay Abramson, Arizona State
Prentice Hall Algebra Correlated to: South Dakota Mathematics Standards, (Grades 9-12)
 High School Algebra Indicator 1: Use procedures to transform algebraic expressions. 9-12.A.1.1. (Comprehension)Write equivalent forms of algebraic expressions using properties of the set of real numbers.
High School Algebra Indicator 1: Use procedures to transform algebraic expressions. 9-12.A.1.1. (Comprehension)Write equivalent forms of algebraic expressions using properties of the set of real numbers.
Mathematics AKS
 Integrated Algebra I A - Process Skills use appropriate technology to solve mathematical problems (GPS) (MAM1_A2009-1) build new mathematical knowledge through problem-solving (GPS) (MAM1_A2009-2) solve
Integrated Algebra I A - Process Skills use appropriate technology to solve mathematical problems (GPS) (MAM1_A2009-1) build new mathematical knowledge through problem-solving (GPS) (MAM1_A2009-2) solve
Integrated Math III. IM3.1.2 Use a graph to find the solution set of a pair of linear inequalities in two variables.
 Standard 1: Algebra and Functions Students solve inequalities, quadratic equations, and systems of equations. They graph polynomial, rational, algebraic, and piece-wise defined functions. They graph and
Standard 1: Algebra and Functions Students solve inequalities, quadratic equations, and systems of equations. They graph polynomial, rational, algebraic, and piece-wise defined functions. They graph and
ALGEBRA (SMR Domain 1) Algebraic Structures (SMR 1.1)...1
 TABLE OF CONTENTS Page Numbers ALGEBRA (SMR Domain 1)...1 0001 Algebraic Structures (SMR 1.1)...1 Apply basic properties of real and complex numbers in constructing mathematical arguments (e.g., if a
TABLE OF CONTENTS Page Numbers ALGEBRA (SMR Domain 1)...1 0001 Algebraic Structures (SMR 1.1)...1 Apply basic properties of real and complex numbers in constructing mathematical arguments (e.g., if a
Maths Years 9 to 10. Boardworks Maths Years 9 to 10. Presentations: 3-D problems 9 slides. Algebraic fractions 22 slides
 Boardworks Presentations: 3-D problems 9 slides Calculating features of 3-D shapes. Algebraic fractions 22 slides Fractions involving algebraic terms. Angle and chord properties 26 slides Arcs, sectors,
Boardworks Presentations: 3-D problems 9 slides Calculating features of 3-D shapes. Algebraic fractions 22 slides Fractions involving algebraic terms. Angle and chord properties 26 slides Arcs, sectors,
Pennsylvania Academic Standards for Mathematics Grade 11
 correlated to the Pennsylvania Academic Standards for Mathematics Grade 11 1/2003 2001 Algebra 1: Concepts and Skills 2001 correlated to the Pennsylvania Academic Standards for Mathematics Grade 11 2.1
correlated to the Pennsylvania Academic Standards for Mathematics Grade 11 1/2003 2001 Algebra 1: Concepts and Skills 2001 correlated to the Pennsylvania Academic Standards for Mathematics Grade 11 2.1
Algebra 2. Chapter 4 Exponential and Logarithmic Functions. Chapter 1 Foundations for Functions. Chapter 3 Polynomial Functions
 Algebra 2 Chapter 1 Foundations for Chapter 2 Quadratic Chapter 3 Polynomial Chapter 4 Exponential and Logarithmic Chapter 5 Rational and Radical Chapter 6 Properties and Attributes of Chapter 7 Probability
Algebra 2 Chapter 1 Foundations for Chapter 2 Quadratic Chapter 3 Polynomial Chapter 4 Exponential and Logarithmic Chapter 5 Rational and Radical Chapter 6 Properties and Attributes of Chapter 7 Probability
General and Specific Learning Outcomes by Strand Applied Mathematics
 General and Specific Learning Outcomes by Strand Applied Mathematics Number Develop number sense. Develop number sense. Specific Learning Outcomes Specific Learning Outcomes Specific Learning Outcomes
General and Specific Learning Outcomes by Strand Applied Mathematics Number Develop number sense. Develop number sense. Specific Learning Outcomes Specific Learning Outcomes Specific Learning Outcomes
NYS Algebra II and Trigonometry Suggested Sequence of Units (P.I's within each unit are NOT in any suggested order)
 1 of 6 UNIT P.I. 1 - INTEGERS 1 A2.A.1 Solve absolute value equations and inequalities involving linear expressions in one variable 1 A2.A.4 * Solve quadratic inequalities in one and two variables, algebraically
1 of 6 UNIT P.I. 1 - INTEGERS 1 A2.A.1 Solve absolute value equations and inequalities involving linear expressions in one variable 1 A2.A.4 * Solve quadratic inequalities in one and two variables, algebraically
Pre AP Algebra. Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Algebra
 Pre AP Algebra Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Algebra 1 The content of the mathematics standards is intended to support the following five goals for students: becoming
Pre AP Algebra Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Algebra 1 The content of the mathematics standards is intended to support the following five goals for students: becoming
Prentice Hall Mathematics: Algebra Correlated to: Michigan High School Math Content Expectations
 STRAND 1: QUANTITATIVE LITERACY AND LOGIC STANDARD L1: REASONING ABOUT NUMBERS, SYSTEMS, AND QUANTITATIVE SITUATIONS Based on their knowledge of the properties of arithmetic, students understand and reason
STRAND 1: QUANTITATIVE LITERACY AND LOGIC STANDARD L1: REASONING ABOUT NUMBERS, SYSTEMS, AND QUANTITATIVE SITUATIONS Based on their knowledge of the properties of arithmetic, students understand and reason
Algebra 1 Math Year at a Glance
 Real Operations Equations/Inequalities Relations/Graphing Systems Exponents/Polynomials Quadratics ISTEP+ Radicals Algebra 1 Math Year at a Glance KEY According to the Indiana Department of Education +
Real Operations Equations/Inequalities Relations/Graphing Systems Exponents/Polynomials Quadratics ISTEP+ Radicals Algebra 1 Math Year at a Glance KEY According to the Indiana Department of Education +
Tennessee s State Mathematics Standards Precalculus
 Tennessee s State Mathematics Standards Precalculus Domain Cluster Standard Number Expressions (N-NE) Represent, interpret, compare, and simplify number expressions 1. Use the laws of exponents and logarithms
Tennessee s State Mathematics Standards Precalculus Domain Cluster Standard Number Expressions (N-NE) Represent, interpret, compare, and simplify number expressions 1. Use the laws of exponents and logarithms
Clinton Community School District K-8 Mathematics Scope and Sequence
 6_RP_1 6_RP_2 6_RP_3 Domain: Ratios and Proportional Relationships Grade 6 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. Understand the
6_RP_1 6_RP_2 6_RP_3 Domain: Ratios and Proportional Relationships Grade 6 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. Understand the
Prentice Hall Algebra Correlated to: Illinois Math Assessment Frameworks (Grade 11)
 Mathematics State Goal 6: Number Sense Grade 11 Standard 6A Representations and Ordering 6.11.01 Recognize, represent, order, compare real numbers, and locate real numbers on a number line (e.g., π, Ö
Mathematics State Goal 6: Number Sense Grade 11 Standard 6A Representations and Ordering 6.11.01 Recognize, represent, order, compare real numbers, and locate real numbers on a number line (e.g., π, Ö
NEW YORK ALGEBRA TABLE OF CONTENTS
 NEW YORK ALGEBRA TABLE OF CONTENTS CHAPTER 1 NUMBER SENSE & OPERATIONS TOPIC A: Number Theory: Properties of Real Numbers {A.N.1} PART 1: Closure...1 PART 2: Commutative Property...2 PART 3: Associative
NEW YORK ALGEBRA TABLE OF CONTENTS CHAPTER 1 NUMBER SENSE & OPERATIONS TOPIC A: Number Theory: Properties of Real Numbers {A.N.1} PART 1: Closure...1 PART 2: Commutative Property...2 PART 3: Associative
DESK Secondary Math II
 Mathematical Practices The Standards for Mathematical Practice in Secondary Mathematics I describe mathematical habits of mind that teachers should seek to develop in their students. Students become mathematically
Mathematical Practices The Standards for Mathematical Practice in Secondary Mathematics I describe mathematical habits of mind that teachers should seek to develop in their students. Students become mathematically
Algebra I Alignment between former TN DOE Mathematics Standards and new TN DOE Mathematics Standards page 1 of 17
 Algebra I Alignment between former TN DOE Mathematics Standards and new TN DOE Mathematics Standards page 1 of 17 Algebra I Transition to New TN Mathematics Standards Algebra I Mathematical Processes New
Algebra I Alignment between former TN DOE Mathematics Standards and new TN DOE Mathematics Standards page 1 of 17 Algebra I Transition to New TN Mathematics Standards Algebra I Mathematical Processes New
7th Grade Curriculum
 Unit #1 Number Systems 1.1 Number Systems 7th Grade Curriculum Distinguish between the various subsets of real numbers (Counting/natural numbers, whole numbers, integers, rational numbers, and irrational
Unit #1 Number Systems 1.1 Number Systems 7th Grade Curriculum Distinguish between the various subsets of real numbers (Counting/natural numbers, whole numbers, integers, rational numbers, and irrational
xvi xxiii xxvi Construction of the Real Line 2 Is Every Real Number Rational? 3 Problems Algebra of the Real Numbers 7
 About the Author v Preface to the Instructor xvi WileyPLUS xxii Acknowledgments xxiii Preface to the Student xxvi 1 The Real Numbers 1 1.1 The Real Line 2 Construction of the Real Line 2 Is Every Real
About the Author v Preface to the Instructor xvi WileyPLUS xxii Acknowledgments xxiii Preface to the Student xxvi 1 The Real Numbers 1 1.1 The Real Line 2 Construction of the Real Line 2 Is Every Real
Appendix C: Event Topics per Meet
 Appendix C: Event Topics per Meet Meet 1 1A Pre-algebra Topics Fractions to add and express as the quotient of two relatively prime integers Complex fractions and continued fractions Decimals, repeating
Appendix C: Event Topics per Meet Meet 1 1A Pre-algebra Topics Fractions to add and express as the quotient of two relatively prime integers Complex fractions and continued fractions Decimals, repeating
Mathematics skills framework
 Mathematics skills framework The framework for MYP mathematics outlines four branches of mathematical study. Schools can use the framework for mathematics as a tool for curriculum mapping when designing
Mathematics skills framework The framework for MYP mathematics outlines four branches of mathematical study. Schools can use the framework for mathematics as a tool for curriculum mapping when designing
Algebra 2 Khan Academy Video Correlations By SpringBoard Activity
 SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
HPS Scope and Sequence Created Trigonometry. Michigan Standards High School Content Expectations (HSCEs) Code & Language
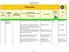 Sub-Categy Quarter 1 Unit 1: The Trigonometric Functions L3.2.1 Know and use the terms of basic logic. Quadratic Identification. Quiz Tests L1.2.4 Organize and summarize a data set in a table, plot, chart,
Sub-Categy Quarter 1 Unit 1: The Trigonometric Functions L3.2.1 Know and use the terms of basic logic. Quadratic Identification. Quiz Tests L1.2.4 Organize and summarize a data set in a table, plot, chart,
MATH II CCR MATH STANDARDS
 RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
Algebra 2 Khan Academy Video Correlations By SpringBoard Activity
 SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
SB Activity Activity 1 Creating Equations 1-1 Learning Targets: Create an equation in one variable from a real-world context. Solve an equation in one variable. 1-2 Learning Targets: Create equations in
