Linear Classifiers 1
|
|
|
- Heather Burke
- 5 years ago
- Views:
Transcription
1 Linear Classifiers 1
2 Outline Framework Exact Minimize Mistakes (Perceptron Training) Matrix inversion Logistic Regression Model Max Likelihood Estimation (MLE) of P( y x ) Gradient descent (MSE; MLE) Linear Discriminant Analysis Max Likelihood Estimation (MLE) of P( y, x ) Direct Computation 2
3 Diagnosing Butterfly-itis Hmmm perhaps Butterfly-it is?? 3
4 Classifier: Decision Boundaries Classifier: partitions input space X into decision regions #wings #antennae Linear threshold unit has a linear decision boundary Defn: Set of points that can be separated by linear decision boundary is linearly separable" 4
5 Linear Separators Draw separating line - #wings ? #antennae If #antennae 2, then butterfly-itis So? is Not butterfly-itis. 5
6 Can be angled #wings ? - - #antennae 2.3 #w #a = 0 If 2.3 #Wings #antennae then butterfly-itis > 0 6
7 Linear Separators, in General Given data (many features) F1 Temp. F2 Press Fn Color diseasex? Class Pale No Clear Yes Yes : : : : Pale No find weights {w1, w2,, wn, w0} such that w1 F1 + + wn Fn + w0 > 0 means Class = Yes 7
8 Linear Separator 35 F1 w1 95 F2 w2 : : 3 Fn wn Just view F0 = 0, so w0 Σi w F i i Yes No 8
9 Linear Separator F F2 7.5 : : 3 Fn i 21 Yes Yes No Given {wi}, and values for instance, compute response Learning i Performance Σi w F Given labeled data, find correct {wi} Linear Threshold Unit Perceptron 9
10 Linear Separators Facts GOOD NEWS: If data is linearly separated, Then FAST ALGORITHM finds correct {wi}! But
11 Linear Separators Facts GOOD NEWS: If data is linearly separated, Then FAST ALGORITHM finds correct {wi}! But Some data sets are NOT linearly separatable! ay t S! d e n tu 11
12 Geometric View ( [1.0, 1.0]; 1 ) ( [0.5; 3.0]; 1 ) ( [2.0; 2.0]; 0 ) Consider 3 training examples: Want classifier that looks like... 12
13 Linear Equation is Hyperplane Equation w x = i wi xi is plane y(x) = 1 0 if w x > 0 otherwise 13
14 Linear Threshold Unit: Perceptron Squashing function: sgn: ℜ {-1, +1 } sgn(r) = 1 0 if r > 0 otherwise ( heaviside ) Actually w x > b but... Create extra input x0 fixed at 1 Corresponding w0 corresponds to -b 14
15 Learning Perceptrons Can represent Linearly-Separated surface... any hyper-plane between two half-spaces Remarkable learning algorithm: [Rosenblatt 1960] If function f can be represented by perceptron, then learning alg guaranteed to quickly converge to f! enormous popularity, early / mid 60's But some simple fns cannot be represented (Boolean XOR) [Minsky/Papert 1969] Killed the field temporarily! 15
16 Perceptron Learning Hypothesis space is... Fixed Size: O(2n^2) distinct perceptrons over n boolean features Deterministic Continuous Parameters Learning algorithm: Various: Local search, Direct computation,... Eager Online / Batch 16
17 Task Input: labeled data Transformed to Output: w ℜr+1 Goal: Want w s.t. i sgn( w [1, x(i) ]) = y(i)... minimize mistakes wrt data... 17
18 Error Function Given data { [x(i), y(i) ] }i=1..m, optimize Classification error Perceptron Training; Matrix Inversion 2. Mean-squared error Matrix Inversion; Gradient Descent m 1 err Class w = I [ y i o w x i ] m i =1 m 1 1 err MSE w = [ y i o w x i ]2 m i = (Log) Conditional Probability m 1 LCL w = log P w y i x i m i =1 MSE Gradient Descent; LCL Gradient Descent 4. (Log) Joint Probability Direct Computation m 1 LL w = log P w y i, x i m i =1 18
19 #1: Optimal Classification Error For each labeled instance [x, y] Err = y ow(x) y = f(x) is target value ow(x) = sgn(w x) is perceptron output Idea: Move weights in appropriate direction, to push Err 0 If Err > 0 (error on POSITIVE example) need to increase sgn(w x) need to increase w x ple) m a x e Input j contributes wj xj to w x VE I T A G E N n o r if xj > 0, increasing wj will increase w x o err ( 0 < r If Erwj will increase wx j x if xj < 0, decreasing w j wj 19 w w + x
20 #1a: Mistake Bound Perceptron Alg Initialize w = 0 Do until bored Predict + iff w x > 0 else " Mistake on positive: w w + x Mistake on negative: w w x Weights Instance Action [0 0 0] #1 +x [1 0 0] #2 -x [0-1 0] #3 +x [1 0 1] #1 OK [1 0 1] #2 -x [0-1 1] #3 +x [1 0 2] #1 OK [1 0 2] #2 -x [0-1 2] #3 OK [1-1 2] #1 +x [1-1 2] #2 OK [1-1 2] #3 OK [1-1 2] #1 OK 20
21 Mistake Bound Theorem Theorem: [Rosenblatt 1960] If data is consistent w/some linear threshold w, then number of mistakes is (1/ )2, where measures wiggle room available: If x = 1, then is max, over all consistent planes, of minimum distance of example to that plane w is to separator, as w x = 0 at boundary So w x is projection of x onto plane, PERPENDICULAR to boundary line ie, is distance from x to that line (once normalized) 21
22 Proof of Convergence x wrong wrt w iff w x < 0 Let w* be unit vector rep'ning target plane = minx { w* x } Let w be hypothesis plane Consider: On each mistake, add x to w w = Σ{x x w<0} x 22
23 Proof (con't) If w is mistake = minx { w* x } w = Σ{x x w<0} x 23
24 #1b: Perceptron Training Rule For each labeled instance [x, y] Err( [x, y] ) = y ow(x) { -1, 0, +1 } If Err( [x, y] ) = 0 Correct! Do nothing! w = 0 Err( [x, y] ) x If Err( [x, y] ) = +1 Mistake on positive! Increment by +x w = +x Err( [x, y] ) x If Err( [x, y] ) = -1 Mistake on negative! Increment by -x w = -x Err( [x, y] ) x In all cases... w(i) = Err( [x(i), y(i) ] ) x(i) = [y(i) ow(x(i))] x(i) Batch Mode: do ALL updates at once! wj = i wj(i) = i x(i)j ( y(i) ow(x(i)) ) wj += η w j 24
25 0. ww 0. Fix New 1. For each row i, compute a. w = 0 b. E(i) = y(i) ow(x(i)) c. w += E(i) x(i) feature j x(i) x(i)j w wj [ wj += E(i) x(i)j ] 2. Increment w += η w E(i) 25
26 Correctness Rule is intuitive: Climbs in correct direction... Thrm: Converges to correct answer, if... training data is linearly separable sufficiently small η Proof: Weight space has EXACTLY 1 minimum! (no non-global minima) with enough examples, finds correct function! Explains early popularity If η too large, may overshoot If η too small, takes too long So often η = η(k) which decays with # of iterations, k 26
27 #1c: Matrix Version? 27
28 Issues 1. Why restrict to only yi { 1, +1 }? If from discrete set yi { 0, 1,, m } : General (non-binary) classification If ARBITRARY yi ℜ: Regression 2. What if NO w works?...x is singular; overconstrained... Could try to minimize residual i I[ y(i) w x(i) ] y X w 1 = i y(i) w x(i) y X w 2 = i ( y(i) w x(i) )2 NP-Hard! Easy! 28
29 L2 error vs 0/1-Loss 0/1 Loss function not smooth, differentiable MSE error is smooth, differentiable and is overbound... 29
30 Gradient Descent for Perceptron? Why not Gradient Descent for THRESHOLDed perceptron? Needs gradient (derivative), not Gradient Descent is General approach. Requires + continuously parameterized hypothesis + error must be differentiatable wrt parameters But... can be slow (many iterations) 30 may only find LOCAL opt
31 #1. LMS version of Classifier View as Regression Find best linear mapping w from X to Y w* = argmin ErrLMS(X, Y)(w) Err LMS (X, Y) Threshold: (w) = i ( y(i) w x(i) )2 if w.x > 0.5, return 1; else 0 See Chapter 3 31
32 Use Linear Regression for Classification? 1. Use regression to find weights w 2. Classify new instance x as sgn( w x ) But regression minimizes sum of squared errors on target function which gives strong influence to outliers Great separation Bad separation 32
33 #3: Logistic Regression Want to compute Pw(y=1 x)... based on parameters w But w x has range [-, ] probability must be in range [0; 1] Need squashing function [-, ] [0, 1] 1 σ x = x 1 e 33
34 Alternative Derivation P x y P y P y x = P x y P y P x y P y 1 = 1 exp a P x y P y a= ln P x y P y 34
35 Logistic Regression (con t) Assume 2 classes: 1 P w y x =σ w x = 1 e x w x w 1 e P w y x = 1 = x w x w 1 e 1 e Log Odds: P w y x log = x w P w y x 35
36 How to learn parameters w? depends on goal? A: Minimize MSE? i ( y(i) ow(x(i)) )2 B: Maximize likelihood? i log Pw(y(i) x(i)) 36
37 MSError Gradient for Sigmoid Unit Error: j ( y(j) ow(x(j)) )2 = j E(j) σ z = For single training instance Input: x(j) = [x(j)1,, x(j)k] Computed Output: o(j) = σ( i x(j)i wi ) = σ( z(j) ) where 1 1 e z z(j) = i x(j)i wi using current { wi } Correct output: y(j) Stochastic Error Gradient (Ignore (j) superscript) 37
38 Derivative of Sigmoid d d 1 σ a = da da 1 e a 1 d 1 a a = 1 e = e a 2 da a 2 1 e 1 e a a e 1 e = = = σ a [ 1 σ a ] a 2 a a 1 e 1 e 1 e 38
39 Updating LR Weights (MSE) Update wi += wi where 39
40 B: Or... Learn Conditional Probability As fitting probability distribution, better to return probability distribution ( w) that is most likely, given training data, S Bayes Rules As P(S) does not depend on w As P(w) is uniform As log is monotonic 40
41 ML Estimation P( S w) likelihood function L(w) = log P( S w) w* = argmaxw L(w) is maximum likelihood estimator (MLE) 41
42 Computing the Likelihood As training examples [x(i), y(i)] are iid drawn independently from same (unknown) prob Pw(x, y) log P( S w) = log Πi Pw(x(i), y(i) ) = i log Pw(x(i), y(i) ) = i log Pw(y(i) x(i)) + i log Pw( x(i)) Here Pw(x(i)) = 1/n not dependent on w, over empirical sample S w* = argmaxw i log Pw(y(i) x(i)) 42
43 Fit Logistic Regression by Gradient Ascent Want w* = argmaxw J(w) J(w) For = i r(y(i), x(i), w) y {0, 1} r(y, x, w) = log Pw( y x ) = y log( Pw( y=1 x ))+(1 y) log(1 Pw( y=1 x )) J w = So climb along wj i i r y, x,w w i j 43
44 Gradient Descent r y, x,w = [ y log p1 1 y log 1 p1 wj wj y p1 p1 y p1 1 y p1 = 1 = p1 w j 1 p1 w j p1 1 p1 w j p1 P w y=1 x = = σ x w wj wj wj x w = p1 1 p1 x ij =σ x w [ 1 σ x w ] wj i i J w r y, x,w = = wj i wj i = y i P w y=1 x x ij i y i p1 p1 1 p1 x ij p 1 1 p 1 44
45 Gradient Ascent for Logistic Regression (MLE) w p1 i y(i) wj p1 i η w 45
46 Comments on MLE Algorithm This is BATCH; obvious online alg (stochastic gradient ascent) Can use second-order (Newton-Raphson) alg for faster convergence weighted least squares computation; aka Iteratively-Reweighted Least Squares (IRLS) 46
47 Use Logistic Regression for Classification Return YES iff P y=1 x P y=1 x P y=0 x P y=1 x ln P y=0 x 1 / 1 exp w x ln exp w x / 1 exp w x 1 ln =w x 0 exp w x P y=0 x stic i g Lo r g e R n o i s es ns r a le! TU L a 47
48 Logistic Regression for K > 2 Classes No t e: e k-1 di ffe ach of d rent w ime nsio i weight s, n x 48
49 Learning LR Weights 1 1 exp w x exp w x 1 exp w x if y=1 0 1 if y=0 w(i)j = (o(i) y(i)) o(i) (1 o(i) ) w(i)j = (y(i) p(1 x(i) )) x(i)j 49
50 (LMS) (MaxProb) feature j x(i) x(i)j w wj 0. ww 0. Fix New 1. For each row i, compute a. w = 0 (i) (i) (i) (o yw(i)(x) (i)o(i))(i)))(1 o(i) ) b. E(i) = y(y op(1 x c. w += E(i) x(i) [ wj += E(i) x(i)j ] 2. Increment w += η w E(i) 50
51 Logistic Regression Algs for LTUs Learns Conditional Probability Distribution P( y x ) Local Search: Begin with initial weight vector; iteratively modify to maximize objective function log likelihood of the data (ie, seek w s.t. probability distribution Pw( y x ) is most likely given data.) Eager: Classifier constructed from training examples, which can then be discarded. Online or batch 51
52 #4: Linear Discriminant Analysis LDA learns joint distribution P( y, x ) As P( y, x ) P( y x ); optimizing P( y, x ) optimizing P( y x ) generative model P( y,x ) model of how data is generated Eg, factor P( y, x ) = P( y ) P( x y ) P( y ) generates value for y; then P( x y ) generates value for x given this y Belief net: Y X 52
53 Linear Discriminant Analysis, con't P( y, x ) = P( y ) P( x y ) P( y ) is a simple discrete distribution Eg: P( y = 0 ) = 0.31; P( y = 1 ) = 0.69 (31% negative examples; 69% positive examples) Assume P( x y ) is multivariate normal, with mean µk and covariance 53
54 Estimating LDA Model Linear discriminant analysis assumes form P( x,y) = µy is mean for examples belonging to class y; covariance matrix is shared by all classes! Can estimate LDA directly: mk = #training examples in class y = k Estimate of P( y = k ): pk = mk / m 1 μ k = {i : y =k } x i i m Σ = 1 x μ x i μ y T i m i i yi (Subtract each xi from corresponding μ y i 54 before taking outer product)
55 Example of Estimation on d : e N ot e-pe r p OT m=7 examples; m+ = 3 positive; m- = 4 negative p+ = 3/7 p- = 4/7 1! = x 0 nd 4 55
56 Estimation z(7) := 56
57 Classifying, Using LDA How to classify new instance, given estimates Class for instance x = [5, 14, 6]? 57
58 LDA learns an LTU Consider 2-class case with a 0/1 loss function Classify ŷ = 1 if iff 58
59 LDA Learns an LTU (2) (x µ1)t -1 (x µ1) (x µ0)t -1 (x µ0) = xt -1 (µ0 µ1) + (µ0 µ1)t -1 x + µ1t -1 µ1 µ0t -1 µ0 As -1 is symmetric, = 2 xt -1 (µ0 µ1)+ µ1t -1 µ1 µ0t -1 µ0 59
60 LDA Learns an LTU (3) So let Classify ŷ = 1 iff LTU!! w x+c>0 60
61 Variants of LDA Covariance matrix n features; k classes Same for all classes? Diagonal #param s + + k + - n2 LDA kn Naïve Gaussian Classifier k n2 General Gaussian Classifier Name 61
62 Generalizations of LDA General Gaussian Classifier Allow each class k to have its own k Classifier quadratic threshold unit (not LTU) Naïve Gaussian Classifier Allow each class k to have its own k but require each k be diagonal. within each class, any pair of features xi and xj are independent Classifier is still quadratic threshold unit but with a restricted form 62
63 Summary of Linear Discriminant Analysis Learns Joint Probability Distr'n P( y, x ) Direct Computation. MLEstimate of P( y, x ) computed directly from data without search. But need to invert matrix, which is O(n3) Eager: Classifier constructed from training examples, which can then be discarded. Batch: Only a batch algorithm. An online LDA alg requires online alg for incrementally updating -1 [Easy if -1 is diagonal... ] 63
64 Two Geometric Views of LDA View 1: Mahalanobis Distance Squared Mahalanobis distance between x and µ DM2(x, µ) = (x µ)t -1 (x µ) -1 linear distortion converts standard Euclidean distance into Mahalanobis distance. LDA classifies x as 0 if DM2(x, µ0) < DM2(x, µ1) log P( x y = k ) log πk ½ DM2(x, µk) 64
65 View 2: Most Informative Low Dimensional Projection nt a in LDA Finds K 1 dim hyperplane (K = number of classes) Project x and { µk } to that hyperplane Classify x as nearest µk within hyperplane r's e h Fis L ar e in rim c Dis Goal: Hyperplane that maximally separates projection of x's wrt -1 project onto: vertical axis LDA's w 65
66 Fisher Linear Discriminant Recall any vector w projects ℜn ℜ Goal: Want w that separates classes Each w x+ far from each w x Perhaps project on m+ m? Still overlap why? 66
67 Fisher Linear Discriminant Problem with m+ m : Doesn t consider scatter within class Goal: Want w that separates classes Each w x+ far from each w x Positive x+'s: w x+ close to each other Negative x 's: w x close to each other scatter of +instance; instance s 2 = i y(i) (w x(i) m+)2 s 2 = i (1 y(i) ) (w x(i) m+)2 + 67
68 Fisher Linear Discriminant Recall any vector w projects ℜn ℜ Goal: Want w that separates classes Positive x+'s: w x+ close to each other Negative x 's: w x close to each other Each w x+ far from each w x scatter of +instance; instance s 2 = i y(i) (w x(i) m+)2 s 2 = i (1 y(i) ) (w x(i) m+)2 + 68
69 FLD, con't Separate means m and m+ maximize (m m+)2 Minimize each spead s+2, s 2 maximize (s+2 + s 2) Objective function: maximize J S w = m m s s #1:(m m+)2 = ( wt m+ wt m )2 = wt (m+ m )(m+ m )T w = wt SB w between-class scatter SB = (m+ m )(m+ m )T 69
70 FLD, III J S w = m m s s s+2 = i y(i) (w x(i) m+)2 = i wt y(i) (x(i) m+) (x(i) m+)t w = wt S+ w S+ = i y(i) (x(i) m+) (x(i) m+)t within-class scatter matrix for + S = i (1 y(i)) (x(i) m ) (x(i) m )T within-class scatter matrix for Sw = S+ + S so s+2 + s 2 = wt SW w 70
71 FLD, IV J S w = Solving m m s s = wt S B w T w Sw w J S w =0 wj = w T m1 m2 2 wt S w w w = α SB-1(m+ m ) 71
72 m m 2 FLD, V J S w = Solving J S w =0 wj When P( x yi ) ~ N(µi; ) s 2 s 2 = wt S B w T w Sw w = w T m1 m2 2 wt S w w w = α SB-1(m+ m ) LINEAR DISCRIMINANT: w = -1(µ+ µ ) FLD is optimal classifier, if classes normally distributed Can use even if not normal: After projecting d-dim to 1, just use any classification method Analogous derivation for K > 2 classes 72
73 Comparing LMS, Logistic Regression, LDA Which is best: LMS, LR, LDA? Ongoing debate within machine learning community about relative merits of direct classifiers [ LMS ] conditional models P( y x ) [ LR ] generative models P( y, x ) [ LDA ] Stay tuned... 73
74 Issues in Debate Statistical efficiency If generative model P( y, x ) is correct, then usually gives better accuracy, particularly if training sample is small Computational efficiency Generative models typically easiest to compute (LDA computed directly, without iteration) Robustness to changing loss functions LMS must re-train the classifier when the loss function changes. no retraining for generative and conditional models Robustness to model assumptions. Generative model usually performs poorly when the assumptions are violated. Eg, LDA works poorly if P( x y ) is non-gaussian. Logistic Regression is more robust, LMS is even more robust Robustness to missing values and noise. In many applications, some of the features xij may be missing or corrupted for some of the training examples. Generative models typically provide better ways of handling this than non-generative models. 74
75 Other Algorithms for learning LTUs Naive Bayes [Discuss later] For K = 2 classes, produces LTU Winnow [?Discuss later?] Can handle large numbers of irrelevant" features (features whose weights should be zero) 75
HTF: Ch4 B: Ch4. Linear Classifiers. R Greiner Cmput 466/551
 HTF: Ch4 B: Ch4 Linear Classifiers R Greiner Cmput 466/55 Outline Framework Eact Minimize Mistakes Perceptron Training Matri inversion LMS Logistic Regression Ma Likelihood Estimation MLE of P Gradient
HTF: Ch4 B: Ch4 Linear Classifiers R Greiner Cmput 466/55 Outline Framework Eact Minimize Mistakes Perceptron Training Matri inversion LMS Logistic Regression Ma Likelihood Estimation MLE of P Gradient
Machine Learning (CS 567) Lecture 5
 Machine Learning (CS 567) Lecture 5 Time: T-Th 5:00pm - 6:20pm Location: GFS 118 Instructor: Sofus A. Macskassy (macskass@usc.edu) Office: SAL 216 Office hours: by appointment Teaching assistant: Cheol
Machine Learning (CS 567) Lecture 5 Time: T-Th 5:00pm - 6:20pm Location: GFS 118 Instructor: Sofus A. Macskassy (macskass@usc.edu) Office: SAL 216 Office hours: by appointment Teaching assistant: Cheol
CS534: Machine Learning. Thomas G. Dietterich 221C Dearborn Hall
 CS534: Machine Learning Thomas G. Dietterich 221C Dearborn Hall tgd@cs.orst.edu http://www.cs.orst.edu/~tgd/classes/534 1 Course Overview Introduction: Basic problems and questions in machine learning.
CS534: Machine Learning Thomas G. Dietterich 221C Dearborn Hall tgd@cs.orst.edu http://www.cs.orst.edu/~tgd/classes/534 1 Course Overview Introduction: Basic problems and questions in machine learning.
Linear Models for Classification
 Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Introduction to Machine Learning
 Introduction to Machine Learning Thomas G. Dietterich tgd@eecs.oregonstate.edu 1 Outline What is Machine Learning? Introduction to Supervised Learning: Linear Methods Overfitting, Regularization, and the
Introduction to Machine Learning Thomas G. Dietterich tgd@eecs.oregonstate.edu 1 Outline What is Machine Learning? Introduction to Supervised Learning: Linear Methods Overfitting, Regularization, and the
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Machine Learning 2017
 Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Linear Classification. CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington
 Linear Classification CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Example of Linear Classification Red points: patterns belonging
Linear Classification CSE 6363 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 Example of Linear Classification Red points: patterns belonging
Logistic Regression Review Fall 2012 Recitation. September 25, 2012 TA: Selen Uguroglu
 Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Machine Learning Lecture 7
 Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Lecture 5: Logistic Regression. Neural Networks
 Lecture 5: Logistic Regression. Neural Networks Logistic regression Comparison with generative models Feed-forward neural networks Backpropagation Tricks for training neural networks COMP-652, Lecture
Lecture 5: Logistic Regression. Neural Networks Logistic regression Comparison with generative models Feed-forward neural networks Backpropagation Tricks for training neural networks COMP-652, Lecture
Ch 4. Linear Models for Classification
 Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
LINEAR MODELS FOR CLASSIFICATION. J. Elder CSE 6390/PSYC 6225 Computational Modeling of Visual Perception
 LINEAR MODELS FOR CLASSIFICATION Classification: Problem Statement 2 In regression, we are modeling the relationship between a continuous input variable x and a continuous target variable t. In classification,
LINEAR MODELS FOR CLASSIFICATION Classification: Problem Statement 2 In regression, we are modeling the relationship between a continuous input variable x and a continuous target variable t. In classification,
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Linear Discrimination Functions
 Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Logistic Regression. Vibhav Gogate The University of Texas at Dallas. Some Slides from Carlos Guestrin, Luke Zettlemoyer and Dan Weld.
 Logistic Regression Vibhav Gogate The University of Texas at Dallas Some Slides from Carlos Guestrin, Luke Zettlemoyer and Dan Weld. Generative vs. Discriminative Classifiers Want to Learn: h:x Y X features
Logistic Regression Vibhav Gogate The University of Texas at Dallas Some Slides from Carlos Guestrin, Luke Zettlemoyer and Dan Weld. Generative vs. Discriminative Classifiers Want to Learn: h:x Y X features
Linear discriminant functions
 Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods.
 Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Probabilistic classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2016
 Probabilistic classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2016 Topics Probabilistic approach Bayes decision theory Generative models Gaussian Bayes classifier
Probabilistic classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2016 Topics Probabilistic approach Bayes decision theory Generative models Gaussian Bayes classifier
Linear Models in Machine Learning
 CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
ECE521 week 3: 23/26 January 2017
 ECE521 week 3: 23/26 January 2017 Outline Probabilistic interpretation of linear regression - Maximum likelihood estimation (MLE) - Maximum a posteriori (MAP) estimation Bias-variance trade-off Linear
ECE521 week 3: 23/26 January 2017 Outline Probabilistic interpretation of linear regression - Maximum likelihood estimation (MLE) - Maximum a posteriori (MAP) estimation Bias-variance trade-off Linear
Linear and logistic regression
 Linear and logistic regression Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Linear and logistic regression 1/22 Outline 1 Linear regression 2 Logistic regression 3 Fisher discriminant analysis
Linear and logistic regression Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Linear and logistic regression 1/22 Outline 1 Linear regression 2 Logistic regression 3 Fisher discriminant analysis
Engineering Part IIB: Module 4F10 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers
 Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Outline. Supervised Learning. Hong Chang. Institute of Computing Technology, Chinese Academy of Sciences. Machine Learning Methods (Fall 2012)
 Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Linear Models for Regression Linear Regression Probabilistic Interpretation
Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Linear Models for Regression Linear Regression Probabilistic Interpretation
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines
 Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Lecture 9: Large Margin Classifiers. Linear Support Vector Machines Perceptrons Definition Perceptron learning rule Convergence Margin & max margin classifiers (Linear) support vector machines Formulation
Neural Network Training
 Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
1 Machine Learning Concepts (16 points)
 CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Regression with Numerical Optimization. Logistic
 CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
Midterm exam CS 189/289, Fall 2015
 Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Midterm exam CS 189/289, Fall 2015 You have 80 minutes for the exam. Total 100 points: 1. True/False: 36 points (18 questions, 2 points each). 2. Multiple-choice questions: 24 points (8 questions, 3 points
Midterm Review CS 6375: Machine Learning. Vibhav Gogate The University of Texas at Dallas
 Midterm Review CS 6375: Machine Learning Vibhav Gogate The University of Texas at Dallas Machine Learning Supervised Learning Unsupervised Learning Reinforcement Learning Parametric Y Continuous Non-parametric
Midterm Review CS 6375: Machine Learning Vibhav Gogate The University of Texas at Dallas Machine Learning Supervised Learning Unsupervised Learning Reinforcement Learning Parametric Y Continuous Non-parametric
CSC242: Intro to AI. Lecture 21
 CSC242: Intro to AI Lecture 21 Administrivia Project 4 (homeworks 18 & 19) due Mon Apr 16 11:59PM Posters Apr 24 and 26 You need an idea! You need to present it nicely on 2-wide by 4-high landscape pages
CSC242: Intro to AI Lecture 21 Administrivia Project 4 (homeworks 18 & 19) due Mon Apr 16 11:59PM Posters Apr 24 and 26 You need an idea! You need to present it nicely on 2-wide by 4-high landscape pages
Machine Learning Lecture 5
 Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
Machine Learning Lecture 5 Linear Discriminant Functions 26.10.2017 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Course Outline Fundamentals Bayes Decision Theory
Logistic regression and linear classifiers COMS 4771
 Logistic regression and linear classifiers COMS 4771 1. Prediction functions (again) Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random
Logistic regression and linear classifiers COMS 4771 1. Prediction functions (again) Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random
Machine Learning Tom M. Mitchell Machine Learning Department Carnegie Mellon University. September 20, 2012
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University September 20, 2012 Today: Logistic regression Generative/Discriminative classifiers Readings: (see class website)
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University September 20, 2012 Today: Logistic regression Generative/Discriminative classifiers Readings: (see class website)
Midterm Review CS 7301: Advanced Machine Learning. Vibhav Gogate The University of Texas at Dallas
 Midterm Review CS 7301: Advanced Machine Learning Vibhav Gogate The University of Texas at Dallas Supervised Learning Issues in supervised learning What makes learning hard Point Estimation: MLE vs Bayesian
Midterm Review CS 7301: Advanced Machine Learning Vibhav Gogate The University of Texas at Dallas Supervised Learning Issues in supervised learning What makes learning hard Point Estimation: MLE vs Bayesian
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Basics Lecture 2: Linear Classification. Princeton University COS 495 Instructor: Yingyu Liang
 Machine Learning Basics Lecture 2: Linear Classification Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d.
Machine Learning Basics Lecture 2: Linear Classification Princeton University COS 495 Instructor: Yingyu Liang Review: machine learning basics Math formulation Given training data x i, y i : 1 i n i.i.d.
Learning Neural Networks
 Learning Neural Networks Neural Networks can represent complex decision boundaries Variable size. Any boolean function can be represented. Hidden units can be interpreted as new features Deterministic
Learning Neural Networks Neural Networks can represent complex decision boundaries Variable size. Any boolean function can be represented. Hidden units can be interpreted as new features Deterministic
Midterm: CS 6375 Spring 2015 Solutions
 Midterm: CS 6375 Spring 2015 Solutions The exam is closed book. You are allowed a one-page cheat sheet. Answer the questions in the spaces provided on the question sheets. If you run out of room for an
Midterm: CS 6375 Spring 2015 Solutions The exam is closed book. You are allowed a one-page cheat sheet. Answer the questions in the spaces provided on the question sheets. If you run out of room for an
The Perceptron algorithm
 The Perceptron algorithm Tirgul 3 November 2016 Agnostic PAC Learnability A hypothesis class H is agnostic PAC learnable if there exists a function m H : 0,1 2 N and a learning algorithm with the following
The Perceptron algorithm Tirgul 3 November 2016 Agnostic PAC Learnability A hypothesis class H is agnostic PAC learnable if there exists a function m H : 0,1 2 N and a learning algorithm with the following
The classifier. Theorem. where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know
 The Bayes classifier Theorem The classifier satisfies where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know Alternatively, since the maximum it is
The Bayes classifier Theorem The classifier satisfies where the min is over all possible classifiers. To calculate the Bayes classifier/bayes risk, we need to know Alternatively, since the maximum it is
The classifier. Linear discriminant analysis (LDA) Example. Challenges for LDA
 The Bayes classifier Linear discriminant analysis (LDA) Theorem The classifier satisfies In linear discriminant analysis (LDA), we make the (strong) assumption that where the min is over all possible classifiers.
The Bayes classifier Linear discriminant analysis (LDA) Theorem The classifier satisfies In linear discriminant analysis (LDA), we make the (strong) assumption that where the min is over all possible classifiers.
Logistic Regression. William Cohen
 Logistic Regression William Cohen 1 Outline Quick review classi5ication, naïve Bayes, perceptrons new result for naïve Bayes Learning as optimization Logistic regression via gradient ascent Over5itting
Logistic Regression William Cohen 1 Outline Quick review classi5ication, naïve Bayes, perceptrons new result for naïve Bayes Learning as optimization Logistic regression via gradient ascent Over5itting
Statistical Data Mining and Machine Learning Hilary Term 2016
 Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Machine Learning. Regression-Based Classification & Gaussian Discriminant Analysis. Manfred Huber
 Machine Learning Regression-Based Classification & Gaussian Discriminant Analysis Manfred Huber 2015 1 Logistic Regression Linear regression provides a nice representation and an efficient solution to
Machine Learning Regression-Based Classification & Gaussian Discriminant Analysis Manfred Huber 2015 1 Logistic Regression Linear regression provides a nice representation and an efficient solution to
SGN (4 cr) Chapter 5
 SGN-41006 (4 cr) Chapter 5 Linear Discriminant Analysis Jussi Tohka & Jari Niemi Department of Signal Processing Tampere University of Technology January 21, 2014 J. Tohka & J. Niemi (TUT-SGN) SGN-41006
SGN-41006 (4 cr) Chapter 5 Linear Discriminant Analysis Jussi Tohka & Jari Niemi Department of Signal Processing Tampere University of Technology January 21, 2014 J. Tohka & J. Niemi (TUT-SGN) SGN-41006
Generative v. Discriminative classifiers Intuition
 Logistic Regression (Continued) Generative v. Discriminative Decision rees Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University January 31 st, 2007 2005-2007 Carlos Guestrin 1 Generative
Logistic Regression (Continued) Generative v. Discriminative Decision rees Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University January 31 st, 2007 2005-2007 Carlos Guestrin 1 Generative
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 305 Part VII
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 305 Part VII
Artificial Neural Networks
 Artificial Neural Networks 鮑興國 Ph.D. National Taiwan University of Science and Technology Outline Perceptrons Gradient descent Multi-layer networks Backpropagation Hidden layer representations Examples
Artificial Neural Networks 鮑興國 Ph.D. National Taiwan University of Science and Technology Outline Perceptrons Gradient descent Multi-layer networks Backpropagation Hidden layer representations Examples
Lecture 4: Types of errors. Bayesian regression models. Logistic regression
 Lecture 4: Types of errors. Bayesian regression models. Logistic regression A Bayesian interpretation of regularization Bayesian vs maximum likelihood fitting more generally COMP-652 and ECSE-68, Lecture
Lecture 4: Types of errors. Bayesian regression models. Logistic regression A Bayesian interpretation of regularization Bayesian vs maximum likelihood fitting more generally COMP-652 and ECSE-68, Lecture
Introduction to Machine Learning
 1, DATA11002 Introduction to Machine Learning Lecturer: Antti Ukkonen TAs: Saska Dönges and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer,
1, DATA11002 Introduction to Machine Learning Lecturer: Antti Ukkonen TAs: Saska Dönges and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer,
Linear Regression (continued)
 Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Introduction to Machine Learning
 1, DATA11002 Introduction to Machine Learning Lecturer: Teemu Roos TAs: Ville Hyvönen and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer
1, DATA11002 Introduction to Machine Learning Lecturer: Teemu Roos TAs: Ville Hyvönen and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer
Overfitting, Bias / Variance Analysis
 Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Stochastic Gradient Descent
 Stochastic Gradient Descent Machine Learning CSE546 Carlos Guestrin University of Washington October 9, 2013 1 Logistic Regression Logistic function (or Sigmoid): Learn P(Y X) directly Assume a particular
Stochastic Gradient Descent Machine Learning CSE546 Carlos Guestrin University of Washington October 9, 2013 1 Logistic Regression Logistic function (or Sigmoid): Learn P(Y X) directly Assume a particular
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University February 2, 2015 Today: Logistic regression Generative/Discriminative classifiers Readings: (see class website)
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University February 2, 2015 Today: Logistic regression Generative/Discriminative classifiers Readings: (see class website)
COMP 652: Machine Learning. Lecture 12. COMP Lecture 12 1 / 37
 COMP 652: Machine Learning Lecture 12 COMP 652 Lecture 12 1 / 37 Today Perceptrons Definition Perceptron learning rule Convergence (Linear) support vector machines Margin & max margin classifier Formulation
COMP 652: Machine Learning Lecture 12 COMP 652 Lecture 12 1 / 37 Today Perceptrons Definition Perceptron learning rule Convergence (Linear) support vector machines Margin & max margin classifier Formulation
Machine Learning and Data Mining. Linear classification. Kalev Kask
 Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
Online Learning With Kernel
 CS 446 Machine Learning Fall 2016 SEP 27, 2016 Online Learning With Kernel Professor: Dan Roth Scribe: Ben Zhou, C. Cervantes Overview Stochastic Gradient Descent Algorithms Regularization Algorithm Issues
CS 446 Machine Learning Fall 2016 SEP 27, 2016 Online Learning With Kernel Professor: Dan Roth Scribe: Ben Zhou, C. Cervantes Overview Stochastic Gradient Descent Algorithms Regularization Algorithm Issues
Generative v. Discriminative classifiers Intuition
 Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 24 th, 2007 1 Generative v. Discriminative classifiers Intuition Want to Learn: h:x a Y X features
Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 24 th, 2007 1 Generative v. Discriminative classifiers Intuition Want to Learn: h:x a Y X features
Logistic Regression. Machine Learning Fall 2018
 Logistic Regression Machine Learning Fall 2018 1 Where are e? We have seen the folloing ideas Linear models Learning as loss minimization Bayesian learning criteria (MAP and MLE estimation) The Naïve Bayes
Logistic Regression Machine Learning Fall 2018 1 Where are e? We have seen the folloing ideas Linear models Learning as loss minimization Bayesian learning criteria (MAP and MLE estimation) The Naïve Bayes
Midterm, Fall 2003
 5-78 Midterm, Fall 2003 YOUR ANDREW USERID IN CAPITAL LETTERS: YOUR NAME: There are 9 questions. The ninth may be more time-consuming and is worth only three points, so do not attempt 9 unless you are
5-78 Midterm, Fall 2003 YOUR ANDREW USERID IN CAPITAL LETTERS: YOUR NAME: There are 9 questions. The ninth may be more time-consuming and is worth only three points, so do not attempt 9 unless you are
NONLINEAR CLASSIFICATION AND REGRESSION. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
Multiclass Classification-1
 CS 446 Machine Learning Fall 2016 Oct 27, 2016 Multiclass Classification Professor: Dan Roth Scribe: C. Cheng Overview Binary to multiclass Multiclass SVM Constraint classification 1 Introduction Multiclass
CS 446 Machine Learning Fall 2016 Oct 27, 2016 Multiclass Classification Professor: Dan Roth Scribe: C. Cheng Overview Binary to multiclass Multiclass SVM Constraint classification 1 Introduction Multiclass
The perceptron learning algorithm is one of the first procedures proposed for learning in neural network models and is mostly credited to Rosenblatt.
 1 The perceptron learning algorithm is one of the first procedures proposed for learning in neural network models and is mostly credited to Rosenblatt. The algorithm applies only to single layer models
1 The perceptron learning algorithm is one of the first procedures proposed for learning in neural network models and is mostly credited to Rosenblatt. The algorithm applies only to single layer models
April 9, Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá. Linear Classification Models. Fabio A. González Ph.D.
 Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá April 9, 2018 Content 1 2 3 4 Outline 1 2 3 4 problems { C 1, y(x) threshold predict(x) = C 2, y(x) < threshold, with threshold
Depto. de Ing. de Sistemas e Industrial Universidad Nacional de Colombia, Bogotá April 9, 2018 Content 1 2 3 4 Outline 1 2 3 4 problems { C 1, y(x) threshold predict(x) = C 2, y(x) < threshold, with threshold
Multilayer Perceptron
 Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Introduction 2 Single Perceptron 3 Boolean Function Learning 4
Outline Hong Chang Institute of Computing Technology, Chinese Academy of Sciences Machine Learning Methods (Fall 2012) Outline Outline I 1 Introduction 2 Single Perceptron 3 Boolean Function Learning 4
Introduction to Machine Learning
 Introduction to Machine Learning Logistic Regression Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Introduction to Machine Learning Logistic Regression Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Least Squares Regression
 CIS 50: Machine Learning Spring 08: Lecture 4 Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may not cover all the
CIS 50: Machine Learning Spring 08: Lecture 4 Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may not cover all the
Support Vector Machines
 Support Vector Machines Hypothesis Space variable size deterministic continuous parameters Learning Algorithm linear and quadratic programming eager batch SVMs combine three important ideas Apply optimization
Support Vector Machines Hypothesis Space variable size deterministic continuous parameters Learning Algorithm linear and quadratic programming eager batch SVMs combine three important ideas Apply optimization
Input layer. Weight matrix [ ] Output layer
![Input layer. Weight matrix [ ] Output layer Input layer. Weight matrix [ ] Output layer](/thumbs/94/121286844.jpg) MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.034 Artificial Intelligence, Fall 2003 Recitation 10, November 4 th & 5 th 2003 Learning by perceptrons
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.034 Artificial Intelligence, Fall 2003 Recitation 10, November 4 th & 5 th 2003 Learning by perceptrons
Machine Learning, Fall 2012 Homework 2
 0-60 Machine Learning, Fall 202 Homework 2 Instructors: Tom Mitchell, Ziv Bar-Joseph TA in charge: Selen Uguroglu email: sugurogl@cs.cmu.edu SOLUTIONS Naive Bayes, 20 points Problem. Basic concepts, 0
0-60 Machine Learning, Fall 202 Homework 2 Instructors: Tom Mitchell, Ziv Bar-Joseph TA in charge: Selen Uguroglu email: sugurogl@cs.cmu.edu SOLUTIONS Naive Bayes, 20 points Problem. Basic concepts, 0
Gaussian and Linear Discriminant Analysis; Multiclass Classification
 Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
11 More Regression; Newton s Method; ROC Curves
 More Regression; Newton s Method; ROC Curves 59 11 More Regression; Newton s Method; ROC Curves LEAST-SQUARES POLYNOMIAL REGRESSION Replace each X i with feature vector e.g. (X i ) = [X 2 i1 X i1 X i2
More Regression; Newton s Method; ROC Curves 59 11 More Regression; Newton s Method; ROC Curves LEAST-SQUARES POLYNOMIAL REGRESSION Replace each X i with feature vector e.g. (X i ) = [X 2 i1 X i1 X i2
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
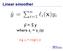 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Intelligent Systems Discriminative Learning, Neural Networks
 Intelligent Systems Discriminative Learning, Neural Networks Carsten Rother, Dmitrij Schlesinger WS2014/2015, Outline 1. Discriminative learning 2. Neurons and linear classifiers: 1) Perceptron-Algorithm
Intelligent Systems Discriminative Learning, Neural Networks Carsten Rother, Dmitrij Schlesinger WS2014/2015, Outline 1. Discriminative learning 2. Neurons and linear classifiers: 1) Perceptron-Algorithm
Single layer NN. Neuron Model
 Single layer NN We consider the simple architecture consisting of just one neuron. Generalization to a single layer with more neurons as illustrated below is easy because: M M The output units are independent
Single layer NN We consider the simple architecture consisting of just one neuron. Generalization to a single layer with more neurons as illustrated below is easy because: M M The output units are independent
Reading Group on Deep Learning Session 1
 Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Reading Group on Deep Learning Session 1 Stephane Lathuiliere & Pablo Mesejo 2 June 2016 1/31 Contents Introduction to Artificial Neural Networks to understand, and to be able to efficiently use, the popular
Linear Classifiers and the Perceptron
 Linear Classifiers and the Perceptron William Cohen February 4, 2008 1 Linear classifiers Let s assume that every instance is an n-dimensional vector of real numbers x R n, and there are only two possible
Linear Classifiers and the Perceptron William Cohen February 4, 2008 1 Linear classifiers Let s assume that every instance is an n-dimensional vector of real numbers x R n, and there are only two possible
Mining Classification Knowledge
 Mining Classification Knowledge Remarks on NonSymbolic Methods JERZY STEFANOWSKI Institute of Computing Sciences, Poznań University of Technology COST Doctoral School, Troina 2008 Outline 1. Bayesian classification
Mining Classification Knowledge Remarks on NonSymbolic Methods JERZY STEFANOWSKI Institute of Computing Sciences, Poznań University of Technology COST Doctoral School, Troina 2008 Outline 1. Bayesian classification
Linear Models for Classification
 Catherine Lee Anderson figures courtesy of Christopher M. Bishop Department of Computer Science University of Nebraska at Lincoln CSCE 970: Pattern Recognition and Machine Learning Congradulations!!!!
Catherine Lee Anderson figures courtesy of Christopher M. Bishop Department of Computer Science University of Nebraska at Lincoln CSCE 970: Pattern Recognition and Machine Learning Congradulations!!!!
Logistic Regression. Some slides adapted from Dan Jurfasky and Brendan O Connor
 Logistic Regression Some slides adapted from Dan Jurfasky and Brendan O Connor Naïve Bayes Recap Bag of words (order independent) Features are assumed independent given class P (x 1,...,x n c) =P (x 1
Logistic Regression Some slides adapted from Dan Jurfasky and Brendan O Connor Naïve Bayes Recap Bag of words (order independent) Features are assumed independent given class P (x 1,...,x n c) =P (x 1
Mark Gales October y (x) x 1. x 2 y (x) Inputs. Outputs. x d. y (x) Second Output layer layer. layer.
 University of Cambridge Engineering Part IIB & EIST Part II Paper I0: Advanced Pattern Processing Handouts 4 & 5: Multi-Layer Perceptron: Introduction and Training x y (x) Inputs x 2 y (x) 2 Outputs x
University of Cambridge Engineering Part IIB & EIST Part II Paper I0: Advanced Pattern Processing Handouts 4 & 5: Multi-Layer Perceptron: Introduction and Training x y (x) Inputs x 2 y (x) 2 Outputs x
Statistical Machine Learning Hilary Term 2018
 Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Machine Learning - Waseda University Logistic Regression
 Machine Learning - Waseda University Logistic Regression AD June AD ) June / 9 Introduction Assume you are given some training data { x i, y i } i= where xi R d and y i can take C different values. Given
Machine Learning - Waseda University Logistic Regression AD June AD ) June / 9 Introduction Assume you are given some training data { x i, y i } i= where xi R d and y i can take C different values. Given
Data Mining. Linear & nonlinear classifiers. Hamid Beigy. Sharif University of Technology. Fall 1396
 Data Mining Linear & nonlinear classifiers Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Data Mining Fall 1396 1 / 31 Table of contents 1 Introduction
Data Mining Linear & nonlinear classifiers Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Data Mining Fall 1396 1 / 31 Table of contents 1 Introduction
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
Machine Learning
 Machine Learning 10-701 Tom M. Mitchell Machine Learning Department Carnegie Mellon University February 1, 2011 Today: Generative discriminative classifiers Linear regression Decomposition of error into
Machine Learning 10-701 Tom M. Mitchell Machine Learning Department Carnegie Mellon University February 1, 2011 Today: Generative discriminative classifiers Linear regression Decomposition of error into
Least Squares Regression
 E0 70 Machine Learning Lecture 4 Jan 7, 03) Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in the lecture. They are not a substitute
E0 70 Machine Learning Lecture 4 Jan 7, 03) Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in the lecture. They are not a substitute
Logistic Regression. COMP 527 Danushka Bollegala
 Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
Learning from Data Logistic Regression
 Learning from Data Logistic Regression Copyright David Barber 2-24. Course lecturer: Amos Storkey a.storkey@ed.ac.uk Course page : http://www.anc.ed.ac.uk/ amos/lfd/ 2.9.8.7.6.5.4.3.2...2.3.4.5.6.7.8.9
Learning from Data Logistic Regression Copyright David Barber 2-24. Course lecturer: Amos Storkey a.storkey@ed.ac.uk Course page : http://www.anc.ed.ac.uk/ amos/lfd/ 2.9.8.7.6.5.4.3.2...2.3.4.5.6.7.8.9
MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE
 MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE March 28, 2012 The exam is closed book. You are allowed a double sided one page cheat sheet. Answer the questions in the spaces provided on
MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE March 28, 2012 The exam is closed book. You are allowed a double sided one page cheat sheet. Answer the questions in the spaces provided on
Support Vector Machines. CAP 5610: Machine Learning Instructor: Guo-Jun QI
 Support Vector Machines CAP 5610: Machine Learning Instructor: Guo-Jun QI 1 Linear Classifier Naive Bayes Assume each attribute is drawn from Gaussian distribution with the same variance Generative model:
Support Vector Machines CAP 5610: Machine Learning Instructor: Guo-Jun QI 1 Linear Classifier Naive Bayes Assume each attribute is drawn from Gaussian distribution with the same variance Generative model:
Machine Learning, Midterm Exam: Spring 2009 SOLUTION
 10-601 Machine Learning, Midterm Exam: Spring 2009 SOLUTION March 4, 2009 Please put your name at the top of the table below. If you need more room to work out your answer to a question, use the back of
10-601 Machine Learning, Midterm Exam: Spring 2009 SOLUTION March 4, 2009 Please put your name at the top of the table below. If you need more room to work out your answer to a question, use the back of
EE 511 Online Learning Perceptron
 Slides adapted from Ali Farhadi, Mari Ostendorf, Pedro Domingos, Carlos Guestrin, and Luke Zettelmoyer, Kevin Jamison EE 511 Online Learning Perceptron Instructor: Hanna Hajishirzi hannaneh@washington.edu
Slides adapted from Ali Farhadi, Mari Ostendorf, Pedro Domingos, Carlos Guestrin, and Luke Zettelmoyer, Kevin Jamison EE 511 Online Learning Perceptron Instructor: Hanna Hajishirzi hannaneh@washington.edu
Classification. Sandro Cumani. Politecnico di Torino
 Politecnico di Torino Outline Generative model: Gaussian classifier (Linear) discriminative model: logistic regression (Non linear) discriminative model: neural networks Gaussian Classifier We want to
Politecnico di Torino Outline Generative model: Gaussian classifier (Linear) discriminative model: logistic regression (Non linear) discriminative model: neural networks Gaussian Classifier We want to
Machine Learning. Lecture 3: Logistic Regression. Feng Li.
 Machine Learning Lecture 3: Logistic Regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2016 Logistic Regression Classification
Machine Learning Lecture 3: Logistic Regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2016 Logistic Regression Classification
