Invariant Manifolds and dispersive Hamiltonian Evolution Equations
|
|
|
- Albert Reginald Phillips
- 5 years ago
- Views:
Transcription
1 Invariant Manifolds and dispersive Hamiltonian Evolution Equations W. Schlag, schlag Boston, January 5, 2012
2 Old-fashioned string theory How does a guitar string evolve in time? Ancient Greece: observed that musical intervals such as an octave, a fifth etc. were based on integer ratios. Post Newton: mechanistic model, use calculus and F = ma. Assume displacement u = u(t, x) is small. Force proportional to curvature: F = ku xx. Figure: Forces acting on pieces of string Dynamical law u tt = c 2 u xx. Write as u = 0. This is an idealization, or model!
3 Solving for the string Cauchy problem: d Alembert solution: u = 0, u(0) = f, t u(0) = g ( 2 t c 2 2 x)u = ( t c x )( t + c x )u = 0 Reduction to first order, transport equations u t + cu x = 0 u(t, x) = ϕ(x ct) u t cu x = 0 u(t, x) = ψ(x + ct) Adjust for initial conditions, gives d Alembert formula: u(t, x) = 1 1 x+ct (f(x ct) + f(x + ct)) + g(y) dy 2 2c x ct If g = 0, the initial position f splits into left- and right-moving waves.
4 d Alembert solution
5 Standing waves Clamped string: u(t, 0) = u(t, L) = 0 for all t 0, u = 0. Special solutions (with c = 1) with n 1 an integer u n (t, x) = sin(πnx/l) [ a n sin(πnt/l) + b n cos(πnt/l) ] Fourier s claim: All solutions are superpositions of these! Ω R d bounded domain, or compact manifold. Let Ω ϕ n = λ 2 nϕ n, with Dirichlet boundary condition in the former case. Then u(t, x) = c n,± e ±iλnt ϕ n (x) n 0,± solves u = 0 (with boundary condition).
6 Drum membranes Two-dimensional waves on a drum: u tt u = 0 with u = 0 on the boundary. Figure: Four basic harmonics of the drum First, third pictures u(t, r) = cos(tλ)j 0 (λr), where J 0 (λ) = 0. Second, fourth pictures u(t, r) = cos(tµ)j m (µr) cos(mθ), where J m (µ) = 0. The J m are Bessel functions.
7 Electrification of waves Maxwell s equations: E(t, x) and B(t, x) vector fields div E = ε 1 0 ρ, div B = 0 curl E + t B = 0, curl B µ 0 ε 0 t E = µ 0 J ε 0 electric constant, µ 0 magnetic constant, ρ charge density, J current density. In vaccum ρ = 0, J = 0. Differentiate fourth equation in time: curl B t µ 0 ε 0 E tt = 0 curl (curl E) + µ 0 ε 0 E tt = 0 (div E) E + µ 0 ε 0 E tt = 0 E tt c 2 E = 0 Similarly B tt c 2 B = 0. In 1861 Maxwell noted that c is the speed of light, and concluded that light should be an electromagnetic wave! Wave equation appears as a fundamental equation! Loss of Galilei invariance!
8 Visualization of EM fields Figure: E&B fields
9 Least action Principle of Least Action: Paths (x(t), ẋ(t)), for t 0 t t 1 with endpoints x(t 0 ) = x 0, and x(t 1 ) = x 1 fixed. The physical path determined by kinetic energy K(x, ẋ) and potential energy P(x, ẋ) minimizes the action: S := t1 t 0 (K P)(x(t), ẋ(t)) dt = t1 t 0 L(x(t), ẋ(t)) dt with L the Lagrangian. In fact: equations of motion equal Euler-Lagrange equation d dt L ẋ + L x = 0 and the physical trajectories are the critical points of S. For L = 1 2 mẋ2 U(x), we obtain mẍ(t) = U (x(t)), which is Newton s F = ma.
10 Waves from a Lagrangian Let L(u, t u) := R 1+d t,x R 1+d t,x 1( u 2 2 t + u 2) (t, x) dtdx (1) Substitute u = u 0 + εv. Then L(u, t u) = L 0 + ε ( u 0 )(t, x)v(t, x) dtdx + O(ε 2 ) where = tt. In other words, u 0 is a critical point of L if and only if u 0 = 0. Significance: Underlying symmetries invariances Conservation laws Conservation of energy, momentum, angular momentum Lagrangian formulation has a universal character, and is flexible, versatile.
11 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x M smooth. What is a wave into M? Lagrangian L(u, t u) = R 1+d t,x 1 2 ( tu 2 g + d j u g) 2 dtdx Critical points L (u, t u) = 0 satisfy manifold-valued wave equation. M R N imbedded, this equation is u T u M or u = A(u)( u, u), A being the second fundamental form. For example, M = S n 1, then j=1 u = u( t u 2 + u 2 ) Note: Nonlinear wave equation, null-form! Harmonic maps are solutions. Intrinsic formulation: D α α u = η αβ D β α u = 0, in coordinates u i tt + ui + Γ i jk (u) αu j α u k = 0 η = ( 1, 1, 1,..., 1) Minkowski metric
12 Maxwell from Lagrangian To formulate electro-magnetism in a Lagrangian frame work, introduce vector potential: A = (A 0, A) with B = curl A, E = A 0 t A Define curvature tensor F αβ := α A β β A α Maxwell s equations: α F αβ = 0. Lagrangian: L = R 1+3 t,x Lorentz invariance: Minkowski metric 1 4 F αβf αβ dtdx [x, y] := η αβ x α y β = x 0 y 0 + Σ 3 j=1 x jy j Linear maps S : R 4 R 4 with [Sx, y] = [x, y] for all x, y R 1+3 t,x are called Lorentz transforms. Note: u = 0 (u S) = 0. For L: ξ = (t, x) η = (s, y), F αβ Fα β = F αβ ξα η α ξ β η β.
13 Lorentz transformations 1 t x 1 x 2 x 3 = cosh α sinh α 0 0 sinh α cosh α t x 1 x 2 x 3 W. Schlag, schlag Figure: Causal structure Dispersive of space-time Hamiltonian PDEs
14 Lorentz transformations 2 Figure: Snapshots of Lorentz transforms Lorentz transforms (hyperbolic rotations) are for the d Alembertian what Euclidean rotations are for the Laplacian.
15 Gauge invariance We obtain the same E, B fields after A A + (φ t, φ). B = curl (A + φ) = curl (A) E = (A 0 + φ t ) t (A + φ) = A 0 t A Curvature F αβ invariant under such gauge transforms. Impose a gauge: α A α = 0 (Lorentz), div A = 0 (Coulomb). These pick out a unique representative in the equivalence class of vector potentials. Make Klein-Gordon equation u m 2 u = α α u m 2 u = 0 gauge invariant: u e iϕ u with ϕ = ϕ(t, x) does not leave solutions invariant. How to modify? KG-Lagrangian is L 0 := R 1+3 t,x R 1+3 t,x 1( α u α u + m 2 u 2) dtdx 2 Need to replace α with D α = α ia α. Bad choice: 1( L 1 := Dα ud α u + m 2 u 2) dtdx 2
16 Maxwell-Klein-Gordon system How is A α determined? Need to add a piece to the Lagrangian to rectify that: a simple and natural choice is the Maxwell Lagrangian. So obtain L MKG := R 1+3 t,x ( 1 4 F αβf αβ D αud α u + m2 2 u 2) dtdx Dynamical equations, as Euler-Lagrange equation of L MKG : α F αβ = Im (φ D β φ) D α D α φ m 2 φ = 0 Coupled system, Maxwell with current J β = Im (φ D β φ) which is determined by scalar field φ. Lorentz and U(1) gauge invariant. Maxwell-Klein-Gordon system.
17 Noncommutative gauge theory, Yang-Mills Nonabelian gauge theory: G Lie (matrix) group, Lie algebra g. Connection 1-form: A = A α dx α with A α : R 1+d g. Covariant differentiation: D α = α + A α. Gauge transform: Ã α = GA α G 1 ( α G)G 1. Curvature is gauge invariant: F αβ = α A β β A α + [A α, A β ] = D α D β D β D α D [ α, β ] Yang-Mills equation (nonlinear!): 1 L := R 1+d 4 trace(f αβf αβ ) dtdx, D α F αβ = 0 In Lorentz gauge t A j=1 ja j = 0 one has schematically A = [A, A] + [A, [A, A]] Eardley-Moncrief: global existence, Klainerman-Machedon: same in energy topology, null-forms!
18 Invariances and conservation laws: Noether s theorem Scalar field ϕ, Lagrangian L := R 1+d t,x L(ϕ, dϕ) dtdx 1-parameter groups of symmetries conservation laws Ψ ε (t, x) = (t, x ), ϕ (t, x ) = ϕ(t, x), and for all regions V L(ϕ, d ϕ ) dt dx = L(ϕ, dϕ) dtdx ε 1 V V Then stress-energy tensor Θ β α = ( β ϕ) αϕ δ β αl satisfies β J β = 0, J β = Θ β αξ α, ξ α = ε Ψ α ε provided L (ϕ) = 0 For example: (t, x) (t + ε, x), gives t Θ 0 0 = jθ j 0 Energy conservation! t Θ R 0 dx = 0. d 0 L ε=0
19 Invariances and conservation laws: Noether s theorem II spatial translations: (t, x) (t, x + εe j ), one has t Θ 0 j = k Θ k j Momentum conservation! t R d Θ 0 j dx = 0 for all 1 j d. Energy conservation for specific Lagrangians: u m 2 u = 0, Θ 0 0 = 1 2 ( tu 2 + u 2 ) Wave maps, Θ 0 0 = 1 2 ( tu 2 g + u 2 g) Maxwell equations, Θ 0 0 = 1 2 ( E 2 + B 2 ) MKG, Θ 0 0 = 1 2 ( E 2 + B 2 + d α=0 D (A) α u 2 + m 2 u 2 ) Hamiltonian equations refers to the existence of a conserved energy (in contrast to dissipative systems). Momentum conservation for KG: t R d u t u dx = 0
20 Basic mathematical questions (for nonlinear problems) Wellposedness: Existence, uniqueness, continuous dependence on the data, persistence of regularity. At first, one needs to understand this locally in time. Global behavior: Finite time break down (some norm, such as L, becomes unbounded in finite time)? Or global existence: smooth solutions for all times if the data are smooth? Blow up dynamics: If the solution breaks down in finite time, can one describe the mechanism by which it does so? For example, via energy concentration at the tip of a light cone? Often, symmetries (in a wider sense) play a crucial role here. Scattering to a free wave: If the solutions exists for all t 0, does it approach a free wave? u = N(u), then v with v = 0 and ( u v)(t) 0 as t in a suitable norm? Here u = (u, t u). If scattering occurs, then we have local energy decay.
21 Basic questions 2 Special solutions: If the solution does not approach a free wave, does it scatter to something else? A stationary nonzero solution, for example? Some physical equations exhibit nonlinear bound states, which represent elementary particles. Stability theory: If special solutions exist such as stationary or time-periodic ones, are they orbitally stable? Are they asymptotically stable? Multi-bump solutions: Is it possible to construct solutions which asymptotically split into moving solitons plus radiation? Lorentz invariance dictates the dynamics of the single solitons. Resolution into multi-bumps: Do all solutions decompose in this fashion? Suppose solutions for all t 0: either scatter to a free wave, or the energy collects in pockets formed by such solitons? Quantization of energy.
22 The wave map system 1 u : R 1+d S N 1 R N, smooth, solves u = u( t u 2 + u 2 ), u(0) = u 0, t u(0) = u 1 How to solve Cauchy problem? Data in X := H σ H σ 1, u(t) = S 0 (t)(u 0, u 1 ) + t S 0 (t)(u 0, u 1 ) = cos(t )u 0 + sin(t ) u 1 0 S 0 (t s)a(u)( u, u)(s) ds Energy estimate: provided σ > d 2 + 1, via Sobolev embedding, u(t) X ( t C u(0) X + C ( u(0) X + Small time well-posedness 0 t 0 A(u)( u, u)(s) H σ 1 ds ) u(s) 3 X ds)
23 The wave map system 2 What can we say about all times t 0? The energy method is very weak, does not allow for global solutions of small energy. Problems: Sobolev spaces H σ defined via the Laplacian, so they are elliptic objects. We need to invoke dispersion. This refers to property of waves in higher dimensions to spread. In R 3 : u = 0, u(0) = 0, t u(0) = g, u(t, x) = t g(x + y) σ(dy) ts 2 If g supported on B(0, 1), then u(t, x) supported on t x 1. Huygens principle. Decay of the wave: u(t, ) Ct 1 Dg 1 In general dimensions the decay is t d 1 2. To invoke this dispersion, we introduce hyperbolic Sobolev spaces, called X σ,b spaces (Beals, Bourgain, Klainerman-Machedon).
24 Domain of influence Figure: Huygens principle
25 The wave map system 3 Idea: To solve u = f write u = 1 f. To solve u = F write u = 1 F. Characteristic variety of is ξ = 0, but of is τ ξ = 0. This leads to the norm F X σ,b = ξ σ τ ξ b ˆF L 2 τ,ξ where ξ = (1 + ξ 2 ) 1 2. Using X σ,b and null forms, Klainerman-Machedon around 1993 were able to show local wellposedness of WM in H σ H σ 1 with σ > d 2. Nonlinearity is special: anihilates self-interactions of waves. Scaling critical exponent σ c = d 2. Rescaling u(t, x) u(λt, λx) preserves solutions. The Sobolev space which is invariant under this scaling is Ḣ d 2 Ḣ d 2 1 (R d ). So what? Any local existence result in this space is automatically global! Just rescale. Hence the hunt for a low-regularity solution theory.
26 The wave map system 4 Tataru, Tao around 2000: Showed that smooth data of small (Ḣ d 2 Ḣ d 2 1 )(R d ) norm lead to global smooth solutions. Low dimensions, especially d = 2 are particularly difficult due to the slow dispersion. Shatah-Struwe 2004 found much simplified argument for d 4 using moving frames in Coulomb gauge. Large data: Conserved energy gives Ḣ 1 L 2 a priori control: 1( ) E = t u 2 g + u 2 g dx R d 2 So d = 2 is energy critical, d 3 energy super critical. Shatah 1987: self-similar blowup solution u(t, r, φ) = (φ, q(r/t)) for d 3 (sphere as target). Struwe 2000: for d = 2 equivariant wave maps, if blowup happens, then it must be via a rescaling of a harmonic map. Self-similar excluded, follows from a fundamental estimate of Christodoulou, Tahvildar-Zadeh. Cuspidal rescaling.
27 Cuspidal energy concentration
28 The wave map system 5 Krieger-S-Tataru 2006: There exist equivariant blowup solutions Q(rt ν ) + o(1) as t 0+ for ν > 3 2 and Q(r) = 2 arctan r. Rodnianski-Sterbenz, Raphael-Rodnianski also constructed blowup, but of a completely different nature, closer to the t 1 rate. For negatively curved targets one has something completely different: Cauchy problem for wave maps R 1+2 t,x H 2, has global smooth solutions for smooth data, and energy disperses to infinity ( scattering ). Krieger-S 2009, based on Kenig-Merle approach to global regularity problem for energy critical equations, to appear as a book with EMS. Tao 2009, similar result, arxiv. Sterbenz-Tataru theorem, Comm. Math. Physics: Cauchy problem for wave maps R 1+2 t,x M with data of energy E < E 0 which is the smallest energy attained by a non-constant harmonic map R 2 M. Then global smooth solutions exist.
29 Semilinear focusing equations Energy subcritical equations: Energy critical case: u + u = u p 1 u in R 1+1 t,x (even), R1+3 t,x i t u + u = u 2 u in radial R 1+3 t,x For d = 3 one has 2 = 6. u = u 2 2 u in radial R 1+d t,x (2) Goals: Describe transition between blowup/global existence and scattering, Soliton resolution conjecture. Results apply only to the case where the energy is at most slightly larger than the energy of the ground state soliton.
30 Basic well-posedness, focusing cubic NLKG in R 3 u[0] H there! strong solution u C([0, T); H 1 ), u C 1 ([0, T); L 2 ) for some T T 0 ( u[0] H ) > 0. Properties: continuous dependence on data; persistence of regularity; energy conservation: ( 1 E(u, u) = 2 u u u 2 1 ) 4 u 4 dx R 3 If u[0] H 1, then global existence; let T > 0 be maximal forward time of existence: T < = u L 3 ([0,T ),L 6 (R 3 )) =. If T = and u L 3 ([0,T ),L 6 (R 3 )) <, then u scatters: (ũ 0, ũ 1 ) H s.t. for v(t) = S 0 (t)(ũ 0, ũ 1 ) one has (u(t), u(t)) = (v(t), v(t)) + o H (1) t S 0 (t) free KG evol. If u scatters, then u L 3 ([0, ),L 6 (R 3 )) <. Finite prop.-speed: if u = 0 on { x x 0 < R}, then u(t, x) = 0 on { x x 0 < R t, 0 < t < min(t, R)}.
31 Finite time blowup, forward scattering set T > 0, exact solution to cubic NLKG ϕ T (t) c(t t) α as t T + α = 1, c = 2. Use finite prop-speed to cut off smoothly to neighborhood of cone x < T t. Gives smooth solution to NLKG, blows up at t = T or before. Small data: global existence and scattering. Large data: can have finite time blowup. Is there a criterion to decide finite time blowup/global existence? Forward scattering set: S(t) = nonlinear evolution { S + := (u 0, u 1 ) H := H 1 L 2 u(t) := S(t)(u 0, u 1 ) time } and scatters to zero, i.e., u L 3 ([0, );L 6 ) <
32 Forward Scattering set S + satisfies the following properties: S + B δ (0), a small ball in H, S + H, S + is an open set in H, S + is path-connected. Some natural questions: 1 Is S + bounded in H? 2 Is S + a smooth manifold or rough? 3 If S + is a smooth mfld, does it separate regions of FTB/GE? 4 Dynamics starting from S +? Any special solutions on S +?
33 Stationary solutions, ground state Stationary solution u(t, x) = ϕ(x) of NLKG, weak solution of Minimization problem ϕ + ϕ = ϕ 3 (3) inf { ϕ 2 H 1 ϕ H 1, ϕ 4 = 1 } has radial solution ϕ > 0, decays exponentially, ϕ = λϕ satisfies (3) for some λ > 0. Coffman: unique ground state Q. Minimizes the stationary energy (or action) ( 1 J(ϕ) := 2 ϕ ϕ 2 1 ) 4 ϕ 4 dx R 3 amongst all nonzero solutions of (3). Payne-Sattinger dilation functional K 0 (ϕ) = J (ϕ) ϕ = ( ϕ 2 + ϕ 2 ϕ 4 )(x) dx R 3
34 Some answers Theorem (Nakanishi-S) Let E(u 0, u 1 ) < E(Q, 0) + ε 2, (u 0, u 1 ) H rad. In t 0 for NLKG: 1 finite time blowup 2 global existence and scattering to 0 3 global existence and scattering to Q: u(t) = Q + v(t) + O H 1(1) as t, and u(t) = v(t) + O L 2(1) as t, v + v = 0, (v, v) H. All 9 combinations of this trichotomy allowed as t ±. Applies to dim = 3, cubic power, or dim = 1, all p > 5. Under energy assumption (EA) S + is connected, smooth mfld, which gives (3), separating regions (1) and (2). S + contains (±Q, 0). S + forms the center stable manifold associated with (±Q, 0). 1-dimensional stable, unstable mflds at (±Q, 0). Stable mfld: Duyckaerts-Merle, Duyckaerts-Holmer-Roudenko
35 The invariant manifolds Figure: Stable, unstable, center-stable manifolds
36 Hyperbolic dynamics ẋ = Ax + f(x), f(0) = 0, Df(0) = 0, R n = X s + X u + X c, A-invariant spaces, A X s has evals in Re z < 0, A X u has evals in Re z > 0, A X c has evals in ir. If X c = {0}, Hartmann-Grobman theorem: conjugation to e ta. If X c {0}, Center Manifold Theorem: local invariant mflds M u, M s, M c around x = 0, tangent to X u, X s, X c, respectively. Example: M s = { x 0 < ε x(t) 0 exponentially as t } M u = { x 0 < ε x(t) 0 exponentially as spec(a) = {1, 1, i, i} ẋ = x + O( x 2 ) t }
37 Hyperbolic dynamics near ±Q Linearized operator L + = + 1 3Q 2. L + Q Q = 2 Q 4 4 < 0 L + ρ = k 2 ρ unique negative eigenvalue, no kernel over radial functions Gap property: L + has no eigenvalues in (0, 1], no threshold resonance (delicate! Costin-Huang-S, 2011) Plug u = Q + v into cubic NLKG: v + L + v = N(Q, v) = 3Qv 2 + v 3 Rewrite as a Hamiltonian system: ( ) [ ] ( 0 1 v t = v v L + 0 v ) ( + 0 N(Q, v) Then spec(a) = {k, k} i[1, ) i(, 1] with ±k simple evals. Formally: X s = P 1 L 2, X u = P 1 L 2. X c is the rest. )
38 Schematic depiction of J, K 0 Figure: The splitting of J(u) < J(Q) by the sign of K = K 0 Energy near ±Q a saddle surface : x 2 y 2 0 Explains mechanism of Payne-Sattinger theorem, 1975 Similar picture for E(u, u) < J(Q). Solution trapped by K 0, K < 0 in that set.
39 Variational structure above J(Q) (Noneffective!) Figure: Signs of K = K 0 away from (±Q, 0) δ > 0 ε 0 (δ), κ 0, κ 1 (δ) > 0 s.t. u H with E( u) < J(Q) + ε 0 (δ) 2, d Q ( u) δ, one has following dichotomy: K 0 (u) κ 1 (δ) and K 2 (u) κ 1 (δ), or K 0 (u) min(κ 1 (δ), κ 0 u 2 H 1 ) and K 2 (u) min(κ 1 (δ), κ 0 u 2 L 2 ).
40 Numerical 2-dim section through S + (with R. Donninger) Figure: (Q + Ae r2, Be r2 ) soliton at (A, B) = (0, 0), (A, B) vary in [ 9, 2] [ 9, 9] RED: global existence, WHITE: finite time blowup, GREEN: PS, BLUE: PS + Our results apply to a neighborhood of (Q, 0), boundary of the red region looks smooth (caution!)
41 One-pass theorem I Crucial no-return property: Trajectory does not return to balls around (±Q, 0). Use virial identity, A = 1 2 (x + x), t w u Au = K 2 (u(t))+error, K 2 (u) = ( u u 4 ) dx (4) where w = w(t, x) is a space-time cutoff that lives on a rhombus, and the error is controlled by the external energy. Figure: Space-time cutoff for the virial identity
42 One-pass theorem II Finite propagation speed error controlled by free energy outside large balls at times T 1, T 2. Integrating between T 1, T 2 gives contradiction; the bulk of the integral of K 2 (u(t)) here comes from exponential ejection mechanism near (±Q, 0). Figure: Possible returning trajectories
43 EMS/AMS book
Long-term dynamics of nonlinear wave equations
 Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Construction of concentrating bubbles for the energy-critical wave equation
 Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
Dynamics of energy-critical wave equation
 Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere
 Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Recent developments on the global behavior to critical nonlinear dispersive equations. Carlos E. Kenig
 Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
arxiv:math/ v1 [math.ap] 24 Apr 2003
![arxiv:math/ v1 [math.ap] 24 Apr 2003 arxiv:math/ v1 [math.ap] 24 Apr 2003](/thumbs/95/122489725.jpg) ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
ICM 2002 Vol. III 1 3 arxiv:math/0304397v1 [math.ap] 24 Apr 2003 Nonlinear Wave Equations Daniel Tataru Abstract The analysis of nonlinear wave equations has experienced a dramatic growth in the last ten
THE UNIVERSITY OF CHICAGO ON THE GLOBAL BEHAVIOR OF WAVE MAPS A DISSERTATION SUBMITTED TO THE FACULTY OF THE DIVISION OF THE PHYSICAL SCIENCES
 THE UNIVERSITY OF CHICAGO ON THE GLOBAL BEHAVIOR OF WAVE MAPS A DISSERTATION SUBMITTED TO THE FACULTY OF THE DIVISION OF THE PHYSICAL SCIENCES IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY DEPARTMENT
THE UNIVERSITY OF CHICAGO ON THE GLOBAL BEHAVIOR OF WAVE MAPS A DISSERTATION SUBMITTED TO THE FACULTY OF THE DIVISION OF THE PHYSICAL SCIENCES IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY DEPARTMENT
A Variational Analysis of a Gauged Nonlinear Schrödinger Equation
 A Variational Analysis of a Gauged Nonlinear Schrödinger Equation Alessio Pomponio, joint work with David Ruiz Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Variational and Topological
A Variational Analysis of a Gauged Nonlinear Schrödinger Equation Alessio Pomponio, joint work with David Ruiz Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Variational and Topological
Alexei F. Cheviakov. University of Saskatchewan, Saskatoon, Canada. INPL seminar June 09, 2011
 Direct Method of Construction of Conservation Laws for Nonlinear Differential Equations, its Relation with Noether s Theorem, Applications, and Symbolic Software Alexei F. Cheviakov University of Saskatchewan,
Direct Method of Construction of Conservation Laws for Nonlinear Differential Equations, its Relation with Noether s Theorem, Applications, and Symbolic Software Alexei F. Cheviakov University of Saskatchewan,
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG
 CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
DISPERSIVE EQUATIONS: A SURVEY
 DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
Overview of the proof of the Bounded L 2 Curvature Conjecture. Sergiu Klainerman Igor Rodnianski Jeremie Szeftel
 Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
Overview of the proof of the Bounded L 2 Curvature Conjecture Sergiu Klainerman Igor Rodnianski Jeremie Szeftel Department of Mathematics, Princeton University, Princeton NJ 8544 E-mail address: seri@math.princeton.edu
arxiv: v1 [math.ap] 1 May 2017
![arxiv: v1 [math.ap] 1 May 2017 arxiv: v1 [math.ap] 1 May 2017](/thumbs/92/108638608.jpg) LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
LOW REGULARITY LOCAL WELL-POSEDNESS FOR THE (N+1)-DIMENSIONAL MAXWELL-KLEIN-GORDON EQUATIONS IN LORENZ GAUGE arxiv:1705.00599v1 [math.ap] 1 May 017 HARTMUT PECHER FACHBEREICH MATHEMATIK UND NATURWISSENSCHAFTEN
Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche
 Scuola di Dottorato THE WAVE EQUATION Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Lucio Demeio - DIISM wave equation 1 / 44 1 The Vibrating String Equation 2 Second
Scuola di Dottorato THE WAVE EQUATION Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Lucio Demeio - DIISM wave equation 1 / 44 1 The Vibrating String Equation 2 Second
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space
 Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
Blow-up on manifolds with symmetry for the nonlinear Schröding
 Blow-up on manifolds with symmetry for the nonlinear Schrödinger equation March, 27 2013 Université de Nice Euclidean L 2 -critical theory Consider the one dimensional equation i t u + u = u 4 u, t > 0,
Blow-up on manifolds with symmetry for the nonlinear Schrödinger equation March, 27 2013 Université de Nice Euclidean L 2 -critical theory Consider the one dimensional equation i t u + u = u 4 u, t > 0,
Conservation Laws: Systematic Construction, Noether s Theorem, Applications, and Symbolic Computations.
 Conservation Laws: Systematic Construction, Noether s Theorem, Applications, and Symbolic Computations. Alexey Shevyakov Department of Mathematics and Statistics, University of Saskatchewan, Saskatoon,
Conservation Laws: Systematic Construction, Noether s Theorem, Applications, and Symbolic Computations. Alexey Shevyakov Department of Mathematics and Statistics, University of Saskatchewan, Saskatoon,
Late-time tails of self-gravitating waves
 Late-time tails of self-gravitating waves (non-rigorous quantitative analysis) Piotr Bizoń Jagiellonian University, Kraków Based on joint work with Tadek Chmaj and Andrzej Rostworowski Outline: Motivation
Late-time tails of self-gravitating waves (non-rigorous quantitative analysis) Piotr Bizoń Jagiellonian University, Kraków Based on joint work with Tadek Chmaj and Andrzej Rostworowski Outline: Motivation
Scattering for cubic-quintic nonlinear Schrödinger equation on R 3
 Scattering for cubic-quintic nonlinear Schrödinger equation on R 3 Oana Pocovnicu Princeton University March 9th 2013 Joint work with R. Killip (UCLA), T. Oh (Princeton), M. Vişan (UCLA) SCAPDE UCLA 1
Scattering for cubic-quintic nonlinear Schrödinger equation on R 3 Oana Pocovnicu Princeton University March 9th 2013 Joint work with R. Killip (UCLA), T. Oh (Princeton), M. Vişan (UCLA) SCAPDE UCLA 1
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY
 SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
Lattice Gauge Theory and the Maxwell-Klein-Gordon equations
 Lattice Gauge Theory and the Maxwell-Klein-Gordon equations Tore G. Halvorsen Centre of Mathematics for Applications, UiO 19. February 2008 Abstract In this talk I will present a discretization of the
Lattice Gauge Theory and the Maxwell-Klein-Gordon equations Tore G. Halvorsen Centre of Mathematics for Applications, UiO 19. February 2008 Abstract In this talk I will present a discretization of the
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS
 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
The stability of Kerr-de Sitter black holes
 The stability of Kerr-de Sitter black holes András Vasy (joint work with Peter Hintz) July 2018, Montréal This talk is about the stability of Kerr-de Sitter (KdS) black holes, which are certain Lorentzian
The stability of Kerr-de Sitter black holes András Vasy (joint work with Peter Hintz) July 2018, Montréal This talk is about the stability of Kerr-de Sitter (KdS) black holes, which are certain Lorentzian
8.821 String Theory Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.81 String Theory Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.81 F008 Lecture 1: Boundary of AdS;
MIT OpenCourseWare http://ocw.mit.edu 8.81 String Theory Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.81 F008 Lecture 1: Boundary of AdS;
Chapter 3 Second Order Linear Equations
 Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Partial Differential Equations (Math 3303) A Ë@ Õæ Aë áöß @. X. @ 2015-2014 ú GA JË@ É Ë@ Chapter 3 Second Order Linear Equations Second-order partial differential equations for an known function u(x,
Travelling waves. Chapter 8. 1 Introduction
 Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Global well-posedness for semi-linear Wave and Schrödinger equations. Slim Ibrahim
 Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games
 Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
Mechanics Physics 151
 Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
Quasi-local Mass in General Relativity
 Quasi-local Mass in General Relativity Shing-Tung Yau Harvard University For the 60th birthday of Gary Horowtiz U. C. Santa Barbara, May. 1, 2015 This talk is based on joint work with Po-Ning Chen and
Quasi-local Mass in General Relativity Shing-Tung Yau Harvard University For the 60th birthday of Gary Horowtiz U. C. Santa Barbara, May. 1, 2015 This talk is based on joint work with Po-Ning Chen and
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS
 8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
B.7 Lie Groups and Differential Equations
 96 B.7. LIE GROUPS AND DIFFERENTIAL EQUATIONS B.7 Lie Groups and Differential Equations Peter J. Olver in Minneapolis, MN (U.S.A.) mailto:olver@ima.umn.edu The applications of Lie groups to solve differential
96 B.7. LIE GROUPS AND DIFFERENTIAL EQUATIONS B.7 Lie Groups and Differential Equations Peter J. Olver in Minneapolis, MN (U.S.A.) mailto:olver@ima.umn.edu The applications of Lie groups to solve differential
arxiv: v2 [math.ap] 4 Jul 2010
![arxiv: v2 [math.ap] 4 Jul 2010 arxiv: v2 [math.ap] 4 Jul 2010](/thumbs/95/124841836.jpg) GLOBAL DYNAMICS ABOVE THE GROUND STATE ENERGY FOR THE FOCUSING NONLINEAR KLEIN-GORDON EQUATION K. NAKANISHI AND W. SCHLAG arxiv:1005.4894v2 [math.ap] 4 Jul 2010 Abstract. The analysis of global dynamics
GLOBAL DYNAMICS ABOVE THE GROUND STATE ENERGY FOR THE FOCUSING NONLINEAR KLEIN-GORDON EQUATION K. NAKANISHI AND W. SCHLAG arxiv:1005.4894v2 [math.ap] 4 Jul 2010 Abstract. The analysis of global dynamics
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
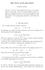 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
General Relativity and Cosmology Mock exam
 Physikalisches Institut Mock Exam Universität Bonn 29. June 2011 Theoretische Physik SS 2011 General Relativity and Cosmology Mock exam Priv. Doz. Dr. S. Förste Exercise 1: Overview Give short answers
Physikalisches Institut Mock Exam Universität Bonn 29. June 2011 Theoretische Physik SS 2011 General Relativity and Cosmology Mock exam Priv. Doz. Dr. S. Förste Exercise 1: Overview Give short answers
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator
 Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
2.3 Calculus of variations
 2.3 Calculus of variations 2.3.1 Euler-Lagrange equation The action functional S[x(t)] = L(x, ẋ, t) dt (2.3.1) which maps a curve x(t) to a number, can be expanded in a Taylor series { S[x(t) + δx(t)]
2.3 Calculus of variations 2.3.1 Euler-Lagrange equation The action functional S[x(t)] = L(x, ẋ, t) dt (2.3.1) which maps a curve x(t) to a number, can be expanded in a Taylor series { S[x(t) + δx(t)]
MATH 131P: PRACTICE FINAL SOLUTIONS DECEMBER 12, 2012
 MATH 3P: PRACTICE FINAL SOLUTIONS DECEMBER, This is a closed ook, closed notes, no calculators/computers exam. There are 6 prolems. Write your solutions to Prolems -3 in lue ook #, and your solutions to
MATH 3P: PRACTICE FINAL SOLUTIONS DECEMBER, This is a closed ook, closed notes, no calculators/computers exam. There are 6 prolems. Write your solutions to Prolems -3 in lue ook #, and your solutions to
On Chern-Simons-Schrödinger equations including a vortex point
 On Chern-Simons-Schrödinger equations including a vortex point Alessio Pomponio Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Workshop in Nonlinear PDEs Brussels, September 7
On Chern-Simons-Schrödinger equations including a vortex point Alessio Pomponio Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Workshop in Nonlinear PDEs Brussels, September 7
Hyperbolic Geometric Flow
 Hyperbolic Geometric Flow Kefeng Liu CMS and UCLA August 20, 2007, Dong Conference Page 1 of 51 Outline: Joint works with D. Kong and W. Dai Motivation Hyperbolic geometric flow Local existence and nonlinear
Hyperbolic Geometric Flow Kefeng Liu CMS and UCLA August 20, 2007, Dong Conference Page 1 of 51 Outline: Joint works with D. Kong and W. Dai Motivation Hyperbolic geometric flow Local existence and nonlinear
Multisolitons for NLS
 Multisolitons for NLS Stefan LE COZ Beijing 2007-07-03 Plan 1 Introduction 2 Existence of multi-solitons 3 (In)stability NLS (NLS) { iut + u + g( u 2 )u = 0 u t=0 = u 0 u : R t R d x C (A0) (regular) g
Multisolitons for NLS Stefan LE COZ Beijing 2007-07-03 Plan 1 Introduction 2 Existence of multi-solitons 3 (In)stability NLS (NLS) { iut + u + g( u 2 )u = 0 u t=0 = u 0 u : R t R d x C (A0) (regular) g
Local smoothing and Strichartz estimates for manifolds with degenerate hyperbolic trapping
 Local smoothing and Strichartz estimates for manifolds with degenerate hyperbolic trapping H. Christianson partly joint work with J. Wunsch (Northwestern) Department of Mathematics University of North
Local smoothing and Strichartz estimates for manifolds with degenerate hyperbolic trapping H. Christianson partly joint work with J. Wunsch (Northwestern) Department of Mathematics University of North
x R d, λ R, f smooth enough. Goal: compute ( follow ) equilibrium solutions as λ varies, i.e. compute solutions (x, λ) to 0 = f(x, λ).
 Continuation of equilibria Problem Parameter-dependent ODE ẋ = f(x, λ), x R d, λ R, f smooth enough. Goal: compute ( follow ) equilibrium solutions as λ varies, i.e. compute solutions (x, λ) to 0 = f(x,
Continuation of equilibria Problem Parameter-dependent ODE ẋ = f(x, λ), x R d, λ R, f smooth enough. Goal: compute ( follow ) equilibrium solutions as λ varies, i.e. compute solutions (x, λ) to 0 = f(x,
Fractal Weyl Laws and Wave Decay for General Trapping
 Fractal Weyl Laws and Wave Decay for General Trapping Jeffrey Galkowski McGill University July 26, 2017 Joint w/ Semyon Dyatlov The Plan The setting and a brief review of scattering resonances Heuristic
Fractal Weyl Laws and Wave Decay for General Trapping Jeffrey Galkowski McGill University July 26, 2017 Joint w/ Semyon Dyatlov The Plan The setting and a brief review of scattering resonances Heuristic
Modern Geometric Structures and Fields
 Modern Geometric Structures and Fields S. P. Novikov I.A.TaJmanov Translated by Dmitry Chibisov Graduate Studies in Mathematics Volume 71 American Mathematical Society Providence, Rhode Island Preface
Modern Geometric Structures and Fields S. P. Novikov I.A.TaJmanov Translated by Dmitry Chibisov Graduate Studies in Mathematics Volume 71 American Mathematical Society Providence, Rhode Island Preface
Dispersive Equations and Nonlinear Waves
 Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
Herbert Koch Daniel Tataru Monica Vi an Dispersive Equations and Nonlinear Waves Generalized Korteweg-de Vries, Nonlinear Schrodinger, Wave and Schrodinger Maps ^ Birkhauser Contents Preface xi Nonlinear
Title. On the stability of the wave-map equation in Kerr spaces. Alexandru D. Ionescu
 Title On the stability of the wave-map equation in Kerr spaces Alexandru D. Ionescu We are interested in the question of the global stability of a stationary axially-symmetric solution of the wave map
Title On the stability of the wave-map equation in Kerr spaces Alexandru D. Ionescu We are interested in the question of the global stability of a stationary axially-symmetric solution of the wave map
Partial Differential Equations
 Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
Part II Partial Differential Equations Year 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2015 Paper 4, Section II 29E Partial Differential Equations 72 (a) Show that the Cauchy problem for u(x,
Quantum Field Theory Notes. Ryan D. Reece
 Quantum Field Theory Notes Ryan D. Reece November 27, 2007 Chapter 1 Preliminaries 1.1 Overview of Special Relativity 1.1.1 Lorentz Boosts Searches in the later part 19th century for the coordinate transformation
Quantum Field Theory Notes Ryan D. Reece November 27, 2007 Chapter 1 Preliminaries 1.1 Overview of Special Relativity 1.1.1 Lorentz Boosts Searches in the later part 19th century for the coordinate transformation
PARTIAL DIFFERENTIAL EQUATIONS. Lecturer: D.M.A. Stuart MT 2007
 PARTIAL DIFFERENTIAL EQUATIONS Lecturer: D.M.A. Stuart MT 2007 In addition to the sets of lecture notes written by previous lecturers ([1, 2]) the books [4, 7] are very good for the PDE topics in the course.
PARTIAL DIFFERENTIAL EQUATIONS Lecturer: D.M.A. Stuart MT 2007 In addition to the sets of lecture notes written by previous lecturers ([1, 2]) the books [4, 7] are very good for the PDE topics in the course.
Nonlinear Modulational Instability of Dispersive PDE Models
 Nonlinear Modulational Instability of Dispersive PDE Models Jiayin Jin, Shasha Liao, and Zhiwu Lin Georgia Tech ICERM workshop on water waves, 4/28/2017 Jiayin Jin, Shasha Liao, and Zhiwu Lin Georgia Tech
Nonlinear Modulational Instability of Dispersive PDE Models Jiayin Jin, Shasha Liao, and Zhiwu Lin Georgia Tech ICERM workshop on water waves, 4/28/2017 Jiayin Jin, Shasha Liao, and Zhiwu Lin Georgia Tech
There is a more global concept that is related to this circle of ideas that we discuss somewhat informally. Namely, a region R R n with a (smooth)
 82 Introduction Liapunov Functions Besides the Liapunov spectral theorem, there is another basic method of proving stability that is a generalization of the energy method we have seen in the introductory
82 Introduction Liapunov Functions Besides the Liapunov spectral theorem, there is another basic method of proving stability that is a generalization of the energy method we have seen in the introductory
Optimal Transportation. Nonlinear Partial Differential Equations
 Optimal Transportation and Nonlinear Partial Differential Equations Neil S. Trudinger Centre of Mathematics and its Applications Australian National University 26th Brazilian Mathematical Colloquium 2007
Optimal Transportation and Nonlinear Partial Differential Equations Neil S. Trudinger Centre of Mathematics and its Applications Australian National University 26th Brazilian Mathematical Colloquium 2007
Lecture No 1 Introduction to Diffusion equations The heat equat
 Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
A semilinear Schrödinger equation with magnetic field
 A semilinear Schrödinger equation with magnetic field Andrzej Szulkin Department of Mathematics, Stockholm University 106 91 Stockholm, Sweden 1 Introduction In this note we describe some recent results
A semilinear Schrödinger equation with magnetic field Andrzej Szulkin Department of Mathematics, Stockholm University 106 91 Stockholm, Sweden 1 Introduction In this note we describe some recent results
BACKGROUND IN SYMPLECTIC GEOMETRY
 BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
BACKGROUND IN SYMPLECTIC GEOMETRY NILAY KUMAR Today I want to introduce some of the symplectic structure underlying classical mechanics. The key idea is actually quite old and in its various formulations
Week 1. 1 The relativistic point particle. 1.1 Classical dynamics. Reading material from the books. Zwiebach, Chapter 5 and chapter 11
 Week 1 1 The relativistic point particle Reading material from the books Zwiebach, Chapter 5 and chapter 11 Polchinski, Chapter 1 Becker, Becker, Schwartz, Chapter 2 1.1 Classical dynamics The first thing
Week 1 1 The relativistic point particle Reading material from the books Zwiebach, Chapter 5 and chapter 11 Polchinski, Chapter 1 Becker, Becker, Schwartz, Chapter 2 1.1 Classical dynamics The first thing
arxiv: v3 [math.ap] 10 Oct 2014
![arxiv: v3 [math.ap] 10 Oct 2014 arxiv: v3 [math.ap] 10 Oct 2014](/thumbs/82/85678438.jpg) THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
THE BOUNDED L 2 CURVATURE CONJECTURE arxiv:1204.1767v3 [math.ap] 10 Oct 2014 SERGIU KLAINERMAN, IGOR RODNIANSKI, AND JEREMIE SZEFTEL Abstract. This is the main paper in a sequence in which we give a complete
Existence, stability and instability for Einstein-scalar field Lichnerowicz equations by Emmanuel Hebey
 Existence, stability and instability for Einstein-scalar field Lichnerowicz equations by Emmanuel Hebey Joint works with Olivier Druet and with Frank Pacard and Dan Pollack Two hours lectures IAS, October
Existence, stability and instability for Einstein-scalar field Lichnerowicz equations by Emmanuel Hebey Joint works with Olivier Druet and with Frank Pacard and Dan Pollack Two hours lectures IAS, October
arxiv: v1 [math.ap] 20 Nov 2007
![arxiv: v1 [math.ap] 20 Nov 2007 arxiv: v1 [math.ap] 20 Nov 2007](/thumbs/79/79495062.jpg) Long range scattering for the Maxwell-Schrödinger system with arbitrarily large asymptotic data arxiv:0711.3100v1 [math.ap] 20 Nov 2007 J. Ginibre Laboratoire de Physique Théorique Université de Paris
Long range scattering for the Maxwell-Schrödinger system with arbitrarily large asymptotic data arxiv:0711.3100v1 [math.ap] 20 Nov 2007 J. Ginibre Laboratoire de Physique Théorique Université de Paris
Interaction energy between vortices of vector fields on Riemannian surfaces
 Interaction energy between vortices of vector fields on Riemannian surfaces Radu Ignat 1 Robert L. Jerrard 2 1 Université Paul Sabatier, Toulouse 2 University of Toronto May 1 2017. Ignat and Jerrard (To(ulouse,ronto)
Interaction energy between vortices of vector fields on Riemannian surfaces Radu Ignat 1 Robert L. Jerrard 2 1 Université Paul Sabatier, Toulouse 2 University of Toronto May 1 2017. Ignat and Jerrard (To(ulouse,ronto)
and the seeds of quantisation
 noncommutative spectral geometry algebra doubling and the seeds of quantisation m.s.,.,, stabile, vitiello, PRD 84 (2011) 045026 mairi sakellariadou king s college london noncommutative spectral geometry
noncommutative spectral geometry algebra doubling and the seeds of quantisation m.s.,.,, stabile, vitiello, PRD 84 (2011) 045026 mairi sakellariadou king s college london noncommutative spectral geometry
NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR SCHRÖDINGER EQUATION
 Journal of Hyperbolic Differential Equations Vol. 7, No. 2 (2010) 279 296 c World Scientific Publishing Company DOI: 10.1142/S0219891610002104 NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR
Journal of Hyperbolic Differential Equations Vol. 7, No. 2 (2010) 279 296 c World Scientific Publishing Company DOI: 10.1142/S0219891610002104 NUMERICAL SIMULATIONS OF THE ENERGY-SUPERCRITICAL NONLINEAR
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD
 INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
The weak null condition, global existence and the asymptotic behavior of solutions to Einstein s equations
 The weak null condition, global existence and the asymptotic behavior of solutions to Einstein s equations The Einstein vacuum equations determine a 4-d manifold M with a Lorentzian metric g, sign( 1,
The weak null condition, global existence and the asymptotic behavior of solutions to Einstein s equations The Einstein vacuum equations determine a 4-d manifold M with a Lorentzian metric g, sign( 1,
Nonlinear stabilization via a linear observability
 via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
Quasi-local mass and isometric embedding
 Quasi-local mass and isometric embedding Mu-Tao Wang, Columbia University September 23, 2015, IHP Recent Advances in Mathematical General Relativity Joint work with Po-Ning Chen and Shing-Tung Yau. The
Quasi-local mass and isometric embedding Mu-Tao Wang, Columbia University September 23, 2015, IHP Recent Advances in Mathematical General Relativity Joint work with Po-Ning Chen and Shing-Tung Yau. The
BIHARMONIC WAVE MAPS INTO SPHERES
 BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
Quasi-local Mass and Momentum in General Relativity
 Quasi-local Mass and Momentum in General Relativity Shing-Tung Yau Harvard University Stephen Hawking s 70th Birthday University of Cambridge, Jan. 7, 2012 I met Stephen Hawking first time in 1978 when
Quasi-local Mass and Momentum in General Relativity Shing-Tung Yau Harvard University Stephen Hawking s 70th Birthday University of Cambridge, Jan. 7, 2012 I met Stephen Hawking first time in 1978 when
Uniqueness of ground state solutions of non-local equations in R N
 Uniqueness of ground state solutions of non-local equations in R N Rupert L. Frank Department of Mathematics Princeton University Joint work with Enno Lenzmann and Luis Silvestre Uniqueness and non-degeneracy
Uniqueness of ground state solutions of non-local equations in R N Rupert L. Frank Department of Mathematics Princeton University Joint work with Enno Lenzmann and Luis Silvestre Uniqueness and non-degeneracy
Asymptotic stability for solitons of the Gross-Pitaevskii and Landau-Lifshitz equations
 Asymptotic stability for solitons of the Gross-Pitaevskii and Landau-Lifshitz equations Philippe Gravejat Cergy-Pontoise University Joint work with F. Béthuel (Paris 6), A. de Laire (Lille) and D. Smets
Asymptotic stability for solitons of the Gross-Pitaevskii and Landau-Lifshitz equations Philippe Gravejat Cergy-Pontoise University Joint work with F. Béthuel (Paris 6), A. de Laire (Lille) and D. Smets
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS
 DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
Dispersive Equations and Hyperbolic Orbits
 Dispersive Equations and Hyperbolic Orbits H. Christianson Department of Mathematics University of California, Berkeley 4/16/07 The Johns Hopkins University Outline 1 Introduction 3 Applications 2 Main
Dispersive Equations and Hyperbolic Orbits H. Christianson Department of Mathematics University of California, Berkeley 4/16/07 The Johns Hopkins University Outline 1 Introduction 3 Applications 2 Main
Applied Math Qualifying Exam 11 October Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems.
 Printed Name: Signature: Applied Math Qualifying Exam 11 October 2014 Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems. 2 Part 1 (1) Let Ω be an open subset of R
Printed Name: Signature: Applied Math Qualifying Exam 11 October 2014 Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems. 2 Part 1 (1) Let Ω be an open subset of R
Wave equation on manifolds and finite speed of propagation
 Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant
 The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant Jared Speck & Igor Rodnianski jspeck@math.princeton.edu University of Cambridge & Princeton University October
The Stability of the Irrotational Euler-Einstein System with a Positive Cosmological Constant Jared Speck & Igor Rodnianski jspeck@math.princeton.edu University of Cambridge & Princeton University October
Math 342 Partial Differential Equations «Viktor Grigoryan
 Math 342 Partial Differential Equations «Viktor Grigoryan 15 Heat with a source So far we considered homogeneous wave and heat equations and the associated initial value problems on the whole line, as
Math 342 Partial Differential Equations «Viktor Grigoryan 15 Heat with a source So far we considered homogeneous wave and heat equations and the associated initial value problems on the whole line, as
YAO LIU. f(x t) + f(x + t)
 DUNKL WAVE EQUATION & REPRESENTATION THEORY OF SL() YAO LIU The classical wave equation u tt = u in n + 1 dimensions, and its various modifications, have been studied for centuries, and one of the most
DUNKL WAVE EQUATION & REPRESENTATION THEORY OF SL() YAO LIU The classical wave equation u tt = u in n + 1 dimensions, and its various modifications, have been studied for centuries, and one of the most
Hylomorphic solitons and their dynamics
 Hylomorphic solitons and their dynamics Vieri Benci Dipartimento di Matematica Applicata U. Dini Università di Pisa 18th May 2009 Vieri Benci (DMA-Pisa) Hylomorphic solitons 18th May 2009 1 / 50 Types
Hylomorphic solitons and their dynamics Vieri Benci Dipartimento di Matematica Applicata U. Dini Università di Pisa 18th May 2009 Vieri Benci (DMA-Pisa) Hylomorphic solitons 18th May 2009 1 / 50 Types
WEYL S LEMMA, ONE OF MANY. Daniel W. Stroock
 WEYL S LEMMA, ONE OF MANY Daniel W Stroock Abstract This note is a brief, and somewhat biased, account of the evolution of what people working in PDE s call Weyl s Lemma about the regularity of solutions
WEYL S LEMMA, ONE OF MANY Daniel W Stroock Abstract This note is a brief, and somewhat biased, account of the evolution of what people working in PDE s call Weyl s Lemma about the regularity of solutions
arxiv:math/ v1 [math.ap] 28 Oct 2005
![arxiv:math/ v1 [math.ap] 28 Oct 2005 arxiv:math/ v1 [math.ap] 28 Oct 2005](/thumbs/72/66322244.jpg) arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
arxiv:math/050643v [math.ap] 28 Oct 2005 A remark on asymptotic completeness for the critical nonlinear Klein-Gordon equation Hans Lindblad and Avy Soffer University of California at San Diego and Rutgers
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
QFT Perturbation Theory
 QFT Perturbation Theory Ling-Fong Li (Institute) Slide_04 1 / 43 Interaction Theory As an illustration, take electromagnetic interaction. Lagrangian density is The combination L = ψ (x ) γ µ ( i µ ea µ
QFT Perturbation Theory Ling-Fong Li (Institute) Slide_04 1 / 43 Interaction Theory As an illustration, take electromagnetic interaction. Lagrangian density is The combination L = ψ (x ) γ µ ( i µ ea µ
Inverse Scattering with Partial data on Asymptotically Hyperbolic Manifolds
 Inverse Scattering with Partial data on Asymptotically Hyperbolic Manifolds Raphael Hora UFSC rhora@mtm.ufsc.br 29/04/2014 Raphael Hora (UFSC) Inverse Scattering with Partial data on AH Manifolds 29/04/2014
Inverse Scattering with Partial data on Asymptotically Hyperbolic Manifolds Raphael Hora UFSC rhora@mtm.ufsc.br 29/04/2014 Raphael Hora (UFSC) Inverse Scattering with Partial data on AH Manifolds 29/04/2014
Some results on the nonlinear Klein-Gordon-Maxwell equations
 Some results on the nonlinear Klein-Gordon-Maxwell equations Alessio Pomponio Dipartimento di Matematica, Politecnico di Bari, Italy Granada, Spain, 2011 A solitary wave is a solution of a field equation
Some results on the nonlinear Klein-Gordon-Maxwell equations Alessio Pomponio Dipartimento di Matematica, Politecnico di Bari, Italy Granada, Spain, 2011 A solitary wave is a solution of a field equation
Chap. 1. Some Differential Geometric Tools
 Chap. 1. Some Differential Geometric Tools 1. Manifold, Diffeomorphism 1.1. The Implicit Function Theorem ϕ : U R n R n p (0 p < n), of class C k (k 1) x 0 U such that ϕ(x 0 ) = 0 rank Dϕ(x) = n p x U
Chap. 1. Some Differential Geometric Tools 1. Manifold, Diffeomorphism 1.1. The Implicit Function Theorem ϕ : U R n R n p (0 p < n), of class C k (k 1) x 0 U such that ϕ(x 0 ) = 0 rank Dϕ(x) = n p x U
Vortex Equations on Riemannian Surfaces
 Vortex Equations on Riemannian Surfaces Amanda Hood, Khoa Nguyen, Joseph Shao Advisor: Chris Woodward Vortex Equations on Riemannian Surfaces p.1/36 Introduction Yang Mills equations: originated from electromagnetism
Vortex Equations on Riemannian Surfaces Amanda Hood, Khoa Nguyen, Joseph Shao Advisor: Chris Woodward Vortex Equations on Riemannian Surfaces p.1/36 Introduction Yang Mills equations: originated from electromagnetism
M ath. Res. Lett. 15 (2008), no. 6, c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION
 M ath. Res. Lett. 15 (2008), no. 6, 1233 1250 c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION Thomas Duyckaerts, Justin Holmer, and Svetlana Roudenko Abstract.
M ath. Res. Lett. 15 (2008), no. 6, 1233 1250 c International Press 2008 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION Thomas Duyckaerts, Justin Holmer, and Svetlana Roudenko Abstract.
RANDOM PROPERTIES BENOIT PAUSADER
 RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
RANDOM PROPERTIES BENOIT PAUSADER. Quasilinear problems In general, one consider the following trichotomy for nonlinear PDEs: A semilinear problem is a problem where the highest-order terms appears linearly
Geometric inequalities for black holes
 Geometric inequalities for black holes Sergio Dain FaMAF-Universidad Nacional de Córdoba, CONICET, Argentina. 3 August, 2012 Einstein equations (vacuum) The spacetime is a four dimensional manifold M with
Geometric inequalities for black holes Sergio Dain FaMAF-Universidad Nacional de Córdoba, CONICET, Argentina. 3 August, 2012 Einstein equations (vacuum) The spacetime is a four dimensional manifold M with
Einstein Toolkit Workshop. Joshua Faber Apr
 Einstein Toolkit Workshop Joshua Faber Apr 05 2012 Outline Space, time, and special relativity The metric tensor and geometry Curvature Geodesics Einstein s equations The Stress-energy tensor 3+1 formalisms
Einstein Toolkit Workshop Joshua Faber Apr 05 2012 Outline Space, time, and special relativity The metric tensor and geometry Curvature Geodesics Einstein s equations The Stress-energy tensor 3+1 formalisms
Corrections to Quantum Theory for Mathematicians
 Corrections to Quantum Theory for Mathematicians B C H January 2018 Thanks to ussell Davidson, Bruce Driver, John Eggers, Todd Kemp, Benjamin ewis, Jeff Margrave, Alexander Mukhin, Josh asmussen, Peter
Corrections to Quantum Theory for Mathematicians B C H January 2018 Thanks to ussell Davidson, Bruce Driver, John Eggers, Todd Kemp, Benjamin ewis, Jeff Margrave, Alexander Mukhin, Josh asmussen, Peter
Quantum Field Theory II
 Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
Particle Physics I Lecture Exam Question Sheet
 Particle Physics I Lecture Exam Question Sheet Five out of these 16 questions will be given to you at the beginning of the exam. (1) (a) Which are the different fundamental interactions that exist in Nature?
Particle Physics I Lecture Exam Question Sheet Five out of these 16 questions will be given to you at the beginning of the exam. (1) (a) Which are the different fundamental interactions that exist in Nature?
Linear Differential Equations. Problems
 Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Course Description for Real Analysis, Math 156
 Course Description for Real Analysis, Math 156 In this class, we will study elliptic PDE, Fourier analysis, and dispersive PDE. Here is a quick summary of the topics will study study. They re described
Course Description for Real Analysis, Math 156 In this class, we will study elliptic PDE, Fourier analysis, and dispersive PDE. Here is a quick summary of the topics will study study. They re described
SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION
 SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION THOMAS DUYCKAERTS, JUSTIN HOLMER, AND SVETLANA ROUDENKO Abstract. Scattering of radial H 1 solutions to the 3D focusing cubic nonlinear
SCATTERING FOR THE NON-RADIAL 3D CUBIC NONLINEAR SCHRÖDINGER EQUATION THOMAS DUYCKAERTS, JUSTIN HOLMER, AND SVETLANA ROUDENKO Abstract. Scattering of radial H 1 solutions to the 3D focusing cubic nonlinear
Nonlinear Schrödinger Equation BAOXIANG WANG. Talk at Tsinghua University 2012,3,16. School of Mathematical Sciences, Peking University.
 Talk at Tsinghua University 2012,3,16 Nonlinear Schrödinger Equation BAOXIANG WANG School of Mathematical Sciences, Peking University 1 1 33 1. Schrödinger E. Schrödinger (1887-1961) E. Schrödinger, (1887,
Talk at Tsinghua University 2012,3,16 Nonlinear Schrödinger Equation BAOXIANG WANG School of Mathematical Sciences, Peking University 1 1 33 1. Schrödinger E. Schrödinger (1887-1961) E. Schrödinger, (1887,
