Variable. Peter W. White Fall 2018 / Numerical Analysis. Department of Mathematics Tarleton State University
|
|
|
- Merilyn Stone
- 5 years ago
- Views:
Transcription
1 Newton s Iterative s Peter W. White white@tarleton.edu Department of Mathematics Tarleton State University Fall 2018 / Numerical Analysis
2 Overview Newton s Iterative s Newton s Iterative s
3 Newton s Iterative s Population Example Malthusian model of population is P (t) = λp(t) with P(0) = P 0. This has solution: P(t) = P 0 e λt. If immigration is permited at a constant rate ν, then the model is p (t) = λp(t) + ν = P(t) = P 0 e λt + ν ( e λt 1 ). λ Question: suppose that P is measured in thousands of individuals, t is years, P 0 = 1, 000, ν = 435 and P(1) = 1, 564, then find λ. That is, find λ where 1, 564 = 1, 000e λ λ ( ) e λ 1
4 Population Example (Continued) Newton s Iterative s In this equation, λ appears both inside and outside a transcendental function. Because of this, it is not currently possible to solve for λ. The methods in this chapter are designed to approximate solutions of problems that can not be solved exactly. Note: If F(x) = f (x) a, then solving f (x) = a for x is equivalent to finding roots (or zeros) of F. That is, f (p) = a if and only if F(p) = 0.
5 Overview Newton s Iterative s Newton s Iterative s
6 Newton s Iterative s Intermediate Value Theorem Theorem 1 Let f be a continuous function on the interval [a, b] with L R between f (a) and f (b). Then there exist c [a, b] such that f (c) = L. Corollary 2 Let f be a continuous function on the interval [a, b] with f (a)f (b) < 0. Then there exists p (a, b) such that f (p) = 0.
7 Newton s Iterative s Bisection Algorithm or Binary-search To find an approximation to the solution of f (x) = 0 given the continuous function f on the interval [a, b], where f (a) and f (b) have opposite signs: INPUT endpoints a, b; tolerance TOL; max number of iterations N 0. OUTPUT approximate solution p or message of failure. Step 1: Set i = 1 and FA = f (a), Step 2: While i N 0 do steps 3-6, Step 3: Set p = a + (b a)/2 and FP = f (p), Step 4: If FP = 0 or (b a)/2 < Tol then OUTPUT(p) and Stop. Step 5: Set i = i + 1. Step 6: If FA FP > 0 then a = p, FA = f (p), else set b = p. Step 7: OUTPUT(" failed, maximum iterations reached") and Stop.
8 Example of Bisection Example 3 Find the square root of 10 accurate to Hint: find the positive root of f (x) = x Newton s Iterative s
9 Homework Homework assignment section 2.1, due: TBA Newton s Iterative s
10 Overview Newton s Iterative s Newton s Iterative s
11 Definition and Example Definition 4 Fixed Point: The number p is a fixed point for a given function g if g(p) = p. Newton s Iterative s Example 5 Determine any fixed points of the function g(x) = x 2 6
12 Newton s Iterative s Sufficient Conditions for Existence Theorem 6 1. If g C[a, b] and g(x) a, b for all x [a, b], then g has at least one fixed point in [a, b]. 2. If, in addition, g (x) exists on (a, b) and a positive constant k < 1 exists with g (x) k, for all x (a, b), then there is exactly one fixed point in [a, b].
13 Example Example 7 Show that g(x) = cos(x) has exactly one fixed point in [0, π/3]. Newton s Iterative s
14 Fixed Point Newton s Iterative s Suppose we generate a sequence {p n } that converges to p with p n+1 = g(p n ) where g is continuous, then p is a fixed point of g. Proof. ( ) p = lim p n+1 = lim g(p n) = g lim p n = g(p). n n n
15 Homework Homework assignment section 2.2, due: TBA Newton s Iterative s
16 Overview Newton s Iterative s Newton s Iterative s
17 Newton s Definition and Example Definition 8 Newton s : Suppose f C 1 (I), where I is an open interval and {p n } be a sequence in I converging to p with p n+1 = p n f (p n) f. Then p is a root (or zero) of f. (p n ) Iterative s Example 9 Determine any roots of the function f (x) = x 2 6
18 Newton s Iterative s Convergence Theorem 10 Let f C 2 [a, b]. If p (a, b) such that f (p) = 0 and f (p) 0, then there exists a δ > 0 such that Newton s method generates a sequence {p n } n=1 converging to p for any initial approximation p 0 [p δ, p + δ]. Note: nothing is said about how small δ might be, or the rate of convergence. In practice, for most reasonable problems, Newton s method will either quickly converge or it will be obvious that it will not converge.
19 Newton s Iterative s Secant Question: What if f (x) is not readily available? In this case replace f (p n ) with an approximation. If p n is close to p n 1, then f (p n ) f (p n) f (p n 1 ) p n p n 1. The Secant method assumes that two initial approximations, p 0 and p 1, are given, then for n = Z +, p n+1 = p n f (p n)(p n p n 1 ) f (p n ) f (p n 1 ).
20 Example Example 11 Use the Secant method with a tolerance of 10 4 to approximate 6. Newton s Iterative s
21 Homework Read: The of False Position at the end of the section and then: Homework assignment section 2.3, due: TBA Newton s Iterative s
22 Overview Newton s Iterative s Newton s Iterative s
23 Newton s Iterative s Order of Convergence Definition 12 Suppose {p n } is a sequence that converges to p, with p n p for all n. If there exists positive constants λ and α with p n+1 p lim n p n p α = λ, then {p n } converges to p of order α, with asymptotic error constant λ. An iterative technique of the form p n+1 = g(p n ) is said to be of order α if the sequence converges to the solution p = g(p) of order α.
24 Newton s Iterative s Order of Convergence (cont.) If α = 1 (and λ < 1), the sequence is linearly convergent. If α = 2, the sequence is quadratically convergent. Example 13 Let p n = 1. Find the order of convergence to zero. 2n
25 Theorem Newton s Iterative s Theorem 14 Let C C[a, b] be such that g(x) [a, b], for all x [a, b]. Suppose, in addition, that g is continuous on (a, b) and that a positive constant k < 1 exists with g (x) k, for all x (a, b). If g (p) 0, then for any number p 0 p in [a, b], the sequence p n+1 = g(p n ) converges only linearly to the unique fixed point p in [a, b].
26 Newton s Iterative s Theorem Theorem 15 Let p be a solution of the equation x = g(x). Suppose that g (p) = 0 and g is continuous with g (x) < M on an open interval I containing p. Then there exists a δ > 0 such that, for p 0 [p δ, p + δ], the sequence defined by p n+1 = g(p n ) converges at a rate at least quadratically to p. Moreover, for sufficiently large n, p n+1 p < M 2 p n p 2.
27 Homework Read: The part about Multiple Roots at the end of the section and then: Homework assignment section 2.4, due: TBA Newton s Iterative s
Solutions of Equations in One Variable. Newton s Method
 Solutions of Equations in One Variable Newton s Method Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011 Brooks/Cole,
Solutions of Equations in One Variable Newton s Method Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011 Brooks/Cole,
Accelerating Convergence
 Accelerating Convergence MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have seen that most fixed-point methods for root finding converge only linearly
Accelerating Convergence MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have seen that most fixed-point methods for root finding converge only linearly
Midterm Review. Igor Yanovsky (Math 151A TA)
 Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Numerical Methods. Root Finding
 Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
ROOT FINDING REVIEW MICHELLE FENG
 ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods
 Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
Numerical Methods Dr. Sanjeev Kumar Department of Mathematics Indian Institute of Technology Roorkee Lecture No 7 Regula Falsi and Secant Methods So welcome to the next lecture of the 2 nd unit of this
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 5 Nonlinear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 5 Nonlinear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Lecture 44. Better and successive approximations x2, x3,, xn to the root are obtained from
 Lecture 44 Solution of Non-Linear Equations Regula-Falsi Method Method of iteration Newton - Raphson Method Muller s Method Graeffe s Root Squaring Method Newton -Raphson Method An approximation to the
Lecture 44 Solution of Non-Linear Equations Regula-Falsi Method Method of iteration Newton - Raphson Method Muller s Method Graeffe s Root Squaring Method Newton -Raphson Method An approximation to the
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 5. Nonlinear Equations
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter 5 Nonlinear Equations Copyright c 2001 Reproduction permitted only for noncommercial, educational
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter 5 Nonlinear Equations Copyright c 2001 Reproduction permitted only for noncommercial, educational
Numerical Methods in Informatics
 Numerical Methods in Informatics Lecture 2, 30.09.2016: Nonlinear Equations in One Variable http://www.math.uzh.ch/binf4232 Tulin Kaman Institute of Mathematics, University of Zurich E-mail: tulin.kaman@math.uzh.ch
Numerical Methods in Informatics Lecture 2, 30.09.2016: Nonlinear Equations in One Variable http://www.math.uzh.ch/binf4232 Tulin Kaman Institute of Mathematics, University of Zurich E-mail: tulin.kaman@math.uzh.ch
Solving Non-Linear Equations (Root Finding)
 Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
Solving Non-Linear Equations (Root Finding) Root finding Methods What are root finding methods? Methods for determining a solution of an equation. Essentially finding a root of a function, that is, a zero
CLASS NOTES Computational Methods for Engineering Applications I Spring 2015
 CLASS NOTES Computational Methods for Engineering Applications I Spring 2015 Petros Koumoutsakos Gerardo Tauriello (Last update: July 2, 2015) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
CLASS NOTES Computational Methods for Engineering Applications I Spring 2015 Petros Koumoutsakos Gerardo Tauriello (Last update: July 2, 2015) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
Outline. Scientific Computing: An Introductory Survey. Nonlinear Equations. Nonlinear Equations. Examples: Nonlinear Equations
 Methods for Systems of Methods for Systems of Outline Scientific Computing: An Introductory Survey Chapter 5 1 Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign
Methods for Systems of Methods for Systems of Outline Scientific Computing: An Introductory Survey Chapter 5 1 Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign
Nonlinear Equations. Chapter The Bisection Method
 Chapter 6 Nonlinear Equations Given a nonlinear function f(), a value r such that f(r) = 0, is called a root or a zero of f() For eample, for f() = e 016064, Fig?? gives the set of points satisfying y
Chapter 6 Nonlinear Equations Given a nonlinear function f(), a value r such that f(r) = 0, is called a root or a zero of f() For eample, for f() = e 016064, Fig?? gives the set of points satisfying y
CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018
 CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018 Petros Koumoutsakos, Jens Honore Walther (Last update: April 16, 2018) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
CLASS NOTES Models, Algorithms and Data: Introduction to computing 2018 Petros Koumoutsakos, Jens Honore Walther (Last update: April 16, 2018) IMPORTANT DISCLAIMERS 1. REFERENCES: Much of the material
Numerical Analysis. EE, NCKU Tien-Hao Chang (Darby Chang)
 Numerical Analysis EE, NCKU Tien-Hao Chang (Darby Chang) 1 In the previous slide Error (motivation) Floating point number system difference to real number system problem of roundoff Introduced/propagated
Numerical Analysis EE, NCKU Tien-Hao Chang (Darby Chang) 1 In the previous slide Error (motivation) Floating point number system difference to real number system problem of roundoff Introduced/propagated
Continuity. MATH 161 Calculus I. J. Robert Buchanan. Fall Department of Mathematics
 Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Root Finding For NonLinear Equations Bisection Method
 Root Finding For NonLinear Equations Bisection Method P. Sam Johnson November 17, 2014 P. Sam Johnson (NITK) Root Finding For NonLinear Equations Bisection MethodNovember 17, 2014 1 / 26 Introduction The
Root Finding For NonLinear Equations Bisection Method P. Sam Johnson November 17, 2014 P. Sam Johnson (NITK) Root Finding For NonLinear Equations Bisection MethodNovember 17, 2014 1 / 26 Introduction The
CS 450 Numerical Analysis. Chapter 5: Nonlinear Equations
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Solution of Algebric & Transcendental Equations
 Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
Page15 Solution of Algebric & Transcendental Equations Contents: o Introduction o Evaluation of Polynomials by Horner s Method o Methods of solving non linear equations o Bracketing Methods o Bisection
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435
 PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
PART I Lecture Notes on Numerical Solution of Root Finding Problems MATH 435 Professor Biswa Nath Datta Department of Mathematical Sciences Northern Illinois University DeKalb, IL. 60115 USA E mail: dattab@math.niu.edu
CS 323: Numerical Analysis and Computing
 CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
CS 323: Numerical Analysis and Computing
 CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
3.1 Introduction. Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x x 1.5 =0, tan x x =0.
 3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
3.1 Introduction Solve non-linear real equation f(x) = 0 for real root or zero x. E.g. x 3 +1.5x 1.5 =0, tan x x =0. Practical existence test for roots: by intermediate value theorem, f C[a, b] & f(a)f(b)
Outline. Math Numerical Analysis. Intermediate Value Theorem. Lecture Notes Zeros and Roots. Joseph M. Mahaffy,
 Outline Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
Outline Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research
Math Numerical Analysis
 Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Math 541 - Numerical Analysis Lecture Notes Zeros and Roots Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center
Chapter 1. Root Finding Methods. 1.1 Bisection method
 Chapter 1 Root Finding Methods We begin by considering numerical solutions to the problem f(x) = 0 (1.1) Although the problem above is simple to state it is not always easy to solve analytically. This
Chapter 1 Root Finding Methods We begin by considering numerical solutions to the problem f(x) = 0 (1.1) Although the problem above is simple to state it is not always easy to solve analytically. This
Math Introduction to Numerical Methods - Winter 2011 Homework 2 Assigned: Friday, January 14, Due: Thursday, January 27,
 Math 371 - Introduction to Numerical Methods - Winter 2011 Homework 2 Assigned: Friday, January 14, 2011. Due: Thursday, January 27, 2011.. Include a cover page. You do not need to hand in a problem sheet.
Math 371 - Introduction to Numerical Methods - Winter 2011 Homework 2 Assigned: Friday, January 14, 2011. Due: Thursday, January 27, 2011.. Include a cover page. You do not need to hand in a problem sheet.
Bisection Method. and compute f (p 1 ). repeat with p 2 = a 2+b 2
 Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
Bisection Method Given continuous function f (x) on the interval [a, b] with f (a) f (b) < 0, there must be a root in (a, b). To find a root: set [a 1, b 1 ] = [a, b]. set p 1 = a 1+b 1 2 and compute f
Nonlinearity Root-finding Bisection Fixed Point Iteration Newton s Method Secant Method Conclusion. Nonlinear Systems
 Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Nonlinear Systems 1 / 24 Part III: Nonlinear Problems Not all numerical problems
Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Nonlinear Systems 1 / 24 Part III: Nonlinear Problems Not all numerical problems
Figure 1: Graph of y = x cos(x)
 Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
Chapter The Solution of Nonlinear Equations f(x) = 0 In this chapter we will study methods for find the solutions of functions of single variables, ie values of x such that f(x) = 0 For example, f(x) =
CHAPTER-II ROOTS OF EQUATIONS
 CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
CHAPTER-II ROOTS OF EQUATIONS 2.1 Introduction The roots or zeros of equations can be simply defined as the values of x that makes f(x) =0. There are many ways to solve for roots of equations. For some
Consequences of Continuity and Differentiability
 Consequences of Continuity and Differentiability We have seen how continuity of functions is an important condition for evaluating limits. It is also an important conceptual tool for guaranteeing the existence
Consequences of Continuity and Differentiability We have seen how continuity of functions is an important condition for evaluating limits. It is also an important conceptual tool for guaranteeing the existence
Math 471. Numerical methods Root-finding algorithms for nonlinear equations
 Math 471. Numerical methods Root-finding algorithms for nonlinear equations overlap Section.1.5 of Bradie Our goal in this chapter is to find the root(s) for f(x) = 0..1 Bisection Method Intermediate value
Math 471. Numerical methods Root-finding algorithms for nonlinear equations overlap Section.1.5 of Bradie Our goal in this chapter is to find the root(s) for f(x) = 0..1 Bisection Method Intermediate value
Numerical Analysis Fall. Roots: Open Methods
 Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Numerical Analysis 2015 Fall Roots: Open Methods Open Methods Open methods differ from bracketing methods, in that they require only a single starting value or two starting values that do not necessarily
Numerical solutions of nonlinear systems of equations
 Numerical solutions of nonlinear systems of equations Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan E-mail: min@math.ntnu.edu.tw August 28, 2011 Outline 1 Fixed points
Numerical solutions of nonlinear systems of equations Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan E-mail: min@math.ntnu.edu.tw August 28, 2011 Outline 1 Fixed points
SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS BISECTION METHOD
 BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
BISECTION METHOD If a function f(x) is continuous between a and b, and f(a) and f(b) are of opposite signs, then there exists at least one root between a and b. It is shown graphically as, Let f a be negative
Numerical Solution of f(x) = 0
 Numerical Solution of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@pdx.edu ME 350: Finding roots of f(x) = 0 Overview Topics covered in these slides
Numerical Solution of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@pdx.edu ME 350: Finding roots of f(x) = 0 Overview Topics covered in these slides
Introductory Numerical Analysis
 Introductory Numerical Analysis Lecture Notes December 16, 017 Contents 1 Introduction to 1 11 Floating Point Numbers 1 1 Computational Errors 13 Algorithm 3 14 Calculus Review 3 Root Finding 5 1 Bisection
Introductory Numerical Analysis Lecture Notes December 16, 017 Contents 1 Introduction to 1 11 Floating Point Numbers 1 1 Computational Errors 13 Algorithm 3 14 Calculus Review 3 Root Finding 5 1 Bisection
MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations.
 MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations. Dmitriy Leykekhman Fall 2008 Goals Learn about different methods for the solution of f(x) = 0, their advantages and disadvantages. Convergence
MATH 3795 Lecture 12. Numerical Solution of Nonlinear Equations. Dmitriy Leykekhman Fall 2008 Goals Learn about different methods for the solution of f(x) = 0, their advantages and disadvantages. Convergence
Fixed-Point Iteration
 Fixed-Point Iteration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation Several root-finding algorithms operate by repeatedly evaluating a function until its
Fixed-Point Iteration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation Several root-finding algorithms operate by repeatedly evaluating a function until its
Jim Lambers MAT 460/560 Fall Semester Practice Final Exam
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Root Finding (and Optimisation)
 Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Chapter 3: Root Finding. September 26, 2005
 Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Lecture 8. Root finding II
 1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
1 Introduction Lecture 8 Root finding II In the previous lecture we considered the bisection root-bracketing algorithm. It requires only that the function be continuous and that we have a root bracketed
Order of convergence
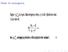 Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Lecture 7. Root finding I. 1 Introduction. 2 Graphical solution
 1 Introduction Lecture 7 Root finding I For our present purposes, root finding is the process of finding a real value of x which solves the equation f (x)=0. Since the equation g x =h x can be rewritten
1 Introduction Lecture 7 Root finding I For our present purposes, root finding is the process of finding a real value of x which solves the equation f (x)=0. Since the equation g x =h x can be rewritten
5 Finding roots of equations
 Lecture notes for Numerical Analysis 5 Finding roots of equations Topics:. Problem statement. Bisection Method 3. Newton s Method 4. Fixed Point Iterations 5. Systems of equations 6. Notes and further
Lecture notes for Numerical Analysis 5 Finding roots of equations Topics:. Problem statement. Bisection Method 3. Newton s Method 4. Fixed Point Iterations 5. Systems of equations 6. Notes and further
Nonlinearity Root-finding Bisection Fixed Point Iteration Newton s Method Secant Method Conclusion. Nonlinear Systems
 Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Nonlinear Systems 1 / 27 Part III: Nonlinear Problems Not
Nonlinear Systems CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Nonlinear Systems 1 / 27 Part III: Nonlinear Problems Not
Zeroes of Transcendental and Polynomial Equations. Bisection method, Regula-falsi method and Newton-Raphson method
 Zeroes of Transcendental and Polynomial Equations Bisection method, Regula-falsi method and Newton-Raphson method PRELIMINARIES Solution of equation f (x) = 0 A number (real or complex) is a root of the
Zeroes of Transcendental and Polynomial Equations Bisection method, Regula-falsi method and Newton-Raphson method PRELIMINARIES Solution of equation f (x) = 0 A number (real or complex) is a root of the
INTRODUCTION TO NUMERICAL ANALYSIS
 INTRODUCTION TO NUMERICAL ANALYSIS Cho, Hyoung Kyu Department of Nuclear Engineering Seoul National University 3. SOLVING NONLINEAR EQUATIONS 3.1 Background 3.2 Estimation of errors in numerical solutions
INTRODUCTION TO NUMERICAL ANALYSIS Cho, Hyoung Kyu Department of Nuclear Engineering Seoul National University 3. SOLVING NONLINEAR EQUATIONS 3.1 Background 3.2 Estimation of errors in numerical solutions
An Improved Hybrid Algorithm to Bisection Method and Newton-Raphson Method
 Applied Mathematical Sciences, Vol. 11, 2017, no. 56, 2789-2797 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2017.710302 An Improved Hybrid Algorithm to Bisection Method and Newton-Raphson
Applied Mathematical Sciences, Vol. 11, 2017, no. 56, 2789-2797 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2017.710302 An Improved Hybrid Algorithm to Bisection Method and Newton-Raphson
Line Search Methods. Shefali Kulkarni-Thaker
 1 BISECTION METHOD Line Search Methods Shefali Kulkarni-Thaker Consider the following unconstrained optimization problem min f(x) x R Any optimization algorithm starts by an initial point x 0 and performs
1 BISECTION METHOD Line Search Methods Shefali Kulkarni-Thaker Consider the following unconstrained optimization problem min f(x) x R Any optimization algorithm starts by an initial point x 0 and performs
Chapter 2 Solutions of Equations of One Variable
 Chapter 2 Solutions of Equations of One Variable 2.1 Bisection Method In this chapter we consider one of the most basic problems of numerical approximation, the root-finding problem. This process involves
Chapter 2 Solutions of Equations of One Variable 2.1 Bisection Method In this chapter we consider one of the most basic problems of numerical approximation, the root-finding problem. This process involves
Finding the Roots of f(x) = 0. Gerald W. Recktenwald Department of Mechanical Engineering Portland State University
 Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Finding the Roots of f(x) = 0
 Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Finding the Roots of f(x) = 0 Gerald W. Recktenwald Department of Mechanical Engineering Portland State University gerry@me.pdx.edu These slides are a supplement to the book Numerical Methods with Matlab:
Unit 2: Solving Scalar Equations. Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright
 cs416: introduction to scientific computing 01/9/07 Unit : Solving Scalar Equations Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright 1 Introduction We now
cs416: introduction to scientific computing 01/9/07 Unit : Solving Scalar Equations Notes prepared by: Amos Ron, Yunpeng Li, Mark Cowlishaw, Steve Wright Instructor: Steve Wright 1 Introduction We now
R x n. 2 R We simplify this algebraically, obtaining 2x n x n 1 x n x n
 Math 42 Homework 4. page 3, #9 This is a modification of the bisection method. Write a MATLAB function similar to bisect.m. Here, given the points P a a,f a and P b b,f b with f a f b,we compute the point
Math 42 Homework 4. page 3, #9 This is a modification of the bisection method. Write a MATLAB function similar to bisect.m. Here, given the points P a a,f a and P b b,f b with f a f b,we compute the point
1. Nonlinear Equations. This lecture note excerpted parts from Michael Heath and Max Gunzburger. f(x) = 0
 Numerical Analysis 1 1. Nonlinear Equations This lecture note excerpted parts from Michael Heath and Max Gunzburger. Given function f, we seek value x for which where f : D R n R n is nonlinear. f(x) =
Numerical Analysis 1 1. Nonlinear Equations This lecture note excerpted parts from Michael Heath and Max Gunzburger. Given function f, we seek value x for which where f : D R n R n is nonlinear. f(x) =
Math 473: Practice Problems for Test 1, Fall 2011, SOLUTIONS
 Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Math 473: Practice Problems for Test 1, Fall 011, SOLUTIONS Show your work: 1. (a) Compute the Taylor polynomials P n (x) for f(x) = sin x and x 0 = 0. Solution: Compute f(x) = sin x, f (x) = cos x, f
Caculus 221. Possible questions for Exam II. March 19, 2002
 Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Homework 2 - Solutions MA/CS 375, Fall 2005
 Homework 2 - Solutions MA/CS 375, Fall 2005 1. Use the bisection method, Newton s method, and the Matlab R function fzero to compute a positive real number x satisfying: sinh x = cos x. For each of the
Homework 2 - Solutions MA/CS 375, Fall 2005 1. Use the bisection method, Newton s method, and the Matlab R function fzero to compute a positive real number x satisfying: sinh x = cos x. For each of the
Numerical Study of Some Iterative Methods for Solving Nonlinear Equations
 International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 5 Issue 2 February 2016 PP.0110 Numerical Study of Some Iterative Methods for Solving Nonlinear
International Journal of Engineering Science Invention ISSN (Online): 2319 6734, ISSN (Print): 2319 6726 Volume 5 Issue 2 February 2016 PP.0110 Numerical Study of Some Iterative Methods for Solving Nonlinear
Numerical Methods Lecture 3
 Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
Numerical Methods Lecture 3 Nonlinear Equations by Pavel Ludvík Introduction Definition (Root or zero of a function) A root (or a zero) of a function f is a solution of an equation f (x) = 0. We learn
x 2 x n r n J(x + t(x x ))(x x )dt. For warming-up we start with methods for solving a single equation of one variable.
 Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Maria Cameron 1. Fixed point methods for solving nonlinear equations We address the problem of solving an equation of the form (1) r(x) = 0, where F (x) : R n R n is a vector-function. Eq. (1) can be written
Homework for Section 1.4, Continuity and One sided Limits. Study 1.4, # 1 21, 27, 31, 37 41, 45 53, 61, 69, 87, 91, 93. Class Notes: Prof. G.
 GOAL: 1. Understand definition of continuity at a point. 2. Evaluate functions for continuity at a point, and on open and closed intervals 3. Understand the Intermediate Value Theorum (IVT) Homework for
GOAL: 1. Understand definition of continuity at a point. 2. Evaluate functions for continuity at a point, and on open and closed intervals 3. Understand the Intermediate Value Theorum (IVT) Homework for
Math 128A: Homework 2 Solutions
 Math 128A: Homework 2 Solutions Due: June 28 1. In problems where high precision is not needed, the IEEE standard provides a specification for single precision numbers, which occupy 32 bits of storage.
Math 128A: Homework 2 Solutions Due: June 28 1. In problems where high precision is not needed, the IEEE standard provides a specification for single precision numbers, which occupy 32 bits of storage.
Continuity. To handle complicated functions, particularly those for which we have a reasonable formula or formulas, we need a more precise definition.
 Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
Continuity Intuitively, a function is continuous if its graph can be traced on paper in one motion without lifting the pencil from the paper. Thus the graph has no tears or holes. To handle complicated
Computational Methods. Solving Equations
 Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
Computational Methods Solving Equations Manfred Huber 2010 1 Solving Equations Solving scalar equations is an elemental task that arises in a wide range of applications Corresponds to finding parameters
Chapter 4. Solution of Non-linear Equation. Module No. 1. Newton s Method to Solve Transcendental Equation
 Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-713209 email: anita.buie@gmail.com 1 . Chapter 4 Solution of Non-linear
Practical Numerical Analysis: Sheet 3 Solutions
 Practical Numerical Analysis: Sheet 3 Solutions 1. We need to compute the roots of the function defined by f(x) = sin(x) + sin(x 2 ) on the interval [0, 3] using different numerical methods. First we consider
Practical Numerical Analysis: Sheet 3 Solutions 1. We need to compute the roots of the function defined by f(x) = sin(x) + sin(x 2 ) on the interval [0, 3] using different numerical methods. First we consider
Root Finding: Close Methods. Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
Root Finding: Close Methods Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Roots Given function f(x), we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the
p 1 p 0 (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- cant method.
 80 CHAP. 2 SOLUTION OF NONLINEAR EQUATIONS f (x) = 0 y y = f(x) (p, 0) p 2 p 1 p 0 x (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- Figure 2.16 cant method. Secant Method The
80 CHAP. 2 SOLUTION OF NONLINEAR EQUATIONS f (x) = 0 y y = f(x) (p, 0) p 2 p 1 p 0 x (p 1, f(p 1 )) (p 0, f(p 0 )) The geometric construction of p 2 for the se- Figure 2.16 cant method. Secant Method The
MA 8019: Numerical Analysis I Solution of Nonlinear Equations
 MA 8019: Numerical Analysis I Solution of Nonlinear Equations Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
MA 8019: Numerical Analysis I Solution of Nonlinear Equations Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
Hence a root lies between 1 and 2. Since f a is negative and f(x 0 ) is positive The root lies between a and x 0 i.e. 1 and 1.
 The Bisection method or BOLZANO s method or Interval halving method: Find the positive root of x 3 x = 1 correct to four decimal places by bisection method Let f x = x 3 x 1 Here f 0 = 1 = ve, f 1 = ve,
The Bisection method or BOLZANO s method or Interval halving method: Find the positive root of x 3 x = 1 correct to four decimal places by bisection method Let f x = x 3 x 1 Here f 0 = 1 = ve, f 1 = ve,
The function graphed below is continuous everywhere. The function graphed below is NOT continuous everywhere, it is discontinuous at x 2 and
 Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Section 1.4 Continuity A function is a continuous at a point if its graph has no gaps, holes, breaks or jumps at that point. If a function is not continuous at a point, then we say it is discontinuous
Motivation: We have already seen an example of a system of nonlinear equations when we studied Gaussian integration (p.8 of integration notes)
 AMSC/CMSC 460 Computational Methods, Fall 2007 UNIT 5: Nonlinear Equations Dianne P. O Leary c 2001, 2002, 2007 Solving Nonlinear Equations and Optimization Problems Read Chapter 8. Skip Section 8.1.1.
AMSC/CMSC 460 Computational Methods, Fall 2007 UNIT 5: Nonlinear Equations Dianne P. O Leary c 2001, 2002, 2007 Solving Nonlinear Equations and Optimization Problems Read Chapter 8. Skip Section 8.1.1.
10.3 Steepest Descent Techniques
 The advantage of the Newton and quasi-newton methods for solving systems of nonlinear equations is their speed of convergence once a sufficiently accurate approximation is known. A weakness of these methods
The advantage of the Newton and quasi-newton methods for solving systems of nonlinear equations is their speed of convergence once a sufficiently accurate approximation is known. A weakness of these methods
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
1. Method 1: bisection. The bisection methods starts from two points a 0 and b 0 such that
 Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
Chapter 4 Nonlinear equations 4.1 Root finding Consider the problem of solving any nonlinear relation g(x) = h(x) in the real variable x. We rephrase this problem as one of finding the zero (root) of a
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 3 Lecture 3 3.1 General remarks March 4, 2018 This
Families of Functions, Taylor Polynomials, l Hopital s
 Unit #6 : Rule Families of Functions, Taylor Polynomials, l Hopital s Goals: To use first and second derivative information to describe functions. To be able to find general properties of families of functions.
Unit #6 : Rule Families of Functions, Taylor Polynomials, l Hopital s Goals: To use first and second derivative information to describe functions. To be able to find general properties of families of functions.
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
SOLVING EQUATIONS OF ONE VARIABLE
 1 SOLVING EQUATIONS OF ONE VARIABLE ELM1222 Numerical Analysis Some of the contents are adopted from Laurene V. Fausett, Applied Numerical Analysis using MATLAB. Prentice Hall Inc., 1999 2 Today s lecture
1 SOLVING EQUATIONS OF ONE VARIABLE ELM1222 Numerical Analysis Some of the contents are adopted from Laurene V. Fausett, Applied Numerical Analysis using MATLAB. Prentice Hall Inc., 1999 2 Today s lecture
Intro to Scientific Computing: How long does it take to find a needle in a haystack?
 Intro to Scientific Computing: How long does it take to find a needle in a haystack? Dr. David M. Goulet Intro Binary Sorting Suppose that you have a detector that can tell you if a needle is in a haystack,
Intro to Scientific Computing: How long does it take to find a needle in a haystack? Dr. David M. Goulet Intro Binary Sorting Suppose that you have a detector that can tell you if a needle is in a haystack,
FIXED POINT ITERATION
 FIXED POINT ITERATION The idea of the fixed point iteration methods is to first reformulate a equation to an equivalent fixed point problem: f (x) = 0 x = g(x) and then to use the iteration: with an initial
FIXED POINT ITERATION The idea of the fixed point iteration methods is to first reformulate a equation to an equivalent fixed point problem: f (x) = 0 x = g(x) and then to use the iteration: with an initial
Bisection and False Position Dr. Marco A. Arocha Aug, 2014
 Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
Bisection and False Position Dr. Marco A. Arocha Aug, 2014 1 Given function f, we seek x values for which f(x)=0 Solution x is the root of the equation or zero of the function f Problem is known as root
MATH 4211/6211 Optimization Basics of Optimization Problems
 MATH 4211/6211 Optimization Basics of Optimization Problems Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 A standard minimization
MATH 4211/6211 Optimization Basics of Optimization Problems Xiaojing Ye Department of Mathematics & Statistics Georgia State University Xiaojing Ye, Math & Stat, Georgia State University 0 A standard minimization
Computational Methods CMSC/AMSC/MAPL 460. Solving nonlinear equations and zero finding. Finding zeroes of functions
 Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
Computational Methods CMSC/AMSC/MAPL 460 Solving nonlinear equations and zero finding Ramani Duraiswami, Dept. of Computer Science Where does it arise? Finding zeroes of functions Solving functional equations
Iterative Methods to Solve Systems of Nonlinear Algebraic Equations
 Western Kentucky University TopSCHOLAR Masters Theses & Specialist Projects Graduate School Spring 018 Iterative Methods to Solve Systems of Nonlinear Algebraic Equations Md Shafiful Alam Western Kentucky
Western Kentucky University TopSCHOLAR Masters Theses & Specialist Projects Graduate School Spring 018 Iterative Methods to Solve Systems of Nonlinear Algebraic Equations Md Shafiful Alam Western Kentucky
Solution of Nonlinear Equations
 Solution of Nonlinear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 14, 017 One of the most frequently occurring problems in scientific work is to find the roots of equations of the form f(x) = 0. (1)
Solution of Nonlinear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 14, 017 One of the most frequently occurring problems in scientific work is to find the roots of equations of the form f(x) = 0. (1)
Numerical Optimization
 Unconstrained Optimization (II) Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Unconstrained Optimization Let f : R R Unconstrained problem min x
Unconstrained Optimization (II) Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Unconstrained Optimization Let f : R R Unconstrained problem min x
Roots of Equations. ITCS 4133/5133: Introduction to Numerical Methods 1 Roots of Equations
 Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Roots of Equations Direct Search, Bisection Methods Regula Falsi, Secant Methods Newton-Raphson Method Zeros of Polynomials (Horner s, Muller s methods) EigenValue Analysis ITCS 4133/5133: Introduction
Nonlinear equations. Norms for R n. Convergence orders for iterative methods
 Nonlinear equations Norms for R n Assume that X is a vector space. A norm is a mapping X R with x such that for all x, y X, α R x = = x = αx = α x x + y x + y We define the following norms on the vector
Nonlinear equations Norms for R n Assume that X is a vector space. A norm is a mapping X R with x such that for all x, y X, α R x = = x = αx = α x x + y x + y We define the following norms on the vector
Today s class. Numerical differentiation Roots of equation Bracketing methods. Numerical Methods, Fall 2011 Lecture 4. Prof. Jinbo Bi CSE, UConn
 Today s class Numerical differentiation Roots of equation Bracketing methods 1 Numerical Differentiation Finite divided difference First forward difference First backward difference Lecture 3 2 Numerical
Today s class Numerical differentiation Roots of equation Bracketing methods 1 Numerical Differentiation Finite divided difference First forward difference First backward difference Lecture 3 2 Numerical
STOP, a i+ 1 is the desired root. )f(a i) > 0. Else If f(a i+ 1. Set a i+1 = a i+ 1 and b i+1 = b Else Set a i+1 = a i and b i+1 = a i+ 1
 53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
53 17. Lecture 17 Nonlinear Equations Essentially, the only way that one can solve nonlinear equations is by iteration. The quadratic formula enables one to compute the roots of p(x) = 0 when p P. Formulas
The Derivative of a Function Measuring Rates of Change of a function. Secant line. f(x) f(x 0 ) Average rate of change of with respect to over,
 The Derivative of a Function Measuring Rates of Change of a function y f(x) f(x 0 ) P Q Secant line x 0 x x Average rate of change of with respect to over, " " " " - Slope of secant line through, and,
The Derivative of a Function Measuring Rates of Change of a function y f(x) f(x 0 ) P Q Secant line x 0 x x Average rate of change of with respect to over, " " " " - Slope of secant line through, and,
MATH 2053 Calculus I Review for the Final Exam
 MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
Simple Iteration, cont d
 Jim Lambers MAT 772 Fall Semester 2010-11 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Simple Iteration, cont d In general, nonlinear equations cannot be solved in a finite sequence
Jim Lambers MAT 772 Fall Semester 2010-11 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Simple Iteration, cont d In general, nonlinear equations cannot be solved in a finite sequence
