tidissomsi D DC if: RELATIVE INVARIANTS AND CLOSURE HARD COPY MICROFICHE MEMORANDUM Q*^M-4209-ARPA ßmf&t&tfa«. Richard Eeliman and John M.
|
|
|
- Carmel Henry
- 5 years ago
- Views:
Transcription
1 if: f 7 f "--is o MEMORANDUM Q*^M-4209-ARPA *** OCTOBER 1964 ^> HARD COPY MICROFICHE ins> i<h«i ^^^.^-a^^^ RELATIVE INVARIANTS AND CLOSURE Richard Eeliman and John M. Richardson PREPARED FOR ADVANCED RESEARCH PROJECTS AGENCY D DC MOV tidissomsi DDC-IRÄ c 7^ ßmf&t&tfa«. SANTA MONICA CAltfO»NIA-
2 ARPA OROBR NO, l«8 «1 MEMORANDUM RM-4209-ARPA OCTOBER 1964 RELATIVE INVARIANTS AND CLOSURE Richard Bellman and John M. Richardson This research is supported by the Advarced Research Projects Agency under Contract /No. SD-79. Any views or conclusions contained in this Memorandun should not be interpreted as representing the official opinion or policy of ARPA. DDC AVAILABILITY NOTICE Qualified requesters may villain copies of this report from the Defence Documentation G-.ter (DDC). Ä nnr0 ve<i for nr? rpk^?* 9 IM 7^e rs"h I I [J foyteuut**»do M«!N S 1 janti KOMICA - Cki'.fQtNik. «O«'*
3 -lii- PREFAGE Part of the research program of The RAND Corporation consists of basic supporting studies in mathematics. This Memorandum presents a method for handling a problem that frequently arises in mathematical physics in connection with equations of heat, radiative transfer, etc., namely, that of replacing a system of nonlinear functional equations with one that is linear-
4 SUHKARY One of the basic problems of mathematical physics ie that of replacing a nonlinear functional equation by a more tractable (analytically and computationally^ linear equation. More generally, one wants to replace a system of nonlinear equations, often ierived from a single equation by means of an expansion in a parameter, an orthogonal expansion^ with a system of linear functional e<]uations. To treat this xlo^ure problem, the authors present a method basea upon the concept cf relative invariants and the use of the multidimensional Lagrange expansion theorem. /\ C ) />
5 -^11- CONTENTS PREFACE. lit SUMMARY v Section 1. INTRODUCTION 1 2. FINITE-DIMENSIONAL CASE 2 3. WHAT IS REQUIRED FOR THIS FORMALISM? 4 4. PRELIMINARY CLOSURE INFINITE-DIMENSIONAL CASE APPLICATION TO THE NONLINEAR HEAT EQUATION.. 7 REFERENCES 9
6 BLANK PAGE
7 RELATIVE INVARIANTS AND CLOSURE 1, INTRODUCTION One of the basic problems of mathematical physics is that of replacing a nonlinear functional equation by an analytically and computationally more tractable linear equation. More generally, the problem is that of replacing a system of nonlinear functional equations by a system of linear functional equations. Often this system of nonlinear equations Is derived from a single equation by means of an expansion in a parameter, or of an orthogonal expansion. Consider, for example, the nonlinear heat equation V-V u t ' u xx + u3 ' with the boundary and initial conditions (1.2) u(x,0) - g(x), 0 < x < 1, If we set u(0,t) - u(l,t) - 0, t > 0. oo (1.3) u = E u (t) sin mrx, n«! substitution in (1.1) yields the infinite system of nonlinear equations (1.4) u;(t).- n 2 u n +. ljn u 1 u j +... ) u n (0).g n, n 1,2,...,
8 " - i - where CD g(x) ^ E g sin nttx, n-1 n We now face the problem of closure (see [1], [2]), which is to say of replacing (1.4) by a finite system of equations, preferably linear. We shall present a method based upon the concept of relative invariants and the use of the imltidimensional Lagrange expansion theorem [2], [3]. In some cases, as in the case above, a preliminary use of approximation methods may be required. 2, FINITE^DIMENSIONAL CASE In order to illustrate the idea of relative invariants, let us first consider a finite system of nonlinear differential equations, say dx. (2.1) ctt 1 " - X i x i + gi< x )' x i (0) - c 1, i - 1,2,...,N, where we suppose that (2.2)(a) Re(X i ) > 0, (b) c. is sufficiently small, (c) g i (x) is a power series in the components of x beginning with quadratic terms. We shall impose another condition upon the X. in a moment.
9 -3- Our aim is to find N functions of the x^ {q)j(x)}, with the properties that d<p. (2.3) ^ = --X iv and (2.4) cp i (x) = x^^ + h i (x) J where the h.(x) are power series in the components of x beginning with quadratic terms. If such functions exist, we have, from (2.3), -X.t (2.5) ^(x) = e ^ cp^c), i * 1,2,...,N. Hence, the x. are obtained as solutions of these N simultaneous equations. Since from (2.4) these equations have the form -X.t (2.6) x i = e * cp i (c) - h^x), i = 1,2,...,N, we are in an ideal position to employ the multidimensional Lagrange expansion to obtain a power series expansion for A, t the x. in terms of the quantities e cp.(c). Cutting this off at any desired stage, we have the required closure. Furthermore, if we so wish, we can employ the Lagrange expansion theorem to calculate N additional functions ^ (x), i - 1,2,...,N, in place of the N functions x^x«,... ^x«.
10 -^ 3> WHAT IS REQITIRED FOR THIS FORMALISM? We mentioned above that a further condition upon the X. was required. In order to Gee how this arises, let us examine the problem of determining the functions '^OO of (2.3).. Write 2 2 (3.1) ^(x) = x i + a lli x 1 + 2a 12i x 1 x 2 + a^x^ +..., and let us restrict ourselves to the case 1=1. We have, dx, dx-, dx, (3.2) ^ ^(x) - ^ + 2a 111 x 1 ^- + 2a 121 ^ x 2 dx 2 dx 2 + 2a 121 x l 3F- + 2a 221 x 2^r + " "- X l x l + 8lll x l + gl2i x l x 2 + " + 2a 111 x 1 [- X 1 x 1 + g 111 x 2 + g^^x,, + - ] + 2a 121 x 2 [- X 1 x 1 + g 111 x2 + g 121 x lx2 +.. ] + 2a 12I x 1 [- X 2 x 2 +g 112 x ] + 2a 22l x 2^~ ' >t 2 x 2 + "'l' L-ät us concentrate solely upon first and second order terms, and, in particular, upon the determination of a Tiw a, 2,, and ^221* We ^^^ froit1 (3.2), (3.3) A ^(x) - - X^ + g ul x2 + g 121 x 1 x 2 + g 221 x X 1 a 111 x i - 2X x a 121 x l x 2 "" 2X 2 a 121 x l x 2 2X 2 a 221 x^
11 2 2 There are no other terms involving x^ ' K i x or 2 x 2' If (3.3) is to hold, for i - 1 we must ha/e, upon equating coefficients, (3.4) g 111-2X 1 a 1L1 = - X 1 a 111, s 121 " ^Xl + 2X 2 )a 121 = ~ X l a 121, s 221 " 2X 2 a 221 " ~ X l a 221* These relations determine the quantities ^ii* a T7ii a 29i uniquely, provided that (3.5) X, ^0, X 1 + 2X 2 ^ 0, 2X 2 - X 1 jfe 0. As far as the determination of all of the coefficients is concerned, we see that we have the condition (3.6) m i^l + m 2^2 + "* + ^^k ^ 0 ' for any nontrivial set of positive or negative integral or zero values of the m.. This is a frequently met condition. This condition is not merely a reflection of the weakness of the method. If, for example, (3.7) x i = - x i^ x i( 0 ) = c i' xl = - 2x 2 + Xp X2(0) - 02» "2t we see that a term of the tc enters. The functions t 2t x-, and Xj are not power series in e and e
12 Observe that we face this situation in treating (1.4), since here X «n X,. n 1 4. PRELIMINARY CLOSURE To avoid a violation of the condition in (3.6), we can use some preliminary closure techniques. Suppose, for example, that 2X X.. =0, which means Chat the third equation in (3.4) is troublesome unless Sooi an^ a««! are both zero. If gooi = 0> we ma y very simply Set a nni = 0» If ^991 ^ } We USe an a PP rox: i- mat i- on 2 technique to replace the g~«,x«by a linear combination of other terms appearing in the expansion of g.(x); see [1], Thus, we can set v^»-*-/ ^221 x 2 = c ll x l C 12 X 2 *'*' where the c., are to be determined by a least squares fit. Various self consistent methods can now be used. 5. INFINITE-DIMENSIONAL CASE Consider now the infinite system of ordinary differential equations dx. (5.1) g~ «- X 1 x i + g i (x), x i (w) - c i, i = 1,2,.., obtained from a nonlinear operator equation (5.2) u t «Au + g(u).
13 where we have used an expansion for u which diagonalizes the operator A. It is easy to see that if the condition of (3.6) is met, we can determine the coefficients of the function? cp. (x) recurrently, solving a single equation for a single unknown at each step. The determination of ^(x) can be carried as far as desired. The stopping ^ule is now a closure technique. Having determined the N functions ( ).(x), i 1,2,...,N, to some degree of accuracy, the N equations -X.t (5.3) cp i (x) - e L ^(c), i * 1,2,...,N, may be solved as indicated above, or in some other way, to yield the x., i = 1,2,...,N. We suppose in (5.3) that on the left-hand side, all terms involving x., i > N + 1, have been omitted. There are many variants of this procedure, each equivalent to a different closure method. 6. APPLICATION TO THE NONLINEAR HEAT EQUATION In applying this method to (1.4), we see that the first violation of (3.6) occurs in connection with the determination of fourth order terms in the functions tp. (x) (since X, = 4X,). Hence, if the deviation from linearity is small, or equivalently if max!g(x) is x small, the method sketched above will yield the second and third-order correction terms for the solution of
14 ^8- oo 2 t (6.1) u^cx^t) = I g e sin ntrx 1 n n-1 in a convenient fashion.
15 -9- REFEREFCES 1. Bellman, R,, and J. M. Richardson, "On Some Questions Arising in the Approximate Solution of Nonlinear Differential Equations," Q. Appl. Math., Vol. 20, 1963, pp Bellman, R., Perturbation Technicmes in Mathematics, Physics, and Engineering, 3blt, Rinehart ~än3 Winston, Inc., New York, 1964, 3. Good, I. J., "Generalizations to Several Variables of Lagrange's Expansion, with Applications to Stochastic Processes," Proc. Cambridge Phil. Soc, Vol. 56, 1960, pp. 36T?m:
ON ANALOGUES OF POINCARE-LYAPUNOV THEORY FOR MULTIPOINT BOUNDARY-VALUE PROBLEMS
 . MEMORANDUM RM-4717-PR SEPTEMBER 1965 ON ANALOGUES OF POINCARE-LYAPUNOV THEORY FOR MULTIPOINT BOUNDARY-VALUE PROBLEMS Richard Bellman This research is sponsored by the United StUes Air Force under Project
. MEMORANDUM RM-4717-PR SEPTEMBER 1965 ON ANALOGUES OF POINCARE-LYAPUNOV THEORY FOR MULTIPOINT BOUNDARY-VALUE PROBLEMS Richard Bellman This research is sponsored by the United StUes Air Force under Project
ON THE CONSTRUCTION OF
 ON THE CONSTRUCTION OF A MATHEMATICAL THEORY OF THE IDENTIFICATION OF SYSTEMS RICHARD BELLMAN THE RAND CORPORATION 1. Summary Let us consider a complex system consisting of a set of interacting subsystems.
ON THE CONSTRUCTION OF A MATHEMATICAL THEORY OF THE IDENTIFICATION OF SYSTEMS RICHARD BELLMAN THE RAND CORPORATION 1. Summary Let us consider a complex system consisting of a set of interacting subsystems.
[mill ^ DDC A NOTE ON THE SOLUTION OF POLYNOMIAL CONGRUENCES. 7^ RflOD (2ttji0uUcöH SANTA MONICA CALIFORNIA
 1 MEMORANDUM ^ RM-3898-PR 3 MARCH 1965 "COPY ^ A ^ f\ "> r» w A NOTE ON THE SOLUTION OF POLYNOMIAL CONGRUENCES Richard Bellman DDC MAR 2 9 196b I PREPARED FOR: UNITED STATES AIR FORCE PROJECT RAND DDCIRA
1 MEMORANDUM ^ RM-3898-PR 3 MARCH 1965 "COPY ^ A ^ f\ "> r» w A NOTE ON THE SOLUTION OF POLYNOMIAL CONGRUENCES Richard Bellman DDC MAR 2 9 196b I PREPARED FOR: UNITED STATES AIR FORCE PROJECT RAND DDCIRA
I-l~ARD COPY $ M IC R O F IC H E $ C V Q B -to R A N D U -- WENGERT S NUMIRICb MIT ORI PARIAL DRIVATIVS'O 'UNITED STATES AR FORCF'RJCTRN
 C V Q B -to R A N D U -- I-l~ARD COPY $ M IC R O F IC H E $ 4v,AB,-R1964 WENGERT S NUMIRICb MIT ORI PARIAL DRIVATIVS'O 1 ji~t ~PART ATODAE QTJASILINEARIZATIO DETFRMINTION ANR. Beilaan H. Iragiwada an~d
C V Q B -to R A N D U -- I-l~ARD COPY $ M IC R O F IC H E $ 4v,AB,-R1964 WENGERT S NUMIRICb MIT ORI PARIAL DRIVATIVS'O 1 ji~t ~PART ATODAE QTJASILINEARIZATIO DETFRMINTION ANR. Beilaan H. Iragiwada an~d
ON SOME QUESTIONS ARISING IN THE APPROXIMATE SOLUTION OF NONLINEAR DIFFERENTIAL EQUATIONS*
 333 ON SOME QUESTIONS ARISING IN THE APPROXIMATE SOLUTION OF NONLINEAR DIFFERENTIAL EQUATIONS* By R. BELLMAN, BAND Corporation, Santa Monica, California AND J. M. RICHARDSON, Hughes Research Laboratories,
333 ON SOME QUESTIONS ARISING IN THE APPROXIMATE SOLUTION OF NONLINEAR DIFFERENTIAL EQUATIONS* By R. BELLMAN, BAND Corporation, Santa Monica, California AND J. M. RICHARDSON, Hughes Research Laboratories,
BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES
 1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
^lüüfn mi. ünnsi DDC. ": i. a's'dw ON A NEW APPROACH TO- NUMERICAL SOLUTION OF A CLASS OF PARTIAL DIFFERENTIAL INTEGRAL EQUATIONS OF TRANSPORT THEORY
 m^^ ^" MEMORANDUM RM-4667-PR JULY 1965 Ci CD ": i. a's'dw ON A NEW APPROACH TO- NUMERICAL SOLUTION OF A CLASS OF PARTIAL DIFFERENTIAL INTEGRAL EQUATIONS OF TRANSPORT THEORY / H PREPARED FOR: UNITED STATES
m^^ ^" MEMORANDUM RM-4667-PR JULY 1965 Ci CD ": i. a's'dw ON A NEW APPROACH TO- NUMERICAL SOLUTION OF A CLASS OF PARTIAL DIFFERENTIAL INTEGRAL EQUATIONS OF TRANSPORT THEORY / H PREPARED FOR: UNITED STATES
ENGI 4430 PDEs - d Alembert Solutions Page 11.01
 ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 4430 PDEs - d Alembert Solutions Page 11.01 11. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients
 Cent. Eur. J. Eng. 4 24 64-7 DOI:.2478/s353-3-4-6 Central European Journal of Engineering The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients
Cent. Eur. J. Eng. 4 24 64-7 DOI:.2478/s353-3-4-6 Central European Journal of Engineering The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients
Sufficient conditions for functions to form Riesz bases in L 2 and applications to nonlinear boundary-value problems
 Electronic Journal of Differential Equations, Vol. 200(200), No. 74, pp. 0. ISSN: 072-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Sufficient conditions
Electronic Journal of Differential Equations, Vol. 200(200), No. 74, pp. 0. ISSN: 072-669. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu (login: ftp) Sufficient conditions
UNCLASSIFIED UNCLASSIFIED DEFENSE DOCUMENTATION CENTER SCIENTIFK AND TECHNICAL INFORMATION FOR CAMEROW STATION, ALEXANDRIA, VIRGINIA
 UNCLASSIFIED AD 4384 38 DEFENSE DOCUMENTATION CENTER FOR SCIENTIFK AND TECHNICAL INFORMATION CAMEROW STATION, ALEXANDRIA, VIRGINIA UNCLASSIFIED _ NOTICE: When government or other dravings, specifications
UNCLASSIFIED AD 4384 38 DEFENSE DOCUMENTATION CENTER FOR SCIENTIFK AND TECHNICAL INFORMATION CAMEROW STATION, ALEXANDRIA, VIRGINIA UNCLASSIFIED _ NOTICE: When government or other dravings, specifications
minimize x subject to (x 2)(x 4) u,
 Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Math 5311 Constrained Optimization Notes
 ath 5311 Constrained Optimization otes February 5, 2009 1 Equality-constrained optimization Real-world optimization problems frequently have constraints on their variables. Constraints may be equality
ath 5311 Constrained Optimization otes February 5, 2009 1 Equality-constrained optimization Real-world optimization problems frequently have constraints on their variables. Constraints may be equality
Chapter 4: Interpolation and Approximation. October 28, 2005
 Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 27 (2011), ISSN
 Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 27 20, 233 243 www.emis.de/journals ISSN 786-009 CERTAIN ESTIMATES FOR DOUBLE SINE SERIES WITH MULTIPLE-MONOTONE COEFFICIENTS XHEVAT Z. KRASNIQI
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 27 20, 233 243 www.emis.de/journals ISSN 786-009 CERTAIN ESTIMATES FOR DOUBLE SINE SERIES WITH MULTIPLE-MONOTONE COEFFICIENTS XHEVAT Z. KRASNIQI
CONTROL SYSTEMS, ROBOTICS AND AUTOMATION Vol. XI Stochastic Stability - H.J. Kushner
 STOCHASTIC STABILITY H.J. Kushner Applied Mathematics, Brown University, Providence, RI, USA. Keywords: stability, stochastic stability, random perturbations, Markov systems, robustness, perturbed systems,
STOCHASTIC STABILITY H.J. Kushner Applied Mathematics, Brown University, Providence, RI, USA. Keywords: stability, stochastic stability, random perturbations, Markov systems, robustness, perturbed systems,
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae Pavel Drábek Remarks on multiple periodic solutions of nonlinear ordinary differential equations Commentationes Mathematicae Universitatis Carolinae,
Commentationes Mathematicae Universitatis Carolinae Pavel Drábek Remarks on multiple periodic solutions of nonlinear ordinary differential equations Commentationes Mathematicae Universitatis Carolinae,
Math 2930 Worksheet Final Exam Review
 Math 293 Worksheet Final Exam Review Week 14 November 3th, 217 Question 1. (* Solve the initial value problem y y = 2xe x, y( = 1 Question 2. (* Consider the differential equation: y = y y 3. (a Find the
Math 293 Worksheet Final Exam Review Week 14 November 3th, 217 Question 1. (* Solve the initial value problem y y = 2xe x, y( = 1 Question 2. (* Consider the differential equation: y = y y 3. (a Find the
EN Applied Optimal Control Lecture 8: Dynamic Programming October 10, 2018
 EN530.603 Applied Optimal Control Lecture 8: Dynamic Programming October 0, 08 Lecturer: Marin Kobilarov Dynamic Programming (DP) is conerned with the computation of an optimal policy, i.e. an optimal
EN530.603 Applied Optimal Control Lecture 8: Dynamic Programming October 0, 08 Lecturer: Marin Kobilarov Dynamic Programming (DP) is conerned with the computation of an optimal policy, i.e. an optimal
New Identities for Weak KAM Theory
 New Identities for Weak KAM Theory Lawrence C. Evans Department of Mathematics University of California, Berkeley Abstract This paper records for the Hamiltonian H = p + W (x) some old and new identities
New Identities for Weak KAM Theory Lawrence C. Evans Department of Mathematics University of California, Berkeley Abstract This paper records for the Hamiltonian H = p + W (x) some old and new identities
ON THE MAXIMUM OF A NORMAL STATIONARY STOCHASTIC PROCESS 1 BY HARALD CRAMER. Communicated by W. Feller, May 1, 1962
 ON THE MAXIMUM OF A NORMAL STATIONARY STOCHASTIC PROCESS 1 BY HARALD CRAMER Communicated by W. Feller, May 1, 1962 1. Let x(t) with oo
ON THE MAXIMUM OF A NORMAL STATIONARY STOCHASTIC PROCESS 1 BY HARALD CRAMER Communicated by W. Feller, May 1, 1962 1. Let x(t) with oo
ENGI 9420 Lecture Notes 8 - PDEs Page 8.01
 ENGI 940 Lecture Notes 8 - PDEs Page 8.01 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 940 Lecture Notes 8 - PDEs Page 8.01 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
COEFFICIENTS OF VISCOSITY FOR A FLUID IN A MAGNETIC FIELD OR IN A ROTATING SYSTEM
 Hooyman, G.J. Physica XXI Mazur, P. " 355-359 Groot, S. R. de 1955 COEFFICIENTS OF VISCOSITY FOR A FLUID IN A MAGNETIC FIELD OR IN A ROTATING SYSTEM by G. J. HOOYMAN, P. MAZUR and S. R. DE GROOT Instituut
Hooyman, G.J. Physica XXI Mazur, P. " 355-359 Groot, S. R. de 1955 COEFFICIENTS OF VISCOSITY FOR A FLUID IN A MAGNETIC FIELD OR IN A ROTATING SYSTEM by G. J. HOOYMAN, P. MAZUR and S. R. DE GROOT Instituut
NOTICE WARNING CONCERNING COPYRIGHT RESTRICTIONS: The copyright law of the United States (title 17, U.S. Code) governs the making of photocopies or
 NOTICE WARNING CONCERNING COPYRIGHT RESTRICTIONS: The copyright law of the United States (title 17, U.S. Code) governs the making of photocopies or other reproductions of copyrighted material. Any copying
NOTICE WARNING CONCERNING COPYRIGHT RESTRICTIONS: The copyright law of the United States (title 17, U.S. Code) governs the making of photocopies or other reproductions of copyrighted material. Any copying
PHYS 410/555 Computational Physics Solution of Non Linear Equations (a.k.a. Root Finding) (Reference Numerical Recipes, 9.0, 9.1, 9.
 PHYS 410/555 Computational Physics Solution of Non Linear Equations (a.k.a. Root Finding) (Reference Numerical Recipes, 9.0, 9.1, 9.4) We will consider two cases 1. f(x) = 0 1-dimensional 2. f(x) = 0 d-dimensional
PHYS 410/555 Computational Physics Solution of Non Linear Equations (a.k.a. Root Finding) (Reference Numerical Recipes, 9.0, 9.1, 9.4) We will consider two cases 1. f(x) = 0 1-dimensional 2. f(x) = 0 d-dimensional
::::: OFTECHY. .0D 0 ::: ::_ I;. :.!:: t;0i f::t l. :- - :.. :?:: : ;. :--- :-.-i. .. r : : a o er -,:I :,--:-':: : :.:
 ,-..., -. :', ; -:._.'...,..-.-'3.-..,....; i b... {'.'',,,.!.C.,..'":',-...,'. ''.>.. r : : a o er.;,,~~~~~~~~~~~~~~~~~~~~~~~~~.'. -...~..........".: ~ WS~ "'.; :0:_: :"_::.:.0D 0 ::: ::_ I;. :.!:: t;0i
,-..., -. :', ; -:._.'...,..-.-'3.-..,....; i b... {'.'',,,.!.C.,..'":',-...,'. ''.>.. r : : a o er.;,,~~~~~~~~~~~~~~~~~~~~~~~~~.'. -...~..........".: ~ WS~ "'.; :0:_: :"_::.:.0D 0 ::: ::_ I;. :.!:: t;0i
Plot of temperature u versus x and t for the heat conduction problem of. ln(80/π) = 820 sec. τ = 2500 π 2. + xu t. = 0 3. u xx. + u xt 4.
 10.5 Separation of Variables; Heat Conduction in a Rod 579 u 20 15 10 5 10 50 20 100 30 150 40 200 50 300 x t FIGURE 10.5.5 Example 1. Plot of temperature u versus x and t for the heat conduction problem
10.5 Separation of Variables; Heat Conduction in a Rod 579 u 20 15 10 5 10 50 20 100 30 150 40 200 50 300 x t FIGURE 10.5.5 Example 1. Plot of temperature u versus x and t for the heat conduction problem
Interpolation and Cubature at Geronimus Nodes Generated by Different Geronimus Polynomials
 Interpolation and Cubature at Geronimus Nodes Generated by Different Geronimus Polynomials Lawrence A. Harris Abstract. We extend the definition of Geronimus nodes to include pairs of real numbers where
Interpolation and Cubature at Geronimus Nodes Generated by Different Geronimus Polynomials Lawrence A. Harris Abstract. We extend the definition of Geronimus nodes to include pairs of real numbers where
g(t) = f(x 1 (t),..., x n (t)).
 Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Math 108b: Notes on the Spectral Theorem
 Math 108b: Notes on the Spectral Theorem From section 6.3, we know that every linear operator T on a finite dimensional inner product space V has an adjoint. (T is defined as the unique linear operator
Math 108b: Notes on the Spectral Theorem From section 6.3, we know that every linear operator T on a finite dimensional inner product space V has an adjoint. (T is defined as the unique linear operator
Math 220a - Fall 2002 Homework 6 Solutions
 Math a - Fall Homework 6 Solutions. Use the method of reflection to solve the initial-boundary value problem on the interval < x < l, u tt c u xx = < x < l u(x, = < x < l u t (x, = x < x < l u(, t = =
Math a - Fall Homework 6 Solutions. Use the method of reflection to solve the initial-boundary value problem on the interval < x < l, u tt c u xx = < x < l u(x, = < x < l u t (x, = x < x < l u(, t = =
ENGI 9420 Lecture Notes 8 - PDEs Page 8.01
 ENGI 940 ecture Notes 8 - PDEs Page 8.0 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 940 ecture Notes 8 - PDEs Page 8.0 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
Optimal control problems with PDE constraints
 Optimal control problems with PDE constraints Maya Neytcheva CIM, October 2017 General framework Unconstrained optimization problems min f (q) q x R n (real vector) and f : R n R is a smooth function.
Optimal control problems with PDE constraints Maya Neytcheva CIM, October 2017 General framework Unconstrained optimization problems min f (q) q x R n (real vector) and f : R n R is a smooth function.
PRE-LEAVING CERTIFICATE EXAMINATION, 2010
 L.7 PRE-LEAVING CERTIFICATE EXAMINATION, 00 MATHEMATICS HIGHER LEVEL PAPER (300 marks) TIME : ½ HOURS Attempt SIX QUESTIONS (50 marks each). WARNING: Marks will be lost if all necessary work is not clearly
L.7 PRE-LEAVING CERTIFICATE EXAMINATION, 00 MATHEMATICS HIGHER LEVEL PAPER (300 marks) TIME : ½ HOURS Attempt SIX QUESTIONS (50 marks each). WARNING: Marks will be lost if all necessary work is not clearly
A NEW NORMAL FORM FOR QUARTIC EQUATIONS*
 310 RAYMOND GARVER (May-June, A NEW NORMAL FORM FOR QUARTIC EQUATIONS* BY RAYMOND GARVER 1. Introduction. There are a number of well known normal forms to which the general quartic equation may be reduced
310 RAYMOND GARVER (May-June, A NEW NORMAL FORM FOR QUARTIC EQUATIONS* BY RAYMOND GARVER 1. Introduction. There are a number of well known normal forms to which the general quartic equation may be reduced
Time-optimal control of a 3-level quantum system and its generalization to an n-level system
 Proceedings of the 7 American Control Conference Marriott Marquis Hotel at Times Square New York City, USA, July 11-13, 7 Time-optimal control of a 3-level quantum system and its generalization to an n-level
Proceedings of the 7 American Control Conference Marriott Marquis Hotel at Times Square New York City, USA, July 11-13, 7 Time-optimal control of a 3-level quantum system and its generalization to an n-level
The Bock iteration for the ODE estimation problem
 he Bock iteration for the ODE estimation problem M.R.Osborne Contents 1 Introduction 2 2 Introducing the Bock iteration 5 3 he ODE estimation problem 7 4 he Bock iteration for the smoothing problem 12
he Bock iteration for the ODE estimation problem M.R.Osborne Contents 1 Introduction 2 2 Introducing the Bock iteration 5 3 he ODE estimation problem 7 4 he Bock iteration for the smoothing problem 12
Explicit solution of a class of quartic Thue equations
 ACTA ARITHMETICA LXIV.3 (1993) Explicit solution of a class of quartic Thue equations by Nikos Tzanakis (Iraklion) 1. Introduction. In this paper we deal with the efficient solution of a certain interesting
ACTA ARITHMETICA LXIV.3 (1993) Explicit solution of a class of quartic Thue equations by Nikos Tzanakis (Iraklion) 1. Introduction. In this paper we deal with the efficient solution of a certain interesting
Absorbing Boundary Conditions for Nonlinear Wave Equations
 Absorbing Boundary Conditions for Nonlinear Wave Equations R. B. Gibson December, 2010 1 1 Linear Wave Equations 1.1 Boundary Condition 1 To begin, we wish to solve where with the boundary condition u
Absorbing Boundary Conditions for Nonlinear Wave Equations R. B. Gibson December, 2010 1 1 Linear Wave Equations 1.1 Boundary Condition 1 To begin, we wish to solve where with the boundary condition u
1 Matrices and vector spaces
 Matrices and vector spaces. Which of the following statements about linear vector spaces are true? Where a statement is false, give a counter-example to demonstrate this. (a) Non-singular N N matrices
Matrices and vector spaces. Which of the following statements about linear vector spaces are true? Where a statement is false, give a counter-example to demonstrate this. (a) Non-singular N N matrices
PH.D. PRELIMINARY EXAMINATION MATHEMATICS
 UNIVERSITY OF CALIFORNIA, BERKELEY Dept. of Civil and Environmental Engineering FALL SEMESTER 2014 Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
UNIVERSITY OF CALIFORNIA, BERKELEY Dept. of Civil and Environmental Engineering FALL SEMESTER 2014 Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
On the Periodic Solutions of Certain Fifth Order Nonlinear Vector Differential Equations
 On the Periodic Solutions of Certain Fifth Order Nonlinear Vector Differential Equations Melike Karta Department of Mathematics, Faculty of Science and Arts, Agri Ibrahim Cecen University, Agri, E-mail:
On the Periodic Solutions of Certain Fifth Order Nonlinear Vector Differential Equations Melike Karta Department of Mathematics, Faculty of Science and Arts, Agri Ibrahim Cecen University, Agri, E-mail:
JUST THE MATHS UNIT NUMBER 1.5. ALGEBRA 5 (Manipulation of algebraic expressions) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1.5 ALGEBRA 5 (Manipulation of algebraic expressions) by A.J.Hobson 1.5.1 Simplification of expressions 1.5.2 Factorisation 1.5.3 Completing the square in a quadratic expression
JUST THE MATHS UNIT NUMBER 1.5 ALGEBRA 5 (Manipulation of algebraic expressions) by A.J.Hobson 1.5.1 Simplification of expressions 1.5.2 Factorisation 1.5.3 Completing the square in a quadratic expression
Introduction to Finite Di erence Methods
 Introduction to Finite Di erence Methods ME 448/548 Notes Gerald Recktenwald Portland State University Department of Mechanical Engineering gerry@pdx.edu ME 448/548: Introduction to Finite Di erence Approximation
Introduction to Finite Di erence Methods ME 448/548 Notes Gerald Recktenwald Portland State University Department of Mechanical Engineering gerry@pdx.edu ME 448/548: Introduction to Finite Di erence Approximation
r OF / in < > O .1^ Jl DDC /?/ / P-1176 Revised ODC-IRA B FUNCTIONAL APPROXIMATIONS AND DYNAMIC PROGRAMMINO Richard Bellman Stuart Dreyfua
 or ^ * in < > O
or ^ * in < > O
Simplified Application of Lighthill's Uniformization Technique Using Lagrange Expansion Formulas
 /. Inst. Maths Applies (1967) 3, 16-20 Simplified Application of Lighthill's Uniformization Technique Using Lagrange Expansion Formulas E. DALE MARTIN National Aeronautics and Space Administration, Ames
/. Inst. Maths Applies (1967) 3, 16-20 Simplified Application of Lighthill's Uniformization Technique Using Lagrange Expansion Formulas E. DALE MARTIN National Aeronautics and Space Administration, Ames
CS 450 Numerical Analysis. Chapter 8: Numerical Integration and Differentiation
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS
 CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
PELL S EQUATION, II KEITH CONRAD
 PELL S EQUATION, II KEITH CONRAD 1. Introduction In Part I we met Pell s equation x dy = 1 for nonsquare positive integers d. We stated Lagrange s theorem that every Pell equation has a nontrivial solution
PELL S EQUATION, II KEITH CONRAD 1. Introduction In Part I we met Pell s equation x dy = 1 for nonsquare positive integers d. We stated Lagrange s theorem that every Pell equation has a nontrivial solution
Lagrange Multipliers
 Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
NUMERICAL SIMULATION OF THE TAYLOR-GREEN VORTEX
 NUMERICAL SIMULATION OF THE TAYLOR-GREEN VORTEX Steven A. Orszaq Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts, 02139 U.S.A. INTRODUCTION In a classic paper~
NUMERICAL SIMULATION OF THE TAYLOR-GREEN VORTEX Steven A. Orszaq Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts, 02139 U.S.A. INTRODUCTION In a classic paper~
UNCLASSIFIED. .n ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED
 UNCLASSIFIED.n 260610 ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications or other data are
UNCLASSIFIED.n 260610 ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications or other data are
Ch 10.1: Two Point Boundary Value Problems
 Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
Ch 10.1: Two Point Boundary Value Problems In many important physical problems there are two or more independent variables, so the corresponding mathematical models involve partial differential equations.
PH.D. PRELIMINARY EXAMINATION MATHEMATICS
 UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem.
 STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
Mem. Differential Equations Math. Phys. 36 (2005), T. Kiguradze
 Mem. Differential Equations Math. Phys. 36 (2005), 42 46 T. Kiguradze and EXISTENCE AND UNIQUENESS THEOREMS ON PERIODIC SOLUTIONS TO MULTIDIMENSIONAL LINEAR HYPERBOLIC EQUATIONS (Reported on June 20, 2005)
Mem. Differential Equations Math. Phys. 36 (2005), 42 46 T. Kiguradze and EXISTENCE AND UNIQUENESS THEOREMS ON PERIODIC SOLUTIONS TO MULTIDIMENSIONAL LINEAR HYPERBOLIC EQUATIONS (Reported on June 20, 2005)
Information Structures Preserved Under Nonlinear Time-Varying Feedback
 Information Structures Preserved Under Nonlinear Time-Varying Feedback Michael Rotkowitz Electrical Engineering Royal Institute of Technology (KTH) SE-100 44 Stockholm, Sweden Email: michael.rotkowitz@ee.kth.se
Information Structures Preserved Under Nonlinear Time-Varying Feedback Michael Rotkowitz Electrical Engineering Royal Institute of Technology (KTH) SE-100 44 Stockholm, Sweden Email: michael.rotkowitz@ee.kth.se
Cambridge International Examinations Cambridge Ordinary Level
 www.onlineexamhelp.com Cambridge International Examinations Cambridge Ordinary Level * 2 4 5 9 7 1 6 2 7 8 * ADDITIONAL MATHEMATICS 4037/21 Paper 2 May/June 2014 2 hours Candidates answer on the Question
www.onlineexamhelp.com Cambridge International Examinations Cambridge Ordinary Level * 2 4 5 9 7 1 6 2 7 8 * ADDITIONAL MATHEMATICS 4037/21 Paper 2 May/June 2014 2 hours Candidates answer on the Question
Examination paper for TMA4215 Numerical Mathematics
 Department of Mathematical Sciences Examination paper for TMA425 Numerical Mathematics Academic contact during examination: Trond Kvamsdal Phone: 93058702 Examination date: 6th of December 207 Examination
Department of Mathematical Sciences Examination paper for TMA425 Numerical Mathematics Academic contact during examination: Trond Kvamsdal Phone: 93058702 Examination date: 6th of December 207 Examination
Chapter 2 Optimal Control Problem
 Chapter 2 Optimal Control Problem Optimal control of any process can be achieved either in open or closed loop. In the following two chapters we concentrate mainly on the first class. The first chapter
Chapter 2 Optimal Control Problem Optimal control of any process can be achieved either in open or closed loop. In the following two chapters we concentrate mainly on the first class. The first chapter
Existence and Uniqueness
 Chapter 3 Existence and Uniqueness An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect
Chapter 3 Existence and Uniqueness An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect
Path integrals in quantum mechanics
 Path integrals in quantum mechanics Phys V3500/G8099 handout #1 References: there s a nice discussion of this material in the first chapter of L.S. Schulman, Techniques and applications of path integration.
Path integrals in quantum mechanics Phys V3500/G8099 handout #1 References: there s a nice discussion of this material in the first chapter of L.S. Schulman, Techniques and applications of path integration.
Preliminary algebra. Polynomial equations. and three real roots altogether. Continue an investigation of its properties as follows.
 978-0-51-67973- - Student Solutions Manual for Mathematical Methods for Physics and Engineering: 1 Preliminary algebra Polynomial equations 1.1 It can be shown that the polynomial g(x) =4x 3 +3x 6x 1 has
978-0-51-67973- - Student Solutions Manual for Mathematical Methods for Physics and Engineering: 1 Preliminary algebra Polynomial equations 1.1 It can be shown that the polynomial g(x) =4x 3 +3x 6x 1 has
Coherent and Incoherent Multiple Scattering of Light in Sea Water
 :.-,-... v...~,i:,*-s->:v-=-s -f^«' -i.i-v fwf- «' V-' '.rt'' "/»m'.f '"-.'«TiW^!^.,,.,, ARPA ORDER NO.: 189-1 CO R-778-ARPA August 1971 I'M "^S? Coherent and Incoherent Multiple Scattering of Light in
:.-,-... v...~,i:,*-s->:v-=-s -f^«' -i.i-v fwf- «' V-' '.rt'' "/»m'.f '"-.'«TiW^!^.,,.,, ARPA ORDER NO.: 189-1 CO R-778-ARPA August 1971 I'M "^S? Coherent and Incoherent Multiple Scattering of Light in
MATH 251 Final Examination August 14, 2015 FORM A. Name: Student Number: Section:
 MATH 251 Final Examination August 14, 2015 FORM A Name: Student Number: Section: This exam has 11 questions for a total of 150 points. Show all your work! In order to obtain full credit for partial credit
MATH 251 Final Examination August 14, 2015 FORM A Name: Student Number: Section: This exam has 11 questions for a total of 150 points. Show all your work! In order to obtain full credit for partial credit
EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD
 Stochastic Modeling and Applications Vol.21 No. 1(June 2017) 23-30 EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD RAHMATULLAH IBRAHIM NURUDDEEN AND AMINU M. NASS* Abstract. This
Stochastic Modeling and Applications Vol.21 No. 1(June 2017) 23-30 EXACT SOLUTIONS OF WAVE-TYPE EQUATIONS BY THE ABOODH DECOMPOSITION METHOD RAHMATULLAH IBRAHIM NURUDDEEN AND AMINU M. NASS* Abstract. This
Math 118, Fall 2014 Final Exam
 Math 8, Fall 4 Final Exam True or false Please circle your choice; no explanation is necessary True There is a linear transformation T such that T e ) = e and T e ) = e Solution Since T is linear, if T
Math 8, Fall 4 Final Exam True or false Please circle your choice; no explanation is necessary True There is a linear transformation T such that T e ) = e and T e ) = e Solution Since T is linear, if T
df(x) = h(x) dx Chemistry 4531 Mathematical Preliminaries Spring 2009 I. A Primer on Differential Equations Order of differential equation
 Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
On the N-tuple Wave Solutions of the Korteweg-de Vnes Equation
 Publ. RIMS, Kyoto Univ. 8 (1972/73), 419-427 On the N-tuple Wave Solutions of the Korteweg-de Vnes Equation By Shunichi TANAKA* 1. Introduction In this paper, we discuss properties of the N-tuple wave
Publ. RIMS, Kyoto Univ. 8 (1972/73), 419-427 On the N-tuple Wave Solutions of the Korteweg-de Vnes Equation By Shunichi TANAKA* 1. Introduction In this paper, we discuss properties of the N-tuple wave
13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs)
 13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs) A prototypical problem we will discuss in detail is the 1D diffusion equation u t = Du xx < x < l, t > finite-length rod u(x,
13 PDEs on spatially bounded domains: initial boundary value problems (IBVPs) A prototypical problem we will discuss in detail is the 1D diffusion equation u t = Du xx < x < l, t > finite-length rod u(x,
The Chebyshev Collection Method for Solving Fractional Order Klein-Gordon Equation
 The Chebyshev Collection Method for Solving Fractional Order Klein-Gordon Equation M. M. KHADER Faculty of Science, Benha University Department of Mathematics Benha EGYPT mohamedmbd@yahoo.com N. H. SWETLAM
The Chebyshev Collection Method for Solving Fractional Order Klein-Gordon Equation M. M. KHADER Faculty of Science, Benha University Department of Mathematics Benha EGYPT mohamedmbd@yahoo.com N. H. SWETLAM
256 Summary. D n f(x j ) = f j+n f j n 2n x. j n=1. α m n = 2( 1) n (m!) 2 (m n)!(m + n)!. PPW = 2π k x 2 N + 1. i=0?d i,j. N/2} N + 1-dim.
 56 Summary High order FD Finite-order finite differences: Points per Wavelength: Number of passes: D n f(x j ) = f j+n f j n n x df xj = m α m dx n D n f j j n= α m n = ( ) n (m!) (m n)!(m + n)!. PPW =
56 Summary High order FD Finite-order finite differences: Points per Wavelength: Number of passes: D n f(x j ) = f j+n f j n n x df xj = m α m dx n D n f j j n= α m n = ( ) n (m!) (m n)!(m + n)!. PPW =
Background and Definitions...2. Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and Functions...
 Legendre Polynomials and Functions Reading Problems Outline Background and Definitions...2 Definitions...3 Theory...4 Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and
Legendre Polynomials and Functions Reading Problems Outline Background and Definitions...2 Definitions...3 Theory...4 Legendre s Equation, Functions and Polynomials...4 Legendre s Associated Equation and
Mechanical Systems II. Method of Lagrange Multipliers
 Mechanical Systems II. Method of Lagrange Multipliers Rafael Wisniewski Aalborg University Abstract. So far our approach to classical mechanics was limited to finding a critical point of a certain functional.
Mechanical Systems II. Method of Lagrange Multipliers Rafael Wisniewski Aalborg University Abstract. So far our approach to classical mechanics was limited to finding a critical point of a certain functional.
An Application to Growth Theory
 An Application to Growth Theory First let s review the concepts of solution function and value function for a maximization problem. Suppose we have the problem max F (x, α) subject to G(x, β) 0, (P) x
An Application to Growth Theory First let s review the concepts of solution function and value function for a maximization problem. Suppose we have the problem max F (x, α) subject to G(x, β) 0, (P) x
Department of Applied Mathematics Faculty of EEMCS. University of Twente. Memorandum No Birth-death processes with killing
 Department of Applied Mathematics Faculty of EEMCS t University of Twente The Netherlands P.O. Box 27 75 AE Enschede The Netherlands Phone: +3-53-48934 Fax: +3-53-48934 Email: memo@math.utwente.nl www.math.utwente.nl/publications
Department of Applied Mathematics Faculty of EEMCS t University of Twente The Netherlands P.O. Box 27 75 AE Enschede The Netherlands Phone: +3-53-48934 Fax: +3-53-48934 Email: memo@math.utwente.nl www.math.utwente.nl/publications
Recurrence Relations and Fast Algorithms
 Recurrence Relations and Fast Algorithms Mark Tygert Research Report YALEU/DCS/RR-343 December 29, 2005 Abstract We construct fast algorithms for decomposing into and reconstructing from linear combinations
Recurrence Relations and Fast Algorithms Mark Tygert Research Report YALEU/DCS/RR-343 December 29, 2005 Abstract We construct fast algorithms for decomposing into and reconstructing from linear combinations
MA 201: Method of Separation of Variables Finite Vibrating String Problem Lecture - 11 MA201(2016): PDE
 MA 201: Method of Separation of Variables Finite Vibrating String Problem ecture - 11 IBVP for Vibrating string with no external forces We consider the problem in a computational domain (x,t) [0,] [0,
MA 201: Method of Separation of Variables Finite Vibrating String Problem ecture - 11 IBVP for Vibrating string with no external forces We consider the problem in a computational domain (x,t) [0,] [0,
ON THE "BANG-BANG" CONTROL PROBLEM*
 11 ON THE "BANG-BANG" CONTROL PROBLEM* BY R. BELLMAN, I. GLICKSBERG AND O. GROSS The RAND Corporation, Santa Monica, Calif. Summary. Let S be a physical system whose state at any time is described by an
11 ON THE "BANG-BANG" CONTROL PROBLEM* BY R. BELLMAN, I. GLICKSBERG AND O. GROSS The RAND Corporation, Santa Monica, Calif. Summary. Let S be a physical system whose state at any time is described by an
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
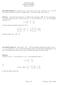 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Introduction. 5-Steps Method : 1. Question. 2. Approach. 3. Formulate. 4. Solve. 5. Interpret
 Introduction 5-Steps Method : 1. Question 2. Approach 3. Formulate 4. Solve 5. Interpret Example #1 A PC manufacturer currently sells 10,000 units/ month of a certain model. The manufacturing cost is $
Introduction 5-Steps Method : 1. Question 2. Approach 3. Formulate 4. Solve 5. Interpret Example #1 A PC manufacturer currently sells 10,000 units/ month of a certain model. The manufacturing cost is $
Optimal Control. Lecture 18. Hamilton-Jacobi-Bellman Equation, Cont. John T. Wen. March 29, Ref: Bryson & Ho Chapter 4.
 Optimal Control Lecture 18 Hamilton-Jacobi-Bellman Equation, Cont. John T. Wen Ref: Bryson & Ho Chapter 4. March 29, 2004 Outline Hamilton-Jacobi-Bellman (HJB) Equation Iterative solution of HJB Equation
Optimal Control Lecture 18 Hamilton-Jacobi-Bellman Equation, Cont. John T. Wen Ref: Bryson & Ho Chapter 4. March 29, 2004 Outline Hamilton-Jacobi-Bellman (HJB) Equation Iterative solution of HJB Equation
The backward continued fraction map and geodesic flow
 Ergod. Th. & Dynam. Sys. (1984), 4, 487-492 Printed in Great Britain The backward continued fraction map and geodesic flow ROY L. ADLER AND LEOPOLD FLATTO IBM Thomas J. Watson Research Center, Yorktown
Ergod. Th. & Dynam. Sys. (1984), 4, 487-492 Printed in Great Britain The backward continued fraction map and geodesic flow ROY L. ADLER AND LEOPOLD FLATTO IBM Thomas J. Watson Research Center, Yorktown
T ((x 1, x 2,..., x n )) = + x x 3. , x 1. x 3. Each of the four coordinates in the range is a linear combination of the three variables x 1
 MATH 37 Linear Transformations from Rn to Rm Dr. Neal, WKU Let T : R n R m be a function which maps vectors from R n to R m. Then T is called a linear transformation if the following two properties are
MATH 37 Linear Transformations from Rn to Rm Dr. Neal, WKU Let T : R n R m be a function which maps vectors from R n to R m. Then T is called a linear transformation if the following two properties are
MATH 251 Final Examination May 3, 2017 FORM A. Name: Student Number: Section:
 MATH 5 Final Examination May 3, 07 FORM A Name: Student Number: Section: This exam has 6 questions for a total of 50 points. In order to obtain full credit for partial credit problems, all work must be
MATH 5 Final Examination May 3, 07 FORM A Name: Student Number: Section: This exam has 6 questions for a total of 50 points. In order to obtain full credit for partial credit problems, all work must be
Handout 1: Introduction to Dynamic Programming. 1 Dynamic Programming: Introduction and Examples
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 1: Introduction to Dynamic Programming Instructor: Shiqian Ma January 6, 2014 Suggested Reading: Sections 1.1 1.5 of Chapter
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 1: Introduction to Dynamic Programming Instructor: Shiqian Ma January 6, 2014 Suggested Reading: Sections 1.1 1.5 of Chapter
UNCLASSIFIED. An QepAaduced. by ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED
 UNCLASSIFIED An 297 954 QepAaduced by ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
UNCLASSIFIED An 297 954 QepAaduced by ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
5 Handling Constraints
 5 Handling Constraints Engineering design optimization problems are very rarely unconstrained. Moreover, the constraints that appear in these problems are typically nonlinear. This motivates our interest
5 Handling Constraints Engineering design optimization problems are very rarely unconstrained. Moreover, the constraints that appear in these problems are typically nonlinear. This motivates our interest
OR MSc Maths Revision Course
 OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
MATH 241 Practice Second Midterm Exam - Fall 2012
 MATH 41 Practice Second Midterm Exam - Fall 1 1. Let f(x = { 1 x for x 1 for 1 x (a Compute the Fourier sine series of f(x. The Fourier sine series is b n sin where b n = f(x sin dx = 1 = (1 x cos = 4
MATH 41 Practice Second Midterm Exam - Fall 1 1. Let f(x = { 1 x for x 1 for 1 x (a Compute the Fourier sine series of f(x. The Fourier sine series is b n sin where b n = f(x sin dx = 1 = (1 x cos = 4
Test 2 Review Math 1111 College Algebra
 Test 2 Review Math 1111 College Algebra 1. Begin by graphing the standard quadratic function f(x) = x 2. Then use transformations of this graph to graph the given function. g(x) = x 2 + 2 *a. b. c. d.
Test 2 Review Math 1111 College Algebra 1. Begin by graphing the standard quadratic function f(x) = x 2. Then use transformations of this graph to graph the given function. g(x) = x 2 + 2 *a. b. c. d.
Lecture 24. Scott Pauls 5/21/07
 Lecture 24 Department of Mathematics Dartmouth College 5/21/07 Material from last class The heat equation α 2 u xx = u t with conditions u(x, 0) = f (x), u(0, t) = u(l, t) = 0. 1. Separate variables to
Lecture 24 Department of Mathematics Dartmouth College 5/21/07 Material from last class The heat equation α 2 u xx = u t with conditions u(x, 0) = f (x), u(0, t) = u(l, t) = 0. 1. Separate variables to
Introduction to Path Integrals
 Introduction to Path Integrals Consider ordinary quantum mechanics of a single particle in one space dimension. Let s work in the coordinate space and study the evolution kernel Ut B, x B ; T A, x A )
Introduction to Path Integrals Consider ordinary quantum mechanics of a single particle in one space dimension. Let s work in the coordinate space and study the evolution kernel Ut B, x B ; T A, x A )
Quantum Mechanics for Scientists and Engineers. David Miller
 Quantum Mechanics for Scientists and Engineers David Miller Vector spaces, operators and matrices Vector spaces, operators and matrices Vector space Vector space We need a space in which our vectors exist
Quantum Mechanics for Scientists and Engineers David Miller Vector spaces, operators and matrices Vector spaces, operators and matrices Vector space Vector space We need a space in which our vectors exist
Eco504, Part II Spring 2010 C. Sims PITFALLS OF LINEAR APPROXIMATION OF STOCHASTIC MODELS
 Eco504, Part II Spring 2010 C. Sims PITFALLS OF LINEAR APPROXIMATION OF STOCHASTIC MODELS 1. A LIST OF PITFALLS Linearized models are of course valid only locally. In stochastic economic models, this usually
Eco504, Part II Spring 2010 C. Sims PITFALLS OF LINEAR APPROXIMATION OF STOCHASTIC MODELS 1. A LIST OF PITFALLS Linearized models are of course valid only locally. In stochastic economic models, this usually
Formulas to remember
 Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Upper Bounds for Partitions into k-th Powers Elementary Methods
 Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 9, 433-438 Upper Bounds for Partitions into -th Powers Elementary Methods Rafael Jaimczu División Matemática, Universidad Nacional de Luján Buenos Aires,
Int. J. Contemp. Math. Sciences, Vol. 4, 2009, no. 9, 433-438 Upper Bounds for Partitions into -th Powers Elementary Methods Rafael Jaimczu División Matemática, Universidad Nacional de Luján Buenos Aires,
Finite Difference and Finite Element Methods
 Finite Difference and Finite Element Methods Georgy Gimel farb COMPSCI 369 Computational Science 1 / 39 1 Finite Differences Difference Equations 3 Finite Difference Methods: Euler FDMs 4 Finite Element
Finite Difference and Finite Element Methods Georgy Gimel farb COMPSCI 369 Computational Science 1 / 39 1 Finite Differences Difference Equations 3 Finite Difference Methods: Euler FDMs 4 Finite Element
DISTRIBUTIONS FUNCTIONS OF PROBABILITY SOME THEOREMS ON CHARACTERISTIC. (1.3) +(t) = eitx df(x),
 SOME THEOREMS ON CHARACTERISTIC FUNCTIONS OF PROBABILITY DISTRIBUTIONS 1. Introduction E. J. G. PITMAN UNIVERSITY OF TASMANIA Let X be a real valued random variable with probability measure P and distribution
SOME THEOREMS ON CHARACTERISTIC FUNCTIONS OF PROBABILITY DISTRIBUTIONS 1. Introduction E. J. G. PITMAN UNIVERSITY OF TASMANIA Let X be a real valued random variable with probability measure P and distribution
