CONVERGENCE OF THE COEFRCIENTS IN A RECURRING POWER SERIES JOSEPH ARK IN Nanuet, New York 1. INTRODUCTION. In this paper we use the following notation
|
|
|
- Clifford Charles
- 5 years ago
- Views:
Transcription
1 CONVERGENCE OF THE COEFRCIENTS IN A RECURRING POWER SERIES JOSEPH ARK IN Nauet, Ne York 1. INTRODUCTION I this paper e use the folloig otatio oo \ k oo 1 \ ^ (k) 1 _ X c x Ev* -E k = / = (For coveiece, e shall rite c istead of c.) We defie Ev = F ( x ) ^ = for a fiite f, t m d v = TT< i -v> = «<*> W= W=l for fiite t ad m, here the d ^ ad are positive itegers. The r fi ad are distict ad e say Jr^ is the greatest r i the jr J. If 2. THEOREM 1 F(x)/Q(x) = 2 ] u x, = 41
2 42 CONVERGENCE OF THE COEFFICIENTS [Feb. the (2.1) lim iu / u.1 (for a fiite j =,1,2,' ) J *>oo j / -j j coverges to rj 9 here the r ^ i Q(x) are distict ith distict moduli ad r A j is the greatest j r i the J r I. Proof* It has bee sho by Poicare [ 1 ] that (2.2) lim u / u, -^>oo / -i coverges to some root (r) i Q(x). i Q(x) is Let (rjj.) (We must the prove that this root (r) m (2.3) MW = J J (l-r x) W, =i here the p are positive itegers or = ad di + P i = d 2 + p 2 =... - p + d = k (k = 1, 2 9 3, ) for a fiite = 1, 2, 3,, m. The* m M(x)Q(x) = " P J (1 - r x ) k =i = k (x) so that (2.4) F(x)M(x)/Q(x)M(x) = F(x)M(x)/<^(x) - Ev* -!> *' =o =o
3 1969] IN A RECURRING POWER SERIES 43 here it is evidet u = c(k,). No let 4 ( x ) = \ = c (here v is fiite), here combiig this ith (2,4), e rite (2.5) F W M W / ^ W - ^ c(k.- 1, )x W oo. = V= / \= ad combiig coefficiets leads to v (2.5.1) cfc-l.) =^cfc-)c = V v W= W= c. k = 2, 3, 4, -. I (2.5.1), e replace k ith k + 1 (here k = 1,2,3, ) here combiig this result ith (2.2) leads to 11m S l ^ o o i c(k + l,)/c(k + l, - 1)1 coverges to some root (r) i Q(x). B For coveiece, e rite the covergece as (2.5.2) c ( k + l, ) = g k + i c ( k + l, - l ).
4 44 CONVERGENCE OF THE COEFFICIENTS [Feb. Combiig (2.5.1) ith k replaced by k + 1 ith (2.5.2), it is easily sho, that for a fiite v, e have (2.5.3) c(k,)/c(k,- 1) = g k v / v = y c ( k + l, - ) c iy c(k + l, - - l ) c = / = = V i > so that (2-5.4) g k + 1 = g k =... = g I. Thus to complete the proof of Theorem 1, it remais to sho that The e cosider the folloig (e refer to (2.3) ) m oo (2.6) (^(x))" 1 = T T (1 - i ^ x ) " 1 = Y ^ e(m,)x (for a fiite m) W=l W= for the covergece properties of e(m, )/e(m, - 1) 9 here the lr distict ad r j is the greatest root NOTE. For coveiece, e rite I W j j are e(m, )/e(m, - j) = ir (for a fiite j =,1, 2, ), i place of I e(m,)/e(m, - j) j coverges to \r j,
5 19^9] IN A RECURRING POWER SERIES For m = 1, e have (2.7) ( i» x)" 1 = ^ e(1 > > x W > = here e(l, ) = r, so that e ( l, ) / e ( l, - j ) = rj For m = 2, e have (2.8) [(1 - r lx ) (1 - rax)]"" 1 = ^ e(2,) = X here e(2 9 ) = (r ' - r )/(v t - r 2 ), so that e(2,)/e(2, - j) = rj It o remais to cosider for fiite m = 3, 4, 5, e / ^ V 1 t s= s=l for a fiite t = 8,4, 5, * 8, here UQ = 1.
6 46 CONVERGENCE OF THE COEFFICIENTS [Feb. Equatig the coefficiets i this leads to (2.1) U = X X ~ s V s s=l t (U = 1 > ad t-1 Ui = U a tral, U 2 = Uia t r a l + U a t ^ % U t = ^ U ^. Also, sice i (2.9), e have e may rite s= t t-1 TTVv> = i -E a s xt " s s=l s= t t-1 (2.1D T f V v = x t - Z v s s=l s= We o combie (2.1) ith (2.11) ad rite (2.12) - ^ + s-1 E ( v E V H r - t-s 8 ) x s=2 V r=l r Multiplyig (2*12) by x ad combiig the result ith t-1 Uixt = Ui S s s=
7 1969] IN A RECURRING POWER SERIES i (2.11) leads to 47 (2.13) x t+i U 2 x t " 1 + E ( U r E U r ^ s V s ^ j r=o s=o ' t-r-2 + Utao. No, multiplyig (2.13) by x ad combiig the r e s u l t ith ^ s=o a s x i (2.11) 9 e the have (2.14) x t+2 U ^ 1 + E ( U r h l - Z U r t - s V s - i ). tr-y-2 r=o + a U 2 We cotiue i the exact ay e foud (2.13) ad (2.14) for - 1 steps to get t-3 (2.15) J**- 1 - U x M + 5 ] r=o u. x t - r - 2 +r+1 JLJ + r - s a t - s - i I s=o ' > i + U au = U x ' R(x) + U a.. -i -i o We o cotiue (2.15) ith (2.11) to get the folloig t equatios r ' +_i = V*" 1 + R(ri) + Vl a ' (2.16) rt+-i = t-l + R ( } t
8 48 CONVERGENCE OF THE COEFFICIENTS [Feb. Next, e cosider the t equatios obtaied from (2.16). These t equatios i the t uko ca be solved by C r a m e r f s rule to obtai (2.17) U D 2 = D l ( ), here Djdi) ad D 2 a r e the determiats give belo: (2.18) Dt() = - t+- t+- r t -1-1 t-2 *r : - ' r i r t 1 1 (2.19) D, = t~i r j r* t-2 r i t-2 r t " r j r t l l 1 We o replace ith - 1 i (2.17) to get (2.2) IT DL 2 = Dj 1 ( - 1), - i ad dividig (2.17) by (2.2), e get (2.21) U / U - i = D l ( ) / D l ( " 1] Sice the r tha the other roots, ad e rite ^ ad a r e distict, the oe root (say r i is g r e a t e r (2.22) U / U - i = t+-2 ^ t+-2^ ( D i ( ) / r p ^ ) / ( D 1 ( - l ) / r r 1 1 ^ ) t+ 7 No i (2.22) e let r i ' (i the umerator) divide every t e r m of the first t+ 2 colum i (2.18) ad r A (i the deomiator) divide every t e r m i the first colum of (2.18) (ith replaced by - 1). The if e let ->oo it i s e v i - det that
9 1969] (2.23) IN A RECURRING POWER SERIES lim ->oo tu /U - i! = I r 1 J. 49 No for a fiite t e rite lim -> oo I U -j. /U -j-i. r J (j =,1, 2,, t - 1), so that (2.24) lim ^ool U /U -tl J Multiplyig the F(x) i (1) ith uu S= i (2.9), e rite (2.25) =o / \ s=o / s=o C x S, s here comparig the coefficiets e have (2.26) Z-^ -i s s=o b s No, sice f is fiite, ad by the results i (2.23), e rite C = ri Y ^ U b = ri C 1 * / J -s-i s -i * s=o
10 5 CONVERGENCE OF THE COEFFICIENTS [Feb. here combiig this ith the r ^ ad are distict (so that e may add that the r, have distict moduli), leads to the completio of the proof for Theorem 1. From (2.7), (2.8), ad (2.17), the folloig corollary is immediate: Corollary. If t s=i s=o here the r s ^ ad are distict, the (2.27) It is alays possible to solve for the U ( =,1, 2,* ) Let as a fuctio of the r. s -k SECTION 3 t =i / =l =o oo (k) c x (CQ r = 1 ad k = 1, 2, 3, ) for a fiite t = 2, 3,4, ad the give roots ^ ad are distict. We also defie s(x) t t = Z E a ^r^+-r" - c ~ xw_1 = =i r= ad b = Z a x 7 W-2 a ;" W=2
11 19691 IN A RECURRING POWER SERIES 51 here *Xi ^ ad is a root i S(x) = 8(x t ) =. We the have the folloig: Theorem 2. If c = 1, ci = aic, c 2 = atcj + a 2 c, e e t-i 3 t ~ J L +i t--i =o ad p.. = a 4 (k + - j) (j = 1, 2, 3,, ), the q m+i = b * " m ^ 2 k + ~ m ~ ^ (m = l, 2, 3, - - -, - l ) (3.1) c ( k ) / c ( k ) = E /G (k, = 1, 2, 3, ), 9 ' -i ' here E ad G are the determiats give belo. Pi 2-1 P2 qa (3.1.1) E = - 1 P3 - i q 4 P4 q 5 - i p - l % - 1 p *It should be oted that sice the a! s are costat for a fixed t, that the root xi ill be determied as a variable* sice it is a fuctio of the c ad ill, of course, chage values for differet -
12 52 CONVERGENCE OF THE COEFFICIENTS [Feb P2 qs o o o 1-1 P3 Q4 (3.1.2) G = -1 p 4 q 5-1 p 5 q 6 Proof. Let (3.2) 1 = 1 IvjfE W=l ' \ W= C X - 1 V i \ \ -1 p (for a fiite ), here the a ad the c are idetical to those i (3). The multiplyig ad combiig the terms i (3.2) leads to S(xi) = S(x) = i (3). No, takig each side of (3.2) to the k poer, e rite (3.3) 1" = 1 E =i a x vk v=o ( k = 2, 3, - - ), (here, of course, xj is a root i (3.3) ). Usig the correspodig values i (3), e rite (3.3) as (3.3.1) 1 = (1 - aix - bx' \=o ( k ) X W + J ( K ) Differetiatio of (3.3.1) leads to k(a lx + 2bx 2 ) I ^ c^k) + J(x) j = (1 - a x x - bx* )l ^ c k) x + W(x) <=o \ = i
13 1969] IN A RECURRING POWER SERIES 53 ad by comparig coefficiets, e coclude that (3.4) c^k) = a i ( k + - l ) c ^ + b(2k + - 2)cf^ for k = 2, 3,..., = 2, 3, -, e (k) = 1 ad c k ) = ajk. (k) Whe e divide (3.4) by c, e get c ( k ) /i. i\ _. M2k + - 2)( - 1) = a! ( k + - l ) + Tgr,. v (,k = 2, 3, ), c ( - l)c - i ^ ~ -2 - i hich i tur, alog ith CQ = 1 ad ci = aik, implies (alog ith the values of p ad q i (3)) 9 (k) (3 c q 2 qs,,, q - i. %. - 5) Jr =^ + ^ +?r + - +^:: + ^ = K() - V i - - i ' We complete the proof of T h e o r e m 2 ith E u l e r f s statemet [2] K W = E / G ; ad e resolve for the case he k = 1 ith (2.27). Corollary. I it is alays possible to solve for TT«-v»- k -h-zv = 1+ 1 \ t \ - k -, ^ (k) = 1 + > e x =i \ =l / =i
14 54 CONVERGENCE OF THE COEFFICIENTS [Feb. (3.6) c k ) / c S i = K ( ) = E / G ( k a d = 2 s 3 f ' ' * ) he t = 2, 3,4, or 5, if the r ^ ad are distict. Proof. I (2.27), it is see that the c maybe determied. No, sice t - 1 = 1, 2, 3, or 4, the the roots (each root is a fuctio of the c ) i S(x).(i 3) may alays be foud, so that e ill obtai values for the p q. We the complete the proof of the corollary by observig that E ad G are both fuctios of the p ad q. I coclusio: We solve he t = 1 ad e rite ad ( 1 - r )" k = f V k ) x (d< k) = l, r ^ O ) X f j W =o No, differetiatig, e have xkrf > d r ' V M = f ^ d ^ k ) x = ' =i ad comparig the coefficiets leads to d(k> o d( k + 1 ) r k -i so that -i J f d f - > = r j j ( k l ) d < ^k+-) =i =o ad e the have d W = r (k + - 1)! /! (k - 1)!
15 1969] IN A RECURRING POWER SERIES 55 REFERENCES 1. L. M. Mile-Thomso, The Calculus of Fiite Differeces, Macmilla ad Co., Ltd., Lodo, 196, p G. Chrystal, Textbook of Algebra, Vol. II, Dover Publicatios, Ic., Ne York, 1961, p. 52. The author ishes to thak L. Carlitz ad V. E. Hoggatt, Jr. for their ecouragemet. *. [Cotiued from p. 4. ] 1. V. E. Hoggatt, J r., "Fiboacci Numbers ad Geeralized Biomial Coefficiets," Fiboacci Quarterly, 5 (1967), pp Dov Jarde, "The Product of Sequeces ith a Commo Liear Recursio Formula of Order 2," publ. i Recurrig Sequeces, Jerusalem, 1958, pp Origial paper appeared i Hebre i Riveo Lematematika, 3 (1949), pp ; 38, beig a joit paper ith Th B Motzki. 12. Dov Jarde, "Nullifyig Coefficiets," Scripta Mathematica, 19(1953), pp Eugee E. Kohlbecker, "O a Geeralizatio of Multiomial Coefficiets for Fiboacci Sequeces," Fiboacci Quarterly, 4 (1966), pp S. G. Mohaty, "Restricted Compositios," Fiboacci Quarterly, 5(1967), pp Roseaa F. Torretto ad J. Alle Fuchs, "Geeralized Biomial Coefficiets," J^bojia^clJ^ 2 (1964), pp Morga Ward, "A Calculus of Sequeces," Amer, J. Math., 58 (1936), pp Stephe K. Jerbic s "Fiboomial Coefficiets A Fe Summatio Properties," Master f s Thesis 8 Sa Jose State College,, Sa Jose* Calif., 1968.
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS
 DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
DIVISIBILITY PROPERTIES OF GENERALIZED FIBONACCI POLYNOMIALS VERNER E. HOGGATT, JR. Sa Jose State Uiversity, Sa Jose, Califoria 95192 ad CALVIN T. LONG Washigto State Uiversity, Pullma, Washigto 99163
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
ANOTHER GENERALIZED FIBONACCI SEQUENCE 1. INTRODUCTION
 ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Theorem: Let A n n. In this case that A does reduce to I, we search for A 1 as the solution matrix X to the matrix equation A X = I i.e.
 Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
GENERALIZATIONS OF ZECKENDORFS THEOREM. TilVIOTHY J. KELLER Student, Harvey Mudd College, Claremont, California
 GENERALIZATIONS OF ZECKENDORFS THEOREM TilVIOTHY J. KELLER Studet, Harvey Mudd College, Claremot, Califoria 91711 The Fiboacci umbers F are defied by the recurrece relatio Fi = F 2 = 1, F = F - + F 0 (
GENERALIZATIONS OF ZECKENDORFS THEOREM TilVIOTHY J. KELLER Studet, Harvey Mudd College, Claremot, Califoria 91711 The Fiboacci umbers F are defied by the recurrece relatio Fi = F 2 = 1, F = F - + F 0 (
EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES
 EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES C A CHURCH Uiversity of North Carolia, Greesboro, North Carolia ad MARJORIE BICKNELL A. C. Wilco High Schl, Sata Clara, Califoria 1. INTRODUCTION
EXPONENTIAL GENERATING FUNCTIONS FOR FIBONACCI IDENTITIES C A CHURCH Uiversity of North Carolia, Greesboro, North Carolia ad MARJORIE BICKNELL A. C. Wilco High Schl, Sata Clara, Califoria 1. INTRODUCTION
LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS
 LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria Give a secod-order liear recursio relatio (.1) T. 1 = a T + b T 1,
LINEAR RECURSION RELATIONS - LESSON FOUR SECOND-ORDER LINEAR RECURSION RELATIONS BROTHER ALFRED BROUSSEAU St. Mary's College, Califoria Give a secod-order liear recursio relatio (.1) T. 1 = a T + b T 1,
Hoggatt and King [lo] defined a complete sequence of natural numbers
![Hoggatt and King [lo] defined a complete sequence of natural numbers Hoggatt and King [lo] defined a complete sequence of natural numbers](/thumbs/96/128001016.jpg) REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
1/(1 -x n ) = \YJ k=0
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E. Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E.WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E. Whitey, Mathematics Departmet,
MDIV. Multiple divisor functions
 MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
MDIV. Multiple divisor fuctios The fuctios τ k For k, defie τ k ( to be the umber of (ordered factorisatios of ito k factors, i other words, the umber of ordered k-tuples (j, j 2,..., j k with j j 2...
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
MATH 31B: MIDTERM 2 REVIEW
 MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
Abstract. 1. Introduction This note is a supplement to part I ([4]). Let. F x (1.1) x n (1.2) Then the moments L x are the Catalan numbers
![Abstract. 1. Introduction This note is a supplement to part I ([4]). Let. F x (1.1) x n (1.2) Then the moments L x are the Catalan numbers Abstract. 1. Introduction This note is a supplement to part I ([4]). Let. F x (1.1) x n (1.2) Then the moments L x are the Catalan numbers](/thumbs/87/95874461.jpg) Abstract Some elemetary observatios o Narayaa polyomials ad related topics II: -Narayaa polyomials Joha Cigler Faultät für Mathemati Uiversität Wie ohacigler@uivieacat We show that Catala umbers cetral
Abstract Some elemetary observatios o Narayaa polyomials ad related topics II: -Narayaa polyomials Joha Cigler Faultät für Mathemati Uiversität Wie ohacigler@uivieacat We show that Catala umbers cetral
(6), (7) and (8) we have easily, if the C's are cancellable elements of S,
 VIOL. 23, 1937 MA THEMA TICS: H. S. VANDIVER 555 where the a's belog to S'. The R is said to be a repetitive set i S, with respect to S', ad with multiplier M. If S cotais a idetity E, the if we set a,
VIOL. 23, 1937 MA THEMA TICS: H. S. VANDIVER 555 where the a's belog to S'. The R is said to be a repetitive set i S, with respect to S', ad with multiplier M. If S cotais a idetity E, the if we set a,
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Some p-adic congruences for p q -Catalan numbers
 Some p-adic cogrueces for p q -Catala umbers Floria Luca Istituto de Matemáticas Uiversidad Nacioal Autóoma de México C.P. 58089, Morelia, Michoacá, México fluca@matmor.uam.mx Paul Thomas Youg Departmet
Some p-adic cogrueces for p q -Catala umbers Floria Luca Istituto de Matemáticas Uiversidad Nacioal Autóoma de México C.P. 58089, Morelia, Michoacá, México fluca@matmor.uam.mx Paul Thomas Youg Departmet
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
AN ALMOST LINEAR RECURRENCE. Donald E. Knuth Calif. Institute of Technology, Pasadena, Calif.
 AN ALMOST LINEAR RECURRENCE Doald E. Kuth Calif. Istitute of Techology, Pasadea, Calif. form A geeral liear recurrece with costat coefficiets has the U 0 = a l* U l = a 2 " ' " U r - l = a r ; u = b, u,
AN ALMOST LINEAR RECURRENCE Doald E. Kuth Calif. Istitute of Techology, Pasadea, Calif. form A geeral liear recurrece with costat coefficiets has the U 0 = a l* U l = a 2 " ' " U r - l = a r ; u = b, u,
sin(n) + 2 cos(2n) n 3/2 3 sin(n) 2cos(2n) n 3/2 a n =
 60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
n=1 a n is the sequence (s n ) n 1 n=1 a n converges to s. We write a n = s, n=1 n=1 a n
 Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
Series. Defiitios ad first properties A series is a ifiite sum a + a + a +..., deoted i short by a. The sequece of partial sums of the series a is the sequece s ) defied by s = a k = a +... + a,. k= Defiitio
I I L an,klr ~ Mr, n~l
 MATHEMATICS ON MATRIX TRANSFORMATIONS OF CERTAIN SEQUENCE SPACES BY H. R. CHILLINGWORTH (Commuicated by Prof. J. F. KoKS!IIA at the meetig of Jue 29, 1957) I this paper we determie the characteristics
MATHEMATICS ON MATRIX TRANSFORMATIONS OF CERTAIN SEQUENCE SPACES BY H. R. CHILLINGWORTH (Commuicated by Prof. J. F. KoKS!IIA at the meetig of Jue 29, 1957) I this paper we determie the characteristics
A FIBONACCI MATRIX AND THE PERMANENT FUNCTION
 A FIBONACCI MATRIX AND THE PERMANENT FUNCTION BRUCE W. KING Burt Hiils-Ballsto Lake High School, Ballsto Lake, New York ad FRANCIS D. PARKER The St. Lawrece Uiversity, Cato, New York The permaet of a -square
A FIBONACCI MATRIX AND THE PERMANENT FUNCTION BRUCE W. KING Burt Hiils-Ballsto Lake High School, Ballsto Lake, New York ad FRANCIS D. PARKER The St. Lawrece Uiversity, Cato, New York The permaet of a -square
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
(2) F j+2 = F J+1 + F., F ^ = 0, F Q = 1 (j = -1, 0, 1, 2, ). Editorial notes This is not our standard Fibonacci sequence.
 ON THE LENGTH OF THE EUCLIDEAN ALGORITHM E. P. IV1ERKES ad DAVSD MEYERS Uiversity of Ciciati, Ciciati, Ohio Throughout this article let a ad b be itegers, a > b >. The Euclidea algorithm geerates fiite
ON THE LENGTH OF THE EUCLIDEAN ALGORITHM E. P. IV1ERKES ad DAVSD MEYERS Uiversity of Ciciati, Ciciati, Ohio Throughout this article let a ad b be itegers, a > b >. The Euclidea algorithm geerates fiite
Infinite Series and Improper Integrals
 8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS
 CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
Hankel determinants of some polynomial sequences. Johann Cigler
 Hael determiats of some polyomial sequeces Joha Cigler Faultät für Mathemati, Uiversität Wie ohacigler@uivieacat Abstract We give simple ew proofs of some Catala Hael determiat evaluatios by Ömer Eğecioğlu
Hael determiats of some polyomial sequeces Joha Cigler Faultät für Mathemati, Uiversität Wie ohacigler@uivieacat Abstract We give simple ew proofs of some Catala Hael determiat evaluatios by Ömer Eğecioğlu
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Unit 4: Polynomial and Rational Functions
 48 Uit 4: Polyomial ad Ratioal Fuctios Polyomial Fuctios A polyomial fuctio y px ( ) is a fuctio of the form p( x) ax + a x + a x +... + ax + ax+ a 1 1 1 0 where a, a 1,..., a, a1, a0are real costats ad
48 Uit 4: Polyomial ad Ratioal Fuctios Polyomial Fuctios A polyomial fuctio y px ( ) is a fuctio of the form p( x) ax + a x + a x +... + ax + ax+ a 1 1 1 0 where a, a 1,..., a, a1, a0are real costats ad
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
The r-generalized Fibonacci Numbers and Polynomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Chapter 4 : Laplace Transform
 4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers
 Quadratic Trasformatios of Hypergeometric Fuctio ad Series with Harmoic Numbers Marti Nicholso I this brief ote, we show how to apply Kummer s ad other quadratic trasformatio formulas for Gauss ad geeralized
Quadratic Trasformatios of Hypergeometric Fuctio ad Series with Harmoic Numbers Marti Nicholso I this brief ote, we show how to apply Kummer s ad other quadratic trasformatio formulas for Gauss ad geeralized
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Created by T. Madas SERIES. Created by T. Madas
 SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
SERIES SUMMATIONS BY STANDARD RESULTS Questio (**) Use stadard results o summatios to fid the value of 48 ( r )( 3r ). 36 FP-B, 66638 Questio (**+) Fid, i fully simplified factorized form, a expressio
Sequences. Notation. Convergence of a Sequence
 Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Sequeces A sequece is essetially just a list. Defiitio (Sequece of Real Numbers). A sequece of real umbers is a fuctio Z (, ) R for some real umber. Do t let the descriptio of the domai cofuse you; it
Fibonacci numbers and orthogonal polynomials
 Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Properties and Tests of Zeros of Polynomial Functions
 Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
MATH 304: MIDTERM EXAM SOLUTIONS
 MATH 304: MIDTERM EXAM SOLUTIONS [The problems are each worth five poits, except for problem 8, which is worth 8 poits. Thus there are 43 possible poits.] 1. Use the Euclidea algorithm to fid the greatest
MATH 304: MIDTERM EXAM SOLUTIONS [The problems are each worth five poits, except for problem 8, which is worth 8 poits. Thus there are 43 possible poits.] 1. Use the Euclidea algorithm to fid the greatest
Interesting Series Associated with Central Binomial Coefficients, Catalan Numbers and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
Q-BINOMIALS AND THE GREATEST COMMON DIVISOR. Keith R. Slavin 8474 SW Chevy Place, Beaverton, Oregon 97008, USA.
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 2008, #A05 Q-BINOMIALS AND THE GREATEST COMMON DIVISOR Keith R. Slavi 8474 SW Chevy Place, Beaverto, Orego 97008, USA slavi@dsl-oly.et Received:
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 2008, #A05 Q-BINOMIALS AND THE GREATEST COMMON DIVISOR Keith R. Slavi 8474 SW Chevy Place, Beaverto, Orego 97008, USA slavi@dsl-oly.et Received:
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Mathematical Series (You Should Know)
 Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
Mathematical Series You Should Kow Mathematical series represetatios are very useful tools for describig images or for solvig/approimatig the solutios to imagig problems. The may be used to epad a fuctio
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS EDITED BY VERNER E, HOGGATT 9 JR 0, SAN JOSE STATE COLLEGE Sed all commuicatios cocerig Advaced P r o b l e m s ad Solutios to Verer E. Hoggatt, J r., Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS EDITED BY VERNER E, HOGGATT 9 JR 0, SAN JOSE STATE COLLEGE Sed all commuicatios cocerig Advaced P r o b l e m s ad Solutios to Verer E. Hoggatt, J r., Mathematics Departmet,
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all couicatios cocerig Advaced Probles ad Solutios to Rayod E. Whitey, Matheatics Departet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND E. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all couicatios cocerig Advaced Probles ad Solutios to Rayod E. Whitey, Matheatics Departet,
Math 120 Answers for Homework 23
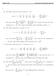 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
A TYPE OF PRIMITIVE ALGEBRA*
 A TYPE OF PRIMITIVE ALGEBRA* BT J. H. M. WEDDERBURN I a recet paper,t L. E. Dickso has discussed the liear associative algebra, A, defied by the relatios xy = yo(x), y = g, where 8 ( x ) is a polyomial
A TYPE OF PRIMITIVE ALGEBRA* BT J. H. M. WEDDERBURN I a recet paper,t L. E. Dickso has discussed the liear associative algebra, A, defied by the relatios xy = yo(x), y = g, where 8 ( x ) is a polyomial
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Unit 6: Sequences and Series
 AMHS Hoors Algebra 2 - Uit 6 Uit 6: Sequeces ad Series 26 Sequeces Defiitio: A sequece is a ordered list of umbers ad is formally defied as a fuctio whose domai is the set of positive itegers. It is commo
AMHS Hoors Algebra 2 - Uit 6 Uit 6: Sequeces ad Series 26 Sequeces Defiitio: A sequece is a ordered list of umbers ad is formally defied as a fuctio whose domai is the set of positive itegers. It is commo
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Sequences and Limits
 Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Polynomials with Rational Roots that Differ by a Non-zero Constant. Generalities
 Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
SOME FIBONACCI AND LUCAS IDENTITIES. L. CARLITZ Dyke University, Durham, North Carolina and H. H. FERNS Victoria, B. C, Canada
 SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
1 Last time: similar and diagonalizable matrices
 Last time: similar ad diagoalizable matrices Let be a positive iteger Suppose A is a matrix, v R, ad λ R Recall that v a eigevector for A with eigevalue λ if v ad Av λv, or equivaletly if v is a ozero
Last time: similar ad diagoalizable matrices Let be a positive iteger Suppose A is a matrix, v R, ad λ R Recall that v a eigevector for A with eigevalue λ if v ad Av λv, or equivaletly if v is a ozero
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
Solutions to Homework 1
 Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Solutios to Homework MATH 36. Describe geometrically the sets of poits z i the complex plae defied by the followig relatios /z = z () Re(az + b) >, where a, b (2) Im(z) = c, with c (3) () = = z z = z 2.
Curve Sketching Handout #5 Topic Interpretation Rational Functions
 Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
Curve Sketchig Hadout #5 Topic Iterpretatio Ratioal Fuctios A ratioal fuctio is a fuctio f that is a quotiet of two polyomials. I other words, p ( ) ( ) f is a ratioal fuctio if p ( ) ad q ( ) are polyomials
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
1. Hydrogen Atom: 3p State
 7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
Are the following series absolutely convergent? n=1. n 3. n=1 n. ( 1) n. n=1 n=1
 Absolute covergece Defiitio A series P a is called absolutely coverget if the series of absolute values P a is coverget. If the terms of the series a are positive, absolute covergece is the same as covergece.
Absolute covergece Defiitio A series P a is called absolutely coverget if the series of absolute values P a is coverget. If the terms of the series a are positive, absolute covergece is the same as covergece.
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
REVIEW 1, MATH n=1 is convergent. (b) Determine whether a n is convergent.
 REVIEW, MATH 00. Let a = +. a) Determie whether the sequece a ) is coverget. b) Determie whether a is coverget.. Determie whether the series is coverget or diverget. If it is coverget, fid its sum. a)
REVIEW, MATH 00. Let a = +. a) Determie whether the sequece a ) is coverget. b) Determie whether a is coverget.. Determie whether the series is coverget or diverget. If it is coverget, fid its sum. a)
AH Checklist (Unit 3) AH Checklist (Unit 3) Matrices
 AH Checklist (Uit 3) AH Checklist (Uit 3) Matrices Skill Achieved? Kow that a matrix is a rectagular array of umbers (aka etries or elemets) i paretheses, each etry beig i a particular row ad colum Kow
AH Checklist (Uit 3) AH Checklist (Uit 3) Matrices Skill Achieved? Kow that a matrix is a rectagular array of umbers (aka etries or elemets) i paretheses, each etry beig i a particular row ad colum Kow
MT5821 Advanced Combinatorics
 MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
Subject: Differential Equations & Mathematical Modeling-III
 Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
9.3 The INTEGRAL TEST; p-series
 Lecture 9.3 & 9.4 Math 0B Nguye of 6 Istructor s Versio 9.3 The INTEGRAL TEST; p-series I this ad the followig sectio, you will study several covergece tests that apply to series with positive terms. Note
Lecture 9.3 & 9.4 Math 0B Nguye of 6 Istructor s Versio 9.3 The INTEGRAL TEST; p-series I this ad the followig sectio, you will study several covergece tests that apply to series with positive terms. Note
Fourier series and the Lubkin W-transform
 Fourier series ad the Lubki W-trasform Jaso Boggess, Departmet of Mathematics, Iowa State Uiversity Eric Buch, Departmet of Mathematics, Baylor Uiversity Charles N. Moore, Departmet of Mathematics, Kasas
Fourier series ad the Lubki W-trasform Jaso Boggess, Departmet of Mathematics, Iowa State Uiversity Eric Buch, Departmet of Mathematics, Baylor Uiversity Charles N. Moore, Departmet of Mathematics, Kasas
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
1, if k = 0. . (1 _ qn) (1 _ qn-1) (1 _ qn+1-k) ... _: =----_...:... q--->1 (1- q) (1 - q 2 ) (1- qk) - -- n! k!(n- k)! n """"' n. k.
 Abstract. We prove the ifiite q-biomial theorem as a cosequece of the fiite q-biomial theorem. 1. THE FINITE q-binomial THEOREM Let x ad q be complex umbers, (they ca be thought of as real umbers if the
Abstract. We prove the ifiite q-biomial theorem as a cosequece of the fiite q-biomial theorem. 1. THE FINITE q-binomial THEOREM Let x ad q be complex umbers, (they ca be thought of as real umbers if the
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
SOLVING LINEAR RECURSIONS OVER ALL FIELDS
 SOLVING LINEAR RECURSIONS OVER ALL FIELDS KEITH CONRAD 1. Itroductio A sequece {a } = a 0, a 1, a,... i a field K satisfies a liear recursio if there are c 1,..., c d K such that 1.1 a = c 1 a 1 + c a
SOLVING LINEAR RECURSIONS OVER ALL FIELDS KEITH CONRAD 1. Itroductio A sequece {a } = a 0, a 1, a,... i a field K satisfies a liear recursio if there are c 1,..., c d K such that 1.1 a = c 1 a 1 + c a
SEQUENCES AND SERIES
 Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
Sequeces ad 6 Sequeces Ad SEQUENCES AND SERIES Successio of umbers of which oe umber is desigated as the first, other as the secod, aother as the third ad so o gives rise to what is called a sequece. Sequeces
ADVANCED PROBLEMS AND SOLUTIONS
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYIVIOWDE. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E D Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYIVIOWDE. WHITNEY Lock Have State College, Lock Have, Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Eaymod E D Whitey, Mathematics Departmet,
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
