OQ4867. Let ABC be a triangle and AA 1 BB 1 CC 1 = {M} where A 1 BC, B 1 CA, C 1 AB. Determine all points M for which ana 1...
|
|
|
- Piers Griffith
- 5 years ago
- Views:
Transcription
1 764 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 Open questions OQ4867. Let ABC be a triangle and AA BB CC = {M} where A BC, B CA, C AB. Determine all points M for which 4 s 2 3r 2 2Rr AA 2 +BB2 +CC2 AA BB BB CC CC AA. OQ4868. Solve in Z the equation n x i x i2...x ik (n + 2) ks x k p =. i <...<i k n p= OQ4869. Let a, a 2,..., a n be digits in the base x. Determine all n N and all x N for which ana...a n a n...a a n n. OQ4870. Compute a a 2...a n a na n...a + a 2a 3...a na a a n...a 2 k= (+d(k))(2+d(k+))...(n+d(k+n )). and Stanciu Nicolae OQ487. Compute k= (+σ(k))(+σ(k+))...(+σ(k+n)). OQ4872. If x (0, ) then compute λ p = lim when p N. OQ4873. Find the sum S k = integer part. We have S = d (n). i <i 2 <...<i k n x ip +ip ip k n i <i 2 <...<i k n h i n k i i 2...i k when [ ] denote the
2 OQ4874. If a i = n n j= k= s nq m a ij i= Open Questions 765 n a ij where a ij > (i =, 2,..., m; j =, 2,..., n), then j= s n mq m a i i= OQ4875. If a k > 0 (k =, 2,..., n), then n n a n k n n Q a n +a 2 a 3...a n Q 2 a 2 +a a n n cyclic. k= a k for all n 3. OQ4876. Let A A 2...A 2n, B B 2...B 2n, C C 2...C 2n convex polygon inscribed in same circle. Diagonals A A n+, A 2 A n+2,..., A n A 2n, B B n+, B 2 B n+2,..., B n B 2n, C C n+, C 2 C n+2,..., C n C 2n intersect at points, Q, R. Determine all polygons such that: ). The triangle QR is equilateral 2). The triangle QR is isoscelle 3). The triangle QR is rightangled OQ4877. Solve in Q the equation x 2 y 3 z 4 = 2x 2 + 3y 3 + 4z 4. OQ4878. Solve in Z the following system: x a xa 2 x a 3 2 xa 4 2 = b 3 = b 2 x a 2n n x a 2n = b n OQ4879. Solve in N the inequation σ 2 (n) ϕ (n) 207 n. OQ4880. Solve in N the inequation σ 3 (n) ϕ 2 (n) 206 n..
3 766 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ488. Consider two n-convex gons that intersect exactly in 2n points. rove that the common area of these n-gons is greather than or equal to half of the area of one of them. OQ4882. If x k R (k =, 2,..., n) and n x 2 k k= = then find all x R (k =, 2,..., n) which maximizes min ( x x 2, x 2 x 3,..., x n x ). OQ4883. Let A A 2...A n be a regular polygon and let M Int (A A 2...A n ). rove that sin (A MA 2 ) > 2π n n 2 + cos π n. OQ4884. Compute n k=0 ( ) k d (k) σ n(n+)(n+2) 3 k(k+)(k+2) 3. OQ4885. If a ij > 0 (i =, 2,..., n; j =, 2,..., m), λ R and n M λ (x, x 2,..., x n ) = n x λ λ i then determine all λ R for which i=! m a j, m a 2j,..., m a nj m M λ (a j, a 2j,..., a nj ). M λ j= j= j= OQ4886. If a ij > 0 (i =, 2,..., m; j =, 2,..., n), then study the monotonicity and the convexity of the function f (x) = n m! x! x x m n a ij. j= a x ij i= i= j= j= OQ4887. If a ij > 0 (i =, 2,..., n; j =, 2,..., m), p i > 0 (i =, 2,..., n) and H (x, x 2,..., x n ) = n p i i= n p i x i= i then
4 H m j= Open Questions 767! a j, m a 2j,..., m a nj m H (a j, a 2j,..., a nj ). j= j= j= OQ4888. If a ij > 0 (i =, 2,..., n; j =, 2,..., m) p i > 0 (i =, 2,..., n) and nq n A (x, x 2,..., x n ) = x p p i i i= i. rove that i=! G m a j, m a 2j,..., m a nj m G (a j, a 2j,..., a nj ). j= j= j= j= OQ4889. If a ij > 0 (i =, 2,..., n; j =, 2,..., m) p i > 0 (i =, 2,..., n) and A (x, x 2,..., x n ) = A m j= n p i x i i= n p i i=,then! a j, m a 2j,..., m a nj m A (a j, a 2j,..., a nj ). j= j= j= OQ4890. If a ij > 0 (i =, 2,..., n; j =, 2,..., m) p i > 0 (i =, 2,..., n) and A (x, x 2,..., x n ) = A n Q j= a j, nq a 2j,..., j= n p i x i i= n p i i=,then! nq Q a nj m A (a j, a 2j,..., a nj ). j= j= OQ489. If a ij > 0 (i =, 2,..., n; j =, 2,..., m) p i > 0 (i =, 2,..., n) and nq n G (x, x 2,..., x n ) = x p p i i i= i, then i=! Q G n nq nq Q a j, a 2j,..., a nj m G (a j, a 2j,..., a nj ). j= j= j= j=
5 768 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4892. If a ij > 0 (i =, 2,..., n; j =, 2,..., m) p i > 0 (i =, 2,..., n) and H (x, x 2,..., x n ) = H n Q j= a j, n p i i= n i= nq a 2j,..., j=,then p i x i! nq a nj j= Q m H (a j, a 2j,..., a nj ). j= OQ4893. If a k > 0 (k =, 2,..., n), A n = n v u 0 then v 2 +A n u 2 +A n n nq k= v 2 +a k u 2 +a k n a k, H n = k= v 2 +H n u 2 +H n n. n n a k= k and OQ4894. Solve in Z the equation n x x +x x k k = n (x + x x k ) x k. k= k= OQ4895. If A n (x, x 2,..., x n ) = n n n s n nq x k, G n (x, x 2,..., x n ) = n x k, k= H n (x, x 2,..., x n ) =, K n (x, x 2,..., x n ) = x 2 k then x k= k= k A n (x, x 2,..., x n ) + G n (x, x 2,..., x n ) H n (x, x 2,..., x n ) + K (x, x 2,..., x n ). OQ4896. If a k > 0 (k =, 2,..., n) then n a 2 k 2 a a 2 ln a ln a 2 a a 2. k= cyclic cyclic s n n k= OQ4897. Let ABC be a triangle and AA, BB, CC his cevians, A (BC), B (CA), C (AB) and AA BB CC = {M}. Denote ω the Brocard angle of the triangle ABC.
6 Open Questions 769 Determine all cevians AA, BB, CC for which 3 2 sin ω AA BB + BB CC + CC AA OQ4898. Determine all a k {0,,..., 9} (k =, 2,..., n) for which a a 2...a n a n a n...a 2 a = a 2n + a2n a2n n. OQ4899. Determine all n, k N such that all divisors a of n and all divisors b of k holds that a + b is divisor of n + k. OQ4900. Determine all a k {0,,..., 9} (k =, 2,..., n) for which a a 2...a n = a n + an an n. OQ490. Determine all a k, b k {0,,..., 9} (k =, 2,..., n) for which a a 2...a n b b 2...b n = (a n + an an n) (b n + bn bn n). OQ4902. Determine all convex polygons A A 2...A 3n for which A A A 3A A 3n A 2 = A 2A A 4A A 3nA 2 2. OQ4903. Determine all numbers for which (a a 2...a n ) k = b b 2...b kn and a a 2...a n = b b 2...b n + b n+...b 2n b kn k+..b kn. OQ4904. Determine all p, p 2, p 3,..., p k prime numbers which dividet the number n N and for which p p 2...p k + dividet n k +. OQ4905. Denote p k the k th prime number. Solve in N the equation nq p r k k = m r. k=
7 770 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4906. ). Solve in N the equation (n!) k + = m p. If k =, p = 2 then (n, m) are the Brown numbers. 2). Solve in N the equation ((n!)!...)! + = m p {z } k time OQ4907. Determine all polindrome numbers a a 2...a 2n for which a a 2...a n and a n+ a n+2...a 2n are polindrome numbers too. OQ4908. Let ABC be a triangle. Determine the best constants a k, b k, c k R (k =, 2, 3, 4) for which a R 2 + b Rr + c r 2 a 2 R + b 2 r R + r 3 c 2 R 2 r p q 3 (a3 R 2 + b 3 Rr + c 3 r 2 ) r 3 (a 4 R + b 4 r) 2 r 3 c 4 s 2 r 3r. OQ4909. A convex quadrilateral ABCD is extremal if and only if a+b 2 = 2bc b+c = cd. rove that ). a + ab + b c + cd + d 2). (a + b c) (a + b) = d (b + c) + bc (d b) 3). Determine all properties of the extremal quadrilateral OQ490. Let be A, B M n n (C), A = (A A) 2, the singular values of A, i.e., the eigenvalues of the operator A, enumerated in decreasing order, will be denoted by S j (A), j =, 2,..., n, then ). (x + y) S j (AB ) S j (xa A + yb B) for all (j =, 2,..., n) and x, y > 0 A K 2). If C M n n (C) such that K 0, then B xa K (x + y) S j (C) S j K for all j =, 2,..., n and x, y > 0 yb m 3). If A i M n (C) (i =, 2,..., m) x i > 0 (i =, 2,..., m), x i =, then i= S j A x Ax Axm m + A x 2 Ax Ax m A xm Ax 2...Ax m m S j (A + A A m ) for all j =, 2,..., n.
8 Open Questions 77 OQ49. Denote F k and L k the k th Fibonacci respective Lucas numbers. Compute: ). A n (r, s, t) = n h F r i k+2 +L s k 2). B n (r, s, t) = n 3). C n (r, s, t) = n F t k= k+ h L r k+2 +Fk s i L t k= k+ h F r k+2 +L s k k= 4). D n (r, s, t) = n k= L r k+2 +F s k i t F s Lk L r F k t, when [ ] denote the integer part. OQ492. Denote F k and L k the k th Fibonacci respective Lucas numbers. Compute: ). A n (r, s, t) = n h L s i k L r k+2 2). B n (r, s, t) = n 3). C n (r, s, t) = n 4). D n (r, s, t) = n F t k= k+ h F s k Fk+2 r L t k= k+ h L s k Fk+2 r F t k= k+ h F s k L r k+2 k= L t k+ i i i, when [ ] denote the integer part. OQ493. Determine all m N for which m is prime, where Fk 2 n= k=n F k denote the k th Fibonacci number, and [ ] the integer part. " # OQ494. If a t = k, then determine all b t i Z (i =, 2,..., m) for which m b t a t = 0. t= k=n
9 772 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ495. If f (k) = " k m + a k m a m k + a m when a, a 2,..., a m N # then compute D t = when [ ] denote the integer part. k=n f t (k) " # OQ496. Denote k the k th ell number. Compute C t = p t k when [ ] denote the integer part. We have n C = n 2 if n is even n + n 2 if n is odd. " # OQ497. Denote L k the k th Lucas number. Compute B t = L t k when [ ] denote the integer part. OQ498. " Denote F k the k th Fibonacci number. Compute # A t = when [ ] denote the integer part. We have: F t k=n k Fn 2 if n is even ). A = F n 2 if n is odd Fn F 2). A 2 = n if n is even F n F n if n is odd OQ499. rove that S t = " k=n # k t = t i=0 k=n k=n a i n i and determine all a 0, a,..., a t where [ ] denote the integer part. We have the followings: ). S 2 = n 2). S 3 = 2n (n ) i 3). S 4 = 3n 2 5n 2 + 4n + 4). S 5 = 4n 4 8n 3 + 9n 2 5n + h (2n+)(n ) 4 h (n+)(n 2) 3 i
10 Open Questions 773 OQ4920. Solve in Z the equations: x k + xk 2 + xk 3 = yk + yk 2 + yk 3, k {2, 4}. If x = a + 3c, x 2 = b + 3c, x 3 = a b + 2c, y = c + d, y 2 = c + e, y 3 = 2c d e, a, b, c, d, e Z, then we obtain a solution. OQ492. Solve in Z the equations: x k + xk 2 + xk 3 + xk 4 + xk 5 = yk + yk 2 + yk 3 + yk 4 + y5 k, k {, 3, 9, 7}. If x = a, x 2 = a + 2c, x 3 = b, x 4 = b + 2c, x 5 = c + d + e, y = a + b c, y 2 = a + b + c, y 3 = d, y 4 = e, y 5 = 3c when a, b, c, d, e Z, then we obtain a solution. OQ4922. Solve in Z the equation 3 64 x 6 k yk 3 6 z 0 k 3 t0 k = 45 u 8 k vk 8 2. If k= k= k= x = a + b + c, x 2 = b + c + d, x 3 = a d, y = c + d + a, y 2 = d + a + b, y 3 = b c, u k = z k = xk, v k = t k = y k (k =, 2, 3) ; a, b, c, d Z, ad = bc, then we obtain a solution. OQ4923. Solve in Z the equation 25 x 3 x3 2 x3 3 + x3 4 x3 5 + x3 6 x 7 x 7 2 x7 3 + x7 4 x7 5 + x7 6 = 2 x 5 x5 2 x5 3 + x5 4 x5 5 + x If x = a + b + c, x 2 = b + c + d, x 3 = a d, x 4 = c + d + a, x 5 = d + a + b, x 6 = b c, a, b, c, d Z, ad = bc, then we obtain a solution. OQ4924. Let be f (n) = ). Compute k= 2). Compute k= 2). Compute n k= f(k) f 2 (k) r +f(k)+f 2 (k) n + q n + p n n +...
11 774 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4925. Denote G k (n) = qn k + kp n k n +... Compute ). 2). 3). n= k= k= G k (n) G 2 k (n) +G k (n)+g 2 k (n) OQ4926. Solve in Z the equation x 3 + x3 2 + x3 3 y 3 + y y3 3 = z 2. If x = 3a 3 +, x 2 = 3a 3 + 2, x 3 = 3a, y = a 3 +, y 2 = a 3 + 2, y 3 = 3a, z = 9a a 3 + 3, a Z, then we obtain a solution. OQ4927. Solve in Z the equation x y 3 + x 2y 3 2 = x 3y 2 3. If x = a + 2b, y = a, x 2 = b, y 2 = 2a + 3b, x 3 = a + b, y 3 = a + 3b, a, b Z, then we obtain a solution. OQ4928. Solve in Z the equation x 3 + y 3 + z 3 = 3t 3. If x = 2a 3 + 6a 8, y = 2a 3 6a 8, z = 6a 2 + 0, t = 2a 2 2, a Z, then we obtain a solution. OQ4929. Solve in Z the equation x 3 + y 3 + z 3 = 6t 3. If x = a 3 + 9a a + 9, y = a 3 9a 2 39a 35, z = 6a a + 70, t = 4a a + 56, a Z, then we obtain a solution. OQ4930. Solve in Z the equation x 4 + 4y 4 = z 4 + 3t 4. If x = 2a 8 6a 4, y = 2a 7, z = 2a 8 + 6a 4, t = 2a, a Z, then we obtain a solution. h i h i OQ493. Denote F (n) = e π n and G (n) = π e n, when [ ] denote the integer part. Compute ). k= F (k) 2). k= G(k) 3). k= F (k)+g(k)
12 Open Questions 775 4). k= ( ) k+ F (k)g(k) 5). k= ( ) k+ F 2 (k)+g 2 (k) OQ4932. Solve in Z the equation x y 2 = 2 n. OQ4933. Solve in Z the equations x 2 207y 2 = 2 n, and z 3 207t 3 = 2 m. OQ4934. Solve in Z the equation 2x 3 + y 3 7z 3 = 3 n. OQ4935. Solve in Z the equation x 4 + 2y 4 = z 4 + 6t 4. If x = 48a 2 2a 4, y = 48a 7, z = 48a 8 + 2a 4, t = 2a, a Z, then we obtain a solution. OQ4936. Solve in Z the equation 2x 3 + y 3 + 7z 3 = t 3. OQ4937. Solve in Z the equation x 6 + y6 + 2z t 6 = x6 2 + y z 2 t 6 2. If x = au 6 + bv 6, y = bu 6 v 6, z = ab a 4 b 4, t = uv 5, x 2 = au 6 bv 6, y 2 = au 6 + bv 6, z 2 = au a 4 b 4, t 2 = u 5 v, when a, b, u, v Z, then we obtain a solution. OQ4938. Solve in Z the equation x 3 + y 3 + z 3 = ut 3. If x = 27a 3 b 9, y = 27a 3 + 9ab 6 + b 9, z = 27a 2 b 3 + 9ab 6, u = a, t = 27a 2 b 2 + 9ab 5 + 3b 8, a, b Z then we obtain a solution. OQ4939. Solve in Z the equation x y z 24 + t 7 = u 7. If x = a, y = a, z = a, t = a , u = a , a Z, then we obtain a solution.
13 776 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4940. Solve in Z the equation 2x 7 + y z 7 = 207 t 7. OQ494. Solve in Z the equation 2x 5 + y z 3 = 207t 3. OQ4942. Solve in Z the equation x n = yz m tu r, when n, m, r N. OQ4943. Solve in Z the equation n k= a k b n k =. OQ4944. Solve in Z the equation x 3 + y 4 + z 5 + t 7 + u 8 = v 8. If x = a 4, y = a, z = a 4, t = a 4, u = a , v = a a Z then we obtain a solution. OQ4945. Solve in Z the equation x 5 = yz 2 tu 2. If x = a b, y = a, z = a 2 + 0ab + 5b 2, t = b, u = 5a 2 + 0ab + b 2, a, b Z then we obtain a solution. OQ4946. Solve in Z the equation x 7 = yz 2 tu 2. If x = a b, y = a, z = a 3 + 2a 2 b + 35ab 2 + 7b 3, t = b, u = 7a a 2 b + 2ab 2 + b 3, a, b Z then we obtain a solution. OQ4947. Solve in N the equation n Q k=0 (m + k) + x p = y r. Remark. If m =, n n, x =, r = 2, then we get n! + = m 2 which have the solutions (n, m) {(4, 5), (5, ), (7, 7)} and Erdős conjectured thad these are the only ones solutions.
14 Open Questions 777 OQ4948. Solve in Z the equation x 3 = yz 2 tu 2. If x = a b, y = a, z = a + 3b, t = b, u = 3a + b, a, b Z then we obtain a solution. OQ4949. Solve in Z the equation x k + y k + 2z k = x k 2 + yk 2 + 2zk 2, when k {, 5}. If x = 8a 6 + 2ab 5, y = 8a 5 b + b 6, z = 8b 6, x 2 = 8a 6 + 2ab 5, y 2 = 8a 5 b b 6, z 2 = a 6, a, b Z then we obtain a solution. OQ4950. Solve in Z the equation x 5 + x5 2 + x5 3 = y5 + y5 2 + y5 3. If x = a a 3 2a 5 + a 9, x 2 = + a 2 2a 6 + 2a 7 + a 8, x 3 = 2a 3 + 2a 4 2a 7, y = a + 3a 3 2a 5 + a 9, y 2 = + a 2 2a 6 2a 7 + a 8, y 3 = 2a 3 + 2a 4 + 2a 7, a Z then we obtain a solution. OQ495. Solve in Z the equation x y 3 + x 2y 3 2 = z t 3 + z 2t 3 2. If x = + 6a 6a 2 + 5a 4 + 7a 6, y = a + 3a 2 2a 3 + a 5 + a 7, x 2 = 2a 8a 3 5a 4 + 6a 5, y 2 = + a 2 2a 4 3a 5 + a 6 z = 6a 6a 2 + 5a 4 + 7a 6 t = a 3a 2 2a 3 + a 5 + a 7 z 2 = 2a 8a 3 + 5a 4 + 6a 5 t 2 = + a 2 2a 4 + 3a 5 + a 6, a Z then we obtain a solution. OQ4952. Solve in Z the equation x 4 + y 4 = z 4 + 2t 4. If x = 92n 7, y = 92n 8 24n 4, z = 92n n 4, t = 2n, n Z then we obtain a solution. OQ4953. Solve in Z the equation 4x 24 + y z 3 = tu 3 +. If x = a, y = 6a 4, z = 92a 8 24a 4, t = 6a 4 +, u = 92a a 4, a Z then we obtain a solution.
15 778 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4954. Solve in Z the equation x 2 y 2 εz 2 =, where ε {, }. If x = 2a 2 + ε, y = 2a 2, z = 2a, a Z then we obtain a solution. OQ4955. Solve in Z the equation x 3 y 3 εz 3 t 3 u 3 = ε, where ε {, }. If x = 3a 2 + ε, y = 3a 3, z = 3a 2, t = 2a, u = a, a Z then we obtain a solution. OQ4956. Solve in Z the equation x 4 y 4 εz 4 εt 4 u 4 v 4 + w 4 =, when ε {, }. If x = 4a 4 + ε, y = 4a 4, z = 4a 3, t = 2a, u = 3a 2, v = 2a 2, w = a 2, a Z then we obtain a solution. OQ4957. Solve in Z the equation x 3 y 4 = 8z u 2 + v 2. If x = a + b, y = a b, z = ab, u = a, v = b, a, b Z then we obtain a solution. OQ4958. Solve in Z the equation x y 3 + z 3 + t 3 6u = 3v s 2 + r 2 + p 2. If x = a + b + c, y = a, z = b, t = c, u = abc, v = a + b + c, s = a, r = b, p = c, a, b, c Z then we obtain a solution. OQ4959. Solve in Z the equation x 3 + 3y 3 + 4z 3 + t 3 = 239. If x = 5, y = 3, z = 2, t = then we obtain a solution. OQ4960. Solve in Z the equation x x 2 x 3 x 4 + y 4 = z 2. If x = a + b, x 2 = a + 2b, x 3 = a + 3b, x 4 = a + 4b, y = b, z = a 2 + 5ab + 5b 2, a, b Z then we obtain a solution. OQ496. Solve in Z the equation x x 2 x 3 x 4 + y 4 = z 2 + t 2.
16 Open Questions 779 OQ4962. Solve in Z the equation x 4 + x4 2 + x4 3 = y4 + y4 2 + y4 3. If x = a 4 b 2b, x 2 = ab 4 + 2a, x 3 = 2a 3 b, y = a 4 b + 2b, y 2 = ab 4 2a, y 3 = 2ab 3, a, b Z then we obtain a solution. OQ4963. Solve in Z the equation x 4 + y 4 + 4z 4 = t 4. If x = a 4 2b 4, y = 2a 3 b, z = 2ab 3, t = a 4 + 2b 4, a, b Z then we obtain a solution. OQ4964. Solve in Z the equation x x 2 x 3 x 4 + y y 2 y 3 y 4 + 2z 4 = u 2 + v 2. If x = a + b, x 2 = a + 2b, x 3 = a + 3b, x 4 = a + 4b, y = a + b, y 2 = 3a + 2b, y 3 = 5a + 3b, y 4 = 5a + b, z = b, u = a 2 + 5ab + 5b 2, v = 5a 2 + 9ab + 5b 2, a, b Z then we obtain a solution. OQ4965. Solve in Z the equation x x 2 x 3 x 4 x 5 x 6 + 9y 6 = z 2. If x = 2a + b, x 2 = 2a + 2b, x 3 = 3a + 3b, x 4 = 2a + 4b, x 5 = 2a + 5b, x 6 = 2a + 6b, y = b, z = 2a s 2 b + 72ab b 3, a, b Z then we obtain a solution. OQ4966. Solve in Z the equation x 2 + y 2 = z 2 + u + v 2 2. If x = a 2 + ab + b 2, y = c 2 + cd + d 2, z = a + b, u = (a + b) (c + d), v = c + d when a, b, c, d Z, then we obtain a solution. OQ4967. Solve in Z the equation x 2 + y 2 = z 2 + t 2 v. If x = a 2 + b 2 a + 2ab 2, y = a 2 + b 2 b + 2a 2 b, z = a, t = b, v = a 4 + 4a 2 b 2 + b 4 ; a, b Z then we obtain a solution. OQ4968. Solve in Z the equation x 2 + y 2 = z 3. If x = a 2 b 2 a 2ab 2, y = a 2 b 2 b + 2a 2 b, z = a 2 + b 2 ; a, b Z then we obtain a solution. OQ4969. Solve in Z the equation x 5 + x5 2 + x5 3 = y5 + y5 2 + y5 3. If x = a b 5, x 2 = a 5 25b 5, x 3 = 0a 3 b 2, y = a b 5, y 2 = a 5 75b 5,
17 780 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 y 3 = 50ab 4 ; a, b Z then we obtain a solution. OQ4970. Solve in Z the equation x 2 + y 2 = 2 + z 2. If x = 2a +, y = 2a 2 + 2a, z = 2a 2 + 2a, a Z then we obtain a solution. OQ497. Solve in Z the equation x 3 + y 3 + z 3 = 2. If x = 6a 3 +, y = 6a 3 +, z = 6a 2 ; a Z then we obtain a solution. OQ4972. Solve in Z the equation x 4 + y 4 + z 4 = 2 + t 4 + u 4. If x = 8a 5 2a, y = 8a 4 +, z = 8a 4, t = 8a 5 + 2a, u = 4a 2 ; a Z then we obtain a solution. OQ4973. Solve in Z the equation x 5 + y 5 + z 5 + t 5 + 2u 5 = 2. If x = 8a 6 + 2a, y = 8a 6 2a, z = 8a 5 +, t = 8a 5 +, u = 8a 6, a Z then we obtain a solution. OQ4974. Solve in Z the equation x k + y k + z k = t k + u k + v k, when k {2, 6}. If x = ad + b, y = c 2d, z = de + f, t = de f, u = c + 2d, v = ad b, a = 4s + r, b = r, c = 2 (s 3r) (s 2r) + r 2, d = s r, e = 2s 3r, f = 2s 5r, s 2 6r 2 = ; s, r Z then we obtain a solution. OQ4975. Let n be a composite number such L n (mod n), this is defined as Lucas pseudoprimes, when L n denote the Lucas number. Denote L the set of Lucas pseudoprimes. Compute p L p 2. OQ4976. Let F k and L k denote the k th Fibonacci respective Lucas numbers, and p be a prime, f a (n) = a n F k and g p k a (n) = a n where [ ] denote the integer part. k=0 k=0 L k p k
18 Open Questions 78 Determine all a, b > 0 and n N for which f a (n) and g a (n) are prime. OQ4977. Denote n the n th ell number. Determine all a, b, a i, b i N (i =, 2,..., r), for which an+b 2 k = an +b + a2n +b arn +b 3 k=0 when a = a + a a r and b = b + b b r. OQ4978. Denote F k the k th Fibonacci number. Determine all p N for p which = n= ( ) n+ F nf n+...f n+p. OQ4979. Determine a recurrence relation for the sequence x n = [π n ] and compute the general form, where [ ] denote the integer part. Same question for the sequence y n = [e n ]. OQ4980. Compute ). α (p) = k= 3). γ (p) = k= ( ) k+ F k F k+...f k+p ( ) k+ k k+... k+p 2). β (p) = k= ( ) k+ L k L k+...l k+p OQ498. Compute ). α (p) = k= 3). γ (n) = k= ( ) k+ F n +F n F n k ( ) k+ n + n n k OQ4982. Compute k= ( ) k+ Fn k +L n k +. k n 2). β (n) = k= ( ) k+ L n +Ln Ln k
19 782 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ4983. Compute OQ4984. Compute ). 2). 3). k= ( ) k+ F k +F 2 k= 2k+ +F 3k F p pn+p ( ) k+ L k +L 2 k= 2k+ +L3 3k Lp pn+p ( ) k+ k + 2 k= 2k+ + 3k p pn+p OQ4985. Compute ). 2). k= k= ( ) k+ (F k +L k ) p +(L k + k ) p +( k +F k ) p ( ) k+ F Lk +L k + Fk 3). ( ) k+ (F k L k ) n +(L k k ) n +( k F k ) n. k= F L k k ( ) k+ +L k k + F k k OQ4986. Compute ). 3). k= k= ( ) k+ F k L k F 2 k +L2 k ( ) k+ F k k F 2 k + 2 k 2). k= ( ) k+ L k k L 2 k + 2 k OQ4987. Compute ). 3). k= ( ) k+ F k L k k F 3 k +L3 k + 3 k ( ) k F k k= k +Lk k + k k 2). k= ( ) k+ F k+k 2 +L k+k 2+ k+k 2
20 Open Questions 783 OQ4988. Solve in Z the equation 2 x 2 + y 2 z 2 t 2 = u 4 v 4. If x = a, y b, z = a + b, t = a b, u = a + b, v = a b, a, b Z, then we obtain a solution. OQ4989. Solve in Z the equation x 3 + y 3 + z 3 + t 3 = 24u. If x = a + b + c, y = a + b c, z = a b + c, t = a b c, u = abc, then we obtain a solution. OQ4990. Solve in Z the equation 6 x 2 + y 2 + z 2 x 3 + x3 2 + x3 3 + x3 4 = 3 x x x5 7 + x5 8. If x = a, y = b, z = c, x = a + b + c, x 2 = a + b + c, x 3 = a b + c, x 4 = a b c, x 5 = a + b + c, x 6 = a + b + c, x 7 = a b + c, x 8 = a b c, a, b, c Z, then we obtain a solution. OQ499. Solve in Z the equation 5 x 2 + y 2 + z 2 + t 2 x 4 + x4 2 + x4 3 + x4 4 x4 5 x4 6 x4 7 8 x4 = y 6 + y6 2 + y6 3 + y6 4 z6 z6 2 z6 3 z6 4. If x = a, y = b, z = c, t = d, x = a + b + c d, x 2 = a + b c + d, x 3 = a + b + c + d, x 4 = a + b + c + d, x 5 = 2a, x 6 = 2b, x 7 = 2c, x 8 = 2d, y = a + b + c + d, y 2 = a + b c + d, y 3 = a + b + c + d, y 4 = a + b + c + d, z = 2a, z 2 = 2b, z 3 = 2c, z 4 = 2d, a, b, c, d Z then we obtain a solution. OQ4992. Solve in Z the equation x 2 + y 2 z 2 + t 2 = u 2 + v 2. If x = a, y = a 2, z = b, t = b 2, u = a b + a 2 b 2, v = a b 2 a 2 b, a, a 2, b, b 2 Z then we obtain a solution. OQ4993. Solve in Z the equation x 2 + x x2 3 y 2 + y2 2 + y3 3 = z 2 + z2 2 + z2 3 + z4 4. If x, x 2, x 3, y, y 2, y 3 Z and z = x y + x 2 y 2 + x 3 y 3, z 2 = x y 2 x 2 y, z 3 = x y 3 x 3 y, z 4 = x 2 y 3 x 3 y 2 then we obtain a solution.
21 784 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 n OQ4994. Solve in Z the equation a 2 k k= n b 2 k k= = n c 2 k + k= i<j n If c k = a k b k (k =, 2,..., n) and d ij = a i b j a j b i ( i, j n) then we obtain a solution. d 2 ij. OQ4995. Solve in Z the equation x 4 x4 2 x4 3 x4 4 + x4 5 + x4 6 + x4 7 x4 8 = 92y. If x = a + b + c + d, x 2 = a b + c + d, x 3 = a + b + c + d, x 4 = a + b + c d, x 5 = a b c + d, x 6 = a b + c + d, x 7 = a + b c d, x 8 = a b c d, y = abcd, a, b, c, d Z, then we obtain a solution. OQ4996. Solve in Z the equation 6 x 2 + y 2 3 = z 6 + t u 6 + v 6. If x = a, y = b, z = a + b, t = a b, u = a, v = b, a, b Z, then we obtain a solution. OQ4997. Solve in Z the equation 2 i= x 6 i = 6 y 2 + y2 2 + y2 3 + k y2 2 4 for k {2, 4}. If x = a + b, x 2 = a + c, x 3 = a + d, x 4 = b + c, x 5 = b + d, x 6 = c + d, x 7 = a b, x 8 = a c, x 9 = a b, x 0 = b c, x = b d, x 2 = c d, y = a, y 2 = b, y 3 = c, y 4 = d, a, b, c, d Z, then we obtain a solution. OQ4998. Solve in Z the equation x 3 + y 3 + z 3 = t 3. If x = a 4 2ab, y = a 3 b + b 4, z = 2a 3 b b 4, t = a 4 + ab 3, a, b Z, then we obtain a solution. OQ4999. Solve in Z the equation x3 +x3 2 +x3 3 +x3 4 = z 3. If x y 3 = ap q, +y3 2 +y3 3 +yy 4 x 2 = bp q, x 3 = cp + q, x 4 = dp + q, y = a, y 2 = b, y 3 = c, y 4 = d, z = a + b + c + d, {p, q} = a + b + c + d, a 2 + b 2 c 2 d 2, then we obtain a solution.
22 OQ5000. Solve in Z the equation Open Questions k= x 5 k = 2. If x = + ax 5, x 2 = ax 5, x 3 = + bx 5, x 4 = bx 5, x 5 = + cx 5, x 6 = cx 5, x 7 = dx 4, {a, b, c, d} = {270, 360, 450, 80}, x Z then we obtain a solution. OQ500. Solve in Z the equation x 3 + y 3 + z 3 + t 3 = 36u 2. If x = a, y = a, z = c +, t = c +, a 2 + 6b 2 = c 2, a, b, c Z, then we obtain a solution. OQ5002. Solve in Z the equation x 5 + x5 2 + x5 3 + x5 4 + x5 5 + x5 6 = 0. If x = a a 3 2a 5 + a 9, x 2 = + a 2 2a 6 + 2a 7 + a 8, x 3 = 2a 3 + 2a 4 2a 7, x 4 = a + 3a 3 2a 5 + a 9, x 5 = + a 2 2a 6 2a 7 + a 8, x 6 = 2a 3 2a 4 2a 7, a Z, then we obtain a solution. OQ5003. Solve in Z the equation x 4 + y 4 = z 4 + 2t 4. If x = 92a 8 24a 4, y = 92a 7, z = 92a a 4, t = 2a, a Z, then we obtain a solution. OQ5004. Solve in Z the equation x 8 + y 8 + z 4 = 2t 2. If x = a + b, y = a b, z = 4ab, t = a 4 + 4a 2 b 2 + b 4, a, b Z, then we obtain a solution. OQ5005. Soolve in Z the equation 2x 4 + 2y 4 + z 4 = t 4. If x = 4a 3, y = 2a, z = 4a 4, t = 4a 4 +, a Z, then we obtain a solution. OQ5006. Solve in Z the equation x 8 + 7y 8 + 7z 8 + t 8 + u 8 = v 8. If x = 2 4 a 7, y = 2 3 a 5, z = 2 2 a 3, t = 2a, u = 6a 8, v = 6a 8 +, a Z, then we obtain a solution.
23 786 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ5007. Solve in Z the equation x x x x x x x6 7 + x x6 9 = 8x6 If x = 2 8 a 5, x 2 = 2 7 a 3, x 3 = 2 6 a, x 4 = 2 5 a 9, x 5 = 2 4 a 7, x 6 = 2 3 a 5, x 7 = 2 2 a 3, x 8 = 2a, x 9 = 256a 6, x 0 = 256a 6 +, a Z, then we obtain a solution. 0. OQ5008. Solve in Z the equation x 8 + 7y 8 + z 8 + t 8 + u 8 = v 8. If x = 2 3n+2, y = 2 5n+3, z = 2 n+, t = 2 7n+4, u = 8 2n+4, v = 2 8n+4 +, n N, then we obtain a solution. OQ5009. Solve in Z the equation 96x y 3 = z 3. If x = a, y = 4a 4, z = 4a 4 +, a Z, then we obtain a solution. OQ500. Solve in Z the equation x y z t 7 = u 7. If x = a, y = a, z = a, t = 6a 8, u = 6a 8 +, a Z, then we obtain a solution. OQ50. Solve in Z the equation x y z t u v w r 5 = s 5. If x = a, y = a, z = a, t = a, u = a, v = a, w = a, r = 256a 6, s = 256a 6 +, a Z, then we obtain a solution. OQ502. Solve in Z the equation x3 y+ + y3 z+ + z3 x+ = 8. OQ503. Solve in Z the equation x 5 y y5 z z5 x+207 = OQ504. Solve in Z the equation x 4 + y 4 = z 4 + t 4. If x = a + 3a 2 2a 3 + a 5 + a 7, y = + a 2 2a 4 3a 5 + a 6, z = a 3a 2 2a 3 + a 5 + a 7, t = + a 2 2a 4 + 3a 5 + a 6, a Z,
24 Open Questions 787 then we obtain a solution. OQ505. If a k > 0 (k =, 2,..., n), then n a a 2 +a a n + a a 2...a n n + n2 n. k= a n k OQ506. Solve in Z the equation n Q k= + x k = n. OQ507. Determin all x k R (k =, 2,..., n), x i 6= x j (i 6= j) for which m m m x x 2 + x2 x xn x N for all m N. OQ508. If a k > 0 (k =, 2,..., n), then n a a +a 2 + a a 2 n a 2 k k= + n2 2. nq OQ509. Let a k 2p (k =, 2,..., n) be positive integers such that k= is divisible by Q a 2p a 2p 2 a a 2p 2. Determine all n, p N cyclic for which (a, a 2,..., a n ) =. OQ5020. Solve in Z the equation n a 2p s n nq x k = a + n x k, when a Z. k= s nq OQ502. Solve in Z the equation n x k = a + k= k= n n k=, when a Z. x k
25 788 Octogon Mathematical Magazine, Vol. 24, No.2, October 206 OQ5022. Determine all magic squares M = (a ij ) i,j n, when a ij = F i + L j, F i the i th Fibonacci number, L j the j th Lucas number. OQ5023. Determine all magic squares M = (a ij ) i,j n where a ij = 0 n sin 2 b ij ( i, j n) when [ ] denote the integer part and b ij = p i+j (p prime). OQ5024. Let be p ij ( i, j n) prime numbers and p ij = 0, a i a i2...a in... (i =, 2,...). Determine all magic squares M = (a ij ) i,j n. OQ5025. Determine all magic squares M = (a ij ) i,j n for which a ij = p k ij ( i, j n) where k N and p ij are prime numbers. OQ5026. rove that don t exist prime p and q such that tgp = q. OQ5027. rove that don t exist prime p and q such that ctgp = q. OQ5028. rove that don t exist prime p and q such that sin p = q. OQ5029. rove that don t exist prime p and q such that cos p = q.
26 OQ5030. If x k > 0 (k =, 2,..., n), then x x 2 x p x 2... x 2 x 2 2 x p +xp Open Questions 789 x x x p 2 +x p 2 x 3, when p N, p 2. OQ503. If a k > s 0 (k =, 2,..., n), then determine all x, y > 0 for which (x + y) n a k x 4 n r n a 4 k + y a ( n a 2. 2) k= k= cyclic OQ5032. Compute n=0 (n!) k (kn+)!(kn+2)!...(kn+k )!. OQ5033. Let ABC be a triangle, determine the best constants u, v, u 2, v 2 0 for which u R+v r m a + m b + m c u 2 R+v 2 r is the best possible. Remark. u = 4 9, v = 9, u 2 = 0, v 2 = is a solution. OQ5034. If x k > 0 (k =, 2,..., n), then n x 6 k k= x 3 x3 2 cyclic + x x 2 cyclic n x 2 k k= 2. OQ5035. Compute + f()+f(2) 2 + f()+f(2)+f(3) f()+f(2)+f(3)+f(4) for the cases: ). f (k) = k 2). f (k) = p k 3). f (k) = F k 4). f (k) = L k
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION. Sunday, March 14, 2004 Time: hours No aids or calculators permitted.
 THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
MeritPath.com. Problems and Solutions, INMO-2011
 Problems and Solutions, INMO-011 1. Let,, be points on the sides,, respectively of a triangle such that and. Prove that is equilateral. Solution 1: c ka kc b kb a Let ;. Note that +, and hence. Similarly,
Problems and Solutions, INMO-011 1. Let,, be points on the sides,, respectively of a triangle such that and. Prove that is equilateral. Solution 1: c ka kc b kb a Let ;. Note that +, and hence. Similarly,
HEAGAN & CO., OPP. f>, L. & W. DEPOT, DOYER, N. J, OUR MOTTO! ould Iwv ia immediate vltlui. VEEY BEST NEW Creamery Butter 22c ib,
 #4 NN N G N N % XX NY N Y FY N 2 88 N 28 k N k F P X Y N Y /» 2«X ««!!! 8 P 3 N 0»9! N k 25 F $ 60 $3 00 $3000 k k N 30 Y F00 6 )P 0» «{ N % X zz» «3 0««5 «N «XN» N N 00/ N 4 GN N Y 07 50 220 35 2 25 0
#4 NN N G N N % XX NY N Y FY N 2 88 N 28 k N k F P X Y N Y /» 2«X ««!!! 8 P 3 N 0»9! N k 25 F $ 60 $3 00 $3000 k k N 30 Y F00 6 )P 0» «{ N % X zz» «3 0««5 «N «XN» N N 00/ N 4 GN N Y 07 50 220 35 2 25 0
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
is equal to = 3 2 x, if x < 0 f (0) = lim h = 0. Therefore f exists and is continuous at 0.
 Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
Madhava Mathematics Competition January 6, 2013 Solutions and scheme of marking Part I N.B. Each question in Part I carries 2 marks. p(k + 1) 1. If p(x) is a non-constant polynomial, then lim k p(k) (a)
Australian Intermediate Mathematics Olympiad 2014
 5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
5. Let 1 a + 1 b = 1 20, where a and b are positive integers. Find the largest value of a + b. [4 marks] A u s t r a l i a n M at h e m at i c a l O ly m p i a d C o m m i t t e e a d e p a r t m e n t
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
INTERNATIONAL MATHEMATICAL OLYMPIADS. Hojoo Lee, Version 1.0. Contents 1. Problems 1 2. Answers and Hints References
 INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
Number Theory Marathon. Mario Ynocente Castro, National University of Engineering, Peru
 Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
Number Theory Marathon. Mario Ynocente Castro, National University of Engineering, Peru
 Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
Number Theory Marathon Mario Ynocente Castro, National University of Engineering, Peru 1 2 Chapter 1 Problems 1. (IMO 1975) Let f(n) denote the sum of the digits of n. Find f(f(f(4444 4444 ))). 2. Prove
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
2008 Euclid Contest. Solutions. Canadian Mathematics Competition. Tuesday, April 15, c 2008 Centre for Education in Mathematics and Computing
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 008 Euclid Contest Tuesday, April 5, 008 Solutions c 008
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
History of Mathematics Workbook
 History of Mathematics Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: April 7, 2014 Student: Spring 2014 Problem A1. Given a square ABCD, equilateral triangles ABX
History of Mathematics Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: April 7, 2014 Student: Spring 2014 Problem A1. Given a square ABCD, equilateral triangles ABX
Collinearity/Concurrence
 Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
Collinearity/Concurrence Ray Li (rayyli@stanford.edu) June 29, 2017 1 Introduction/Facts you should know 1. (Cevian Triangle) Let ABC be a triangle and P be a point. Let lines AP, BP, CP meet lines BC,
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
International Mathematical Talent Search Round 26
 International Mathematical Talent Search Round 26 Problem 1/26. Assume that x, y, and z are positive real numbers that satisfy the equations given on the right. x + y + xy = 8, y + z + yz = 15, z + x +
International Mathematical Talent Search Round 26 Problem 1/26. Assume that x, y, and z are positive real numbers that satisfy the equations given on the right. x + y + xy = 8, y + z + yz = 15, z + x +
CAREER POINT. PRMO EXAM-2017 (Paper & Solution) Sum of number should be 21
 PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
PRMO EXAM-07 (Paper & Solution) Q. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3? Sum
TEST CODE: MMA (Objective type) 2015 SYLLABUS
 TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
The 3rd Olympiad of Metropolises
 The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
= 10 such triples. If it is 5, there is = 1 such triple. Therefore, there are a total of = 46 such triples.
 . Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
. Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
Hanoi Open Mathematical Competition 2016
 Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
Hanoi Open Mathematical Competition 2016 Junior Section Saturday, 12 March 2016 08h30-11h30 Question 1. If then m is equal to 2016 = 2 5 + 2 6 + + 2 m, (A): 8 (B): 9 (C): 10 (D): 11 (E): None of the above.
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
2013 University of New South Wales School Mathematics Competition
 Parabola Volume 49, Issue (201) 201 University of New South Wales School Mathematics Competition Junior Division Problems and s Problem 1 Suppose that x, y, z are non-zero integers with no common factor
Parabola Volume 49, Issue (201) 201 University of New South Wales School Mathematics Competition Junior Division Problems and s Problem 1 Suppose that x, y, z are non-zero integers with no common factor
Moreover this binary operation satisfies the following properties
 Contents 1 Algebraic structures 1 1.1 Group........................................... 1 1.1.1 Definitions and examples............................. 1 1.1.2 Subgroup.....................................
Contents 1 Algebraic structures 1 1.1 Group........................................... 1 1.1.1 Definitions and examples............................. 1 1.1.2 Subgroup.....................................
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
Baltic Way 2016 Solutions
 Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle?
 1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
40th Canadian Mathematical Olympiad
 40th Canadian Mathematical Olympiad Wednesday, March 26, 2008 Solutions - CMO 2008 1. ABCD is a convex quadrilateral in which AB is the longest side. Points M and N are located on sides AB and BC respectively,
40th Canadian Mathematical Olympiad Wednesday, March 26, 2008 Solutions - CMO 2008 1. ABCD is a convex quadrilateral in which AB is the longest side. Points M and N are located on sides AB and BC respectively,
Vectors - Applications to Problem Solving
 BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
BERKELEY MATH CIRCLE 00-003 Vectors - Applications to Problem Solving Zvezdelina Stankova Mills College& UC Berkeley 1. Well-known Facts (1) Let A 1 and B 1 be the midpoints of the sides BC and AC of ABC.
Concurrency and Collinearity
 Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
Concurrency and Collinearity Victoria Krakovna vkrakovna@gmail.com 1 Elementary Tools Here are some tips for concurrency and collinearity questions: 1. You can often restate a concurrency question as a
2007 Mathematical Olympiad Summer Program Tests
 2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
14 th Annual Harvard-MIT Mathematics Tournament Saturday 12 February 2011
 14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
11 is the same as their sum, find the value of S.
 Answers: (998-99 HKMO Final Events) Created by: Mr. Francis Hung Last updated: July 08 Individual Events I P 4 I a 8 I a 6 I4 a I5 a IS a Q 8 b 0 b 7 b b spare b 770 R c c c c 0 c 57 S 0 d 000 d 990 d
Answers: (998-99 HKMO Final Events) Created by: Mr. Francis Hung Last updated: July 08 Individual Events I P 4 I a 8 I a 6 I4 a I5 a IS a Q 8 b 0 b 7 b b spare b 770 R c c c c 0 c 57 S 0 d 000 d 990 d
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
Winter Mathematical Competition Varna, February, 9-11, 2007
 Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE]
![DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] DISCUSSION CLASS OF DAX IS ON 22ND MARCH, TIME : 9-12 BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE]](/thumbs/90/102188445.jpg) DISCUSSION CLASS OF DAX IS ON ND MARCH, TIME : 9- BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] Q. Let y = cos x (cos x cos x). Then y is (A) 0 only when x 0 (B) 0 for all real x (C) 0 for all real x
DISCUSSION CLASS OF DAX IS ON ND MARCH, TIME : 9- BRING ALL YOUR DOUBTS [STRAIGHT OBJECTIVE TYPE] Q. Let y = cos x (cos x cos x). Then y is (A) 0 only when x 0 (B) 0 for all real x (C) 0 for all real x
OLYMON. Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Issue 7:2.
 OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
The Advantage Testing Foundation Olympiad Solutions
 The Advantage Testing Foundation 014 Olympiad Problem 1 Say that a convex quadrilateral is tasty if its two diagonals divide the quadrilateral into four nonoverlapping similar triangles. Find all tasty
The Advantage Testing Foundation 014 Olympiad Problem 1 Say that a convex quadrilateral is tasty if its two diagonals divide the quadrilateral into four nonoverlapping similar triangles. Find all tasty
ISI B.STAT/B.MATH OBJECTIVE QUESTIONS & SOLUTIONS SET 1
 1 Blog: www.ctanujit.in Ph: +91-84053573 ISI B.STAT/B.MATH OBJECTIVE QUESTIONS & SOLUTIONS SET 1 1. How many zeros are at the end of 1000!? (a) 40 (b) 48 (c) 49 (d) None Ans:- (c) The number of two s is
1 Blog: www.ctanujit.in Ph: +91-84053573 ISI B.STAT/B.MATH OBJECTIVE QUESTIONS & SOLUTIONS SET 1 1. How many zeros are at the end of 1000!? (a) 40 (b) 48 (c) 49 (d) None Ans:- (c) The number of two s is
BC Exam Solutions Texas A&M High School Math Contest October 24, p(1) = b + 2 = 3 = b = 5.
 C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
C Exam Solutions Texas &M High School Math Contest October 4, 01 ll answers must be simplified, and If units are involved, be sure to include them. 1. p(x) = x + ax + bx + c has three roots, λ i, with
Math Day at the Beach 2017 Solutions
 Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Solutions. cos ax + cos bx = 0. a sin ax + b sin bx = 0.
 Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
Elementary Differential Equations, Section 2 Prof. Loftin: Practice Test Problems for Test Find the radius of convergence of the power series
 Elementary Differential Equations, Section 2 Prof. Loftin: Practice Test Problems for Test 2 SOLUTIONS 1. Find the radius of convergence of the power series Show your work. x + x2 2 + x3 3 + x4 4 + + xn
Elementary Differential Equations, Section 2 Prof. Loftin: Practice Test Problems for Test 2 SOLUTIONS 1. Find the radius of convergence of the power series Show your work. x + x2 2 + x3 3 + x4 4 + + xn
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
Solutions 2017 AB Exam
 1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
1. Solve for x : x 2 = 4 x. Solutions 2017 AB Exam Texas A&M High School Math Contest October 21, 2017 ANSWER: x = 3 Solution: x 2 = 4 x x 2 = 16 8x + x 2 x 2 9x + 18 = 0 (x 6)(x 3) = 0 x = 6, 3 but x
SOLUTIONS OF 2012 MATH OLYMPICS LEVEL II T 3 T 3 1 T 4 T 4 1
 SOLUTIONS OF 0 MATH OLYMPICS LEVEL II. If T n = + + 3 +... + n and P n = T T T 3 T 3 T 4 T 4 T n T n for n =, 3, 4,..., then P 0 is the closest to which of the following numbers? (a).9 (b).3 (c) 3. (d).6
SOLUTIONS OF 0 MATH OLYMPICS LEVEL II. If T n = + + 3 +... + n and P n = T T T 3 T 3 T 4 T 4 T n T n for n =, 3, 4,..., then P 0 is the closest to which of the following numbers? (a).9 (b).3 (c) 3. (d).6
Math Bootcamp 2012 Miscellaneous
 Math Bootcamp 202 Miscellaneous Factorial, combination and permutation The factorial of a positive integer n denoted by n!, is the product of all positive integers less than or equal to n. Define 0! =.
Math Bootcamp 202 Miscellaneous Factorial, combination and permutation The factorial of a positive integer n denoted by n!, is the product of all positive integers less than or equal to n. Define 0! =.
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
1. Matrices and Determinants
 Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
EGMO 2016, Day 1 Solutions. Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers.
 EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
T-2 In the equation A B C + D E F = G H I, each letter denotes a distinct non-zero digit. Compute the greatest possible value of G H I.
 2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
2016 ARML Local Problems and Solutions Team Round Solutions T-1 All the shelves in a library are the same length. When filled, two shelves side-by-side can hold exactly 12 algebra books and 10 geometry
The Alberta High School Mathematics Competition Solution to Part I, 2014.
 The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
The Alberta High School Mathematics Competition Solution to Part I, 2014. Question 1. When the repeating decimal 0.6 is divided by the repeating decimal 0.3, the quotient is (a) 0.2 (b) 2 (c) 0.5 (d) 0.5
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
International Mathematics TOURNAMENT OF THE TOWNS
 1 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Spring 2006. 1. Assume a convex polygon with 100 vertices is given. Prove that one can chose 50 points inside the polygon in such
1 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Spring 2006. 1. Assume a convex polygon with 100 vertices is given. Prove that one can chose 50 points inside the polygon in such
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca Euclid Contest. Thursday, April 6, 2017
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Euclid Contest Thursday, April 6, 017 (in North America and South America) Friday, April 7, 017 (outside of North America and
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 017 Euclid Contest Thursday, April 6, 017 (in North America and South America) Friday, April 7, 017 (outside of North America and
Sydney University Mathematical Society Problems Competition Solutions.
 Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
Sydney University Mathematical Society Problems Competition 005 Solutions 1 Suppose that we look at the set X n of strings of 0 s and 1 s of length n Given a string ɛ = (ɛ 1,, ɛ n ) X n, we are allowed
PRMO Solution
 PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
PRMO Solution 0.08.07. How many positive integers less than 000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?. Suppose a, b
B.Stat. (Hons.) & B.Math. (Hons.) Admission Test: 2013
 B.Stat. (Hons.) & B.Math. (Hons.) Admission Test: 013 Multiple-Choice Test Time: hours 1. Let i = 1 and S = {i+i + +i n : n 1}. The number of distinct real numbers in the set S is (A) 1 (B) (C) 3 (D) infinite..
B.Stat. (Hons.) & B.Math. (Hons.) Admission Test: 013 Multiple-Choice Test Time: hours 1. Let i = 1 and S = {i+i + +i n : n 1}. The number of distinct real numbers in the set S is (A) 1 (B) (C) 3 (D) infinite..
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD. A High School Competition Conducted by. And Sponsored by FIRST-LEVEL EXAMINATION SOLUTIONS
 46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
46th ANNUAL MASSACHUSETTS MATHEMATICS OLYMPIAD 009 00 A High School Competition Conducted by THE MASSACHUSETTS ASSOCIATION OF MATHEMATICS LEAGUES (MAML) And Sponsored by THE ACTUARIES CLUB OF BOSTON FIRST-LEVEL
2011 Olympiad Solutions
 011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
Math Day at the Beach 2017
 Math Day at the Beach 017 Multiple Choice Write your name and school and mark your answers on the answer sheet. You have 0 minutes to work on these problems. No calculator is allowed. 1. How many integers
Math Day at the Beach 017 Multiple Choice Write your name and school and mark your answers on the answer sheet. You have 0 minutes to work on these problems. No calculator is allowed. 1. How many integers
STEP Support Programme. Hints and Partial Solutions for Assignment 17
 STEP Support Programme Hints and Partial Solutions for Assignment 7 Warm-up You need to be quite careful with these proofs to ensure that you are not assuming something that should not be assumed. For
STEP Support Programme Hints and Partial Solutions for Assignment 7 Warm-up You need to be quite careful with these proofs to ensure that you are not assuming something that should not be assumed. For
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS
 CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
Pre-REGIONAL MATHEMATICAL OLYMPIAD, 2017
 P-RMO 017 NATIONAL BOARD FOR HIGHER MATHEMATICS AND HOMI BHABHA CENTRE FOR SCIENCE EDUCATION TATA INSTITUTE OF FUNDAMENTAL RESEARCH Pre-REGIONAL MATHEMATICAL OLYMPIAD, 017 TEST PAPER WITH SOLUTION & ANSWER
P-RMO 017 NATIONAL BOARD FOR HIGHER MATHEMATICS AND HOMI BHABHA CENTRE FOR SCIENCE EDUCATION TATA INSTITUTE OF FUNDAMENTAL RESEARCH Pre-REGIONAL MATHEMATICAL OLYMPIAD, 017 TEST PAPER WITH SOLUTION & ANSWER
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
Pre-Regional Mathematical Olympiad Solution 2017
 Pre-Regional Mathematical Olympiad Solution 07 Time:.5 hours. Maximum Marks: 50 [Each Question carries 5 marks]. How many positive integers less than 000 have the property that the sum of the digits of
Pre-Regional Mathematical Olympiad Solution 07 Time:.5 hours. Maximum Marks: 50 [Each Question carries 5 marks]. How many positive integers less than 000 have the property that the sum of the digits of
27th Russian Mathematics Olympiad
 27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
Some Basic Logic. Henry Liu, 25 October 2010
 Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
Some Basic Logic Henry Liu, 25 October 2010 In the solution to almost every olympiad style mathematical problem, a very important part is existence of accurate proofs. Therefore, the student should be
Divisibility in the Fibonacci Numbers. Stefan Erickson Colorado College January 27, 2006
 Divisibility in the Fibonacci Numbers Stefan Erickson Colorado College January 27, 2006 Fibonacci Numbers F n+2 = F n+1 + F n n 1 2 3 4 6 7 8 9 10 11 12 F n 1 1 2 3 8 13 21 34 89 144 n 13 14 1 16 17 18
Divisibility in the Fibonacci Numbers Stefan Erickson Colorado College January 27, 2006 Fibonacci Numbers F n+2 = F n+1 + F n n 1 2 3 4 6 7 8 9 10 11 12 F n 1 1 2 3 8 13 21 34 89 144 n 13 14 1 16 17 18
ANSWERS. CLASS: VIII TERM - 1 SUBJECT: Mathematics. Exercise: 1(A) Exercise: 1(B)
 ANSWERS CLASS: VIII TERM - 1 SUBJECT: Mathematics TOPIC: 1. Rational Numbers Exercise: 1(A) 1. Fill in the blanks: (i) -21/24 (ii) -4/7 < -4/11 (iii)16/19 (iv)11/13 and -11/13 (v) 0 2. Answer True or False:
ANSWERS CLASS: VIII TERM - 1 SUBJECT: Mathematics TOPIC: 1. Rational Numbers Exercise: 1(A) 1. Fill in the blanks: (i) -21/24 (ii) -4/7 < -4/11 (iii)16/19 (iv)11/13 and -11/13 (v) 0 2. Answer True or False:
2016 EF Exam Texas A&M High School Students Contest Solutions October 22, 2016
 6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
6 EF Exam Texas A&M High School Students Contest Solutions October, 6. Assume that p and q are real numbers such that the polynomial x + is divisible by x + px + q. Find q. p Answer Solution (without knowledge
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Recreational Mathematics
 Recreational Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2003 Chapters 5 8 Version 030630 Chapter 5 Greatest common divisor 1 gcd(a, b) as an integer combination of
Recreational Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2003 Chapters 5 8 Version 030630 Chapter 5 Greatest common divisor 1 gcd(a, b) as an integer combination of
Discovery Guide. Beautiful, mysterious woman pursued by gunmen. Sounds like a spy story...
 Dv G W C T Gp, A T Af Hk T 39 Sp. M Mx Hk p j p v, f M P v...(!) Af Hk T 39 Sp, B,,, UNMISSABLE! T - f 4 p v 150 f-p f x v. Bf, k 4 p v 150. H k f f x? D,,,, v? W k, pf p f p? W f f f? W k k p? T p xp
Dv G W C T Gp, A T Af Hk T 39 Sp. M Mx Hk p j p v, f M P v...(!) Af Hk T 39 Sp, B,,, UNMISSABLE! T - f 4 p v 150 f-p f x v. Bf, k 4 p v 150. H k f f x? D,,,, v? W k, pf p f p? W f f f? W k k p? T p xp
INVERSION IN THE PLANE BERKELEY MATH CIRCLE
 INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
Using Complex Weighted Centroids to Create Homothetic Polygons. Harold Reiter. Department of Mathematics, University of North Carolina Charlotte,
 Using Complex Weighted Centroids to Create Homothetic Polygons Harold Reiter Department of Mathematics, University of North Carolina Charlotte, Charlotte, NC 28223, USA hbreiter@emailunccedu Arthur Holshouser
Using Complex Weighted Centroids to Create Homothetic Polygons Harold Reiter Department of Mathematics, University of North Carolina Charlotte, Charlotte, NC 28223, USA hbreiter@emailunccedu Arthur Holshouser
2017 China Team Selection Test
 China Team Selection Test 2017 TST 1 1 Find out the maximum value of the numbers of edges of a solid regular octahedron that we can see from a point out of the regular octahedron.(we define we can see
China Team Selection Test 2017 TST 1 1 Find out the maximum value of the numbers of edges of a solid regular octahedron that we can see from a point out of the regular octahedron.(we define we can see
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
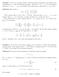 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
JEE/BITSAT LEVEL TEST
 JEE/BITSAT LEVEL TEST Booklet Code A/B/C/D Test Code : 00 Matrices & Determinants Answer Key/Hints Q. i 0 A =, then A A is equal to 0 i (a.) I (b.) -ia (c.) -I (d.) ia i 0 i 0 0 Sol. We have AA I 0 i 0
JEE/BITSAT LEVEL TEST Booklet Code A/B/C/D Test Code : 00 Matrices & Determinants Answer Key/Hints Q. i 0 A =, then A A is equal to 0 i (a.) I (b.) -ia (c.) -I (d.) ia i 0 i 0 0 Sol. We have AA I 0 i 0
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD
 SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
SOUTH AFRICAN TERTIARY MATHEMATICS OLYMPIAD. Determine the following value: 7 August 6 Solutions π + π. Solution: Since π
