Sufficient conditions, fields and the calculus of variations
|
|
|
- Percival Welch
- 5 years ago
- Views:
Transcription
1 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.1 (1-7) Historia Mathematica ( ) Essay Review Sufficient conditions, fields and the calculus of variations Craig G. Fraser Institute for the History and Philosophy of Science and Technology, University of Toronto, Ontario, Canada Von der Bernoullischen Brachistochrone zum Kalibrator-Konzept. Ein historisher Abriß zur Entstehung der Feldtheorie in der Variationsrechnung (hinreichende Bedingungen in der Variationsrechnung) By Rüdiger Thiele. De Diversis Artibus: Collection de Travaux de l Académie Internationale d Histoire des Sciences, vol. 80. Turnhout, Belgium (Brepolis Publishers) ISBN , 828 pp The problem of establishing sufficient conditions for the existence of a maximum or minimum was the outstanding problem of the calculus of variations in the 19th century. By the 1860s the investigation of the second variation had been developed into a successful theory by Carl Jacobi ( ), Alfred Clebsch ( ) and Adolph Mayer ( ). A new approach to the subject was initiated by Karl Weierstrass ( ) in his Berlin lectures of the late 1870s and early 1880s. Although Weierstrass s theory was purely analytic, certain aspects of his approach were amenable to geometric treatment, a fact that was made clear in Adolf Kneser s ( ) exposition in his 1900 Lehrbuch der Variationsrechnung [Kneser, 1900]. Kneser introduced explicitly the concept of a field, a set of solution curves to the Euler Lagrange equations that was essential to the application of Weierstrass s method. In later mathematics Weierstrass s method became identified with the field theoretic approach to the problem of sufficiency. In the same year as Kneser s book, David Hilbert ( ) introduced the concept of the invariant integral that greatly simplified some of the proofs in Weierstrass s theory. It turned out that Hilbert s insight, presented in analytic form, possessed similarities to ideas underlying earlier geometrical work by Eugenio Beltrami ( ) from Beginning in 1904, the Göttingen researcher Constantin Carathéodory ( ) assembled a complex of ideas that extended Kneser s geometric approach, and provided a way of connecting Hamilton Jacobi theory to the calculus of variations. During the 1930s the German mathematicians Hermann Weyl ( ) and Hermann Boerner ( ) and the Belgian researcher Théophile Lepage ( ) investigated the application of Carathéodory s method to variational problems involving multiple integrals. Boerner became something of an apostle for Carathéodory s theory, which he characterized as a royal road to the calculus of variations. (In September of 1943 Boerner delivered a lecture at the Oberwolfach Institute titled Carathéodory s Königsweg ins Herz der Variationsrechnung, a theme that was developed by him in an article published as [Boerner, 1953].) During the 1960s several researchers continued Boerner s line of investigation, including the Leipzig mathematician Rolf Klötzler (b. 1931). Rüdiger Thiele s book is a detailed and comprehensive history of the field theoretic approach to the calculus of variations. In his narrative the crucial moment in the history occurs with the appendix to Carathéodory s 1904 doctoral dissertation. Carathéodory understood his work to be related to some of Johann Bernoulli s ( ) results, originally obtained by Bernoulli in 1697 and published in Hence Thiele begins the book with an account of the work of Johann Bernoulli and then follows this with a survey of Carathéodory s theory. The narrative then moves address: cfraser@chass.utoronto.ca.
2 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.2 (1-7) 2 Essay Review / Historia Mathematica ( ) Fig. 1. Constantin Carathéodory ( ). back in time to a detailed study of Weierstrass s methods and their elaboration and publication by investigators at the end of the century. This is followed by a survey of relevant 19th-century research in dynamics and differential geometry, a prominent figure here being Kneser. A major chapter is devoted to Hilbert s contributions to the calculus of variations and related subjects, and to Mayer s research on fields. There is also an account of work on the field concept in the first decade of the new century by mathematicians in the United States, Germany (mainly the circle around Hilbert), France and Austria. Carathéodory s theory being seen in some sense as the natural culmination of the Weierstrass Kneser Hilbert development, the last part of the book examines how this theory was extended by such researchers as Boerner and Lepage. The term calibrator in the title refers to invariant integrals defined on differential manifolds, objects that occur in parts of recent abstract variational analysis in which some of Carathéodory s original ideas have remained important. The organization of Thiele s book and its valuation of the theory involve a definite perspective on the history of the calculus of variations. Weierstrass s method as modified by Hilbert constitutes the right approach to the problem of sufficiency, and Carathéodory s theory succeeds in a definitive and natural way in connecting this method to a complementary geometric understanding of the subject. The sense of the subject s historical development is a fairly typical reflection of mathematical modernism, of the implicit belief widely held in the first part of the 20th century that the different parts of mathematics had reached their final and natural form. Carathéodory (Fig. 1) in his dissertation did not illustrate his method with concrete examples, working instead at a somewhat more general level of analysis. Although his method was analytic, the following simple example may
3 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.3 (1-7) Essay Review / Historia Mathematica ( ) 3 Abb Synchronenschar (orthogonale Trajektorien der Extremalen) Fig. 2. Figure 1 from p. 49 of Thiele s book. help to illustrate some aspects of his theory. Suppose that space is filled with an optical medium whose index of refraction varies from point to point. The transmission of light in the medium is governed by the variational principle of least time. The family of curves in Fig. 2 originating at the origin are the paths of the rays of light that emanate into the medium from a source located at the origin. In this example the index of refraction decreases with increasing distance below the horizontal y-axis. The set of curved rays constitute a field of extremals for the variational problem. The integral expression for the time taken from the origin to y along a curved ray is known as a field function. Take some given time and consider the locus of points on the rays reached in this time. The curve formed by this locus is a curve of equal time and was called a synchrone by Johann Bernoulli. Physically, the synchrone is the wave front at the given time of the rays emanating from the origin. It turns out that the synchronal curve cuts each of the field curves orthogonally, a fact that was recognized by Christiaan Huygens ( ) in his optical investigations. The family of synchrones make up what Carathéodory called a geodetically equidistant family of curves with respect to the variational problem defined by the principle of least time. In Carathéodory s analytic development the following are connected: The field of extremals consisting of the solution curves to the Euler Lagrange differential equation; The Hamilton Jacobi partial-differential equation satisfied by the field function; The lines defined by setting the field function equal to a constant, these lines being transversal (i.e. normal) to the extremals; The expression that appears in the integrand of the Hilbert invariant integral, and the Legendre and Weierstrass necessary conditions. In order to provide some indication of the analytic character of Carathéodory s theory we show that a curve defined by setting the field function equal to a constant is normal to the extremals. We have the field function φ(x,y) = x 0 f(x,y,y )dx, an integral that is understood to be evaluated along the minimizing or maximizing arc from the origin to (x, y). Setting φ(x,y) = λ where λ is a parameter, we differentiate to obtain φ x dx + φ y pdx= dλ, where fdλ φ x and φ y are the partial derivatives of φ with respect to x and y. The integrand fdxis then equal to φ x +pφ y, where p = y = dy dx. For an extremal or curve of steepest descent the derivative with respect to p of this last expression is
4 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.4 (1-7) 4 Essay Review / Historia Mathematica ( ) equal to zero: or, d( fdλ φ x +pφ y ) = 0, (1) dp f p (φ x + pφ y ) fφ y = 0, (2) where f p is the partial derivative of f(x,y,p) with respect to p. It is possible to show from (2) that the Euler Lagrange equation holds for the given arc. Using this fact, one can differentiate the original field function φ(x,y) = x 0 f(x,y,y )dx with respect to x to obtain the relation f = φ x + pφ y. Combining this relation with (2) there follows f = φ x + pφ y, f p = φ y. (3) The condition that the extremal curve be normal to the curve φ(x,y) = const. at (x, y) is f + (q p)f p = 0, (4) where q is the slope of φ(x,y) = const. at (x, y). Because q = φ x φy (4) becomes ( ) φx f + p f p = 0. (5) φ y It is clear that (5) follows from (3). Hence the extremal is normal or transversal to the curve φ(x,y) = const. An aspect of the history that is not altogether straightforward and merits some discussion concerns the relationship of Johann Bernoulli s research to that of Carathéodory. At the conclusion of a memoir published in 1718, Bernoulli presented two demonstrations that the cycloid is the curve of quickest descent in the brachistochrone problem [Bernoulli, 1718]. He referred to these as his analytic and synthetic solutions. From a modern perspective, the first solution is equivalent to a derivation of the differential equation of the cycloid as a necessary condition, while the second is a proof that the cycloid results in a smaller time than neighboring comparison arcs. Historian Herman Goldstine ( ) characterized the second solution as the first sufficiency proof in the history of the calculus of variations and praised it for its elegance [Goldstine, 1981, 66], an evaluation echoed by Thiele (p. 41) in his account. It is worth noting as a general logical point that all verifications in mathematics can be construed as sufficiency proofs. 1 However, in the calculus of variations such verifications even for very simple examples can give rise to questions of considerable difficulty and subtlety. In his analytic solution Johann Bernoulli worked with an infinitesimal element of the variational integral and minimized this element using the ordinary methods of the calculus. In this approach Carathéodory seemed to find the essence of Bernoulli s method, and to the extent that he regarded his own work to be a continuation of Bernoulli s it was apparently because of this fact. Thus Carathéodory s account in his dissertation of Bernoulli s 1718 paper was primarily a description of the latter s analytic solution; it is only at the end of his account and only in a few sentences that Carathéodory observed that the solution may be verified directly. In a paper published one year later [Carathéodory, 1905, 162] Carathéodory stated explicitly that Bernoulli s method consisted of reducing the problem to one of ordinary calculus; this was the approach followed by Bernoulli in his analytic solution and also followed by Carathéodory in his investigation. 1 There were results before Johann Bernoulli s that could be understood as sufficiency proofs in the calculus of variations. For example, the ray of light that satisfies the law of reflection obeys the principle that light travels the path of shortest distance. Beginning with a broken ray obeying the reflection law (angle of incidence equals angle of reflection), one can show by elementary geometry that the distance along this ray is smaller than the distance along neighboring broken rays. Such an argument is a sufficiency proof and appears in Hero of Alexandria s (ca ) Catoptrics.
5 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.5 (1-7) Essay Review / Historia Mathematica ( ) 5 In his dissertation Carathéodory obtained the differential equation for the general variational problem by ordinary differentiation of an infinitesimal element of the variational integrand, just as Bernoulli had done for the brachistochrone in his analytic solution of It should be noted that there were important differences: Bernoulli differentiated with respect to a variable given in terms of the radius of curvature at a point, while Carathéodory differentiated with respect to the general slope variable p. Also Carathéodory understood his method to be direct (one of his early papers [Carathéodory, 1908] was titled Sur une méthode directe du calcul des variations ), and it would indeed be today grouped with what are called direct methods in the calculus of variations. By contrast, for Bernoulli it was the synthetic solution that was direct; the analytic solution would have been termed indirect because the answer (assuming there was one) was not exhibited at the outset but found by an analytic process. In a historical article published in 1937 Carathéodory commented on the origins of his own early work in the calculus of variations. In his original dissertation he seemed to be saying that his method was a development of Johann Bernoulli s analytic solution of 1718, a fact that was evident in the procedure actually followed in the dissertation. However, in 1937 [Carathéodory, 1937, 98] he suggested that it was Johann s synthetic solution that inspired him. A few years later in another historical essay [Carathéodory, 1945, 111] he reported that this solution contained the germ of the modern ideas of the calculus of variations. Thiele (p. 42) accepts this opinion, stating more specifically that the germ of field theory can be found in Johann s synthetic solution. Thiele implies that the solution may even have been of philosophical significance, in advance of its time, since the proof involved the identification of minimality as a property and a demonstration that the cycloid possessed this property. There are nevertheless some difficulties with Carathéodory s claim. First, it is not clear from a detailed examination of the content of Bernoulli s synthetic solution how the idea of a field is present there. Carathéodory [1937, 106] and Herman Goldstine [1981, 387] claim that Carathéodory s method may be obtained from Johann Bernoulli s synthetic solution if the normals to the brachistochrone are replaced by synchronal curves intersecting this curve. Unfortunately, no details are provided on how this would be done, and it is not at all clear to me that it is possible without moving completely beyond what is in Bernoulli and simply duplicating Carathéodory s analysis. The cycloid is not exhibited as a member of a family of solution curves. The proof depends on a special property of the radius of curvature of the cycloid, a property that is not generalizeable to other curves. Second, it is clear from all of Carathéodory s early writings and from what he actually did during this early period that, if he was indeed following a much older historical precedent, he was following Bernoulli s analytic solution (i.e. derivation of a differential equation as a necessary condition). In order to elaborate on the claim that the idea of field theory and the inspiration for Carathéodory s theory may be found in Johann Bernoulli s writings, Thiele turns to a paper published by Bernoulli in It is in this paper that Bernoulli introduced his famous analogy of the descending body in the brachistochrone problem with the emission of light through a medium of variable refractive index [Bernoulli, 1697]. The latter provides an elementary geometric illustration of some of the ideas in Carathéodory s theory, hence our presentation of it as an example above. Unfortunately, Carathédory in his formative mathematical writings referred only to Johann s paper of 1718, and not once to the article of The Göttingen researcher did mention Huygens, which would indicate he was familiar with some of the more geometric work of the period. In addition, Johann Bernoulli s optical analogy was well known at the time because of its description in Ernst Mach s widely read 1883 book on the historical development of mechanics. Nevertheless, Carathéodory was very specific that the source of his inspiration was the conclusion of Johann s 1718 memoir. Thiele (p. 52, bottom) suggests that the analytic character of this memoir captured Carathéodory s attention; it is also true that the field concept was less apparent in the memoir than it was in Johann s 1697 investigation. In his historical writings Carathéodory s somewhat personal perspective is apparent from his overall opinion of Johann Bernoulli s 1718 memoir. The large majority of the memoir was devoted to an exposition of the methods of Johann s late brother Jakob ( ); the resulting account was historically and mathematically a very important contribution to 18th-century analysis and provided the beginning for Leonhard Euler s ( ) seminal researches on what later became known as the calculus of variations. Carathéodory characterizes the memoir as a rather tedious tract [Carathéodory, 1937, 98] redeemed only by the appearance in its final pages of the synthetic solution. One might also take exception with Carathéodory s estimate of the elegance of this solution [Carathéodory, 1904, 70]. To me it seems interesting but rather complicated; while it does what it is supposed to do, a reader coming to it without any knowledge of the identity of its author may not find it elegant. Certainly no one before Carathédory was impressed enough to even mention it. The concluding section of the 1718 paper acted as a stimulus to Carathéodory s early thinking, and the analytic solution presented there may have given him the idea of using ordinary differentiation
6 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.6 (1-7) 6 Essay Review / Historia Mathematica ( ) to maximize or minimize the differential element of the variational integrand. Beyond this, the value he attributed to it may have been more a reflection of his subjective creative process than of what can sensibly be said to exist in the historical record. Another general point concerning the history being recounted here relates to the assessment of Carathéodory s theory by some of the researchers who followed in his footsteps. Boerner believed that Carathéodory [1935] opened up a royal road to the calculus of variations because of the way in which his theory linked many of the fundamental ideas of the subject. In 1909 Oskar Bolza ( ) had published a major work on the calculus of variations which remains today a valuable guide to the subject; while Carathéodory s theory (then fairly recent) was mentioned [Bolza, 1909, 140-3], the book showed that it is possible to present a coherent and hugely detailed exposition of the subject without invoking this theory as a magic key. Several decades later the American authority Gilbert Bliss ( ) published a rather succinct account [Bliss, 1946, 77 80] of Carathédory s theory in the course of a comprehensive textbook, referring to it as a very interesting approach to the calculus of variations [Bliss, 1946, 77]. The viewpoints of Boerner and Bliss express a certain underlying difference of opinion concerning the centrality of Carathédory s theory. Boerner s perspective may in part have reflected his excitement and the instinctive tendency of the working mathematician to elevate his own research. There is no doubt that Carathéodory s theory is a beautiful part of modern mathematics, not altogether widely known or appreciated today. Thiele s book is a masterful account both of its history as well as of the wider origin and development of field theoretic methods in the calculus of variations. Exhaustive in its coverage, the book is filled with interesting observations and informative comments on many different aspects of its subject. The appendix is a diverting essay discussing in an accessible way the many uses of the field concept in variational mathematics. Von der Bernoullischen Brachistochrone zum Kalibrator-Konzept is the product of decades of historical investigation and reflection on the part of the author, and will become a standard work of reference for the history of modern analysis. References 2 Bliss, Gilbert, Lectures on the Calculus of Variations. University of Chicago Press, Chicago. Bernoulli, Johann, Curvatura radii in diaphanis non uniformibus, Solutionque Problematis a se in Actis 1696, p. 269, propositi, de invenidenda linea Brachystochrona, id est, in qua grave a dato puncto ad datum punctum brevissimo tempore decurrit, & de curva Synchrona seu radiorum unda construenda. Acta Eruditorum, [This memoir is reprinted in Goldstine, Herman H., Radelet-de Grave, Patricia (Eds.), Die Streitschriften von Jacob und Johann Bernoulli, Birkhäuser, Basel, 1991, pp There is a German translation in Stäckel, Paul (Ed.), Abhandlungen über Variations-Rechnung (Ostwald s Klassiker Nr. 46), 1894, pp. 6 13, and an English translation in Struik, Dirk (Ed.), A Source Book in Mathematics, , 1969, pp ] Bernoulli, Johann, Remarques sur ce qu on a donné jusqu ici de solutions des Problêmes sur les Isoperimetres; avec une nouvelle methode courte & facile de les resoudre sans calcul, laquelle s étend aussi à d autres problêmes qui ont rapport à ceux-là. Mémoires de l Académie Royale des Sciences de Paris, [This memoir is reprinted in Die Streitschriften von Jacob und Johann Bernoulli, pp ] Boerner, Hermann, Carathéodory s Eingang zur Variationrechsnung. Jahresbericht der Deutsche Mathematiker- Vereinigung 56, Bolza, Oskar, Vorlesungen über Variationsrechnung. B.G. Teubner, Leipzig. Carathéodory, Constantin, Über die diskontinuierlichen Lösungen in der Variatiosnrechnung. Doktor- Dissertation, Universität Göttingen, 71 pages. Reprinted in Gesammelte Mathematische Schriften, vol. 1, 1954, pp Carathéodory, Constantin, Über das allgemeine Problem der Variationsrechnung. Nachrichten von der K. Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-physikalische Klasse, Reprinted in Gesammelte Mathematische Schriften, vol. 1, 1954, pp Carathéodory, Constantin, Sur une Méthode directe du Calcul des Variations. Rendiconti del Circolo Matematico di Palermo 25, Reprinted in Gesammelte Mathematische Schriften, vol. 1, 1954, pp Carathéodory, Constantin, Variationsrechnung und partielle Differentialgleichungen erster Ordung. Teubner, Leipzig. 2 Page references for Carathéodory are to his writings as published in Gesammelte Mathematische Schriften [Carathéodory, 1954, 1955].
7 JID:YHMAT AID:2660 /BRV [m3sc+; v 1.110; Prn:4/03/2009; 9:01] P.7 (1-7) Essay Review / Historia Mathematica ( ) 7 Carathéodory, Constantin, The beginning of research in the calculus of variations. Osiris 3, Reprinted in Gesammelte Mathematische Schriften, vol. 2, 1955, pp Carathéodory, Constantin, Basel und der Beginn der Variationsrechnung. Festschrift zum 60. Geburtstage von Prof. Dr. Andreas Speiser. Zürich, pp Reprinted in Gesammelte Mathematische Schriften, vol. 2, 1955, pp Carathéodory, Constantin, Gesammelte Mathematische Schriften Volume 1. C.H. Beck sche Verlagsbuchhandlung, Munich. Carathéodory, Constantin, Gesammelte Mathematische Schriften Volume 2. C.H. Beck sche Verlagsbuchhandlung, Munich. Goldstine, Herman H., A History of the Calculus of Variations from the 17th through the 19th Century. Springer- Verlag, New York. Kneser, Adolf, Lehrbuch der Variationsrechnung. Vieweg, Braunschweig.
Leibniz and the Discovery of Calculus. The introduction of calculus to the world in the seventeenth century is often associated
 Leibniz and the Discovery of Calculus The introduction of calculus to the world in the seventeenth century is often associated with Isaac Newton, however on the main continent of Europe calculus would
Leibniz and the Discovery of Calculus The introduction of calculus to the world in the seventeenth century is often associated with Isaac Newton, however on the main continent of Europe calculus would
Brachistochrones with loose ends
 IOP PUBLISHING Eur. J. Phys. 29 (2008) 1191 1199 EUROPEAN JOURNAL OF PHYSICS doi:10.1088/0143-0807/29/6/008 Brachistochrones with loose ends Stephan Mertens 1,2 and Sebastian Mingramm 1 1 Institut für
IOP PUBLISHING Eur. J. Phys. 29 (2008) 1191 1199 EUROPEAN JOURNAL OF PHYSICS doi:10.1088/0143-0807/29/6/008 Brachistochrones with loose ends Stephan Mertens 1,2 and Sebastian Mingramm 1 1 Institut für
O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis. Monday 30th October 2017 (Week 4)
 O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis Monday 30th October 2017 (Week 4) Summary French institutions Fourier series Early-19th-century rigour Limits, continuity,
O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis Monday 30th October 2017 (Week 4) Summary French institutions Fourier series Early-19th-century rigour Limits, continuity,
O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour
 O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour Monday 22nd October 2018 (Week 3) Summary Publication and acceptance of the calculus
O1 History of Mathematics Lecture VI Successes of and difficulties with the calculus: the 18th-century beginnings of rigour Monday 22nd October 2018 (Week 3) Summary Publication and acceptance of the calculus
THE HILBERT INTEGRAL AND MAYER FIELDS FOR THE PROBLEM OF MAYER IN THE CALCULUS OF VARIATIONS*
 THE HILBERT INTEGRAL AND MAYER FIELDS FOR THE PROBLEM OF MAYER IN THE CALCULUS OF VARIATIONS* BY GILLIE A. LAREW One studying the problem of Mayer in the calculus of variations and investigating the sufficient
THE HILBERT INTEGRAL AND MAYER FIELDS FOR THE PROBLEM OF MAYER IN THE CALCULUS OF VARIATIONS* BY GILLIE A. LAREW One studying the problem of Mayer in the calculus of variations and investigating the sufficient
YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM
 YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM GARY BROOKFIELD In 1696 Johann Bernoulli issued a famous challenge to his fellow mathematicians: Given two points A and B in a vertical plane,
YET ANOTHER ELEMENTARY SOLUTION OF THE BRACHISTOCHRONE PROBLEM GARY BROOKFIELD In 1696 Johann Bernoulli issued a famous challenge to his fellow mathematicians: Given two points A and B in a vertical plane,
O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets. Monday 14th November 2016 (Week 6)
 O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets Monday 14th November 2016 (Week 6) Summary Proofs of the Intermediate Value Theorem revisited Convergence
O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets Monday 14th November 2016 (Week 6) Summary Proofs of the Intermediate Value Theorem revisited Convergence
Johann Bernoulli ( )he established the principle of the so-called virtual work for static systems.
 HISTORICAL SURVEY Wilhelm von Leibniz (1646-1716): Leibniz s approach to mechanics was based on the use of mathematical operations with the scalar quantities of energy, as opposed to the vector quantities
HISTORICAL SURVEY Wilhelm von Leibniz (1646-1716): Leibniz s approach to mechanics was based on the use of mathematical operations with the scalar quantities of energy, as opposed to the vector quantities
Euler s Rediscovery of e
 Euler s Rediscovery of e David Ruch May 9, 2018 1 Introduction The famous constant e is used in countless applications across many fields of mathematics, and resurfaces periodically in the evolution of
Euler s Rediscovery of e David Ruch May 9, 2018 1 Introduction The famous constant e is used in countless applications across many fields of mathematics, and resurfaces periodically in the evolution of
O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis. Monday 31st October 2016 (Week 4)
 O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis Monday 31st October 2016 (Week 4) Summary French institutions Fourier series Early-19th-century rigour Limits, continuity,
O1 History of Mathematics Lecture VIII Establishing rigorous thinking in analysis Monday 31st October 2016 (Week 4) Summary French institutions Fourier series Early-19th-century rigour Limits, continuity,
Another theorem of Cauchy which admits exceptions
 Historia Mathematica 39 (2012) 206 210 www.elsevier.com/locate/yhmat Another theorem of Cauchy which admits eceptions R.P. Burn * Eeter University, UK Available online 3 December 2011 Abstract Several
Historia Mathematica 39 (2012) 206 210 www.elsevier.com/locate/yhmat Another theorem of Cauchy which admits eceptions R.P. Burn * Eeter University, UK Available online 3 December 2011 Abstract Several
Paper read at History of Science Society 2014 Annual Meeting, Chicago, Nov. 9,
 Euler s Mechanics as Opposition to Leibnizian Dynamics 1 Nobumichi ARIGA 2 1. Introduction Leonhard Euler, the notable mathematician in the eighteenth century, is also famous for his contributions to mechanics.
Euler s Mechanics as Opposition to Leibnizian Dynamics 1 Nobumichi ARIGA 2 1. Introduction Leonhard Euler, the notable mathematician in the eighteenth century, is also famous for his contributions to mechanics.
Minkowski space - Wikipedia, the free encyclopedia
 1 of 7 27/03/2013 12:38 Minkowski space From Wikipedia, the free encyclopedia In mathematical physics, Minkowski space or Minkowski spacetime (named after the mathematician Hermann Minkowski) is the mathematical
1 of 7 27/03/2013 12:38 Minkowski space From Wikipedia, the free encyclopedia In mathematical physics, Minkowski space or Minkowski spacetime (named after the mathematician Hermann Minkowski) is the mathematical
Einstein s Third Postulate
 Einstein s Third Postulate W. Engelhardt 1, retired from: Max-Planck-Institut für Plasmaphysik, D-85741 Garching, Germany Abstract Einstein s own demonstration of time dilation taken from his book with
Einstein s Third Postulate W. Engelhardt 1, retired from: Max-Planck-Institut für Plasmaphysik, D-85741 Garching, Germany Abstract Einstein s own demonstration of time dilation taken from his book with
Field equations or conservation laws?
 arxiv:1309.4442v2 [physics.hist-ph] 11 Oct 2013 Field equations or conservation laws? Mauro Francaviglia, Marcella Palese and Ekkehart Winterroth Department of Mathematics, University of Torino, Italy
arxiv:1309.4442v2 [physics.hist-ph] 11 Oct 2013 Field equations or conservation laws? Mauro Francaviglia, Marcella Palese and Ekkehart Winterroth Department of Mathematics, University of Torino, Italy
Beyond Newton and Leibniz: The Making of Modern Calculus. Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida
 Beyond Newton and Leibniz: The Making of Modern Calculus Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida Calculus Before Newton & Leibniz Four Major Scientific Problems
Beyond Newton and Leibniz: The Making of Modern Calculus Anthony V. Piccolino, Ed. D. Palm Beach State College Palm Beach Gardens, Florida Calculus Before Newton & Leibniz Four Major Scientific Problems
ALGEBRAISCHE GEOMETRIE
 ERGEBNISSE DER MATHEMATIK UND IHRER GRENZGEBIETE UNTER MITWIRKUNG DER SCHRIFTLEITUNG DES "ZENTRALBLATT FOR MATHEMATIK" HERAUSGEGEBEN VON L.V.AHLFORS R.BAER R.COURANT ].L.DOOB S.EILENBERG P. R. HALMOS.
ERGEBNISSE DER MATHEMATIK UND IHRER GRENZGEBIETE UNTER MITWIRKUNG DER SCHRIFTLEITUNG DES "ZENTRALBLATT FOR MATHEMATIK" HERAUSGEGEBEN VON L.V.AHLFORS R.BAER R.COURANT ].L.DOOB S.EILENBERG P. R. HALMOS.
THE VARIABLE END POINT PROBLEM OF THE CALCULUS OF VARIATIONS INCLUDING A GENERALIZATION OF THE CLASSICAL JACOBI CONDITIONS* A. E.
 THE VARIABLE END POINT PROBLEM OF THE CALCULUS OF VARIATIONS INCLUDING A GENERALIZATION OF THE CLASSICAL JACOBI CONDITIONS* BY A. E. CURRIER 1. Introduction, f In the present paper we treat the variable
THE VARIABLE END POINT PROBLEM OF THE CALCULUS OF VARIATIONS INCLUDING A GENERALIZATION OF THE CLASSICAL JACOBI CONDITIONS* BY A. E. CURRIER 1. Introduction, f In the present paper we treat the variable
NOTES. Reconsidering Leibniz s Analytic Solution of the. Catenary Problem:
 NOTES Reconsidering Leibniz s Analytic Solution of the Catenary Problem: The Letter to Rudolph von Bodenhausen of August 1691 Mike Raugh January 3, 017 Leibniz published his solution of the catenary problem
NOTES Reconsidering Leibniz s Analytic Solution of the Catenary Problem: The Letter to Rudolph von Bodenhausen of August 1691 Mike Raugh January 3, 017 Leibniz published his solution of the catenary problem
Shi Feng Sheng Danny Wong
 Exhibit C A Proof of the Fermat s Last Theorem Shi Feng Sheng Danny Wong Abstract: Prior to the Diophantine geometry, number theory (or arithmetic) was to study the patterns of the numbers and elementary
Exhibit C A Proof of the Fermat s Last Theorem Shi Feng Sheng Danny Wong Abstract: Prior to the Diophantine geometry, number theory (or arithmetic) was to study the patterns of the numbers and elementary
Reviews 341. r 2009 Blackwell Publishing Ltd.
 Reviews 341 Tietz, U. (2003), Über Intentionalität, Regeln und die Intersubjektivität der Bedeutung, Deutsche Zeitschrift für Philosophie, 51: 63 79. Wikforss, Å. (2001), Semantic Normativity, Philosophical
Reviews 341 Tietz, U. (2003), Über Intentionalität, Regeln und die Intersubjektivität der Bedeutung, Deutsche Zeitschrift für Philosophie, 51: 63 79. Wikforss, Å. (2001), Semantic Normativity, Philosophical
O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets. Monday 13th November 2017 (Week 6)
 O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets Monday 13th November 2017 (Week 6) Summary Proofs of the Intermediate Value Theorem revisited Convergence
O1 History of Mathematics Lecture XII 19th-century rigour in real analysis, part 2: real numbers and sets Monday 13th November 2017 (Week 6) Summary Proofs of the Intermediate Value Theorem revisited Convergence
m 5500 Calculus of Variations. Spring Andrej Cherkaev
 m 5500 Calculus of Variations. Spring 2013. Andrej Cherkaev Introduction 1 Subjects of Calculus of variations Optimization The desire for optimality (perfection) is inherent in humans. The search for etremes
m 5500 Calculus of Variations. Spring 2013. Andrej Cherkaev Introduction 1 Subjects of Calculus of variations Optimization The desire for optimality (perfection) is inherent in humans. The search for etremes
A unique representation of polyhedral types. Centering via Möbius transformations
 Mathematische Zeitschrift manuscript No. (will be inserted by the editor) A unique representation of polyhedral types. Centering via Möbius transformations Boris A. Springborn Boris Springborn Technische
Mathematische Zeitschrift manuscript No. (will be inserted by the editor) A unique representation of polyhedral types. Centering via Möbius transformations Boris A. Springborn Boris Springborn Technische
Intuitive infinitesimals in the calculus
 Intuitive infinitesimals in the calculus David Tall Mathematics Education Research Centre University of Warwick COVENTRY, UK Intuitive infinitesimals Intuitive approaches to the notion of the limit of
Intuitive infinitesimals in the calculus David Tall Mathematics Education Research Centre University of Warwick COVENTRY, UK Intuitive infinitesimals Intuitive approaches to the notion of the limit of
S2500 ANALYSIS AND OPTIMIZATION, SUMMER 2016 FINAL EXAM SOLUTIONS
 S25 ANALYSIS AND OPTIMIZATION, SUMMER 216 FINAL EXAM SOLUTIONS C.-M. MICHAEL WONG No textbooks, notes or calculators allowed. The maximum score is 1. The number of points that each problem (and sub-problem)
S25 ANALYSIS AND OPTIMIZATION, SUMMER 216 FINAL EXAM SOLUTIONS C.-M. MICHAEL WONG No textbooks, notes or calculators allowed. The maximum score is 1. The number of points that each problem (and sub-problem)
Lecture 6, September 1, 2017
 Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Engineering Mathematics Fall 07 Lecture 6, September, 07 Escape Velocity Suppose we have a planet (or any large near to spherical heavenly body) of radius R and acceleration of gravity at the surface of
Introduction to the Theory and Application of the Laplace Transformation
 Gustav Doetsch Introduction to the Theory and Application of the Laplace Transformation With 51 Figures and a Table of Laplace Transforms Translation by Walter Nader Springer-Verlag Berlin Heidelberg New
Gustav Doetsch Introduction to the Theory and Application of the Laplace Transformation With 51 Figures and a Table of Laplace Transforms Translation by Walter Nader Springer-Verlag Berlin Heidelberg New
THE MEANING OF RELATIVITY
 THE MEANING OF RELATIVITY Albert Einstein THE MEANING OF RELATIVITY With a new Foreword by W. H. McCREA, F.R.S. CHAPMAN AND HALL SCIENCE PAPERBACKS First published 191111 by Methuen & Co Ltd Se,;iJ'NJ
THE MEANING OF RELATIVITY Albert Einstein THE MEANING OF RELATIVITY With a new Foreword by W. H. McCREA, F.R.S. CHAPMAN AND HALL SCIENCE PAPERBACKS First published 191111 by Methuen & Co Ltd Se,;iJ'NJ
THE FOUNDATIONS OF PHYSICS (SECOND COMMUNICATION)
 DAVID HILBERT THE FOUNDATIONS OF PHYSICS (SECOND COMMUNICATION) Originally published as Die Grundlagen der Physik. (Zweite Mitteilung) in Nachrichten von der Königlichen Gesellschaft zu Göttingen. Math.-phys.
DAVID HILBERT THE FOUNDATIONS OF PHYSICS (SECOND COMMUNICATION) Originally published as Die Grundlagen der Physik. (Zweite Mitteilung) in Nachrichten von der Königlichen Gesellschaft zu Göttingen. Math.-phys.
The Brachistochrone Curve
 The Brachistochrone Curve Paige R MacDonald May 16, 2014 Paige R MacDonald The Brachistochrone Curve May 16, 2014 1 / 1 The Problem In 1696, Johann Bernoulli posed the following problem to the scientific
The Brachistochrone Curve Paige R MacDonald May 16, 2014 Paige R MacDonald The Brachistochrone Curve May 16, 2014 1 / 1 The Problem In 1696, Johann Bernoulli posed the following problem to the scientific
THE CALCULUS OF VARIATIONS*
 1925.] THE CALCULUS OF VARIATIONS 163 THE CALCULUS OF VARIATIONS* BY LEONIDA TONELLI 1. The Purpose of this Note. It is proposed to explain briefly here the method followed in my Fondamenti di Calcolo
1925.] THE CALCULUS OF VARIATIONS 163 THE CALCULUS OF VARIATIONS* BY LEONIDA TONELLI 1. The Purpose of this Note. It is proposed to explain briefly here the method followed in my Fondamenti di Calcolo
Leonhard Euler: Swiss man famous for mathematics, and not his chocolate
 1 Jose Cabrera Dr. Shanyu Ji Math 4388 31 October 2016 Leonhard Euler: Swiss man famous for mathematics, and not his chocolate Leonhard Euler - one of the most revolutionary figures in 18th century mathematics.
1 Jose Cabrera Dr. Shanyu Ji Math 4388 31 October 2016 Leonhard Euler: Swiss man famous for mathematics, and not his chocolate Leonhard Euler - one of the most revolutionary figures in 18th century mathematics.
Chapter One Hilbert s 7th Problem: It s statement and origins
 Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
Chapter One Hilbert s 7th Problem: It s statement and origins At the second International Congress of athematicians in Paris, 900, the mathematician David Hilbert was invited to deliver a keynote address,
On the Origin of the Lorentz Transformation
 On the Origin of the Lorentz Transformation by W. Engelhardt Abstract The Lorentz Transformation, which is considered as constitutive for the Special Relativity Theory, was invented by Voigt in 1887, adopted
On the Origin of the Lorentz Transformation by W. Engelhardt Abstract The Lorentz Transformation, which is considered as constitutive for the Special Relativity Theory, was invented by Voigt in 1887, adopted
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields
 Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
Boyce/DiPrima/Meade 11 th ed, Ch 1.1: Basic Mathematical Models; Direction Fields Elementary Differential Equations and Boundary Value Problems, 11 th edition, by William E. Boyce, Richard C. DiPrima,
Fourier series: Fourier, Dirichlet, Poisson, Sturm, Liouville
 Fourier series: Fourier, Dirichlet, Poisson, Sturm, Liouville Joseph Fourier (1768-1830) upon returning from Egypt in 1801 was appointed by Napoleon Prefect of the Department of Isères (where Grenoble
Fourier series: Fourier, Dirichlet, Poisson, Sturm, Liouville Joseph Fourier (1768-1830) upon returning from Egypt in 1801 was appointed by Napoleon Prefect of the Department of Isères (where Grenoble
Kant and Finitism. Crossing Worlds: Mathematical logisc, philosophy, art: For Juliette Kennedy. Bill Tait. 4 June 2016
 Kant and Finitism Crossing Worlds: Mathematical logisc, philosophy, art: For Juliette Kennedy Bill Tait 4 June 2016 The Problems Kant in The Critique of Pure Reason: How can there be synthetic a priori
Kant and Finitism Crossing Worlds: Mathematical logisc, philosophy, art: For Juliette Kennedy Bill Tait 4 June 2016 The Problems Kant in The Critique of Pure Reason: How can there be synthetic a priori
History of Mathematics: Non-Euclidean Geometry in the 19th Century
 History of Mathematics: Non-Euclidean Geometry in the 19th Century Abstract Title: History of Mathematics Non-Euclidean Geometry in the 19th Century Core Audience: beginning graduate/advanced undergraduate:
History of Mathematics: Non-Euclidean Geometry in the 19th Century Abstract Title: History of Mathematics Non-Euclidean Geometry in the 19th Century Core Audience: beginning graduate/advanced undergraduate:
Paradoxical Euler: Integrating by Differentiating. Andrew Fabian Hieu D. Nguyen. Department of Mathematics Rowan University, Glassboro, NJ 08028
 Paradoxical Euler: Integrating by Differentiating Andrew Fabian Hieu D Nguyen Department of Mathematics Rowan University, Glassboro, NJ 0808 3-3-09 I Introduction Every student of calculus learns that
Paradoxical Euler: Integrating by Differentiating Andrew Fabian Hieu D Nguyen Department of Mathematics Rowan University, Glassboro, NJ 0808 3-3-09 I Introduction Every student of calculus learns that
Brouwer Fixed Point Theorem: A Proof for Economics Students
 Brouwer Fixed Point Theorem: A Proof for Economics Students Takao Fujimoto Abstract This note is one of the efforts to present an easy and simple proof of Brouwer fixed point theorem, which economics students
Brouwer Fixed Point Theorem: A Proof for Economics Students Takao Fujimoto Abstract This note is one of the efforts to present an easy and simple proof of Brouwer fixed point theorem, which economics students
Introduction to the calculus of variations. Bernard Dacorogna
 Introduction to the calculus of variations Bernard Dacorogna iv Contents Prefaces to the English Edition Preface to the French Edition ix xi 0 Introduction 1 0.1 Brief historical comments... 1 0.2 Model
Introduction to the calculus of variations Bernard Dacorogna iv Contents Prefaces to the English Edition Preface to the French Edition ix xi 0 Introduction 1 0.1 Brief historical comments... 1 0.2 Model
214 FIRST PROPOSAL OF THE UNIVERSAL SPEED OF VOL See Deutsches Museum München, Archives, HS 5520
 214 FIRST PROPOSAL OF THE UNIVERSAL SPEED OF VOL. 39 spring 1888, Lorentz sent some of his work on Michelson s experiment to Voigt. In March 1888, Lorentz sent another letter to Voigt. He read some of
214 FIRST PROPOSAL OF THE UNIVERSAL SPEED OF VOL. 39 spring 1888, Lorentz sent some of his work on Michelson s experiment to Voigt. In March 1888, Lorentz sent another letter to Voigt. He read some of
Frederic Brechenmacher. To cite this version: HAL Id: hal
 A controversy and the writing of a history: the discussion of small oscillations (1760-1860) from the standpoint of the controversy between Jordan and Kronecker (1874) Frederic Brechenmacher To cite this
A controversy and the writing of a history: the discussion of small oscillations (1760-1860) from the standpoint of the controversy between Jordan and Kronecker (1874) Frederic Brechenmacher To cite this
Unpublished Manuscripts by G.W. Leibniz Associated with Nondecimal Systems
 UDC 51(091) Unpublished Manuscripts by G.W. Leibniz Associated with Nondecimal Systems E. V. Shukhman, A. E. Shukhman Orenburg State Pedagogical University, Gagarina av. 1, Orenburg, 460001, Russia Orenburg
UDC 51(091) Unpublished Manuscripts by G.W. Leibniz Associated with Nondecimal Systems E. V. Shukhman, A. E. Shukhman Orenburg State Pedagogical University, Gagarina av. 1, Orenburg, 460001, Russia Orenburg
Graduate Texts in Mathematics 51
 Graduate Texts in Mathematics 51 Editorial Board F. W. Gehring P. R. Halmos M anaging Editor c. C. Moore Wilhelm Klingenberg ACoursein Differential Geometry Translated by David Hoffman Springer Science+Business
Graduate Texts in Mathematics 51 Editorial Board F. W. Gehring P. R. Halmos M anaging Editor c. C. Moore Wilhelm Klingenberg ACoursein Differential Geometry Translated by David Hoffman Springer Science+Business
When Cauchy and Hölder Met Minkowski: A Tour through Well-Known Inequalities
 202 MATHEMATICS MAGAZINE When Cauchy and Hölder Met Minkowski: A Tour through Well-Known Inequalities GERHARD J. WOEGINGER Department of Mathematics TU Eindhoven The Netherlands gwoegi@win.tue.nl Many
202 MATHEMATICS MAGAZINE When Cauchy and Hölder Met Minkowski: A Tour through Well-Known Inequalities GERHARD J. WOEGINGER Department of Mathematics TU Eindhoven The Netherlands gwoegi@win.tue.nl Many
TOPICS IN THE HISTORY OF MODERN MATHEMATICS (MHF4401)
 TOPICS IN THE HISTORY OF MODERN MATHEMATICS (MHF4401) Course Theme Laura De Carli The proposed course focuses on the life, the achievements, and the historical times of three scientists whose theories
TOPICS IN THE HISTORY OF MODERN MATHEMATICS (MHF4401) Course Theme Laura De Carli The proposed course focuses on the life, the achievements, and the historical times of three scientists whose theories
General Variation of a Functional
 Lecture 15 General Variation of a Functional Transversality conditions Broken etremals Corner conditions ME 256 at the Indian Institute of Science, Bengaluru G. K. Ananthasuresh Professor, Mechanical Engineering,
Lecture 15 General Variation of a Functional Transversality conditions Broken etremals Corner conditions ME 256 at the Indian Institute of Science, Bengaluru G. K. Ananthasuresh Professor, Mechanical Engineering,
TOOLING UP MATHEMATICS FOR ENGINEERING*
 TOOLING UP MATHEMATICS FOR ENGINEERING* BY THEODORE von KARMAN California Institute of Technology It has often been said that one of the primary objectives of Mathematics is to furnish tools to physicists
TOOLING UP MATHEMATICS FOR ENGINEERING* BY THEODORE von KARMAN California Institute of Technology It has often been said that one of the primary objectives of Mathematics is to furnish tools to physicists
AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY
 AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY AUDREY CURNOCK Abstract. This technical paper is the looking at extreme point structure from an isometric view point,
AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY AUDREY CURNOCK Abstract. This technical paper is the looking at extreme point structure from an isometric view point,
MthEd/Math 300 Williams Fall 2011 Midterm Exam 3
 Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 3 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
Name: MthEd/Math 300 Williams Fall 2011 Midterm Exam 3 Closed Book / Closed Note. Answer all problems. You may use a calculator for numerical computations. Section 1: For each event listed in the first
FUNDAMENTAL FORCES DARK MATTER. Universe: classical matter and energy: 4% dark matter and dark energy: 96%
 LEONHARD EULER (1707 1783) EULER AND THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY Read Euler, he is the master of us all. Marquis de Pierre Simon Laplace (1749 1827) The Euler Calculus of Variations
LEONHARD EULER (1707 1783) EULER AND THE MATHEMATICAL PRINCIPLES OF NATURAL PHILOSOPHY Read Euler, he is the master of us all. Marquis de Pierre Simon Laplace (1749 1827) The Euler Calculus of Variations
A history of Topology
 A history of Topology Version for printing Geometry and topology index History Topics Index Topological ideas are present in almost all areas of today's mathematics. The subject of topology itself consists
A history of Topology Version for printing Geometry and topology index History Topics Index Topological ideas are present in almost all areas of today's mathematics. The subject of topology itself consists
Gottfreid Leibniz = Inventor of Calculus. Rachael, Devan, Kristen, Taylor, Holly, Jolyn, Natalie, Michael, & Tanner
 Gottfreid Leibniz = Inventor of Calculus Rachael, Devan, Kristen, Taylor, Holly, Jolyn, Natalie, Michael, & Tanner Who invented Calculus? Gottfreid Leibniz When did he invent Calculus? 1646-1716 Why he
Gottfreid Leibniz = Inventor of Calculus Rachael, Devan, Kristen, Taylor, Holly, Jolyn, Natalie, Michael, & Tanner Who invented Calculus? Gottfreid Leibniz When did he invent Calculus? 1646-1716 Why he
Albert Einstein THE COLLECTED PAPERS OF. The Principal Ideas of the Theory of Relativity REPRINTED FROM: VOLUME 7
 REPRINTED FROM: THE COLLECTED PAPERS OF Albert Einstein VOLUME 7 THE BERLIN YEARS: WRITINGS, 1918 1921 Michel Janssen, Robert Schulmann, József Illy, Christoph Lehner, and Diana Kormos Buchwald EDITORS
REPRINTED FROM: THE COLLECTED PAPERS OF Albert Einstein VOLUME 7 THE BERLIN YEARS: WRITINGS, 1918 1921 Michel Janssen, Robert Schulmann, József Illy, Christoph Lehner, and Diana Kormos Buchwald EDITORS
Poincaré s cube manifolds*
 Bulletin of the Manifold Atlas (2013) Poincaré s cube manifolds* KLAUS VOLKERT Abstract. In this article we describe an important class of 3-manifolds studied by Poincaré in his papers on analysis situs
Bulletin of the Manifold Atlas (2013) Poincaré s cube manifolds* KLAUS VOLKERT Abstract. In this article we describe an important class of 3-manifolds studied by Poincaré in his papers on analysis situs
The Euler-MacLaurin formula applied to the St. Petersburg problem
 The Euler-MacLaurin formula applied to the St. Petersburg problem Herbert Müller, Switzerland Published in 2013 on http://herbert-mueller.info/ Abstract In the St. Petersburg problem, a person has to decide
The Euler-MacLaurin formula applied to the St. Petersburg problem Herbert Müller, Switzerland Published in 2013 on http://herbert-mueller.info/ Abstract In the St. Petersburg problem, a person has to decide
Instituto Superior Técnico. Calculus of variations and Optimal Control. Problem Series nº 2
 Instituto Superior Técnico Calculus of variations and Optimal Control Problem Series nº P1. Snell s law of refraction and Fermat s Principle of Least Time Consider the situation shown in figure P1-1 where
Instituto Superior Técnico Calculus of variations and Optimal Control Problem Series nº P1. Snell s law of refraction and Fermat s Principle of Least Time Consider the situation shown in figure P1-1 where
Rossby, Ertel, and potential vorticity. R. M. Samelson. College of Oceanic and Atmospheric Sciences. Oregon State University.
 Rossby, Ertel, and potential vorticity R. M. Samelson College of Oceanic and Atmospheric Sciences Oregon State University 104 Oc Adm Bldg Corvallis, OR 97331-5503 USA rsamelson@coas.oregonstate.edu http://www.coas.oregonstate.edu/faculty/samelson.html
Rossby, Ertel, and potential vorticity R. M. Samelson College of Oceanic and Atmospheric Sciences Oregon State University 104 Oc Adm Bldg Corvallis, OR 97331-5503 USA rsamelson@coas.oregonstate.edu http://www.coas.oregonstate.edu/faculty/samelson.html
Positive eigenfunctions for the p-laplace operator revisited
 Positive eigenfunctions for the p-laplace operator revisited B. Kawohl & P. Lindqvist Sept. 2006 Abstract: We give a short proof that positive eigenfunctions for the p-laplacian are necessarily associated
Positive eigenfunctions for the p-laplace operator revisited B. Kawohl & P. Lindqvist Sept. 2006 Abstract: We give a short proof that positive eigenfunctions for the p-laplacian are necessarily associated
Poincaré s homology sphere*
 Bulletin of the Manifold Atlas (2013) Poincaré s homology sphere* KLAUS VOLKERT Abstract. This article presents the history of Poincaré s homology sphere from its start in Poincaré s last paper on topology
Bulletin of the Manifold Atlas (2013) Poincaré s homology sphere* KLAUS VOLKERT Abstract. This article presents the history of Poincaré s homology sphere from its start in Poincaré s last paper on topology
On the Linearization of Second-Order Dif ferential and Dif ference Equations
 Symmetry, Integrability and Geometry: Methods and Applications Vol. (006), Paper 065, 15 pages On the Linearization of Second-Order Dif ferential and Dif ference Equations Vladimir DORODNITSYN Keldysh
Symmetry, Integrability and Geometry: Methods and Applications Vol. (006), Paper 065, 15 pages On the Linearization of Second-Order Dif ferential and Dif ference Equations Vladimir DORODNITSYN Keldysh
Might have Minkowski discovered the cause of gravity before Einstein? Vesselin Petkov Minkowski Institute Montreal, Canada
 Might have Minkowski discovered the cause of gravity before Einstein? Vesselin Petkov Minkowski Institute Montreal, Canada OUTLINE We will never know how physics would have developed had Hermann Minkowski
Might have Minkowski discovered the cause of gravity before Einstein? Vesselin Petkov Minkowski Institute Montreal, Canada OUTLINE We will never know how physics would have developed had Hermann Minkowski
Riemann bilinear relations
 Riemann bilinear relations Ching-Li Chai The Riemann bilinear relations, also called the Riemann period relations, is a set of quadratic relations for period matrices. The ones considered by Riemann are
Riemann bilinear relations Ching-Li Chai The Riemann bilinear relations, also called the Riemann period relations, is a set of quadratic relations for period matrices. The ones considered by Riemann are
Infinite dimensional differential geometry seminar
 Infinite dimensional differential geometry seminar February 19, 2010 1 Introduction 1.1 Why is -dimensional interesting? 1. Mathamatics: 2. Physics: Calculus beyond Banach spaces Infinite dimensional manifolds
Infinite dimensional differential geometry seminar February 19, 2010 1 Introduction 1.1 Why is -dimensional interesting? 1. Mathamatics: 2. Physics: Calculus beyond Banach spaces Infinite dimensional manifolds
Multivariable Calculus with MATLAB
 Multivariable Calculus with MATLAB Ronald L. Lipsman Jonathan M. Rosenberg Multivariable Calculus with MATLAB With Applications to Geometry and Physics Ronald L. Lipsman Department of Mathematics University
Multivariable Calculus with MATLAB Ronald L. Lipsman Jonathan M. Rosenberg Multivariable Calculus with MATLAB With Applications to Geometry and Physics Ronald L. Lipsman Department of Mathematics University
Goethe s Faust and the Minimal Action Principle: a possible Universal message
 Goethe s Faust and the Minimal Action Principle: a possible Universal message Claudio Verzegnassi a and Euro Spallucci c arxiv:1402.1592v1 [physics.pop-ph] 7 Feb 2014 a Dipartimento di Chimica, Fisica
Goethe s Faust and the Minimal Action Principle: a possible Universal message Claudio Verzegnassi a and Euro Spallucci c arxiv:1402.1592v1 [physics.pop-ph] 7 Feb 2014 a Dipartimento di Chimica, Fisica
The Two Careers of Emmy Noether
 The Two Careers of Emmy Noether A notable career in Nineteenth Century Erlangen. 1905 1916 The long Nineteenth Century. EN would be remembered today as a woman in mathematics if she had never done any
The Two Careers of Emmy Noether A notable career in Nineteenth Century Erlangen. 1905 1916 The long Nineteenth Century. EN would be remembered today as a woman in mathematics if she had never done any
Readings for Unit I from Ryan (Topics from linear algebra)
 Readings for Unit I from Ryan (Topics from linear algebra) I.0 : Background Suggested readings. Ryan : pp. 193 202 General convention. In most cases, the background readings for a section of the course
Readings for Unit I from Ryan (Topics from linear algebra) I.0 : Background Suggested readings. Ryan : pp. 193 202 General convention. In most cases, the background readings for a section of the course
Maximum Process Problems in Optimal Control Theory
 J. Appl. Math. Stochastic Anal. Vol. 25, No., 25, (77-88) Research Report No. 423, 2, Dept. Theoret. Statist. Aarhus (2 pp) Maximum Process Problems in Optimal Control Theory GORAN PESKIR 3 Given a standard
J. Appl. Math. Stochastic Anal. Vol. 25, No., 25, (77-88) Research Report No. 423, 2, Dept. Theoret. Statist. Aarhus (2 pp) Maximum Process Problems in Optimal Control Theory GORAN PESKIR 3 Given a standard
Surfaces in the Euclidean 3-Space
 Surfaces in the Euclidean 3-Space by Rolf Sulanke Finished September 24, 2014 Mathematica v. 9, v. 10 Preface In this notebook we develop Mathematica tools for applications to Euclidean differential geometry
Surfaces in the Euclidean 3-Space by Rolf Sulanke Finished September 24, 2014 Mathematica v. 9, v. 10 Preface In this notebook we develop Mathematica tools for applications to Euclidean differential geometry
Final Exam Extra Credit Opportunity
 Final Exam Extra Credit Opportunity For extra credit, counted toward your final exam grade, you can write a 3-5 page paper on (i) Chapter II, Conceptions in Antiquity, (ii) Chapter V, Newton and Leibniz,
Final Exam Extra Credit Opportunity For extra credit, counted toward your final exam grade, you can write a 3-5 page paper on (i) Chapter II, Conceptions in Antiquity, (ii) Chapter V, Newton and Leibniz,
1 The role of gravity The view of physics that is most generally accepted at the moment is that one can divide the discussion of the universe into
 1 The role of gravity The view of physics that is most generally accepted at the moment is that one can divide the discussion of the universe into two parts. First, there is the question of the local laws
1 The role of gravity The view of physics that is most generally accepted at the moment is that one can divide the discussion of the universe into two parts. First, there is the question of the local laws
Dynamics of boundary layer separating from surface to the outer flow
 Dynamics of boundary layer separating from surface to the outer flow Sergey V. Ershkov Sternberg Astronomical Institute, M.V. Lomonosov's Moscow State University, 13 Universitetskij prospect, Moscow 11999,
Dynamics of boundary layer separating from surface to the outer flow Sergey V. Ershkov Sternberg Astronomical Institute, M.V. Lomonosov's Moscow State University, 13 Universitetskij prospect, Moscow 11999,
CARATHÉODORY S ROYAL ROAD OF THE CALCULUS OF VARIATIONS: MISSED EXITS TO THE MAXIMUM PRINCIPLE OF OPTIMAL CONTROL THEORY.
 Manuscript submitted to AIMS Journals Volume X, Number 0X, XX 200X Website: http://aimsciences.org pp. X XX CARATHÉODORY S ROYAL ROAD OF THE CALCULUS OF VARIATIONS: MISSED EXITS TO THE MAXIMUM PRINCIPLE
Manuscript submitted to AIMS Journals Volume X, Number 0X, XX 200X Website: http://aimsciences.org pp. X XX CARATHÉODORY S ROYAL ROAD OF THE CALCULUS OF VARIATIONS: MISSED EXITS TO THE MAXIMUM PRINCIPLE
332 BOOK REVIEWS [March
 332 BOOK REVIEWS [March Lectures on differential geometry. By S. Sternberg. Prentice-Hall, Englewood Cliffs, N. J., 1964. 15+390 pp. $16.00. At last we have a book that begins with the differentiable manifold
332 BOOK REVIEWS [March Lectures on differential geometry. By S. Sternberg. Prentice-Hall, Englewood Cliffs, N. J., 1964. 15+390 pp. $16.00. At last we have a book that begins with the differentiable manifold
Observations on Category Theory. John L. Bell
 Observations on Category Theory John L. Bell 1. Devised by Eilenberg and Mac Lane in the early 1940s, category theory is a presentation of mathematics in terms of the fundamental concepts of transformation,
Observations on Category Theory John L. Bell 1. Devised by Eilenberg and Mac Lane in the early 1940s, category theory is a presentation of mathematics in terms of the fundamental concepts of transformation,
Follow links for Class Use and other Permissions. For more information send to:
 COPYRIGHT NOTICE: John J. Watkins: Topics in Commutative Ring Theory is published by Princeton University Press and copyrighted, 2007, by Princeton University Press. All rights reserved. No part of this
COPYRIGHT NOTICE: John J. Watkins: Topics in Commutative Ring Theory is published by Princeton University Press and copyrighted, 2007, by Princeton University Press. All rights reserved. No part of this
Are All Infinities Created Equal?
 Are All Infinities Created Equal? Guram Bezhanishvili Georg Ferdinand Ludwig Philip Cantor (1845 1918), the founder of set theory, and considered by many as one of the most original minds in the history
Are All Infinities Created Equal? Guram Bezhanishvili Georg Ferdinand Ludwig Philip Cantor (1845 1918), the founder of set theory, and considered by many as one of the most original minds in the history
Unification, decoupling, and identification in the Palatini formalism
 Unification, decoupling, and identification in the Palatini formalism 1 Introduction This paper focuses on several philosophical (and historical) aspects of the Palatini formalism as a metric-affine approach
Unification, decoupling, and identification in the Palatini formalism 1 Introduction This paper focuses on several philosophical (and historical) aspects of the Palatini formalism as a metric-affine approach
Elliptic Curves an Introduction
 Irish Math. Soc. Bulletin 60 (2007), 39 43 39 Elliptic Curves an Introduction BERND KREUSSLER The following four articles constitute expanded versions of talks given during a mini-workshop which took place
Irish Math. Soc. Bulletin 60 (2007), 39 43 39 Elliptic Curves an Introduction BERND KREUSSLER The following four articles constitute expanded versions of talks given during a mini-workshop which took place
Introduction. You know, it would be sufficient to really understand. If I can t picture it, I can t understand it.
 CHAPTER 1 Introduction You know, it would be sufficient to really understand the electron. Albert Einstein [2] If I can t picture it, I can t understand it. Albert Einstein [41] I think it is quite likely,
CHAPTER 1 Introduction You know, it would be sufficient to really understand the electron. Albert Einstein [2] If I can t picture it, I can t understand it. Albert Einstein [41] I think it is quite likely,
Lecture Notes in Physics
 Lecture Notes in Physics Edited by H. Araki, Kyoto, J. Ehlers, M(Jnchen, K. Hepp, Z~rich R. Kippenhahn, MLinchen, H. A. Weidenmeller, Heidelberg and J. Zittartz, K61n 190 Karl Kraus States, Effects, and
Lecture Notes in Physics Edited by H. Araki, Kyoto, J. Ehlers, M(Jnchen, K. Hepp, Z~rich R. Kippenhahn, MLinchen, H. A. Weidenmeller, Heidelberg and J. Zittartz, K61n 190 Karl Kraus States, Effects, and
Leibniz and the Infinite
 Documenta Math. 19 Leibniz and the Infinite Eberhard Knobloch 2010 Mathematics Subject Classification: 01A45, 28-03 Keywords and Phrases: Leibniz, infinite, infinitely small, mathematical rigour, integration
Documenta Math. 19 Leibniz and the Infinite Eberhard Knobloch 2010 Mathematics Subject Classification: 01A45, 28-03 Keywords and Phrases: Leibniz, infinite, infinitely small, mathematical rigour, integration
Gaussian Guesswork: Infinite Sequences and the Arithmetic-Geometric Mean
 Ursinus College Digital Commons @ Ursinus College Calculus Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) Fall 217 Gaussian Guesswork: Infinite Sequences
Ursinus College Digital Commons @ Ursinus College Calculus Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) Fall 217 Gaussian Guesswork: Infinite Sequences
Differential and Complex Geometry: Origins, Abstractions and Embeddings
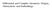 Differential and Complex Geometry: Origins, Abstractions and Embeddings Raymond O. Wells, Jr. Differential and Complex Geometry: Origins, Abstractions and Embeddings 123 Raymond O. Wells, Jr. University
Differential and Complex Geometry: Origins, Abstractions and Embeddings Raymond O. Wells, Jr. Differential and Complex Geometry: Origins, Abstractions and Embeddings 123 Raymond O. Wells, Jr. University
VARIATIONAL PRINCIPLES
 CHAPTER - II VARIATIONAL PRINCIPLES Unit : Euler-Lagranges s Differential Equations: Introduction: We have seen that co-ordinates are the tools in the hands of a mathematician. With the help of these co-ordinates
CHAPTER - II VARIATIONAL PRINCIPLES Unit : Euler-Lagranges s Differential Equations: Introduction: We have seen that co-ordinates are the tools in the hands of a mathematician. With the help of these co-ordinates
Contributions to the general theory of transformations
 Beiträge zur allgemeinen Transformationstheorie, Leipziger Berichte (895), Heft V, VI, submitted on --896, pp. 494-508. Presented at the session on 9-7-895; Gesammelte Abhandlungen, v. VI, art. III. Contributions
Beiträge zur allgemeinen Transformationstheorie, Leipziger Berichte (895), Heft V, VI, submitted on --896, pp. 494-508. Presented at the session on 9-7-895; Gesammelte Abhandlungen, v. VI, art. III. Contributions
Die Grundlehren der mathematischen Wissenschaften
 Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Beriicksichtigung der Anwendungsgebiete Band 52 H erau.fgegeben von J. L. Doob. E. Heinz F. Hirzebruch. E. Hopf H.
Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Beriicksichtigung der Anwendungsgebiete Band 52 H erau.fgegeben von J. L. Doob. E. Heinz F. Hirzebruch. E. Hopf H.
THE CONSTRUCTIVE SECOND NUMBER CLASS*
 224 ALONZO CHURCH [April THE CONSTRUCTIVE SECOND NUMBER CLASS* ALONZO CHURCH The existence of at least a vague distinction between what I shall call the constructive and the non-constructive ordinals of
224 ALONZO CHURCH [April THE CONSTRUCTIVE SECOND NUMBER CLASS* ALONZO CHURCH The existence of at least a vague distinction between what I shall call the constructive and the non-constructive ordinals of
1 Introduction. Erik J. Balder, Mathematical Institute, University of Utrecht, Netherlands
 Comments on Chapters 20 and 21 (Calculus of Variations and Optimal Control Theory) of Introduction to Mathematical Economics (third edition, 2008) by E.T. Dowling Erik J. Balder, Mathematical Institute,
Comments on Chapters 20 and 21 (Calculus of Variations and Optimal Control Theory) of Introduction to Mathematical Economics (third edition, 2008) by E.T. Dowling Erik J. Balder, Mathematical Institute,
How Euler Did It. by Ed Sandifer. Foundations of Calculus. September 2006
 How Euler Did It Foundations of Calculus September 2006 by Ed Sandifer As we begin a new academic year, many of us are introducing another generation of students to the magic of calculus. As always, those
How Euler Did It Foundations of Calculus September 2006 by Ed Sandifer As we begin a new academic year, many of us are introducing another generation of students to the magic of calculus. As always, those
Analytic Projective Geometry
 Chapter 5 Analytic Projective Geometry 5.1 Line and Point Coordinates: Duality in P 2 Consider a line in E 2 defined by the equation X 0 + X 1 x + X 2 y 0. (5.1) The locus that the variable points (x,
Chapter 5 Analytic Projective Geometry 5.1 Line and Point Coordinates: Duality in P 2 Consider a line in E 2 defined by the equation X 0 + X 1 x + X 2 y 0. (5.1) The locus that the variable points (x,
HILBERT S THEOREM ON THE HYPERBOLIC PLANE
 HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century
 The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century Mike Raugh www.mikeraugh.org JMM: Joint Mathematics Meetings, Atlanta January 4, 2017 Copyright 2017 Mike Raugh Catenary: Derived
The Leibniz Catenary Construction: Geometry vs Analysis in the 17 th Century Mike Raugh www.mikeraugh.org JMM: Joint Mathematics Meetings, Atlanta January 4, 2017 Copyright 2017 Mike Raugh Catenary: Derived
Invariant Lagrangian Systems on Lie Groups
 Invariant Lagrangian Systems on Lie Groups Dennis Barrett Geometry and Geometric Control (GGC) Research Group Department of Mathematics (Pure and Applied) Rhodes University, Grahamstown 6140 Eastern Cape
Invariant Lagrangian Systems on Lie Groups Dennis Barrett Geometry and Geometric Control (GGC) Research Group Department of Mathematics (Pure and Applied) Rhodes University, Grahamstown 6140 Eastern Cape
CALCULUS OF VARIATIONS, PARTIAL DIFFERENTIAL EQUATIONS, AND GEOMETRY
 CALCULUS OF VARIATIONS, PARTIAL DIFFERENTIAL EQUATIONS, AND GEOMETRY Fabrice Bethuel Université Pierre et Marie Curie, Paris, France Keywords: Minimization, compactness, minimal surfaces, parameterization,
CALCULUS OF VARIATIONS, PARTIAL DIFFERENTIAL EQUATIONS, AND GEOMETRY Fabrice Bethuel Université Pierre et Marie Curie, Paris, France Keywords: Minimization, compactness, minimal surfaces, parameterization,
226 My God, He Plays Dice! Entanglement. Chapter This chapter on the web informationphilosopher.com/problems/entanglement
 226 My God, He Plays Dice! Entanglement Chapter 29 20 This chapter on the web informationphilosopher.com/problems/entanglement Entanglement 227 Entanglement Entanglement is a mysterious quantum phenomenon
226 My God, He Plays Dice! Entanglement Chapter 29 20 This chapter on the web informationphilosopher.com/problems/entanglement Entanglement 227 Entanglement Entanglement is a mysterious quantum phenomenon
Calculus of Variations Summer Term 2014
 Calculus of Variations Summer Term 2014 Lecture 2 25. April 2014 c Daria Apushkinskaya 2014 () Calculus of variations lecture 2 25. April 2014 1 / 20 Purpose of Lesson Purpose of Lesson: To discuss the
Calculus of Variations Summer Term 2014 Lecture 2 25. April 2014 c Daria Apushkinskaya 2014 () Calculus of variations lecture 2 25. April 2014 1 / 20 Purpose of Lesson Purpose of Lesson: To discuss the
