Lectures on Applied Reactor Technology and Nuclear Power Safety. Lecture No 1. Title: Neutron Life Cycle
|
|
|
- Eustace Heath
- 5 years ago
- Views:
Transcription
1 Lectures on Nuclear Power Safety Lecture No 1 Title: Neutron Life Cycle Department of Energy Technology KTH Spring 2005 Slide No 1
2 Outline of the Lecture Infinite Multiplication Factor, k Four Factor Formula Fast Fission Factor, ε Resonance Escape Probability, p Thermal Utilization Factor, f Reproduction Factor, η Effective Multiplication Factor, k eff Fast Non-Leakage Probability, P fnl Thermal Non-Leakage Probability, P tnl Six Factor Formula Neutron Life Cycle of a Fast Reactor Slide No 2
3 Introduction We start with a short overview of some introductory topics, which are related to today s lecture: Neutron reactions Cross-section for neutron reactions Neutron absorption Nuclear fission Neutron moderation (or slowing down) Slide No 3
4 Neutron reactions (1) Neutrons play a very important role in nuclear reactor operations and their interactions with matter must be studied in details Reaction of neutron with nuclei fall into two broad classes: scattering absorption In scattering reactions, the final result is an exchange of energy between the colliding particles, and neutron remains free after the interaction In absorption, however, neutron is retained by the nucleus and new particles are formed Slide No 4
5 Neutron reactions (2) Inelastic scattering When a neutron undergoes inelastic scattering, it is first captured by the target nucleus to for an excited state of the compound nucleus A neutron of lower kinetic energy is then emitted, leaving the target nucleus in an excited state This excess energy is subsequently emitted as one or two photons of gamma radiation In general, inelastic scattering is limited to some high or low (depending on target mass) neutron energy ranges Slide No 5
6 Neutron reactions (3) Elastic scattering In elastic scattering the kinetic energy is conserved that is the total kinetic energy of neutron and the target nucleus is unchanged due to collision There are two types of elastic scattering: Potential scattering resembling collision of two billiard balls Resonance or compound nucleus scattering (when target nucleus is larger) where neutron is first absorbed and next expelled from nucleus, leaving the target nucleus in the ground state Slide No 6
7 Neutron reactions (4) In considering absorption reactions it is convenient to distinguish between reactions of slow neutrons and of fast neutrons There are four main kinds of slow neutron reactions: these involve capture of the neutron by the target followed by either: The emission of gamma radiation (n,γ) radiative capture The ejection of an alpha particle (n,α) The ejection of an proton (n,p) Fission (n,f) Of these the radiative capture is most common, whereas others are limited to few species. Slide No 7
8 Cross-section for neutron reactions (1) To quantify the probability of a certain reaction of a neutron with matter it is convenient to utilize the concept of cross-sections The cross-section of a target nucleus for any given reaction is thus a measure of the probability of a particular neutron-nucleus interaction and is a property of the nucleus and of the energy of the incident neutron Slide No 8
9 Cross-section for neutron reactions (2) Suppose a uniform, parallel beam of I mono-energetic neutrons per m 2 impinges perpendicularly, for a given time, on a thin layer δx m in thickness, of a target material containing N atoms per m 3, so that Nδx is the number of target nuclei per m 2 (see figure to the right) The nuclear cross section for a specified reaction is then defined as I I δx N R 2 σ = m / nucleus Cross-section unit: 1 b (barn) = ( Nδx) I m 2 /nucleus Where N R is the number of reactions Slide No 9
10 Cross-section for neutron reactions (3) Total cross section of uranium-238 Slide No 10
11 Cross-section for neutron reactions (4) Total cross section of uranium-235 Slide No 11
12 Cross-section for neutron reactions (5) Fission cross section of uranium-235 Slide No 12
13 Cross-section for neutron reactions (6) The cross section σ for a given reaction applies to a single nucleus and is frequently called the microscopic cross section. Since N is the number of target nuclei per m 3, the product Nσ represents the total cross section of the nuclei per m 3 Thus, the macroscopic cross section Σ is introduced as Σ = Nσ m 1 Slide No 13
14 Cross-section for neutron reactions (7) If a target material is an element of atomic weight A, 1 mole has a mass of 10-3 A kg and contains the Avogadro number (N A = ) of atoms. If the element density is ρ kg/m 3, the number of atoms per m 3 N is given as 3 10 ρn = A The macroscopic cross section is thus N A 3 10 ρ Σ = A N A σ Slide No 14
15 Cross-section for neutron reactions (8) For a compound of molecular weight M and density ρ kg/m 3, the number N i of atoms of the i th kind per m 3 is given by the following equation 3 10 ρn A N = ν ν i i M where is the number of atoms of the kind i in a molecule of the compound. The macroscopic cross section for this element in the given target material is then and for compound ρn A 10 ρn Σ i = N iσ i = ν iσ i Σ = A ( ν1σ 1 + ν 2σ 2 +L) M i M Slide No 15
16 Nuclear fission (1) Fission is caused by the absorption of neutron by a certain nuclei of high atomic number When fission takes place the nucleus breaks up into two lighter nuclei: fission fragments Only three nuclides, having sufficient stability to permit storage over a long period of time, namely uranium-233, uranium-235 and plutonium-239, are fissionable by neutrons of all energies Of these nuclides, only uranium-235 occurs in nature The other two are produced artificially from thorium-232 and uranium-238, respectively Slide No 16
17 Nuclear fission (2) Example of a nuclear fission of U-235 Each fission of U-235 is followed by a release of 2 or 3 neutrons (2.42 on average for fission of U-235 with thermal neutrons) Slide No 17
18 Nuclear fission (3) Chain reaction will sustain if there is enough neutrons to cause fissions in coming generations If fission is caused by slow (thermal) neutrons, they have to be moderated (slowed down) before the next fission Slide No 18
19 Nuclear fission (4) Approximate distribution of energy per fission of 235 U: J = 1 pj MeV Kinetic energy of fission products Instantaneous gamma-ray energy Kinetic energy of fission neutrons Beta particles from fission products Gamma rays from fission products Neutrinos Total fission energy Slide No 19
20 Nuclear fission (5) The neutrons released in fission are of two categories: Prompt neutrons (over 99% of all neutrons are prompt) released within s Delayed neutrons emitted during several minutes after fission The average number of neutrons liberated in fission is designed as. Typical values are shown below ν thermal neutrons Fast neutrons Uranium Uranium Plutonium Slide No 20
21 Nuclear fission (6) Neutrons released after fission do not have the same energy Typical energy spectrum is shown in figure Most neutrons have energy between 1 and 2 MeV Slide No 21
22 Nuclear fission (7) Fission of uranium- 235 can end up with 80 different primary fission products The range of mass numbers of products is from 72 to 161 Figure shows fission yield vs mass number Slide No 22
23 Nuclear fission (8) The fission cross section of uranium-235 is very low for fast (high-energy) neutrons To increase the fission rate, it is necessary to slow-down neutrons This subject is treated in the section that follows Slide No 23
24 Slowing down of neutrons (1) After fission, neutrons move in all directions with speed up to km/s Neutrons can not move a longer time with such high speeds, which successively goes down due to collisions with nuclei; this process is called scattering After short period of time the neutron velocities approach the equilibrium velocity, which is about 2200 m/s at 20 C Slide No 24
25 Slowing down of neutrons (2) Neutron scattering can be either: Elastic (in most cases) Inelastic Classical dynamics law are used to describe the elestic scattering process Collision in laboratory system V 1 Neutron before Nucleus before A ψ V 2 Nucleus after Neutron after Collision in a center-of-mass system Centrer of mass V 2 Neutron after Laboratory or Center-ofmass systems are used V 1 -v m Neutron before Nucleus after θ v m Nucleus before Slide No 25
26 Slowing down of neutrons (3) It can be shown that after collision, the minimum value of energy to which neutron can be reduced is αe 1 Where E 1 is the neutron energy before the collision, and A 1 α = A The maximum energy of neutron after collision is E 1 Slide No 26
27 Slowing down of neutrons (4) For hydrogen A = 1 and so And it is possible for neutron to lose all energy in one collision For carbon A = 12 and α = 0 α = The minimum energy of neutron after collision will be equal to 71.6% of that before the collision Slide No 27
28 Slowing down of neutrons (5) A useful quantity in the study of the slowing down of neutrons is the average value of the decrease in the natural logarithm of the neutron energy per collision, or the average logarithmic energy decrement per collision It is the average of all collisions of lne 1 lne 2 = ln(e 1 /E 2 ), where E 1 is the energy of the neutron before and E 2 is that after collision E ξ ln E 1 2 = 1 ln E E d d ( cosθ ) ( cosθ ) Here θ is a collision angle in the C system; integration means averaging over all possible collision angles Slide No 28
29 Slowing down of neutrons (6) Analyzing energy change in scattering, the ratio E 1 /E 2 can be expressed in terms of mass number A and cosine of the collision angle cosθ Using this in the equation in the previous slide, the following is obtained ξ = 1+ ( A 1) 2A 2 ln A 1 A + 1 It can be seen that for Hydrogen (A=1) ξ=1 and for uranium-238 ξ= Slide No 29
30 Slide No 30 Slowing down of neutrons (7) If the moderator is not a single element, but a compound containing n different nuclei, the effective or mean (weighted) value of ξ is given by For example for H 2 O we get sn s s n sn s s σ σ σ ξ σ ξ σ ξ σ ξ = ) ( ) ( ) ( ) ( ) ( O s H s O O s H H s O H σ σ ξ σ ξ σ ξ + + =
31 Slowing down of neutrons (8) An interesting application of the logarithmic energy decrement per collision is to compute the average number of collisions necessary to thermalize a fission neutron It can be shown that this number is = 14.4/ξ One also defines the moderating or slowing down power of a material as: ξσ s However, this parameter is not sufficient to describe how good a given material is as a moderator, since one also whishes the moderator to be a week absorber of neutrons That is why one use moderating ratio = ξσ s / Σ a as a figure of merit Slide No 31
32 Infinite Multiplication Factor (1) Not all neutrons produced by fission will cause new fission: Some will be absorbed by non-fissionable material Some will be absorbed parasitically in fissionable material Others will leak out of the reactor For the maintenance of a self-sustaining chain reaction it is enough that, on the average, at least one neutron produced in fission that causes fission of another nucleus Slide No 32
33 Infinite Multiplication Factor (2) The condition of a self-sustaining chain reaction is conveniently expressed in terms of a multiplication factor The number of neutrons absorbed or leaking out of the reactor will determine the value of this multiplication factor, and will also determine whether a new generation of neutrons is larger, smaller or the same size as the preceding generation Slide No 33
34 Infinite Multiplication Factor (3) Any reactor of a finite size will have neutrons leak out of it Generally, the larger the reactor the lower the fraction the neutron leakage For simplicity consider a reactor that is infinitely large, and therefore has no neutron leakage A measure of the increase or decrease in neutron flux in an infinite reactor is the infinite multiplication factor k Slide No 34
35 Infinite Multiplication Factor (4) The infinite multiplication factor is the ratio of the neutrons produced by fission in one generation to the number of neutrons lost through absorption in the preceding generation: or k = Neutron production from fission in one generation Neutron absorption in the preceding generation k = Rate Rate of of neutron neutron production absorption Slide No 35
36 Infinite Multiplication Factor (5) The condition for criticality, i.e. for a self-sustaining fission chain to be possible, in the infinite system is that the rate of neutron production should be equal to the rate of absorption in the absence of an extraneous source In other words, the requirement for criticality is: k = 1 Slide No 36
37 Four Factor Formula (1) For some thermal reactors, the infinite multiplication factor k can be evaluated with a fair degree of accuracy by means of the four factor formula The basis of this formula is the assumed division of the neutrons into three categories: Fission neutrons with energies in excess of about 1MeV which can cause fission in uranium-238 as well as in uranium-235 Neutrons in the resonance region which may be captured by uranium-238 Thermal neutrons which cause nearly all the fission in uranium- 235 and thereby generate fission neutrons Slide No 37
38 Four Factor Formula (2) A group of fast neutrons can enter into several reactions Some of these reactions reduce the size of the neutron group while other reactions allow the group to increase in size or produce a second generation There are four factors that give the inherent multiplication ability of the fuel and moderator materials: where : ε = Fast fission factor k = ε p f η p f = = Resonance escape probability Thermal utilization factor η = Reproduction factor Slide No 38
39 Fast Fission Factor (1) The first process that the neutrons of one generation may undergo is fast fission Fast fission is fission caused be neutrons that are in the fast energy range In a thermal reactor using slightly enriched or natural uranium fuel, some neutrons, before they have been slowed down appreciably, will cause fission of both uranium-235 and uranium-238 nuclei Slide No 39
40 Fast Fission Factor (2) At neutron energies greater than about 1 MeV, most of the fast neutron fissions will be of uranium-238, because of its larger proportions in the fuel Fast fission results in the net increase in the fast neutron population of the reactor core The cross-section for fast fission in uranium-235 and uranium-238 is small The fast neutron population in one generation is thus increased by a factor called the fast fission factor Slide No 40
41 Fast Fission Factor (3) The fast fission factor is defined as the ratio of the net number of fast neutrons produced by all fissions to the number of fast neutrons produced by thermal fissions ε = Number of fast neutrons produced by all fissions Number of fast neutrons produced by thermal fissions In order for a neutron to be absorbed by a fuel nucleus as a fast neutron, it must pass close to a fuel nucleus while it is a fast neutron Slide No 41
42 Fast Fission Factor (4) The value of ε will be affected by the arrangement and concentrations of the fuel and the moderator The value of ε is essentially 1.00 for a homogenous reactor where the fuel atoms are surrounded by moderator atoms However, in a heterogeneous reactor, all the fuel atoms are packed closely together in elements such as pins, rods or pellets Thus neutrons emitted from one fission can pass close to another fuel atom The arrangement in heterogeneous reactors results in ε~ Slide No 42
43 Resonance Escape Probability (1) As already discussed, neutrons increase in number as a result of fast fission After that neutrons continue to diffuse through the reactor As the neutrons move they collide with nuclei of fuel and non-fuel material and moderator in the reactor loosing part of their energy While they are slowing down there is a chance that some neutrons will be captured by uranium-238 nuclei Slide No 43
44 Resonance Escape Probability (2) Absorption cross-section of uranium-238 has several resonance peaks for neutron energies between 6 to 200 ev The peak values can be as high as barns, whereas below 6 ev, the absorption cross-section is as low as 10 barns The probability that the neutron will not be absorbed by a resonance peak is called the resonance escape probability, p Slide No 44
45 Resonance Escape Probability (3) the resonance escape probability, p is defined as the ratio of the number of neutrons that reach thermal energies to the number of fast neutrons that start to slow down p = Number of neutrons that reach thermal energy Number of fast neutrons that start to slow down The value of resonance escape probability is determined largely by the fuel-moderator arrangement and the amount of enrichment of uranium-235 Slide No 45
46 Resonance Escape Probability (4) In a homogeneous reactor the neutrons slow down in a region close to fuel nuclei and thus the probability of being absorbed by uranium-238 is high In the heterogeneous reactor neutrons slow down in the moderator where there are no atoms of uranium-238 and the probability of undergoing resonance absorption is low Slide No 46
47 Resonance Escape Probability (5) The value of the resonance escape probability is not significantly affected by pressure or poison concentration In water moderated, low uranium-235 enrichment reactors, raising the temperature of the fuel will rise the resonance absorption in uranium-238 due to the Doppler effect (i.e.. An apparent broadening of normally narrow resonance peaks due to thermal motion of nuclei) The increase in resonance absorption lowers the resonance escape probability Slide No 47
48 Resonance Escape Probability (6) The resonance escape probability can be found from the following formula: p( E) exp N F I ξ Σ s where: ξ is the weighted average logarithmic energy decrement for both moderator and absorber, N F is the number of fuel nuclei per unit volume of the system, I is the effective resonance integral and Σ s is the total macroscopic cross section for scattering in the system Slide No 48
49 Resonance Escape Probability (7) Experimental measurements of the resonance integral for a system of isolated rods give the following formula: I = a + b A M I where a and b are constants for a given fuel material (= 2.95 and 81.5 resp for uranium and 4.45 and 84.5 for uranium dioxide, such that I will be in barns), A is the area (in m 2 ) and M is the mass (in kg) of a fuel rod A = UO + 2 M A M [] b ; I = [] b uranium 5 Slide No 49
50 Resonance Escape Probability (8) The integral I depends on temperature as follows: [ + β ( 300) ] I( T ) = I(300 K) 1 T Here I(300 K) is the value of the integral at T = 300 K and β is a constant which depends on the nature of the fuel and the radius of fuel rods in heterogeneous systems For UO 2 and typical fuel rods used in LWRs β = 6x10-3 Slide No 50
51 Resonance Escape Probability (7) Example: Calculate the resonance integral I for fuel rods containing UO 2 (density kg m -3 ); the rod diameter is 8 mm. Solution: For 1 m long fuel rod its surface area is equal to A =1* πd = m 2 and its mass is M = 1* πd 2 /4*ρ = π* /4*10200 = kg. Thus the integral I is obtained as I = = b Slide No 51
52 Resonance Escape Probability (8) Since neutrons absorbed by resonance capture in uranium-238 are lost and unable to take part in sustaining the fission chain, most thermal reactors are design to maximize the resonance escape probability as far as possible In a homogeneous mixture of natural uranium fuel and carbon graphite moderator the highest value of k is hence a fission chain can not possibly be sustained Heterogeneous arrangement of the same materials can lead to k as high as 1.08 due to the increase in the resonance escape probability Slide No 52
53 Thermal Utilization Factor (1) Once thermalized, the neutrons continue to diffuse throughout the reactor and are subject to absorption by other materials in the reactor as well as the fuel The thermal utilization factor f is defined as the ratio of the number of thermal neutrons absorbed in the fuel to the number of thermal neutrons absorbed in all reactor material: f = Number of thermal neutrons absorbed in the fuel Number of thermal neutrons absorbed in all reactor materials Slide No 53
54 Thermal Utilization Factor (2) The thermal utilization factor can be expressed as follows: f = Σ U a U φ V U + Σ m a U U Σa φ V m m φ V + Σ c a U c φ V c + Σ p a p φ V p where superscripts U, m, p and c refer to uranium, moderator, poison and construction material (clad, spacers, etc), respectively. In a heterogeneous reactor the flux will be different in the fuel region than in the moderator region due to the high absorption rate by the fuel Slide No 54
55 Thermal Utilization Factor (3) In the homogenous reactor the neutron flux seen by the fuel, moderator, poisons and the construction material will be the same and the equation for f can be rewritten as f = Σ U a + Σ m a U Σa + Σ p a + Σ c a Slide No 55
56 Thermal Utilization Factor (4) The coefficient f will not in general depend on the temperature However, in heterogeneous water moderated reactors the moderator (water) expands with temperature and number of moderator atoms will decrease and this results in increase of thermal utilization Because of this effect the temperature coefficient for the thermal utilization factor is positive Slide No 56
57 Reproduction Factor (1) Most of the neutrons absorbed in the fuel cause fission, but some do not The reproduction factor is defined as the ratio of the fast neutrons produced by thermal fission to the number of thermal neutrons absorbed in the fuel η = Number of fast neutrons produced by thermal fission Number of thermal neutrons absorbed in the fuel Slide No 57
58 Reproduction Factor (2) The reproduction factor can also be stated as a ratio of rates as shown below: The rate of production of fast neutrons by thermal fission = U U fission reaction rate ( Σ f φ ) Χ the average number of neutrons produced per fission ( ν ) U U The rate of absorption of thermal neutrons by the fuel ( Σ φ ) When fuel contains several fissionable materials, it is necessary to account for each material, e.g. η U U Σ f φ ν Σ η = = ν U Σ φ Σ U a N σ ν U f U a U 235 U 235 f = U 235 U 235 U 238 U 238 N σ a + N σ a a Slide No 58
59 Effective Multiplication Factor (1) The infinite multiplication factor can fully represent only a reactor that is infinitely large To completely describe the neutron life cycle in a real, finite reactor, it is necessary to account for neutrons that leak out The multiplication factor that takes leakage into account is the effective multiplication factor k eff Slide No 59
60 Effective Multiplication Factor (2) For critical reactor the neutron population is neither increasing nor decreasing and k eff = 1 If the neutron production is grater than the absorption and leakage, the reactor is called supercritical; k eff > 1 If the neutron production is less than the absorption and leakage, the reactor is called subcritical; k eff < 1 k eff = k x P FNL x P TNL, where P FNL is the fast nonleakage probability and P FNL is the thermal nonleakage probability Slide No 60
61 Fast Non-Leakage Probability (1) In a realistic reactor of finite size some of the fast neutrons leak out of the boundaries of the reactor core before they begin the slowing down process The fast non-leakage probability P FNL is defined as the ratio of the number of fast neutrons that do not leak from the reactor to the number of fast neutrons produced by all fissions P FNL = Number of fast neutrons that do not leak from reactor Number of fast neutrons produced by all fissions Slide No 61
62 Thermal Non-Leakage Probability (1) Neutrons can also leak out of a finite reactor after they reach thermal energies The thermal non-leakage probability is defined as the ratio of the number of thermal neutrons that do not leak from the reactor core to the number of neutrons that reach thermal energies P TNL = Number of thermal neutrons that do not leak from reactor Number of neutrons that reach the thermal energies Slide No 62
63 Six Factor Formula (1) k eff = k x P FNL x P TNL Inclusion of expression for k (four-factor formula) yields k eff = ε P p P f η FNL TNL Slide No 63
64 40 neutrons net increase Fast fission Six Factor Formula (2) N0 ε = 1040 Fast nonleakage 140 fast neutrons leak N0 εp FNL = 900 Resonance escape 180 neutrons absorbed ε = 1.04 N 0 =1000 neutrons at start of generation N0 εpfnl pptnl fη = 1000 P FNL = neutrons absorbed in non-fuel p = 0.80 N0 εp FNL p = 720 reproduction η = neutrons net increase N0 εpfnl pptnl f = 495 Thermal utilization f = N0 εp FNL pp TNL = 620 Thermal nonleakage P TNL = Slide No neutrons leak
65 Neutron Life Cycle of a Fast Reactor (1) Neutron life cycle in a fast reactor is markedly different than that for a thermal reactor In a fast reactor, care is taken during the reactor design to minimize thermalization of neutrons Virtually all fissions taking place in fast reactor are caused by fast neutrons Resonance escape probability is not significant since very few neutrons exist at energies where it is significant Slide No 65
66 Exercises (1) 10:15-10:30 - Divide into groups of 4-5 students and solve the following problem: Exercise 1: The microscopic cross-section for the capture of thermal neutrons by hydrogen is 0.33 b and for oxygen b. Calculate the macroscopic capture cross section of the water molecule for thermal neutrons assuming that water density is 1000 kg/m 3 Hint: use the formula for compounds: 3 10 ρn Σ = A M ( ν σ + ν σ +L) Slide No 66
67 Exercises (2) 10:30-10:45 - solve the following problem: Exercise 2: Disregarding the uranium-234, the natural uranium may be taken to be a homogeneous mixture of weight percent of uranium-238 (absorption cross section 2.7 b) and 0.72 weight percent of uranium-235 (absorption cross section 681 b). The density of natural uranium metal is 19.0 x 10 3 kg m -3. Determine the total macroscopic and microscopic absorption cross sections of this material Hint: first find mass of U-235 and U-238 per unit volume of mixture and then number of nuclei per cubic meter of U-235 and U-238 Slide No 67
68 Exercises (3) 10:45-11:00 solve the following problem: Exercise 3: Calculate the thermal utilization factor for a homogenized core composed of (in % by volume): UO 2 35% and H 2 O 65%. The enrichment of the fuel is 3.2% (by weight). Microscopic cross sections [b] for absorption are as follows: water 0.66 [b], oxygen O: 2x10-4 [b], U- 235: 681 [b], U-238: 2.7 [b]. Density of UO 2 : kg/m 3 Density of water: 800 kg/m 3 Slide No 68
69 Exercises (4) Exercise 4: Calculate the moderating power and the moderating ratio for H 2 O (density 1000 kg/m 3 ) and Carbon (density 1600 kg/m 3 ). The macroscopic cross sections are given below: Isotope microscopic cross sections [b] absorption scattering Hydrogen Oxygen 27x Carbon Slide No 69
70 Exercises (5) Exercise 5: Calculate the resonance escape probability for a reactor as in Exercise 3 assuming the fuel temperature T = 1500 K and the effective resonance integral for fuel at T = 300 K equal to 25 [b]. Microscopic cross sections for scattering are as follows: water 103 [b], oxygen O: 6 [b], U-235: 8 [b], U-238: 8.3 [b]. Slide No 70
71 Home Assignment #1 due Description and data for problems 1 and 2 A homogenized core has the following composition (in % by volume): UO 2-32%, Zr 10%, H 2 O 58%. The enrichment of the fuel is 3.5% (weight). The material data are given in the Table below. Component density σ a σ kg m -3 barn barn barn f σ s ν H 2 O Zr UO U U O - 2x Slide No 71
72 Home Assignment #1 due Problem 1 (5 points): Calculate the thermal utilization factor in such a core. Problem 2 (5 points): Calculate k for an identical core as in Problem 1 assuming that the resonance escape probability p is known and equal to 0.69 and the fast fission factor is 1.04 Slide No 72
Neutron Interactions Part I. Rebecca M. Howell, Ph.D. Radiation Physics Y2.5321
 Neutron Interactions Part I Rebecca M. Howell, Ph.D. Radiation Physics rhowell@mdanderson.org Y2.5321 Why do we as Medical Physicists care about neutrons? Neutrons in Radiation Therapy Neutron Therapy
Neutron Interactions Part I Rebecca M. Howell, Ph.D. Radiation Physics rhowell@mdanderson.org Y2.5321 Why do we as Medical Physicists care about neutrons? Neutrons in Radiation Therapy Neutron Therapy
Cross-Sections for Neutron Reactions
 22.05 Reactor Physics Part Four Cross-Sections for Neutron Reactions 1. Interactions: Cross-sections deal with the measurement of interactions between moving particles and the material through which they
22.05 Reactor Physics Part Four Cross-Sections for Neutron Reactions 1. Interactions: Cross-sections deal with the measurement of interactions between moving particles and the material through which they
Reactors and Fuels. Allen G. Croff Oak Ridge National Laboratory (ret.) NNSA/DOE Nevada Support Facility 232 Energy Way Las Vegas, NV
 Reactors and Fuels Allen G. Croff Oak Ridge National Laboratory (ret.) NNSA/DOE Nevada Support Facility 232 Energy Way Las Vegas, NV July 19-21, 2011 This course is partially based on work supported by
Reactors and Fuels Allen G. Croff Oak Ridge National Laboratory (ret.) NNSA/DOE Nevada Support Facility 232 Energy Way Las Vegas, NV July 19-21, 2011 This course is partially based on work supported by
Today, I will present the first of two lectures on neutron interactions.
 Today, I will present the first of two lectures on neutron interactions. I first need to acknowledge that these two lectures were based on lectures presented previously in Med Phys I by Dr Howell. 1 Before
Today, I will present the first of two lectures on neutron interactions. I first need to acknowledge that these two lectures were based on lectures presented previously in Med Phys I by Dr Howell. 1 Before
Elastic scattering. Elastic scattering
 Elastic scattering Now we have worked out how much energy is lost when a neutron is scattered through an angle, θ We would like to know how much energy, on average, is lost per collision In order to do
Elastic scattering Now we have worked out how much energy is lost when a neutron is scattered through an angle, θ We would like to know how much energy, on average, is lost per collision In order to do
VI. Chain Reaction. Two basic requirements must be filled in order to produce power in a reactor:
 VI. Chain Reaction VI.1. Basic of Chain Reaction Two basic requirements must be filled in order to produce power in a reactor: The fission rate should be high. This rate must be continuously maintained.
VI. Chain Reaction VI.1. Basic of Chain Reaction Two basic requirements must be filled in order to produce power in a reactor: The fission rate should be high. This rate must be continuously maintained.
6 Neutrons and Neutron Interactions
 6 Neutrons and Neutron Interactions A nuclear reactor will not operate without neutrons. Neutrons induce the fission reaction, which produces the heat in CANDU reactors, and fission creates more neutrons.
6 Neutrons and Neutron Interactions A nuclear reactor will not operate without neutrons. Neutrons induce the fission reaction, which produces the heat in CANDU reactors, and fission creates more neutrons.
Nuclear Reactions A Z. Radioactivity, Spontaneous Decay: Nuclear Reaction, Induced Process: x + X Y + y + Q Q > 0. Exothermic Endothermic
 Radioactivity, Spontaneous Decay: Nuclear Reactions A Z 4 P D+ He + Q A 4 Z 2 Q > 0 Nuclear Reaction, Induced Process: x + X Y + y + Q Q = ( m + m m m ) c 2 x X Y y Q > 0 Q < 0 Exothermic Endothermic 2
Radioactivity, Spontaneous Decay: Nuclear Reactions A Z 4 P D+ He + Q A 4 Z 2 Q > 0 Nuclear Reaction, Induced Process: x + X Y + y + Q Q = ( m + m m m ) c 2 x X Y y Q > 0 Q < 0 Exothermic Endothermic 2
Nuclear Fission. 1/v Fast neutrons. U thermal cross sections σ fission 584 b. σ scattering 9 b. σ radiative capture 97 b.
 Nuclear Fission 1/v Fast neutrons should be moderated. 235 U thermal cross sections σ fission 584 b. σ scattering 9 b. σ radiative capture 97 b. Fission Barriers 1 Nuclear Fission Q for 235 U + n 236 U
Nuclear Fission 1/v Fast neutrons should be moderated. 235 U thermal cross sections σ fission 584 b. σ scattering 9 b. σ radiative capture 97 b. Fission Barriers 1 Nuclear Fission Q for 235 U + n 236 U
Chapter V: Interactions of neutrons with matter
 Chapter V: Interactions of neutrons with matter 1 Content of the chapter Introduction Interaction processes Interaction cross sections Moderation and neutrons path For more details see «Physique des Réacteurs
Chapter V: Interactions of neutrons with matter 1 Content of the chapter Introduction Interaction processes Interaction cross sections Moderation and neutrons path For more details see «Physique des Réacteurs
NUCLEAR SCIENCE ACAD BASIC CURRICULUM CHAPTER 5 NEUTRON LIFE CYCLE STUDENT TEXT REV 2. L th. L f U-235 FUEL MODERATOR START CYCLE HERE THERMAL NEUTRON
 ACAD BASIC CURRICULUM NUCLEAR SCIENCE CHAPTER 5 NEUTRON LIFE CYCLE 346 RESONANCE LOSSES p 038 THERMAL NEUTRON 2 THERMAL NEUTRON LEAKAGE 52 THERMAL ABSORBED BY NON-FUEL ATOMS L th 07 THERMAL f 965 THERMAL
ACAD BASIC CURRICULUM NUCLEAR SCIENCE CHAPTER 5 NEUTRON LIFE CYCLE 346 RESONANCE LOSSES p 038 THERMAL NEUTRON 2 THERMAL NEUTRON LEAKAGE 52 THERMAL ABSORBED BY NON-FUEL ATOMS L th 07 THERMAL f 965 THERMAL
Control of the fission chain reaction
 Control of the fission chain reaction Introduction to Nuclear Science Simon Fraser University Spring 2011 NUCS 342 April 8, 2011 NUCS 342 (Lecture 30) April 8, 2011 1 / 29 Outline 1 Fission chain reaction
Control of the fission chain reaction Introduction to Nuclear Science Simon Fraser University Spring 2011 NUCS 342 April 8, 2011 NUCS 342 (Lecture 30) April 8, 2011 1 / 29 Outline 1 Fission chain reaction
B. Rouben McMaster University Course EP 4D03/6D03 Nuclear Reactor Analysis (Reactor Physics) 2015 Sept.-Dec.
 2: Fission and Other Neutron Reactions B. Rouben McMaster University Course EP 4D03/6D03 Nuclear Reactor Analysis (Reactor Physics) 2015 Sept.-Dec. 2015 September 1 Contents Concepts: Fission and other
2: Fission and Other Neutron Reactions B. Rouben McMaster University Course EP 4D03/6D03 Nuclear Reactor Analysis (Reactor Physics) 2015 Sept.-Dec. 2015 September 1 Contents Concepts: Fission and other
X. Assembling the Pieces
 X. Assembling the Pieces 179 Introduction Our goal all along has been to gain an understanding of nuclear reactors. As we ve noted many times, this requires knowledge of how neutrons are produced and lost.
X. Assembling the Pieces 179 Introduction Our goal all along has been to gain an understanding of nuclear reactors. As we ve noted many times, this requires knowledge of how neutrons are produced and lost.
Quiz, Physics & Chemistry
 Eight Sessions 1. Pressurized Water Reactor 2. Quiz, Thermodynamics & HTFF 3. Quiz, Physics & Chemistry 4. Exam #1, Electrical Concepts & Systems 5. Quiz, Materials Science 6. Quiz, Strength of Materials
Eight Sessions 1. Pressurized Water Reactor 2. Quiz, Thermodynamics & HTFF 3. Quiz, Physics & Chemistry 4. Exam #1, Electrical Concepts & Systems 5. Quiz, Materials Science 6. Quiz, Strength of Materials
NEUTRON MODERATION. LIST three desirable characteristics of a moderator.
 Reactor Theory (eutron Characteristics) DOE-HDBK-1019/1-93 EUTRO MODERATIO EUTRO MODERATIO In thermal reactors, the neutrons that cause fission are at a much lower energy than the energy level at which
Reactor Theory (eutron Characteristics) DOE-HDBK-1019/1-93 EUTRO MODERATIO EUTRO MODERATIO In thermal reactors, the neutrons that cause fission are at a much lower energy than the energy level at which
Lecture 20 Reactor Theory-V
 Objectives In this lecture you will learn the following We will discuss the criticality condition and then introduce the concept of k eff.. We then will introduce the four factor formula and two group
Objectives In this lecture you will learn the following We will discuss the criticality condition and then introduce the concept of k eff.. We then will introduce the four factor formula and two group
Nuclear Physics 2. D. atomic energy levels. (1) D. scattered back along the original direction. (1)
 Name: Date: Nuclear Physics 2. Which of the following gives the correct number of protons and number of neutrons in the nucleus of B? 5 Number of protons Number of neutrons A. 5 6 B. 5 C. 6 5 D. 5 2. The
Name: Date: Nuclear Physics 2. Which of the following gives the correct number of protons and number of neutrons in the nucleus of B? 5 Number of protons Number of neutrons A. 5 6 B. 5 C. 6 5 D. 5 2. The
Write down the nuclear equation that represents the decay of neptunium 239 into plutonium 239.
 Q1.A rod made from uranium 238 ( U) is placed in the core of a nuclear reactor where it absorbs free neutrons. When a nucleus of uranium 238 absorbs a neutron it becomes unstable and decays to neptunium
Q1.A rod made from uranium 238 ( U) is placed in the core of a nuclear reactor where it absorbs free neutrons. When a nucleus of uranium 238 absorbs a neutron it becomes unstable and decays to neptunium
Neutron reproduction. factor ε. k eff = Neutron Life Cycle. x η
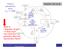 Neutron reproduction factor k eff = 1.000 What is: Migration length? Critical size? How does the geometry affect the reproduction factor? x 0.9 Thermal utilization factor f x 0.9 Resonance escape probability
Neutron reproduction factor k eff = 1.000 What is: Migration length? Critical size? How does the geometry affect the reproduction factor? x 0.9 Thermal utilization factor f x 0.9 Resonance escape probability
17 Neutron Life Cycle
 17 Neutron Life Cycle A typical neutron, from birth as a prompt fission neutron to absorption in the fuel, survives for about 0.001 s (the neutron lifetime) in a CANDU. During this short lifetime, it travels
17 Neutron Life Cycle A typical neutron, from birth as a prompt fission neutron to absorption in the fuel, survives for about 0.001 s (the neutron lifetime) in a CANDU. During this short lifetime, it travels
Physics 3204 UNIT 3 Test Matter Energy Interface
 Physics 3204 UNIT 3 Test Matter Energy Interface 2005 2006 Time: 60 minutes Total Value: 33 Marks Formulae and Constants v = f λ E = hf h f = E k + W 0 E = m c 2 p = h λ 1 A= A T 0 2 t 1 2 E k = ½ mv 2
Physics 3204 UNIT 3 Test Matter Energy Interface 2005 2006 Time: 60 minutes Total Value: 33 Marks Formulae and Constants v = f λ E = hf h f = E k + W 0 E = m c 2 p = h λ 1 A= A T 0 2 t 1 2 E k = ½ mv 2
VIII. Neutron Moderation and the Six Factors
 Introduction VIII. Neutron Moderation and the Six Factors 130 We continue our quest to calculate the multiplication factor (keff) and the neutron distribution (in position and energy) in nuclear reactors.
Introduction VIII. Neutron Moderation and the Six Factors 130 We continue our quest to calculate the multiplication factor (keff) and the neutron distribution (in position and energy) in nuclear reactors.
neutrons in the few kev to several MeV Neutrons are generated over a wide range of energies by a variety of different processes.
 Neutrons 1932: Chadwick discovers the neutron 1935: Goldhaber discovers 10 B(n,α) 7 Li reaction 1936: Locher proposes boron neutron capture as a cancer therapy 1939: Nuclear fission in 235 U induced by
Neutrons 1932: Chadwick discovers the neutron 1935: Goldhaber discovers 10 B(n,α) 7 Li reaction 1936: Locher proposes boron neutron capture as a cancer therapy 1939: Nuclear fission in 235 U induced by
Neutron interactions and dosimetry. Eirik Malinen Einar Waldeland
 Neutron interactions and dosimetry Eirik Malinen Einar Waldeland Topics 1. Neutron interactions 1. Scattering 2. Absorption 2. Neutron dosimetry 3. Applications The neutron Uncharged particle, mass close
Neutron interactions and dosimetry Eirik Malinen Einar Waldeland Topics 1. Neutron interactions 1. Scattering 2. Absorption 2. Neutron dosimetry 3. Applications The neutron Uncharged particle, mass close
Binding Energy and Mass defect
 Binding Energy and Mass defect Particle Relative Electric Charge Relative Mass Mass (kg) Charge (C) (u) Electron -1-1.60 x 10-19 5.485779 x 10-4 9.109390 x 10-31 Proton +1 +1.60 x 10-19 1.007276 1.672623
Binding Energy and Mass defect Particle Relative Electric Charge Relative Mass Mass (kg) Charge (C) (u) Electron -1-1.60 x 10-19 5.485779 x 10-4 9.109390 x 10-31 Proton +1 +1.60 x 10-19 1.007276 1.672623
EEE4101F / EEE4103F Radiation Interactions & Detection
 EEE4101F / EEE4103F Radiation Interactions & Detection 1. Interaction of Radiation with Matter Dr. Steve Peterson 5.14 RW James Department of Physics University of Cape Town steve.peterson@uct.ac.za March
EEE4101F / EEE4103F Radiation Interactions & Detection 1. Interaction of Radiation with Matter Dr. Steve Peterson 5.14 RW James Department of Physics University of Cape Town steve.peterson@uct.ac.za March
Chapter 10. Answers to examination-style questions. Answers Marks Examiner s tips. 1 (a) (i) 238. (ii) β particle(s) 1 Electron antineutrinos 1
 (a) (i) 238 92 U + 0 n 239 92 U (ii) β particle(s) Electron antineutrinos (b) For: Natural uranium is 98% uranium-238 which would be otherwise unused. Plutonium-239 would not need to be stored long-term
(a) (i) 238 92 U + 0 n 239 92 U (ii) β particle(s) Electron antineutrinos (b) For: Natural uranium is 98% uranium-238 which would be otherwise unused. Plutonium-239 would not need to be stored long-term
Chapter Three (Nuclear Radiation)
 Al-Mustansiriyah University College of Science Physics Department Fourth Grade Nuclear Physics Dr. Ali A. Ridha Chapter Three (Nuclear Radiation) (3-1) Nuclear Radiation Whenever a nucleus can attain a
Al-Mustansiriyah University College of Science Physics Department Fourth Grade Nuclear Physics Dr. Ali A. Ridha Chapter Three (Nuclear Radiation) (3-1) Nuclear Radiation Whenever a nucleus can attain a
Neutron Interactions with Matter
 Radioactivity - Radionuclides - Radiation 8 th Multi-Media Training Course with Nuclides.net (Institute Josžef Stefan, Ljubljana, 13th - 15th September 2006) Thursday, 14 th September 2006 Neutron Interactions
Radioactivity - Radionuclides - Radiation 8 th Multi-Media Training Course with Nuclides.net (Institute Josžef Stefan, Ljubljana, 13th - 15th September 2006) Thursday, 14 th September 2006 Neutron Interactions
NUCLEI. Atomic mass unit
 13 NUCLEI Atomic mass unit It is a unit used to express the mass of atoms and particles inside it. One atomic mass unit is the mass of atom. 1u = 1.660539 10. Chadwick discovered neutron. The sum of number
13 NUCLEI Atomic mass unit It is a unit used to express the mass of atoms and particles inside it. One atomic mass unit is the mass of atom. 1u = 1.660539 10. Chadwick discovered neutron. The sum of number
Nuclear Reactor Physics I Final Exam Solutions
 .11 Nuclear Reactor Physics I Final Exam Solutions Author: Lulu Li Professor: Kord Smith May 5, 01 Prof. Smith wants to stress a couple of concepts that get people confused: Square cylinder means a cylinder
.11 Nuclear Reactor Physics I Final Exam Solutions Author: Lulu Li Professor: Kord Smith May 5, 01 Prof. Smith wants to stress a couple of concepts that get people confused: Square cylinder means a cylinder
Fundamentals of Power Reactors. Module One Science & Engineering Fundamentals. Copyright Notice
 Fundamentals of Power Reactors Module One Science & Engineering Fundamentals Copyright Notice HER MAJESTY THE QUEEN IN RIGHT OF CANADA (1993) as represented by the Atomic Energy Control Board All rights
Fundamentals of Power Reactors Module One Science & Engineering Fundamentals Copyright Notice HER MAJESTY THE QUEEN IN RIGHT OF CANADA (1993) as represented by the Atomic Energy Control Board All rights
Introduction to Nuclear Reactor Physics
 Introduction to Nuclear Reactor Physics J. Frýbort, L. Heraltová Department of Nuclear Reactors 19 th October 2017 J. Frýbort, L. Heraltová (CTU in Prague) Introduction to Nuclear Reactor Physics 19 th
Introduction to Nuclear Reactor Physics J. Frýbort, L. Heraltová Department of Nuclear Reactors 19 th October 2017 J. Frýbort, L. Heraltová (CTU in Prague) Introduction to Nuclear Reactor Physics 19 th
SHAWNEE ENVIRONMENTAL SERVICES, INC Identify the definitions of the following terms: a. Nucleon b. Nuclide c. Isotope
 Course Title: Radiological Control Technician Module Title: uclear Physics Module umber: 1.04 Objectives: 1.04.01 Identify the definitions of the following terms: a. ucleon b. uclide c. Isotope 1.04.02
Course Title: Radiological Control Technician Module Title: uclear Physics Module umber: 1.04 Objectives: 1.04.01 Identify the definitions of the following terms: a. ucleon b. uclide c. Isotope 1.04.02
Chemical Engineering 412
 Chemical Engineering 412 Introductory Nuclear Engineering Exam 1 Review 1 Chapter 1 - Fundamentals 2 Nuclear units Elementary particles/particle physics Isotopic nomenclature Atomic weight/number density
Chemical Engineering 412 Introductory Nuclear Engineering Exam 1 Review 1 Chapter 1 - Fundamentals 2 Nuclear units Elementary particles/particle physics Isotopic nomenclature Atomic weight/number density
Reactivity Balance & Reactor Control System
 Reactivity Balance & Reactor Control System K.S. Rajan Professor, School of Chemical & Biotechnology SASTRA University Joint Initiative of IITs and IISc Funded by MHRD Page 1 of 6 Table of Contents 1 MULTIPLICATION
Reactivity Balance & Reactor Control System K.S. Rajan Professor, School of Chemical & Biotechnology SASTRA University Joint Initiative of IITs and IISc Funded by MHRD Page 1 of 6 Table of Contents 1 MULTIPLICATION
Nuclear Theory - Course 127 FISSION
 Nuclear Theory - Course 127 FISSION After having looked at neutron reactions in general, we shall use this lesson to describe the fission reaction and its products in some detail. The Fission Reaction
Nuclear Theory - Course 127 FISSION After having looked at neutron reactions in general, we shall use this lesson to describe the fission reaction and its products in some detail. The Fission Reaction
State the main interaction when an alpha particle is scattered by a gold nucleus
 Q1.(a) Scattering experiments are used to investigate the nuclei of gold atoms. In one experiment, alpha particles, all of the same energy (monoenergetic), are incident on a foil made from a single isotope
Q1.(a) Scattering experiments are used to investigate the nuclei of gold atoms. In one experiment, alpha particles, all of the same energy (monoenergetic), are incident on a foil made from a single isotope
Chemistry: The Central Science. Chapter 21: Nuclear Chemistry
 Chemistry: The Central Science Chapter 21: Nuclear Chemistry A nuclear reaction involves changes in the nucleus of an atom Nuclear chemistry the study of nuclear reactions, with an emphasis in their uses
Chemistry: The Central Science Chapter 21: Nuclear Chemistry A nuclear reaction involves changes in the nucleus of an atom Nuclear chemistry the study of nuclear reactions, with an emphasis in their uses
Energy. on this world and elsewhere. Visiting today: Prof. Paschke
 Energy on this world and elsewhere Visiting today: Prof. Paschke Instructor: Gordon D. Cates Office: Physics 106a, Phone: (434) 924-4792 email: cates@virginia.edu Course web site available at www.phys.virginia.edu,
Energy on this world and elsewhere Visiting today: Prof. Paschke Instructor: Gordon D. Cates Office: Physics 106a, Phone: (434) 924-4792 email: cates@virginia.edu Course web site available at www.phys.virginia.edu,
CHARGED PARTICLE INTERACTIONS
 CHARGED PARTICLE INTERACTIONS Background Charged Particles Heavy charged particles Charged particles with Mass > m e α, proton, deuteron, heavy ion (e.g., C +, Fe + ), fission fragment, muon, etc. α is
CHARGED PARTICLE INTERACTIONS Background Charged Particles Heavy charged particles Charged particles with Mass > m e α, proton, deuteron, heavy ion (e.g., C +, Fe + ), fission fragment, muon, etc. α is
SOURCES of RADIOACTIVITY
 Section 9: SOURCES of RADIOACTIVITY This section briefly describes various sources of radioactive nuclei, both naturally occurring and those produced artificially (man-made) in, for example, reactors or
Section 9: SOURCES of RADIOACTIVITY This section briefly describes various sources of radioactive nuclei, both naturally occurring and those produced artificially (man-made) in, for example, reactors or
Nuclear Physics Fundamentals and Application Prof. H.C. Verma Department of Physics Indian Institute of Technology, Kanpur
 Nuclear Physics Fundamentals and Application Prof. H.C. Verma Department of Physics Indian Institute of Technology, Kanpur Lecture - 34 Nuclear fission of uranium So, we talked about fission reactions
Nuclear Physics Fundamentals and Application Prof. H.C. Verma Department of Physics Indian Institute of Technology, Kanpur Lecture - 34 Nuclear fission of uranium So, we talked about fission reactions
Nuclear Physics and Nuclear Reactions
 Slide 1 / 33 Nuclear Physics and Nuclear Reactions The Nucleus Slide 2 / 33 Proton: The charge on a proton is +1.6x10-19 C. The mass of a proton is 1.6726x10-27 kg. Neutron: The neutron is neutral. The
Slide 1 / 33 Nuclear Physics and Nuclear Reactions The Nucleus Slide 2 / 33 Proton: The charge on a proton is +1.6x10-19 C. The mass of a proton is 1.6726x10-27 kg. Neutron: The neutron is neutral. The
General Physics (PHY 2140)
 General Physics (PHY 2140) Lecture 20 Modern Physics Nuclear Energy and Elementary Particles Fission, Fusion and Reactors Elementary Particles Fundamental Forces Classification of Particles Conservation
General Physics (PHY 2140) Lecture 20 Modern Physics Nuclear Energy and Elementary Particles Fission, Fusion and Reactors Elementary Particles Fundamental Forces Classification of Particles Conservation
1.1 ALPHA DECAY 1.2 BETA MINUS DECAY 1.3 GAMMA EMISSION 1.4 ELECTRON CAPTURE/BETA PLUS DECAY 1.5 NEUTRON EMISSION 1.6 SPONTANEOUS FISSION
 Chapter NP-3 Nuclear Physics Decay Modes and Decay Rates TABLE OF CONTENTS INTRODUCTION OBJECTIVES 1.0 RADIOACTIVE DECAY 1.1 ALPHA DECAY 1.2 BETA MINUS DECAY 1.3 GAMMA EMISSION 1.4 ELECTRON CAPTURE/BETA
Chapter NP-3 Nuclear Physics Decay Modes and Decay Rates TABLE OF CONTENTS INTRODUCTION OBJECTIVES 1.0 RADIOACTIVE DECAY 1.1 ALPHA DECAY 1.2 BETA MINUS DECAY 1.3 GAMMA EMISSION 1.4 ELECTRON CAPTURE/BETA
1 v. L18.pdf Spring 2010, P627, YK February 22, 2012
 L18.pdf Spring 2010, P627, YK February 22, 2012 18 T2 Nuclear Information Service at LANL: http://t2.lanl.gov/data/ ENDF/B VI Neutron Data : http://t2.lanl.gov/cgi bin/nuclides/endind Thermal neutron x
L18.pdf Spring 2010, P627, YK February 22, 2012 18 T2 Nuclear Information Service at LANL: http://t2.lanl.gov/data/ ENDF/B VI Neutron Data : http://t2.lanl.gov/cgi bin/nuclides/endind Thermal neutron x
Nuclear Reactions. This is an example of nuclear reaction. Now consider a chemical reaction
 Nuclear Reactions. Introduction REDs are important while yellow is less. Nuclear reactions are the transformations that occur when two nuclei collide. The first such reaction was observed by Rutherford
Nuclear Reactions. Introduction REDs are important while yellow is less. Nuclear reactions are the transformations that occur when two nuclei collide. The first such reaction was observed by Rutherford
turbine (a) (i) Which part of the power station provides thermal (heat) energy from a chain reaction?
 Nuclear fission and radiation 1 The diagram shows parts of a nuclear power station. control rods boiler steam generator electricity out turbine condenser nuclear reactor (a) (i) Which part of the power
Nuclear fission and radiation 1 The diagram shows parts of a nuclear power station. control rods boiler steam generator electricity out turbine condenser nuclear reactor (a) (i) Which part of the power
Introduction to Radiological Sciences Neutron Detectors. Theory of operation. Types of detectors Source calibration Survey for Dose
 Introduction to Radiological Sciences Neutron Detectors Neutron counting Theory of operation Slow neutrons Fast neutrons Types of detectors Source calibration Survey for Dose 2 Neutrons, what are they?
Introduction to Radiological Sciences Neutron Detectors Neutron counting Theory of operation Slow neutrons Fast neutrons Types of detectors Source calibration Survey for Dose 2 Neutrons, what are they?
Nuclear Fission. Q for 238 U + n 239 U is 4.??? MeV. E A for 239 U 6.6 MeV MeV neutrons are needed.
 Q for 235 U + n 236 U is 6.54478 MeV. Table 13.11 in Krane: Activation energy E A for 236 U 6.2 MeV (Liquid drop + shell) 235 U can be fissioned with zero-energy neutrons. Q for 238 U + n 239 U is 4.???
Q for 235 U + n 236 U is 6.54478 MeV. Table 13.11 in Krane: Activation energy E A for 236 U 6.2 MeV (Liquid drop + shell) 235 U can be fissioned with zero-energy neutrons. Q for 238 U + n 239 U is 4.???
2. The Steady State and the Diffusion Equation
 2. The Steady State and the Diffusion Equation The Neutron Field Basic field quantity in reactor physics is the neutron angular flux density distribution: Φ( r r, E, r Ω,t) = v(e)n( r r, E, r Ω,t) -- distribution
2. The Steady State and the Diffusion Equation The Neutron Field Basic field quantity in reactor physics is the neutron angular flux density distribution: Φ( r r, E, r Ω,t) = v(e)n( r r, E, r Ω,t) -- distribution
We completed our discussion of nuclear modeling with a discussion of the liquid drop and shell models We began discussing radioactivity
 Modern Physics (PHY 3305) Lecture Notes Modern Physics (PHY 3305) Lecture Notes Nuclear Physics: Fission and Fusion (11.7) SteveSekula, 19 April 010 (created 1 April 010) Review no tags We completed our
Modern Physics (PHY 3305) Lecture Notes Modern Physics (PHY 3305) Lecture Notes Nuclear Physics: Fission and Fusion (11.7) SteveSekula, 19 April 010 (created 1 April 010) Review no tags We completed our
Chapter 12: Nuclear Reaction
 Chapter 12: Nuclear Reaction A nuclear reaction occurs when a nucleus is unstable or is being bombarded by a nuclear particle. The product of a nuclear reaction is a new nuclide with an emission of a nuclear
Chapter 12: Nuclear Reaction A nuclear reaction occurs when a nucleus is unstable or is being bombarded by a nuclear particle. The product of a nuclear reaction is a new nuclide with an emission of a nuclear
Lewis 2.1, 2.2 and 2.3
 Chapter 2(and 3) Cross-Sections TA Lewis 2.1, 2.2 and 2.3 Learning Objectives Understand different types of nuclear reactions Understand cross section behavior for different reactions Understand d resonance
Chapter 2(and 3) Cross-Sections TA Lewis 2.1, 2.2 and 2.3 Learning Objectives Understand different types of nuclear reactions Understand cross section behavior for different reactions Understand d resonance
Nuclear Chemistry. Decay Reactions The most common form of nuclear decay reactions are the following:
 Nuclear Chemistry Nuclear reactions are transmutation of the one element into another. We can describe nuclear reactions in a similar manner as regular chemical reactions using ideas of stoichiometry,
Nuclear Chemistry Nuclear reactions are transmutation of the one element into another. We can describe nuclear reactions in a similar manner as regular chemical reactions using ideas of stoichiometry,
Lesson 8: Slowing Down Spectra, p, Fermi Age
 Lesson 8: Slowing Down Spectra, p, Fermi Age Slowing Down Spectra in Infinite Homogeneous Media Resonance Escape Probability ( p ) Resonance Integral ( I, I eff ) p, for a Reactor Lattice Semi-empirical
Lesson 8: Slowing Down Spectra, p, Fermi Age Slowing Down Spectra in Infinite Homogeneous Media Resonance Escape Probability ( p ) Resonance Integral ( I, I eff ) p, for a Reactor Lattice Semi-empirical
Chapter Four (Interaction of Radiation with Matter)
 Al-Mustansiriyah University College of Science Physics Department Fourth Grade Nuclear Physics Dr. Ali A. Ridha Chapter Four (Interaction of Radiation with Matter) Different types of radiation interact
Al-Mustansiriyah University College of Science Physics Department Fourth Grade Nuclear Physics Dr. Ali A. Ridha Chapter Four (Interaction of Radiation with Matter) Different types of radiation interact
Lectures on Applied Reactor Technology and Nuclear Power Safety. Lecture No 5. Title: Reactor Kinetics and Reactor Operation
 Lectures on Nuclear Power Safety Lecture No 5 Title: Reactor Kinetics and Reactor Operation Department of Energy Technology KTH Spring 2005 Slide No 1 Outline of the Lecture (1) Reactor Kinetics Reactor
Lectures on Nuclear Power Safety Lecture No 5 Title: Reactor Kinetics and Reactor Operation Department of Energy Technology KTH Spring 2005 Slide No 1 Outline of the Lecture (1) Reactor Kinetics Reactor
Radioactivity is the spontaneous disintegration of nuclei. The first radioactive. elements discovered were the heavy atoms thorium and uranium.
 Chapter 16 What is radioactivity? Radioactivity is the spontaneous disintegration of nuclei. The first radioactive elements discovered were the heavy atoms thorium and uranium. These heavy atoms and others
Chapter 16 What is radioactivity? Radioactivity is the spontaneous disintegration of nuclei. The first radioactive elements discovered were the heavy atoms thorium and uranium. These heavy atoms and others
The number of protons in the nucleus is known as the atomic number Z, and determines the chemical properties of the element.
 I. NUCLEAR PHYSICS I.1 Atomic Nucleus Very briefly, an atom is formed by a nucleus made up of nucleons (neutrons and protons) and electrons in external orbits. The number of electrons and protons is equal
I. NUCLEAR PHYSICS I.1 Atomic Nucleus Very briefly, an atom is formed by a nucleus made up of nucleons (neutrons and protons) and electrons in external orbits. The number of electrons and protons is equal
Interaction of Ionizing Radiation with Matter
 Type of radiation charged particles photonen neutronen Uncharged particles Charged particles electrons (β - ) He 2+ (α), H + (p) D + (d) Recoil nuclides Fission fragments Interaction of ionizing radiation
Type of radiation charged particles photonen neutronen Uncharged particles Charged particles electrons (β - ) He 2+ (α), H + (p) D + (d) Recoil nuclides Fission fragments Interaction of ionizing radiation
NE 495 Elements of Nuclear Engineering
 Name: NE 495 Elements of Nuclear Engineering Open Books and Notes Final Examination, Spring 2009 1. Indicate whether the following statements are true (T) or false (F). [50 ( ) The energy of a photon is
Name: NE 495 Elements of Nuclear Engineering Open Books and Notes Final Examination, Spring 2009 1. Indicate whether the following statements are true (T) or false (F). [50 ( ) The energy of a photon is
UNIT 13: NUCLEAR CHEMISTRY
 UNIT 13: NUCLEAR CHEMISTRY REVIEW: ISOTOPE NOTATION An isotope notation is written as Z A X, where X is the element, A is the mass number (sum of protons and neutrons), and Z is the atomic number. For
UNIT 13: NUCLEAR CHEMISTRY REVIEW: ISOTOPE NOTATION An isotope notation is written as Z A X, where X is the element, A is the mass number (sum of protons and neutrons), and Z is the atomic number. For
Activation Analysis. Characteristic decay mechanisms, α, β, γ Activity A reveals the abundance N:
 2.5. Isotope analysis and neutron activation techniques The previously discussed techniques of material analysis are mainly based on the characteristic atomic structure of the elements and the associated
2.5. Isotope analysis and neutron activation techniques The previously discussed techniques of material analysis are mainly based on the characteristic atomic structure of the elements and the associated
MCRT L8: Neutron Transport
 MCRT L8: Neutron Transport Recap fission, absorption, scattering, cross sections Fission products and secondary neutrons Slow and fast neutrons Energy spectrum of fission neutrons Nuclear reactor safety
MCRT L8: Neutron Transport Recap fission, absorption, scattering, cross sections Fission products and secondary neutrons Slow and fast neutrons Energy spectrum of fission neutrons Nuclear reactor safety
molar mass = 0.239kg (1) mass needed = = kg (1) [7]
![molar mass = 0.239kg (1) mass needed = = kg (1) [7] molar mass = 0.239kg (1) mass needed = = kg (1) [7]](/thumbs/77/75861066.jpg) PhysicsAndMathsTutor.com 1 1. (a) (i) proton number 82 and nucleon number 214 (ii) Pb 2 (b) (i) kinetic energy [or electrostatic potential energy] (ii) m = 8.6 E 2 c 1 10 = 8 2 (10 ) = 9.6 10 0 kg [5]
PhysicsAndMathsTutor.com 1 1. (a) (i) proton number 82 and nucleon number 214 (ii) Pb 2 (b) (i) kinetic energy [or electrostatic potential energy] (ii) m = 8.6 E 2 c 1 10 = 8 2 (10 ) = 9.6 10 0 kg [5]
Physics of Radiotherapy. Lecture II: Interaction of Ionizing Radiation With Matter
 Physics of Radiotherapy Lecture II: Interaction of Ionizing Radiation With Matter Charge Particle Interaction Energetic charged particles interact with matter by electrical forces and lose kinetic energy
Physics of Radiotherapy Lecture II: Interaction of Ionizing Radiation With Matter Charge Particle Interaction Energetic charged particles interact with matter by electrical forces and lose kinetic energy
Nuclear Power MORE CHAPTER 11, #6. Nuclear Fission Reactors
 MORE CHAPTER 11, #6 Nuclear Power Nuclear Fission Reactors The discovery that several neutrons are emitted in the fission process led to speculation concerning the possibility of using these neutrons to
MORE CHAPTER 11, #6 Nuclear Power Nuclear Fission Reactors The discovery that several neutrons are emitted in the fission process led to speculation concerning the possibility of using these neutrons to
CHEM 312 Lecture 7: Fission
 CHEM 312 Lecture 7: Fission Readings: Modern Nuclear Chemistry, Chapter 11; Nuclear and Radiochemistry, Chapter 3 General Overview of Fission Energetics The Probability of Fission Fission Product Distributions
CHEM 312 Lecture 7: Fission Readings: Modern Nuclear Chemistry, Chapter 11; Nuclear and Radiochemistry, Chapter 3 General Overview of Fission Energetics The Probability of Fission Fission Product Distributions
Fundamentals of Nuclear Reactor Physics
 Fundamentals of Nuclear Reactor Physics E. E. Lewis Professor of Mechanical Engineering McCormick School of Engineering and Applied Science Northwestern University AMSTERDAM BOSTON HEIDELBERG LONDON NEW
Fundamentals of Nuclear Reactor Physics E. E. Lewis Professor of Mechanical Engineering McCormick School of Engineering and Applied Science Northwestern University AMSTERDAM BOSTON HEIDELBERG LONDON NEW
Operational Reactor Safety
 Operational Reactor Safety 22.091/22.903 Professor Andrew C. Kadak Professor of the Practice Lecture 3 Reactor Kinetics and Control Page 1 Topics to Be Covered Time Dependent Diffusion Equation Prompt
Operational Reactor Safety 22.091/22.903 Professor Andrew C. Kadak Professor of the Practice Lecture 3 Reactor Kinetics and Control Page 1 Topics to Be Covered Time Dependent Diffusion Equation Prompt
Nuclear reactions and nuclear ssion
 Nuclear reactions and nuclear ssion March 19, 2002 1 Cross sections and reaction rates ² Consider a thin target of thickness dx and number density of targets n t being bombarded by a beam of number density
Nuclear reactions and nuclear ssion March 19, 2002 1 Cross sections and reaction rates ² Consider a thin target of thickness dx and number density of targets n t being bombarded by a beam of number density
Characteristics and Structure of Matter Perry Sprawls, Ph.D.
 Online Textbook Perry Sprawls, Ph.D. Table of Contents INTRODUCTION AND OVERVIEW NUCLEAR STRUCTURE Composition Nuclides Isotopes Isobars Isomers Isotones NUCLEAR STABILITY Radioactivity NUCLEAR ENERGY
Online Textbook Perry Sprawls, Ph.D. Table of Contents INTRODUCTION AND OVERVIEW NUCLEAR STRUCTURE Composition Nuclides Isotopes Isobars Isomers Isotones NUCLEAR STABILITY Radioactivity NUCLEAR ENERGY
Nuclear Fission Fission discovered by Otto Hahn and Fritz Strassman, Lisa Meitner in 1938
 Fission Readings: Modern Nuclear Chemistry, Chapter 11; Nuclear and Radiochemistry, Chapter 3 General Overview of Fission Energetics The Probability of Fission Fission Product Distributions Total Kinetic
Fission Readings: Modern Nuclear Chemistry, Chapter 11; Nuclear and Radiochemistry, Chapter 3 General Overview of Fission Energetics The Probability of Fission Fission Product Distributions Total Kinetic
Step 2: Calculate the total amount of U-238 present at time=0. Step 4: Calculate the rate constant for the decay process.
 LP#9. A meteor contains 0.556 g of Pb-206 to every 1.00g U-238. Determine the age of the meteor. Step 1: Calculate the moles of each nuclide present. 0.566g Pb-206 x 1.00g U-238 x Step 2: Calculate the
LP#9. A meteor contains 0.556 g of Pb-206 to every 1.00g U-238. Determine the age of the meteor. Step 1: Calculate the moles of each nuclide present. 0.566g Pb-206 x 1.00g U-238 x Step 2: Calculate the
Introduction to Nuclear Engineering. Ahmad Al Khatibeh
 Introduction to Nuclear Engineering Ahmad Al Khatibeh CONTENTS INTRODUCTION (Revision) RADIOACTIVITY Radioactive Decay Rates Units of Measurement for Radioactivity Variation of Radioactivity Over Time.
Introduction to Nuclear Engineering Ahmad Al Khatibeh CONTENTS INTRODUCTION (Revision) RADIOACTIVITY Radioactive Decay Rates Units of Measurement for Radioactivity Variation of Radioactivity Over Time.
Reactor Operation Without Feedback Effects
 22.05 Reactor Physics - Part Twenty-Six Reactor Operation Without Feedback Effects 1. Reference Material: See pp. 363-368 of the article, Light Water Reactor Control Systems, in Wiley Encyclopedia of Electrical
22.05 Reactor Physics - Part Twenty-Six Reactor Operation Without Feedback Effects 1. Reference Material: See pp. 363-368 of the article, Light Water Reactor Control Systems, in Wiley Encyclopedia of Electrical
1. Explain the significance of negative energy of electron in an orbit. askiitians
 Class: 12 Subject: Physics Topic: Atoms and Nuclei No. of Questions: 30 1. Explain the significance of negative energy of electron in an orbit. The energy of an electron in the orbits of an atom is negative.
Class: 12 Subject: Physics Topic: Atoms and Nuclei No. of Questions: 30 1. Explain the significance of negative energy of electron in an orbit. The energy of an electron in the orbits of an atom is negative.
Radiation Detection for the Beta- Delayed Alpha and Gamma Decay of 20 Na. Ellen Simmons
 Radiation Detection for the Beta- Delayed Alpha and Gamma Decay of 20 Na Ellen Simmons 1 Contents Introduction Review of the Types of Radiation Charged Particle Radiation Detection Review of Semiconductor
Radiation Detection for the Beta- Delayed Alpha and Gamma Decay of 20 Na Ellen Simmons 1 Contents Introduction Review of the Types of Radiation Charged Particle Radiation Detection Review of Semiconductor
NUCLEI, RADIOACTIVITY AND NUCLEAR REACTIONS
 NUCLEI, RADIOACTIVITY AND NUCLEAR REACTIONS VERY SHORT ANSWER QUESTIONS Q-1. Which of the two is bigger 1 kwh or 1 MeV? Q-2. What should be the approximate minimum energy of a gamma ray photon for pair
NUCLEI, RADIOACTIVITY AND NUCLEAR REACTIONS VERY SHORT ANSWER QUESTIONS Q-1. Which of the two is bigger 1 kwh or 1 MeV? Q-2. What should be the approximate minimum energy of a gamma ray photon for pair
Slowing down the neutrons
 Slowing down the neutrons Clearly, an obvious way to make a reactor work, and to make use of this characteristic of the 3 U(n,f) cross-section, is to slow down the fast, fission neutrons. This can be accomplished,
Slowing down the neutrons Clearly, an obvious way to make a reactor work, and to make use of this characteristic of the 3 U(n,f) cross-section, is to slow down the fast, fission neutrons. This can be accomplished,
Atomic and nuclear physics
 Chapter 4 Atomic and nuclear physics INTRODUCTION: The technologies used in nuclear medicine for diagnostic imaging have evolved over the last century, starting with Röntgen s discovery of X rays and Becquerel
Chapter 4 Atomic and nuclear physics INTRODUCTION: The technologies used in nuclear medicine for diagnostic imaging have evolved over the last century, starting with Röntgen s discovery of X rays and Becquerel
Radioactivity III: Measurement of Half Life.
 PHY 192 Half Life Spring 2010 1 Radioactivity III: Measurement of Half Life. Introduction This experiment will once again use the apparatus of the first experiment, this time to measure radiation intensity
PHY 192 Half Life Spring 2010 1 Radioactivity III: Measurement of Half Life. Introduction This experiment will once again use the apparatus of the first experiment, this time to measure radiation intensity
General Physics (PHY 2140)
 General Physics (PHY 140) Lecture 18 Modern Physics Nuclear Physics Nuclear properties Binding energy Radioactivity The Decay Process Natural Radioactivity Last lecture: 1. Quantum physics Electron Clouds
General Physics (PHY 140) Lecture 18 Modern Physics Nuclear Physics Nuclear properties Binding energy Radioactivity The Decay Process Natural Radioactivity Last lecture: 1. Quantum physics Electron Clouds
Lecture 14, 8/9/2017. Nuclear Reactions and the Transmutation of Elements Nuclear Fission; Nuclear Reactors Nuclear Fusion
 Lecture 14, 8/9/2017 Nuclear Reactions and the Transmutation of Elements Nuclear Fission; Nuclear Reactors Nuclear Fusion Nuclear Reactions and the Transmutation of Elements A nuclear reaction takes place
Lecture 14, 8/9/2017 Nuclear Reactions and the Transmutation of Elements Nuclear Fission; Nuclear Reactors Nuclear Fusion Nuclear Reactions and the Transmutation of Elements A nuclear reaction takes place
PHYSICS A2 UNIT 2 SECTION 1: RADIOACTIVITY & NUCLEAR ENERGY
 PHYSICS A2 UNIT 2 SECTION 1: RADIOACTIVITY & NUCLEAR ENERGY THE ATOMIC NUCLEUS / NUCLEAR RADIUS & DENSITY / PROPERTIES OF NUCLEAR RADIATION / INTENSITY & BACKGROUND RADIATION / EXPONENTIAL LAW OF DECAY
PHYSICS A2 UNIT 2 SECTION 1: RADIOACTIVITY & NUCLEAR ENERGY THE ATOMIC NUCLEUS / NUCLEAR RADIUS & DENSITY / PROPERTIES OF NUCLEAR RADIATION / INTENSITY & BACKGROUND RADIATION / EXPONENTIAL LAW OF DECAY
Elements, atoms and more. Contents. Atoms. Binding energy per nucleon. Nuclear Reactors. Atom: cloud of electrons around a nucleus
 Delft University of Technology Nuclear Reactors Jan Leen Kloosterman, Reactor Institute Delft, TU-Delft 8-6-0 Challenge the future Contents Elements, atoms and more Introductory physics Reactor physics
Delft University of Technology Nuclear Reactors Jan Leen Kloosterman, Reactor Institute Delft, TU-Delft 8-6-0 Challenge the future Contents Elements, atoms and more Introductory physics Reactor physics
Subcritical Multiplication and Reactor Startup
 22.05 Reactor Physics - Part Twenty-Five Subcritical Multiplication and Reactor Startup 1. Reference Material See pp. 357-363 of the article, Light Water Reactor Control Systems, in Wiley Encyclopedia
22.05 Reactor Physics - Part Twenty-Five Subcritical Multiplication and Reactor Startup 1. Reference Material See pp. 357-363 of the article, Light Water Reactor Control Systems, in Wiley Encyclopedia
Lecture PowerPoints. Chapter 31 Physics: Principles with Applications, 7th edition Giancoli
 Lecture PowerPoints Chapter 31 Physics: Principles with Applications, 7th edition Giancoli This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching
Lecture PowerPoints Chapter 31 Physics: Principles with Applications, 7th edition Giancoli This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching
22.54 Neutron Interactions and Applications (Spring 2004) Chapter 1 (2/3/04) Overview -- Interactions, Distributions, Cross Sections, Applications
 .54 Neutron Interactions and Applications (Spring 004) Chapter 1 (/3/04) Overview -- Interactions, Distributions, Cross Sections, Applications There are many references in the vast literature on nuclear
.54 Neutron Interactions and Applications (Spring 004) Chapter 1 (/3/04) Overview -- Interactions, Distributions, Cross Sections, Applications There are many references in the vast literature on nuclear
Sustainable Power Generation Applied Heat and Power Technology. Equations, diagrams and tables
 Sustainable Power Generation Applied Heat and Power Technology Equations, diagrams and tables 1 STEAM CYCLE Enthalpy of liquid water h = c p,liquid (T T ref ) T ref = 273 K (normal conditions). The specific
Sustainable Power Generation Applied Heat and Power Technology Equations, diagrams and tables 1 STEAM CYCLE Enthalpy of liquid water h = c p,liquid (T T ref ) T ref = 273 K (normal conditions). The specific
There are 82 protons in a lead nucleus. Why doesn t the lead nucleus burst apart?
 Question 32.1 The Nucleus There are 82 protons in a lead nucleus. Why doesn t the lead nucleus burst apart? a) Coulomb repulsive force doesn t act inside the nucleus b) gravity overpowers the Coulomb repulsive
Question 32.1 The Nucleus There are 82 protons in a lead nucleus. Why doesn t the lead nucleus burst apart? a) Coulomb repulsive force doesn t act inside the nucleus b) gravity overpowers the Coulomb repulsive
General Physics (PHY 2140)
 General Physics (PHY 2140) Lecture 37 Modern Physics Nuclear Physics Radioactivity Nuclear reactions http://www.physics.wayne.edu/~apetrov/phy2140/ Chapter 29 1 Lightning Review Last lecture: 1. Nuclear
General Physics (PHY 2140) Lecture 37 Modern Physics Nuclear Physics Radioactivity Nuclear reactions http://www.physics.wayne.edu/~apetrov/phy2140/ Chapter 29 1 Lightning Review Last lecture: 1. Nuclear
Introduction to Nuclear Physics and Nuclear Decay
 Introduction to Nuclear Physics and Nuclear Decay Larry MacDonald macdon@uw.edu Nuclear Medicine Basic Science Lectures September 6, 2011 toms Nucleus: ~10-14 m diameter ~10 17 kg/m 3 Electron clouds:
Introduction to Nuclear Physics and Nuclear Decay Larry MacDonald macdon@uw.edu Nuclear Medicine Basic Science Lectures September 6, 2011 toms Nucleus: ~10-14 m diameter ~10 17 kg/m 3 Electron clouds:
Chem 481 Lecture Material 4/22/09
 Chem 481 Lecture Material 4/22/09 Nuclear Reactors Poisons The neutron population in an operating reactor is controlled by the use of poisons in the form of control rods. A poison is any substance that
Chem 481 Lecture Material 4/22/09 Nuclear Reactors Poisons The neutron population in an operating reactor is controlled by the use of poisons in the form of control rods. A poison is any substance that
Chapter 37. Nuclear Chemistry. Copyright (c) 2011 by Michael A. Janusa, PhD. All rights reserved.
 Chapter 37 Nuclear Chemistry Copyright (c) 2 by Michael A. Janusa, PhD. All rights reserved. 37. Radioactivity Radioactive decay is the process in which a nucleus spontaneously disintegrates, giving off
Chapter 37 Nuclear Chemistry Copyright (c) 2 by Michael A. Janusa, PhD. All rights reserved. 37. Radioactivity Radioactive decay is the process in which a nucleus spontaneously disintegrates, giving off
Class XII Chapter 13 - Nuclei Physics
 Question 13.1: (a) Two stable isotopes of lithium and have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium. (b)
Question 13.1: (a) Two stable isotopes of lithium and have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium. (b)
Nuclear Chemistry. The Nucleus. Isotopes. Slide 1 / 43. Slide 2 / 43. Slide 3 / 43
 Slide 1 / 43 Nuclear Chemistry The Nucleus Slide 2 / 43 Remember that the nucleus is comprised of the two nucleons, protons and neutrons. The number of protons is the atomic number. The number of protons
Slide 1 / 43 Nuclear Chemistry The Nucleus Slide 2 / 43 Remember that the nucleus is comprised of the two nucleons, protons and neutrons. The number of protons is the atomic number. The number of protons
