Basic Tools CMSC 641. Running Time. Problem. Problem. Algorithmic Design Paradigms. lg (n!) (lg n)! (lg n) lgn n.2
|
|
|
- Beatrix Richardson
- 5 years ago
- Views:
Transcription
1 Baic Tool CMSC April, Review Aympoic Noaion Order of Growh Recurrence relaion Daa Srucure Li, Heap, Graph, Tree, Balanced Tree, Hah Table Advanced daa rucure: Binomial Heap, Fibonacci Heap Soring Mehod Heapor, Quickor Linear ime or (bucke/couning/radix) Selecion elec he median in linear ime Running Time Problem Heap Operaion make-heap iner find-min delee-min union decreae-key delee Linked Li N N N Binary N Binomial Fibonacci Find he large ube of hee funcion ha belong o he ame equivalence cla: n lg lg n lg (n!) (lg n)! (lg n) lgn n. lg lgn i-empy amorized Algorihmic Deign Paradigm Problem Divide and Conquer Dynamic Programming Greedy Algorihm Minimum Spanning Tree Krukal and Prim Shore Pah Dijkra algorihm Bellman Ford Floyd Warhall Forre Gump i a good runner. He can run mile uninerruped bu afer ha he need o op o ea a box of chocolae. He wan o run acro America along a cerain rou. He know he locaion of he ore along he roue ha ell hi favorie chocolae. He wan o op a FEW ime a poible. Deign an algorihm for chooing where Gump hould op. Inpu: ored array A[,,,n] of diance of chocolae hop from he aring poin Aume ha he la chocolae hop i a he end of he roue
2 Soluion Inuiion Behind Greedy MST Greedy Work! Chooe he op ha i FARTHEST (among all poible op) from he curren op. Variable: currensop, nexsop Greedy Choice : chooe he nexsop uch ha A[nexSop] A[currenSop] <, and A[nexSop+] A[currenSop] > You need o prove ha he oluion i opimal Ue a proof by conradicion We mainain in a ube of edge A, which will iniially be empy, and we will add edge one a a ime, unil equal he MST. We ay ha a ube A E i viable if A i a ube of edge in ome MST. We ay ha an edge (u,v) E-A i afe if A {(u,v)} i viable. Baically, he choice (u,v) i a afe choice o add o ha A can ill be exended o form an MST. Noe ha if A i viable i canno conain a cycle. A generic greedy algorihm operae by repeaedly adding any afe edge o he curren panning ree. Generic-MST (G, w) Definiion. A // A rivially aifie invarian // line - mainain he invarian. while A doe no form a panning ree. do find an edge (u,v) ha i afe for A. A A {(u,v)}. reurn A // A i now a MST A cu (S, V-S) i ju a pariion of he verice ino dijoin ube. An edge (u, v) croe he cu if one endpoin i in S and he oher i in V-S. Given a ube of edge A, we ay ha a cu repec A if no edge in A croe he cu. An edge of E i a ligh edge croing a cu, if among all edge croing he cu, i ha he minimum weigh (he ligh edge may no be unique if here are duplicae edge weigh). When i an Edge Safe? MST Lemma If we have compued a parial MST, and we wih o know which edge can be added ha do NOT induce a cycle in he curren MST, any edge ha croe a repecing cu i a poible candidae. Inuiion ay ha ince all edge croing a repecing cu do no induce a cycle, hen he lighe edge croing a cu i a naural choice. Lemma: Le G = (V, E) be a conneced, undireced graph wih real-value weigh on he edge. Le A be a viable ube of E (i.e. a ube of ome MST), le (S, V-S) be any cu ha repec A, and le (u,v) be a ligh edge croing hi cu. Then, he edge i afe for A. Poin of Lemma: Greedy raegy work!
3 Baic of Krukal Algorihm Deecing a Cycle Aemp o add edge o A in increaing order of weigh (lighe edge fir) If he nex edge doe no induce a cycle among he curren e of edge, hen i i added o A. If i doe, hen hi edge i paed over, and we conider he nex edge in order. A hi algorihm run, he edge of A will induce a fore on he verice and he ree of hi fore are merged ogeher unil we have a ingle ree conaining all verice. We can perform a DFS on ubgraph induced by he edge of A, bu hi ake oo much ime. Ue dijoin e UNION-FIND daa rucure. Thi daa rucure uppor operaion: Creae-Se(u): creae a e conaining u. Find-Se(u): Find he e ha conain u. Union(u, v): Merge he e conaining u and v. Each can be performed in O(lg n) ime. The verice of he graph will be elemen o be ored in he e; he e will be verice in each ree of A (ored a a imple li of edge). MST-Krukal(G, w) Inuiion behind Prim Algorihm. A // iniially A i empy. for each verex v V[G] // line - ake O(V) ime. do Creae-Se(v) // creae e for each verex. or he edge of E by non-decreaing weigh w. for each edge (u,v) E, in order by non-decreaing weigh. do if Find-Se(u) Find-Se(v) // u&v on differen ree. hen A A {(u,v)}. Union(u,v). reurn A Conider he e of verice S currenly par of he ree, and i complemen (V-S). We have a cu of he graph and he curren e of ree edge A i repeced by hi cu. Which edge hould we add nex? Ligh edge! Toal running ime i O(E lg E). Baic of Prim Algorihm Implemenaion: Prioriy Queue I work by adding leave one a a ime o he curren ree. Sar wih he roo verex r (i can be any verex). A any ime, he ube of edge A form a ingle ree. S = verice of A. A each ep, a ligh edge connecing a verex in S o a verex in V- S i added o he ree. The ree grow unil i pan all he verice in V. Implemenaion Iue: How o updae he cu efficienly? How o deermine he ligh edge quickly? Prioriy queue implemened uing heap can uppor he following operaion in O(lg n) ime: Iner (Q, u, key): Iner u wih he key value key in Q u = Exrac_Min(Q): Exrac he iem wih minimum key value in Q Decreae_Key(Q, u, new_key): Decreae he value of u key value o new_key All he verice ha are no in he S (he verice of he edge in A) reide in a prioriy queue Q baed on a key field. When he algorihm erminae, Q i empy.
4 MST-Prim(G, w, r) Analyi of Prim. Q V[G]. for each verex u Q // iniializaion: O(V) ime. do key[u]. key[r] // ar a he roo. π[r] NIL // e paren of r o be NIL. while Q // unil all verice in MST. do u Exrac-Min(Q) // verex wih lighe edge. for each v adj[u]. do if v Q and w(u,v) < key[v]. hen π[v] u. key[v] w(u,v) // new ligher edge ou of v. decreae_key(q, v, key[v]) Exracing he verex from he queue: O(lg n) For each inciden edge, decreaing he key of he neighboring verex: O(lg n) where n = V The oher ep are conan ime. The overall running ime i, where e = E and n = V, T(n) = u V (lg n + deg(u)lgn) = u V (+ deg(u)) lg n = lg n (n + e) = O((n + e)lgn) Eenially ame a Krukal : O((n+e) lg n) ime Can be made o run faer in O(n lg n) ime How? Problem There ha been a lo of hype recenly abou The Marix Reloaded wih he releae of new hearical railer. For hi problem, uppoe you are managing he conrucion of billboard on he Neo Memorial Highway, a heavily-raveled rech of road ha run we-ea for M mile. The poible ie for billboard are given by number x x, x n, each in he inerval [.M] (pecified by heir poiion along he highway meaured in mile from i weern end). If you place a billboard a locaion x i, you receive a revenue of r i > You wan o place billboard a a ube of he ie in x x, x n o a o maximize your oal revenue, ubjec o he following rericion: DP Soluion OPT[i] = he maximum revenue one can receive given he conrain and elecing a ube of he ie beween x and x i Noice ha if we don build a x i, we imply wan he be hing ha happened o far, i.e. OPT[i ] If we do build a x i, we wan he be hing ha happened up o : x i, i.e. or OPT[j] + r i where x j < x i Recurrence: OPT[i] = max OPT[i ] OPT[j] + r i where </ j </ i x j < x i Running ime?. Environmenal Conrain. You canno build wo billboard wihin le han mile of one anoher on he highway. Definiion for Shore Pah Single-Source Shore Pah Think of verice a ciie and he edge weigh a he diance from one ciy o anoher. Define he lengh of a pah o be he um of edge weigh along he pah. Define he diance beween wo verice, u and v, δ(u,v) o be he lengh of he minimum lengh pah from u o v. Given a direced graph G = (V, E) wih edge weigh and a diinguihed ource verex, V, deermine he diance from he ource verex o every verex in he graph. BFS find hor-pah from a ingle ource verex o all oher verice in O(n+e) ime, auming he graph ha no edge weigh. Edge weigh can be negaive; bu in order for he problem o be well-defined here mu be no cycle whoe oal co i negaive. A hore pah from verex u o verex v i hen defined a any pah p wih weigh w(p) = δ(u,v).
5 Relaxaion Relax (u, v) Mainain an eimae of he hore pah for each verex v, call i d[v]. Iniially d[v] will be he lengh of he hore pah ha he algorihm of know from o v. Thi value will alway be greaer han or equal o he rue hore pah diance from o v. Iniially, we know of no pah, o all d[v]= & d[]=. A he algorihm goe on and ee more verice, i rie o updae d[v] for each verex in he graph, unil all d[v] value converge o rue hore diance.. if d[u] + w(u,v) < d[v] // i he pah hru u horer?. hen d[v] d[u] + w(u,v); // ye, hen ake i.. π[v] u; // he hore way back o he ource i hrough u by updaing he predeceor poiner NOTE: If we perform Relax (u, v) repeaedly over all edge of he graph, all he d[v] value will evenually converge o he rue final diance value from. How o do hi mo efficienly? Dijkra Algorihm Dijkra(G, w, ) Mainain a ube of verice, S V, for which we know heir rue diance d[u]=δ(,u). Iniially S = and we e d[]= and all oher o. One by one we elec verice from V - S o add o S. For each verex u V-S, we have compued a diance eimae d[u]. The greedy approach i o ake he verex for which d[u] i minimum, i.e. ake unproceed verex ha i cloe o. We ore he verice of V - S in a prioriy queue (heap), where he key value of each verex u i d[u]. All operaion can be done in O(lg n) ime.. Q V[G] and S. for each verex u Q // iniializaion: O(V) ime. do d[u] and π[u] NIL. d[] // ar a he ource. π[] NIL // e paren of o be NIL. while Q // ill all verice proceed. do u Exrac-Min(Q) // elec cloe o S S {u}. for each v adj[u]. do if v Q and (d[u] + w(u,v) < d[v]). hen π[v] u. d[v] d[u] + w(u,v) // Relax (u,v). decreae_key(q, v, d[v]) More on Shore Pah Problem Running ime of Dijkra Bellman Ford Deec negaive weigh cycle Floyd Warhall All pair Shore Pah Dynamic Programming Algorihm There are n ciie conneced by m bue. For each bu, we are given i aring ciy, erminu ciy, aring ime and ime a which i reache he erminu. The bu doe no op anywhere in he middle, o you may board i only from he aring erminu. You ar a ciy a AM and wan o find he earlie ime you can reach a ciy X uing any number of bu op. Decribe a polynomial ime algorihm o accomplih hi.
6 Soluion Max Flow Nework Conruc a graph G Verice repreen ciie Edge repreen bu roue Can we ue Bellman Ford o find he earlie ime o reach any ciy from ciy in polynomial ime? Need o modify he relaxaion procedure Max flow nework: G = (V, E,,, u). (V, E) = direced graph, no parallel arc. Two diinguihed node: = ource, = ink. u(e) = capaciy of arc e. RELAX(Ciy u, Ciy v){ if d[u] < arime(u,v) and d[v] > endime(u,v) hen d[v] := endime(u,v) } where, d[v] i he earlie ime o far o reach ciy u from ciy. Capaciy Flow Flow An - flow i a funcion f: E R ha aifie: For each e E: f(e) u(e) (capaciy) For each v V {, }: f ( e) (conervaion) e in o v e ou of v An - flow i a funcion f: E R ha aifie: For each e E: f(e) u(e) (capaciy) For each v V {, }: f ( e) (conervaion) e in o v ou of v e MAX FLOW: find - flow ha maximize ne flow ou of he ource. f e ou of Capaciy Flow Capaciy Flow Value = Flow Flow An - flow i a funcion f: E R ha aifie: For each e E: f(e) u(e) (capaciy) For each v V {, }: f ( e) (conervaion) e in o v e ou of v MAX FLOW: find - flow ha maximize ne flow ou of he ource. An - flow i a funcion f: E R ha aifie: For each e E: f(e) u(e) (capaciy) For each v V {, }: f ( e) (conervaion) e in o v e ou of v MAX FLOW: find - flow ha maximize ne flow ou of he ource. Capaciy Flow Value = Capaciy Flow Value =
7 Cu Cu An - cu i a node pariion (S, T) uch ha S, T. The capaciy of an - cu (S, T) i: u( e) : = u( v, w). e ou of S ( v, w) E v S, w T Min - cu: find an - cu of minimum capaciy. An - cu i a node pariion (S, T) uch ha S, T. The capaciy of an - cu (S, T) i: u( e) : = u( v, w ). e ou of S ( v, w ) v S E, w T Min - cu: find an - cu of minimum capaciy. Capaciy = Capaciy = Cu Max Flow and Min Cu An - cu i a node pariion (S, T) uch ha S, T. The capaciy of an - cu (S, T) i: u( e) : = u( v, w). e ou of S ( v, w ) E v S, w T Min - cu: find an - cu of minimum capaciy. Corollary. Le f be a flow, and le (S, T) be a cu. If f = cap(s, T), hen f i a max flow and (S, T) i a min cu. Capaciy = Cu capaciy = Flow value = Max-Flow Min-Cu Theorem Max-Flow Min-Cu Theorem MAX-FLOW MIN-CUT THEOREM (Ford-Fulkeron, ): In any nework, he value of he max flow i equal o he value of he min cu. Augmening pah heorem (Ford-Fulkeron, ): A flow f i a max flow if and only if here are no augmening pah. Cu capaciy = Flow value = MAX-FLOW MIN-CUT THEOREM (Ford-Fulkeron, ): he value of he max flow i equal o he value of he min cu. We prove boh imulaneouly by howing he TFAE: (i)f i a max flow. (ii)there i no augmening pah relaive o f. (iii)there exi a cu (S, T) uch ha f = cap(s, T).
8 Chooing Good Augmening Pah Shore Augmening Pah Ue care when elecing augmening pah. Some choice lead o exponenial algorihm. Clever choice lead o polynomial algorihm. Goal: chooe augmening pah o ha: Can find augmening pah efficienly. Few ieraion. Edmond-Karp (): chooe augmening pah wih Max boleneck capaciy. (fa pah) Sufficienly large capaciy. (capaciy-caling) Fewe number of arc. (hore pah) Inuiion: chooing pah via breadh fir earch. Eay o implemen. may implemen by coincidence! Find augmening pah wih fewe number of arc. ShoreAugmeningPah(V, E,, ) FOREACH e E f(e) G f reidual graph WHILE (here exi augmening pah) find uch a pah P by BFS f augmen(f, P) updae G f RETURN f Hiory Year... Dicoverer Danzig Mehod Simplex Big-Oh mn U Ford, Fulkeron Augmening pah mnu Edmond-Karp Shore pah m n Diniz Shore pah mn Edmond-Karp, Diniz Capaciy caling m log U Diniz-Gabow Capaciy caling mn log U Karzanov Preflow-puh n Sleaor-Tarjan Dynamic ree mn log n Goldberg-Tarjan FIFO preflow-puh mn log (n / m) Goldberg-Rao Lengh funcion m / log (n / m) log U mn / log (n / m) log U
Max Flow, Min Cut COS 521. Kevin Wayne Fall Soviet Rail Network, Cuts. Minimum Cut Problem. Flow network.
 Sovie Rail Nework, Max Flow, Min u OS Kevin Wayne Fall Reference: On he hiory of he ranporaion and maximum flow problem. lexander Schrijver in Mah Programming, :,. Minimum u Problem u Flow nework.! Digraph
Sovie Rail Nework, Max Flow, Min u OS Kevin Wayne Fall Reference: On he hiory of he ranporaion and maximum flow problem. lexander Schrijver in Mah Programming, :,. Minimum u Problem u Flow nework.! Digraph
Soviet Rail Network, 1955
 Sovie Rail Nework, 1 Reference: On he hiory of he ranporaion and maximum flow problem. Alexander Schrijver in Mah Programming, 1: 3,. Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic
Sovie Rail Nework, 1 Reference: On he hiory of he ranporaion and maximum flow problem. Alexander Schrijver in Mah Programming, 1: 3,. Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic
The Residual Graph. 12 Augmenting Path Algorithms. Augmenting Path Algorithm. Augmenting Path Algorithm
 Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
The Residual Graph. 11 Augmenting Path Algorithms. Augmenting Path Algorithm. Augmenting Path Algorithm
 Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Problem Set If all directed edges in a network have distinct capacities, then there is a unique maximum flow.
 CSE 202: Deign and Analyi of Algorihm Winer 2013 Problem Se 3 Inrucor: Kamalika Chaudhuri Due on: Tue. Feb 26, 2013 Inrucion For your proof, you may ue any lower bound, algorihm or daa rucure from he ex
CSE 202: Deign and Analyi of Algorihm Winer 2013 Problem Se 3 Inrucor: Kamalika Chaudhuri Due on: Tue. Feb 26, 2013 Inrucion For your proof, you may ue any lower bound, algorihm or daa rucure from he ex
Flow networks. Flow Networks. A flow on a network. Flow networks. The maximum-flow problem. Introduction to Algorithms, Lecture 22 December 5, 2001
 CS 545 Flow Nework lon Efra Slide courey of Charle Leieron wih mall change by Carola Wenk Flow nework Definiion. flow nework i a direced graph G = (V, E) wih wo diinguihed verice: a ource and a ink. Each
CS 545 Flow Nework lon Efra Slide courey of Charle Leieron wih mall change by Carola Wenk Flow nework Definiion. flow nework i a direced graph G = (V, E) wih wo diinguihed verice: a ource and a ink. Each
Graphs III - Network Flow
 Graph III - Nework Flow Flow nework eup graph G=(V,E) edge capaciy w(u,v) 0 - if edge doe no exi, hen w(u,v)=0 pecial verice: ource verex ; ink verex - no edge ino and no edge ou of Aume every verex v
Graph III - Nework Flow Flow nework eup graph G=(V,E) edge capaciy w(u,v) 0 - if edge doe no exi, hen w(u,v)=0 pecial verice: ource verex ; ink verex - no edge ino and no edge ou of Aume every verex v
! Abstraction for material flowing through the edges. ! G = (V, E) = directed graph, no parallel edges.
 Sovie Rail Nework, haper Nework Flow Slide by Kevin Wayne. opyrigh Pearon-ddion Weley. ll righ reerved. Reference: On he hiory of he ranporaion and maximum flow problem. lexander Schrijver in Mah Programming,
Sovie Rail Nework, haper Nework Flow Slide by Kevin Wayne. opyrigh Pearon-ddion Weley. ll righ reerved. Reference: On he hiory of he ranporaion and maximum flow problem. lexander Schrijver in Mah Programming,
1 Motivation and Basic Definitions
 CSCE : Deign and Analyi of Algorihm Noe on Max Flow Fall 20 (Baed on he preenaion in Chaper 26 of Inroducion o Algorihm, 3rd Ed. by Cormen, Leieron, Rive and Sein.) Moivaion and Baic Definiion Conider
CSCE : Deign and Analyi of Algorihm Noe on Max Flow Fall 20 (Baed on he preenaion in Chaper 26 of Inroducion o Algorihm, 3rd Ed. by Cormen, Leieron, Rive and Sein.) Moivaion and Baic Definiion Conider
Today: Max Flow Proofs
 Today: Max Flow Proof COSC 58, Algorihm March 4, 04 Many of hee lide are adaped from everal online ource Reading Aignmen Today cla: Chaper 6 Reading aignmen for nex cla: Chaper 7 (Amorized analyi) In-Cla
Today: Max Flow Proof COSC 58, Algorihm March 4, 04 Many of hee lide are adaped from everal online ource Reading Aignmen Today cla: Chaper 6 Reading aignmen for nex cla: Chaper 7 (Amorized analyi) In-Cla
CSE 521: Design & Analysis of Algorithms I
 CSE 52: Deign & Analyi of Algorihm I Nework Flow Paul Beame Biparie Maching Given: A biparie graph G=(V,E) M E i a maching in G iff no wo edge in M hare a verex Goal: Find a maching M in G of maximum poible
CSE 52: Deign & Analyi of Algorihm I Nework Flow Paul Beame Biparie Maching Given: A biparie graph G=(V,E) M E i a maching in G iff no wo edge in M hare a verex Goal: Find a maching M in G of maximum poible
Algorithmic Discrete Mathematics 6. Exercise Sheet
 Algorihmic Dicree Mahemaic. Exercie Shee Deparmen of Mahemaic SS 0 PD Dr. Ulf Lorenz 7. and 8. Juni 0 Dipl.-Mah. David Meffer Verion of June, 0 Groupwork Exercie G (Heap-Sor) Ue Heap-Sor wih a min-heap
Algorihmic Dicree Mahemaic. Exercie Shee Deparmen of Mahemaic SS 0 PD Dr. Ulf Lorenz 7. and 8. Juni 0 Dipl.-Mah. David Meffer Verion of June, 0 Groupwork Exercie G (Heap-Sor) Ue Heap-Sor wih a min-heap
Maximum Flow. Contents. Max Flow Network. Maximum Flow and Minimum Cut
 Conen Maximum Flow Conen. Maximum low problem. Minimum cu problem. Max-low min-cu heorem. Augmening pah algorihm. Capaciy-caling. Shore augmening pah. Princeon Univeriy COS Theory o Algorihm Spring Kevin
Conen Maximum Flow Conen. Maximum low problem. Minimum cu problem. Max-low min-cu heorem. Augmening pah algorihm. Capaciy-caling. Shore augmening pah. Princeon Univeriy COS Theory o Algorihm Spring Kevin
Algorithm Design and Analysis
 Algorihm Deign and Analyi LECTURES 17 Nework Flow Dualiy of Max Flow and Min Cu Algorihm: Ford-Fulkeron Capaciy Scaling Sofya Rakhodnikova S. Rakhodnikova; baed on lide by E. Demaine, C. Leieron, A. Smih,
Algorihm Deign and Analyi LECTURES 17 Nework Flow Dualiy of Max Flow and Min Cu Algorihm: Ford-Fulkeron Capaciy Scaling Sofya Rakhodnikova S. Rakhodnikova; baed on lide by E. Demaine, C. Leieron, A. Smih,
Network Flow. Data Structures and Algorithms Andrei Bulatov
 Nework Flow Daa Srucure and Algorihm Andrei Bulao Algorihm Nework Flow 24-2 Flow Nework Think of a graph a yem of pipe We ue hi yem o pump waer from he ource o ink Eery pipe/edge ha limied capaciy Flow
Nework Flow Daa Srucure and Algorihm Andrei Bulao Algorihm Nework Flow 24-2 Flow Nework Think of a graph a yem of pipe We ue hi yem o pump waer from he ource o ink Eery pipe/edge ha limied capaciy Flow
Soviet Rail Network, 1955
 7.1 Nework Flow Sovie Rail Nework, 19 Reerence: On he hiory o he ranporaion and maximum low problem. lexander Schrijver in Mah Programming, 91: 3, 00. (See Exernal Link ) Maximum Flow and Minimum Cu Max
7.1 Nework Flow Sovie Rail Nework, 19 Reerence: On he hiory o he ranporaion and maximum low problem. lexander Schrijver in Mah Programming, 91: 3, 00. (See Exernal Link ) Maximum Flow and Minimum Cu Max
Main Reference: Sections in CLRS.
 Maximum Flow Reied 09/09/200 Main Reference: Secion 26.-26. in CLRS. Inroducion Definiion Muli-Source Muli-Sink The Ford-Fulkeron Mehod Reidual Nework Augmening Pah The Max-Flow Min-Cu Theorem The Edmond-Karp
Maximum Flow Reied 09/09/200 Main Reference: Secion 26.-26. in CLRS. Inroducion Definiion Muli-Source Muli-Sink The Ford-Fulkeron Mehod Reidual Nework Augmening Pah The Max-Flow Min-Cu Theorem The Edmond-Karp
Algorithms and Data Structures 2011/12 Week 9 Solutions (Tues 15th - Fri 18th Nov)
 Algorihm and Daa Srucure 2011/ Week Soluion (Tue 15h - Fri 18h No) 1. Queion: e are gien 11/16 / 15/20 8/13 0/ 1/ / 11/1 / / To queion: (a) Find a pair of ube X, Y V uch ha f(x, Y) = f(v X, Y). (b) Find
Algorihm and Daa Srucure 2011/ Week Soluion (Tue 15h - Fri 18h No) 1. Queion: e are gien 11/16 / 15/20 8/13 0/ 1/ / 11/1 / / To queion: (a) Find a pair of ube X, Y V uch ha f(x, Y) = f(v X, Y). (b) Find
Maximum Flow and Minimum Cut
 // Sovie Rail Nework, Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy. Nework Flow Flow nework.
// Sovie Rail Nework, Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy. Nework Flow Flow nework.
CS 473G Lecture 15: Max-Flow Algorithms and Applications Fall 2005
 CS 473G Lecure 1: Max-Flow Algorihm and Applicaion Fall 200 1 Max-Flow Algorihm and Applicaion (November 1) 1.1 Recap Fix a direced graph G = (V, E) ha doe no conain boh an edge u v and i reveral v u,
CS 473G Lecure 1: Max-Flow Algorihm and Applicaion Fall 200 1 Max-Flow Algorihm and Applicaion (November 1) 1.1 Recap Fix a direced graph G = (V, E) ha doe no conain boh an edge u v and i reveral v u,
Network Flows: Introduction & Maximum Flow
 CSC 373 - lgorihm Deign, nalyi, and Complexiy Summer 2016 Lalla Mouaadid Nework Flow: Inroducion & Maximum Flow We now urn our aenion o anoher powerful algorihmic echnique: Local Search. In a local earch
CSC 373 - lgorihm Deign, nalyi, and Complexiy Summer 2016 Lalla Mouaadid Nework Flow: Inroducion & Maximum Flow We now urn our aenion o anoher powerful algorihmic echnique: Local Search. In a local earch
Maximum Flow. How do we transport the maximum amount data from source to sink? Some of these slides are adapted from Lecture Notes of Kevin Wayne.
 Conen Conen. Maximum flow problem. Minimum cu problem. Max-flow min-cu heorem. Augmening pah algorihm. Capaciy-caling. Shore augmening pah. Chaper Maximum How do we ranpor he maximum amoun daa from ource
Conen Conen. Maximum flow problem. Minimum cu problem. Max-flow min-cu heorem. Augmening pah algorihm. Capaciy-caling. Shore augmening pah. Chaper Maximum How do we ranpor he maximum amoun daa from ource
MAXIMUM FLOW. introduction Ford-Fulkerson algorithm maxflow-mincut theorem
 MAXIMUM FLOW inroducion Ford-Fulkeron algorihm maxflow-mincu heorem Mincu problem Inpu. An edge-weighed digraph, ource verex, and arge verex. each edge ha a poiive capaciy capaciy 9 10 4 15 15 10 5 8 10
MAXIMUM FLOW inroducion Ford-Fulkeron algorihm maxflow-mincu heorem Mincu problem Inpu. An edge-weighed digraph, ource verex, and arge verex. each edge ha a poiive capaciy capaciy 9 10 4 15 15 10 5 8 10
CS4445/9544 Analysis of Algorithms II Solution for Assignment 1
 Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Randomized Perfect Bipartite Matching
 Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Greedy. I Divide and Conquer. I Dynamic Programming. I Network Flows. Network Flow. I Previous topics: design techniques
 Algorihm Deign Technique CS : Nework Flow Dan Sheldon April, reedy Divide and Conquer Dynamic Programming Nework Flow Comparion Nework Flow Previou opic: deign echnique reedy Divide and Conquer Dynamic
Algorihm Deign Technique CS : Nework Flow Dan Sheldon April, reedy Divide and Conquer Dynamic Programming Nework Flow Comparion Nework Flow Previou opic: deign echnique reedy Divide and Conquer Dynamic
16 Max-Flow Algorithms and Applications
 Algorihm A proce canno be underood by opping i. Underanding mu move wih he flow of he proce, mu join i and flow wih i. The Fir Law of Mena, in Frank Herber Dune (196) There a difference beween knowing
Algorihm A proce canno be underood by opping i. Underanding mu move wih he flow of he proce, mu join i and flow wih i. The Fir Law of Mena, in Frank Herber Dune (196) There a difference beween knowing
Admin MAX FLOW APPLICATIONS. Flow graph/networks. Flow constraints 4/30/13. CS lunch today Grading. in-flow = out-flow for every vertex (except s, t)
 /0/ dmin lunch oday rading MX LOW PPLIION 0, pring avid Kauchak low graph/nework low nework direced, weighed graph (V, ) poiive edge weigh indicaing he capaciy (generally, aume ineger) conain a ingle ource
/0/ dmin lunch oday rading MX LOW PPLIION 0, pring avid Kauchak low graph/nework low nework direced, weighed graph (V, ) poiive edge weigh indicaing he capaciy (generally, aume ineger) conain a ingle ource
CSC 364S Notes University of Toronto, Spring, The networks we will consider are directed graphs, where each edge has associated with it
 CSC 36S Noe Univeriy of Torono, Spring, 2003 Flow Algorihm The nework we will conider are direced graph, where each edge ha aociaed wih i a nonnegaive capaciy. The inuiion i ha if edge (u; v) ha capaciy
CSC 36S Noe Univeriy of Torono, Spring, 2003 Flow Algorihm The nework we will conider are direced graph, where each edge ha aociaed wih i a nonnegaive capaciy. The inuiion i ha if edge (u; v) ha capaciy
Wrap up: Weighted, directed graph shortest path Minimum Spanning Tree. Feb 25, 2019 CSCI211 - Sprenkle
 Objecive Wrap up: Weighed, direced graph hore pah Minimum Spanning Tree eb, 1 SI - Sprenkle 1 Review Wha are greedy algorihm? Wha i our emplae for olving hem? Review he la problem we were working on: Single-ource,
Objecive Wrap up: Weighed, direced graph hore pah Minimum Spanning Tree eb, 1 SI - Sprenkle 1 Review Wha are greedy algorihm? Wha i our emplae for olving hem? Review he la problem we were working on: Single-ource,
6/3/2009. CS 244 Algorithm Design Instructor: t Artur Czumaj. Lecture 8 Network flows. Maximum Flow and Minimum Cut. Minimum Cut Problem.
 Maximum Flow and Minimum Cu CS lgorihm Deign Inrucor: rur Czumaj Lecure Nework Max and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy.
Maximum Flow and Minimum Cu CS lgorihm Deign Inrucor: rur Czumaj Lecure Nework Max and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy.
CSE 421 Introduction to Algorithms Winter The Network Flow Problem
 CSE 42 Inroducion o Algorihm Winer 202 The Nework Flow Problem 2 The Nework Flow Problem 5 a 4 3 x 3 7 6 b 4 y 4 7 6 c 5 z How much uff can flow from o? 3 Sovie Rail Nework, 955 Reference: On he hiory
CSE 42 Inroducion o Algorihm Winer 202 The Nework Flow Problem 2 The Nework Flow Problem 5 a 4 3 x 3 7 6 b 4 y 4 7 6 c 5 z How much uff can flow from o? 3 Sovie Rail Nework, 955 Reference: On he hiory
18 Extensions of Maximum Flow
 Who are you?" aid Lunkwill, riing angrily from hi ea. Wha do you wan?" I am Majikhie!" announced he older one. And I demand ha I am Vroomfondel!" houed he younger one. Majikhie urned on Vroomfondel. I
Who are you?" aid Lunkwill, riing angrily from hi ea. Wha do you wan?" I am Majikhie!" announced he older one. And I demand ha I am Vroomfondel!" houed he younger one. Majikhie urned on Vroomfondel. I
Algorithm Design and Analysis
 Algorihm Deign and Analyi LECTURE 0 Nework Flow Applicaion Biparie maching Edge-dijoin pah Adam Smih 0//0 A. Smih; baed on lide by E. Demaine, C. Leieron, S. Rakhodnikova, K. Wayne La ime: Ford-Fulkeron
Algorihm Deign and Analyi LECTURE 0 Nework Flow Applicaion Biparie maching Edge-dijoin pah Adam Smih 0//0 A. Smih; baed on lide by E. Demaine, C. Leieron, S. Rakhodnikova, K. Wayne La ime: Ford-Fulkeron
Maximum Flow in Planar Graphs
 Maximum Flow in Planar Graph Planar Graph and i Dual Dualiy i defined for direced planar graph a well Minimum - cu in undireced planar graph An - cu (undireced graph) An - cu The dual o he cu Cu/Cycle
Maximum Flow in Planar Graph Planar Graph and i Dual Dualiy i defined for direced planar graph a well Minimum - cu in undireced planar graph An - cu (undireced graph) An - cu The dual o he cu Cu/Cycle
Please Complete Course Survey. CMPSCI 311: Introduction to Algorithms. Approximation Algorithms. Coping With NP-Completeness. Greedy Vertex Cover
 Pleae Complee Coure Survey CMPSCI : Inroducion o Algorihm Dealing wih NP-Compleene Dan Sheldon hp: //owl.oi.uma.edu/parner/coureevalsurvey/uma/ Univeriy of Maachue Slide Adaped from Kevin Wayne La Compiled:
Pleae Complee Coure Survey CMPSCI : Inroducion o Algorihm Dealing wih NP-Compleene Dan Sheldon hp: //owl.oi.uma.edu/parner/coureevalsurvey/uma/ Univeriy of Maachue Slide Adaped from Kevin Wayne La Compiled:
Matching. Slides designed by Kevin Wayne.
 Maching Maching. Inpu: undireced graph G = (V, E). M E i a maching if each node appear in a mo edge in M. Max maching: find a max cardinaliy maching. Slide deigned by Kevin Wayne. Biparie Maching Biparie
Maching Maching. Inpu: undireced graph G = (V, E). M E i a maching if each node appear in a mo edge in M. Max maching: find a max cardinaliy maching. Slide deigned by Kevin Wayne. Biparie Maching Biparie
Flow networks, flow, maximum flow. Some definitions. Edmonton. Saskatoon Winnipeg. Vancouver Regina. Calgary. 12/12 a.
 Flow nework, flow, maximum flow Can inerpre direced graph a flow nework. Maerial coure hrough ome yem from ome ource o ome ink. Source produce maerial a ome eady rae, ink conume a ame rae. Example: waer
Flow nework, flow, maximum flow Can inerpre direced graph a flow nework. Maerial coure hrough ome yem from ome ource o ome ink. Source produce maerial a ome eady rae, ink conume a ame rae. Example: waer
Flow Networks. Ma/CS 6a. Class 14: Flow Exercises
 0/0/206 Ma/CS 6a Cla 4: Flow Exercie Flow Nework A flow nework i a digraph G = V, E, ogeher wih a ource verex V, a ink verex V, and a capaciy funcion c: E N. Capaciy Source 7 a b c d e Sink 0/0/206 Flow
0/0/206 Ma/CS 6a Cla 4: Flow Exercie Flow Nework A flow nework i a digraph G = V, E, ogeher wih a ource verex V, a ink verex V, and a capaciy funcion c: E N. Capaciy Source 7 a b c d e Sink 0/0/206 Flow
Reminder: Flow Networks
 0/0/204 Ma/CS 6a Cla 4: Variou (Flow) Execie Reminder: Flow Nework A flow nework i a digraph G = V, E, ogeher wih a ource verex V, a ink verex V, and a capaciy funcion c: E N. Capaciy Source 7 a b c d
0/0/204 Ma/CS 6a Cla 4: Variou (Flow) Execie Reminder: Flow Nework A flow nework i a digraph G = V, E, ogeher wih a ource verex V, a ink verex V, and a capaciy funcion c: E N. Capaciy Source 7 a b c d
4/12/12. Applications of the Maxflow Problem 7.5 Bipartite Matching. Bipartite Matching. Bipartite Matching. Bipartite matching: the flow network
 // Applicaion of he Maxflow Problem. Biparie Maching Biparie Maching Biparie maching. Inpu: undireced, biparie graph = (, E). M E i a maching if each node appear in a mo one edge in M. Max maching: find
// Applicaion of he Maxflow Problem. Biparie Maching Biparie Maching Biparie maching. Inpu: undireced, biparie graph = (, E). M E i a maching if each node appear in a mo one edge in M. Max maching: find
Network Flows UPCOPENCOURSEWARE number 34414
 Nework Flow UPCOPENCOURSEWARE number Topic : F.-Javier Heredia Thi work i licened under he Creaive Common Aribuion- NonCommercial-NoDeriv. Unpored Licene. To view a copy of hi licene, vii hp://creaivecommon.org/licene/by-nc-nd/./
Nework Flow UPCOPENCOURSEWARE number Topic : F.-Javier Heredia Thi work i licened under he Creaive Common Aribuion- NonCommercial-NoDeriv. Unpored Licene. To view a copy of hi licene, vii hp://creaivecommon.org/licene/by-nc-nd/./
Algorithms. Algorithms 6.4 MAXIMUM FLOW
 Algorihm ROBERT SEDGEWICK KEVIN WAYNE 6.4 MAXIMUM FLOW Algorihm F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE hp://alg4.c.princeon.edu inroducion Ford Fulkeron algorihm maxflow mincu heorem analyi
Algorihm ROBERT SEDGEWICK KEVIN WAYNE 6.4 MAXIMUM FLOW Algorihm F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE hp://alg4.c.princeon.edu inroducion Ford Fulkeron algorihm maxflow mincu heorem analyi
Introduction to Congestion Games
 Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
23 Maximum Flows and Minimum Cuts
 A proce canno be underood by opping i. Underanding mu move wih he flow of he proce, mu join i and flow wih i. The Fir Law of Mena, in Frank Herber Dune (196) Conrary o expecaion, flow uually happen no
A proce canno be underood by opping i. Underanding mu move wih he flow of he proce, mu join i and flow wih i. The Fir Law of Mena, in Frank Herber Dune (196) Conrary o expecaion, flow uually happen no
CMPS 6610/4610 Fall Flow Networks. Carola Wenk Slides adapted from slides by Charles Leiserson
 CMP 6610/4610 Fall 2016 Flow Nework Carola Wenk lide adaped rom lide by Charle Leieron Max low and min c Fndamenal problem in combinaorial opimizaion Daliy beween max low and min c Many applicaion: Biparie
CMP 6610/4610 Fall 2016 Flow Nework Carola Wenk lide adaped rom lide by Charle Leieron Max low and min c Fndamenal problem in combinaorial opimizaion Daliy beween max low and min c Many applicaion: Biparie
Average Case Lower Bounds for Monotone Switching Networks
 Average Cae Lower Bound for Monoone Swiching Nework Yuval Filmu, Toniann Piai, Rober Robere, Sephen Cook Deparmen of Compuer Science Univeriy of Torono Monoone Compuaion (Refreher) Monoone circui were
Average Cae Lower Bound for Monoone Swiching Nework Yuval Filmu, Toniann Piai, Rober Robere, Sephen Cook Deparmen of Compuer Science Univeriy of Torono Monoone Compuaion (Refreher) Monoone circui were
Dynamic Programming 11/8/2009. Weighted Interval Scheduling. Weighted Interval Scheduling. Unweighted Interval Scheduling: Review
 //9 Algorihms Dynamic Programming - Weighed Ineral Scheduling Dynamic Programming Weighed ineral scheduling problem. Insance A se of n jobs. Job j sars a s j, finishes a f j, and has weigh or alue j. Two
//9 Algorihms Dynamic Programming - Weighed Ineral Scheduling Dynamic Programming Weighed ineral scheduling problem. Insance A se of n jobs. Job j sars a s j, finishes a f j, and has weigh or alue j. Two
They were originally developed for network problem [Dantzig, Ford, Fulkerson 1956]
![They were originally developed for network problem [Dantzig, Ford, Fulkerson 1956] They were originally developed for network problem [Dantzig, Ford, Fulkerson 1956]](/thumbs/89/98635862.jpg) 6. Inroducion... 6. The primal-dual algorihmn... 6 6. Remark on he primal-dual algorihmn... 7 6. A primal-dual algorihmn for he hore pah problem... 8... 9 6.6 A primal-dual algorihmn for he weighed maching
6. Inroducion... 6. The primal-dual algorihmn... 6 6. Remark on he primal-dual algorihmn... 7 6. A primal-dual algorihmn for he hore pah problem... 8... 9 6.6 A primal-dual algorihmn for he weighed maching
7. NETWORK FLOW I. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley. Last updated on 11/22/17 6:11 AM
 7. NETWORK FLOW I max-flow and min-cu problem Ford Fulkeron algorihm max-flow min-cu heorem capaciy-caling algorihm hore augmening pah blocking-flow algorihm imple uni-capaciy nework Lecure lide by Kevin
7. NETWORK FLOW I max-flow and min-cu problem Ford Fulkeron algorihm max-flow min-cu heorem capaciy-caling algorihm hore augmening pah blocking-flow algorihm imple uni-capaciy nework Lecure lide by Kevin
26.1 Flow networks. f (u,v) = 0.
 26 Maimum Flow Ju a we can model a road map a a direced graph in order o find he hore pah from one poin o anoher, we can alo inerpre a direced graph a a flow nework and ue i o anwer queion abou maerial
26 Maimum Flow Ju a we can model a road map a a direced graph in order o find he hore pah from one poin o anoher, we can alo inerpre a direced graph a a flow nework and ue i o anwer queion abou maerial
16 Max-Flow Algorithms
 A process canno be undersood by sopping i. Undersanding mus move wih he flow of he process, mus join i and flow wih i. The Firs Law of Mena, in Frank Herber s Dune (196) There s a difference beween knowing
A process canno be undersood by sopping i. Undersanding mus move wih he flow of he process, mus join i and flow wih i. The Firs Law of Mena, in Frank Herber s Dune (196) There s a difference beween knowing
7. NETWORK FLOW I. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley. Last updated on 11/22/17 6:11 AM
 7. NETWORK FLOW I max-flow and min-cu problem Ford Fulkeron algorihm max-flow min-cu heorem capaciy-caling algorihm hore augmening pah blocking-flow algorihm imple uni-capaciy nework Lecure lide by Kevin
7. NETWORK FLOW I max-flow and min-cu problem Ford Fulkeron algorihm max-flow min-cu heorem capaciy-caling algorihm hore augmening pah blocking-flow algorihm imple uni-capaciy nework Lecure lide by Kevin
Geometric Path Problems with Violations
 Click here o view linked Reference 1 1 1 0 1 0 1 0 1 0 1 Geomeric Pah Problem wih Violaion Anil Mahehwari 1, Subha C. Nandy, Drimi Paanayak, Saanka Roy and Michiel Smid 1 1 School of Compuer Science, Carleon
Click here o view linked Reference 1 1 1 0 1 0 1 0 1 0 1 Geomeric Pah Problem wih Violaion Anil Mahehwari 1, Subha C. Nandy, Drimi Paanayak, Saanka Roy and Michiel Smid 1 1 School of Compuer Science, Carleon
Today s topics. CSE 421 Algorithms. Problem Reduction Examples. Problem Reduction. Undirected Network Flow. Bipartite Matching. Problem Reductions
 Today opic CSE Algorihm Richard Anderon Lecure Nework Flow Applicaion Prolem Reducion Undireced Flow o Flow Biparie Maching Dijoin Pah Prolem Circulaion Loweround conrain on flow Survey deign Prolem Reducion
Today opic CSE Algorihm Richard Anderon Lecure Nework Flow Applicaion Prolem Reducion Undireced Flow o Flow Biparie Maching Dijoin Pah Prolem Circulaion Loweround conrain on flow Survey deign Prolem Reducion
3/3/2015. Chapter 7. Network Flow. Maximum Flow and Minimum Cut. Minimum Cut Problem
 // Chaper Nework Flow Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy. Nonrivial applicaion /
// Chaper Nework Flow Maximum Flow and Minimum Cu Max flow and min cu. Two very rich algorihmic problem. Cornerone problem in combinaorial opimizaion. Beauiful mahemaical dualiy. Nonrivial applicaion /
Discussion Session 2 Constant Acceleration/Relative Motion Week 03
 PHYS 100 Dicuion Seion Conan Acceleraion/Relaive Moion Week 03 The Plan Today you will work wih your group explore he idea of reference frame (i.e. relaive moion) and moion wih conan acceleraion. You ll
PHYS 100 Dicuion Seion Conan Acceleraion/Relaive Moion Week 03 The Plan Today you will work wih your group explore he idea of reference frame (i.e. relaive moion) and moion wih conan acceleraion. You ll
Introduction to SLE Lecture Notes
 Inroducion o SLE Lecure Noe May 13, 16 - The goal of hi ecion i o find a ufficien condiion of λ for he hull K o be generaed by a imple cure. I urn ou if λ 1 < 4 hen K i generaed by a imple curve. We will
Inroducion o SLE Lecure Noe May 13, 16 - The goal of hi ecion i o find a ufficien condiion of λ for he hull K o be generaed by a imple cure. I urn ou if λ 1 < 4 hen K i generaed by a imple curve. We will
Graph Theory: Network Flow
 Univeriy of Wahingon Mah 336 Term Paper Graph Theory: Nework Flow Auhor: Ellio Broard Advier: Dr. Jame Morrow 3 June 200 Conen Inroducion...................................... 2 2 Terminology......................................
Univeriy of Wahingon Mah 336 Term Paper Graph Theory: Nework Flow Auhor: Ellio Broard Advier: Dr. Jame Morrow 3 June 200 Conen Inroducion...................................... 2 2 Terminology......................................
Ford Fulkerson algorithm max-flow min-cut theorem. max-flow min-cut theorem capacity-scaling algorithm
 7. NETWORK FLOW I 7. NETWORK FLOW I max-flow and min-cu problem max-flow and min-cu problem Ford Fulkeron algorihm Ford Fulkeron algorihm max-flow min-cu heorem max-flow min-cu heorem capaciy-caling algorihm
7. NETWORK FLOW I 7. NETWORK FLOW I max-flow and min-cu problem max-flow and min-cu problem Ford Fulkeron algorihm Ford Fulkeron algorihm max-flow min-cu heorem max-flow min-cu heorem capaciy-caling algorihm
arxiv: v1 [cs.cg] 21 Mar 2013
![arxiv: v1 [cs.cg] 21 Mar 2013 arxiv: v1 [cs.cg] 21 Mar 2013](/thumbs/87/97053008.jpg) On he rech facor of he Thea-4 graph Lui Barba Proenji Boe Jean-Lou De Carufel André van Renen Sander Verdoncho arxiv:1303.5473v1 [c.cg] 21 Mar 2013 Abrac In hi paper we how ha he θ-graph wih 4 cone ha
On he rech facor of he Thea-4 graph Lui Barba Proenji Boe Jean-Lou De Carufel André van Renen Sander Verdoncho arxiv:1303.5473v1 [c.cg] 21 Mar 2013 Abrac In hi paper we how ha he θ-graph wih 4 cone ha
Physics 240: Worksheet 16 Name
 Phyic 4: Workhee 16 Nae Non-unifor circular oion Each of hee proble involve non-unifor circular oion wih a conan α. (1) Obain each of he equaion of oion for non-unifor circular oion under a conan acceleraion,
Phyic 4: Workhee 16 Nae Non-unifor circular oion Each of hee proble involve non-unifor circular oion wih a conan α. (1) Obain each of he equaion of oion for non-unifor circular oion under a conan acceleraion,
Selfish Routing. Tim Roughgarden Cornell University. Includes joint work with Éva Tardos
 Selfih Rouing Tim Roughgarden Cornell Univeriy Include join work wih Éva Tardo 1 Which roue would you chooe? Example: one uni of raffic (e.g., car) wan o go from o delay = 1 hour (no congeion effec) long
Selfih Rouing Tim Roughgarden Cornell Univeriy Include join work wih Éva Tardo 1 Which roue would you chooe? Example: one uni of raffic (e.g., car) wan o go from o delay = 1 hour (no congeion effec) long
I. Introduction to place/transition nets. Place/Transition Nets I. Example: a vending machine. Example: a vending machine
 Inroducory Tuorial I. Inroducion o place/ransiion nes Place/Transiion Nes I Prepared by: Jörg Desel, Caholic Universiy in Eichsä and Karsen Schmid, Humbold-Universiä zu Berlin Speaker: Wolfgang Reisig,
Inroducory Tuorial I. Inroducion o place/ransiion nes Place/Transiion Nes I Prepared by: Jörg Desel, Caholic Universiy in Eichsä and Karsen Schmid, Humbold-Universiä zu Berlin Speaker: Wolfgang Reisig,
April 3, The maximum flow problem. See class notes on website.
 5.05 April, 007 The maximum flow problem See cla noe on webie. Quoe of he day You ge he maxx for he minimum a TJ Maxx. -- ad for a clohing ore Thi wa he mo unkinde cu of all -- Shakepeare in Juliu Caear
5.05 April, 007 The maximum flow problem See cla noe on webie. Quoe of he day You ge he maxx for he minimum a TJ Maxx. -- ad for a clohing ore Thi wa he mo unkinde cu of all -- Shakepeare in Juliu Caear
, the. L and the L. x x. max. i n. It is easy to show that these two norms satisfy the following relation: x x n x = (17.3) max
 ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
CHAPTER 7: SECOND-ORDER CIRCUITS
 EEE5: CI RCUI T THEORY CHAPTER 7: SECOND-ORDER CIRCUITS 7. Inroducion Thi chaper conider circui wih wo orage elemen. Known a econd-order circui becaue heir repone are decribed by differenial equaion ha
EEE5: CI RCUI T THEORY CHAPTER 7: SECOND-ORDER CIRCUITS 7. Inroducion Thi chaper conider circui wih wo orage elemen. Known a econd-order circui becaue heir repone are decribed by differenial equaion ha
introduction Ford-Fulkerson algorithm
 Algorihm ROBERT SEDGEWICK KEVIN WAYNE. MAXIMUM FLOW. MAXIMUM FLOW inroducion inroducion Ford-Fulkeron algorihm Ford-Fulkeron algorihm Algorihm F O U R T H E D I T I O N maxflow-mincu heorem analyi of running
Algorihm ROBERT SEDGEWICK KEVIN WAYNE. MAXIMUM FLOW. MAXIMUM FLOW inroducion inroducion Ford-Fulkeron algorihm Ford-Fulkeron algorihm Algorihm F O U R T H E D I T I O N maxflow-mincu heorem analyi of running
Longest Common Prefixes
 Longes Common Prefixes The sandard ordering for srings is he lexicographical order. I is induced by an order over he alphabe. We will use he same symbols (,
Longes Common Prefixes The sandard ordering for srings is he lexicographical order. I is induced by an order over he alphabe. We will use he same symbols (,
introduction Ford-Fulkerson algorithm
 Algorihm ROBERT SEDGEWICK KEVIN WAYNE. MAXIMUM FLOW. MAXIMUM FLOW inroducion inroducion Ford-Fulkeron algorihm Ford-Fulkeron algorihm Algorihm F O U R T H E D I T I O N maxflow-mincu heorem analyi of running
Algorihm ROBERT SEDGEWICK KEVIN WAYNE. MAXIMUM FLOW. MAXIMUM FLOW inroducion inroducion Ford-Fulkeron algorihm Ford-Fulkeron algorihm Algorihm F O U R T H E D I T I O N maxflow-mincu heorem analyi of running
u(t) Figure 1. Open loop control system
 Open loop conrol v cloed loop feedbac conrol The nex wo figure preen he rucure of open loop and feedbac conrol yem Figure how an open loop conrol yem whoe funcion i o caue he oupu y o follow he reference
Open loop conrol v cloed loop feedbac conrol The nex wo figure preen he rucure of open loop and feedbac conrol yem Figure how an open loop conrol yem whoe funcion i o caue he oupu y o follow he reference
Mechtild Stoer * Frank Wagner** Abstract. fastest algorithm known. The runtime analysis is straightforward. In contrast to
 SERIE B INFORMATIK A Simple Min Cu Algorihm Mechild Soer * Frank Wagner** B 9{1 May 199 Abrac We preen an algorihm for nding he minimum cu of an edge-weighed graph. I i imple in every repec. I ha a hor
SERIE B INFORMATIK A Simple Min Cu Algorihm Mechild Soer * Frank Wagner** B 9{1 May 199 Abrac We preen an algorihm for nding he minimum cu of an edge-weighed graph. I i imple in every repec. I ha a hor
24 Single-Source Shortest Paths
 Single-Source Shore Pah Profeor Parick wihe o find he hore poible roue from Phoeni o Indianapoli. Given a road map of he Unied Sae on which he diance beween each pair of adjacen inerecion i marked, how
Single-Source Shore Pah Profeor Parick wihe o find he hore poible roue from Phoeni o Indianapoli. Given a road map of he Unied Sae on which he diance beween each pair of adjacen inerecion i marked, how
EE202 Circuit Theory II
 EE202 Circui Theory II 2017-2018, Spring Dr. Yılmaz KALKAN I. Inroducion & eview of Fir Order Circui (Chaper 7 of Nilon - 3 Hr. Inroducion, C and L Circui, Naural and Sep epone of Serie and Parallel L/C
EE202 Circui Theory II 2017-2018, Spring Dr. Yılmaz KALKAN I. Inroducion & eview of Fir Order Circui (Chaper 7 of Nilon - 3 Hr. Inroducion, C and L Circui, Naural and Sep epone of Serie and Parallel L/C
Network flows. The problem. c : V V! R + 0 [ f+1g. flow network G = (V, E, c), a source s and a sink t uv not in E implies c(u, v) = 0
 Nework flow The problem Seing flow nework G = (V, E, c), a orce and a ink no in E implie c(, ) = 0 Flow from o capaciy conrain kew-ymmery flow-coneraion ale of he flow jfj = P 2V Find a maximm flow from
Nework flow The problem Seing flow nework G = (V, E, c), a orce and a ink no in E implie c(, ) = 0 Flow from o capaciy conrain kew-ymmery flow-coneraion ale of he flow jfj = P 2V Find a maximm flow from
5.2 GRAPHICAL VELOCITY ANALYSIS Polygon Method
 ME 352 GRHICL VELCITY NLYSIS 52 GRHICL VELCITY NLYSIS olygon Mehod Velociy analyi form he hear of kinemaic and dynamic of mechanical yem Velociy analyi i uually performed following a poiion analyi; ie,
ME 352 GRHICL VELCITY NLYSIS 52 GRHICL VELCITY NLYSIS olygon Mehod Velociy analyi form he hear of kinemaic and dynamic of mechanical yem Velociy analyi i uually performed following a poiion analyi; ie,
What is maximum Likelihood? History Features of ML method Tools used Advantages Disadvantages Evolutionary models
 Wha i maximum Likelihood? Hiory Feaure of ML mehod Tool ued Advanage Diadvanage Evoluionary model Maximum likelihood mehod creae all he poible ree conaining he e of organim conidered, and hen ue he aiic
Wha i maximum Likelihood? Hiory Feaure of ML mehod Tool ued Advanage Diadvanage Evoluionary model Maximum likelihood mehod creae all he poible ree conaining he e of organim conidered, and hen ue he aiic
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
CMU-Q Lecture 3: Search algorithms: Informed. Teacher: Gianni A. Di Caro
 CMU-Q 5-38 Lecure 3: Search algorihms: Informed Teacher: Gianni A. Di Caro UNINFORMED VS. INFORMED SEARCH Sraegy How desirable is o be in a cerain inermediae sae for he sake of (effecively) reaching a
CMU-Q 5-38 Lecure 3: Search algorihms: Informed Teacher: Gianni A. Di Caro UNINFORMED VS. INFORMED SEARCH Sraegy How desirable is o be in a cerain inermediae sae for he sake of (effecively) reaching a
2. VECTORS. R Vectors are denoted by bold-face characters such as R, V, etc. The magnitude of a vector, such as R, is denoted as R, R, V
 ME 352 VETS 2. VETS Vecor algebra form he mahemaical foundaion for kinemaic and dnamic. Geomer of moion i a he hear of boh he kinemaic and dnamic of mechanical em. Vecor anali i he imehonored ool for decribing
ME 352 VETS 2. VETS Vecor algebra form he mahemaical foundaion for kinemaic and dnamic. Geomer of moion i a he hear of boh he kinemaic and dnamic of mechanical em. Vecor anali i he imehonored ool for decribing
Laplace Transform. Inverse Laplace Transform. e st f(t)dt. (2)
 Laplace Tranform Maoud Malek The Laplace ranform i an inegral ranform named in honor of mahemaician and aronomer Pierre-Simon Laplace, who ued he ranform in hi work on probabiliy heory. I i a powerful
Laplace Tranform Maoud Malek The Laplace ranform i an inegral ranform named in honor of mahemaician and aronomer Pierre-Simon Laplace, who ued he ranform in hi work on probabiliy heory. I i a powerful
13.1 Circuit Elements in the s Domain Circuit Analysis in the s Domain The Transfer Function and Natural Response 13.
 Chaper 3 The Laplace Tranform in Circui Analyi 3. Circui Elemen in he Domain 3.-3 Circui Analyi in he Domain 3.4-5 The Tranfer Funcion and Naural Repone 3.6 The Tranfer Funcion and he Convoluion Inegral
Chaper 3 The Laplace Tranform in Circui Analyi 3. Circui Elemen in he Domain 3.-3 Circui Analyi in he Domain 3.4-5 The Tranfer Funcion and Naural Repone 3.6 The Tranfer Funcion and he Convoluion Inegral
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Stationary Distribution. Design and Analysis of Algorithms Andrei Bulatov
 Saionary Disribuion Design and Analysis of Algorihms Andrei Bulaov Algorihms Markov Chains 34-2 Classificaion of Saes k By P we denoe he (i,j)-enry of i, j Sae is accessible from sae if 0 for some k 0
Saionary Disribuion Design and Analysis of Algorihms Andrei Bulaov Algorihms Markov Chains 34-2 Classificaion of Saes k By P we denoe he (i,j)-enry of i, j Sae is accessible from sae if 0 for some k 0
Network Flow Applications
 Hopial problem Neork Flo Applicaion Injured people: n Hopial: k Each peron need o be brough o a hopial no more han 30 minue aay Each hopial rea no more han n/k" people Gien n, k, and informaion abou people
Hopial problem Neork Flo Applicaion Injured people: n Hopial: k Each peron need o be brough o a hopial no more han 30 minue aay Each hopial rea no more han n/k" people Gien n, k, and informaion abou people
Myriad of applications
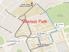 Shortet Path Myriad of application Finding hortet ditance between location (Google map, etc.) Internet router protocol: OSPF (Open Shortet Path Firt) i ued to find the hortet path to interchange package
Shortet Path Myriad of application Finding hortet ditance between location (Google map, etc.) Internet router protocol: OSPF (Open Shortet Path Firt) i ued to find the hortet path to interchange package
Warm Up. Correct order: s,u,v,y,x,w,t
 Warm Up Rn Breadh Fir Search on hi graph aring from. Wha order are erice placed on he qee? When proceing a erex iner neighbor in alphabeical order. In a direced graph, BFS only follow an edge in he direcion
Warm Up Rn Breadh Fir Search on hi graph aring from. Wha order are erice placed on he qee? When proceing a erex iner neighbor in alphabeical order. In a direced graph, BFS only follow an edge in he direcion
20/20 20/20 0/5 0/5 20/20 20/20 5/5 0/5 0/5 5/5 0/20 25/30 20/20 30/30 20/20 0/5 5/5 20/20 0/5 0/5 15/20 15/25 20/20 10/10
 Annoncemen CSEP Applied Algorihm Richard Anderon Lecre 9 Nework Flow Applicaion Reading for hi week 7.-7.. Nework flow applicaion Nex week: Chaper 8. NP-Compleene Final exam, March 8, 6:0 pm. A UW. hor
Annoncemen CSEP Applied Algorihm Richard Anderon Lecre 9 Nework Flow Applicaion Reading for hi week 7.-7.. Nework flow applicaion Nex week: Chaper 8. NP-Compleene Final exam, March 8, 6:0 pm. A UW. hor
Computer-Aided Analysis of Electronic Circuits Course Notes 3
 Gheorghe Asachi Technical Universiy of Iasi Faculy of Elecronics, Telecommunicaions and Informaion Technologies Compuer-Aided Analysis of Elecronic Circuis Course Noes 3 Bachelor: Telecommunicaion Technologies
Gheorghe Asachi Technical Universiy of Iasi Faculy of Elecronics, Telecommunicaions and Informaion Technologies Compuer-Aided Analysis of Elecronic Circuis Course Noes 3 Bachelor: Telecommunicaion Technologies
To become more mathematically correct, Circuit equations are Algebraic Differential equations. from KVL, KCL from the constitutive relationship
 Laplace Tranform (Lin & DeCarlo: Ch 3) ENSC30 Elecric Circui II The Laplace ranform i an inegral ranformaion. I ranform: f ( ) F( ) ime variable complex variable From Euler > Lagrange > Laplace. Hence,
Laplace Tranform (Lin & DeCarlo: Ch 3) ENSC30 Elecric Circui II The Laplace ranform i an inegral ranformaion. I ranform: f ( ) F( ) ime variable complex variable From Euler > Lagrange > Laplace. Hence,
ARTIFICIAL INTELLIGENCE. Markov decision processes
 INFOB2KI 2017-2018 Urech Univeriy The Neherland ARTIFICIAL INTELLIGENCE Markov deciion procee Lecurer: Silja Renooij Thee lide are par of he INFOB2KI Coure Noe available from www.c.uu.nl/doc/vakken/b2ki/chema.hml
INFOB2KI 2017-2018 Urech Univeriy The Neherland ARTIFICIAL INTELLIGENCE Markov deciion procee Lecurer: Silja Renooij Thee lide are par of he INFOB2KI Coure Noe available from www.c.uu.nl/doc/vakken/b2ki/chema.hml
The Primal Simplex Approach to the QoS Routing Problem
 The Primal Simplex Approach o he QoS Rouing Problem Ying Xiao, Krihnaiyan Thulairaman Univeriy of Oklahoma, Norman, OK {ying_xiao, hulai}@ou.edu Guoliang Xue Arizona Sae Univeriy, Tempe, AZ xue@au.edu
The Primal Simplex Approach o he QoS Rouing Problem Ying Xiao, Krihnaiyan Thulairaman Univeriy of Oklahoma, Norman, OK {ying_xiao, hulai}@ou.edu Guoliang Xue Arizona Sae Univeriy, Tempe, AZ xue@au.edu
Designing Information Devices and Systems I Spring 2019 Lecture Notes Note 17
 EES 16A Designing Informaion Devices and Sysems I Spring 019 Lecure Noes Noe 17 17.1 apaciive ouchscreen In he las noe, we saw ha a capacior consiss of wo pieces on conducive maerial separaed by a nonconducive
EES 16A Designing Informaion Devices and Sysems I Spring 019 Lecure Noes Noe 17 17.1 apaciive ouchscreen In he las noe, we saw ha a capacior consiss of wo pieces on conducive maerial separaed by a nonconducive
Random Walk with Anti-Correlated Steps
 Random Walk wih Ani-Correlaed Seps John Noga Dirk Wagner 2 Absrac We conjecure he expeced value of random walks wih ani-correlaed seps o be exacly. We suppor his conjecure wih 2 plausibiliy argumens and
Random Walk wih Ani-Correlaed Seps John Noga Dirk Wagner 2 Absrac We conjecure he expeced value of random walks wih ani-correlaed seps o be exacly. We suppor his conjecure wih 2 plausibiliy argumens and
DETC2004/CIE ALGORITHMIC FOUNDATIONS FOR CONSISTENCY-CHECKING OF INTERACTION-STATES OF MECHATRONIC SYSTEMS
 Proceeding of DETC 04 ASME 2004 Deign Engineering Technical Conference and Compuer and Informaion in Engineering Conference Sal Lake Ciy, Uah, USA, Sepember 28-Ocober 2, 2004 DETC2004/CIE-79 ALGORITHMIC
Proceeding of DETC 04 ASME 2004 Deign Engineering Technical Conference and Compuer and Informaion in Engineering Conference Sal Lake Ciy, Uah, USA, Sepember 28-Ocober 2, 2004 DETC2004/CIE-79 ALGORITHMIC
Notes for Lecture 17-18
 U.C. Berkeley CS278: Compuaional Complexiy Handou N7-8 Professor Luca Trevisan April 3-8, 2008 Noes for Lecure 7-8 In hese wo lecures we prove he firs half of he PCP Theorem, he Amplificaion Lemma, up
U.C. Berkeley CS278: Compuaional Complexiy Handou N7-8 Professor Luca Trevisan April 3-8, 2008 Noes for Lecure 7-8 In hese wo lecures we prove he firs half of he PCP Theorem, he Amplificaion Lemma, up
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Civil and Environmental Engineering
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deparmen of Civil and Environmenal Engineering 1.731 Waer Reource Syem Lecure 17 River Bain Planning Screening Model Nov. 7 2006 River Bain Planning River bain planning
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Deparmen of Civil and Environmenal Engineering 1.731 Waer Reource Syem Lecure 17 River Bain Planning Screening Model Nov. 7 2006 River Bain Planning River bain planning
Maximum Flow 5/6/17 21:08. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Maximm Flo 5/6/17 21:08 Preenaion for e ih he exbook, Algorihm Deign and Applicaion, by M. T. Goodrich and R. Tamaia, Wiley, 2015 Maximm Flo χ 4/6 4/7 1/9 2015 Goodrich and Tamaia Maximm Flo 1 Flo Neork
Maximm Flo 5/6/17 21:08 Preenaion for e ih he exbook, Algorihm Deign and Applicaion, by M. T. Goodrich and R. Tamaia, Wiley, 2015 Maximm Flo χ 4/6 4/7 1/9 2015 Goodrich and Tamaia Maximm Flo 1 Flo Neork
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
UT Austin, ECE Department VLSI Design 5. CMOS Gate Characteristics
 La moule: CMOS Tranior heory Thi moule: DC epone Logic Level an Noie Margin Tranien epone Delay Eimaion Tranior ehavior 1) If he wih of a ranior increae, he curren will ) If he lengh of a ranior increae,
La moule: CMOS Tranior heory Thi moule: DC epone Logic Level an Noie Margin Tranien epone Delay Eimaion Tranior ehavior 1) If he wih of a ranior increae, he curren will ) If he lengh of a ranior increae,
