Explosion Protection of Buildings
|
|
|
- Georgiana Banks
- 5 years ago
- Views:
Transcription
1 Explosion Protection of Buildings Author: Miroslav Mynarz
2 Explosion Protection of Buildings Introduction to the Problems of Determination of Building Structure's Response
3 3 Classification of actions According to response of the structure: Static (no significant accelerations originate in the structure) Dynamic (significant accelerations originate in the structure)
4 4 Classification of actions According to its nature: Force (including moments) Deformation or inematic (forced by displacement or rotation)
5 5 Types of actions Deterministic: Periodical (repeating regularly) Non-periodical (repeating irregularly)
6 6 Types of actions Periodical: Harmonic (simple) y = A sinωt e. g. rotary motion of unbalanced movement of machine advance motion of piston in cylinder simple tone of musical instrument movement of a bell etc.
7 7 Types of actions Periodical : Compact of i-harmonic components F(t) = F st + F i sin(ω i t + φ i ) (Fourier transform) e. g. movement of a floor loaded by more machines movement of bridge dec loaded by more vehicles compound tones, noises etc.
8 8 Types of actions Non-periodical: Impuls (impuls of various shape) I = t F (τ) Δτ e. g. effects of explosions or blast waves push of drop hammers, ramming of piles acoustic stroes etc.
9 9 Types of actions Non-periodical: Non-periodical force F t Combination: Periodical impulses F t e. g. effects of flat wheels to bridge forging of repeated pushes of drop hammer
10 0 Types of actions Non-deterministic (random, stochastic): Stationary (steady, still) Non-stationary (unsteady, unstable)
11 Dynamic ~ time variable load Dynamic load load whose size, direction or place is changing in time. Response of building structure to dynamic load final deformations of the structure (deflections, displacements or rotations) and their derivation in time (velocity, acceleration) as well as internal forces (normal and shear forces or bending moments) and stresses are variable in time.
12 Dynamic ~ time variable load Determination of dynamic response analysis of the structure at dynamic load. Methods depend on character of the load: deterministic load, non-deterministic load.
13 3 Dynamic ~ time variable load Deterministic procedures: time course is nown; material and shape of the structure is nown; boundary conditions (for example founding of the structure) are defined.
14 4 Dynamic ~ time variable load Non-deterministic procedures: time course of load is not nown fully; character of load is variable; character of material properties of the structure is variable.
15 5 Analysis of the response of the building structure Determination of deformation quantities displacements, deflections; rotations; their time derivations. Following force quantities are derivated from deformation quantities internal forces; stress.
16 6 Building structure Number of degrees of freedom (number of components of possible displacements or rotations of structure s mass in particular points which are not precluded by sliding supports): real structures infinite number of degrees of freedom; solid body in 3-D space (point mass in space) 6 degrees of freedom; solid slab in plane (point mass in plane) 3 degrees of freedom. For each degree of freedom, equation of equilibrium (equation of motion) can be written.
17 7 Building structure Characteristics of the structure (material, structural arrangement and boundary conditions): stiffness; mass of inertia (weight); damping properties. Tuning of the structure spectrum of natural frequencies and corresponding free vibration mode shapes (function of stiffness and mass of the structures).
18 8 Building structure Mode shape (antinode versus node): natural mode shape; free vibration; forced vibration.
19 9 Quantities displacement (deflection) s(t)=s 0 f(t) rotation φ(t)=φ 0 f(t) velocity of vibration v(t)=ds/dt φ(t)=dφ/dt acceleration of vibration a(t)=d s/dt φ(t)=d φ /dt momentum of (point) mass H(t)=m v(t) momentum of body inertia force H(t)= V v(t) dm F(t)= m a(t)
20 0 Quantities in direction: of coordinate axes; related to the structure (e. g. in the middle of a span); related to trajectory (e. g. radial, tangential, centrifugal, centripetal). Equation of motion (summary condition of equilibrium of forces in direction of appropriate degree of freedom): displacement; rotational (spin, angular).
21 Quantities Newton's second law: F(t) = d/dt (m ds/dt) = m d s/dt = m a(t) F(t) force vector s(t) trajectory (displacement, rotation) ~ position vector p(t) = s(t) internal forces in the structure (elastic) m a(t) P(t) inertia forces in the structure (volume) external forces (load)
22 Quantities p(t) = s(t) m a(t) P(t) internal forces in the structure (elastic) inertia forces in the structure (volume) external forces (load) d Alembert's principle (motion of a point mass ~ a body) : P(t) - m d s/dt = 0
23 3 Equations of motion Structure under dynamic load: The course of load F(t) is variable in time whereas time change of load is usually in order of seconds or milliseconds. More precise definition of time change of load results from comparison of time change of load F(t) and natural periods of the structure T(i). When time changes of load are long-term, thus in order of hours, days, years, we usually do not tal about dynamic load but about variability of static load.
24 4 Equations of motion Equations of motion (control equations of the system): Equations of motion (control equations of the system) are derivated from equations of equilibrium in appropriate possible direction of motion (deflection or rotation) which is denoted as degrees of freedom: F I (t) + F D (t) + F E (t) = F(t)
25 5 Equations of motion Time change of displacement y(t) is considered as a solution of equation of equilibrium, inertia forces F I (t) = m y (t) thus product of mass m and acceleration of vibration y (t) (from Newton's second law); damping forces F D (t) = C y (t) are usually formulated as product of dumping constant C and velocity of vibration y (t); elastic forces F E (t) = y (t) product of stiffness of the structure and displacement of vibration y(t).
26 6 Equations of motion M y (t) + C y (t) + K y (t) = F where M, C and K are mass, damping and stiffness matrixes of the system; y, y, y are vectors of acceleration, velocity and displacement of vibration; F is a vector of the right sides (load of single parts points of the structure).
27 7 Equations of motion Members of a mass matrix after discretization of a system consist of masses of moving point masses and mass moments of inertia of rotating point masses. Particular elements m ij of a mass matrix can be determined as forces in a point i corresponding to a unit acceleration y in a point j.
28 8 Equations of motion Mass matrix: When using software, consistent mass matrix is usually used; it means a mass matrix with nonzero elements even at non-diagonal positions. More simply, generally for manual calculation or computation of small systems or systems with limited number of degrees of freedom, only lumped mass matrix is used it is diagonal matrix with zero elements at non-diagonal positions. It means that inertia forces in i-th point of the system generated by the load applied to this point do not induce inertia response of other points.
29 9 Equations of motion Let s divide bent beam to several particular elements where mass of single elements is focused into nodes of discrete system. If diagonal matrix is used for calculation then at each position of diagonal, mass of particular node is placed there and it performs only advanced motion. If we tae into account that masses in nodes can also rotate then mass matrix has nonzero elements even at non-diagonal positions it is considered as consistent mass matrix.
30 30 Equations of motion Damping matrix: For compilation of damping matrix C it is usually assumed that damping is directly proportional to velocity of motion (see formulation of damping forces of equation of motion) this damping is denoted as viscous damping. Then single elements of damping matrix correspond to force in node i at action of unit vector of velocity y in point j: F D = c y
31 3 Equations of motion In software, implementation of damping to equation of motion with help of coefficients a and b is used with advantage. In this case, damping matrix C is more simply considered to be linear combination of mass matrix and stiffness matrix C = a M + b K Simplification consists especially in determination of damping size with only two parameters a and b that are valid for all frequency components of vibration.
32 3 Equations of motion De facto, damping of vibrations is usually higher on higher frequencies it means that calculated dynamic response of the structure can be actually different.
33 33 Equations of motion Stiffness matrix: Particular elements of this matrix correspond to static stiffnesses of single nodal points of 3D discretizated system at unit displacements (and also rotations) of these relevant nodal points. As well as in the cases of mass and damping matrixes, single elements of stiffness matrix ij correspond to a force (moment) in a node i at action of unit displacement (rotation) y in point j: F E = y
34 34 Equations of motion Calculation decomposes in two cases: - equation without right side (unloaded structure): calculation of natural vibration (tuning of the structure); - equation with right side (loaded structure): calculation of forced vibration. There are many methods for solution of free and forced vibration. The user of particular software should now used method of solution. It is not advisable to use the software as a blac box through which the user gains the results and believes them absolutely. He or she should then now the possibilities of the method in so far to estimate its proximities bringing into the results of response calculation.
35 35 Equations of motion Development to the free vibration mode shapes: In this case, it highly depends on a number of mode shapes used for calculation. For small amount of mode shapes (up to 5 or 0 shapes), the calculation could involve only 50 to 60 % intensity of a real response. According to Eurocode 8, minimum number of considered global mode shapes is: 3 n or T 0. s n is a number of floors above the foundation or solid subsoil.
36 36 Equations of motion Damping of vibrations: A size of damping can affect even calculated quantities of the response especially in the case when the response of the structure is close to resonant frequency. It is usually assumed that damping is proportional to the velocity of vibration. This damping is called viscous. Most software generally enables the implementation of viscous damping to the calculation. Viscous damping is also suitable approximation to other assumptions about damping (e. g. hysteretic damping that is proportional to the deflection of vibrations).
37 37 Equations of motion Damping of vibrations: For determination of a level of viscous damping, it is suitable to result from parameters measured at particular structure. Damping is frequency-dependent. Generally, structural damping is lowest on lowest natural frequencies and damping is increasing with increasing frequency. Relation between the damping ratio D and the logarithmic decrement of damping δ follows: D δ f ω i i δ π
38 38 Equations of motion Damping of vibrations: - chosen values of the logarithmic decrement of damping δ and the damping ratio D (according to ČSN ) Material Constructive system, element D (%) Steel Masonry Timber Concrete engineering structures (building, halls) towers, smoestacs, high-rise structures single elements columns, beams springs (wound) vertical bric masonry (walls, partition walls) masonry vaults in steel beams stone masonry on lime mortar stone masonry on cement-lime mortar glued beams nailed beams roof trusses tower structures compression elements without cracs elements with tension (without cracs) elements with cracs slab and rib floors crane beams and columns high prefabricated houses ,
39 deflection y VŠB Technical University of Ostrava 39 Equations of motion Experimental methods for determination of damping: deflection in resonance frequency of excitation f
40 40 VŠB Technical University of Ostrava Experimental methods for determination of damping: Equations of motion the logarithmic decrement of damping m n n n n y y ln m y y ln δ the damping ratio from rezonant gain pea st y y D method of the width of the resonance curve f f f f D
41 4 Equations of motion Implementation of a size of damping to the calculation: In software, Rayleigh formulation of damping is generally implemented (through method of integration of equations of motion). It results from solution of matrix equation of motion whose damping matrix C is considered as a linear combination of mass matrix M and stiffness matrix K: C = α M + β K
42 4 Equations of motion Implementation of a size of damping to the calculation: For a system with one degree of freedom: α D ω β It could be derived even for a system with more degrees of freedom it is then necessary to now relevant number of natural frequencies. D ω
43 43 Equations of motion Implementation of a size of damping to the calculation: At calculation of systems with more dominant frequency components of excitation or at excitation with general time course of a load, it is necessary to decide which size of damping will be used for which frequency component. At other frequency components whose damping is not nown more precisely a size of response is burdened with bigger or smaller error.
44 44 Standards requirements for determination of dynamic response of the structure Standards usually do not specify process of calculation and chosen method. For example, standards (ČSN , Eurocode 8 or UBC 997 etc.) enable simplified (seismic this procedure can be applied even to the blast effects) calculation of simpler structures at use of cantilever model (the object is replaced by a bar model cantilever with masses focused in single floors).
45 45 Standards requirements for determination of dynamic response of the structure Simplification of geometry (numerical model) versus calculation method Cantilever model is suitable for high slender structures but not for structures with wide plan (e. g. industrial halls), underground structures, indented buildings or structures with dominant effect in vertical direction (bridges, huge cantilever length of floors in buildings). In such cases it is correct to use 3D or at least D model and to perform dynamic computation on these models. Simplification of input data: material characteristic and load.
46 46 Damping of system with one degree of freedom Natural undamped vibration: F in F re m d v dt d v m dt v t t t v m mass of a system t 0 - inertia force - restoring force of the spring v(t) vertical displacement of the spring stiffness (the spring constant)
47 47 Damping of system with one degree of freedom v Natural undamped vibration: t A sinω t B cosω t v sinω t A φ0 0 v0 cos φ0 B v sinφ v A B φ 0 B A 0 0 B φ arcg 0 A 0 0
48 48 Damping of system with one degree of freedom Initial conditions: t dv v t ω A cosω t B sinω t dt v0 ω0 cos ω0t φ0 v0 ω0 sin ω0t φ t π d v v t ω A sinω t B cosω t dt ω t φ v ω sinω t φ π v0 ω0 sin
49 49 Damping of system with one degree of freedom π T0 π f ω 0 0 m ω 0 m f 0 0 T 0 ω π π m Natural frequency f 0 = f ()
50 50 Damping of system with one degree of freedom v Natural damped vibration: d v m dt d v dt t t ω dv b dt b dv dt t t v ω t 0 t 0 For solution in shape of v(t)=e αt it has characteristic equation: with roots α α ω α ω b ω ω ω, b b 0 ωbt ωbt t e A sinω t B cosω t v e sinω t d d d d v 0 d φ 0
51 5 Damping of system with one degree of freedom Following three cases can occur: - critical damping, when ω b = ω 0, b r = ; characteristic equation has one real, double root: α, =-ω b, - overdamping, when ω b > ω 0, b r > ; characteristic equation has two different real roots: α ω ω ω, b b 0 - underdamping, when ω b < ω 0, b r < ; characteristic equation has two imaginary complex conjugate roots: α ω i ω ω ω iω, b 0 b b d ω d ω ω 0 b is natural angular (circular) frequency of damping vibration.
52 5 Damping of system with one degree of freedom υ ln v v ω f b ωbt d d πω ω d b υ πω ω d b b r π b r υ πb r the damping ratio b r = D
53 53 Damping of system with one degree of freedom Harmonic excitation undamped vibration: m d v dt t v v t v t sinωt F sinωt v F F ω0 v st mω m ω ω ω ω 0 0 v st δ
54 54 Damping of system with one degree of freedom Harmonic excitation undamped vibration: force force resonance deflection deflection
55 55 Damping of system with one degree of freedom Harmonic excitation undamped vibration: v m d v dt d v dt t t ω c b dv dt t t dv dt v ω 0 v t t Ft t F m t A sinωt B cosωt v sinωt φ v F A t B F sinωt tgφ B A
56 56 VŠB Technical University of Ostrava Damping of system with one degree of freedom Harmonic excitation undamped vibration: η b η η F ω ω ω ω ω ω m F A r b 0 4 b η η b η F ω ω ω ω ωω m F B r r b b 4 4 η π υ η η υ π υ η δ
57 57 Damping of system with one degree of freedom Harmonic excitation undamped vibration: π Under-resonant area for η= resonance δ υ over-resonant area. v v st F mω ω b m ω ω ω 0 ω ω 0 4ω ω b 0 v st δ F 4ω ωb
58 58 Damping of system with two degrees of freedom Simple beam undamped vibration: m m d v dt t v d v dt t t v t 0 v t v t 0 ω, m m 4 m m m m a v v 0 0 m ω m ω a v v 0 0 m ω m ω
59 59 Damping of system with two degrees of freedom Simple beam undamped vibration: I m d ζ dt t d u dt t a ζζ uu a ζ u m m t ut 0 ζu t ζ t 0 uζ I m a b
60 60 Damping of system with two degrees of freedom Simple beam undamped vibration: EI b b ζζ l l l 6EI b EI 3 l l uu l ζu ω, uu m ζζ I 4 uu m ζζ I uζ mi a a i i I m
61 6 VŠB Technical University of Ostrava Damping of system with two degrees of freedom 0 t v t v dt t v d m Simple beam undamped vibration: 0 t v t v dt t v d m 4 m m m m m m ω,
62 6 Damping of system with three degrees of freedom
63 63 Than you for your attention.
Introduction to structural dynamics
 Introduction to structural dynamics p n m n u n p n-1 p 3... m n-1 m 3... u n-1 u 3 k 1 c 1 u 1 u 2 k 2 m p 1 1 c 2 m2 p 2 k n c n m n u n p n m 2 p 2 u 2 m 1 p 1 u 1 Static vs dynamic analysis Static
Introduction to structural dynamics p n m n u n p n-1 p 3... m n-1 m 3... u n-1 u 3 k 1 c 1 u 1 u 2 k 2 m p 1 1 c 2 m2 p 2 k n c n m n u n p n m 2 p 2 u 2 m 1 p 1 u 1 Static vs dynamic analysis Static
Dr.Vinod Hosur, Professor, Civil Engg.Dept., Gogte Institute of Technology, Belgaum
 STRUCTURAL DYNAMICS Dr.Vinod Hosur, Professor, Civil Engg.Dept., Gogte Institute of Technology, Belgaum Overview of Structural Dynamics Structure Members, joints, strength, stiffness, ductility Structure
STRUCTURAL DYNAMICS Dr.Vinod Hosur, Professor, Civil Engg.Dept., Gogte Institute of Technology, Belgaum Overview of Structural Dynamics Structure Members, joints, strength, stiffness, ductility Structure
Dynamics of Machinery
 Dynamics of Machinery Two Mark Questions & Answers Varun B Page 1 Force Analysis 1. Define inertia force. Inertia force is an imaginary force, which when acts upon a rigid body, brings it to an equilibrium
Dynamics of Machinery Two Mark Questions & Answers Varun B Page 1 Force Analysis 1. Define inertia force. Inertia force is an imaginary force, which when acts upon a rigid body, brings it to an equilibrium
Dynamics of structures
 Dynamics of structures 2.Vibrations: single degree of freedom system Arnaud Deraemaeker (aderaema@ulb.ac.be) 1 Outline of the chapter *One degree of freedom systems in real life Hypothesis Examples *Response
Dynamics of structures 2.Vibrations: single degree of freedom system Arnaud Deraemaeker (aderaema@ulb.ac.be) 1 Outline of the chapter *One degree of freedom systems in real life Hypothesis Examples *Response
Structural Dynamics. Spring mass system. The spring force is given by and F(t) is the driving force. Start by applying Newton s second law (F=ma).
 Structural Dynamics Spring mass system. The spring force is given by and F(t) is the driving force. Start by applying Newton s second law (F=ma). We will now look at free vibrations. Considering the free
Structural Dynamics Spring mass system. The spring force is given by and F(t) is the driving force. Start by applying Newton s second law (F=ma). We will now look at free vibrations. Considering the free
CE 6701 Structural Dynamics and Earthquake Engineering Dr. P. Venkateswara Rao
 CE 6701 Structural Dynamics and Earthquake Engineering Dr. P. Venkateswara Rao Associate Professor Dept. of Civil Engineering SVCE, Sriperumbudur Difference between static loading and dynamic loading Degree
CE 6701 Structural Dynamics and Earthquake Engineering Dr. P. Venkateswara Rao Associate Professor Dept. of Civil Engineering SVCE, Sriperumbudur Difference between static loading and dynamic loading Degree
WEEKS 8-9 Dynamics of Machinery
 WEEKS 8-9 Dynamics of Machinery References Theory of Machines and Mechanisms, J.J.Uicker, G.R.Pennock ve J.E. Shigley, 2011 Mechanical Vibrations, Singiresu S. Rao, 2010 Mechanical Vibrations: Theory and
WEEKS 8-9 Dynamics of Machinery References Theory of Machines and Mechanisms, J.J.Uicker, G.R.Pennock ve J.E. Shigley, 2011 Mechanical Vibrations, Singiresu S. Rao, 2010 Mechanical Vibrations: Theory and
Introduction to Vibration. Professor Mike Brennan
 Introduction to Vibration Professor Mie Brennan Introduction to Vibration Nature of vibration of mechanical systems Free and forced vibrations Frequency response functions Fundamentals For free vibration
Introduction to Vibration Professor Mie Brennan Introduction to Vibration Nature of vibration of mechanical systems Free and forced vibrations Frequency response functions Fundamentals For free vibration
CIVL 8/7117 Chapter 12 - Structural Dynamics 1/75. To discuss the dynamics of a single-degree-of freedom springmass
 CIV 8/77 Chapter - /75 Introduction To discuss the dynamics of a single-degree-of freedom springmass system. To derive the finite element equations for the time-dependent stress analysis of the one-dimensional
CIV 8/77 Chapter - /75 Introduction To discuss the dynamics of a single-degree-of freedom springmass system. To derive the finite element equations for the time-dependent stress analysis of the one-dimensional
COPYRIGHTED MATERIAL. Index
 Index A Admissible function, 163 Amplification factor, 36 Amplitude, 1, 22 Amplitude-modulated carrier, 630 Amplitude ratio, 36 Antinodes, 612 Approximate analytical methods, 647 Assumed modes method,
Index A Admissible function, 163 Amplification factor, 36 Amplitude, 1, 22 Amplitude-modulated carrier, 630 Amplitude ratio, 36 Antinodes, 612 Approximate analytical methods, 647 Assumed modes method,
STRUCTURAL DYNAMICS BASICS:
 BASICS: STRUCTURAL DYNAMICS Real-life structures are subjected to loads which vary with time Except self weight of the structure, all other loads vary with time In many cases, this variation of the load
BASICS: STRUCTURAL DYNAMICS Real-life structures are subjected to loads which vary with time Except self weight of the structure, all other loads vary with time In many cases, this variation of the load
Section 3.7: Mechanical and Electrical Vibrations
 Section 3.7: Mechanical and Electrical Vibrations Second order linear equations with constant coefficients serve as mathematical models for mechanical and electrical oscillations. For example, the motion
Section 3.7: Mechanical and Electrical Vibrations Second order linear equations with constant coefficients serve as mathematical models for mechanical and electrical oscillations. For example, the motion
Modeling and Experimentation: Mass-Spring-Damper System Dynamics
 Modeling and Experimentation: Mass-Spring-Damper System Dynamics Prof. R.G. Longoria Department of Mechanical Engineering The University of Texas at Austin July 20, 2014 Overview 1 This lab is meant to
Modeling and Experimentation: Mass-Spring-Damper System Dynamics Prof. R.G. Longoria Department of Mechanical Engineering The University of Texas at Austin July 20, 2014 Overview 1 This lab is meant to
Vibrations Qualifying Exam Study Material
 Vibrations Qualifying Exam Study Material The candidate is expected to have a thorough understanding of engineering vibrations topics. These topics are listed below for clarification. Not all instructors
Vibrations Qualifying Exam Study Material The candidate is expected to have a thorough understanding of engineering vibrations topics. These topics are listed below for clarification. Not all instructors
UNIT-I (FORCE ANALYSIS)
 DHANALAKSHMI SRINIVASAN INSTITUTE OF RESEACH AND TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING QUESTION BANK ME2302 DYNAMICS OF MACHINERY III YEAR/ V SEMESTER UNIT-I (FORCE ANALYSIS) PART-A (2 marks)
DHANALAKSHMI SRINIVASAN INSTITUTE OF RESEACH AND TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING QUESTION BANK ME2302 DYNAMICS OF MACHINERY III YEAR/ V SEMESTER UNIT-I (FORCE ANALYSIS) PART-A (2 marks)
Chapter 2: Rigid Bar Supported by Two Buckled Struts under Axial, Harmonic, Displacement Excitation..14
 Table of Contents Chapter 1: Research Objectives and Literature Review..1 1.1 Introduction...1 1.2 Literature Review......3 1.2.1 Describing Vibration......3 1.2.2 Vibration Isolation.....6 1.2.2.1 Overview.
Table of Contents Chapter 1: Research Objectives and Literature Review..1 1.1 Introduction...1 1.2 Literature Review......3 1.2.1 Describing Vibration......3 1.2.2 Vibration Isolation.....6 1.2.2.1 Overview.
A Guide to linear dynamic analysis with Damping
 A Guide to linear dynamic analysis with Damping This guide starts from the applications of linear dynamic response and its role in FEA simulation. Fundamental concepts and principles will be introduced
A Guide to linear dynamic analysis with Damping This guide starts from the applications of linear dynamic response and its role in FEA simulation. Fundamental concepts and principles will be introduced
Outline of parts 1 and 2
 to Harmonic Loading http://intranet.dica.polimi.it/people/boffi-giacomo Dipartimento di Ingegneria Civile Ambientale e Territoriale Politecnico di Milano March, 6 Outline of parts and of an Oscillator
to Harmonic Loading http://intranet.dica.polimi.it/people/boffi-giacomo Dipartimento di Ingegneria Civile Ambientale e Territoriale Politecnico di Milano March, 6 Outline of parts and of an Oscillator
Introduction to Vibration. Mike Brennan UNESP, Ilha Solteira São Paulo Brazil
 Introduction to Vibration Mike Brennan UNESP, Ilha Solteira São Paulo Brazil Vibration Most vibrations are undesirable, but there are many instances where vibrations are useful Ultrasonic (very high
Introduction to Vibration Mike Brennan UNESP, Ilha Solteira São Paulo Brazil Vibration Most vibrations are undesirable, but there are many instances where vibrations are useful Ultrasonic (very high
Codal Provisions IS 1893 (Part 1) 2002
 Abstract Codal Provisions IS 1893 (Part 1) 00 Paresh V. Patel Assistant Professor, Civil Engineering Department, Nirma Institute of Technology, Ahmedabad 38481 In this article codal provisions of IS 1893
Abstract Codal Provisions IS 1893 (Part 1) 00 Paresh V. Patel Assistant Professor, Civil Engineering Department, Nirma Institute of Technology, Ahmedabad 38481 In this article codal provisions of IS 1893
Structural Dynamics A Graduate Course in Aerospace Engineering
 Structural Dynamics A Graduate Course in Aerospace Engineering By: H. Ahmadian ahmadian@iust.ac.ir The Science and Art of Structural Dynamics What do all the followings have in common? > A sport-utility
Structural Dynamics A Graduate Course in Aerospace Engineering By: H. Ahmadian ahmadian@iust.ac.ir The Science and Art of Structural Dynamics What do all the followings have in common? > A sport-utility
Introduction to Continuous Systems. Continuous Systems. Strings, Torsional Rods and Beams.
 Outline of Continuous Systems. Introduction to Continuous Systems. Continuous Systems. Strings, Torsional Rods and Beams. Vibrations of Flexible Strings. Torsional Vibration of Rods. Bernoulli-Euler Beams.
Outline of Continuous Systems. Introduction to Continuous Systems. Continuous Systems. Strings, Torsional Rods and Beams. Vibrations of Flexible Strings. Torsional Vibration of Rods. Bernoulli-Euler Beams.
Chapter 23: Principles of Passive Vibration Control: Design of absorber
 Chapter 23: Principles of Passive Vibration Control: Design of absorber INTRODUCTION The term 'vibration absorber' is used for passive devices attached to the vibrating structure. Such devices are made
Chapter 23: Principles of Passive Vibration Control: Design of absorber INTRODUCTION The term 'vibration absorber' is used for passive devices attached to the vibrating structure. Such devices are made
Final Exam Solution Dynamics :45 12:15. Problem 1 Bateau
 Final Exam Solution Dynamics 2 191157140 31-01-2013 8:45 12:15 Problem 1 Bateau Bateau is a trapeze act by Cirque du Soleil in which artists perform aerial maneuvers on a boat shaped structure. The boat
Final Exam Solution Dynamics 2 191157140 31-01-2013 8:45 12:15 Problem 1 Bateau Bateau is a trapeze act by Cirque du Soleil in which artists perform aerial maneuvers on a boat shaped structure. The boat
Dynamics of Structures: Theory and Analysis
 1. Free vibrations 2. Forced vibrations 3. Transient response 4. Damping mechanisms Dynamics of Structures: Theory and Analysis Steen Krenk Technical University of Denmark 5. Modal analysis I: Basic idea
1. Free vibrations 2. Forced vibrations 3. Transient response 4. Damping mechanisms Dynamics of Structures: Theory and Analysis Steen Krenk Technical University of Denmark 5. Modal analysis I: Basic idea
Preliminary Examination - Dynamics
 Name: University of California, Berkeley Fall Semester, 2018 Problem 1 (30% weight) Preliminary Examination - Dynamics An undamped SDOF system with mass m and stiffness k is initially at rest and is then
Name: University of California, Berkeley Fall Semester, 2018 Problem 1 (30% weight) Preliminary Examination - Dynamics An undamped SDOF system with mass m and stiffness k is initially at rest and is then
Laboratory notes. Torsional Vibration Absorber
 Titurus, Marsico & Wagg Torsional Vibration Absorber UoB/1-11, v1. Laboratory notes Torsional Vibration Absorber Contents 1 Objectives... Apparatus... 3 Theory... 3 3.1 Background information... 3 3. Undamped
Titurus, Marsico & Wagg Torsional Vibration Absorber UoB/1-11, v1. Laboratory notes Torsional Vibration Absorber Contents 1 Objectives... Apparatus... 3 Theory... 3 3.1 Background information... 3 3. Undamped
on the figure. Someone has suggested that, in terms of the degrees of freedom x1 and M. Note that if you think the given 1.2
 1) A two-story building frame is shown below. The mass of the frame is assumed to be lumped at the floor levels and the floor slabs are considered rigid. The floor masses and the story stiffnesses are
1) A two-story building frame is shown below. The mass of the frame is assumed to be lumped at the floor levels and the floor slabs are considered rigid. The floor masses and the story stiffnesses are
Chapter a. Spring constant, k : The change in the force per unit length change of the spring. b. Coefficient of subgrade reaction, k:
 Principles of Soil Dynamics 3rd Edition Das SOLUTIONS MANUAL Full clear download (no formatting errors) at: https://testbankreal.com/download/principles-soil-dynamics-3rd-editiondas-solutions-manual/ Chapter
Principles of Soil Dynamics 3rd Edition Das SOLUTIONS MANUAL Full clear download (no formatting errors) at: https://testbankreal.com/download/principles-soil-dynamics-3rd-editiondas-solutions-manual/ Chapter
Structural Dynamics Lecture Eleven: Dynamic Response of MDOF Systems: (Chapter 11) By: H. Ahmadian
 Structural Dynamics Lecture Eleven: Dynamic Response of MDOF Systems: (Chapter 11) By: H. Ahmadian ahmadian@iust.ac.ir Dynamic Response of MDOF Systems: Mode-Superposition Method Mode-Superposition Method:
Structural Dynamics Lecture Eleven: Dynamic Response of MDOF Systems: (Chapter 11) By: H. Ahmadian ahmadian@iust.ac.ir Dynamic Response of MDOF Systems: Mode-Superposition Method Mode-Superposition Method:
Introduction to Mechanical Vibration
 2103433 Introduction to Mechanical Vibration Nopdanai Ajavakom (NAV) 1 Course Topics Introduction to Vibration What is vibration? Basic concepts of vibration Modeling Linearization Single-Degree-of-Freedom
2103433 Introduction to Mechanical Vibration Nopdanai Ajavakom (NAV) 1 Course Topics Introduction to Vibration What is vibration? Basic concepts of vibration Modeling Linearization Single-Degree-of-Freedom
T1 T e c h n i c a l S e c t i o n
 1.5 Principles of Noise Reduction A good vibration isolation system is reducing vibration transmission through structures and thus, radiation of these vibration into air, thereby reducing noise. There
1.5 Principles of Noise Reduction A good vibration isolation system is reducing vibration transmission through structures and thus, radiation of these vibration into air, thereby reducing noise. There
Lecture XXVI. Morris Swartz Dept. of Physics and Astronomy Johns Hopkins University November 5, 2003
 Lecture XXVI Morris Swartz Dept. of Physics and Astronomy Johns Hopins University morris@jhu.edu November 5, 2003 Lecture XXVI: Oscillations Oscillations are periodic motions. There are many examples of
Lecture XXVI Morris Swartz Dept. of Physics and Astronomy Johns Hopins University morris@jhu.edu November 5, 2003 Lecture XXVI: Oscillations Oscillations are periodic motions. There are many examples of
AA242B: MECHANICAL VIBRATIONS
 AA242B: MECHANICAL VIBRATIONS 1 / 50 AA242B: MECHANICAL VIBRATIONS Undamped Vibrations of n-dof Systems These slides are based on the recommended textbook: M. Géradin and D. Rixen, Mechanical Vibrations:
AA242B: MECHANICAL VIBRATIONS 1 / 50 AA242B: MECHANICAL VIBRATIONS Undamped Vibrations of n-dof Systems These slides are based on the recommended textbook: M. Géradin and D. Rixen, Mechanical Vibrations:
Structural Dynamics Lecture 2. Outline of Lecture 2. Single-Degree-of-Freedom Systems (cont.)
 Outline of Single-Degree-of-Freedom Systems (cont.) Linear Viscous Damped Eigenvibrations. Logarithmic decrement. Response to Harmonic and Periodic Loads. 1 Single-Degreee-of-Freedom Systems (cont.). Linear
Outline of Single-Degree-of-Freedom Systems (cont.) Linear Viscous Damped Eigenvibrations. Logarithmic decrement. Response to Harmonic and Periodic Loads. 1 Single-Degreee-of-Freedom Systems (cont.). Linear
Some Aspects of Structural Dynamics
 Appendix B Some Aspects of Structural Dynamics This Appendix deals with some aspects of the dynamic behavior of SDOF and MDOF. It starts with the formulation of the equation of motion of SDOF systems.
Appendix B Some Aspects of Structural Dynamics This Appendix deals with some aspects of the dynamic behavior of SDOF and MDOF. It starts with the formulation of the equation of motion of SDOF systems.
D : SOLID MECHANICS. Q. 1 Q. 9 carry one mark each.
 GTE 2016 Q. 1 Q. 9 carry one mark each. D : SOLID MECHNICS Q.1 single degree of freedom vibrating system has mass of 5 kg, stiffness of 500 N/m and damping coefficient of 100 N-s/m. To make the system
GTE 2016 Q. 1 Q. 9 carry one mark each. D : SOLID MECHNICS Q.1 single degree of freedom vibrating system has mass of 5 kg, stiffness of 500 N/m and damping coefficient of 100 N-s/m. To make the system
Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter.
 Chapter 3 Mechanical Systems A. Bazoune 3.1 INRODUCION Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter. 3. MECHANICAL ELEMENS Any mechanical system consists
Chapter 3 Mechanical Systems A. Bazoune 3.1 INRODUCION Mathematical Modeling and response analysis of mechanical systems are the subjects of this chapter. 3. MECHANICAL ELEMENS Any mechanical system consists
EVALUATING DYNAMIC STRESSES OF A PIPELINE
 EVALUATING DYNAMIC STRESSES OF A PIPELINE by K.T. TRUONG Member ASME Mechanical & Piping Division THE ULTRAGEN GROUP LTD 2255 Rue De La Province Longueuil (Quebec) J4G 1G3 This document is provided to
EVALUATING DYNAMIC STRESSES OF A PIPELINE by K.T. TRUONG Member ASME Mechanical & Piping Division THE ULTRAGEN GROUP LTD 2255 Rue De La Province Longueuil (Quebec) J4G 1G3 This document is provided to
EN40: Dynamics and Vibrations. Final Examination Wed May : 2pm-5pm
 EN40: Dynamics and Vibrations Final Examination Wed May 10 017: pm-5pm School of Engineering Brown University NAME: General Instructions No collaboration of any kind is permitted on this examination. You
EN40: Dynamics and Vibrations Final Examination Wed May 10 017: pm-5pm School of Engineering Brown University NAME: General Instructions No collaboration of any kind is permitted on this examination. You
Oscillatory Motion SHM
 Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
Chapter 15 Oscillatory Motion SHM Dr. Armen Kocharian Periodic Motion Periodic motion is motion of an object that regularly repeats The object returns to a given position after a fixed time interval A
EQUIVALENT SINGLE-DEGREE-OF-FREEDOM SYSTEM AND FREE VIBRATION
 1 EQUIVALENT SINGLE-DEGREE-OF-FREEDOM SYSTEM AND FREE VIBRATION The course on Mechanical Vibration is an important part of the Mechanical Engineering undergraduate curriculum. It is necessary for the development
1 EQUIVALENT SINGLE-DEGREE-OF-FREEDOM SYSTEM AND FREE VIBRATION The course on Mechanical Vibration is an important part of the Mechanical Engineering undergraduate curriculum. It is necessary for the development
This equation of motion may be solved either by differential equation method or by graphical method as discussed below:
 2.15. Frequency of Under Damped Forced Vibrations Consider a system consisting of spring, mass and damper as shown in Fig. 22. Let the system is acted upon by an external periodic (i.e. simple harmonic)
2.15. Frequency of Under Damped Forced Vibrations Consider a system consisting of spring, mass and damper as shown in Fig. 22. Let the system is acted upon by an external periodic (i.e. simple harmonic)
KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY OSCILLATIONS AND WAVES PRACTICE EXAM
 KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY-10012 OSCILLATIONS AND WAVES PRACTICE EXAM Candidates should attempt ALL of PARTS A and B, and TWO questions from PART C. PARTS A and B should be answered
KEELE UNIVERSITY PHYSICS/ASTROPHYSICS MODULE PHY-10012 OSCILLATIONS AND WAVES PRACTICE EXAM Candidates should attempt ALL of PARTS A and B, and TWO questions from PART C. PARTS A and B should be answered
Structural System, Machines and Load Cases
 Machine-Induced Vibrations Machine-Induced Vibrations In the following example the dynamic excitation of two rotating machines is analyzed. A time history analysis in the add-on module RF-DYNAM Pro - Forced
Machine-Induced Vibrations Machine-Induced Vibrations In the following example the dynamic excitation of two rotating machines is analyzed. A time history analysis in the add-on module RF-DYNAM Pro - Forced
Dynamics of structures
 Dynamics of structures 2.Vibrations: single degree of freedom system Arnaud Deraemaeker (aderaema@ulb.ac.be) 1 One degree of freedom systems in real life 2 1 Reduction of a system to a one dof system Example
Dynamics of structures 2.Vibrations: single degree of freedom system Arnaud Deraemaeker (aderaema@ulb.ac.be) 1 One degree of freedom systems in real life 2 1 Reduction of a system to a one dof system Example
Lecture 27: Structural Dynamics - Beams.
 Chapter #16: Structural Dynamics and Time Dependent Heat Transfer. Lectures #1-6 have discussed only steady systems. There has been no time dependence in any problems. We will investigate beam dynamics
Chapter #16: Structural Dynamics and Time Dependent Heat Transfer. Lectures #1-6 have discussed only steady systems. There has been no time dependence in any problems. We will investigate beam dynamics
Exam Question 6/8 (HL/OL): Circular and Simple Harmonic Motion. February 1, Applied Mathematics: Lecture 7. Brendan Williamson.
 in a : Exam Question 6/8 (HL/OL): Circular and February 1, 2017 in a This lecture pertains to material relevant to question 6 of the paper, and question 8 of the Ordinary Level paper, commonly referred
in a : Exam Question 6/8 (HL/OL): Circular and February 1, 2017 in a This lecture pertains to material relevant to question 6 of the paper, and question 8 of the Ordinary Level paper, commonly referred
Identification Methods for Structural Systems. Prof. Dr. Eleni Chatzi Lecture March, 2016
 Prof. Dr. Eleni Chatzi Lecture 4-09. March, 2016 Fundamentals Overview Multiple DOF Systems State-space Formulation Eigenvalue Analysis The Mode Superposition Method The effect of Damping on Structural
Prof. Dr. Eleni Chatzi Lecture 4-09. March, 2016 Fundamentals Overview Multiple DOF Systems State-space Formulation Eigenvalue Analysis The Mode Superposition Method The effect of Damping on Structural
Step 1: Mathematical Modeling
 083 Mechanical Vibrations Lesson Vibration Analysis Procedure The analysis of a vibrating system usually involves four steps: mathematical modeling derivation of the governing uations solution of the uations
083 Mechanical Vibrations Lesson Vibration Analysis Procedure The analysis of a vibrating system usually involves four steps: mathematical modeling derivation of the governing uations solution of the uations
4.9 Free Mechanical Vibrations
 4.9 Free Mechanical Vibrations Spring-Mass Oscillator When the spring is not stretched and the mass m is at rest, the system is at equilibrium. Forces Acting in the System When the mass m is displaced
4.9 Free Mechanical Vibrations Spring-Mass Oscillator When the spring is not stretched and the mass m is at rest, the system is at equilibrium. Forces Acting in the System When the mass m is displaced
The... of a particle is defined as its change in position in some time interval.
 Distance is the. of a path followed by a particle. Distance is a quantity. The... of a particle is defined as its change in position in some time interval. Displacement is a.. quantity. The... of a particle
Distance is the. of a path followed by a particle. Distance is a quantity. The... of a particle is defined as its change in position in some time interval. Displacement is a.. quantity. The... of a particle
Table of Contents. Preface... 13
 Table of Contents Preface... 13 Chapter 1. Vibrations of Continuous Elastic Solid Media... 17 1.1. Objective of the chapter... 17 1.2. Equations of motion and boundary conditions of continuous media...
Table of Contents Preface... 13 Chapter 1. Vibrations of Continuous Elastic Solid Media... 17 1.1. Objective of the chapter... 17 1.2. Equations of motion and boundary conditions of continuous media...
Chapter 14 Oscillations. Copyright 2009 Pearson Education, Inc.
 Chapter 14 Oscillations Oscillations of a Spring Simple Harmonic Motion Energy in the Simple Harmonic Oscillator Simple Harmonic Motion Related to Uniform Circular Motion The Simple Pendulum The Physical
Chapter 14 Oscillations Oscillations of a Spring Simple Harmonic Motion Energy in the Simple Harmonic Oscillator Simple Harmonic Motion Related to Uniform Circular Motion The Simple Pendulum The Physical
International Journal of Emerging Technologies in Computational and Applied Sciences (IJETCAS)
 International Association of Scientific Innovation and Research (IASIR) (An Association Unifying the Sciences, Engineering, and Applied Research) International Journal of Emerging Technologies in Computational
International Association of Scientific Innovation and Research (IASIR) (An Association Unifying the Sciences, Engineering, and Applied Research) International Journal of Emerging Technologies in Computational
Chapter 15. Oscillatory Motion
 Chapter 15 Oscillatory Motion Part 2 Oscillations and Mechanical Waves Periodic motion is the repeating motion of an object in which it continues to return to a given position after a fixed time interval.
Chapter 15 Oscillatory Motion Part 2 Oscillations and Mechanical Waves Periodic motion is the repeating motion of an object in which it continues to return to a given position after a fixed time interval.
LANMARK UNIVERSITY OMU-ARAN, KWARA STATE DEPARTMENT OF MECHANICAL ENGINEERING COURSE: MECHANICS OF MACHINE (MCE 322). LECTURER: ENGR.
 LANMARK UNIVERSITY OMU-ARAN, KWARA STATE DEPARTMENT OF MECHANICAL ENGINEERING COURSE: MECHANICS OF MACHINE (MCE 322). LECTURER: ENGR. IBIKUNLE ROTIMI ADEDAYO SIMPLE HARMONIC MOTION. Introduction Consider
LANMARK UNIVERSITY OMU-ARAN, KWARA STATE DEPARTMENT OF MECHANICAL ENGINEERING COURSE: MECHANICS OF MACHINE (MCE 322). LECTURER: ENGR. IBIKUNLE ROTIMI ADEDAYO SIMPLE HARMONIC MOTION. Introduction Consider
Physics 8 Monday, December 4, 2017
 Physics 8 Monday, December 4, 2017 HW12 due Friday. Grace will do a review session Dec 12 or 13. When? I will do a review session: afternoon Dec 17? Evening Dec 18? Wednesday, I will hand out the practice
Physics 8 Monday, December 4, 2017 HW12 due Friday. Grace will do a review session Dec 12 or 13. When? I will do a review session: afternoon Dec 17? Evening Dec 18? Wednesday, I will hand out the practice
202 Index. failure, 26 field equation, 122 force, 1
 Index acceleration, 12, 161 admissible function, 155 admissible stress, 32 Airy's stress function, 122, 124 d'alembert's principle, 165, 167, 177 amplitude, 171 analogy, 76 anisotropic material, 20 aperiodic
Index acceleration, 12, 161 admissible function, 155 admissible stress, 32 Airy's stress function, 122, 124 d'alembert's principle, 165, 167, 177 amplitude, 171 analogy, 76 anisotropic material, 20 aperiodic
Engineering Science OUTCOME 2 - TUTORIAL 3 FREE VIBRATIONS
 Unit 2: Unit code: QCF Level: 4 Credit value: 5 Engineering Science L/60/404 OUTCOME 2 - TUTORIAL 3 FREE VIBRATIONS UNIT CONTENT OUTCOME 2 Be able to determine the behavioural characteristics of elements
Unit 2: Unit code: QCF Level: 4 Credit value: 5 Engineering Science L/60/404 OUTCOME 2 - TUTORIAL 3 FREE VIBRATIONS UNIT CONTENT OUTCOME 2 Be able to determine the behavioural characteristics of elements
ENG1001 Engineering Design 1
 ENG1001 Engineering Design 1 Structure & Loads Determine forces that act on structures causing it to deform, bend, and stretch Forces push/pull on objects Structures are loaded by: > Dead loads permanent
ENG1001 Engineering Design 1 Structure & Loads Determine forces that act on structures causing it to deform, bend, and stretch Forces push/pull on objects Structures are loaded by: > Dead loads permanent
Dynamic analysis of a reinforced concrete shear wall with strain rate effect. Synopsis. Introduction
 Dynamic analysis of a reinforced concrete shear wall with strain rate effect Synopsis A simplified analysis method for a reinforced concrete shear wall structure considering strain rate effects is presented.
Dynamic analysis of a reinforced concrete shear wall with strain rate effect Synopsis A simplified analysis method for a reinforced concrete shear wall structure considering strain rate effects is presented.
MATH 251 Week 6 Not collected, however you are encouraged to approach all problems to prepare for exam
 MATH 51 Week 6 Not collected, however you are encouraged to approach all problems to prepare for exam A collection of previous exams could be found at the coordinator s web: http://www.math.psu.edu/tseng/class/m51samples.html
MATH 51 Week 6 Not collected, however you are encouraged to approach all problems to prepare for exam A collection of previous exams could be found at the coordinator s web: http://www.math.psu.edu/tseng/class/m51samples.html
Measurement Techniques for Engineers. Motion and Vibration Measurement
 Measurement Techniques for Engineers Motion and Vibration Measurement Introduction Quantities that may need to be measured are velocity, acceleration and vibration amplitude Quantities useful in predicting
Measurement Techniques for Engineers Motion and Vibration Measurement Introduction Quantities that may need to be measured are velocity, acceleration and vibration amplitude Quantities useful in predicting
Chapter 14 Periodic Motion
 Chapter 14 Periodic Motion 1 Describing Oscillation First, we want to describe the kinematical and dynamical quantities associated with Simple Harmonic Motion (SHM), for example, x, v x, a x, and F x.
Chapter 14 Periodic Motion 1 Describing Oscillation First, we want to describe the kinematical and dynamical quantities associated with Simple Harmonic Motion (SHM), for example, x, v x, a x, and F x.
Structural Dynamics Lecture 4. Outline of Lecture 4. Multi-Degree-of-Freedom Systems. Formulation of Equations of Motions. Undamped Eigenvibrations.
 Outline of Multi-Degree-of-Freedom Systems Formulation of Equations of Motions. Newton s 2 nd Law Applied to Free Masses. D Alembert s Principle. Basic Equations of Motion for Forced Vibrations of Linear
Outline of Multi-Degree-of-Freedom Systems Formulation of Equations of Motions. Newton s 2 nd Law Applied to Free Masses. D Alembert s Principle. Basic Equations of Motion for Forced Vibrations of Linear
ANALYSIS OF HIGHRISE BUILDING STRUCTURE WITH SETBACK SUBJECT TO EARTHQUAKE GROUND MOTIONS
 ANALYSIS OF HIGHRISE BUILDING SRUCURE WIH SEBACK SUBJEC O EARHQUAKE GROUND MOIONS 157 Xiaojun ZHANG 1 And John L MEEK SUMMARY he earthquake response behaviour of unframed highrise buildings with setbacks
ANALYSIS OF HIGHRISE BUILDING SRUCURE WIH SEBACK SUBJEC O EARHQUAKE GROUND MOIONS 157 Xiaojun ZHANG 1 And John L MEEK SUMMARY he earthquake response behaviour of unframed highrise buildings with setbacks
Materials: engineering, science, processing and design, 2nd edition Copyright (c)2010 Michael Ashby, Hugh Shercliff, David Cebon.
 Modes of Loading (1) tension (a) (2) compression (b) (3) bending (c) (4) torsion (d) and combinations of them (e) Figure 4.2 1 Standard Solution to Elastic Problems Three common modes of loading: (a) tie
Modes of Loading (1) tension (a) (2) compression (b) (3) bending (c) (4) torsion (d) and combinations of them (e) Figure 4.2 1 Standard Solution to Elastic Problems Three common modes of loading: (a) tie
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Introduction to vibration
 Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Introduction to vibration Module 15 Lecture 38 Vibration of Rigid Bodies Part-1 Today,
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Introduction to vibration Module 15 Lecture 38 Vibration of Rigid Bodies Part-1 Today,
Lecture 9: Harmonic Loads (Con t)
 Lecture 9: Harmonic Loads (Con t) Reading materials: Sections 3.4, 3.5, 3.6 and 3.7 1. Resonance The dynamic load magnification factor (DLF) The peak dynamic magnification occurs near r=1 for small damping
Lecture 9: Harmonic Loads (Con t) Reading materials: Sections 3.4, 3.5, 3.6 and 3.7 1. Resonance The dynamic load magnification factor (DLF) The peak dynamic magnification occurs near r=1 for small damping
The student will experimentally determine the parameters to represent the behavior of a damped oscillatory system of one degree of freedom.
 Practice 3 NAME STUDENT ID LAB GROUP PROFESSOR INSTRUCTOR Vibrations of systems of one degree of freedom with damping QUIZ 10% PARTICIPATION & PRESENTATION 5% INVESTIGATION 10% DESIGN PROBLEM 15% CALCULATIONS
Practice 3 NAME STUDENT ID LAB GROUP PROFESSOR INSTRUCTOR Vibrations of systems of one degree of freedom with damping QUIZ 10% PARTICIPATION & PRESENTATION 5% INVESTIGATION 10% DESIGN PROBLEM 15% CALCULATIONS
JEPPIAAR ENGINEERING COLLEGE
 JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
JEPPIAAR ENGINEERING COLLEGE Jeppiaar Nagar, Rajiv Gandhi Salai 600 119 DEPARTMENT OFMECHANICAL ENGINEERING QUESTION BANK VI SEMESTER ME6603 FINITE ELEMENT ANALYSIS Regulation 013 SUBJECT YEAR /SEM: III
TOPIC E: OSCILLATIONS EXAMPLES SPRING Q1. Find general solutions for the following differential equations:
 TOPIC E: OSCILLATIONS EXAMPLES SPRING 2019 Mathematics of Oscillating Systems Q1. Find general solutions for the following differential equations: Undamped Free Vibration Q2. A 4 g mass is suspended by
TOPIC E: OSCILLATIONS EXAMPLES SPRING 2019 Mathematics of Oscillating Systems Q1. Find general solutions for the following differential equations: Undamped Free Vibration Q2. A 4 g mass is suspended by
MECHANICS OF STRUCTURES SCI 1105 COURSE MATERIAL UNIT - I
 MECHANICS OF STRUCTURES SCI 1105 COURSE MATERIAL UNIT - I Engineering Mechanics Branch of science which deals with the behavior of a body with the state of rest or motion, subjected to the action of forces.
MECHANICS OF STRUCTURES SCI 1105 COURSE MATERIAL UNIT - I Engineering Mechanics Branch of science which deals with the behavior of a body with the state of rest or motion, subjected to the action of forces.
Chapter 5 Design. D. J. Inman 1/51 Mechanical Engineering at Virginia Tech
 Chapter 5 Design Acceptable vibration levels (ISO) Vibration isolation Vibration absorbers Effects of damping in absorbers Optimization Viscoelastic damping treatments Critical Speeds Design for vibration
Chapter 5 Design Acceptable vibration levels (ISO) Vibration isolation Vibration absorbers Effects of damping in absorbers Optimization Viscoelastic damping treatments Critical Speeds Design for vibration
FLEXIBILITY METHOD FOR INDETERMINATE FRAMES
 UNIT - I FLEXIBILITY METHOD FOR INDETERMINATE FRAMES 1. What is meant by indeterminate structures? Structures that do not satisfy the conditions of equilibrium are called indeterminate structure. These
UNIT - I FLEXIBILITY METHOD FOR INDETERMINATE FRAMES 1. What is meant by indeterminate structures? Structures that do not satisfy the conditions of equilibrium are called indeterminate structure. These
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License.
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 015 14. Oscillations Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License This wor
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 015 14. Oscillations Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License This wor
Final Exam. June 10, 2008, 1:00pm
 PHYSICS 101: Fundamentals of Physics Final Exam Final Exam Name TA/ Section # June 10, 2008, 1:00pm Recitation Time You have 2 hour to complete the exam. Please answer all questions clearly and completely,
PHYSICS 101: Fundamentals of Physics Final Exam Final Exam Name TA/ Section # June 10, 2008, 1:00pm Recitation Time You have 2 hour to complete the exam. Please answer all questions clearly and completely,
Study of coupling between bending and torsional vibration of cracked rotor system supported by radial active magnetic bearings
 Applied and Computational Mechanics 1 (2007) 427-436 Study of coupling between bending and torsional vibration of cracked rotor system supported by radial active magnetic bearings P. Ferfecki a, * a Center
Applied and Computational Mechanics 1 (2007) 427-436 Study of coupling between bending and torsional vibration of cracked rotor system supported by radial active magnetic bearings P. Ferfecki a, * a Center
Rutgers University Department of Physics & Astronomy. 01:750:271 Honors Physics I Fall Lecture 19. Home Page. Title Page. Page 1 of 36.
 Rutgers University Department of Physics & Astronomy 01:750:271 Honors Physics I Fall 2015 Lecture 19 Page 1 of 36 12. Equilibrium and Elasticity How do objects behave under applied external forces? Under
Rutgers University Department of Physics & Astronomy 01:750:271 Honors Physics I Fall 2015 Lecture 19 Page 1 of 36 12. Equilibrium and Elasticity How do objects behave under applied external forces? Under
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CHAPTER 3 VIBRATION THEORY. Single Degree of Freedom Systems (SDOF) Stiffness, k Member Stiffness (Member Rigidity).
 HPTER 3 VIRTION THEORY Single egree of Freedom Systems (SOF).. 3- Stiffness, k. 3- Member Stiffness (Member Rigidity). 3-3 Natural Period.. 3-3 Natural Frequency... 3-5 ngular Natural Frequency 3-5 Structural
HPTER 3 VIRTION THEORY Single egree of Freedom Systems (SOF).. 3- Stiffness, k. 3- Member Stiffness (Member Rigidity). 3-3 Natural Period.. 3-3 Natural Frequency... 3-5 ngular Natural Frequency 3-5 Structural
Chapter 7 Vibration Measurement and Applications
 Chapter 7 Vibration Measurement and Applications Dr. Tan Wei Hong School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) Pauh Putra Campus ENT 346 Vibration Mechanics Chapter Outline 7.1
Chapter 7 Vibration Measurement and Applications Dr. Tan Wei Hong School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) Pauh Putra Campus ENT 346 Vibration Mechanics Chapter Outline 7.1
Springs: Part I Modeling the Action The Mass/Spring System
 17 Springs: Part I Second-order differential equations arise in a number of applications We saw one involving a falling object at the beginning of this text (the falling frozen duck example in section
17 Springs: Part I Second-order differential equations arise in a number of applications We saw one involving a falling object at the beginning of this text (the falling frozen duck example in section
Seismic design of bridges
 NAIONAL ECHNICAL UNIVERSIY OF AHENS LABORAORY FOR EARHQUAKE ENGINEERING Seismic design of bridges Lecture 4 Ioannis N. Psycharis Seismic isolation of bridges I. N. Psycharis Seismic design of bridges 2
NAIONAL ECHNICAL UNIVERSIY OF AHENS LABORAORY FOR EARHQUAKE ENGINEERING Seismic design of bridges Lecture 4 Ioannis N. Psycharis Seismic isolation of bridges I. N. Psycharis Seismic design of bridges 2
2007 Problem Topic Comment 1 Kinematics Position-time equation Kinematics 7 2 Kinematics Velocity-time graph Dynamics 6 3 Kinematics Average velocity
 2007 Problem Topic Comment 1 Kinematics Position-time equation Kinematics 7 2 Kinematics Velocity-time graph Dynamics 6 3 Kinematics Average velocity Energy 7 4 Kinematics Free fall Collisions 3 5 Dynamics
2007 Problem Topic Comment 1 Kinematics Position-time equation Kinematics 7 2 Kinematics Velocity-time graph Dynamics 6 3 Kinematics Average velocity Energy 7 4 Kinematics Free fall Collisions 3 5 Dynamics
Translational Motion Rotational Motion Equations Sheet
 PHYSICS 01 Translational Motion Rotational Motion Equations Sheet LINEAR ANGULAR Time t t Displacement x; (x = rθ) θ Velocity v = Δx/Δt; (v = rω) ω = Δθ/Δt Acceleration a = Δv/Δt; (a = rα) α = Δω/Δt (
PHYSICS 01 Translational Motion Rotational Motion Equations Sheet LINEAR ANGULAR Time t t Displacement x; (x = rθ) θ Velocity v = Δx/Δt; (v = rω) ω = Δθ/Δt Acceleration a = Δv/Δt; (a = rα) α = Δω/Δt (
Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras
 Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras Module - 01 Lecture - 09 Characteristics of Single Degree - of -
Dynamics of Ocean Structures Prof. Dr. Srinivasan Chandrasekaran Department of Ocean Engineering Indian Institute of Technology, Madras Module - 01 Lecture - 09 Characteristics of Single Degree - of -
Study Sheet for Exam #3
 Physics 121 Spring 2003 Dr. Dragt Study Sheet for Exam #3 14. Physics knowledge, like all subjects having some substance, is cumulative. You are still responsible for all material on the Study Sheets for
Physics 121 Spring 2003 Dr. Dragt Study Sheet for Exam #3 14. Physics knowledge, like all subjects having some substance, is cumulative. You are still responsible for all material on the Study Sheets for
Computational Simulation of Dynamic Response of Vehicle Tatra T815 and the Ground
 IOP Conference Series: Earth and Environmental Science PAPER OPEN ACCESS Computational Simulation of Dynamic Response of Vehicle Tatra T815 and the Ground To cite this article: Jozef Vlek and Veronika
IOP Conference Series: Earth and Environmental Science PAPER OPEN ACCESS Computational Simulation of Dynamic Response of Vehicle Tatra T815 and the Ground To cite this article: Jozef Vlek and Veronika
Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee
 Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee Module - 1 Review of Basics of Mechanical Vibrations Lecture - 2 Introduction
Vibration Control Prof. Dr. S. P. Harsha Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee Module - 1 Review of Basics of Mechanical Vibrations Lecture - 2 Introduction
Problem 1: Find the Equation of Motion from the static equilibrium position for the following systems: 1) Assumptions
 Problem 1: Find the Equation of Motion from the static equilibrium position for the following systems: 1) Assumptions k 2 Wheels roll without friction k 1 Motion will not cause block to hit the supports
Problem 1: Find the Equation of Motion from the static equilibrium position for the following systems: 1) Assumptions k 2 Wheels roll without friction k 1 Motion will not cause block to hit the supports
Design of Reinforced Concrete Structures (II)
 Design of Reinforced Concrete Structures (II) Discussion Eng. Mohammed R. Kuheil Review The thickness of one-way ribbed slabs After finding the value of total load (Dead and live loads), the elements are
Design of Reinforced Concrete Structures (II) Discussion Eng. Mohammed R. Kuheil Review The thickness of one-way ribbed slabs After finding the value of total load (Dead and live loads), the elements are
1859. Forced transverse vibration analysis of a Rayleigh double-beam system with a Pasternak middle layer subjected to compressive axial load
 1859. Forced transverse vibration analysis of a Rayleigh double-beam system with a Pasternak middle layer subjected to compressive axial load Nader Mohammadi 1, Mehrdad Nasirshoaibi 2 Department of Mechanical
1859. Forced transverse vibration analysis of a Rayleigh double-beam system with a Pasternak middle layer subjected to compressive axial load Nader Mohammadi 1, Mehrdad Nasirshoaibi 2 Department of Mechanical
Free Vibration of Single-Degree-of-Freedom (SDOF) Systems
 Free Vibration of Single-Degree-of-Freedom (SDOF) Systems Procedure in solving structural dynamics problems 1. Abstraction/modeling Idealize the actual structure to a simplified version, depending on the
Free Vibration of Single-Degree-of-Freedom (SDOF) Systems Procedure in solving structural dynamics problems 1. Abstraction/modeling Idealize the actual structure to a simplified version, depending on the
Effects of Damping Ratio of Restoring force Device on Response of a Structure Resting on Sliding Supports with Restoring Force Device
 Effects of Damping Ratio of Restoring force Device on Response of a Structure Resting on Sliding Supports with Restoring Force Device A. Krishnamoorthy Professor, Department of Civil Engineering Manipal
Effects of Damping Ratio of Restoring force Device on Response of a Structure Resting on Sliding Supports with Restoring Force Device A. Krishnamoorthy Professor, Department of Civil Engineering Manipal
Impact. m k. Natural Period of Vibration τ. Static load Gray area Impact load t > 3 τ. Absorbing energy. Carrying loads
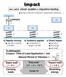 Impact also called shock, sudden or impulsive loading driving a nail with a hammer, automobile collisions. dashpot a) Rapidly moving vehicles crossing a bridge To distinguish: b) Suddenly applied c) Direct
Impact also called shock, sudden or impulsive loading driving a nail with a hammer, automobile collisions. dashpot a) Rapidly moving vehicles crossing a bridge To distinguish: b) Suddenly applied c) Direct
Stochastic Dynamics of SDOF Systems (cont.).
 Outline of Stochastic Dynamics of SDOF Systems (cont.). Weakly Stationary Response Processes. Equivalent White Noise Approximations. Gaussian Response Processes as Conditional Normal Distributions. Stochastic
Outline of Stochastic Dynamics of SDOF Systems (cont.). Weakly Stationary Response Processes. Equivalent White Noise Approximations. Gaussian Response Processes as Conditional Normal Distributions. Stochastic
CAEFEM v9.5 Information
 CAEFEM v9.5 Information Concurrent Analysis Corporation, 50 Via Ricardo, Thousand Oaks, CA 91320 USA Tel. (805) 375 1060, Fax (805) 375 1061 email: info@caefem.com or support@caefem.com Web: http://www.caefem.com
CAEFEM v9.5 Information Concurrent Analysis Corporation, 50 Via Ricardo, Thousand Oaks, CA 91320 USA Tel. (805) 375 1060, Fax (805) 375 1061 email: info@caefem.com or support@caefem.com Web: http://www.caefem.com
Dynamic Loads CE 543. Examples. Harmonic Loads
 CE 543 Structural Dynamics Introduction Dynamic Loads Dynamic loads are time-varying loads. (But time-varying loads may not require dynamic analysis.) Dynamics loads can be grouped in one of the following
CE 543 Structural Dynamics Introduction Dynamic Loads Dynamic loads are time-varying loads. (But time-varying loads may not require dynamic analysis.) Dynamics loads can be grouped in one of the following
