Chapter I Vector Analysis
|
|
|
- Oswin Griffith
- 5 years ago
- Views:
Transcription
1 . Chpte I Vecto nlss
2 . Vecto lgeb j It s well-nown tht n vecto cn be wtten s Vectos obe the followng lgebc ules: scl s ) ( j v v cos ) ( e Commuttv ) ( ssoctve C C ) ( ) ( v j ) ( ) ( ) ( ) (
3 (v) he lw of cosnes C Let C C C cos C commuttve not () ple Poduct C C C ) ( C cos volume of pllelepped ule cb bc ) ( C C C (v) j
4 Poston, Dsplcement, & Septon Vectos he poston vecto of pont n 3-D s epessed n Ctesn coodntes s j P(,,) he nfntesml dsplcement vecto s dl d dj d souce pont s the pont whee n e. chge s locted. feld pont s the pont t whch ou e clcultng electc o mgnetc fled. Souce pont he septon vecto fom the souce pont to the feld pont s defned s d feld pont
5 Dffeentl Clculus df d df tht s f s chnged b d, the functon chnges b df wth d Odn Devtves It s nown tht df d popotonlt fcto. s the In othe wods we s tht the devtve s smll f the functon ves slowl wth nd lge f the functon ves pdl wth. df Geometcll we s tht s the slope of the gph f() vs.. d Gdent (Dectonl Devtve) Let be scl functon of 3-vbles,.e., (,, ) d d d d () hs tells us how ves s we go smll dstnce (d, d, d) w fom the pont (,, ). Let us ewte Eq. () s
6 d o d dl wth j j d d j d () s clled the gdent of the functon. he smbol j s clled the del opeto. Le n vecto the gdent hs mgntude nd decton. Now Eq. (3) cn be wtten s d dl cos Fo fed dl, d s mmum when, tht s d s mmum when we move n the sme decton s. (3) (4) (5)
7 he gdent ponts n the decton of mmum ncese of the functon. he mgntude gves the slope long ths mml decton. s dected noml to the level sufce of though the pont beng consdeed,.e., s pependcul to the sufce =constnt. Emple Fnd the gdent of the poston vecto. Souton In Ctesn coodntes the mgntude of the poston vecto s j j hs mens tht the dstnce fom the ogn nceses most pdl n the dl decton.
8 It s lso defned s the net te of flow pe unt volume,.e., denst the souce Emple Fnd the dvegence of the vectos Souton: Snce nd,, j Dvegence he dvegence of vecto s defned s j j he dvegence s mesue of how much the vecto speds out (dvege) fom the pont n queston. 3
9 he Cul he cul of vecto s defned s j he cul of vecto s mesue of how much the vecto cul ound the pont n queston. Emple Fnd the cul of the vectos Souton: j j nd j j
10 j j he Del Opeto Opetons ) ( ) ( ) ( v ) (
11 Integl Clculus Lne Integl he lne ntegl s epessed s b dl whee s vecto functon nd s n nfntesml dsplcement vecto long pth fom pont to pont b. If the pth foms closed loop, ccle s put on the ntegl sgn,.e., dl If the lne ntegl s ndependent on the pth followed, the vecto consevtve dl s clled
12 Emple Let j fnd b dl fom pont =(,,) to pont b=(,,) long the sold pth (pth ) nd long the dshed pth (pth ). Souton: dl d dj d b we hve fo the fst pth b b dl d b d d d d c c b c d d Now long the pth c =, nd long the pth cb =. hs leds to b dl d 4 d
13 Fo the second pth we hve = nd ths gves b dl d d d d d d Note tht the two esults e dffeent,.e., the vecto s not consevtve. Sufce Integl S ds he sufce ntegl s epessed s ds whee s vecto functon nd s n nfntesml element of e. gn f the sufce s closed we put ccle on the ntegl sgn, tht s ds ds he decton of s pependcul to the sufce n dected outwd fo closed sufces nd bt fo open sufces.
14 Emple Let ds j 3 Fnd S ove the 5-sdes of cube of sde, s shown n the fgue (ecludng the bottom). Souton: Fo the top sde ds top dd dd ds 3 dd top ut on the top sde = ds d 4 d top Fo the ght sde ds ght ddj ds dd d d ght ds left ddj ds dd left Fo the font sde ds dd ds dd font ut on the top sde = ds 4 d 6 d font Fo the bc sde ds dd ds dd bc ut on the top sde = ds bc dd Fo the left sde d d dd
15 Volume Integl he volume ntegl s epessed s V d whee s vecto functon nd d s n nfntesml element of volume. he Fundmentl heoem of Clculus bdf d d f ( b) f ( ) he Fundmentl heoem of Gdent whee =(,,) be scl functon of thee vbles, then b dl ( b) ( ) Snce the ght sde of the lst equton depends onl on the end ponts nd not on the pth followed we conclude tht
16 b Cooll : dl s ndependent on the pth followed fom to b. Cooll dl Emple: Let Chec the fundmentl theoem of gdent b tng two pths fom pont (,,) to pont b (,,). Souton: he fst pth s -steps: step () long the -s nd then up step (). Now dl d dj d nd j b b Fo the st pth dl d dj () () () () d d b () dl u fo step () =, nd fo step () = Fo the nd pth b dl d d d d d d 3 d ( ) 4 4
17 he Fundmentl heoem of Dvegence v d S ds It sttes tht the ntegl of dvegence ove volume s equl to the vlue of the functon t the bound. In nothe wold, the dvegence theoem sttes tht the outwd flu of vecto feld though sufce s equl to the tple ntegl of the dvegence on the egon nsde the sufce. Emple: Chec the dvegence theoem usng the vecto j Ove the unt cube stuted t the ogn. Soluton: v d ddd
18 o fnd S the fces: ds ds top we hve to clculte the ntegl ove ll dd dd ut fo the top sde =, so we hve top ds ds d bottom d dd ut fo the top sde =, so we hve ds ght ds dd bottom dd dd ut fo the ght sde =, so we hve ds d d 3 4 ght dd
19 ds dd left ut fo the left sde =, so we hve ds d 3 ds font ds bc S ds Stoes' heoem S dd dd ds left dl d d d 3 d Snce the bound lne fo n closed sufce shn down to pont, then S ds 3
20 Emple: Chec the Stoes' theoem usng the vecto 3 j 4 Ove the sque sufce shown. Soluton: 4 S ds dd ds 4 dd ut on the sufce =, so we hve S ds 4 dd 3 4
21 dl bottom dj ght d top dj d left long the bottom sde ==, so we hve dj bottom 3 d long the top sde =, = so we hve dj 3 d top long the ght sde =, = so we hve d 4 d 3 4 ght long the left sde =, = so we hve d 4 d left dl
22 Integton b Pts d d It s nown tht fg f dg d b Integtng both sdes we get fgd f d g d d d g df d Usng the fundmentl theoem of clculus we get b f dg d d fg b b g df d d Emple: Evlute the ntegl e d Soluton: It s nown tht e d e d e d e b d d dg d b df d
23 Sphecl coodntes (,,) Cuvlne Coodntes : s the dstnce fom the ogn (fom to ) : the pol ngle, s the ngle between nd the -s (fom to ) : the muthl ngle s the ngle between the pojecton of to the - plne nd the -s (fom to ) he elton between the Ctesn coodntes nd the sphecl coodntes cn be wtten s sn cos sn sn sncos he unt vectos ssocted wth the sphecl coodntes e elted to the coespondng unt vectos n the Ctesn coodntes s sn cos sn snj cos cos cos cos snj sn sn cosj
24 he nfntesml dsplcement vecto n sphecl coodntes s epessed s dl d d sn d he volume element s epessed s d dl dl dl sn ddd Fo the sufce elements we hve ds dl dl dd s constnt ds sn dl dl dd s constnt ds3 dl dl sn dd s constnt o fnd the volume of sphee of dus R we hve V d R sn d d d 4 3 R 3
25 o fnd the gdent n sphecl coodntes let = (,, ) so ) ( sn d d d dl d () d d d d Equtng the bove two equtons we get, sn sn o sn Smll, one cn fnd the dvegence nd the cul n sphecl coodntes
26 sn sn sn sn sn sn sn sn sn he Lplcn s defned s
27 Clndcl coodntes (,, ) : s the dstnce fom the -s (fom to ) : the muthl ngle s the ngle between nd the -s (fom to ) : the dstnce fom the - plne (fom - to ) he elton between the Ctesn coodntes nd the clndcl coodntes cn be wtten s cos sn he unt vectos ssocted wth the clndcl coodntes e elted to the coespondng unt vectos n the Ctesn coodntes s cos sn j sn cos j
28 he nfntesml dsplcement vecto n clndcl coodntes s epessed s dl d d d he volume element s epessed s d dl dl dl ddd Fo the sufce elements we hve ds dl dl d d ds dl dl dd ds dl dl d d 3 s constnt s constnt s constnt
29 he Del he Dvegence he Cul sn he Lplcn
30 he Dc Delt Functon Consde the functon Now sn nd d d ds S ut fom the dvegence theoem we now tht 4 sn d d S v ds d He we hve contdcton. he poblem s the pont =, whee the vecto blows up. He we hve contdcton. he poblem s the pont =, whee the vecto blows up. So we wte 3 4
31 Whee () s clled the Dc delt functon wth the followng popetes: 3 F d d F Usng theses popetes we hve v d 4 d 4 v 3 s epected
Chapter I Matrices, Vectors, & Vector Calculus 1-1, 1-9, 1-10, 1-11, 1-17, 1-18, 1-25, 1-27, 1-36, 1-37, 1-41.
 Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
Chapte I Matces, Vectos, & Vecto Calculus -, -9, -0, -, -7, -8, -5, -7, -36, -37, -4. . Concept of a Scala Consde the aa of patcles shown n the fgue. he mass of the patcle at (,) can be epessed as. M (,
PHYS 2421 Fields and Waves
 PHYS 242 Felds nd Wves Instucto: Joge A. López Offce: PSCI 29 A, Phone: 747-7528 Textook: Unvesty Physcs e, Young nd Feedmn 23. Electc potentl enegy 23.2 Electc potentl 23.3 Clcultng electc potentl 23.4
PHYS 242 Felds nd Wves Instucto: Joge A. López Offce: PSCI 29 A, Phone: 747-7528 Textook: Unvesty Physcs e, Young nd Feedmn 23. Electc potentl enegy 23.2 Electc potentl 23.3 Clcultng electc potentl 23.4
EN2210: Continuum Mechanics. Homework 4: Balance laws, work and energy, virtual work Due 12:00 noon Friday February 4th
 EN: Contnuum Mechncs Homewok 4: Blnce lws, wok nd enegy, vtul wok Due : noon Fdy Feuy 4th chool of Engneeng Bown Unvesty. how tht the locl mss lnce equton t cn e e-wtten n sptl fom s xconst v y v t yconst
EN: Contnuum Mechncs Homewok 4: Blnce lws, wok nd enegy, vtul wok Due : noon Fdy Feuy 4th chool of Engneeng Bown Unvesty. how tht the locl mss lnce equton t cn e e-wtten n sptl fom s xconst v y v t yconst
MATHEMATICS II PUC VECTOR ALGEBRA QUESTIONS & ANSWER
 MATHEMATICS II PUC VECTOR ALGEBRA QUESTIONS & ANSWER I One M Queston Fnd the unt veto n the deton of Let ˆ ˆ 9 Let & If Ae the vetos & equl? But vetos e not equl sne the oespondng omponents e dstnt e detons
MATHEMATICS II PUC VECTOR ALGEBRA QUESTIONS & ANSWER I One M Queston Fnd the unt veto n the deton of Let ˆ ˆ 9 Let & If Ae the vetos & equl? But vetos e not equl sne the oespondng omponents e dstnt e detons
6.6 The Marquardt Algorithm
 6.6 The Mqudt Algothm lmttons of the gdent nd Tylo expnson methods ecstng the Tylo expnson n tems of ch-sque devtves ecstng the gdent sech nto n tetve mtx fomlsm Mqudt's lgothm utomtclly combnes the gdent
6.6 The Mqudt Algothm lmttons of the gdent nd Tylo expnson methods ecstng the Tylo expnson n tems of ch-sque devtves ecstng the gdent sech nto n tetve mtx fomlsm Mqudt's lgothm utomtclly combnes the gdent
Uniform Circular Motion
 Unfom Ccul Moton Unfom ccul Moton An object mong t constnt sped n ccle The ntude of the eloct emns constnt The decton of the eloct chnges contnuousl!!!! Snce cceleton s te of chnge of eloct:!! Δ Δt The
Unfom Ccul Moton Unfom ccul Moton An object mong t constnt sped n ccle The ntude of the eloct emns constnt The decton of the eloct chnges contnuousl!!!! Snce cceleton s te of chnge of eloct:!! Δ Δt The
Lecture 5 Single factor design and analysis
 Lectue 5 Sngle fcto desgn nd nlss Completel ndomzed desgn (CRD Completel ndomzed desgn In the desgn of expements, completel ndomzed desgns e fo studng the effects of one pm fcto wthout the need to tke
Lectue 5 Sngle fcto desgn nd nlss Completel ndomzed desgn (CRD Completel ndomzed desgn In the desgn of expements, completel ndomzed desgns e fo studng the effects of one pm fcto wthout the need to tke
Electric Potential. and Equipotentials
 Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
Rigid Body Dynamics. CSE169: Computer Animation Instructor: Steve Rotenberg UCSD, Winter 2018
 Rg Bo Dnmcs CSE169: Compute Anmton nstucto: Steve Roteneg UCSD, Wnte 2018 Coss Pouct k j Popetes of the Coss Pouct Coss Pouct c c c 0 0 0 c Coss Pouct c c c c c c 0 0 0 0 0 0 Coss Pouct 0 0 0 ˆ ˆ 0 0 0
Rg Bo Dnmcs CSE169: Compute Anmton nstucto: Steve Roteneg UCSD, Wnte 2018 Coss Pouct k j Popetes of the Coss Pouct Coss Pouct c c c 0 0 0 c Coss Pouct c c c c c c 0 0 0 0 0 0 Coss Pouct 0 0 0 ˆ ˆ 0 0 0
U>, and is negative. Electric Potential Energy
 Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
Collection of Formulas
 Collection of Fomuls Electomgnetic Fields EITF8 Deptment of Electicl nd Infomtion Technology Lund Univesity, Sweden August 8 / ELECTOSTATICS field point '' ' Oigin ' Souce point Coulomb s Lw The foce F
Collection of Fomuls Electomgnetic Fields EITF8 Deptment of Electicl nd Infomtion Technology Lund Univesity, Sweden August 8 / ELECTOSTATICS field point '' ' Oigin ' Souce point Coulomb s Lw The foce F
Electric Field F E. q Q R Q. ˆ 4 r r - - Electric field intensity depends on the medium! origin
 1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
The Shape of the Pair Distribution Function.
 The Shpe of the P Dstbuton Functon. Vlentn Levshov nd.f. Thope Deptment of Phscs & stonom nd Cente fo Fundmentl tels Resech chgn Stte Unvest Sgnfcnt pogess n hgh-esoluton dffcton epements on powde smples
The Shpe of the P Dstbuton Functon. Vlentn Levshov nd.f. Thope Deptment of Phscs & stonom nd Cente fo Fundmentl tels Resech chgn Stte Unvest Sgnfcnt pogess n hgh-esoluton dffcton epements on powde smples
General Physics II. number of field lines/area. for whole surface: for continuous surface is a whole surface
 Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
Integral Vector Operations and Related Theorems Applications in Mechanics and E&M
 Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
Dola Bagayoko (0) Integal Vecto Opeatons and elated Theoems Applcatons n Mechancs and E&M Ι Basc Defnton Please efe to you calculus evewed below. Ι, ΙΙ, andιιι notes and textbooks fo detals on the concepts
Physics 11b Lecture #11
 Physics 11b Lectue #11 Mgnetic Fields Souces of the Mgnetic Field S&J Chpte 9, 3 Wht We Did Lst Time Mgnetic fields e simil to electic fields Only diffeence: no single mgnetic pole Loentz foce Moving chge
Physics 11b Lectue #11 Mgnetic Fields Souces of the Mgnetic Field S&J Chpte 9, 3 Wht We Did Lst Time Mgnetic fields e simil to electic fields Only diffeence: no single mgnetic pole Loentz foce Moving chge
DEPARTMENT OF CIVIL AND ENVIRONMENTAL ENGINEERING FLUID MECHANICS III Solutions to Problem Sheet 3
 DEPATMENT OF CIVIL AND ENVIONMENTAL ENGINEEING FLID MECHANICS III Solutions to Poblem Sheet 3 1. An tmospheic vote is moelle s combintion of viscous coe otting s soli boy with ngul velocity Ω n n iottionl
DEPATMENT OF CIVIL AND ENVIONMENTAL ENGINEEING FLID MECHANICS III Solutions to Poblem Sheet 3 1. An tmospheic vote is moelle s combintion of viscous coe otting s soli boy with ngul velocity Ω n n iottionl
This immediately suggests an inverse-square law for a "piece" of current along the line.
 Electomgnetic Theoy (EMT) Pof Rui, UNC Asheville, doctophys on YouTube Chpte T Notes The iot-svt Lw T nvese-sque Lw fo Mgnetism Compe the mgnitude of the electic field t distnce wy fom n infinite line
Electomgnetic Theoy (EMT) Pof Rui, UNC Asheville, doctophys on YouTube Chpte T Notes The iot-svt Lw T nvese-sque Lw fo Mgnetism Compe the mgnitude of the electic field t distnce wy fom n infinite line
Chapter 28 Sources of Magnetic Field
 Chpte 8 Souces of Mgnetic Field - Mgnetic Field of Moving Chge - Mgnetic Field of Cuent Element - Mgnetic Field of Stight Cuent-Cying Conducto - Foce Between Pllel Conductos - Mgnetic Field of Cicul Cuent
Chpte 8 Souces of Mgnetic Field - Mgnetic Field of Moving Chge - Mgnetic Field of Cuent Element - Mgnetic Field of Stight Cuent-Cying Conducto - Foce Between Pllel Conductos - Mgnetic Field of Cicul Cuent
Homework 3 MAE 118C Problems 2, 5, 7, 10, 14, 15, 18, 23, 30, 31 from Chapter 5, Lamarsh & Baratta. The flux for a point source is:
 . Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
. Homewok 3 MAE 8C Poblems, 5, 7, 0, 4, 5, 8, 3, 30, 3 fom Chpte 5, msh & Btt Point souces emit nuetons/sec t points,,, n 3 fin the flux cuent hlf wy between one sie of the tingle (blck ot). The flux fo
24-2: Electric Potential Energy. 24-1: What is physics
 D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
D. Iyad SAADEDDIN Chapte 4: Electc Potental Electc potental Enegy and Electc potental Calculatng the E-potental fom E-feld fo dffeent chage dstbutons Calculatng the E-feld fom E-potental Potental of a
Physics 11b Lecture #2. Electric Field Electric Flux Gauss s Law
 Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
Physcs 11b Lectue # Electc Feld Electc Flux Gauss s Law What We Dd Last Tme Electc chage = How object esponds to electc foce Comes n postve and negatve flavos Conseved Electc foce Coulomb s Law F Same
CHAPTER 3 DIPOLE AND QUADRUPOLE MOMENTS
 CHAPTE DIPOLE AND QUADUPOLE MOMENTS. Intoducton τ p E FIGUE III. Consde body whch s on the whole electclly neutl, but n whch thee s septon of chge such tht thee s moe postve chge t one end nd moe negtve
CHAPTE DIPOLE AND QUADUPOLE MOMENTS. Intoducton τ p E FIGUE III. Consde body whch s on the whole electclly neutl, but n whch thee s septon of chge such tht thee s moe postve chge t one end nd moe negtve
ELECTRO - MAGNETIC INDUCTION
 NTRODUCTON LCTRO - MAGNTC NDUCTON Whenee mgnetic flu linked with cicuit chnges, n e.m.f. is induced in the cicuit. f the cicuit is closed, cuent is lso induced in it. The e.m.f. nd cuent poduced lsts s
NTRODUCTON LCTRO - MAGNTC NDUCTON Whenee mgnetic flu linked with cicuit chnges, n e.m.f. is induced in the cicuit. f the cicuit is closed, cuent is lso induced in it. The e.m.f. nd cuent poduced lsts s
Neural Network Introduction. Hung-yi Lee
 Neu Neto Intoducton Hung- ee Reve: Supevsed enng Mode Hpothess Functon Set f, f : : (e) Tnng: Pc the est Functon f * Best Functon f * Testng: f Tnng Dt : functon nput : functon output, ˆ,, ˆ, Neu Neto
Neu Neto Intoducton Hung- ee Reve: Supevsed enng Mode Hpothess Functon Set f, f : : (e) Tnng: Pc the est Functon f * Best Functon f * Testng: f Tnng Dt : functon nput : functon output, ˆ,, ˆ, Neu Neto
Class Summary. be functions and f( D) , we define the composition of f with g, denoted g f by
 Clss Summy.5 Eponentil Functions.6 Invese Functions nd Logithms A function f is ule tht ssigns to ech element D ectly one element, clled f( ), in. Fo emple : function not function Given functions f, g:
Clss Summy.5 Eponentil Functions.6 Invese Functions nd Logithms A function f is ule tht ssigns to ech element D ectly one element, clled f( ), in. Fo emple : function not function Given functions f, g:
Topics for Review for Final Exam in Calculus 16A
 Topics fo Review fo Finl Em in Clculus 16A Instucto: Zvezdelin Stnkov Contents 1. Definitions 1. Theoems nd Poblem Solving Techniques 1 3. Eecises to Review 5 4. Chet Sheet 5 1. Definitions Undestnd the
Topics fo Review fo Finl Em in Clculus 16A Instucto: Zvezdelin Stnkov Contents 1. Definitions 1. Theoems nd Poblem Solving Techniques 1 3. Eecises to Review 5 4. Chet Sheet 5 1. Definitions Undestnd the
Math 4318 : Real Analysis II Mid-Term Exam 1 14 February 2013
 Mth 4318 : Rel Anlysis II Mid-Tem Exm 1 14 Febuy 2013 Nme: Definitions: Tue/Flse: Poofs: 1. 2. 3. 4. 5. 6. Totl: Definitions nd Sttements of Theoems 1. (2 points) Fo function f(x) defined on (, b) nd fo
Mth 4318 : Rel Anlysis II Mid-Tem Exm 1 14 Febuy 2013 Nme: Definitions: Tue/Flse: Poofs: 1. 2. 3. 4. 5. 6. Totl: Definitions nd Sttements of Theoems 1. (2 points) Fo function f(x) defined on (, b) nd fo
Physics 604 Problem Set 1 Due Sept 16, 2010
 Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Angular Momentum in Spherical Symmetry
 Angu Moentu n Sphec Set Angu Moentu n Sphec Set 6 Quntu Mechncs Pof. Y. F. Chen Angu Moentu n Sphec Set The concept of ngu oentu ps cuc oe n the theedenson 3D Schödnge we equton. The ethod of septon w
Angu Moentu n Sphec Set Angu Moentu n Sphec Set 6 Quntu Mechncs Pof. Y. F. Chen Angu Moentu n Sphec Set The concept of ngu oentu ps cuc oe n the theedenson 3D Schödnge we equton. The ethod of septon w
1 Using Integration to Find Arc Lengths and Surface Areas
 Novembe 9, 8 MAT86 Week Justin Ko Using Integtion to Find Ac Lengths nd Sufce Aes. Ac Length Fomul: If f () is continuous on [, b], then the c length of the cuve = f() on the intevl [, b] is given b s
Novembe 9, 8 MAT86 Week Justin Ko Using Integtion to Find Ac Lengths nd Sufce Aes. Ac Length Fomul: If f () is continuous on [, b], then the c length of the cuve = f() on the intevl [, b] is given b s
CSJM University Class: B.Sc.-II Sub:Physics Paper-II Title: Electromagnetics Unit-1: Electrostatics Lecture: 1 to 4
 CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
CSJM Unvesty Class: B.Sc.-II Sub:Physcs Pape-II Ttle: Electomagnetcs Unt-: Electostatcs Lectue: to 4 Electostatcs: It deals the study of behavo of statc o statonay Chages. Electc Chage: It s popety by
DCDM BUSINESS SCHOOL NUMERICAL METHODS (COS 233-8) Solutions to Assignment 3. x f(x)
 DCDM BUSINESS SCHOOL NUMEICAL METHODS (COS -8) Solutons to Assgnment Queston Consder the followng dt: 5 f() 8 7 5 () Set up dfference tble through fourth dfferences. (b) Wht s the mnmum degree tht n nterpoltng
DCDM BUSINESS SCHOOL NUMEICAL METHODS (COS -8) Solutons to Assgnment Queston Consder the followng dt: 5 f() 8 7 5 () Set up dfference tble through fourth dfferences. (b) Wht s the mnmum degree tht n nterpoltng
Engineering Mechanics. Force resultants, Torques, Scalar Products, Equivalent Force systems
 Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
Engneeng echancs oce esultants, Toques, Scala oducts, Equvalent oce sstems Tata cgaw-hll Companes, 008 Resultant of Two oces foce: acton of one bod on anothe; chaacteed b ts pont of applcaton, magntude,
COMP 465: Data Mining More on PageRank
 COMP 465: Dt Mnng Moe on PgeRnk Sldes Adpted Fo: www.ds.og (Mnng Mssve Dtsets) Powe Iteton: Set = 1/ 1: = 2: = Goto 1 Exple: d 1/3 1/3 5/12 9/24 6/15 = 1/3 3/6 1/3 11/24 6/15 1/3 1/6 3/12 1/6 3/15 Iteton
COMP 465: Dt Mnng Moe on PgeRnk Sldes Adpted Fo: www.ds.og (Mnng Mssve Dtsets) Powe Iteton: Set = 1/ 1: = 2: = Goto 1 Exple: d 1/3 1/3 5/12 9/24 6/15 = 1/3 3/6 1/3 11/24 6/15 1/3 1/6 3/12 1/6 3/15 Iteton
Chapter Fifiteen. Surfaces Revisited
 Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
Chapte Ffteen ufaces Revsted 15.1 Vecto Descpton of ufaces We look now at the vey specal case of functons : D R 3, whee D R s a nce subset of the plane. We suppose s a nce functon. As the pont ( s, t)
( ) D x ( s) if r s (3) ( ) (6) ( r) = d dr D x
 SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
SIO 22B, Rudnick dpted fom Dvis III. Single vile sttistics The next few lectues e intended s eview of fundmentl sttistics. The gol is to hve us ll speking the sme lnguge s we move to moe dvnced topics.
Chapter Newton-Raphson Method of Solving a Nonlinear Equation
 Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
School of Electrical and Computer Engineering, Cornell University. ECE 303: Electromagnetic Fields and Waves. Fall 2007
 School of Electicl nd Compute Engineeing, Conell Univesity ECE 303: Electomgnetic Fields nd Wves Fll 007 Homewok 4 Due on Sep. 1, 007 by 5:00 PM Reding Assignments: i) Review the lectue notes. ii) Relevnt
School of Electicl nd Compute Engineeing, Conell Univesity ECE 303: Electomgnetic Fields nd Wves Fll 007 Homewok 4 Due on Sep. 1, 007 by 5:00 PM Reding Assignments: i) Review the lectue notes. ii) Relevnt
Set of square-integrable function 2 L : function space F
 Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
Set of squae-ntegable functon L : functon space F Motvaton: In ou pevous dscussons we have seen that fo fee patcles wave equatons (Helmholt o Schödnge) can be expessed n tems of egenvalue equatons. H E,
FI 2201 Electromagnetism
 FI 1 Electomgnetism Alexnde A. Isknd, Ph.D. Physics of Mgnetism nd Photonics Resech Goup Electosttics ELECTRIC PTENTIALS 1 Recll tht we e inteested to clculte the electic field of some chge distiution.
FI 1 Electomgnetism Alexnde A. Isknd, Ph.D. Physics of Mgnetism nd Photonics Resech Goup Electosttics ELECTRIC PTENTIALS 1 Recll tht we e inteested to clculte the electic field of some chge distiution.
1 - ELECTRIC CHARGE AND ELECTRIC FIELD Page 1
 . Eectc Chge ELECTRIC CHARGE AND ELECTRIC IELD Pge Of most moe thn fundment ptces of mtte, thee most mpotnt e eecton, poton nd neuton. The msses e m e 9. g, m p m n.6 7 g espectvey. Gvtton foce of ttcton
. Eectc Chge ELECTRIC CHARGE AND ELECTRIC IELD Pge Of most moe thn fundment ptces of mtte, thee most mpotnt e eecton, poton nd neuton. The msses e m e 9. g, m p m n.6 7 g espectvey. Gvtton foce of ttcton
Electricity & Magnetism Lecture 6: Electric Potential
 Electicity & Mgnetism Lectue 6: Electic Potentil Tody s Concept: Electic Potenl (Defined in tems of Pth Integl of Electic Field) Electicity & Mgnesm Lectue 6, Slide Stuff you sked bout:! Explin moe why
Electicity & Mgnetism Lectue 6: Electic Potentil Tody s Concept: Electic Potenl (Defined in tems of Pth Integl of Electic Field) Electicity & Mgnesm Lectue 6, Slide Stuff you sked bout:! Explin moe why
Rigid Bodies: Equivalent Systems of Forces
 Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
Engneeng Statcs, ENGR 2301 Chapte 3 Rgd Bodes: Equvalent Sstems of oces Intoducton Teatment of a bod as a sngle patcle s not alwas possble. In geneal, the se of the bod and the specfc ponts of applcaton
PHY126 Summer Session I, 2008
 PHY6 Summe Sesson I, 8 Most of nfomaton s avalable at: http://nngoup.phscs.sunsb.edu/~chak/phy6-8 ncludng the sllabus and lectue sldes. Read sllabus and watch fo mpotant announcements. Homewok assgnment
PHY6 Summe Sesson I, 8 Most of nfomaton s avalable at: http://nngoup.phscs.sunsb.edu/~chak/phy6-8 ncludng the sllabus and lectue sldes. Read sllabus and watch fo mpotant announcements. Homewok assgnment
Chapter Linear Regression
 Chpte 6.3 Le Regesso Afte edg ths chpte, ou should be ble to. defe egesso,. use sevel mmzg of esdul cte to choose the ght cteo, 3. deve the costts of le egesso model bsed o lest sques method cteo,. use
Chpte 6.3 Le Regesso Afte edg ths chpte, ou should be ble to. defe egesso,. use sevel mmzg of esdul cte to choose the ght cteo, 3. deve the costts of le egesso model bsed o lest sques method cteo,. use
Effects of polarization on the reflected wave
 Lecture Notes. L Ros PPLIED OPTICS Effects of polrzton on the reflected wve Ref: The Feynmn Lectures on Physcs, Vol-I, Secton 33-6 Plne of ncdence Z Plne of nterfce Fg. 1 Y Y r 1 Glss r 1 Glss Fg. Reflecton
Lecture Notes. L Ros PPLIED OPTICS Effects of polrzton on the reflected wve Ref: The Feynmn Lectures on Physcs, Vol-I, Secton 33-6 Plne of ncdence Z Plne of nterfce Fg. 1 Y Y r 1 Glss r 1 Glss Fg. Reflecton
Chapter 3 Vector Integral Calculus
 hapte Vecto Integal alculus I. Lne ntegals. Defnton A lne ntegal of a vecto functon F ove a cuve s F In tems of components F F F F If,, an ae functon of t, we have F F F F t t t t E.. Fn the value of the
hapte Vecto Integal alculus I. Lne ntegals. Defnton A lne ntegal of a vecto functon F ove a cuve s F In tems of components F F F F If,, an ae functon of t, we have F F F F t t t t E.. Fn the value of the
Optimization. x = 22 corresponds to local maximum by second derivative test
 Optimiztion Lectue 17 discussed the exteme vlues of functions. This lectue will pply the lesson fom Lectue 17 to wod poblems. In this section, it is impotnt to emembe we e in Clculus I nd e deling one-vible
Optimiztion Lectue 17 discussed the exteme vlues of functions. This lectue will pply the lesson fom Lectue 17 to wod poblems. In this section, it is impotnt to emembe we e in Clculus I nd e deling one-vible
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
 1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
Chapter 21: Electric Charge and Electric Field
 Chpte : lectc Chge nd lectc Feld lectc Chge Known b ncent Geeks s el s 600 BC Sttc electct: electc chge v fcton (see lso fg.) (Attempted) pth bll demo nd/o scotch tpe demo: knds of popetes objects wth
Chpte : lectc Chge nd lectc Feld lectc Chge Known b ncent Geeks s el s 600 BC Sttc electct: electc chge v fcton (see lso fg.) (Attempted) pth bll demo nd/o scotch tpe demo: knds of popetes objects wth
Chapter 7. Kleene s Theorem. 7.1 Kleene s Theorem. The following theorem is the most important and fundamental result in the theory of FA s:
 Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
Jens Siebel (University of Applied Sciences Kaiserslautern) An Interactive Introduction to Complex Numbers
 Jens Sebel (Unversty of Appled Scences Kserslutern) An Interctve Introducton to Complex Numbers 1. Introducton We know tht some polynoml equtons do not hve ny solutons on R/. Exmple 1.1: Solve x + 1= for
Jens Sebel (Unversty of Appled Scences Kserslutern) An Interctve Introducton to Complex Numbers 1. Introducton We know tht some polynoml equtons do not hve ny solutons on R/. Exmple 1.1: Solve x + 1= for
Answers to test yourself questions
 Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
13.5. Torsion of a curve Tangential and Normal Components of Acceleration
 13.5 osion of cuve ngentil nd oml Components of Acceletion Recll: Length of cuve '( t) Ac length function s( t) b t u du '( t) Ac length pmetiztion ( s) with '( s) 1 '( t) Unit tngent vecto '( t) Cuvtue:
13.5 osion of cuve ngentil nd oml Components of Acceletion Recll: Length of cuve '( t) Ac length function s( t) b t u du '( t) Ac length pmetiztion ( s) with '( s) 1 '( t) Unit tngent vecto '( t) Cuvtue:
The Schur-Cohn Algorithm
 Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
The Formulas of Vector Calculus John Cullinan
 The Fomuls of Vecto lculus John ullinn Anlytic Geomety A vecto v is n n-tuple of el numbes: v = (v 1,..., v n ). Given two vectos v, w n, ddition nd multipliction with scl t e defined by Hee is bief list
The Fomuls of Vecto lculus John ullinn Anlytic Geomety A vecto v is n n-tuple of el numbes: v = (v 1,..., v n ). Given two vectos v, w n, ddition nd multipliction with scl t e defined by Hee is bief list
Physics 1502: Lecture 2 Today s Agenda
 1 Lectue 1 Phsics 1502: Lectue 2 Tod s Agend Announcements: Lectues posted on: www.phs.uconn.edu/~cote/ HW ssignments, solutions etc. Homewok #1: On Mstephsics this Fid Homewoks posted on Msteingphsics
1 Lectue 1 Phsics 1502: Lectue 2 Tod s Agend Announcements: Lectues posted on: www.phs.uconn.edu/~cote/ HW ssignments, solutions etc. Homewok #1: On Mstephsics this Fid Homewoks posted on Msteingphsics
Scalars and Vectors Scalar
 Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
Scalas and ectos Scala A phscal quantt that s completel chaacteed b a eal numbe (o b ts numecal value) s called a scala. In othe wods a scala possesses onl a magntude. Mass denst volume tempeatue tme eneg
ESCI 342 Atmospheric Dynamics I Lesson 1 Vectors and Vector Calculus
 ESI 34 tmospherc Dnmcs I Lesson 1 Vectors nd Vector lculus Reference: Schum s Outlne Seres: Mthemtcl Hndbook of Formuls nd Tbles Suggested Redng: Mrtn Secton 1 OORDINTE SYSTEMS n orthonorml coordnte sstem
ESI 34 tmospherc Dnmcs I Lesson 1 Vectors nd Vector lculus Reference: Schum s Outlne Seres: Mthemtcl Hndbook of Formuls nd Tbles Suggested Redng: Mrtn Secton 1 OORDINTE SYSTEMS n orthonorml coordnte sstem
Radial geodesics in Schwarzschild spacetime
 Rdil geodesics in Schwzschild spcetime Spheiclly symmetic solutions to the Einstein eqution tke the fom ds dt d dθ sin θdϕ whee is constnt. We lso hve the connection components, which now tke the fom using
Rdil geodesics in Schwzschild spcetime Spheiclly symmetic solutions to the Einstein eqution tke the fom ds dt d dθ sin θdϕ whee is constnt. We lso hve the connection components, which now tke the fom using
CISE 301: Numerical Methods Lecture 5, Topic 4 Least Squares, Curve Fitting
 CISE 3: umercl Methods Lecture 5 Topc 4 Lest Squres Curve Fttng Dr. Amr Khouh Term Red Chpter 7 of the tetoo c Khouh CISE3_Topc4_Lest Squre Motvton Gven set of epermentl dt 3 5. 5.9 6.3 The reltonshp etween
CISE 3: umercl Methods Lecture 5 Topc 4 Lest Squres Curve Fttng Dr. Amr Khouh Term Red Chpter 7 of the tetoo c Khouh CISE3_Topc4_Lest Squre Motvton Gven set of epermentl dt 3 5. 5.9 6.3 The reltonshp etween
ELECTROSTATICS. 4πε0. E dr. The electric field is along the direction where the potential decreases at the maximum rate. 5. Electric Potential Energy:
 LCTROSTATICS. Quntiztion of Chge: Any chged body, big o smll, hs totl chge which is n integl multile of e, i.e. = ± ne, whee n is n intege hving vlues,, etc, e is the chge of electon which is eul to.6
LCTROSTATICS. Quntiztion of Chge: Any chged body, big o smll, hs totl chge which is n integl multile of e, i.e. = ± ne, whee n is n intege hving vlues,, etc, e is the chge of electon which is eul to.6
Chapter Newton-Raphson Method of Solving a Nonlinear Equation
 Chpter 0.04 Newton-Rphson Method o Solvng Nonlner Equton Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
Chpter 0.04 Newton-Rphson Method o Solvng Nonlner Equton Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
Course Updates. Reminders: 1) Assignment #8 available. 2) Chapter 28 this week.
 Couse Updtes http://www.phys.hwii.edu/~vne/phys7-sp1/physics7.html Remindes: 1) Assignment #8 vilble ) Chpte 8 this week Lectue 3 iot-svt s Lw (Continued) θ d θ P R R θ R d θ d Mgnetic Fields fom long
Couse Updtes http://www.phys.hwii.edu/~vne/phys7-sp1/physics7.html Remindes: 1) Assignment #8 vilble ) Chpte 8 this week Lectue 3 iot-svt s Lw (Continued) θ d θ P R R θ R d θ d Mgnetic Fields fom long
Review of linear algebra. Nuno Vasconcelos UCSD
 Revew of lner lgebr Nuno Vsconcelos UCSD Vector spces Defnton: vector spce s set H where ddton nd sclr multplcton re defned nd stsf: ) +( + ) (+ )+ 5) λ H 2) + + H 6) 3) H, + 7) λ(λ ) (λλ ) 4) H, - + 8)
Revew of lner lgebr Nuno Vsconcelos UCSD Vector spces Defnton: vector spce s set H where ddton nd sclr multplcton re defned nd stsf: ) +( + ) (+ )+ 5) λ H 2) + + H 6) 3) H, + 7) λ(λ ) (λλ ) 4) H, - + 8)
π,π is the angle FROM a! TO b
 Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Section 35 SHM and Circular Motion
 Section 35 SHM nd Cicul Motion Phsics 204A Clss Notes Wht do objects do? nd Wh do the do it? Objects sometimes oscillte in simple hmonic motion. In the lst section we looed t mss ibting t the end of sping.
Section 35 SHM nd Cicul Motion Phsics 204A Clss Notes Wht do objects do? nd Wh do the do it? Objects sometimes oscillte in simple hmonic motion. In the lst section we looed t mss ibting t the end of sping.
3.1 Magnetic Fields. Oersted and Ampere
 3.1 Mgnetic Fields Oested nd Ampee The definition of mgnetic induction, B Fields of smll loop (dipole) Mgnetic fields in mtte: ) feomgnetism ) mgnetiztion, (M ) c) mgnetic susceptiility, m d) mgnetic field,
3.1 Mgnetic Fields Oested nd Ampee The definition of mgnetic induction, B Fields of smll loop (dipole) Mgnetic fields in mtte: ) feomgnetism ) mgnetiztion, (M ) c) mgnetic susceptiility, m d) mgnetic field,
Homework: Study 6.2 #1, 3, 5, 7, 11, 15, 55, 57
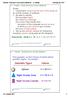 Gols: 1. Undestnd volume s the sum of the es of n infinite nume of sufces. 2. Be le to identify: the ounded egion the efeence ectngle the sufce tht esults fom evolution of the ectngle ound n xis o foms
Gols: 1. Undestnd volume s the sum of the es of n infinite nume of sufces. 2. Be le to identify: the ounded egion the efeence ectngle the sufce tht esults fom evolution of the ectngle ound n xis o foms
u(r, θ) = 1 + 3a r n=1
 Mth 45 / AMCS 55. etuck Assignment 8 ue Tuesdy, Apil, 6 Topics fo this week Convegence of Fouie seies; Lplce s eqution nd hmonic functions: bsic popeties, computions on ectngles nd cubes Fouie!, Poisson
Mth 45 / AMCS 55. etuck Assignment 8 ue Tuesdy, Apil, 6 Topics fo this week Convegence of Fouie seies; Lplce s eqution nd hmonic functions: bsic popeties, computions on ectngles nd cubes Fouie!, Poisson
UNIT10 PLANE OF REGRESSION
 UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
UIT0 PLAE OF REGRESSIO Plane of Regesson Stuctue 0. Intoducton Ojectves 0. Yule s otaton 0. Plane of Regesson fo thee Vaales 0.4 Popetes of Resduals 0.5 Vaance of the Resduals 0.6 Summay 0.7 Solutons /
Test 1 phy What mass of a material with density ρ is required to make a hollow spherical shell having inner radius r i and outer radius r o?
 Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
Test 1 phy 0 1. a) What s the pupose of measuement? b) Wte all fou condtons, whch must be satsfed by a scala poduct. (Use dffeent symbols to dstngush opeatons on ectos fom opeatons on numbes.) c) What
ELECTROMAGNETISM. at a point whose position vector with respect to a current element i d l is r. According to this law :
 ELECTROMAGNETISM ot-svt Lw: Ths w s used to fnd the gnetc fed d t pont whose poston vecto wth espect to cuent eeent d s. Accodng to ths w : µ d ˆ d = 4π d d The tot fed = d θ P whee ˆ s unt vecto n the
ELECTROMAGNETISM ot-svt Lw: Ths w s used to fnd the gnetc fed d t pont whose poston vecto wth espect to cuent eeent d s. Accodng to ths w : µ d ˆ d = 4π d d The tot fed = d θ P whee ˆ s unt vecto n the
Ch 26 - Capacitance! What s Next! Review! Lab this week!
 Ch 26 - Cpcitnce! Wht s Next! Cpcitnce" One week unit tht hs oth theoeticl n pcticl pplictions! Cuent & Resistnce" Moving chges, finlly!! Diect Cuent Cicuits! Pcticl pplictions of ll the stuff tht we ve
Ch 26 - Cpcitnce! Wht s Next! Cpcitnce" One week unit tht hs oth theoeticl n pcticl pplictions! Cuent & Resistnce" Moving chges, finlly!! Diect Cuent Cicuits! Pcticl pplictions of ll the stuff tht we ve
Generalized q-integrals via neutrices: Application to the q-beta function
 Flomt 7:8 3), 473 483 DOI.98/FIL38473S Publshed by Fculty of Scences nd Mthemtcs, Unvesty of Nš, Seb Avlble t: http://www.pmf.n.c.s/flomt Genelzed q-ntegls v neutces: Applcton to the q-bet functon Ahmed
Flomt 7:8 3), 473 483 DOI.98/FIL38473S Publshed by Fculty of Scences nd Mthemtcs, Unvesty of Nš, Seb Avlble t: http://www.pmf.n.c.s/flomt Genelzed q-ntegls v neutces: Applcton to the q-bet functon Ahmed
CENTROID (AĞIRLIK MERKEZİ )
 CENTOD (ĞLK MEKEZİ ) centrod s geometrcl concept rsng from prllel forces. Tus, onl prllel forces possess centrod. Centrod s tougt of s te pont were te wole wegt of pscl od or sstem of prtcles s lumped.
CENTOD (ĞLK MEKEZİ ) centrod s geometrcl concept rsng from prllel forces. Tus, onl prllel forces possess centrod. Centrod s tougt of s te pont were te wole wegt of pscl od or sstem of prtcles s lumped.
1. The sphere P travels in a straight line with speed
 1. The sphee P tels in stight line with speed = 10 m/s. Fo the instnt depicted, detemine the coesponding lues of,,,,, s mesued eltie to the fixed Oxy coodinte system. (/134) + 38.66 1.34 51.34 10sin 3.639
1. The sphee P tels in stight line with speed = 10 m/s. Fo the instnt depicted, detemine the coesponding lues of,,,,, s mesued eltie to the fixed Oxy coodinte system. (/134) + 38.66 1.34 51.34 10sin 3.639
Remember: When an object falls due to gravity its potential energy decreases.
 Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
Chapte 5: lectc Potental As mentoned seveal tmes dung the uate Newton s law o gavty and Coulomb s law ae dentcal n the mathematcal om. So, most thngs that ae tue o gavty ae also tue o electostatcs! Hee
( ) ( )()4 x 10-6 C) ( ) = 3.6 N ( ) = "0.9 N. ( )ˆ i ' ( ) 2 ( ) 2. q 1 = 4 µc q 2 = -4 µc q 3 = 4 µc. q 1 q 2 q 3
 3 Emple : Three chrges re fed long strght lne s shown n the fgure boe wth 4 µc, -4 µc, nd 3 4 µc. The dstnce between nd s. m nd the dstnce between nd 3 s lso. m. Fnd the net force on ech chrge due to the
3 Emple : Three chrges re fed long strght lne s shown n the fgure boe wth 4 µc, -4 µc, nd 3 4 µc. The dstnce between nd s. m nd the dstnce between nd 3 s lso. m. Fnd the net force on ech chrge due to the
If there are k binding constraints at x then re-label these constraints so that they are the first k constraints.
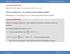 Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
Mathematcal Foundatons -1- Constaned Optmzaton Constaned Optmzaton Ma{ f ( ) X} whee X {, h ( ), 1,, m} Necessay condtons fo to be a soluton to ths mamzaton poblem Mathematcally, f ag Ma{ f ( ) X}, then
Fundamental Theorem of Calculus
 Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
Fundmentl Theorem of Clculus Recll tht if f is nonnegtive nd continuous on [, ], then the re under its grph etween nd is the definite integrl A= f() d Now, for in the intervl [, ], let A() e the re under
of Technology: MIT OpenCourseWare). (accessed MM DD, YYYY). License: Creative Commons Attribution- Noncommercial-Share Alike.
 MIT OpenouseWe http://ocw.mit.edu 6.1/ESD.1J Electomgnetics nd pplictions, Fll 25 Plese use the following cittion fomt: Mkus Zhn, Eich Ippen, nd Dvid Stelin, 6.1/ESD.1J Electomgnetics nd pplictions, Fll
MIT OpenouseWe http://ocw.mit.edu 6.1/ESD.1J Electomgnetics nd pplictions, Fll 25 Plese use the following cittion fomt: Mkus Zhn, Eich Ippen, nd Dvid Stelin, 6.1/ESD.1J Electomgnetics nd pplictions, Fll
E-Companion: Mathematical Proofs
 E-omnon: Mthemtcl Poo Poo o emm : Pt DS Sytem y denton o t ey to vey tht t ncee n wth d ncee n We dene } ] : [ { M whee / We let the ttegy et o ech etle n DS e ]} [ ] [ : { M w whee M lge otve nume oth
E-omnon: Mthemtcl Poo Poo o emm : Pt DS Sytem y denton o t ey to vey tht t ncee n wth d ncee n We dene } ] : [ { M whee / We let the ttegy et o ech etle n DS e ]} [ ] [ : { M w whee M lge otve nume oth
Algebra Based Physics. Gravitational Force. PSI Honors universal gravitation presentation Update Fall 2016.notebookNovember 10, 2016
 Newton's Lw of Univesl Gvittion Gvittionl Foce lick on the topic to go to tht section Gvittionl Field lgeb sed Physics Newton's Lw of Univesl Gvittion Sufce Gvity Gvittionl Field in Spce Keple's Thid Lw
Newton's Lw of Univesl Gvittion Gvittionl Foce lick on the topic to go to tht section Gvittionl Field lgeb sed Physics Newton's Lw of Univesl Gvittion Sufce Gvity Gvittionl Field in Spce Keple's Thid Lw
Learning Enhancement Team
 Lernng Enhnement Tem Worsheet: The Cross Produt These re the model nswers for the worsheet tht hs questons on the ross produt etween vetors. The Cross Produt study gude. z x y. Loong t mge, you n see tht
Lernng Enhnement Tem Worsheet: The Cross Produt These re the model nswers for the worsheet tht hs questons on the ross produt etween vetors. The Cross Produt study gude. z x y. Loong t mge, you n see tht
Chapter 21: Electric Charge and Electric Field
 Chpte 1: Electic Chge nd Electic Field Electic Chge Ancient Gees ~ 600 BC Sttic electicit: electic chge vi fiction (see lso fig 1.1) (Attempted) pith bll demonsttion: inds of popeties objects with sme
Chpte 1: Electic Chge nd Electic Field Electic Chge Ancient Gees ~ 600 BC Sttic electicit: electic chge vi fiction (see lso fig 1.1) (Attempted) pith bll demonsttion: inds of popeties objects with sme
CHAPTER 18: ELECTRIC CHARGE AND ELECTRIC FIELD
 ollege Physics Student s Mnul hpte 8 HAPTR 8: LTRI HARG AD LTRI ILD 8. STATI LTRIITY AD HARG: OSRVATIO O HARG. ommon sttic electicity involves chges nging fom nnocoulombs to micocoulombs. () How mny electons
ollege Physics Student s Mnul hpte 8 HAPTR 8: LTRI HARG AD LTRI ILD 8. STATI LTRIITY AD HARG: OSRVATIO O HARG. ommon sttic electicity involves chges nging fom nnocoulombs to micocoulombs. () How mny electons
Abhilasha Classes Class- XII Date: SOLUTION (Chap - 9,10,12) MM 50 Mob no
 hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
Fluids & Bernoulli s Equation. Group Problems 9
 Goup Poblems 9 Fluids & Benoulli s Eqution Nme This is moe tutoil-like thn poblem nd leds you though conceptul development of Benoulli s eqution using the ides of Newton s 2 nd lw nd enegy. You e going
Goup Poblems 9 Fluids & Benoulli s Eqution Nme This is moe tutoil-like thn poblem nd leds you though conceptul development of Benoulli s eqution using the ides of Newton s 2 nd lw nd enegy. You e going
Previously. Extensions to backstepping controller designs. Tracking using backstepping Suppose we consider the general system
 436-459 Advnced contol nd utomtion Extensions to bckstepping contolle designs Tcking Obseves (nonline dmping) Peviously Lst lectue we looked t designing nonline contolles using the bckstepping technique
436-459 Advnced contol nd utomtion Extensions to bckstepping contolle designs Tcking Obseves (nonline dmping) Peviously Lst lectue we looked t designing nonline contolles using the bckstepping technique
Go over vector and vector algebra Displacement and position in 2-D Average and instantaneous velocity in 2-D Average and instantaneous acceleration
 Mh Csquee Go oe eco nd eco lgeb Dsplcemen nd poson n -D Aege nd nsnneous eloc n -D Aege nd nsnneous cceleon n -D Poecle moon Unfom ccle moon Rele eloc* The componens e he legs of he gh ngle whose hpoenuse
Mh Csquee Go oe eco nd eco lgeb Dsplcemen nd poson n -D Aege nd nsnneous eloc n -D Aege nd nsnneous cceleon n -D Poecle moon Unfom ccle moon Rele eloc* The componens e he legs of he gh ngle whose hpoenuse
3.1 Electrostatic Potential Energy and Potential Difference
 3. lectostatc Potental negy and Potental Dffeence RMMR fom mechancs: - The potental enegy can be defned fo a system only f consevatve foces act between ts consttuents. - Consevatve foces may depend only
3. lectostatc Potental negy and Potental Dffeence RMMR fom mechancs: - The potental enegy can be defned fo a system only f consevatve foces act between ts consttuents. - Consevatve foces may depend only
VEKTORANALYS FLUX INTEGRAL LINE INTEGRAL. and. Kursvecka 2. Kapitel 4 5. Sidor 29 50
 VEKTORANAYS Ksecka INE INTEGRA and UX INTEGRA Kaptel 4 5 Sdo 9 5 A wnd TARGET PROBEM We want to psh a mne cat along a path fom A to B. Bt the wnd s blowng. How mch enegy s needed? (.e. how mch s the wok?
VEKTORANAYS Ksecka INE INTEGRA and UX INTEGRA Kaptel 4 5 Sdo 9 5 A wnd TARGET PROBEM We want to psh a mne cat along a path fom A to B. Bt the wnd s blowng. How mch enegy s needed? (.e. how mch s the wok?
6 Roots of Equations: Open Methods
 HK Km Slghtly modfed 3//9, /8/6 Frstly wrtten t Mrch 5 6 Roots of Equtons: Open Methods Smple Fed-Pont Iterton Newton-Rphson Secnt Methods MATLAB Functon: fzero Polynomls Cse Study: Ppe Frcton Brcketng
HK Km Slghtly modfed 3//9, /8/6 Frstly wrtten t Mrch 5 6 Roots of Equtons: Open Methods Smple Fed-Pont Iterton Newton-Rphson Secnt Methods MATLAB Functon: fzero Polynomls Cse Study: Ppe Frcton Brcketng
Quiz: Experimental Physics Lab-I
 Mxmum Mrks: 18 Totl tme llowed: 35 mn Quz: Expermentl Physcs Lb-I Nme: Roll no: Attempt ll questons. 1. In n experment, bll of mss 100 g s dropped from heght of 65 cm nto the snd contner, the mpct s clled
Mxmum Mrks: 18 Totl tme llowed: 35 mn Quz: Expermentl Physcs Lb-I Nme: Roll no: Attempt ll questons. 1. In n experment, bll of mss 100 g s dropped from heght of 65 cm nto the snd contner, the mpct s clled
Energy in Closed Systems
 Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
Enegy n Closed Systems Anamta Palt palt.anamta@gmal.com Abstact The wtng ndcates a beakdown of the classcal laws. We consde consevaton of enegy wth a many body system n elaton to the nvese squae law and
The formulae in this booklet have been arranged according to the unit in which they are first
 Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
The formulae in this booklet have been arranged according to the unit in which they are first
 Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge ccog to the ut whch the e fst touce. Thus cte sttg ut m e eque to use the fomule tht wee touce peceg ut e.g. ctes sttg C mght e epecte to use
Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge ccog to the ut whch the e fst touce. Thus cte sttg ut m e eque to use the fomule tht wee touce peceg ut e.g. ctes sttg C mght e epecte to use
( ) ( ) ( ) ( ) ( ) # B x ( ˆ i ) ( ) # B y ( ˆ j ) ( ) # B y ("ˆ ( ) ( ) ( (( ) # ("ˆ ( ) ( ) ( ) # B ˆ z ( k )
 Emple 1: A positie chge with elocit is moing though unifom mgnetic field s shown in the figues below. Use the ight-hnd ule to detemine the diection of the mgnetic foce on the chge. Emple 1 ˆ i = ˆ ˆ i
Emple 1: A positie chge with elocit is moing though unifom mgnetic field s shown in the figues below. Use the ight-hnd ule to detemine the diection of the mgnetic foce on the chge. Emple 1 ˆ i = ˆ ˆ i
