Topics in statistical inference for massive data and high-dimensional data
|
|
|
- Eileen Hutchinson
- 5 years ago
- Views:
Transcription
1 Graduate Theses and Dissertations Iowa State University Capstones, Theses and Dissertations 2017 Topics in statistical inference for massive data and high-dimensional data Liuhua Peng Iowa State University Follow this and additional works at: Part of the Statistics and Probability Commons Recommended Citation Peng, Liuhua, "Topics in statistical inference for massive data and high-dimensional data" (2017). Graduate Theses and Dissertations This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact
2 Topics in statistical inference for massive data and high-dimensional data by Liuhua Peng A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Statistics Program of Study Committee: Song Xi Chen, Co-major Professor Dan Nettleton, Co-major Professor Yehua Li Raymond Wong Zhengyuan Zhu Iowa State University Ames, Iowa 2017 Copyright c Liuhua Peng, All rights reserved.
3 ii DEDICATION To Mingqi, Ethan and Zoe
4 iii TABLE OF CONTENTS LIST OF TABLES vi LIST OF FIGURES viii ACKNOWLEDGEMENTS ABSTRACT xi xii CHAPTER 1. GENERAL INTRODUCTION CHAPTER 2. DISTRIBUTED STATISTICAL INFERENCE FOR MAS- SIVE DATA Introduction Symmetric statistics Distributed statistics Computing issues and selection of K Asymptotic distribution of T Bootstrap procedures Entire sample bootstrap U-statistics as an example BLB and SDB Distributed bootstrap Pseudo-distributed bootstrap Comparison of the distributed bootstrap, the pseudo-distributed bootstrap, the BLB and the SDB Applications Numerical studies
5 iv Gini s mean difference Distance covariance Real data analysis Conclusion Appendix Proof of Theorem Proof of Theorem Proof of Theorem Proof of Theorem Proof of Corollary Proof of Corollary Proof of Theorem CHAPTER 3. MORE POWERFUL TESTS FOR SPARSE HIGH DIMEN- SIONAL COVARIANCES MATRICES Introduction Motivations and preliminaries Testing procedures Identity test Power of the identity test Sphericity test Selection of k Numerical results Simulation studies Empirical study Discussion Appendix Critical lemmas Proof of Proposition Proof of Theorem
6 v Proof of Theorem Proof of Theorem Proof of Theorem More numerical results CHAPTER 4. VARIABLE IMPORTANCE ASSESSMENT AND BACK- WARD VARIABLE SELECTION FOR HIGH-DIMENSIONAL DATA Introduction Variable importance The multi-response permutation procedure An MRPP-based importance measure An alternative importance measure Backward selection A modified MRPP Real data analysis Simulations Backward selection Modified MRPP Conclusion CHAPTER 5. GENERAL CONCLUSIONS BIBLIOGRAPHY
7 vi LIST OF TABLES Table 2.1 Algorithm for the distributed bootstrap Table 2.2 Algorithm for the pseudo-distributed bootstrap Table 2.3 Comparison of the distributed bootstrap (DB), the pseudo-distributed bootstrap (PDB), the BLB and the SDB Table 2.4 Number of iterations completed in 10 seconds for each method. DB: the distributed bootstrap, PDB: the pseudo-distributed bootstrap, BLB: the bag of little bootstrap, SDB: the subsampled double bootstrap Table 2.5 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Gaussian data. 43 Table 2.6 Sizes of independence tests based on dcov 2 (Y, Z). T Var: test using variance estimation in (2.17); T PDB : test using the pseudo-distributed bootstrap Table 2.7 Powers of independence tests based on dcov 2 (Y, Z) for ϱ = Table 2.8 Powers of independence tests based on dcov 2 (Y, Z) for ϱ = Table 2.9 U and S 2 U for airline on-time dataset along with computing time (in seconds) given in the parentheses Table 2.10 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Gamma data. 62 Table 2.11 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Poisson data. 62 Table 3.1 Empirical power with respect to k for the identity test
8 vii Table 3.2 Empirical sizes of the proposed test (IT) for the identity hypothesis, along with those of the tests by Chen, Zhang and Zhong (2010) (CZZ) and Ledoit and Wolf (2002) (LW) Table 3.3 Number of identified gene-sets against null hypotheses. ST and IT stand for the proposed sphericity and identity tests, respectively. The last column reports the means and standard deviations for k qc Table 3.4 Computational time (in seconds) for a single sphericity test under the alternative Σ = (σ ij ) 1 i,j p with σ ij = I(i = j) + θ i j ρ I(i j) with different n and p Table 3.5 Empirical sizes of the proposed test (ST) for the sphericity hypothesis, along with those of the tests by Chen, Zhang and Zhong (2010) (CZZ) and Ledoit and Wolf (2002) (LW) Table 4.1 Number of gene sets for which each method ranks 1, 2, or 3 with respect to false positive rate. (Rank 1 is best and 3 is worst) Table 4.2 Combinations of n 1 and n 2 considered in the simulations Table 4.3 Empirical sizes of original MRPP (MRPP Org ) and modified MRPP with different choices of R 0. For Mod S(L), R 0 is chosen as the cardinality of S(L). For Mod 2, Mod 4, Mod 8, Mod 16 and Mod R, R 0 is pre-specified as 2, 4, 8, 16 and R, respectively
9 viii LIST OF FIGURES Figure 2.1 A diagram summary of the BLB procedure Figure 2.2 MSE(U )/MSE(U N ) and MSE(N 1 S 2 U )/MSE(N 1 S 2 UN ) against the number of blocks K for each scenario Figure 2.3 Bias(N 1 SU 2 ) / Bias(N 1 SUN 2 ) and Var(N 1 SU 2 )/Var(N 1 SUN 2 ) against the number of blocks K for each scenario Figure 2.4 Time evolution of relative errors under Gaussian scenario Figure 2.5 Time evolution of estimated confidence interval width Figure 2.6 Time evolution of relative errors under Gamma scenario Figure 2.7 Time evolution of relative errors under Poisson scenario Figure 3.1 Empirical size of the 5% sphericity test with respect to the banding width k for various sample sizes and dimensions Figure 3.2 Proportions of the banding width selected by the method of Qiu and Chen (2015) Figure 3.3 Empirical powers for the identity tests against the alternative in the diagonal form with the Gaussian distributed innovation Figure 3.4 Empirical powers for the identity tests against the alternative in the diagonal form with the Gamma distributed innovation Figure 3.5 Empirical powers for the identity tests against the alternatives in either the bandable or banded forms of the proposed test with either the Gaussian or Gamma distributed innovation Figure 3.6 Empirical powers for the sphericity tests against the alternative in the diagonal form with the Gaussian distributed innovation
10 ix Figure 3.7 Empirical powers for the sphericity tests against the alternative in the diagonal form with the Gamma distributed innovation Figure 3.8 Empirical powers for the sphericity tests against the alternatives in either the bandable or banded forms of the proposed test with either the Gaussian or Gamma distributed innovation Figure 3.9 Comparison of heat maps of correlation matrices before and after reordering of a gene set, GO: from BP category in NEG group Figure 3.10 Histograms of p-values for identity hypotheses (right panels) and sphericity hypotheses (left panels) for the three gene ontologies by the proposed tests Figure 4.1 The MRPP p-values on the sets of selected and deleted genes in each iteration Figure 4.2 Summary of 859 gene sets selected for simulations: (a) Histogram of the number of genes in each gene set; (b) Histogram of MRPP test p-values for each gene set Figure 4.3 Number of genes selected by each method for each gene set Figure 4.4 Comparison of average false positive rate for three methods, ρ t for twosample t-test, ρ l for limma and ρ bs for backward selection. (a) ρ t ρ bs ; (b) ρ l ρ bs ; (c) ρ t ρ l ; (d) the proportion of 1000 simulation replications in which each method has the lowest false positive rate across gene sets with of varying size Figure 4.5 (a): Histogram of number of genes in the 61 gene sets for which all three methods initially selected the same number of genes. (b) to (d): Comparison of average false positive rate for three methods when applied to the 61 gene sets Figure 4.6 Empirical powers of the original MRPP and modified MRPP with different choices of R 0 for ν =
11 x Figure 4.7 Empirical powers of the original MRPP and modified MRPP with different choices of R 0 for ν = Figure 4.8 Empirical powers of the original MRPP and modified MRPP with different choices of R 0 for ν =
12 xi ACKNOWLEDGEMENTS I would like to thank my major professor, Dr. Song Xi Chen and Dr. Dan Nettleton, for their extremely helpful guidance and support during my Ph.D. study. They showed me their great patience and encouragement, which have often inspired me for completing my graduate education and pursuing my future research. I have learned so much from them and will be indebted to them for everything they have taught me. I would also like to thank my remaining committee members, Dr. Yehua Li, Dr. Raymond Wong and Dr. Zhenyuan Zhu, for their interests and efforts for this work. Finally, I would like to thank my family and friends for their endless love and support.
13 xii ABSTRACT This dissertation consists of three research papers that deal with three different problems in statistics concerning high-volume datasets. The first paper studies the distributed statistical inference for massive data. With the increasing size of the data, computational complexity and feasibility should be taken into consideration for statistical analyses. We investigate the statistical efficiency of the distributed version of a general class of statistics. Distributed bootstrap algorithms are proposed to approximate the distribution of the distributed statistics. These approaches relief the computational burdens of conventional methods while preserving adequate statistical efficiency. The second paper deals with testing the identity and sphericity hypotheses problem regarding high-dimensional covariance matrices, with a focus on improving the power of existing methods. By taking advantage of the sparsity in the underlying covariance matrices, the power improvement is accomplished by utilizing the banding estimator for the covariance matrices, which leads to a significant reduction in the variance of the test statistics. The last paper considers variable selection for high-dimensional data. Distance-based variable importance measures are proposed to rank and select variables with dependence structures being taken into consideration. The importance measures are inspired by the multi-response permutation procedure (MRPP) and the energy distance. A backward selection algorithm is developed to discover important variables and to improve the power of the original MRPP for high-dimensional data.
14 1 CHAPTER 1. GENERAL INTRODUCTION Datasets with high volume are becoming increasingly prevalent as advances in technology have allowed for the generation of such datasets. Two different types of high-volume datasets are considered in this thesis. The first type is the massive data with large sample size and the second category is the high-dimensional data with a large number of variables. Analyzing those type of datasets demands new technologies that meet the inherent properties of the datasets. For massive data, with the growth in the size of the datasets, classical statistical methods can be computationally expensive, or infeasible, even though they can achieve favorable statistical efficiency. Thus, computational efficiency is also an important criterion when comparing different statistical approaches for massive data. Specifically, in the first paper, we consider distributed statistical inference for massive data. Among the techniques developed for analyzing massive datasets, there are two categories that are most important. One is the split-and-conquer method (Zhang, Duchi and Wainwright, 2013; Chen and Xie, 2014; Battey, et al., 2015), and the other one is the resampling-based methods (Kleiner, et al., 2014; Sengupta, Volgushev and Shao, 2016). In this paper, we consider a general class of symmetric statistics (Lai and Wang, 1993; Jing and Wang, 2010) that encompasses many commonly used statistics, for example, the U and L-statistics. By following the procedure of split-and-conquer, we formulate a distributed version of the statistics. The distributed statistic has advantages in computation over the statistic based on the whole dataset, including computing time, storage and memory requirement. Moreover, we study the statistical efficiency of the distributed statistic and compare it with the full sample one. It is shown that for non-degenerate statistics, with a properly selected number of data blocks, the distributed statistic can maintain the same leading order efficiency as the full sample statistic. By recognizing the appealing properties of the distributed statistic, approximating its distribu-
15 2 tion function is of great interest. Two bootstrap algorithms (the distributed bootstrap and the pseudo-distributed bootstrap) that can be implemented distributively are proposed to achieve this goal. Being distributed in computing makes the algorithms adaptive to massive datasets. It is also shown that the distributed approaches can preserve a sufficient level of statistical efficiency. For high-dimensional data, due to the large amount of variables, classical statistical approaches are no longer powerful or even not applicable. In the second paper, we consider testing the identity and sphericity hypotheses for high-dimensional covariance matrices, where traditional likelihood based tests fail under the high-dimensional setting as the sample covariance matrix is no long a consistent estimator of the population covariance matrix (Bai, Silverstein and Yin, 1988; Bai and Yin, 1993). Inspired by the existing U-statistic based tests for highdimensional covariance matrices proposed in Chen, Zhang and Zhong (2010) and the natural feature of sparsity for high-dimensional data, we formulate two new test statistics by employing the banded covariance estimator (Bickel and Levina, 2008a) incorporate with two discrepancy measures for the identity and sphericity hypotheses. This enables us to take advantage of the sparsity of the underlying covariance matrices and thus leads to the power improvement. Theoretical results are established to ensure the consistency of the proposed tests and to reveal the reason for power improvement, which is due to the reduction in the variance of the test statistics. Variable selection is in great need for high-dimensional data. For example, identifying differentially expressed genes for gene expression data is of great interest in genomic analysis. For this type of applications, an important feature of the data is that only a limit number of experimental subjects can be measured, which leads to the so-called small n, large p problem. In the third paper, we consider variable selection problem under the high-dimensional scenario. Existing methods for solving this problem have some limitations. The multi-response permutation procedure (MRPP) (Mielke and Berry, 2007) is a powerful tool for detecting differences between multivariate distributions. By imposing a hypothetical perturbation that tilts each dimension in the Euclidean distance between two data vectors, we introduce distancebased variable importance measures that takes the covariance structure into consideration. In
16 3 addition, a backward selection algorithm based on the importance measure is proposed to discover importance variables. By eliminating irrelevant variables in each iteration, we can focus on a subset of important variables. Besides identifying important variables, we modify the original MRPP based on the backward selection algorithm, with focusing on the important subset of the variables. This leads to a power improvement of the original MRPP when detecting differences between multivariate distributions. The rest of this dissertation is organized as followings. We present the results concerning the distributed inference for massive data in Chapter 2, where theoretical supports are given; In Chapter 3, we propose two more powerful tests for testing the identity and sphericity hypothesis for high-dimensional covariance matrices; In Chapter 4, we introduce the concept of variable importance inspired by the MRPP and propose a backward selection algorithm, which can be used to discover importance variables and improve the original MRPP. A general conclusion is included in Chapter 5, with discussions on future studies.
17 4 CHAPTER 2. DISTRIBUTED STATISTICAL INFERENCE FOR MASSIVE DATA Liuhua Peng and Song Xi Chen Abstract This paper studies distributed statistical inference for a general type of statistics that encompasses U-statistics and M-estimator in the context of massive data. When the data are stored on multiple platforms, it is usually expensive and slow to do data communication. To deal with this issue, we formulate the distributed statistics which can be computed distributively and hence reduces computational time significantly. We investigate properties of the distributed statistics from the perspective of mean square error of estimation and their asymptotic distributions. In addition, we propose two distributed bootstrap algorithms which are computationally effective and consistent theoretically. Applications of our approaches and numerical studies are provided to support them. 2.1 Introduction In the past decade, massive data with rapidly increasing size are generated in many fields of scientific studies that create needs for statistical analyses. Not only the sheer size of the data is an issue, but also the fact that these datasets are often stored in multiple locations or clouds, where each contains a subset of the data which can be massive in its own right. This implies that a statistical procedure that involves the entire data has to involve data communication between different storage facilities or clouds, which is usually slow and expensive. For statistical analyzes involving a massive data set, the computational and data storage implications of a
18 5 statistical procedure should be taken into consideration in additional to the usual criteria of statistical inference. Two kinds of methods have been developed to deal with these new challenges with massive data. One is the so-called split-and-conquer (SaC) method (Zhang, Duchi and Wainwright, 2013; Chen and Xie, 2014; Battey, et al., 2015); and the other one is the resampling-based methods advocated by Kleiner, et al. (2014) and Sengupta, Volgushev and Shao (2016). From the estimation point of view, the SaC first partitions the entire dataset into blocks with relatively smaller sizes, performs the estimation on each data block and then aggregate the estimators from each block to get the final estimator. SaC has been used in different settings under the massive data scenario, for instance the M-estimation by Zhang, Duchi and Wainwright (2013), the generalized linear models by Chen and Xie (2014), and other studies by Huang and Huo (2015), Battey, et al. (2015) and Lee, et al. (2015). The other method involves making the bootstrap procedure adaptive to the massive data setting in order to obtain standard errors or confidence intervals for statistical inference. As the conventional bootstrap resampling of the entire dataset is not feasible for massive data due to its being computationally too expensive, Kleiner, et al. (2014) introduced the bag of little bootstrap (BLB) that incorporates subsampling and the m out of n bootstrap to assess the quality of estimators for various inference purposes. Sengupta, Volgushev and Shao (2016) proposed the subsampled double bootstrap (SDB) method based on the idea of the BLB and a fast double bootstrap (Davidson and MacKinnon, 2002; Chang and Hall, 2015). However, both the BLB and the SDB have some limitations. Firstly, the core idea of the BLB and the SDB is to construct subsets of small size from the entire dataset, and then resample these small subsets to obtain weighted resamples of the subset such that the resample size is equal to the size of the entire data. Hence, the computational efficiency of the BLB and the SDB heavily rely on an assumption that the estimator of interest admitted a weighted subsample representation (Kleiner, et al., 2014), which is usually satisfied for linear statistics. Secondly, the SDB requires resampling from the entire dataset, which is computationally expensive and hard to accomplish when the data are stored in different locations.
19 6 In this paper, we consider distributed statistical inference for a class of symmetric statistics that does the SaC step for a distributed formulation of the statistics followed by two versions of the bootstrap specifically designed for the distributed statistic formulation. We first divide the entire dataset into K data blocks (which is similar to SaC) and then formulate a distributed statistic by averaging the statistics obtained on each data block. The distributed statistic has computational advantage over the statistics based on the entire (massive) data. Besides the computational issue, we consider achieving the best estimation efficiency for the distributed estimation, that touches on the issue of selecting the number of data blocks. After studying the relative efficiency of the distributed statistic relative to the full sample statistics, we device computationally efficient bootstrap algorithms to approximate the distribution of the distributed statistics, which can be used in various inferential tasks of the statistical inference. The latter is carried out by recognizing the limitations of the BLB and the SDB. Specifically, we develop a distributed bootstrap (DB) and a pseudo-distributed bootstrap (PDB) to approximate the distribution of the distributed statistics. Both strains of the bootstrap method can be implemented distributively and are suitable to parallel and distributed computing platforms. It is shown that being distributed in both the statistical formulation and the subsequent bootstrap makes the computation much suited to the massive data setting while maintaining sufficient level of statistical efficiency and accuracy in the inference. The rest of the paper is organized as follows. The class of symmetric statistics considered in this paper is introduced in Section 2.2. The distributed statistic is formulated in Section 2.3 together with its statistical efficiency. Section 2.4 discusses the issues concerning computational complexity and the selection of the number of data blocks. In Section 2.5, asymptotic distributions of the distributed statistics are established for both non-degenerate and degenerate cases. Bootstrap procedures which are designed to approximate the distribution of the distributed statistics are discussed through Section 2.6 to Section 2.9. Application of the distributed inference procedures on the distance covariance is presented in Section Section 2.11 provides numerical studies to support our theoretical results. All technical proofs along with additional simulation results are provided in the appendix.
20 7 2.2 Symmetric statistics Let X N = {X 1,..., X N } be a sequence of independent random vectors taking values in a measurable space (X, B) with a common distribution F. The statistic of interest T N = T (X N ) is a statistic that admits a general non-linear form T N = θ + N 1 N α(x i ; F ) + N 2 i=1 1 i<j N β(x i, X j ; F ) + R N, (2.1) where θ = θ(f ) is the parameter of interest, α(x; F ) and β(x, y; F ) are known measurable functions satisfying the conditions given in Condition 2.1. In (2.1), R N = R(X N ; F ) is a remainder term which may be viewed as the approximation error of the expansion that constitutes the first three terms on the right side. In summary, T N may be considered as an estimator of θ and E(R N ) is the estimation bias, while both the linear and quadratic terms contribute to the variation of T N. The statistic T N encompasses many commonly used statistics, for example, the U and L- statistics, and the smoothed functions of the sample means. The form (2.1) was introduced in Lai and Wang (1993) while Edgeworth expansions for T N were studied in Jing and Wang (2010). In both Lai and Wang (1993) and Jing and Wang (2010), it is assumed that α(x 1 ; F ) is non-lattice distributed and R N is of smaller order of the quadratic term involving β. For instance, T N can be a U-statistic with α(x i ; F ) and β(x i, X j ; F ) terms to be the first and second order terms in its Hoeffding decomposition (Hoeffding, 1948; Serfling, 1980). In this case, E(R N ) = 0 and Var(R N ) = O(N 3 ). In this paper, we relax the conditions in Lai and Wang (1993) and Jing and Wang (2010) such that T N includes more types of statistics. The linear term involving α(x i ; F ) can vanish, for instance in the case of the degenerate U-statistics. Furthermore, the M-estimators are included in (2.1) with R N having certain order of magnitude depending on the forms of the score functions. When the score function of the M-estimator is twice differentiable and its second derivative is Lipschitz continuous, the M-estimator can be expressed in the form of (2.1) with an explicit β and the reminder term R N = O p (N 1 ) (Lahiri, 1994). However, when the score function is not smooth enough, the M-estimator may not be expanded to the second-order β(x i, X j ; F ) term. In this situation, we can absorb the term involving β into R N, which is often of order O p (N 3/4 ) (He and Shao, 1996).
21 8 We assume the following condition regarding α and β. Condition 2.1. The functions α(x; F ) and β(x, y; F ) are known measurable functions of x and y, satisfying E{α(X 1 ; F )} = 0 and Var{α(X 1 ; F )} = σα 2 [0, ), and β(x, y; F ) is symmetric in x and y such that E{β(X 1, X 2 ; F ) X 1 } = 0 and E {β(x 1, X 2 ; F )} 2 = σβ 2 [0, ). 2.3 Distributed statistics To improve the computation of T N in the context of massive data, we divide the full dataset X N into K data blocks. Let X (k) = {X k,1,..., X k,nk } be the k-th data block of size n k, for k = 1,..., K. Sometimes, such division is not needed when X N storage facilities. Otherwise, the blocks can be obtained by random sampling. is naturally stored over K We have the following conditions concerning the sizes of data blocks {n k } K k=1 and the number of blocks K. Condition 2.2. There exist finite positive constants c 1 and c 2 such that c 1 inf k1,k 2 n k1 /n k2 sup k1,k 2 n k1 /n k2 c 2. In addition, K can be either finite or diverging to infinity as long as it satisfies that K/N 0 as N. Condition 2.2 implies that {n k } K k=1 are of the same order and the number of data blocks K should be of a smaller order of N. For k = 1,..., K, let T (k) = T ( X (k) ) be a version of TN, but is based on the k-th data block X (k) such that T (k) = θ + n 1 k n k i=1 α(x k,i ; F ) + n 2 k, 1 i<j n k β(x k,i, X k,j ; F ) + R (k) where R (k) = R( X (k) ; F ) is the remainder term specific to the k-th block. By doing a weighted average of the K block-wise statistics, we arrive at the distributed statistic which can be expressed as T = θ + N 1 N i=1 T = N 1 α(x i ; F ) + N 1 K k=1 K k=1 n 1 k n k T (k), (2.2) 1 i<j n k β(x k,i, X k,j ; F ) + R, (2.3)
22 9 where R = N 1 K k=1 n kr (k). It is clear that the first two terms (containing θ and α) of T and T N are the same. The difference between them occurs at the terms involving β and the remainders. To facilitate analyzes on T, we assume the following assumption. Condition 2.3. If E(R N ) = b 1 N τ 1 +o(n τ 1 ) and Var(R N ) = o(n τ 2 ) for some b 1 0, τ 1 1 and τ 2 1, then E ( R (k) ) = b1,k n τ 1 k + o(n τ 1 k ) for some b 1,k 0 and Var ( R (k) ) = o(n τ 2 k ), for k = 1,..., K. Condition 2.3 describes a divisible property of R N in its first two moments with respect to the sample size N. That is, { R (k) } K k=1 inherit the first two moments properties of R N with N substituted by n k. First, we present results concerning T N to provide baseline results. Proposition 2.1. Under Condition 2.1, if E(R N ) = b 1 N τ 1 +o(n τ 1 ) for some b 1 0, τ 1 1, and Var(R N ) = o(n 2 ), then Bias(T N ) = b 1 N τ 1 + o(n τ 1 ) and Var(T N ) = σ 2 αn σ 2 β N 2 + N 1 N i=1 Cov {α(x i ; F ), R N } + o(n 2 ). The bias of T N is totally determined by the expectation of R N. In the variance expression, we keep the term involving the covariance between α(x i, F ) and R N as it may not be negligible in a general case. For the special case when R N is uncorrelated with α(x i ; F ), which is the case for the U-statistics, the covariance term is negligible. Then, the mean square error (MSE) of T N is MSE(T N ) = σαn σβ 2 N 2 + b 2 1N 2τ 1 N + N 1 Cov {α(x i ; F ), R N } + o(n 2 + N 2τ 1 ). (2.4) i=1 The results of T is given in the following theorems.
23 10 Theorem 2.1. Under Conditions 2.1, 2.2, 2.3, if E(R N ) = b 1 N τ 1 +o(n τ 1 ) for some b 1 0, τ 1 1, and Var(R N ) = o(n 2 ), then Bias(T ) = N 1 K k=1 Var(T ) = σ 2 αn σ 2 β KN 2 + N 2 b 1,k n 1 τ 1 k + o(k τ 1 N τ 1 ) and K n k n k k=1 i=1 { } Cov α(x k.i ; F ), R (k) + o(kn 2 ). If T N is an unbiased estimator of θ, namely τ 1 =, T is also unbiased so that E(T ) = θ. Thus the distributed approach can preserve the unbiasedness of the statistics. For the biased case of τ 1 <, according to Theorem 2.1, as N 1 K k=1 b 1,kn 1 τ 1 k is of order O(K τ 1 N τ 1 ) under Condition 2.2, the bias is enlarged by a factor of K τ 1 for T relative to that of T N. This indicates that the data blocking accumulates the biases from each data block, leading to an increase in the bias of the distributed statistic. For the more common case that the bias of T N is at the order of O(N 1 ), the bias of T is O(KN 1 ). For the variance, we note there is an increase in the factor of K in the term that involves σ 2 β N 2 due to the data blocking. For the covariance term in Var(T ), under the conditions in Theorem 2.1, as Var { N 1 N i=1 α(x i; F ) } = O(N 1 ) and Var(R N ) = o(n 2 ), by utilizing Cauchy-Schwarz inequality we have { Cov N 1 N i=1 α(x i ; F ), R N } = o(n 3/2 ). Similarly, N 2 K k=1 n nk k i=1 Cov{ α(x k.i ; F ), R } (k) = o(k 1/2 N 3/2 ) by the independence between each data block. Thus, an increase of order K 1/2 occurs in the covariance term. Moreover, the covariance term in Var(T ) is always at a smaller order of N 1 as K = o(n), while it may exceed the KN 2 order term. For the case of σ 2 α > 0, the variance inflation happens in the second order term without altering the leading order term. However, for the degenerate case of σ 2 α = 0, but σ 2 β > 0, the variance inflation appears in the leading order via a factor of K.
24 11 Combining the bias and variance from Theorem 2.1, we have MSE(T ) =σ 2 αn σ 2 β KN 2 + N 2 ( K + N 2 K k=1 n k n k i=1 k=1 b 1,k n 1 τ 1 k ) 2 { } Cov α(x k.i ; F ), R (k) + o(kn 2 + K 2τ 1 N 2τ 1 ). (2.5) To compare the MSEs of T N and T, we first consider the non-degenerate case of σ 2 α > 0. By comparing (2.4) with (2.5). If ( ) K = o N 1 1/(2τ 1) (2.6) then K 2τ 1 N 2τ 1 = o(n 1 ), and MSE(T N ) and MSE(T ) share the same leading order term σ 2 αn 1. We note that 1 1/(2τ 1 ) is an increasing function of τ 1, ranging from 1/2 (when τ 1 = 1) to 1 (when τ 1 ). For the case of τ 1 = 1 when T N has a bias of order N 1, the number of blocks K is required to be at a smaller order of N 1/2 such that T maintains the same leading order efficiency as T N in terms of MSEs. The increase in the variance due to the data blocking is reflected in the MSE, although it is of the second order unless in the degenerate case. In summary, we see that the data blocking increases the bias and variance of the distributed statistic T. This may be viewed as a price paid to gain computational scalability for massive data. Despite this, there is room to select K properly to minimize the increases. For instance, by choosing K to satisfy (2.6), the increase in the bias is confined in the second order. Also, for non-degenerate situation, the impact of the data blocking can be largely limited to the second order as reflected in the MSE expression (2.5). 2.4 Computing issues and selection of K The rationale for carrying out the distributed formulation is in reducing the computing time and data storage significantly in the context of massive data while maintaining the best level of the estimation accuracy given a computational and storage budget. In this section, we will discuss this issue with the U-statistics as an example. First, the distributed approach can reduce the computing time significantly when the inferences involved is computationally intensive. For example, if the computational complexity
25 12 of calculating T N is at the order of O(N a ) with a > 1, then computing T only needs K O((N/K) a ), that is O(K 1 a N a ) steps. So calculating T is a factor of O(K a 1 ) faster than computing T N directly. Similar statement can be found from Theorem 5 in Chen and Xie (2014). In our distributed approach, the computing effort of the average step is only at the order of K, which is negligible. Besides the saving in computing cost, the distributed approach requires less memory space. Suppose the memory needed for computing T N is O(N b ) for some b 1. Then for T, the requirement on the size of memory is at the order of O((N/K) b + K). This means a memory saving by a factor of 1 K b when K = O(N b/(1+b) ), or 1 KN b when KN b/(1+b), for the distributed approach. Now we use the U-statistics as an example to demonstrate the savings in computing. Consider a U-statistic U N of degree m 2 with a symmetric kernel function h such that ( ) N 1 U N = h(x i1,..., X im ) m 1 i 1 <...<i m N N =θ U + N 1 α U (X i ; F ) + N 2 i=1 1 i<j N where θ U = E(U N ), α U (x; F ) = m [E {h(x, X 2,..., X m )} θ U ], β U (X i, X j ; F ) + R UN, β U (x, y; F ) = (m 1) [me {h(x, y, X 3,..., X m )} α U (x; F ) α U (y; F ) mθ U ], R UN is the remainder term satisfies E(R UN ) = 0 and Var(R UN ) = O(N 3 ) under the condition that E(h 2 ) <. It is clear that U N can be represented in the form of (2.1). This representation is called the Hoeffding s decomposition of U-statistics and it is initially from Hoeffding (1948, 1961). If we need s steps to calculate the h function, then the computing cost of U N is (s + 1) ( N m), which is at the order of O(N m ). Assume the entire dataset of size N is divided evenly into K subsets with each of size n = N/K, denote U (k) as the U-statistic using data in the k-th block. Then the distributed U-statistic is U U,K = K 1 K k=1 U (k). Notice that the number of computing steps for U is K (s + 1) ( n m), which is of order O(K 1 m N m ). Thus, the computing steps of the distributed statistic is a factor of K m 1 less than that of the full sample U-statistic U N.
26 13 Now we consider the problem of selecting K. As we discussed earlier, using a larger K would reduce the computing burden and make computation more feasible. However, the mean square error of T is an increasing function of K, which indicates that there would be a loss in the estimation efficiency for using a large K. Thus, in practice, the selection of K should be a result of a compromise between the statistical accuracy and the computational cost and feasibility. First of all, the storage and memory bottleneck require K to be big enough such that the data points in each data block are manageable. Suppose that K K 0 is a hard requirement to meet the capacity of memory and storage. As the mean square error of T is increasing with respect to K, so the minimum mean square error we can get is MSE(T 0 ), which is achieved when K = K 0. This statement is based on the assumption that we have plenty enough time to fulfill all computing procedures. In practice, we might have fixed time budget. In this situation, denote the computing cost as C(K) and the fixed time budget as C 0. It is reasonable to assume that the computing cost C(K) is a decreasing function of K. Denote K 0 = min{k C(K) C 0}, then the optimal K is min(k 0, K 0 ). This result suggests us to select the smallest K that meet the limits of memory, storage and computing time budget, to attain the best statistical efficiency. 2.5 Asymptotic distribution of T Now we investigate the asymptotic distribution of T and compare it with that of T N. First, we have the following theorem presenting the asymptotic distribution of T N when σ 2 α > 0. Theorem 2.2. Under Condition 2.1 and σ 2 α > 0, if R N = o p (N 1/2 ), then as N, N 1/2 σ 1 α (T N θ) d N (0, 1). Here N (0, 1) denotes the standard normal distribution. This theorem is a consequence of the central limit theorem and the assumption that R N = o p (N 1/2 ). The requirement that R N = o p (N 1/2 ) is easy to achieve and one sufficient assumption for it is E(R 2 N ) = o(n 1 ). Next, we have the following theorem concerning the asymptotic distribution of T.
27 14 Theorem 2.3. Under Conditions 2.1, 2.2, 2.3 and σ 2 α > 0, if E(R N ) = b 1 N τ 1 + o(n τ 1 ), Var(R N ) = o(n τ 2 ) for some τ 1 1, τ 2 1, and K = o ( N 1 1/(2τ 1) ), then as N, N 1/2 σ 1 α (T θ) d N (0, 1). The condition K = o ( N 1 1/(2τ 1) ) indicates that, under Conditions and the assumption that σα 2 > 0, the smaller order R N is, the higher order K can be so that T can attain the same asymptotic normal distribution as T N. Thus the condition on K is determined by the order of the remainder term R N. The conditions on K coincides with the requirement on K (2.6) in order that MSE(T N ) and MSE(T ) have the same leading order term, and T has the same efficiency as T N. Furthermore, we can attain the uniform convergence of the distribution of T to that of T N. Before that, we need the following assumption on α. Condition 2.4. There exists a positive constant δ 1 such that E α(x 1 ; F ) 2+δ <. This condition is commonly used in obtaining the uniform convergence, for instance in Petrov (1998). Theorem 2.4. Under Conditions 2.1, 2.2, 2.3, 2.4 and σ 2 α > 0, assume E(R N ) = b 1 N τ 1 + o(n τ 1 ) and Var(R N ) = o(n τ 2 ) for some τ 1 1 and τ 2 > 1, if K = O(N τ ) for a positive constant τ such that τ < 1 1/(2τ 1 ), then as N, { } sup P N 1/2 σα 1 (T θ) x x R { P N 1/2 σα 1 (T N θ) x} = o(1). It is noticed that the uniform convergence requires K = O(N τ ) for 0 < τ < 1 1/(2τ 1 ), which is slightly stronger than K = o ( N 1 1/(2τ 1) ) assumed in Theorem 2.3. With all these results, for the case of σ 2 α > 0, as long as the number of data blocks K does not diverges too fast, T can maintain the same estimation efficiency as T N and they have the same asymptotic distribution. Thus T is a good substitute of T N as an estimator of θ. For the degenerate case where σ 2 α = 0, an increase of order K in the variance has been shown in Theorem 2.1. This means that T can not achieve the same efficiency as T N. We want to explore the asymptotic distribution of T in the degenerate case and compare it with
28 15 the one of T N. It is noticed that when σ 2 α = 0 and σ 2 β > 0, and T N θ = N 2 T θ = N 1 K k=1 n 1 k 1 i<j N β(x i, X j ; F ) + R N 1 i<j n k β(x k,i, X k,j ; F ) + R. (2.7) Thus, the leading order term of T θ is no longer the same as that of T N θ, which leads to an order of K increase in the variance as shown in Theorem 2.1. Before investigating the asymptotic distributions of T N and T, we introduce the notations in the spectral decomposition of β. As β is a symmetric function of two variables, when it has finite second moment, there exist sequences of eigenvalues {λ l } l=1 and eigenfunctions {β l} l=1 in connection with β such that β admits the following expansion (Dunford and Schwartz, 1963; Serfling, 1980) β(x, y; F ) = λ l β l (x; F )β l (y; F ), (2.8) l=1 such that lim E L β(x 1, X 2 ; F ) L 2 λ l β l (X 1 ; F )β l (X 2 ; F ) = 0. l=1 Here β l satisfies E {β l (X 1 ; F )} = 0 for all l Z and 1 l 1 = l 2, E {β l1 (X 1 ; F )β l2 (X 1 ; F )} = 0 l 1 l 2. Moreover, {λ l } l=1 satisfy l=1 λ2 l = σ2 β <. The following theorem establishes the asymptotic distribution of T N under the degenerate case. Theorem 2.5. Under Condition 2.1, σα 2 = 0 and σβ 2 > 0, if R N = o p (N 1 ), then as N, 2N(T N θ) d λ l (χ 2 1l 1), where {χ 2 1l } l=1 are independent chi-square random variables with one degree of freedom. l=1
29 16 This theorem is a direct result of the asymptotic distribution of degenerate U-statistics (Serfling, 1980) and the condition that R N = o p (N 1 ). Note that from (2.7), T can be viewed as a weighted average of K independent statistics, the asymptotic behavior of degenerate T is given in the following theorem. Theorem 2.6. Under Conditions 2.1, 2.2, σα 2 = 0 and σβ 2 > 0, then (i) If K is finite and R = o p (N 1 ), then as N, 2N(T θ) d λ l (χ 2 Kl K), l=1 where {χ 2 Kl } l=1 are independent chi-square random variables with K degrees of freedom. (ii) If K, there exists a constant δ > 0 such that E β(x 1, X 2 ; F ) 2+δ <, and R = o p (K 1/2 N 1 ), then as N, 2 1/2 K 1/2 Nσ 1 β (T θ) d N (0, 1). From this theorem, we get two different types of limit distribution for T depending on whether K is finite or diverging. This is easy to interpret because T may be viewed as an average of K independent random variables. So with the data divided into increasingly many data blocks, the distribution of T is asymptotically normal. When K is finite, the condition R = o p (N 1 ) is a directly result of R (k) = o p(n 1 ). When K diverges to infinity, under k Condition 2.3 which prescribes the divisibility of R N with respect to the sample size N, so that E(R ) = N 1 K k=1 b 1,kn 1 τ 1 k +o(k τ 1 N τ 1 ) and Var(R ) = o(kn 2 ). Thus in order that R = o p (K 1/2 N 1 ), it requires that K τ 1 N τ 1 = o(k 1/2 N 1 ), that is, ( ) K = o N 1 1/(2τ 1 1). If τ 1 = 1 with b 1 0, E(R ) = O(KN 1 ) which means that R = o p (K 1/2 N 1 ) is not achievable in this case. It is of interest to mention that when K, the normalizing factor is of order K 1/2 N, which is of smaller order of N, the normalizing factor for T N. This indicates that the distributed statistic T is less efficient than T N, and this property coincides with the increase in the variance of T as discussed in Theorem 2.1.
30 Bootstrap procedures We have studied the asymptotic properties of T by focusing on its mean square error and asymptotic distributions in the previous sections. An important remaining issue is how to approximate the distribution of T under different conditions on σα 2 and K? This motivates the bootstrap. The bootstrap is a powerful tool for statistical analysis, especially in approximating distributions of statistics. First, we investigate the properties of the conventional bootstrap when applied to the distributed statistics for massive data. Then we review two novel bootstrap algorithms, the BLB and the SDB, designed for massive data. After recognizing the limitations of the BLB and the SDB, we propose two distributed bootstrap procedures that adapt the distributed statistics T under the massive data scenario Entire sample bootstrap In order to approximate the distribution of T, we consider resampling the entire sample to construct bootstrap resamples by following the procedures of the conventional bootstrap. By calculating the corresponding distributed statistic for each resample, we can use the empirical distribution of the bootstrap distributed statistics to estimate the distribution of T. As T is a distributed type statistic and the sample size N is large, in order to construct resamples of size N and get the bootstrap version of T, one may carry out the resampling procedure in the following two steps: Step 1. For k = 1,..., K, randomly sample a set X (k) = { X k,1,..., X k,n k } from XN with replacement and compute the corresponding statistic as T (k) = T ( X (k) ). Step 2. Obtain the bootstrap distributed statistic T = N 1 K k=1 n k T (k). By carrying out this two steps resampling procedure, it ensures that the resample X N = { (1) X,..., } X (K) are conditionally independently and identically distributed from the empirical distribution of X N, denoted as F N, and they are split into K subsets automatically. So the storage space requirement of the resampling procedure is scale in K 1 N, rather than N and it is easy to be paralleled.
31 18 Next, we explore the asymptotic properties of the entire sample bootstrap procedure. To facilitate the working of the bootstrap procedure, we need T to admit an expansion similar to T in (2.3). Suppose that for k = 1,..., K, T (k) = T ( X (k) ) has the following form T (k) = θ N + n 1 k n k i=1 α(x k,i ; F N) + n 2 k β(xk,i, X k,j ; F N) + R (k), 1 i<j n k where θn = θ(f N), R (k) = R( X (k) ; F ) (k) N are the analog of θ and R under F N. Then T = θ N + N 1 K n k α(xk,i ; F N) + N 1 k=1 i=1 K k=1 n 1 k 1 i<j n k β(x k,i, X k,j ; F N) + R, where R = N 1 K k=1 n kr (k). Here, α(x; F N) and β(x, y; F N ) can be viewed as the empirical version of α(x; F ) and β(x, y; F ). Denote S(F ) as the support of F, we need to regulate them as in the following condition. (2.9) Condition 2.5. α(x; F N ) and β(x, y; F N ) are functions depend on F N. α(x; F N ) satisfies N i=1 α(x i; F N ) = 0 and sup α(x; F N ) α(x; F ) = o p (1), and β(x, y; F N ) is symmetric x S(F ) in x and y such that N i=1 {β(x i, y; F N )} = 0 for any y S(F ) and sup β(x, y; F N ) x,y S(F ) β(x, y; F ) = o p (1). Condition 2.5 indicates that for X k,i with distribution F N, E { α(x k,i ; F N) F N } = 0 and E { β(x k,i, y; F N) F N } = 0 for any y S(F ). Moreover, it requires that α(x; FN ) and β(x, y; F N ) are close to α(x; F ) and β(x, y; F ). Explicit discussions on these conditions will be given shortly in the context of U-statistics. The following theorem establishes the theoretical properties of the bootstrap distributed statistic which is inspired by Lai and Wang (1993). For specific statistics, we need to check the bootstrap distributed statistic admits the form (2.9) and satisfies other assumptions assumed in the theorem to get the corresponding results. Theorem 2.7. Under the conditions of Theorem 2.4 and E β(x 1, X 1 ; F ) 2 <, suppose that there exist functions α(x; F N ) and β(x, y; F N ) satisfy Condition 2.5, let T = θ N + N 1 K n k α(xk,i ; F N) + N 1 k=1 i=1 K k=1 n 1 k 1 i<j n k β(x k,i, X k,j ; F N) + R,
32 19 where R satisfies P{ R N 1/2 (lnn) 1 F N } = op (1), then as N, { 1 sup P N 1/2ˆσ α,n (T θn) x } { FN P N 1/2 σα 1 (T θ) x} = op (1), x R and ˆσ 2 α,n σ2 α = o p (1) where ˆσ 2 α,n = E { α 2 (X 1,1 ; F N) F N }. This theorem offers theoretical support for the entire sample bootstrap method. Repeat step 1 to 2 a number (B) of times, we get B bootstrap distributed statistics, denote them as T 1,..., T B. Then, the empirical distribution of { ( } 1 N 1/2ˆσ α,n T b N) θ, b = 1,..., B can be used to approximate the distribution of N 1/2 σα 1 (T θ) U-statistics as an example We would like to use U-statistics as an example to demonstrate the conditions in Theorem 2.7 are appropriate. Suppose U N = U(X N ) is a U-statistic of degree 2 with a symmetric kernel function h, that is, U N =2{N(N 1)} 1 h(x i, X j ) 1 i<j N N =θ U + N 1 α U (X i ; F ) + N 2 β U (X i, X j ; F ) + R UN, (2.10) i=1 1 i<j N where θ U = E(U N ), α U (x; F ) = 2 [E {h(x, X 2 )} θ U ], β U (x, y; F ) = 2h(x, y) α U (x; F ) α U (y; F ) 2θ U, and R UN is the remainder term. Obviously U N is in the form of (2.1). Under the condition that E{h(X 1, X 2 )} 2 <, it can be shown that α U and β U meet Condition 2.1 and R UN satisfies E(R UN ) = 0 and E(R 2 UN ) = O(N 4 ) (Hoeffding, 1948; Serfling, 1980). Let U (k) = U( X (k) ) be the corresponding U-statistic obtained from the k-th data block, for k = 1,..., K, then the distributed U-statistic is U =N 1 where R U K k=1 n 1 k U (k) N =θ U + N 1 α U (X i ; F ) + N 1 i=1 satisfies E(R U ) = 0 and E K k=1 n 1 k ( ) RU 2 1 i<j n k β U (X k,i, X k,j ; F ) + R U, = O(K 3 N 4 ) under Condition 2.2. According to Theorem 2.4, if E α U (X 1 ; F ) 2+δ < and K = O(N τ ) for some positive δ and
33 20 τ < 1, then as N, { } { sup P N 1/2 σ 1 α,u (U θ U ) x P N 1/2 σ 1 α,u (U N θ U ) x} = o(1). x R Now we consider the bootstrap version of the distributed U-statistic. Let X (1),..., X (K) be an i.i.d. sample from the empirical distribution F N and U (k) = U( X (k) ) be the corresponding U-statistic based on X (k), for k = 1,..., K, then U (k) =2{n k(n k 1)} 1 =θ UN + n 1 k n k i=1 1 i<j n k h(x k,i, X k,j ) α U (X k,i ; F N) + n 2 k where θun = E( U (k) ) FN = N 2 N N i=1 j=1 h(x i, X j ), and β U (Xk,i, X k,j ; F N) + R (k) U, 1 i<j n k α U (x; F N ) = 2 [ E { h(x, X k,2 ) F N} θ UN ], β U (x, y; F N ) = 2h(x, y) α U (x; F N ) α U (y; F N ) 2θ UN. Thus, the bootstrap distributed statistic U = N 1 K k=1 n ku (k) is in the form of (2.9) with reminder term R U = N 1 K k=1 n kr (k) U. Represent α U(x; F N ) and β U (x, y; F N ) in term of α U (x; F ) and β U (x, y; F ), we have and α U (x; F N ) =α U (x; F ) N 1 N 2 N i=1 j=1 β U (x, y; F N ) =β U (x, y; F ) N 1 + N 2 N i=1 j=1 N i=1 α U (X i ; F ) + N 1 N β U (X i, X j ; F ), N i=1 N β U (X i, X j ; F ). N i=1 β U (x, X i ; F ) N 1 β U (x, X i ; F ) N i=1 β U (X i, y; F ) By simple algebra, it is checked that N i=1 α U(X i ; F N ) = 0, β U (x, y; F N ) is symmetric in x and y, and N i=1 {β U(X i, y; F N )} = 0 for any y S(F ). Furthermore, according to the condition E{h(X 1, X 2 )} 2 <, sup x S(F ) α U (x; F N ) α U (x; F ) = o p (1) and sup x,y S(F ) β U (x, y; F N ) β U (x, y; F ) = o p (1) are easily verifiable by law of large numbers.
34 Note that R (k) U = 2n 2 k (n k 1) 1 1 i<j n k β U (Xk,i, X k,j ; F N), E ( R (k) E ( R (k)2 ) FN = Op (n 4 ), from which U k 21 P { RU N 1/2 (lnn) 1 } F N = o p (1) U ) FN = 0 and can be verified by Cauchy-Schwarz inequality and the condition that K = O(N τ ) for a positive τ < 1. Thus the conditions in Theorem 2.7 are all satisfied by the U-statistic. Finally, let ˆσ α,un 2 = E { αu 2 (X 1,1 ; F } N) F N, if E {h(x1, X 1 )} 2 <, Theorem 2.7 implies that { } sup P 1 N 1/2ˆσ α,un (U θun) { x F N P N 1/2 σ 1 α,u (U θ U ) x} = o p (1), x R and ˆσ 2 α,un σ2 α,u = o p(1). Even the entire sample bootstrap enjoys nice theoretical properties, it has several limitations when applied to massive data. Data communication expenditure is the most serious issue. Resampling from the whole dataset X N is expensive for huge datasets. Moreover, the whole data may be stored in different locations, which makes the entire sample bootstrap require data communication among different data clusters at different locations. In addition, θ N = θ(f N) has the same computational complexity as T N. For instance, for the U-statistics discussed above, θ UN = N 2 N i=1 N j=1 h(x i, X j ) which is computationally expensive for massive data BLB and SDB The bag of little bootstrap (Kleiner, et al., 2014) and the subsampled double bootstrap (Sengupta, Volgushev and Shao, 2016) are two novel resampling-based methods for massive data with emphasis on accessing the quality of estimators. Suppose ˆθ N = ˆθ N (F N ) is an estimator of θ = θ(f ) based on sample X N = {X 1,..., X N }. Let u(ˆθ N, θ) be some quantity concerning ˆθ N, and Q N (F ) be its sampling distribution, which is unknown because it depends on the underlying distribution F. We are interested in an assessment ξ {Q N (F )} of u(θ N, θ), regarding an aspect of Q N (F ). For example, if u(ˆθ N, θ) = ˆθ N θ is the estimation error of ˆθ N, ξ {Q N (F )} is the expectation of u(ˆθ N, θ) representing the bias of ˆθ N. Similarly, ξ {Q N (F )} can define the mean square error of ˆθ N or a confidence interval of θ. Resampling methods like the bootstrap can be used to estimate ξ {Q N (F )}. The basic idea of the bootstrap is, first estimate the unknown sampling distribution Q N (F ) by an empirical
35 22 distribution, which can be derived by resampling the observed data, then estimate ξ {Q N (F )} by plug in the empirical distribution as an estimate of Q N (F ). For the conventional bootstrap, by resampling on the entire data, we can obtain a number (B) of resamples, denoted as X (b) N = {X (b) 1,..., X (b) (b) N }, b = 1,..., B. For each resample, we calculate u(ˆθ N, ˆθ (b) N ) where ˆθ N = ( (b) ) (b) ˆθ N F N with F N be the empirical distribution of X (b) N. Then the empirical distribution of {u(ˆθ (b) N, ˆθ N ), b = 1,..., B}, denoted as Q N, can be used to estimate Q N(F ). Finally, ξ{q N } is used to estimate ξ {Q N (F )}. For massive data, calculating ˆθ N and ˆθ (b) N for each resample in the conventional bootstrap can be computationally expansive. Kleiner, et al. (2014) proposed the bags of little bootstrap (BLB) to obtain an estimate of ξ {Q N (F )} for massive datasets. estimators ˆθ N and ˆθ (b) N To avoid calculating the directly, the first step of the BLB is randomly sampling subsets of small size from the entire data. In the BLB, S subsets of size n (chosen to be n = N ς for some 0 < ς < 1) are sampled from the original dataset X N without replacement (these subsets can be disjoint predefined subsets of X N ). Denote the s-th subset as X s,n = {X s,1,..., X s,n } and its empirical distribution as F s,n, for s = 1,..., S. Then calculating the corresponding estimator ˆθ s,n = ˆθ n (F s,n ) for each subset is computationally economical. The next step is constructing estimates of Q N (F ) for each subset. Instead of using Q n (F s,n ), the key idea of the BLB is the usage of Q N (F s,n ), even though F s,n has its support on only n points (Kleiner, et al., 2014). Then the BLB s estimate of ξ {Q N (F )} is S 1 S s=1 ξ {Q N(F s,n )}. For each subset X s,n, in order to approximate ξ {Q N (F s,n )}, we generate B resamples of size N from the subset and denote them as X (b) s,n = { X (b) s,1,..., X (b) s,n }, b = 1,..., B. Actually, in order to generate the resample X (b) s,n, it is equivalent to draw a multinomial random vector with index N and parameter n 1 1 n, denoted as W (b) s,n the frequencies for each datum in X s,n in the resample. ( Xs,n, W (b) ) s,n, for s = 1,..., S and b = 1,..., B. ˆθ (b) s,n Let F (b) s,n = ˆθ N ( F (b) s,n = ( w (b) s,1,..., w (b) s,n Thus X (b) s,n ), which represents can be represented as be the empirical distribution of the resample ( X s,n, W (b) ) s,n. Calculate the estimator ) (ˆθ (b) and compute u s,n, ˆθ s,n ) for each resample. Then for each subset Xs,n, the empirical distribution of { u (ˆθ (b) s,n, ˆθ s,n ), b = 1,..., B }, denoted as Q N ( Fs,n ), is used to estimate Q N (F s,n ). Finally, the estimate of ξ {Q N (F )} is obtained by averaging ξ { Q N (F s,n) }
36 23 over S different subsets, that is S 1 S s=1 ξ {Q N (F s,n)}. A diagram summary of the BLB procedure is shown in Figure 2.1. Kleiner, et al. (2014) proved that under some conditions, S 1 S s=1 ξ {Q N (F s,n)} convergence to ξ {Q N (F )} in probability as n goes into infinity. (X 1,1,..., X 1,n ) Multinomial N, 1 n,..., 1 n (1) (1) (w 1,1..., w1,n ) X 1,1,..., X 1,n (1) (1) X 1,1,..., X1,N. (1) θ 1,n. θ u(θ 1 1,n, θ 1,n ). ξ{q N (F 1,n )} θ 1,n (B) (B) X 1,1,..., X1,N (B) θ 1,n u(θ B 1,n, θ 1,n ) X 1,..., X N. S S 1 ξ{q N (F s,n )} s=1 θ N X S,1,..., X S,n (1) (1) X S,1,..., XS,N. (1) θ S,n θ. u(θ 1 S,n, θ S,n ). ξ{q N (F S,n )} θ S,n (B) (B) X S,1,..., XS,N (B) θ S,n u(θ B S,n, θ S,n ) Figure 2.1 A diagram summary of the BLB procedure. Sengupta, Volgushev and Shao (2016) proposed a method based on the idea of the BLB and a fast double bootstrap (Davidson and MacKinnon, 2002; Chang and Hall, 2015), called the subsampled double bootstrap (SDB). For the SDB, a large number (S) of random subsets of size n are sampled from the original dataset, which is similar as in the BLB. Then for each subset X s,n = { X s,1,..., X s,n}, instead of using B resamples, only one resample X (1) s,n = { X (1) s,1,..., } X (1) s,n is generated in the SDB. So for each subset, only one u(ˆθ (1) s,n, ˆθ s,n) is obtained, here ˆθ s,n = ˆθ N (F s,n) and ˆθ (1) s,n = ˆθ N (Fs,n (1) ), where Fs,n and Fs,n (1) are the empirical distributions of X s,n and X (1) s,n, respectively. Then the empirical distribution of { u(ˆθ (1) s,n, ˆθ s,n), s = 1,..., S }, denoted as Q N,n,S, is used to estimate Q N(F ), and ξ { Q N,n,S} is the SDB s estimate of ξ {Q N (F )}.
37 24 The key idea of the BLB and the SDB is generating resamples with sizes equal to the size of the original data by resampling a small subset, and this can be done by sampling a multinomial distributed random vector (W (b) s,n ) of length n. The BLB and the SDB have computational advantages only when the estimator can be calculated directly with the weighted data representation ( X s,n, W (b) ) s,n, for example, general M-estimators. In those cases, the computational requirement of calculating ˆθ (b) s,n is scale in n, rather than N. There are several differences between the BLB and the SDB. First, the number of subsets S in the BLB can be either finite or infinite, while for the SDB, S needs to diverge to infinity. In the BLB, we get an estimate of ξ{q N (F )} for each subset by generating B resamples. In contrast, only one u(ˆθ (1) s,n, ˆθ s,n) is derived from the each subset X s,n in the SDB and the estimate of ξ{q N (F )} is based on these X s,n s across the subsets. Thus the SDB requires resampling from the entire dataset X N to get the random subsets {X s,n, s = 1,..., S}. For massive data that stored in different locations, resampling from the entire dataset in the SDB would reduce its computational appeal. The BLB can be applied with the subsets {X s,n, s = 1,..., S} chosen as each data block and the following procedures can all be done within each data block. Data communication are only needed for the final average step which is cheap and convenient. So the BLB can be implemented distributively and thus is suitable for massive data that stored in different locations. There are several limitations of the BLB, as mentioned in Sengupta, Volgushev and Shao (2016). First, Kleiner, et al. (2014) suggests using a small number of subsets (small S) but a large number of resamples for each subset (big B), which leads to that only a small portion of the whole data is used to get the BLB estimator. Second, using too many resamples for each subset can increase the computational burden. Last, it is unclear how to choose S and R for the BLB to achieve optimal statistical efficiency. To overcome these limitations, we propose a distributed bootstrap method which does not require communication among different data blocks.
38 Distributed bootstrap We are interested in approximating the distribution of N 1/2 (T θ) for massive datasets, especially when the data are stored in different locations. In this case, resampling from the entire dataset could be computationally costly. By recognizing the natural formation of the distributed statistics, we consider doing resampling within each data block. Suppose the entire data have already been divided into K subsets: X (1),..., X(K). For each subset X (k), we generate B resamples of the same size n k, denote them X 1(k),..., X B(k) Compute the corresponding statistic T b(k) = T ( X b(k) k = 1,..., K. Average them over K subsets leads to for b = 1,..., B. Let F (k) T b = N 1 K k=1 n k T b(k) be the empirical distribution of X(k). ) for each resampled data block, for and θ (k) = θ( F (k) ) be the analogy of θ under X (k). Define θ = N 1 K k=1 n kθ (k), then the empirical distribution of { N 1/2 (T b θ ), b = 1,..., B} is used to approximate the distribution of N 1/2 (T θ). The algorithm is outlined in Table 2.1. Table 2.1 Algorithm for the distributed bootstrap. Input: data X (1),..., X(K) ; n 1,..., n K, subset sizes; B, number of Monte Carlo iterations; T, function deriving statistic Output: an estimate of the distribution of N 1/2 (T θ) For k 1 to K do end End compute θ (k) = θ(f (k) ) for b 1 to B do generate resample X b(k) compute T b(k) = T ( X b(k) from X(k) Compute θ = N 1 K k=1 n kθ (k) For b 1 to B do compute T b = N 1 K k=1 n kt b(m) End ) and N 1/2 (T b θ )
39 26 We call this algorithm the distributed bootstrap because all the sampling procedures can be fulfilled within each data block. For each subset in each iteration, we can calculate T b(k) and θ (k) totally locally and avoid data communication between different data blocks. These make the distributed bootstrap suitable for the massive data setting. Besides the advantages in computing, we want to investigate the asymptotic properties of the distributed bootstrap. Similar as the technique used in establishing theoretical properties of the entire sample bootstrap, we need to make assumptions on the statistics derived from each resampled data block. For k = 1,..., K, denote F (k) as the empirical distribution of X (k), let X (k) = { Xk,1,..., } X (k) k,n k be i.i.d. resamples drawn from F. Suppose that for k = 1,..., K, T (k) = T (X (k) ) has the following form T (k) = θ (k) + n 1 k n k i=1 α ( Xk,i ; F (k) ) + n 2 k 1 i<j n k β ( X k,i, Xk,j ; F (k) ) (k) + R, where θ (k) = θ( F (k) ) (k), R = R( X (k) ; F (k) ) (k) are the analog of θ and R Then T = N 1 K k=1 n kt (k) can be written as T = θ + N 1 K n k k=1 i=1 α ( Xk,i ; F (k) ) + N 1 K k=1 n 1 k 1 i<j n k β where θ = N 1 K k=1 n kθ (k) and R = N 1 K k=1 n kr (k) We have the following assumptions on α ( x; F (k) Condition 2.6. For k = 1,..., K, the functions α ( x; F (k) F (k), satisfy n k i=1 α( X k,i ; F (k) ) = 0 and sup is symmetric in x and y, n k i=1 x S(F ). ) and β ( x, y; F (k) ). α ( x; F (k) under F (k). ( X k,i, X k,j ; F (k) ) + R, ) ( (k) and β x, y; F ), depending on ) α(x; F ) = o p (1); β ( x, y; F (k) ) { β ( Xk,i, y; F (k) )} = 0 for any y S(F ) and ( sup (k) β x, y; F ) β(x, y; F ) = op (1). x,y S(F ) The following theorem establishes the consistency of the distributed bootstrap. Theorem 2.8. Under the conditions of Theorem 2.4 and E β(x 1, X 1 ; F ) 2 <, suppose there exist functions α ( x; F (k) ) ( (k) and β x, y; F ), k = 1,..., K satisfy Condition 2.6, let T = θ + N 1 K n k k=1 i=1 α ( Xk,i ; F (k) ) + N 1 K k=1 n 1 k 1 i<j n k β ( X k,i, X k,j ; F (k) ) + R,
40 27 { where R satisfies P R N 1/2 (lnn) 1 } (1) F,..., F (K) = o p (1), then as N, { sup P N x R 1/2ˆσ 1 } α, (T θ) { x F (1),..., F (K) P N 1/2 σα 1 (T θ) x} and ˆσ α, 2 σ2 α = o p (1) where ˆσ α, 2 = N 1 { K k=1 n ke α 2( Xk,1 ; F (k) ) } (k) F. = o p (1), Theorem 2.8 gives theoretical support for the distributed bootstrap, which works for both finite and infinite K, as long as K is at a proper order of N. The condition on K is hidden in the assumption P { R N 1/2 (lnn) 1 F (1),..., F (K) a U-statistic defined in (2.10), R (k) U satisfies E ( R (k) U } = op (1). For example, for ) ( ) = 0 and E R (k)2 (k) U F = F (k) O p (n 4 k ), for k = 1,..., K. Thus the consistency of the distributed bootstrap for the U-statistic is ensured as long as K = O(N τ ) for a positive τ < 1. Again, for specific statistics, we need to check the bootstrap distributed statistic satisfies the conditions assumed in Theorem 2.8. It is worth mentioning that the underlying empirical distribution for each subset are different, as we are resampling from each subset, the bootstrap resamples { X (1),..., X (K) } are not identically distributed. This theorem ensures that the distributed bootstrap procedure can be utilized in a broad range by combining it with the continuous mapping theorem and delta method, for instance in the variance estimation and confidence interval establishing. Let ˆσ 2 DB = B 1 B b=1 ( T b B 1 B l=1 T l ) 2 be the sample variance of {T b, b = 1,..., B}. Then ˆσ2 DB is a consistent estimator of N 1 σ 2 α, hence it is a consistent estimator of Var(T ). In addition, denote u τ as the lower τ quantile of the empirical distribution of { N 1/2( T b θ ), b = 1,..., B }, then an equal-tail two-sided confidence interval for θ with level 1 τ can be constructed as ( ) T N 1/2 u 1 τ/2, T N 1/2 u τ/2.
41 Pseudo-distributed bootstrap Even the distributed bootstrap can save computing time substantially, it can still be computationally expensive when the size of the data is huge. The reason is that the distributed statistic need to be recalculated for each resample in the distributed bootstrap procedure. To avoid this issue, we consider another way for approximating the distribution of T under the assumption that K diverges (K ). The idea comes from the expression T = N 1 K k=1 n k T (k) = K 1 K (Kn k /N)T (k) which indicates that T is the average of K independent random variables. So when K is large enough, approximating the distribution of T is similar to the problem that approximating the distribution of the sample mean of a sequence of independent but not necessary identically distributed samples. In view of this point, if K, we can propose a computational more efficient bootstrap strategy, which directly resamples { T } (k) K rather than the original data. k=1 We state our approach in a more general way, not restricted to T with the form (2.3). Denote T (k) = T( X (k) ), k = 1,..., K as a sequence of statistics obtained from each sub- ) = θk and Var ( T (k) ) = σ 2 k where σk 2 (0, ) for k = 1,..., K, also set. Suppose E ( T (k) k=1, denote θ = K 1 K k=1 θ k and σ 2 = K 1 K k=1 σ2 k. Let T = K 1 K k=1 T(k) be the average of { T (k) } K k=1. To estimate the distribution of K1/2 ( T θ ), we randomly draw B resamples T b(1),..., T b(k), b = 1,..., B from F K,T, where F K,T is the empirical distribution of { T (k) } K. Denote T b k=1 = K 1 K k=1 T b(k) for b = 1,..., B, then the empirical distribution of { K 1/2( T b T )} B b=1 is used to estimate the one of K1/2 ( T θ ). We call this algorithm the pseudo-distributed bootstrap and its procedure is summarized in Table 2.2. The pseudo-distributed bootstrap is the conventional bootstrap procedure carried out on the statistics { T (k) K }, which are independent but not necessary identically distributed. The k=1 bootstrap procedures under non-i.i.d. models has been studied in Liu (1988). The key idea is that even the statistics { T (k) K } are not i.i.d., the bootstrap still draws i.i.d. samples. The k=1 following proposition establishes the asymptotic properties of the pseudo-distributed bootstrap, which is an immediate result of Theorem 1 in Liu (1988).
42 29 Table 2.2 Algorithm for the pseudo-distributed bootstrap. Input: data X (1),..., X(K) ; K, number of subsets; B, number of Monte Carlo iterations; T, function deriving statistic Output: an estimate of the distribution of K 1/2 ( T θ ) For k 1 to K do compute T (k) = T( X (k) ) End Compute T = K 1 K k=1 T(k) For b 1 to B do generate resample T b(1),..., T b(k) compute T b = K 1 K k=1 T b(k) End For b 1 to B do compute K 1/2( T b T End ) from T(1),..., T(K) Proposition 2.2. Let T (1),..., T(K) be a sequence of statistics derived from each subset X (k), with E( T (k) ) = θk and Var ( T (k) ) = σ 2 k, k = 1,..., K. Denote T = K 1 K k=1 T(k) and θ = K 1 K k=1 θ K. Let T (1),..., T (K) be an i.i.d. sample from F K,T, where F K,T is the empirical distribution of { T (k) } K k=1. Denote T = K 1 K k=1 T (k). Suppose inf k σk 2 > 0 and sup k E (k) T 2+δ < for some positive δ. Moreover, assume K 1 K ( k=1 θk θ ) 2 0 as K. Then with probability 1, as K, } sup {K P 1/2 (T T ) x F K,T x R { P K 1/2 (T θ) x} = o(1). (2.11) This proposition ensures that under the conditions on the moments of { T (k) } K k=1, the pseudo-distributed bootstrap is asymptotic consistent. This result is quite general because we do not impose any other conditions on T (k) rather than its moments. That is, T(k) is not required to be in the form of (2.1). For specific statistics, we only need to check the moment conditions in Proposition 2.2 to get the consistency result. The following corollaries indicate that the pseudo-distributed bootstrap works for the distributed statistics in the form (2.3) under mild conditions.
43 30 Corollary 2.1. For T in (2.3) with σ 2 α > 0, under the conditions assumed in Theorem 2.4, let T (k) = N 1/2 K 1/2 n k T (k) for k = 1,..., K and F K,T be the empirical distribution of {T (k) }K k=1. (1) Suppose T,..., T (K) is an i.i.d. sample from F K,T and denote T = K 1 K k=1 T (k). Assume E β(x 1, X 2 ; F ) 2+δ < and sup k E n 1/2 k R(k) 2+δ <, in addition, sup k N 1/2 K 1/2 n k NK 1 0 as N, then with probability 1, as K, sup {K P 1/2 (T N 1/2 K 1/2 T ) x F K,T x R } { P N 1/2 (T θ) x} = o(1). Corollary 2.1 shows that under moderate conditions on n k, K and the moments of T (k), the pseudo-distributed bootstrap is asymptotic consistent when σ 2 α > 0. The resampling procedure is carried out on the scaled statistics { T (k) } K k=1 as we have different sample size for each subset. The condition sup k N 1/2 K 1/2 n k NK 1 0 requires that the sample size of each subset should not be too far away from each other and this associates with the condition K 1 K k=1 ( θk θ ) 2 0 in Proposition 2.2. Comparing with the distributed bootstrap, besides the gain in computing, an appealing property of the pseudo-distributed bootstrap is that it does not require the bootstrap statistic has certain form as assumed in Theorem 2.7 and 2.8. This makes the pseudo-distributed bootstrap more versatile and easier to verify. In addition, we would like to claim that the pseudo-distributed bootstrap has appropriate convergence rate. First, we assume that the remainder terms {R (k) }K k=1, are small enough such that they can be dominated and thus omitted in the following discussion. Furthermore, suppose n k = NK 1 for k = 1,..., K. Under the conditions E α(x 1 ; F ) 4 < and E β(x 1, X 2 ; F ) 4 <, by Theorem 5.18 of Petrov (1998), { P K 1/2 s } 1 (T N 1/2 K 1/2 T ) x F K,T =Φ(x) 6 1 K 1/2 s { ( ) } 3 E T (1) 3 N 1/2 K 1/2 T F K,T (x 2 1)φ(x) + O p (K 1 ) uniformly in x R where s 2 = K 1 ( K 2. k=1 T (k) ) T Mentioned that E { ( T (1) N 1/2 K 1/2 T ) 3 F K,T } = O p (n 1/2 k + K 1/2 ),
44 31 this clearly implies sup {K P 1/2 s } 1 (T N 1/2 K 1/2 T ) x F K,T Φ(x) = O p(n 1/2 + K 1 ). x R According to the proof of Theorem 2.4, { } sup P N 1/2 σα 1 (T θ) x Φ(x) = O(N 1/2 ), x R it follows that sup {K P 1/2 s 1 (T N 1/2 K 1/2 T ) x F K,T x R =O p (N 1/2 + K 1 ). } { P N 1/2 σα 1 (T θ) x} This result indicates that the convergence rate of the pseudo-distributed bootstrap is at the order of O p (N 1/2 + K 1 ). The next corollary gives theoretical support for the pseudo-distributed bootstrap when applied to the distributed statistics in the form (2.3) under degeneracy. Corollary 2.2. For T in (2.3) with σ 2 α = 0 but σ 2 β > 0, under Conditions 2.1, 2.3 where E(R N ) = b 1 N τ 1 + o(n τ 1 ) and Var(R N ) = o(n τ 2 ) for some τ 1 > 1, τ 2 2, assume n k = NK 1 for k = 1,..., K and K = O(N τ ) for some positive constant τ < 1 1/(2τ 1 1). Let T (k) = n kt (k) for k = 1,..., K and F K,T be the empirical distribution function of {T (k) }K k=1. Suppose T (1),..., T (K) is an i.i.d. sample from F K,T and denote T = K 1 K. Assume E β(x 1, X 2 ; F ) 2+δ < and sup k E n k R (k) 2+δ < for some positive constant δ, then with probability 1, as K, sup {K P 1/2 (T NK 1 T ) x F K,T x R k=1 T (k) } { P NK 1/2 (T θ) x} = o(1). Comparing with the case of σ 2 α > 0, stronger conditions are needed for the degenerate statistics. First, τ 1 should be strictly larger than 1 such that R can be dominated by the quadratic term involving β. Second, n k is assumed to be the same for all subsets and K is required to have a smaller order. Last, stronger moment condition is needed for R (k). These two corollaries reveal the versatility of the pseudo-distributed bootstrap. It works for both non-degenerate and degenerate statistics, the procedures are the same except that different scalers are used.
45 Comparison of the distributed bootstrap, the pseudo-distributed bootstrap, the BLB and the SDB In this section, we compare the distributed bootstrap (DB), the pseudo-distributed bootstrap (PDB), the bag of little bootstrap (BLB) and the subsampled double bootstrap (SDB) in approximating the distribution function of T. First, we compare them regarding their computational complexity. In order to make our discussion more straightforward, we assume that the entire data are divided evenly into K blocks, that is, n 1 = = n K = K 1 N. Suppose that the time cost for calculating the statistic in (2.1) on a sample of size m is t(m), then the computing time of the BLB with B resamples for each of the S subsets is S { BKt(K 1 N) + t(n) }, where n is the size of the subsets {X s,n, s = 1,..., S}. For the SDB with S random subsets of size n, its computational complexity is S { Kt(K 1 N) + t(n) }. If we generate B resamples in the distributed bootstrap, the computational cost would be (B +1)Kt(K 1 N) for the distributed bootstrap. In addition, the pseudo-distributed bootstrap requires Kt(K 1 N) + BK time to fulfill its implementation with B pseudo resamples. Thus the pseudo-distributed bootstrap is the fastest among these four resampling strategies, which is due to that the PDB benefits from avoiding recalculating the distributed statistic for each iteration. The distributed bootstrap and the SDB have similar computational cost if S is close to B. However, the SDB can not be implemented distributively. For the BLB, its computational complexity depends on both S and B. Moreover, if given a fixed time budget, it is not clear how to select S and B to achieve the optimal statistical accuracy, see more discussions in Sengupta, Volgushev and Shao (2016). For massive dataset that stored in different locations, the advantage of the SDB is limited because it requires random sampling from the entire dataset, while the other three methods can be implemented distributively within each data block. Furthermore, only the pseudodistributed bootstrap requires K diverges, the other three approaches work for both cases when K is finite or diverging. Comparison of these four resampling methods is summarized in Table 2.3.
46 33 Table 2.3 Comparison of the distributed bootstrap (DB), the pseudo-distributed bootstrap (PDB), the BLB and the SDB. Computing Time Distributed or Not Requirement on K DB (B + 1)Kt(K 1 N) distributed finite or diverging PDB Kt(K 1 N) + BK distributed diverging BLB S { BKt(K 1 N) + t(n) } distributed finite or diverging SDB S { Kt(K 1 N) + t(n) } not distributed finite or diverging 2.10 Applications Distance covariance and distance correlation, introduced in Székely, Rizzo and Bakirov (2007), are distance based methods that measuring and testing dependence between two random vectors. The distance covariance and correlation of two random vectors are equal to zero if and only if these two random vectors are independent. This attractive property makes the distance variance and correlation more versatile in detecting dependence than the classic Pearson correlation, especially for non-linear dependence. Distance covariance and correlation have been used in many literatures, for example, feature screening (Li, Zhong and Zhu, 2012), sufficient dimension reduction diagnostic (Chen, Cook and Zou, 2015) and testing mutual independence under high-dimensionality (Yao, Zhang and Shao, 2016). In this section, we focus on the distance covariance and its usage in testing independence for massive data. Suppose Y and Z are two random vectors having finite first moments and taking values in R p and R q, respectively. Let φ Y (t) and φ Z (s) be the characteristic functions of Y and Z, and φ Y,Z (t, s) be the joint characteristic function of Y and Z. The distance covariance between Y and Z is defined as dcov 2 (Y, Z) = φ Y,Z (t, s) φ Y (t)φ Z (s) 2 ω(t, s)dtds, (2.12) R p+q where ω(t, s) = ( c p c q t 1+p p s 1+q q ) 1 is a weight function with cd = π (1+d)/2 /Γ {(1 + d)/2} and a d is the Euclidean norm of a R d. For a complex-valued function φ, φ 2 = φ φ where φ is the conjugate of φ. Denote X = (Y T, Z T ) T, under the condition that E Y p +E Z q <, dcov 2 (Y, Z) = E Y Y p Z Z q 2E Y Y p Z Z q + E Y Y p E Z Z q, where X = (Y T, Z T ) T and X = (Y T, Z T ) T are independent copies of X.
47 34 Suppose that X N = {X 1,..., X N } is an observed sample from F, the joint distribution of X, and X i = (Y T i, ZT i )T for i = 1,..., N. Define A ij = X i X j p and B ij = Y i Y j q for i, j = 1,..., N. In this paper, we consider the U-centered version of empirical distance covariance (Székely and Rizzo, 2014; Yao, Zhang and Shao, 2016) which is defined by dcov 2 N(Y, Z) = {N(N 3)} 1 i j à ij Bij, (2.13) where and à ij = A ij (N 2) 1 B ij = B ij (N 2) 1 N l 1 =1 N l 1 =1 for i j. By simple algebra, A l1 j (N 2) 1 B l1 j (N 2) 1 dcov 2 N(Y, Z) = {N(N 1)} 1 i j N l 2 =1 N l 2 =1 A il2 + {(N 1)(N 2)} 2 B il2 + {(N 1)(N 2)} 2 A ij B ij + {N(N 1)(N 2)} 1 + {N(N 1)(N 2)(N 3)} 1 i j l 1 l 2 A ij B l1 l 2, N l 1 =1 l 2 =1 N l 1 =1 l 2 =1 i j l 1 A ij B il1 N A l1 l 2, N B l1 l 2, from which we can see that dcov 2 N (Y, Z) is an unbiased estimator of dcov2 (Y, Z). Moreover, dcovn 2 (Y, Z) is a U-statistic of degree 4. When the sample size N is large, there are two issues when computing dcovn 2 (Y, Z). First, the computational complexity of dcov 2 N (Y, Z) is at the order of O(N 2 ), which is expensive when N is large. Second, the memory requirement in calculating dcovn 2 (Y, Z) is of order O(N 2 ), which makes the computing less feasible for a larger N. For example, when N = 10 5, it requires more than 70 Gigabyte storage in memory in order to complete the calculation of dcovn 2 (Y, Z). Thus we employ a distributed version of the distance covariance under the massive data scenario. Suppose the entire data X N are divided into K sub-samples with the k-th subset X (k) = {X k,1,..., X k,nk } of size n k for k = 1,..., K. Denote dcov 2(k) (Y, Z) as the empirical distance covariance based on X (k). Then the distributed distance covariance is defined as dcov 2 (Y, Z) = N 1 K k=1 n k dcov 2(k) (Y, Z). (2.14)
48 35 It is easy to see that dcov 2 (Y, Z) is also an unbiased estimator of the population distance covariance dcov 2 (Y, Z). The distributed distance covariance enjoys two advantages in computing. Assume that n k, k = 1,..., K have the same order, then the computing time of dcov 2 (Y, Z) is of order O(K 1 N 2 ), which is much less than O(N 2 ), the computational complexity of dcovn 2 (Y, Z). Moreover, the memory requirement of computing dcov2 (Y, Z) is only O(K 2 N 2 ), which makes dcov 2 (Y, Z) more feasible when the size of the data is large. Besides that, computing dcov 2 (Y, Z) can be easily parallelized which is suited to modern parallel and distributed computing architectures. Now we consider testing independence between Y and Z using the distance covariance. That is to test the hypothesis H 0 : Y and Z are independent versus H 1 : Y and Z are dependent. (2.15) Under the null hypothesis that Y and Z are independent, if E Y 2 p + E Z 2 q <, then the empirical distance covariance dcovn 2 (Y, Z) is a degenerate U-statistic that has the following representation (Yao, Zhang and Shao, 2016): dcov 2 N(Y, Z) = N 2 1 i<j N β(x i, X j ; F ) + R N, where β(x i, X j ; F ) = 2U(Y i, Y j )V(Z i, Z j ) with U(y, y ) = y y p E y Y p E Y y p + E Y Y p and V(z, z ) = z z q E z Z q E Z z q + E Z Z q, and R N = R(X N ; F ) is the reminder term satisfies E(R N ) = 0 and Var(R N ) = O(N 3 ). It is easy to verify that under the null hypothesis, E{β(X 1, X 2 ; F ) X 1 } = 0 and E {β(x 1, X 2 ; F )} 2 = 4E {U(Y 1, Y 2 )} 2 E {V(Z 1, Z 2 )} 2 σ 2 β <. If the empirical distance covariance dcovn 2 (Y, Z) in (2.13) is used as the test statistic, we need to obtain a reference distribution for dcovn 2 (Y, Z) using the bootstrap on the entire dataset (Arcones and Giné, 1992) or random permutation (Székely, Rizzo and Bakirov, 2007). For massive dataset, computing dcovn 2 (Y, Z) itself is a big issue as discussed before. Moreover, the bootstrap and random permutation on the entire dataset are both computationally expensive as we need to recalculate the distance covariance for each resample or permutation. Thus we consider using the distributed distance covariance dcov 2 (Y, Z) as the test statistic. Under
49 36 the null hypothesis, if E Y 2 p + E Z 2 q <, dcov 2 (Y, Z) can be rewritten as dcov 2 (Y, Z) = N 1 K k=1 n 1 k 1 i<j n k β(x k,i, X k,j ; F ) + R, (2.16) where R = N 1 K k=1 n kr ( X (k) ; F ) is the remainder term that satisfies E(R ) = 0 and Var(R ) = O(K 2 N 3 ). Thus according to Theorem 2.6, we have the following asymptotic result concerning dcov 2 (Y, Z). Corollary 2.3. Assume there exists a constant δ > 0 such that E Y 2+δ p + E Z 2+δ q <. There exist positive constants c 1 and c 2 such that c 1 inf k1,k 2 n k1 /n k2 sup k1,k 2 n k1 /n k2 c 2. In addition, if K and K = o(n), then under the null hypothesis that Y and Z are independent, 2 1/2 K 1/2 Nσ 1 β dcov2 (Y, Z) d N (0, 1) as N, where σ 2 β = 4E {U(Y 1, Y 2 )} 2 E {V(Z 1, Z 2 )} 2. In order to carry out the test using this asymptotic normality result, we need to get a consistent estimator of σ 2 β, or equivalently, estimators of E {U(Y 1, Y 2 )} 2 and E {V(Z 1, Z 2 )} 2. Mentioned that dcov 2 (Y, Y) = E {U(Y 1, Y 2 )} 2 and dcov 2 (Z, Z) = E {V(Z 1, Z 2 )} 2 are the distance variances (Székely, Rizzo and Bakirov, 2007) of Y and Z, respectively, it is straightforward to use the distributed version of the empirical distance variances to estimate dcov 2 (Y, Y) and dcov 2 (Z, Z). Let then ˆσ 2 β, = 4 { dcov 2(k) (Y, Y) = {n k(n k 3)} 1 dcov 2(k) (Z, Z) = {n k(n k 3)} 1 N 1 is an unbiased estimator of σ 2 β K k=1 n k dcov 2(k) (Y, Y) estimator is established in the next theorem. } { Ã 2 (k,i)(k,j), 1 i j n k B2 (k,i)(k,j), 1 i j n k N 1 under the null hypothesis. K k=1 n k dcov 2(k) (Z, Z) } The consistency of this variance
50 37 Theorem 2.9. Under the conditions in Corollary 2.3, if E Y 4 p+e Z 4 q <, then as N, ˆσ 2 β, /σ2 β p 1. Combine Corollary 2.3 and Theorem 2.9 with Slutsky s theorem, we have 2 1/2 K 1/2 N ˆσ 1 β, dcov2 (Y, Z) d N (0, 1) under the null hypothesis. Therefore, a test with nominal significant level τ reject H 0 if 2 1/2 K 1/2 N ˆσ 1 β, dcov2 (Y, Z) > z τ, (2.17) where z τ is the τ upper-quantile of the standard normal distribution, and the test procedure is ensured to have the nominal level of significance asymptotically. Furthermore, the implementation of the test includes calculating dcov 2 (Y, Z) and ˆσ2 β,, which both require O(K 1 N 2 ) order computing time. This feature makes the testing procedure based on the distributed distance covariance more friendly to massive datasets. For each subset X (k), after getting à (k,i)(k,j) and B (k,i)(k,j) for different i and j, we can obtain dcov 2(k) (Y, Z), dcov2(k) (Y, Y) and dcov 2(k) (Z, Z) for k = 1,..., K, which are sufficient to fulfill the test. Next we consider using the pseudo-distributed bootstrap to approximate the distribution of dcov 2 (Y, Z) under the null hypothesis, and as a consequence, to implement the independence test. Assume the sizes of all subsets are equal, that is n k = NK 1 for k = 1,..., K. Let F K,dcov be the empirical distribution of { dcov 2(1) (Y, Z),..., dcov2(k) (Y, Z)}. For b = 1,..., B, draw resample dcov 2 b(1) (Y, Z),..., dcov2 b(k) (Y, Z) from F K,dcov. Then dcov 2 b (Y, Z) = K 1 K k=1 dcov 2 b(k) (Y, Z), b = 1,..., B can be used to approximate the critical value of the test. According to Corollary 2.2, we have the following theoretical result supporting the pseudo-distributed bootstrap approach. Corollary 2.4. Under the conditions in Corollary 2.3, assume n k = NK 1 for k = 1,..., K. Let F K,dcov be the empirical distribution of dcov 2(1) (Y, Z),..., dcov2(k) (Y, Z). Suppose that dcov 2 (k) (Y, Z), k = 1,..., K are i.i.d. from F K,dcov and denote dcov 2 (Y, Z) = K 1 K k=1 dcov 2 (k) (Y, Z).
51 38 Then with probability 1, as K, { sup P 2 1/2 K 1/2 Ndcov(Y, 2 Z) x F K,T x R } { P 2 1/2 K 1/2 Ndcov(Y, 2 Z) x} = o(1). This corollary ensures that the test based on the pseudo-distributed bootstrap is consistent. Comparing with Theorem 2.9, fourth finite moment condition is not needed for the pseudodistributed bootstrap approach. In addition, the procedure based on the pseudo-distributed bootstrap is computational competitive. We will compare these two different approaches in the simulation studies Numerical studies In this section, we report numerical studies, using both simulated and real datasets, to valuate the performance of our proposed distributed approach and bootstrap algorithms. We also compare our approaches with the BLB (Kleiner, et al., 2014) and the SDB (Sengupta, Volgushev and Shao, 2016) to reveal the advantages of our methods. We focus on two different setups, one is the Gini s mean difference which measures the variability of a distribution, the other one is testing independence using the distance covariance. We fix the sample size as N = and vary the number of subsets K for different scenarios in the simulation studies. All the experiments executed in this section are ran in R with a single Intel(R) Core(TM) i7 GHz processor Gini s mean difference The Gini s mean difference is defined as U N = {N(N 1)} 1 1 i j N X i X j, which is a U-statistic of degree two, and it is an unbiased estimator of the dispersion parameter θ = E X i X j, which measures the variability of a distribution. Then U N has the formation as in (2.10). For massive data, we introduce the distributed version of U N. Suppose the entire data are divided into K data blocks, with each of size n k. For each block, denote U (k) as the Gini s mean difference obtained from the k-th data block, then the distributed Gini s mean
52 39 difference is U = N 1 K k=1 n ku (k). As U N is an unbiased estimator of θ, as long as K = o(n), U attains the same estimation efficiency as U N. For U N, we can use the jackknife (Efron and Stein, 1981) to estimate its variance, denoted as N 1 S 2 UN, where S 2 UN = 4(N 1)(N 2) 2 N i=1 (N 1) 1 j i 2 X i X j U N, and S 2 UN can be expanded as S 2 UN = σ 2 α,u + N 1 N i=1 γ U (X i, F ) + H UN, with γ U (X i, F ) = {α U (X i, F )} 2 σ 2 α,u + 2g(X i) and g(x) = E {α U (X 1, F )β U (x, X 1 ; F )}, the remainder term H UN satisfies E(H UN ) = O(N 2 ) and E(H 2 UN ) = O(N 2 ) (Callaert and Veraverbeke, 1981). Then S 2 UN is in the form of (2.1) with vanished quadratic term. As an estimator of Var(U N ), N 1 S 2 UN has a bias of order N 2. Because the variance of N 1 S 2 UN is of order O(N 3 ), the mean square error of N 1 S 2 UN is of order O(N 3 ). For the distributed statistic U, we propose a distributed jackknife variance estimator. Denote n 1 k S(k)2 (k) U as the jackknife variance estimator of U for the k-th block, then the distributed variance estimator for U is defined as N 1 S 2 U with S2 U = N 1 K k=1 n ks (k)2 U. According to Theorem 2.1, the mean square error of N 1 S 2 U as an estimator of Var(U ) is O(N 3 + K 2 N 4 ), which is still of order N 3 if K = o(n 1/2 ). Also the mean square error of N 1 S 2 U increases at the order of K2 when KN 1/2 diverges. In the simulations, we consider X 1,..., X N from three different distributions, thus we consider the following three scenarios. (I). N (1, 1): Normal distribution with mean 1 and unit variance; (II). Gamma(3, 1): Gamma distribution with shape parameter 3 and scale parameter 1; (III). P oisson(4): Poisson distribution with parameter 4. The first two distributions are continuous while the third one is discrete, and the true values of θ and Var(U ) can be calculated algebraically for the first two distributions. For Poisson distribution, the corresponding θ and Var(U ) can be approximated to a certain accuracy due to its discreteness. See Lomnicki (1952) for reference.
53 40 First, we want to study the performance of U as an estimator of θ by comparing it with U N, which is a special case of U when K = 1. In addition, we examine how N 1 S 2 U works as the estimator of the variance of U in terms of mean square errors (MSE). Let K = {5, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000} be the set of values for K we considered here. For the sake of convenience, we divide the whole dataset into blocks with equal size N/K in the simulations. And we use the notation MSE( ) to denote the mean square error of an estimator. With the distributions and parameters set up above, for each simulation, we generate {X i, i = 1,..., N} i.i.d. from the three distributions respectively. For each dataset, we calculate U N and its variance estimator N 1 SUN 2. Then for each K K, we estimate θ using U and estimate the variance of U by N 1 SU 2. Thus by carrying out a number of simulations, we can get MSE(U N ), MSE(N 1 S 2 UN ) and MSE(U ), MSE(N 1 S 2 U ) for each K K under three scenarios. We summarize the average mean square errors of U and N 1 SU 2 for all three scenarios in Figure 2.2, with each based on 2000 simulations. In order to compare the results of U with U N more intuitively, we plot the mean square error of U and N 1 S 2 U divided by those of U N and N 1 S 2 N,U respectively, that is, each point in Figure 2.2 is the average of MSE(U )/MSE(U N ) (Figure 2.2(a)) or MSE(SU 2 )/MSE(S2 UN ) (Figure 2.2(b)) for K K. Figure 2.2(a) shows that, the mean square error of U keeps increasing slowly as K goes bigger when K is not too large. Thus the distributed estimator U is almost as good as U N for relatively small K, this coincides with our theoretical results that U is unbiased and the variance increment occurs only in the second order term, so as long as O(N 1 ) is still the dominate order of the variance of U when K = o(n), the increment in mean square error of U is negligible. From the plot we can see that even when K is as large as 5000, which means that each block only contains 20 data points, the relative increase of mean square error is less than 10 percent for all three distributions. Thus U is still an reasonable substitute of U N as an estimator of θ in this situation. For N 1 S 2 U, Figure 2.2(b) shows that N 1 S 2 U is still comparable to N 1 S 2 N,U in the sense of mean square error for relatively small K. But the mean square error for N 1 S 2 U increases very fast for K lager than 200, and the outcomes vary for different underlying distribu-
54 41 MSE(U )/MSE(U N ) Normal Gamma Poisson ) )/MSE(N 1 S UN 2 MSE(N 1 S U Normal Gamma Poisson (a) MSE(U )/MSE(U N ) K (b) MSE(N 1 S 2 U)/MSE(N 1 S 2 UN ) K Figure 2.2 MSE(U )/MSE(U N ) and MSE(N 1 SU 2 )/MSE(N 1 SUN 2 ) against the number of blocks K for each scenario. tions. As we discussed before, the mean square error of N 1 SU 2 is of order O(N 3 +K 2 N 4 ) where the second order term increases at the order K 2. So for large K such that the O(K 2 N 4 ) order term dominates the term of order O(N 3 ), the mean square error of N 1 SU 2 would increase at the order of K 2, as demonstrated in Figure 2.2(b). In addition, Figure 2.3 depicts the variation of the absolute bias and variance of N 1 SU 2 that contributes to its mean square error. Clearly, by comparing Figure 2.3(a) with Figure 2.3(b), we see that the relative increment in the mean square error of N 1 S 2 U is mainly due to its bias increase, which agrees with the investigation concerning MSE(N 1 SU 2 ) before. Now we turn to study the performance of the distributed bootstrap and the pseudodistributed bootstrap, and compare them with the BLB and the SDB. In this simulation, we consider constructing the 95% confidence intervals for θ based on U for the number of subsets K {20, 50, 100, 200, 500, 1000} using the distributed bootstrap, the pseudo-distributed bootstrap, the BLB and the SDB, respectively. For each simulated dataset and K, we use these four methods to estimate the width of confidence intervals and each method is allowed to run for 10 seconds in order to take the computing time into consideration. Under this setup, we can compare the performances of these methods within certain fixed time budget. For the BLB,
55 42 ) ) / Bias(N 1 S UN 2 Bias(N 1 S U Normal Gamma Poisson ) )/Var(N 1 S UN 2 Var(N 1 S U Normal Gamma Poisson (a) Bias(N 1 S 2 U) / Bias(N 1 S 2 UN ) K (b) Var(N 1 S 2 U)/Var(N 1 S 2 UN ) K Figure 2.3 Bias(N 1 S 2 U ) / Bias(N 1 S 2 UN ) and Var(N 1 S 2 U )/Var(N 1 S 2 UN ) against the number of blocks K for each scenario. we fix the number of resamples B = 100 as in Kleiner, et al. (2014) and Sengupta, Volgushev and Shao (2016), the subset X s,n are chosen as the s-th data block, thus the size of the subset X s,n is equal to N/K. For the SDB, the size of the random subset X s,n is also chosen as N/K. Table 2.4 gives the summary of the number of iterations completed for each method within 10 seconds for different K. From this table, we can see that the pseudo-distributed bootstrap is the fastest one that has the most iterations among all these methods. The bag of little bootstrap is the slowest method, when K = 20, the BLB can not even finish one iteration in 10 seconds. The distributed bootstrap and the subsampled double bootstrap have similar performance. However, it is worth to mention that these results do not take the time expenditure of data communication between each data block into account, for the SDB which can not be implemented distributively, the communication between each block can be costly that slows down the SDB hugely. In order to evaluate these four methods, we conduct 500 simulation replications and report the coverage rates and widths of the 95% confidence intervals for different methods, the results for Gaussian scenario is given in Table 2.5 and the results for Gamma and Poisson data can be found in Table 2.10 and Table 2.11 in the appendix. Table 2.5 shows that the coverage rates
56 43 Table 2.4 Number of iterations completed in 10 seconds for each method. DB: the distributed bootstrap, PDB: the pseudo-distributed bootstrap, BLB: the bag of little bootstrap, SDB: the subsampled double bootstrap. K DB PDB BLB SDB are a little bit far away from the nominal confidence level 95% for relatively small K. When K = 20, the reason why the distributed bootstrap and the subsampled double bootstrap do not have good performances is that they can not finish enough iterations to ensure the convergence of their algorithms. As the pseudo-distributed bootstrap is based on the assumption that k diverges, the coverage rate is still not good when K = 20 even it can complete enough iterations in 10 seconds. For relatively large K, the performances of the DB, the PDB and the SDB are reasonable and comparable to each other. For the bag of little bootstrap, its performance depends on the choices of the number of resamples B and the subset size n. Table 2.5 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Gaussian data. K DB ( ) ( ) ( ) ( ) ( ) ( ) PDB ( ) ( ) ( ) ( ) ( ) ( ) BLB NA (NA) ( ) ( ) ( ) ( ) ( ) SDB ( ) ( ) ( ) ( ) ( ) ( ) Next we calculate the relative errors of the confidence interval widths for each method. If d is the true width and ˆd is an estimator of the confidence interval width, the relative error is defined as ˆd d /d. We approximate the true width by 5000 Monte Carlo simulations and the relative errors are averaged over 500 simulations. Follow the comparison strategy in
57 44 Sengupta, Volgushev and Shao (2016), these four methods are compared with respect to the time evolution of relative errors. This is a way to explore which method can produce more precise result given a fixed time budget. For each method, we calculate its relative error for each iteration along with the computing time. For the BLB and the SDB, one iteration means the completion of estimation procedure for one subset. The relative error is assigned to be 1 before the first iteration is completed. Figure 2.4 shows the evolution of relative errors across time for the distributed bootstrap, the pseudo-distributed bootstrap, the BLB and the SDB with different number of blocks, the data are generated from N (1, 1). First, we can see that the pseudo-distributed bootstrap is the fastest method to converge for all K. It takes time for the BLB to complete one iteration, especially when K is small, for example, when K = 20, the BLB can not even finish one iteration in 10 seconds. Also when K = 20, the relative error of the pseudo-distributed bootstrap is not reliable which means it can not produce a reasonable estimate of the confidence interval width in this case. This is expectable because the convergence rate of the pseudo-distributed bootstrap relies on the order of K. In contrast, as K increases, the relative errors of the pseudodistributed bootstrap will decrease to an acceptable rate. For a sufficient large K (K 200), its relative error is comparable with those of the distributed bootstrap, the BLB and the SDB. The distributed bootstrap and the SDB have performance close to each other. However, the SDB is not a distributed resampling approach, which would limit its usage when the entire data are stored in different locations. Results for Gamma and Poisson scenarios are shown in Figure 2.6 and Figure 2.7. In conclusion, with a small time budget, the other three methods have advantages over the BLB, especially when K is small. When K is relatively large, the pseudo-distributed bootstrap has advantage in computing and can produce reasonable estimators. The SDB has limitation that it can not be implemented distributively. The distributed bootstrap is designed distributively and can work for a wide range of K.
58 45 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (a) K = 20 (b) K = 50 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (c) K = 100 (d) K = 200 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (e) K = 500 (f) K = 1000 Figure 2.4 Time evolution of relative errors under Gaussian scenario.
59 Distance covariance The distributed version of distance covariance and its usage in testing independence between two multivariate random vectors has been studied in Section By formulating the distributed distance covariance, we can reduce the requirements on computing time and memory space, which makes it meet the demands for handling massive datasets. In this section, we investigate the performance of the distributed distance covariance dcov 2 (Y, Z) in testing independence by numerical studies. It is worth noting that for the conventional distance covariance dcovn 2 (Y, Z), random permutations are needed to implement the test (Székely, Rizzo and Bakirov, 2007), which could increase the computing cost dramatically. While for distributed distance covariance dcov 2 (Y, Z), we can use the result in (2.17) based on the variance estimator ˆσ 2 β, or the pseudo-distributed bootstrap (Corollary 2.4) to implement the test, where permutations are not needed. Moreover, the testing procedures based on dcov 2 (Y, Z) only need O(K 2 N 2 ) memory space, which is much less than that of dcovn 2 (Y, Z), which is at the order of O(N 2 ). All simulation results in this section were based on 1000 iterations with the nominal significant level at 5%. The sample size is fixed at N = and the number of data blocks K is selected in the set {20, 50, 100, 200, 500, 1000, 2000, 5000}. For the null hypothesis, we generate Y and Z independently from distribution G 1 and G 2, respectively. Three different combinations of G 1 and G 2 are considered: (I) G 1 and G 2 are both N (0 p, I p ), where I p is the p-dimensional identity matrix.; (II) G 1 is N (0 p, I p ), for G 2, its p components are i.i.d. from student-t distribution with 3 degrees of freedom, that is, for Z = (Z 1,..., Z p ) T, Z i t(3) and Z i and Z j are independent for i, j = 1,..., p; (III) For both G 1 and G 2, their marginal components are i.i.d. from student-t distribution with 3 degrees of freedom. Scenario (I) and (III) are also employed in Székely, Rizzo and Bakirov (2007). The dimension p is chosen as 5, 10, 20 and 40 for each scenario. Table 2.6 reports the empirical sizes of the tests based on the distributed distance covariance dcov 2 (Y, Z). T Var stands for the testing procedure based on the variance estimator ˆσ 2 β, in (2.17) and T PDB represents the test using the pseudo-distributed bootstrap. Table 2.6 shows that the empirical sizes of both methods are close to the nominal level 5% for all combinations
60 47 of p and K under all three scenarios. Thus, these two tests for independence based on the distributed distance covariance both have good control of Type-I error for a wide range of K. In addition, the performance of these two methods is very comparable to each other. However, for relatively large K, T PDB has slightly better control of the empirical sizes than T Var. To compare the powers of these two tests, we generate p-dimensional random vectors Y G 1 and Z G 2, and the same three different combinations of G 1 and G 2 are considered as in the simulation setups for the null hypothesis. For Y = (Y 1,..., Y p ) T and Z = (Z 1,..., Z p ) T under each scenario, we simulate cor(y i, Z j ) = ϱ i j p for i, j = 1,..., p and ϱ = 0.05, 0.1 are considered. The dimension parameter p is taken to be 5, 10, 20 and 40. Under these setups, Y and Z are dependent with each other. Two testing procedures based on the distributed distance covariance dcov 2 (Y, Z) are carried out to testing the independence between Y and Z. Table 2.7 and 2.8 give the empirical powers of T Var and T PDB. From Table 2.7 and 2.8, it is clear that the empirical powers of these two distributed distance covariance based tests decrease as the dimension p increases. In addition, as the number of data blocks K increases, the empirical powers of the tests also decrease. This is due to the increase in the variance of dcov 2 (Y, Z) when K increases. This is the price we need to pay for using the distributed distance covariance. The computing time and memory requirement can be reduced by increasing the number of data blocks, however, this will result in the power loss of the tests for independence. This coincides with the discussions on degenerate T N and the asymptotic efficiency of T Real data analysis In this section, we use the 2016 airline on-time performance data as a case study to illustrate how our proposed distributed inference work for massive data. The data is publicly available from the Bureau of Transportation Statistics website ( The dataset consists of the arrival and departure details for total 5, 617, 658 commercial flights within the USA in We are interested in the arrival delay variable which presents the difference in minutes between scheduled and actual arrival time for each flight, and negative values stand for early arrivals. After removing missing and extreme values, we arrive at 5, 536, 426 data points.
61 48 Table 2.6 Sizes of independence tests based on dcov 2 (Y, Z). T Var: test using variance estimation in (2.17); T PDB : test using the pseudo-distributed bootstrap. K p = 5 p = 10 p = 20 p = 40 T Var T PDB T Var T PDB T Var T PDB T Var T PDB scenario I scenario II scenario III
62 49 Table 2.7 Powers of independence tests based on dcov 2 (Y, Z) for ϱ = K p = 5 p = 10 p = 20 p = 40 T Var T PDB T Var T PDB T Var T PDB T Var T PDB scenario I scenario II scenario III
63 50 Table 2.8 Powers of independence tests based on dcov 2 (Y, Z) for ϱ = 0.1. K p = 5 p = 10 p = 20 p = 40 T Var T PDB T Var T PDB T Var T PDB T Var T PDB scenario I scenario II scenario III
64 51 In this case study, we treat the dataset as an univariate i.i.d. sample of size N = 5, 536, 426. The parameter of interest is the dispersion parameter θ = E X i X j, which can be estimated by the Gini s mean difference U N = {N(N 1)} 1 X i X j. 1 i j N Due to the massive size of the dataset, we consider using the distributed version of U N to do inferences on θ. Denote U as the distributed version of the Gini s mean difference with the entire data randomly divided evenly into K blocks. Table 2.9 presents the values of U and its jackknife variance estimator N 1 S 2 U for different K along with their computing time. According to Table 2.9, it is clear that the computing time of both T and S 2 U is linearly decreasing in K, and the value of S 2 U is increasing in K. The computing time for S 2 U when K = is about a factor of less than the case when K = 1, however, the estimated variance only has 0.3% increase. This result indicates that for the Gini s mean difference, the distributed statistic T can maintain sufficient estimation efficiency while decrease computing time massively. Next we applied the distributed bootstrap, the pseudo-distributed bootstrap, the BLB and the SDB on this dataset to estimate the 95% confidence interval width of θ based on T with different number of blocks K {50, 200, 500, 2000, 5000, 20000}. Same as in the simulation studies, we chose the subset size n = N/K for the BLB and the SDB, and the number of resamples B was chosen as 100 for the BLB. Each method was allowed to run for 60 minutes and the time evolution of the estimated confidence interval width is shown in Figure 2.5. The BLB is the slowest to converge and the pseudo-distributed bootstrap is the fastest to stabilized. Thus, the pseudo-distributed bootstrap has advantage for small time budgets. For relatively large K, these four methods tend to obtain similar estimates of the confidence interval width Conclusion We considered distributed inferences for massive data with a concentration on a general type of statistics T N. To conquer computational issues, we formulated the distributed statistics T and studied its statistical efficiency under a general approach. We also focused on
65 52 Table 2.9 U and S U 2 for airline on-time dataset along with computing time (in seconds) given in the parentheses. K U ( ) ( ) ( ) ( ) (857.74) (328.38) (165.78) (82.99) S U ( ) ( ) ( ) ( ) ( ) ( ) (947.36) (477.83) K U (32.96) (16.17) (8.17) (3.31) (1.67) (0.88) (0.37) (0.22) S U (189.43) (94.95) (47.97) (19.31) (10.03) (5.92) (4.73) (6.40)
66 53 Confidence Interval Width DB PDB BLB SDB Time (min) Confidence Interval Width DB PDB BLB SDB Time (min) (a) K = 50 (b) K = 200 Confidence Interval Width DB PDB BLB SDB Time (min) Confidence Interval Width DB PDB BLB SDB Time (min) (c) K = 500 (d) K = 2000 Confidence Interval Width DB PDB BLB SDB Time (min) Confidence Interval Width DB PDB BLB SDB Time (min) (e) K = 5000 (f) K = Figure 2.5 Time evolution of estimated confidence interval width.
67 54 the degenerate case when the linear term in T N vanishes. Furthermore, regarding the computational advantages of T against T N, we proposed bootstrap algorithms to approximate the distribution function of T. Theoretical properties of the proposed methods were established and we applied them on the independence test using the distance covariance regarding massive datasets. Finally, we used numerical studies to illustrate our theoretical results. In practice, an important issue of the distributed approaches is the choice of the number of blocks K. Increasing K would decrease the computational cost, however, this leads to a loss in statistical efficiency. This topic has been touched in Section 2.4, where storage and memory requirement are considered. However, it is still an issue on how to select K in practice that balances the computing time and statistical efficiency. Instead of giving fixed time budget, another problem is to minimize computing time subject to attaining certain statistical efficiency. This is similar to a sample size determination problem. We leave these for future study. We focused our development of the distributed approaches on i.i.d. data. It is still unclear how these methods work for dependent data. Furthermore, in Kleiner, et al. (2014), higher order accuracy of BLB has been studied. Thus, it is of interest to investigate higher order correctness and convergence rates of our proposed distributed approaches, and we plan to investigate this in the future Appendix In this section, we present the proofs of main theorems in this paper. Before stating the proofs of the main theorems, we give several lemmas that will be frequently used later. The first lemma is a generalization of Esseen s inequality which we may refer to Theorem 5.7 in Petrov (1998). Lemma 2.1. Let Y 1,..., Y N be independent random variables. For i = 1,..., N, E(Y i ) = 0 and E Y i 2+δ < for some positive δ 1. Then ( ) N sup P B 1/2 N N Y i x Φ(x) C 1B 1 δ/2 N E Y j 2+δ, x R i=1 where B N = N i=1 Var(Y i) and C 1 is a positive constant. i=1
68 55 The second lemma is a modified version of Marcinkiewicz-Zygmund strong law of larger numbers and its proof can be found in Liu (1988). Lemma 2.2. Let Y 1,..., Y N be independent random variables with E Y i η+ε < for some positive η, 0 < η < 2 and ε > 0. Then as N, N 1/η N i=1 (Y i a i ) 0 almost surely, where a i = EY i if η 1 and a i = 0 otherwise Proof of Theorem 2.4 Proof. According to Lemma 2.1, we know that where V N = N 1/2 σ 1 α = N 1/2 σ 1 α sup P (V N x) Φ(x) N δ/2 C 1 σα 2 δ E α(x 1 ; F ) 2+δ, x R N i=1 α(x i; F ). Denote N = N 3/2 σα 1 K k=1 n 1 k 1 i<j N β(x i, X j ; F ) and 1 i<j n k β(x k,i, X k,j ; F ), then by Cauchy-Schwarz inequality, P ( N (lnn) 1) = O(N 1 (lnn) 2 ), P ( (lnn) 1) = O(KN 1 (lnn) 2 ). If E(R N ) = b 1 N τ 1 + o(n τ 1 ) and Var(R N ) = o(n τ 2 ), under Condition 2.3 and the assumption K = O(N τ ), E(R ) = O(N τ 1τ τ 1 ) and Var(R ) = o(n τ 2τ τ τ 2 ), again by Cauchy-Schwarz inequality, ( P R N N 1/2 (lnn) 1) = o(n 1 τ 2 (lnn) 2 ), ( P R N 1/2 (lnn) 1) = o(n τ 2τ τ τ 2 +1 (lnn) 2 ), under the condition that τ < 1 1/(2τ 1 ). Finally, by the fact that we complete the proof of Theorem 2.4. sup Φ(x + t) Φ(x) = o(1), x R, t <(lnn) 1
69 Proof of Theorem 2.6 Proof. When M is finite, the result can be easily obtained from independence between each subset and the classic limit theorem for degenerate U-statistic (Serfling, 1980). Now we focus on the case when K. Without loss of generality, assume θ = 0. Denote T (k) = (k) + R(k) where (k) 1 i<j n k β (X k,i, X k,j ; F ). Under the condition = n 2 k that R = o p (K 1/2 N 1 ), it is sufficient to prove that 2 1/2 K 1/2 Nσ 1 β convergence to standard normal distribution as K, N, here Rewrite = N 1 K k=1 n k (k) = N 1 2 1/2 K 1/2 Nσ 1 β = where (k) = 21/2 K 1/2 n k σ 1 β (k) K k=1 K k=1 satisfies E ( n 1 k 2 1/2 K 1/2 n k σ 1 β (k) (k) 1 i<j n k β (X k,i, X k,j ; F ). K ) = 0 and Var k=1 (k), ( (k) ) = K 1 (1 n 1 k ) for k = 1,..., K. As (k), k = 1,..., K are independent, it is enough to check the Lindeberg condition for (k). Note that s2 ( ) K k=1 Var (k) = 1 K 1 K k=1 n 1, then for every ε > 0, s 2 =s 2 s 2 K k=1 K k=1 k=1 C 2 s 2 [ (k) E 2 { } (k) ] 1 > εs [ K K 1 (1 n 1 k )E 1/2 (k) 2 { K 1 1/2 (k) > εs K 1/2}] K K 1 (1 n 1 k (εs ) K 1/2) δ E K 1/2 (k) K k=1 0, as K. K 1 (1 n 1 k ) ( εs K 1/2) δ 2+δ k The next-to-last line is from the moment inequalities of U-statistics (Koroljuk and Borovskich, 1994) and C 2 is a positive constant. Thus we finish the proof of Theorem 2.6.
70 Proof of Theorem 2.7 Proof. According to the proof of Theorem 2.4, under the conditions assumed in Theorem 2.4, we have { sup P x R N 1/2 σ 1 α } (T θ) x Φ(x) = o(1), thus, it is sufficient to show that under the conditions assumed in the theorem { 1 sup P N 1/2ˆσ α,n (T θn) x } FN Φ(x) = o p (1). (2.18) x R We proceed to show that E { α(x 1 ; F N) 2+δ F N } is bounded in probability. Note that E { α(x 1; F N ) 2+δ } FN N =N 1 α(x i ; F N ) 2+δ i=1 N N 1 i=1 C δ { α(x i ; F N ) α(x i ; F ) 2+δ + α(x i ; F ) 2+δ}, By the condition that sup α(x; F N ) α(x; F ) = o p (1) and the strong law of large numbers, we x R have E { α(x1 ; F N) 2+δ } F N = Op (1). Similarly, we can show that E { β(x1, X 2 ; F N) 2 } F N < in probability. Thus, under the condition P { R N 1/2 (lnn) 1 } F N = o p (1), by carrying out similar procedures in the proof of Theorem 2.4, we can prove (2.18) which leads to the result that { sup P N x R In addition, 1/2ˆσ 1 } α,n (T θn) { x F N P N 1/2 σα 1 (T θ) x} = o p (1). ˆσ α,n 2 σα 2 =E { α 2 (X1; F N ) } F N σ 2 α N =N 1 α 2 (X i ; F N ) σα 2 i=1 N =N 1 {α(x i ; F N ) α(x i ; F )} 2 + N 1 N i=1 i=1 N + N 1 { α 2 (X i ) σα} 2 =o p (1). i=1 2α(X i ; F ) {α(x i ; F N ) α(x i ; F )}
71 Proof of Theorem 2.8 Proof. The proof of Theorem 2.8 is similar with the one of Theorem 2.7 and thus is omitted here Proof of Corollary 2.1 Proof. Let T (k) = T (k) N 1/2 K 1/2 θ. Denote ( ) ( ) θ k = E T (k) = N 1/2 K 1/2 (n k NK 1 )θ + N 1/2 K 1/2 n k E R (k) ( ) and σk 2 = Var T (k) = N 1 Kn k σα 2 {1 + o(1)} for k = 1,..., K, then θ = K 1 K k=1 θ k = N 1/2 K 1/2 K k=1 ( ) n k E R (k). Denote T (k) = T (k) N 1/2 K 1/2 θ, then T (k), k = 1,..., K are i.i.d. from F K,T (x + N 1/2 K 1/2 θ). Since E α(x 1 ; F ) 2+δ <, E β(x 1, X 2 ; F ) 2+δ < and sup k E n 1/2 k R(k) 2+δ < ( T (k), we have sup k E 2+δ) <. This immediately results in { T } (k) E 2+δ 1 K FK,T = K 1 T (k) k=1 2+δ 1 < with probability 1 for some δ 1 satisfies 0 < δ 1 < δ (Lemma 2.2). Define T = K 1 K k=1 T (k) = T N 1/2 K 1/2 θ, then T T = T N 1/2 K 1/2 T where T = K 1 K k=1 T(k). Denote σ2 = K 1 K k=1 σ2 k and s 2 = K 1 K k=1 then sup k N 1/2 K 1/2 n k NK 1 0 implies that s 2 σ 2 = K 1 K k=1 ( T (k) T ) 2, { ( T (k) θ k + θ k θ + θ T ) 2 σ 2 k } 0
72 59 almost surely. According to Lemma 2.1, sup {K P 1/2 s } 1 (T N 1/2 K 1/2 T ) x F K,T Φ(x) x R { T } C 1 s 2 δ 1 K δ1/2 (k) E T 2+δ 1 FK,T [ { T } ] C 2 s 2 δ 1 K δ 1/2 (k) E 2+δ 1 FK,T + T 2+δ 1 0 almost surely as K. It has been shown in the proof of Theorem 2.4 that { sup P x R N 1/2 σ 1 α } (T θ) x Φ(x) = o(1). Combine this with the fact that s 2 σ 2 α 0 with probability 1, we complete the proof of this corollary Proof of Corollary 2.2 Proof. Use similar techniques as in the proof of Corollary 2.1, let T (k) = T (k) NK 1 θ = ( ) ( ) ( ) n k (T (k) θ), denote θ k = E T (k) = n k E R (k) and σk 2 = Var T (k) = 2 1 σβ 2 {1 + o(1)} for k = 1,..., K, then T = K 1 N K 1 ( ) K k=1 n ke R (k). k=1 T(k) = NK 1 (T θ) and θ = K 1 K k=1 θ k = Under the conditions that E β(x 1, X 2 ; F ) 2+δ < and sup k E n k R (k) obtain sup k E n k (T (k) θ) 2+δ <, which in turn implies that { sup P NK 1/2 σ } 1 (T θ) x Φ(x) = o(1), x R where σ 2 = K 1 K k=1 σ2 k. 2+δ <, we Denote T (k) = T (k) NK 1 θ, then T (k), k = 1,..., K are i.i.d. from F K,T (x+nk 1 θ). ( T (k) As sup k E 2+δ ) <, this immediately results in { T } (k) E 2+δ 2 K FK,T = K 1 T (k) k=1 2+δ 2 <
73 60 with probability 1 and δ 2 satisfies 0 < δ 2 < δ (Lemma 2.2). Define T = K 1 K k=1 T (k) = T NK 1 θ, then T T = T NK 1 T. Denote s 2 = K 1 K k=1 s 2 σ 2 = K 1 K k=1 ( T (k) T ) 2, then { ( T (k) θ k + θ k θ + θ T ) 2 σ 2 k }, which convergence to 0 almost surely. According to Lemma 2.1, sup {K P 1/2 s } 1 (T NK 1 T ) x F K,T Φ(x) x R { T } C 1 s 2 δ 2 K δ2/2 (k) E T 2+δ 2 FK,T 0 almost surely as K, thus we finish the proof of Corollary Proof of Theorem 2.9 ( ) ( ) Proof. Under the null hypothesis, E ˆσ β, 2 = σβ 2, thus it is sufficient to show that Var ˆσ β, 2 = o(1) as N. Mentioned that Var (ˆσ [ { β, 2 ) =Var 4 =16E { N 1 N 1 K k=1 K k=1 n k dcov 2(k) (Y, Y ) } { n k dcov 2(k) (Y, Y )} 2 E 16dcov 4 (Y, Y )dcov 4 (Z, Z) =16N 2 K k=1 + 16N 2 K { N 1 N 1 K k=1 K k=1 n 2 k Var { dcov 2(k) (Y, Y ) } dcov 4 (Z, Z) k=1 + 16N 4 [ K k=1 n 2 k Var { dcov 2(k) (Z, Z) } dcov 4 (Y, Y ) n k dcov 2(k) (Z, Z) n k dcov 2(k) (Z, Z) }] ] [ { } K ] n 2 k Var dcov 2(k) (Y, Y ) { } n 2 k Var dcov 2(k) (Z, Z). k=1 } 2
74 61 Since dcov 2(k) (Y, Y ) and dcov2(k) (Z, Z) are U-statistics of degree 4, under the condition that { } { } E Y 4 p + E Z 4 q <, Var dcov 2(k) (Y, Y ) = O(n 1 k ) and Var dcov 2(k) (Z, Z) = O(n 1 k ( ) ), these two results immediately leads to Var ˆσ β, 2 = o(1) and the proof is complete.
75 62 Table 2.10 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Gamma data. K PDB ( ) ( ) ( ) ( ) ( ) ( ) DB ( ) ( ) ( ) ( ) ( ) ( ) BLB NA (NA) ( ) ( ) ( ) ( ) ( ) SDB ( ) ( ) ( ( ) ( ) ( ) Table 2.11 Coverage rates and confidence interval widths (in parentheses) of the 95% confidence intervals with 10 seconds time budget for Poisson data. K PDB ( ) ( ) ( ) ( ) ( ) ( ) DB ( ) ( ) ( ) ( ) ( ) ( ) BLB NA (NA) ( ) ( ) ( ) ( ) ( ) SDB ( ) ( ) ( ) ( ) ( ) ( )
76 63 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (a) K = 20 (b) K = 50 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (c) K = 100 (d) K = 200 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (e) K = 500 (f) K = 1000 Figure 2.6 Time evolution of relative errors under Gamma scenario.
77 64 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (a) K = 20 (b) K = 50 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (c) K = 100 (d) K = 200 Relative Error PDB DB BLB SDB Time (sec) Relative Error PDB DB BLB SDB Time (sec) (e) K = 500 (f) K = 1000 Figure 2.7 Time evolution of relative errors under Poisson scenario.
78 65 CHAPTER 3. MORE POWERFUL TESTS FOR SPARSE HIGH DIMENSIONAL COVARIANCES MATRICES A paper accepted by Journal of Multivariate Analysis Liuhua Peng, Song Xi Chen, Wen Zhou Abstract This paper considers improving the power of tests for the identity and sphericity hypotheses regarding high dimensional covariance matrices. The power improvement is achieved by employing the banding estimator for the covariance matrices, which leads to significant reduction in the variance of the test statistics in high dimension. Theoretical justification and simulation experiments are provided to ensure the validity of the proposed tests. The tests are used to analyze a dataset from an acute lymphoblastic leukemia gene expression study for an illustration. 3.1 Introduction This paper is interested in testing hypothesis for high-dimensional covariance matrices, Σ, of a p-dimensional random vector X. In practice, it is often of scientific interest to test whether or not a prescribed dependence structure is supported by data, for instance H 0 : Σ = Σ 0 vs. H 1 : Σ Σ 0 (3.1) and H 0 : Σ = σ 2 Σ 0 vs. H 1 : Σ σ 2 Σ 0 for some unknown σ 2 > 0, (3.2)
79 66 for a known non-degenerate covariance matrix Σ 0. Among many practical applications, genomic studies usually motivate (3.1) or (3.2): it is not uncommon to postulate a grouping structure among genes of interest such that genes are not correlated across groups (Katsani et al., 2014), i.e. Σ is presumed in a diagonal block shape upon permutations. Additionally, in the fields of image segmentation, epidemiology and ecology, large numbers of pixels or population abundances are collected across the spatial domain. Certain spatial autocorrelations are usually prescribed for fitting data to a parametric or semiparametric model for predictions (Bolker, 2008; Cressie, 1993). It is important to verify whether or not these hypothetical dependence structures are supported by data. For identically and independently distributed data X 1,..., X n with unknown common mean µ and covariance Σ 0, linear transform Σ 1/2 0 X i reduces (3.1) and (3.2) to H 0 : Σ = I p vs. H 1 : Σ I p, (3.3) and H 0 : Σ = σ 2 I p vs. H 1 : Σ σ 2 I p, (3.4) where I p is the p-dimensional identity matrix. Hypotheses (3.3) and (3.4) are called the identity and sphericity hypothesis, respectively. For fixed p, likelihood ratio test has been developed and widely applied. We refer to Anderson (2003) for more details. Let Σ be the sample covariance matrix. John (1971, 1972) and Nagao (1973) showed that for a fixed p, test statistics { ( ) } 2 V n = p 1 tr Σ Ip and [ { U n = p 1 tr p Σ/tr( Σ) } ] 2 I p (3.5) provide the most powerful invariant tests for both the identity and sphericity hypotheses against the local alternatives. Traditional tests, however, are not applicable to the large p, small n paradigm since the sample covariance matrix is singular with probability one whenever p > n and is no longer a consistent estimator if p is not a smaller order of n (Bai and Yin, 1993; Bai, Silverstein and Yin, 1988). Tests for covariance matrices suited for the high dimensionality have been developed over the recent years. Ledoit and Wolf (2002) established the asymptotic properties of statistics in
80 67 (3.5) for p/n c (0, + ) and proposed tests for identity (3.3) and sphericity (3.4) under the Gaussian assumption. Jiang (2004) developed a sphericity test based on the max-type statistic L n = max 1 i<j p ˆρ ij, where ˆρ ij denotes the sample correlation coefficient between the i-th and j-th components of X. With the aid of the random matrix theory, Bai et al. (2009) proposed a modified likelihood ratio statistic for testing (3.3) for p/n y (0, 1). To avoid the issue of inconsistency of Σ when p > n, Chen, Zhang and Zhong (2010) proposed U-statistic based testing procedures for both the identity and sphericity hypotheses. Their tests require much relaxed assumptions on the data distribution, and allow p diverges in n in any rates. See, for example, Cai and Jiang (2011); Hallin and Paindaveine (2006); Srivastava and Yanagihara (2010); Srivastava and Reid (2012); Srivastava, Yanagihara and Kubokawa (2014); Zou et al., (2014) for alternative test formulations, and Bai et al. (2009); Schott (2005); Zheng et al., (2014); Qiu and Chen (2012) for related works. One limitation of these high dimensional tests is a loss of power under sparse high dimension situations, largely due to a rapid increase in the variance of the test statistic as the p gets larger. For instance, in the formulation of the identity test, estimation of the discrepancy measure p 1 tr{( Σ I p ) 2 } involves all the entries of the sample covariance. As a result, the test statistics incurs larger variation as the dimension gets larger. The increased variance dilutes the signal p 1 tr{( Σ I p ) 2 } of the test and hence brings down its power. While we are gathering more dimensions in the data as more features are recorded, the information content of the data is not necessarily increasing at the same rate as the dimension. Indeed, it is commonly acknowledged that parameters associated with high dimensional data can be sparse in the sense of that many of the parameters are either zero or taking small values. This was the rationale behind the proposal of LASSO in Tibshirani (1996) as well as other regularization-based estimations in regression and covariance matrices; see Bickel and Levina (2008b); Cai, Zhang and Zhou (2010); Fan and Li (2001); Rothman, Levina and Zhu (2009). We consider in this paper tests for covariance matrices by utilizing the regularization-based estimation constructed for a specific class of sparse covariance matrices, the so-called bandable covariances, introduced by Bickel and Levina (2008a). The bandable class is naturally suited as alternative hypotheses to the null identity and the sphericity hypotheses. Specifically, we
81 68 formulate the test statistics by employing the banded covariance estimator proposed in Bickel and Levina (2008a). This allows us to take advantage of the knowledge of sparsity in the Σ. We demonstrate in this paper that the new test formulations have a remarkable power enhancement over the existing high dimensional tests for the covariance which do not utilize the sparsity information. The rest of the paper is organized as follows. We introduce our motivations in Section 3.2 and present the testing procedures in Section 3.3. The theoretical properties of the proposed tests are also investigated in Section 3.3. Section 3.4 is devoted to a discussion on the selection of k for the proposed tests. Numerical results are displayed in Section 3.5 to investigate the performance of the tests in practice. Both simulation studies and applications of the proposed tests to an acute lymphoblastic leukemia gene expression dataset are reported. Section 3.6 concludes the article with a brief discussion. Technical proofs and supplementary material contains more details on the numerical studies are given in Section Motivations and preliminaries Our investigation is motivated by the notion of the bandable covariance class introduced by Bickel and Levina (2008a), which is defined as U(ε 0, C, α) = { Σ = (σ ij ) 1 i,j p : max σ ij Ck j 0 α for all k 0 0, i j >k 0 0 < ε 0 λ min (Σ) λ max (Σ) 1/ε 0 }, (3.6) where ε 0, C and α are positive constants. The bandable covariance prescribes a general decaying pair-wise covariances σ ij for large i j. The increasing sparsity as the pair-wise covariance moves away from the main diagonal is ideally suited as alternative models for the identity and sphericity hypotheses. It is noted that the Σ of the original random vector X may not be bandable. We assume there is a permutation of X such that the corresponding covariance is bandable. There are algorithms, for instance the angle-based ordering algorithm (Friendly, 2002) or the Isoband algorithm (Wagaman and Levina, 2009), which may be used to permute the data so that Σ under the permutation is more bandable.
82 69 For the above bandable covariance class, Bickel and Levina (2008a) proposes the banding covariance estimator. Let k < p be a positive integer and write the sample covariance matrix Σ = (ˆσ ij ) 1 i,j p. The banding estimator of Σ with bandwidth k is ˆΣ k,p ˆΣ k = B k ( Σ) = (ˆσ ij I{ i j k}) 1 i,j p. For Σ U(ε 0, C, α), Bickel and Levina (2008a) established the consistency of B k ( Σ) to Σ under the spectral norm by letting k divergence at the rate (n 1 lnp) 1/{2(α+1)} for sub-gaussian distributed data when lnp/n 0. Encouraged by this important advance in high dimensional covariance estimation, we consider replacing Σ in (3.5) by B k ( Σ) leads to the following test statistics [ { p 1 tr B k ( Σ) } ] [ 2 { I p and p 1 tr pb k ( Σ)/tr( Σ) } ] 2 I p. (3.7) Comparing with the statistics V n and U n given in (3.5), the above formulations based on the banding estimator B k ( Σ) are expected to be less variable since those pair-wise sample covariances ˆσ ij located further away from the k-th superdiagonals (subdiagonals) are excluded due to the banding operation. Indeed, for Σ in the bandable class, most of the signals (those larger σ ij ) are located closer to the main diagonals. This form of sparsity suggests us to discount covariances which are far away from the main diagonals. It is obvious that the formulation is critically dependent on the choice of the banding width k. Recently, Qiu and Chen (2015) have proposed a data driven method for choosing k by minimizing an empirical version of B k (Σ) Σ F, where F denotes the Frobenius norm. The seemingly natural constructions given in (3.7) need to be refined in order to be suitable for more relaxed relationship between p and n and without the sub-gaussian assumption in Bickel and Levina (2008a). Our aim here is to obtain unbiased estimators for tr{b k (Σ)} and tr[{b k (Σ)} 2 ] for Σ U(ε 0, C, α). Denote X i = (x i1,..., x ip ) for each i, and let L n1 (i, j) = 1 Pn 2 x l1 ix l1 jx l2 ix l2 j, L n2 (i, j) = 1 P 3 x l1 ix l2 jx l3 ix l3 j, l 1 l n 2 l 1,l 2,l 3 L n3 (i, j) = 1 Pn 4 x l1 ix l2 jx l3 ix l4 j, L n4 (i) = 1 n x 2 li n, L n 5 (i) = 1 P 2 x l1 ix l2 i, l 1,l 2,l 3,l 4 l=1 n l 1 l 2 where P r n = n!/(n r)! for r = 2, 3, 4 and denotes the summation over mutually different indices. Notice that p i=1 { L n 4 (i) L n5 (i)} and i j k { L n 1 (i, j) 2 L n2 (i, j) + L n3 (i, j)} are unbiased estimators of tr(σ) and tr[{b k (Σ)} 2 ], respectively.
83 70 We consider two discrepancy measures for the identity and sphericity hypotheses: p 1 tr[{b k (Σ) I p } 2 ] = p 1 tr[{b k (Σ)} 2 ] 2p 1 tr(σ) + 1, and [ { } ] 1 p tr B k (Σ) 2 (1/p)tr{B k (Σ)} I p = ptr[{b k(σ)} 2 ] {tr(σ)} 2 1, upon which, we propose the following two unbiased estimators to these two measures and V n,k = p 1 i j k { L n1 (i, j) 2 L n2 (i, j) + L n3 (i, j)} 2p 1 p { L n4 (i) L n5 (i)} + 1, (3.8) [ i j k U n,k = p { L ] n 1 (i, j) 2 L n2 (i, j) + L n3 (i, j)} { p i=1 ( L n 4 (i) L n5 (i))} 2 1. (3.9) It is noted that V n,k and U n,k reduce to the statistics in Chen, Zhang and Zhong (2010) i=1 when the banding width k = p 1 which involves all the sample covariances. Thus, V n,k and U n,k are regularized versions of those proposed by Chen, Zhang and Zhong (2010). By utilizing the sparse information that Σ U(ε 0, C, α), those ˆσ ij beyond the k-th superdiagonal are avoided which makes V n,k and U n,k have less variations and hence more powerful tests as we will demonstrate later. It is easy to see that V n,k and U n,k are invariant under the location shift. Hence, without loss of generality, we assume data has been centered such that µ = 0. Assumption 3.1. Σ U(ε 0, C, α) for some constants ε 0, C and α which are unrelated to p. Similarly to Bai and Saranadasa (1996) and Chen, Zhang and Zhong (2010), we assume the following multivariate model for X i. Assumption 3.2. Data X 1,..., X n are independent and identically distributed p-dimensional random vectors such that X i = ΓZ i for i = 1,..., n, (3.10) where Γ = (Γ ij ) 1 i p,1 j m is a constant loading matrix with p m and ΓΓ = Σ, Z i = (z i1,..., z im ) s are independent and identically p-dimensional random vectors with zero mean
84 71 and identity covariance. Furthermore, we assume sup j E(z 8 1j ) < C 1 for some constant C 1 > 0 and there exists a constant < such that E(z 4 1j ) = 3 + for each j. For any integer l v 0 with q v=1 l v 8, E(z l 1 1i 1... z lq 1i q ) = E(z l 1 1i 1 )... E(z lq 1i q ) (3.11) whenever i 1,..., i q are distinct. This model, first employed by Bai and Saranadasa (1996) for testing high-dimensional mean vectors, ensures that the observations X i are linearly generated by m-variate Z i consisted of white noises. The dimension m of Z i is finite but diverge to infinity as p and n both go to infinity. So the dimension of Z i is arbitrary as long as m p that equips the model flexibility in generating X i with covariance Σ. The distribution of Z i is not restricted to particular families, and is therefore nonparametric. Assumption 3.2 has been extensively employed in high dimensional multivariate testing problems, for example see Chen, Zhang and Zhong (2010); Touloumis, Tavaré and Marioni (2015). 3.3 Testing procedures Identity test We first derive the mean and variance of the test statistic V n,k for the identity hypothesis. Derivations given in Lemma 3.1 in the appendix show that under Assumptions 3.1 and 3.2, as n, p and k, if k = o(min(n 1/2, p 1/2 )), E(V n,k ) = p 1 tr[{b k (Σ) I p } 2 ] and Var(V n,k ) = p 2 σ 2 V n,k {1 + o(1)} (3.12) where σv 2 n,k = τn,k 2 (Σ) + 8n 1 tr [Σ {B k (Σ) I p }] 2 [{ } { }] + 4 n 1 tr Γ (B k (Σ) I p )Γ Γ (B k (Σ) I p )Γ, (3.13)
85 τ 2 n,k (Σ) = 4 n(n 1) + 8 n(n 1) i 1 j 1 k i 2 j 2 k i 1 j 1 k i 2 j 2 k 72 σ 2 i 1 i 2 σ 2 j 1 j n(n 1) σ i1 i 2 σ j1 j 2 f i1 j 1 i 2 j 2 (Σ) + i 1 j 1 k i 2 j 2 k 2 2 n(n 1) i 1 j 1 k i 2 j 2 k σ i1 i 2 σ j1 j 2 σ i1 j 2 σ j1 i 2 f 2 i 1 j 1 i 2 j 2 (Σ), (3.14) and denotes the Hadamard product of matrices. In (3.14), f i1 j 1 i 2 j 2 (Σ) = m r=1 Γ i 1 rγ j1 rγ i2 rγ j2 r for the loading matrix Γ = (Γ jl ) p m in Assumption 3.2. Based on (3.12), the following theorem establishes the asymptotic normality of V n,k. Theorem 3.1. Under Assumptions 3.1 and 3.2, as n, p and k, if k = o(min(n 1/2, p 1/2 )), in distribution. σ 1 V n,k {pv n,k tr[{b k (Σ) I p } 2 ]} N (0, 1) (3.15) In Theorem 3.1, no explicit restrictions on the growth rates of p and n are imposed. We note that the banding width prescribed in Bickel and Levina (2008a) that allows consistent estimation was k = (n 1 lnp) 1/{2(α+1)} for the sub-gaussian distributed data and k = (n 1/2 p 2/β ) 1/(1+α+2/β) for data with bounded β-th moment, where α is the sparsity index in the bandable class. For both cases, the condition k = o(min(n 1/2, p 1/2 )) assumed in Theorem 3.1 allows wider range of the banding width than that in Bickel and Levina (2008a). This is because testing hypotheses usually requires less stringent assumptions than the estimation. It is also noted that the asymptotic normality holds even for a fixed k, but σ 2 V n,k will be in a more involved form with more terms than those in (3.13). Under the null identity hypothesis H 0 in (3.3), E(V n,k ) = 0 and Var(V n,k ) = p 2 σ 2 V n,k 0 + o(p 2 σ 2 V n,k 0 ) where σ 2 V n,k 0 = τ 2 n,k (I p) = 4{n(n 1)} 1 (2pk + 2p k 2 k) + 8 {n(n 1)} {n(n 1)} 1 i 1 j 1 k i 2 j 2 k From Theorem 3.1, the asymptotic null distribution of V n,k is f 2 i 1 j 1 i 2 j 2 (I p ). i j k f iijj (I p ) pσ 1 V n,k 0 V n,k d N (0, 1). (3.16)
86 73 To facilitate testing, we need to estimate σv 2 n,k 0. Given that the loading matrix Γ is not observable, it is difficult to estimate f iijj (I p ) and f 2 i 1 j 1 i 2 j 2 (I p ) directly from data. However, we note that under the H 0 σ 2 V n,k 0 = 2{n(n 1)} 1 i 1 j 1 k i 2 j 2 k {E(x li1 x lj1 x li2 x lj2 ) σ i1 j 1 σ i2 j 2 } 2, which suggests that σ 2 V n,k 0 can be estimated by ˆσ 2 V n,k 0 = 2{n(n 1)} 1 i 1 j 1 k i 2 j 2 k { 1 P 2 n 2 P 3 n + 1 P 4 n x l1 i 1 x l1 j 1 x l1 i 2 x l1 j 2 x l2 i 1 x l2 j 1 x l2 i 2 x l2 j 2 l 1 l 2 x l1 i 1 x l1 j 1 x l2 i 2 x l2 j 2 x l3 i 1 x l3 j 1 x l3 i 2 x l3 j 2 l 1,l 2,l 3 l 1,l 2,l 3,l 4 x l1 i 1 x l1 j 1 x l2 i 2 x l2 j 2 x l3 i 1 x l3 j 1 x l4 i 2 x l4 j 2 }. (3.17) The consistency of ˆσ 2 V n,k 0 is implied from the following proposition. Proposition 3.1. Under Assumptions 3.1 and 3.2, and if µ = 0, then ( ) ( ) E ˆσ V 2 n,k 0 = σv 2 n,k 0 and Var ˆσ V 2 n,k 0/σV 2 n,k 0 = O(k 2 n 1 + n 1 ). In practice, to cater for the case of µ 0, we can replace x il by x il x l where x l = n 1 n l=1 x il for each l to center the data so that µ = 0 is satisfied. As Proposition 3.1 implies ˆσ 2 V n,k 0 /σ2 V n,k 0 1 in probability under the H 0. We have pˆσ 1 V n,k 0 V n,k N (0, 1) (3.18) in distribution under the H 0. Therefore, a regularized identity test with a nominal significant level α rejects H 0 : Σ = I p if pˆσ 1 V n,k 0 V n,k > z α where z α is the α upper-quantile of N (0, 1). As long as k = o(min(n 1/2, p 1/2 )), the asymptotic normality given in (3.18) ensures the nominal level of significance asymptotically.
87 Power of the identity test To evaluate the power of the test for the identity hypothesis, let δ Vn,k = tr[{b k (Σ) I p } 2 ], which can be viewed as the signal of the test problem under the alternative. The power of the regularized identity test ( ) β Vn,k (α) = Pr pσ 1 V n,k 0 V n,k z α { } = Pr σ 1 V n,k (pv n,k tr[{b k (Σ) I p } 2 ]) σ 1 V n,k σ Vn,k 0z α σ 1 V n,k δ Vn,k ( ) = 1 Φ σ 1 V n,k σ Vn,k 0z α σ 1 V n,k δ Vn,k, where Φ is the standard normal distribution. It can be shown that σ 1 V n,k σ Vn,k 0 is bounded. Hence, the power of the proposed identity test is largely determined by σ 1 V n,k δ Vn,k, which may be regarded as the signal to noise ratio of the test. We now discuss the role of the banding width on the power of the test. We note that both δ Vn,k and σ 2 V n,k are increasing with respect to k. For two banding widths k 2 > k 1, suppose that δ Vn,k1 > 0, it may be shown that σ 1 V n,k2 δ Vn,k2 σ 1 V n,k1 δ Vn,k1 if and only if (δ Vn,k2 δ Vn,k1 )/δ Vn,k1 + 1 {(σ 2 V n,k2 σ 2 V n,k1 )/σ 2 V n,k1 + 1} 1/2. Therefore, if the relative signal increment (δ Vn,k2 δ Vn,k1 )/δ Vn,k1 can off-set the relative increase in the noise as specified above, the test with the larger k 2 is more powerful than that with the smaller k 1. On the contrary, if the relative increase in the signal cannot off-set the relative increase in the noise, using the large k leads to a loss of power. To answer the question that when will the increase of the banding width not bring in more power, we note that and for a positive constant c, δ Vn,k2 δ Vn,k1 = σ 2 V n,k2 σ 2 V n,k1 4n(n 1) 1 This implies that a necessary condition for σ 1 V n,k2 δ Vn,k2 k 1 < i j k 2 σ 2 ij k 1 < i j k 2 σ 2 iiσ 2 jj c(k 2 k 1 )pn 2. σ 1 V n,k1 δ Vn,k1 (δ Vn,k2 δ Vn,k1 )/δ Vn,k1 c 1 (k 2 k 1 )n 1 is
88 75 for a positive constant c 1. Hence, if the relative signal increment is smaller than c 1 (k 2 k 1 )n 1, using the larger k 2 will result in a loss in the power. To gain further insight, let us consider the case of banded covariance in which Σ = B k(σ) for a k. In this case, δ Vn,k = δ Vn, k while σ 2 V n,k keeps increasing for all k k. This means that σ 1 V n,k δ Vn,k gets smaller and a loss of power occurs as k gets larger beyond k. Since our proposed test is identical to the one in Chen, Zhang and Zhong (2010) if k = p 1, the proposed identity test is asymptotically more powerful for a properly selected k under the banded scenario. The following theorem establishes the consistency of the proposed identity test. Theorem 3.2. Under Assumptions 3.1 and 3.2, p, k and k = o(min(n 1/2, p 1/2 )), as n, β Vn,k 1 provided {τ n,k (Σ)} 1 δ Vn,k. We note here that τ n,k (Σ) defined in (3.14) is the first term of σv 2 n,k. Theorem 3.2 implies that the proposed identity test is able to detect alternatives with power tending to 1 when {τ n,k (Σ)} 1 δ Vn,k. We note that when {τ n,k (Σ)} 1 δ Vn,k, τn,k 2 (Σ) dominates the other two terms of σ 2 V n,k in (3.13), which means σ 1 V n,k δ Vn,k. It may be shown that τ 2 n,k (Σ) is at most O(k2 pn 2 ) under Assumptions 3.1 and 3.2. Hence, the test has power approaching to one as long as p 1 δ Vn,k is a larger order of kp 1/2 n 1, which is much weaker than n 1, the corresponding lower limit for the test of Chen, Zhang and Zhong (2010) Sphericity test We firstly establish the asymptotic properties of U n,k. Let σu 2 τn,k 2 n,k = (Σ) [ { tr 2 {B k (Σ)Σ} + 2 n tr Bk (Σ)Σ tr(b k (Σ)Σ) Σ } ] 2 tr(σ) + ([ { n tr Γ Bk (Σ) tr(b k (Σ)Σ) I } ] [ { p Γ Γ Bk (Σ) tr(σ) tr(b k (Σ)Σ) I } ]) p Γ. tr(σ) Theorem 3.3. Under Assumptions 3.1 and 3.2, as n, p and k, if k = o(min(n 1/2, p 1/2 )), [{ tr 2 } ( ) ] (Σ) Un,k + 1 U n,k 1 N (0, 1) (3.19) tr(b k (Σ)Σ) p σ 1 in distribution.
89 76 The asymptotic variance under the null hypothesis is σ 2 U n,k 0 = σ 8 p 2 [ 4{n(n 1)} 1 (2pk k 2 k + 2p) + 8 {n(n 1)} {n(n 1)} 1 i 1 j 1 k i 2 j 2 k ] fi 2 1 j 1 i 2 j 2 (I p ). Then, Theorem 3.3 implies that under the null sphericity hypothesis i j k f ijij (I p ) σ 1 U n,k 0 U n,k N (0, 1) (3.20) in distribution. Using a similar approach to estimating the null variance σv 2 n,k 0 in Section 3.3.1, an estimator of the null variance σ 2 U n,k 0 is ˆσ U 2 n,k 0 = ˆσ V 2 n,k 0 It may be shown that ˆσ 2 U n,k 0 σ2 U n,k 0 i j k ( L 1,ij 2 L 2,ij + L 3,ij ) in probability and ˆσ 1 U n,k 0 U n,k converges to N (0, 1) in distribution. These lead to a sphericity test with a nominal significance level α that rejects H 0 : Σ = σ 2 I p if ˆσ 1 U n,k 0 U n,k > z α. (3.21) Let δ Un,k = 1 {tr 2 (Σ)}/[ptr{B k (Σ)Σ}]. The power of the sphericity test is β Un,k (α) = Pr(σ 1 U n,k 0 U n,k z α ) [{ tr 2 } ( ) (Σ) σun,k 0 = 1 Φ z α δ ] U n,k. ptr(b k (Σ)Σ) σ Un,k σ Un,k 2. As tr 2 (Σ)/[ptr{B k (Σ)Σ}] and σ Un,k 0/σ Un,k are both bounded, the power is largely influenced by δ Un,k /σ Un,k, which can be viewed as the signal to noise ratio of the testing problem. To gain insight on the power, we study the signal to noise ratio as what we did for the identity test in section It can be shown that for k 2 > k 1, σ 1 U n,k2 δ Un,k2 and only if (δ Un,k2 δ Un,k1 )/δ Un,k1 + 1 {(σ 2 U n,k2 σ 2 U n,k1 )/σ 2 U n,k1 + 1} 1/2. σ 1 U n,k1 δ Un,k1 if We also note that, for k 2 > k 1 δ Un,k2 δ Un,k1 = p 1 tr 2 k (Σ) 1 < i j k 2 σij 2 tr{b 2 k 1 (Σ)}tr{B 2 k 2 (Σ)},
90 77 which indicates that the increase in the signal is largely driven by k 1 < i j k 2 σ 2 ij, those σ ij between the k 1 and k 2 -th superdiagonals. At the same time, it can be shown that σ 2 U n,k is increasing with respect to k at a rate at least p 1 n 2. Hence, a power-enhancing strategy is to use the smallest k that captures the most signals. The following theorem establishes the consistency of the proposed sphericity test (3.21). Theorem 3.4. Under Assumptions 3.1 and 3.2, p, k and k = o(min(n 1/2, p 1/2 )) as n, if tr{b k (Σ)Σ}{τ n,k (Σ)} 1 δ Un,k then β Un,k 1. It can be shown that τ n,k (Σ)/tr{B k (Σ)Σ} is at most O(kp 1/2 n 1 ). Hence, the proposed sphericity test is consistent as long as δ Un,k is a larger order of kp 1/2 n 1, which is much lower than the corresponding lower limit of the test of Chen, Zhang and Zhong (2010) since k = o(p 1/2 ). The latter test requires δ Un,p 1 is a larger order of n Selection of k Given the beneficial power property of the tests based on the banding operation, we report numerical results of the proposed tests with respect to k in this section. We start with evaluating the impacts of k on the size of the tests. Clearly, under the null hypotheses for both (3.3) and (3.4), Σ U(ε 0, C, α). Given the established asymptotic normality for the two test statistics, the size of the proposed tests are expected to be close to the nominal significance level for a wider range of k as long as k = o(min(n 1/2, p 1/2 )). To confirm this, we ran simulations for the sphericity test. We generated independent and identically distributed random vectors X i from N (0, Σ) where Σ = 2I p and considered k = a i n 1/3 for {a i } 10 i=1 = {0, 0.1, 0.3, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0}. The sample size and the dimensions considered were n = 20, 40 and 60, and p = 38, 89 and 181, respectively. Figure 3.1 displays the empirical size of the proposed sphericity test with respect to k s for the combinations of n and p based on 1000 simulations. The figure shows that the empirical size was largely close to the nominal 5% level for the wider choices of k s. To gain information on the role of k on the power of the tests, we considered the identity test at 5% level of significance under the alternative where Σ 1 = I p Ω, Ω = (ω ij ) 1 i,j p
91 78 Figure 3.1 Empirical size of the 5% sphericity test with respect to the banding width k for various sample sizes and dimensions. with ω ij = I( i j = l) for a fixed integer l. According to Theorem 3.2, the proposed identity test is powerful if {τ n,k (Σ 1 )} 1 δ Vn,k. For the given covariance structure, δ Vn,k = 0 for k < l and δ Vn,k = (p l) for k l. In the meanwhile, τ 2 n,k (Σ 1) is strictly increasing along with k. Thus, {τ n,k (Σ 1 )} 1 δ Vn,k is maximized at k = l for any given n and p, namely the power would be maximized if k agreed with the underlying bandwidth l. We carried out a simulation experiment for N (0, Σ 1 ) distributed data with Σ 1 defined as above and l = 2, and n = 20 and p = 20. Table 3.1 reports the empirical power of the proposed identity test with banding widths ranging from 0 to 7 based on 1000 replications. It shows that the test gained powers as k was increased to l = 2, peaked at k = l = 2, and then declined afterward. This power profile was highly consistent with the discussion made toward the end of Section regarding the signals and the noise of the test statistic. Table 3.1 Empirical power with respect to k for the identity test. k Power While the above results were assuring, we need a practical way to select the banding width k in order to carry out the tests. Qiu and Chen (2015) proposed a selection method by minimizing an empirical estimate of E B k (S n ) Σ 2 F. They demonstrated that the approach has superior performance than the cross-validation approach based on random sample splitting proposed in
92 79 Bickel and Levina (2008a). The cross-validation was formulated based on a score function of k that measured the discrepancy between B k (S n ) based on one part of the split sample, and the sample covariance based on the remaining sample. The issue with the cross-validation was that the use of the inconsistent sample covariance makes the approach unreliable in high dimension. We carried out 1000 simulation experiments to investigate the performance of the banding width denoted as k qc prescribed by Qiu and Chen (2015) for the same Gaussian model with covariance matrix Σ 1 in the setting for Table 3.1 for the identity test. We considered n = 20, 40, 80 and p = 20, 60, 100, 160, 200, 300 in the simulations. Figure 3.2 reports the empirical proportion that the selected banding width k qc agreed with the true value, which was l = 2, and otherwise. Red solid lines with squares report the proportion of times that the selected k agrees with the true value l = 2, the green dashed lines with circles report the proportion that the selected k < 2, and the blue dot-dash lines with triangles report the proportion that the k > 2. The performance of the banding width selection algorithm was satisfactory. Figure 3.2 shows that even when n was small at 20, the algorithm could still identify the true banding width with sufficient probability, and the precision improved as the dimension p was increased. When n was 40, the proportion of correct selection started to be close to 100%. The corresponding empirical powers of the proposed identity test using k qc were close to one for most combinations of n and p. Hence, this numerical study provided support to using k qc for the regularized tests for high dimensional covariance matrices. Figure 3.2 Proportions of the banding width selected by the method of Qiu and Chen (2015).
93 Numerical results Simulation studies We report results of simulation experiments which were designed to evaluate the performance of the proposed tests for identity and sphericity of high dimensional Σ. To demonstrate the improvement in power of the proposed tests, we also experimented two existing high dimensional tests: the one by Chen, Zhang and Zhong (2010) (CZZ hereafter) and the test by Ledoit and Wolf (2002) (LW hereafter). The LW test is applicable for Gaussian data only. The test statistics of CZZ and LW tests include all the components of the sample covariance matrix in their formulation and were expected to have lower power as the test statistics can bear larger variation. We considered two types of innovations for generating data according to Assumption 3.2: the Gaussian innovation where Z i were N (0 m, I m ) distributed; and the Gamma innovation where Z i had m independent and identically distributed components, and each component was the standardized Gamma random variable with parameters 4 and 0.5 such that it had zero mean and unit variance. In the simulations for the sphericity test, the null hypothesis was H 0 : Σ = 2I p. When evaluating the powers of the tests for both identity and sphericity hypotheses, we considered the following three forms of Σ. Diagonal Form: Set Σ = diag(4 1 [vp], 2 1 p [vp] ]) where [x] denotes the integer truncation of x and v characterizes the sparsity of the signals. We chose v = 0.05 and 0.1. Banded Form: Σ = (σ ij ) 1 i,j p with σ ij = ρ i j I{ i j 1} and ρ = Bandable Form: Take Σ = (σ ij ) 1 i,j p with σ ij = I(i = j) + θ i j ρ I(i j) with θ = 1.2 and ρ = 0.16, which prescribed a polynomial decay as considered by Qiu and Chen (2015). To mimic the large p, small n scenario, we set n = 20, 40, 60 and 80, and for each n let p = 38, 55, 89, 159, 181, 331, 343, 642, also set m = p when generating the data according to Assumption 3.2. All the simulation results were based on 1000 iterations with nominal
94 81 significance level at 5%. The parameter k was determined by k = k qc + 1 where k qc was the banding width by the method of Qiu and Chen (2015). We add 1 to k qc was to ensure the banding estimator B k ( ˆΣ) contains enough signals. Table 3.2 displays the empirical sizes of the proposed identity test, the CZZ and LW tests for testing (3.3). It shows that for the Gaussian data the LW test maintained the size better than the other two tests as the LW test was designed for Gaussian data. It is observed that as the sample size was increased, both the proposed identity test and the CZZ test had empirical sizes approaching to the nominal significance level. For the Gamma distributed innovation, as displayed in Table 3.2, the proposed identity test and the CZZ test had the empirical sizes close to the nominal level, while the LW test failed to control the size. The empirical sizes of the three tests for testing the sphericity hypothesis are reported in the appendix, which were quite similar to those of the identity tests in Table 3.2. To compare the powers of the tests, we considered n = 40, 60, 80 for p set as above. For the Gamma distributed data, only the proposed identity and the CZZ tests were considered since the LW test was no longer applicable. Figures display the empirical powers of the of the proposed identity test, the CZZ and LW tests. It was very clear that the proposed identity test outperformed the other two tests for both data generating distributions and the covariance models considered in the simulation. For the alternative Σ with the diagonal form (in Figures 3.3 and 3.4), the powers of all three tests were improved for all tests when v is large as expected; the LW and CZZ tests have comparable powers for the Gaussian data (Figure 3.3). Figure 3.5 reports the empirical power for the bandable and banded alternative. It shows that the proposed identity test outperformed the other two tests. For the alternative in the bandable form, neither the CZZ test nor the LW test gained extra powers as p was increased, while the proposed identity test had its power increased as p was increased as shown in panels (a) and (b) of Figure 3.5). As n was increased, all three tests gained powers as expected. Given the slow decay rate of off-diagonal entries, the alternative in the banded form had a relatively larger banding width than other two types of alternatives. For the banded alternative, all tests gain powers in growing p or n and the CZZ test has power approaching to the proposed identity test as n increasing (panels (c) and (d) in Figure 3.5).
95 82 Table 3.2 Empirical sizes of the proposed test (IT) for the identity hypothesis, along with those of the tests by Chen, Zhang and Zhong (2010) (CZZ) and Ledoit and Wolf (2002) (LW). IT CZZ LW IT CZZ LW IT CZZ LW IT CZZ LW n = 20 n = 40 n = 60 n = 80 p Gaussian distributed innovation Gamma distributed innovation
96 83 Figure 3.3 Empirical powers for the identity tests against the alternative in the diagonal form with the Gaussian distributed innovation. Figure 3.4 Empirical powers for the identity tests against the alternative in the diagonal form with the Gamma distributed innovation.
97 84 (a) Bandable alternative with Gaussian innovations. (b) Bandable alternative with Gaussian innovations. (c) Banded alternative with Gaussian innovations. (d) Banded alternative with Gamma innovations. Figure 3.5 Empirical powers for the identity tests against the alternatives in either the bandable or banded forms of the proposed test with either the Gaussian or Gamma distributed innovation.
98 85 Figure 3.6 Empirical powers for the sphericity tests against the alternative in the diagonal form with the Gaussian distributed innovation. Figure 3.7 Empirical powers for the sphericity tests against the alternative in the diagonal form with the Gamma distributed innovation.
99 86 (a) Bandable alternative with Gaussian innovations. (b) Bandable alternative with Gaussian innovations. (c) Banded alternative with Gaussian innovations. (d) Banded alternative with Gamma innovations. Figure 3.8 Empirical powers for the sphericity tests against the alternatives in either the bandable or banded forms of the proposed test with either the Gaussian or Gamma distributed innovation.
100 87 The power performance of the proposed test for the sphericity along with the CZZ and LW tests are reported in Figures , which suggest that the proposed sphericity test was much more powerful than the other two tests under the three forms of the alternatives Σ. More simulation results are reported in the appendix Empirical study We analyzed an acute lymphoblastic leukemia (ALL) data reported in Chiaretti et al. (2004) to demonstrate the proposed regularized tests for identity and sphericity. The data contain microarray expressions for patients having acute lymphoblastic leukemia of either T- lymphocyte type or B-lymphocyte type. We focused on the sub-sample of B-lymphocyte type leukemia in this analysis. The 78 patients of B-lymphocyte type leukemia were classified into two groups: the BCR/ABL fusion (36 patients) and cytogenetically normal NEG (42 patients). The original dataset has been analyzed by Chen and Qin (2010); Chiaretti et al. (2004), and Dudoit, Keles and van der Laan (2011), using different methodologies. Our analysis is to study the covariance structures for sets of genes defined within the gene ontology (GO) framework. It is known that genes tend to work collectively to achieve certain biological tasks, which gave rise to the identification of gene-sets (also called GO terms) with respect to three broader categories of biological functions: biological processes (BP), cellular components (CC) and molecular functions (MF). The gene-sets are technically defined in the gene ontology (GO) system via structured vocabularies which produce unique name for a geneset. After a preliminary screening with the gene-filtering approach advocated in Gentleman et al. (2005), there left 2694 unique gene-sets in the BP category, 352 in the CC category and 419 in the MF category for the ALL data. The largest gene-set had 3048, 3140 and 303 genes in BP, CC and MF, respectively. Our aim was to study the dependence structures in the expression levels of gene-sets between the BCR/ABL and NEG groups for each of the three functional categories by testing hypotheses (3.3) and (3.4) for appropriately transformed data. The procedure is described as following. To attain bandable covariance structure so that we can apply the proposed tests, we employed the re-ordering algorithm in Friendly (2002) to each gene-set in both the NEG and the BCR/ABL
101 88 fusion groups to obtain a permutation of the genes in that gene-set so that the covariance was more bandable. As a demonstration of this data re-ordering algorithm, we compare the heat maps of the correlation matrices before and after the re-ordering based on samples from the NEG group for the gene-set GO: (G2/M transition of mitotic cell cycle), which has 63 genes, in Figure 3.9 in the appendix. For a gene-set of a functional category with the NEG sample, say the g-th gene-set, its covariance Σ neg,g was estimated by using the banding estimator, denoted as Σ neg,g with the banding width determined by the method in Qiu and Chen (2015). And to transform the same gene-set in the BCR/ABL group. Σ 1/2 neg,g was used For each transformed gene-set in the BCR/ABL group, we tested the hypotheses (3.3) and (3.4) using the proposed regularized identity and sphericity tests when p > 10 and use the tests by John (1971, 1972) for those genesets with smaller dimensions. For the proposed tests, k was chosen as k qc + 1. We essentially tested hypotheses H 0 : Σ neg,g = Σ BCR/ABL,g or Σ neg,g = σ 2 gσ BCR/ABL,g for some σ 2 g > 0 for each g = 1,..., G where G is the total number of gene-sets in the category. The test of Chen, Zhang and Zhong (2010) was also performed to serve as a comparison. By controlling the false discovery rate (FDR) (Benjamini and Hochberg, 1995) at 0.001, we have identified gene-sets that have significantly different covariance structures between the NEG and BCR/ABL groups. Table 3.3 provides a broad classification for the gene-sets identified by the proposed test and the test of Chen, Zhang and Zhong (2010). The table shows that the dependence structure between NEG and BCR/ABL were largely different with quite a large number of significantly differential expressed gene-sets, which was due to a large number of very small p-values (Figure 3.10 in the appendix). Biologically speaking, the NEG and BCR/ABL cases have different genetic mechanisms that cytogenetically normal leukemia is not associated with large chromosomal abnormalities while the BCR/ABL leukemia involves fusion of BCR and ABL genes in Philadelphia chromosome (Pakakasama et al., 2008). Table 3.3 reveals that the proposed tests identified more gene-sets than the CZZ test. It is interesting to notice that the proposed sphericity test has identified GO: and GO: as diseases-associated gene-sets in the MF category while they were missed by the CZZ test, and biologically these two gene-sets correspond to exonuclease activity and endopeptidase in-
102 89 Table 3.3 Number of identified gene-sets against null hypotheses. ST and IT stand for the proposed sphericity and identity tests, respectively. The last column reports the means and standard deviations for k qc. GO Sphericity hypothesis (3.4) Identity hypothesis (3.3) k after Total Category ST only Both CZZ only IT only Both CZZ only re-ordering BP (14.11, 10.03) CC (14.57, 9.51) MF (13.57, 9.33) hibitor activity, which have been recognized associated to the disease development of different types of leukemia recently (Shi et al., 2015; Tsakou et al., 2012). 3.6 Discussion In this paper, we introduced two powerful tests for the identity and sphericity hypotheses of large covariance matrices and showed that the proposed testing procedures perform particularly well against sparse alternatives from some particular classes. The proposed tests leverage the sparsity information of the alternatives in high dimensional settings that leads to significant reduction in the variance of the test statistics. The theoretical properties of the proposed tests were established. We also explored how the proposed tests improve the powers comparing to the test by Chen, Zhang and Zhong (2010). Furthermore, we discussed the selection of k for the proposed tests in practice. Finally, we examined the proposed tests by numerical studies and illustrated its applications in real data analysis. The forms of the identity hypothesis that Σ = I p and the sphericity hypothesis that Σ = σ 2 I p are two idealized hypotheses. Despite being idealized, they play central roles in either the classical multivariate analysis where the dimension of data p is fixed or the high dimensional multivariate analysis where p is diverging and can be larger than the sample size as treated in this paper. The literature of the classical multivariate analysis include those of Anderson (2003), John (1971, 1972) and Nagao (1973), while the contemporary literature includes Chen, Zhang and Zhong (2010) and Ledoit and Wolf (2002) among others. The identity hypothesis in (3.3) actually covers the hypothesis H 0 : Σ = Σ 0 for a known invertible covariance matrix Σ 0. By transforming the data via left multiplying Σ 1/2 0, the
103 90 identity hypothesis can be carried out for the transformed data. The sphericity hypothesis can be treated similarly. In practice, the hypotheses Σ 0 can be postulated based on the empirical estimates of Σ. This was what we have done in the case study by first permuting the data to rearrange the data components so that those with high correlations are grouped closer than those with low correlation. After the permutation, we employed the banding estimator of the high dimensional covariance matrix of Bickel and Levina (2008a) to attain a banded form for Σ, which are used to standardize the data. We are aware that using the estimated Σ 0 would introduce issues of inference as the estimation error may affect the asymptotic distribution. While this would not be a big issue in the classical fixed dimensional context, it would be an issue when p diverges. We would consider this issue in a future study. Another issue is a concern on the computational costs required in carrying out the proposed test procedures. The main cost of computation is in computing the raw test statistics and in estimating their variance. To gain information on the computation time needed, we report in Table 3.4 the time needed to accomplish a single sphericity test under the alternative bandable form Σ in the simulation study for different n and p on a PC with Intel(R) Core(MT) i7-4790k processor and CPU speed of 4.0GHz. The computing times in the table suggest that the computation burden for carrying out the test procedure is manageable even for relatively larger values of n and p with a quite standard computational capacity. Table 3.4 Computational time (in seconds) for a single sphericity test under the alternative Σ = (σ ij ) 1 i,j p with σ ij = I(i = j) + θ i j ρ I(i j) with different n and p. n p Appendix We begin this appendix by presenting some notation and technical preliminaries that will be used in the proof of the main results. For a matrix M = (m ij ) 1 i,j p, we denote λ(m) the
104 91 eigenvalues of M with λ min (M) and λ max (M) the smallest and largest eigenvalues of M, respectively, and denote the matrix norms by M 1 max j i m ij, M { λ max (M M) } 1/2, and M max i j m ij. For symmetric Σ U(ε 0, C, α), we have the following properties (1) Σ 1/ε 0 and B k (Σ) Σ 1 Ck α ; (2) B k (Σ) 1/ε 0 + Ck α ; (3) λ min {B k (Σ)} λ min (Σ) Ck α ; and (4) there exist C 1, C 2 > 0 such that C 1 min i σ ii max i σ ii C 2 for Σ = (σ ij ) 1 i,j p. Properties (2) and (3) imply that for sufficiently large k, there exits a positive constant δ 0 such that 0 < δ 0 λ min {B k (Σ)} λ max {B k (Σ)} 1/δ 0, which means tr(σ) = O(p) and tr{b k (Σ)} = O(p) for sufficiently large k. In addition, some algebraic computations yield following useful results in remaining derivations: (i) i 1 j 1 k p i 2 =1 σ i 1 j 1 f i1 j 1 i 2 i 2 (Σ) = tr [{ Γ B k (Σ)Γ } (Γ Γ) ] tr{b k (Σ)Σ 2 }; (ii) i 1 j 1 k i 2 j 2 k σ i 1 j 1 σ i2 j 2 f i1 j 1 i 2 j 2 (Σ) = tr [{ Γ B k (Σ)Γ } { Γ B k (Σ)Γ }] tr [ {B k (Σ)Σ} 2] ; (iii) i 1 j 1 k i 2 j 2 k σ2 i 1 i 2 σj 2 1 j 2 (2k + 1) 2 tr{(σ Σ) 2 }, i 1 j 1 k i 2 j 2 k σ i 1 i 2 σ j1 j 2 σ i1 j 2 σ j1 i 2 (2k + 1) 2 tr{(σ Σ) 2 }; (iv) i 1 j 1 k (v) i 1 j 1 k i 2 j 2 k σ i 1 i 2 σ j1 j 2 f i1 j 1 i 2 j 2 (Σ) (2k + 1) 2 tr{(γ Γ)(Γ Γ) (Σ Σ)}; and, i 2 j 2 k f 2 i 1 j 1 i 2 j 2 (Σ) (2k + 1) 2 tr [ {(Γ Γ)(Γ Γ) } 2 ] Critical lemmas In this section, we collect some technical lemmas that will be used in the proofs. The first lemma provides algebraic representations of the variances and covariances of L n1, L n2, L n3, L n4 and L n5.
105 92 Lemma 3.1. Under Assumptions 3.1 and 3.2, for τ 2 n,k (Σ) defined in (3.14) and n = n(n 1)(n 2)(n 3) Var L n1 (i, j) = τ n,k 2 (Σ) + 8n 1 tr [ {B k (Σ)Σ} 2] Var i j k i j k L n2 (i, j) = 2 n(n 1) tr {B k(σ)σb k (Σ)Σ} + i 2 j 2 k Var L n3 (i, j) = 8 n i j k i 1 j 1 k { p } Var L n4 (i) = 2n 1 tr(σ 2 ) + n 1 tr i=1 [{ } { }] + 4 n 1 tr Γ B k (Σ)Γ Γ B k (Σ)Γ, 1 n(n 1)(n 2) i 1 j 1 k { } (σ i1 i 2 σ j1 j 2 + σ i1 j 2 σ j1 i 2 ) 2 + (σ i1 i 2 σ j1 j 2 + σ i1 j 2 σ j1 i 2 )f i1 j 1 i 2 j 2 (Σ), i 2 j 2 k { p } Var L n5 (i) = 2{n(n 1)} 1 tr(σ 2 ), i=1 σ 2 i 1 i 2 σ 2 j 1 j n {( Γ Γ ) ( )} Γ Γ, i 1 j 1 k i 2 j 2 k σ i1 i 2 σ i1 j 2 σ j1 i 2 σ j1 j 2, and furthermore, p Cov L n1 (i, j), L n4 (i) = 4n 1 tr { B k (Σ)Σ 2} [{ } ] + 2 n 1 tr Γ B k (Σ)Γ (Γ Γ), i j k i=1 { p } p Cov L n4 (i), L n5 (i) = 0. i=1 i=1 The proof of Lemma 3.1 is based on standard yet tedious computations that we omit here. Lemma 3.1 implies that Var{ i j k L n 3 (i, j)} = O ( n 2 Var{ i j k L n 1 (i, j)} ), and under the assumption that k and k = o(min(n 1/2, p 1/2 )), it yields Var L n2 (i, j) = o Var L n1 (i, j) and i j k { p } Var L 5,i = o Var i=1 i j k i j k L n1 (i, j). The next lemma is on the asymptotic normality of statistics T n,k.
106 93 Lemma 3.2. Under Assumptions 3.1 and 3.2, for any real sequences {a n } n=1 and {b n} n=1, T n,k = a n i j k L n 1 (i, j) + b n p i=1 L n 4 (i) satisfies {Var(T n,k )} 1/2 {T n,k E(T n,k )} N (0, 1) (3.22) in distribution provided k = o(min(n 1/2, p 1/2 )). Proof. Let F 0 = {, Ω} and F t = σ{x 1,..., X t } for t = 1,..., n be the sequence of σ-fields generated by data, and denote E t ( ) E( F t ) and E( ) E 0 ( ). Write T n,k E(T n,k ) = n t=1 D t,k, where D t,k = E t (T n,k ) E t 1 (T n,k ). It is easy to see that D t,k is F t measurable and E t 1 (D t,k ) = 0 for each t 1 so that for every n, {D t,k, F t } 1 t n is a martingale difference array. By the martingale central limit theorem, (3.22) is straightforward once one can show that, as n, n t=1 σ2 t,k Var(T n,k ) p 1 and n t=1 E(D4 t,k ) Var 2 (T n,k ) 0, (3.23) with σ 2 t,k = E t 1(D 2 t,k ). As E( n t=1 σ2 t,k ) = Var(T n,k), it suffices to show that Var( n t=1 σ2 t,k ) = o(var2 (T n,k )) to derive the first part of (3.23). By Lemma 3.1, Var(T n,k ) = a 2 nτn,k 2 (Σ) + 2n 1 tr [{2a n B k (Σ) + b n I p } Σ] 2 + n 1 tr [ { } Γ (2a n B k (Σ) + b n I p ) Γ { ]. Γ (2a n B k (Σ) + b n I p ) Γ} Also, notice that [ ] D t,k = 2a n {n(n 1)} 1 X t B k (Q t 1 )X t tr{b k (Q t 1 )Σ} [ ] { } + 2a n n 1 X t B k (Σ)X t tr{b k (Σ)Σ} + b n n 1 X t X t tr(σ), where Q t 1 = (Q i,j t 1 ) 1 i,j p = t 1 s=1 (X sx s Σ) with Q i,j t 1 = t 1 s=1 (x six sj σ ij ), so n σt,k 2 = R 1,n + R 2,n + R 3,n + R 4,n + nc, t=1
107 94 for some constant C and R 1,n = 8a n {n 2 (n 1)} 1 R 2,n = 4 a n {n 2 (n 1)} 1 R 3,n = 8a 2 n{n 2 (n 1) 2 } 1 n tr [B k (Q t 1 )Σ {2a n B k (Σ) + b n I p } Σ], t=1 R 4,n = 4 a 2 n{n 2 (n 1) 2 } 1 n t=1 [{ } { }] tr Γ B k (Q t 1 )Γ Γ (2a n B k (Σ) + b n I p ) Γ, n tr [ {B k (Q t 1 )Σ} 2], t=1 n t=1 [{ } { }] tr Γ B k (Q t 1 )Γ Γ B k (Q t 1 )Γ, It is sufficient to show Var(R i,n ) = o(var 2 (T n,k )) for i = 1, 2, 3, 4 to obtain Var( n t=1 σ2 t,k ) = o(var 2 (T n,k )). We first study R 1,n. Denote Ω k = Σ {2a n B k (Σ) + b n I p } Σ. Recall the fact that tr{b k (A)C} = tr{ab k (C)} for symmetric matrices A and C with conformable sizes, we have Therefore, for each s 1 t 1 [ ] tr {B k (Q t 1 )Ω k } = X s B k (Ω k )X s tr{b k (Σ)Ω k }. s=1 [ ] [{ } { }] Var X s B k (Ω k )X s tr{b k (Σ)Ω k } = 2tr{ΣB k (Ω k )} 2 + tr Γ B k (Ω)Γ Γ B k (Ω)Γ. By the algebraic properties summarized before, it holds for some constant γ > 0 that tr{σb k (Ω k )} 2 γtr[{b k (Σ)Σ} 2 ]tr [{2a n B k (Σ) + b n I p } Σ] 2 = o { n 3 Var 2 (T n,k ) }, and also tr [{ Γ B k (Ω k )Γ } { Γ B k (Ω k )Γ }] tr{σb k (Ω k )} 2. We therefore conclude that there exist constant C > 0 such that Var(R 1,n ) Cn 3 Var [tr {B k (Q t 1 )Ω k }] = o(var 2 (T n,k )). For R 3,n, denote for any 1 s 1, s 2 n, Y s1 s 2 = σ i1 i 2 σ j1 j 2 (x s1 i 1 x s1 j 1 σ i1 j 1 )(x s2 i 2 x s2 j 2 σ i2 j 2 ). i 1 j 1 k i 2 j 2 k Then tr [ {B k (Q t 1 )Σ} 2] t 1 = Y ss + Y s1 s 2. s=1 s 1 s 2
108 95 Notice that E(Y s1 s 2 ) = 0 for any s 1 s 2 and E(Y s1 s 2 Y s3 s 4 ) = 0 for any (s 1, s 2, s 3, s 4 ) except s 1 = s 2 = s 3 = s 4, s 1 = s 3 and s 2 = s 4 or s 1 = s 4 and s 2 = s 3. Hence, for any t l Cov ( tr [ {B k (Q t 1 )Σ} 2], tr [ {B k (Q l 1 )Σ} 2]) = (t 1)Var(Y 11 ) + 2(t 1)(t 2)Var(Y 12 ). It is therefore sufficiently to show Var(Y 11 ) = o ( n 5 Var 2 (T n,k ) ) and Var(Y 12 ) = o ( n 4 Var 2 (T n,k ) ). As k = o(n 1/2 ), then for constant C 1 > 0 E(Y 2 11) = i 1 j 1 k i 2 j 2 k i 3 j 3 k i 4 j 4 k [ σ i1 i 2 σ j1 j 2 σ i3 i 4 σ j3 j 4 ] E{(x 1i1 x 1j1 σ i1 j 1 )(x 1i2 x 1j2 σ i2 j 2 )(x 1i3 x 1j3 σ i3 j 3 )(x 1i4 x 1j4 σ i4 j 4 )} C 1 (2k + 1) 4 tr 2 (Σ 4 ) = o ( n 5 Var 2 (T n,k ) ), so that Var(Y 11 ) = o { n 5 Var 2 (T n,k ) }. Similarly, for some constant C 2 > 0 Var(Y 12 ) = [ σ i1 i 2 σ j1 j 2 σ i3 i 4 σ j3 j 4 i 1 j 1 k i 2 j 2 k i 3 j 3 k i 4 j 4 k ] {σ i1 i 3 σ j1 j 3 + σ i1 j 3 σ j1 i 3 + f i1 j 1 i 3 j 3 (Σ)}{σ i2 i 4 σ j2 j 4 + σ i2 j 4 σ j2 i 4 + f i2 j 2 i 4 j 4 (Σ)} C 2 (2k + 1) 4 tr(σ 8 ) = o ( n 4 Var 2 (T n,k ) ). Thus, Var [ tr{(b k (Q t 1 )Σ) 2 } ] = t 2 o ( n 4 Var 2 (T n,k ) ), which implies that for some positive constants γ, γ 1 and γ 2 [ n Var(R 3,n ) γn 8 Var tr { (B k (Q t 1 )Σ) 2}] γ 1 n 5 Var(Y 11 ) + γ 2 n 4 Var(Y 12 ) t=1 = o(var 2 (T n,k )). Likewise, we can show that Var(R i,n ) = o(var 2 (T n,k )) for i = 2, 4, by which we obtain the first part of (3.23) using the concentration property. It remains to show the second part of (3.23). By standard algebraic computations, one can show that D t,k = M t,1 + M t,2 where [ ] M t,1 = 2a n {n(n 1)} 1 X t B k (Q t 1 )X t tr{b k (Q t 1 )Σ}, [ ] M t,2 = n 1 X t {2a n B k (Σ) + b n I p }X t tr {(2a n B k (Σ) + b n I p )Σ}.
109 96 Since n t=1 E(D4 t,k ) C { n t=1 E(M4 t,1 ) + n t=1 E(M4 t,2 )} for constant C > 0, it suffices to show E(M 4 t,i ) = o(var2 (T n,k )) for i = 1, 2. By Cauchy-Schwartz inequality, for some constant c > 0, E [ X t B k (Q t 1 )X t tr {B k (Q t 1 )Σ} ] 4 ce [ tr 2 {(B k (Q t 1 )Σ) 2 } ]. On the other hand, E [ tr{(b k (Q t 1 )Σ) 2 } ] = (t 1) and i 1 j 1 k i 2 j 2 k Var [ tr{(b k (Q t 1 )Σ) 2 } ] = t 2 o ( n 2 Var(T n,k ) ) 2, {σ i1 i 2 σ j1 j 2 + σ i1 j 2 σ i2 j 1 + f i1 j 1 i 2 j 2 (Σ)} σ i1 i 2 σ j1 j 2, we have E [ tr 2 {(B k (Q t 1 )Σ) 2 } ] = t 2 O ( n 2 Var(T n,k ) ) 2. Therefore, it yields n E(M 4 t,1) = 16a 4 nn 8 t=1 n t=1 [ ] 4 E Xt B k (Q t 1 )X t tr {B k (Q t 1 )Σ} n 5 O ( n 2 Var(T n,k ) ) 2 = o(var(tn,k )). Similarly, for some constant C > 0, n E(M 4 t,2) = n 4 t=1 n t=1 [ ] 4 E X t {2a n B k (Σ) + b n I p }X t tr {(2a n B k (Σ) + b n I p )Σ} Cn 3 tr 2 [{2a n B k (Σ) + b n I p }Σ] 2, which implies n t=1 E(M4 t,2 ) = o ( Var 2 (T n,k ) ). We therefore obtain the second part in (3.23), and derive the assertion of Lemma Proof of Proposition 3.1 where Simple algebraic computations yield Π 1 = 1 P 2 n Π 2 = 1 P 3 n Π 3 = 1 P 4 n ˆσ 2 V n,k 0 = 2{n(n 1)} 1 i 1 j 1 k i 2 j 2 k {Π 1 2Π 2 + Π 3 }, {(x 11 i 1 x 11 j 1 σ i1 j 1 )(x 11 i 2 x 11 j 2 σ i2 j 2 )(x 12 i 1 x 12 j 1 σ i1 j 1 )(x 12 i 2 x 12 j 2 σ i2 j 2 )}, l 1 l 2 {(x 11 i 1 x 11 j 1 σ i1 j 1 )(x 12 i 2 x 12 j 2 σ i2 j 2 )(x 13 i 1 x 13 j 1 σ i1 j 1 )(x 13 i 2 x 13 j 2 σ i2 j 2 )}, l 1,l 2,l 3 {(x 11 i 1 x 11 j 1 σ i1 j 1 )(x 12 i 2 x 12 j 2 σ i2 j 2 )(x 13 i 1 x 13 j 1 σ i1 j 1 )(x 14 i 2 x 14 j 2 σ i2 j 2 )}. l 1,l 2,l 3,l 4
110 97 Thus, E(ˆσ V 2 n,k 0 ) = σ2 V n,k 0. Similar to Lemma 3.1, Var ( [ = 4n 1 i 1 j 1 k i 2 j 2 k i 3 j 3 k i 4 j 4 k Π 1 i 1 j 1 k i 2 j 2 k {E(x li1 x lj1 x li2 x lj2 ) σ i1 j 1 σ i2 j 2 } 2 ] 2 + 4n 1 i 1 j 1 k i 2 j 2 k [ {E(x li1 x lj1 x li2 x lj2 ) σ i1 j 1 σ i2 j 2 } {E(x li3 x lj3 x li4 x lj4 ) σ i3 j 3 σ i4 j 4 } ]) {1 E{(x 1i1 x 1j1 σ i1 j 1 )(x 1i2 x 1j2 σ i2 j 2 )(x 1i3 x 1j3 σ i3 j 3 )(x 1i4 x 1j4 σ i4 j 4 )} + O(n 1 ) } ( ) = O (n 3 + k 2 n 3 )σv 2 n,k 0. The variances for the remaining terms of ˆσ V 2 n,k 0 can be estimated similarly and the proposition follows Proof of Theorem 3.1 Denote Ṽ n,k = p L n1 (i, j) 2 L n4 (i) + p. i j k i=1 Under Assumptions 3.1 and 3.2, E(Ṽn,k) = tr[{b k (Σ) I p } 2 ]. From Lemma 3.1, we have Var(Ṽn,k) = σ 2 V n,k + o(σ 2 V n,k ), Var{ i j k L n 2 (i, j)} = o(σ 2 V n,k ), Var{ i j k L n 3 (i, j)} = o(σ 2 V n,k ), and Var { p i=1 L n 5 (i)} = o(σ 2 V n,k ). Theorem 3.1 therefore follows Lemma 3.2 and Slutsky s Theorem Proof of Theorem 3.2 It follows Theorems 3.1 and (3.16) that ( ) β Vn,k = 1 Φ σ 1 V n,k σ Vn,k 0z α σ 1 V n,k [tr{(b k (Σ) I p ) 2 }]. As discussed before, it can be seen that σ Vn,k tr [ ( {B k (Σ) I p } 2] τn,k 2 (Σ) ) 1/2 tr 2 [{B k (Σ) I p } 2 ] tr[σ{b k (Σ) I p }] 2 n tr 2 [{B k (Σ) I p } 2, ]
111 98 so that under the condition {τ n,k (Σ)} 1 tr [ {B k (Σ) I p } 2], it suffices to show provided σ 1 V n,k σ Vn,k 0 is bounded. tr[σ{b k (Σ) I p }] 2 ntr 2 [{B k (Σ) I p } 2 0, (3.24) ] Denote λ 1 λ p the eigenvalues of B k (Σ) that for some δ 0, 0 < δ 0 λ 1 λ p δ 1 0 for sufficiently large k. Standard algebraic computations give tr [Σ{B k (Σ) I p }] 2 = tr [B k (Σ){B k (Σ) I p }] 2 + tr [{Σ B k (Σ)}{B k (Σ) I p }] 2 + 2tr [B k (Σ){B k (Σ) I p }{Σ B k (Σ)}{B k (Σ) I p }] I 1 + I 2 + I 3. By the fact that Σ B k (Σ) Ck α, I i = o ( ntr 2 [ {B k (Σ) I p } 2]) for i = 2, 3. Notice that tr [B k (Σ){B k (Σ) I p }] 2 = p i=1 λ 2 i (λ i 1) 2 δ 2 0 from which (3.24) follows. We therefore obtain Theorem 3.2. p i=1 (λ i 1) 2 = δ 2 0 tr [ {B k (Σ) I p } 2], Proof of Theorem 3.3 Denote Ũ n,k = i j k L n 1 (i, j) tr{b k (Σ)Σ} 2 p i=1 L n 4 (i) + 1. tr(σ) By Lemmas 3.1 and 3.2, we have Var(Ũn,k) = σu 2 n,k {1 + o(1)} and σ 1 U n,k Ũ n,k N (0, 1) [ ] in distribution. Together with results that Var i j k L n 2 (i, j)/tr{b k (Σ)Σ} = o(σu 2 n,k ), Var { [ p ] i=1 L n 5 (i)/tr(σ)} = o(σu 2 n,k ) and Var i j k L n 3 (i, j)/tr{b k (Σ)Σ} = o(σu 2 n,k ), we have σ 1 U n,k Û n,k N (0, 1) in distribution, where i j k Û n,k = { L n 1 (i, j) 2 L n2 (i, j) + L n3 (i, j)} 2 p i=1 { L n 4 (i) L n5 (i)} + 1. tr{b k (Σ)Σ} tr(σ) Denote ɛ n = [ p i=1 { L n 4 (i) L n5 (i)} tr(σ)] /tr(σ) with E(ɛ n ) = 0, then Var(ɛ n ) = tr 2 (Σ) [ {( ) ( )} ] 2n 1 tr(σ 2 ) + n 1 tr Γ Γ Γ Γ + 2{n(n 1)} 1 tr(σ 2 ) [ (2 + )n 1 + 2{n(n 1)} 1] tr 2 (Σ)tr(Σ 2 ) = o(σ Un ).
112 99 Thus, Theorem 3.3 follows from ( tr 2 (Σ) tr{b k (Σ)Σ} Proof of Theorem 3.4 It follows Theorems 3.3 and (3.21) ([ tr 2 (Σ) β Un,k = 1 Φ ptr{b k (Σ)Σ} Since σ Un,k 0/σ Un,k ) ( Un,k + 1 p ] ( σun,k 0 σ Un,k ) 1 = Ûn,k ɛ 2 n (1 + ɛ 2 n) 2. and p 1 tr 2 (Σ)/tr{B k (Σ)Σ} are bounded and [ τn,k 2 σ Un,k (Σ) tr 2 {(B k (Σ)Σ)} tr n ) z α σ 1 tr U n,k [1 2 ]) (Σ). ptr{b k (Σ)Σ} { ( Bk (Σ)Σ tr(b k (Σ)Σ) Σ ) }] 2 1/2, tr(σ) similar to Theorem 3.2, under the condition {τ n,k (Σ)} 1 [tr{b k (Σ)Σ tr 2 (Σ)/p}], it is sufficient to show n 1 tr [ { Σ 2 tr(σ 2 ) Standard algebra and definition in (3.6) implies that [ {Σ tr 2 tr 1 (Σ)tr(Σ 2 )Σ } ] 2 ɛ 2 0 p { λi (Σ) tr 1 (Σ)tr(Σ 2 ) } 2 i=1 = ɛ 2 0 tr2 (Σ) = ɛ 2 0 tr2 (Σ) Σ } 2 ] { } 2 1 tr2 (Σ) tr(σ) ptr(σ 2 0. (3.25) ) p { tr 1 (Σ)λ i (Σ) p 1 + p 1 tr 2 (Σ)tr(Σ 2 ) } 2 i=1 [ tr { (tr 1 (Σ)Σ p 1 I p ) 2 } + p { p 1 tr 2 (Σ)tr(Σ 2 ) } 2 ], and {tr(σ 2 ) p 1 tr 2 (Σ)} 2 = tr 2 (Σ)tr { tr 1 (Σ)Σ p 1 I p } 2, which implies (3.25) and Theorem 3.4 follows More numerical results
113 100 Table 3.5 Empirical sizes of the proposed test (ST) for the sphericity hypothesis, along with those of the tests by Chen, Zhang and Zhong (2010) (CZZ) and Ledoit and Wolf (2002) (LW). IT CZZ LW IT CZZ LW IT CZZ LW IT CZZ LW n = 20 n = 40 n = 60 n = 80 p Gaussian distributed innovation Gamma distributed innovation
114 101 (a) Before reordering (b) After reordering Figure 3.9 Comparison of heat maps of correlation matrices before and after reordering of a gene set, GO: from BP category in NEG group.
Experimental designs for multiple responses with different models
 Graduate Theses and Dissertations Graduate College 2015 Experimental designs for multiple responses with different models Wilmina Mary Marget Iowa State University Follow this and additional works at:
Graduate Theses and Dissertations Graduate College 2015 Experimental designs for multiple responses with different models Wilmina Mary Marget Iowa State University Follow this and additional works at:
Empirical Likelihood Tests for High-dimensional Data
 Empirical Likelihood Tests for High-dimensional Data Department of Statistics and Actuarial Science University of Waterloo, Canada ICSA - Canada Chapter 2013 Symposium Toronto, August 2-3, 2013 Based on
Empirical Likelihood Tests for High-dimensional Data Department of Statistics and Actuarial Science University of Waterloo, Canada ICSA - Canada Chapter 2013 Symposium Toronto, August 2-3, 2013 Based on
Lecture 7 Introduction to Statistical Decision Theory
 Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
More powerful tests for sparse high-dimensional covariances matrices
 Accepted Manuscript More powerful tests for sparse high-dimensional covariances matrices Liu-hua Peng, Song Xi Chen, Wen Zhou PII: S0047-259X(16)30004-5 DOI: http://dx.doi.org/10.1016/j.jmva.2016.03.008
Accepted Manuscript More powerful tests for sparse high-dimensional covariances matrices Liu-hua Peng, Song Xi Chen, Wen Zhou PII: S0047-259X(16)30004-5 DOI: http://dx.doi.org/10.1016/j.jmva.2016.03.008
Divide-and-combine Strategies in Statistical Modeling for Massive Data
 Divide-and-combine Strategies in Statistical Modeling for Massive Data Liqun Yu Washington University in St. Louis March 30, 2017 Liqun Yu (WUSTL) D&C Statistical Modeling for Massive Data March 30, 2017
Divide-and-combine Strategies in Statistical Modeling for Massive Data Liqun Yu Washington University in St. Louis March 30, 2017 Liqun Yu (WUSTL) D&C Statistical Modeling for Massive Data March 30, 2017
INFORMATION APPROACH FOR CHANGE POINT DETECTION OF WEIBULL MODELS WITH APPLICATIONS. Tao Jiang. A Thesis
 INFORMATION APPROACH FOR CHANGE POINT DETECTION OF WEIBULL MODELS WITH APPLICATIONS Tao Jiang A Thesis Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the
INFORMATION APPROACH FOR CHANGE POINT DETECTION OF WEIBULL MODELS WITH APPLICATIONS Tao Jiang A Thesis Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the
Nonconcave Penalized Likelihood with A Diverging Number of Parameters
 Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Statistical Inference On the High-dimensional Gaussian Covarianc
 Statistical Inference On the High-dimensional Gaussian Covariance Matrix Department of Mathematical Sciences, Clemson University June 6, 2011 Outline Introduction Problem Setup Statistical Inference High-Dimensional
Statistical Inference On the High-dimensional Gaussian Covariance Matrix Department of Mathematical Sciences, Clemson University June 6, 2011 Outline Introduction Problem Setup Statistical Inference High-Dimensional
Numerical computation of an optimal control problem with homogenization in one-dimensional case
 Retrospective Theses and Dissertations Iowa State University Capstones, Theses and Dissertations 28 Numerical computation of an optimal control problem with homogenization in one-dimensional case Zhen
Retrospective Theses and Dissertations Iowa State University Capstones, Theses and Dissertations 28 Numerical computation of an optimal control problem with homogenization in one-dimensional case Zhen
Inferences on a Normal Covariance Matrix and Generalized Variance with Monotone Missing Data
 Journal of Multivariate Analysis 78, 6282 (2001) doi:10.1006jmva.2000.1939, available online at http:www.idealibrary.com on Inferences on a Normal Covariance Matrix and Generalized Variance with Monotone
Journal of Multivariate Analysis 78, 6282 (2001) doi:10.1006jmva.2000.1939, available online at http:www.idealibrary.com on Inferences on a Normal Covariance Matrix and Generalized Variance with Monotone
Confidence intervals for kernel density estimation
 Stata User Group - 9th UK meeting - 19/20 May 2003 Confidence intervals for kernel density estimation Carlo Fiorio c.fiorio@lse.ac.uk London School of Economics and STICERD Stata User Group - 9th UK meeting
Stata User Group - 9th UK meeting - 19/20 May 2003 Confidence intervals for kernel density estimation Carlo Fiorio c.fiorio@lse.ac.uk London School of Economics and STICERD Stata User Group - 9th UK meeting
Examining the accuracy of the normal approximation to the poisson random variable
 Eastern Michigan University DigitalCommons@EMU Master's Theses and Doctoral Dissertations Master's Theses, and Doctoral Dissertations, and Graduate Capstone Projects 2009 Examining the accuracy of the
Eastern Michigan University DigitalCommons@EMU Master's Theses and Doctoral Dissertations Master's Theses, and Doctoral Dissertations, and Graduate Capstone Projects 2009 Examining the accuracy of the
The properties of L p -GMM estimators
 The properties of L p -GMM estimators Robert de Jong and Chirok Han Michigan State University February 2000 Abstract This paper considers Generalized Method of Moment-type estimators for which a criterion
The properties of L p -GMM estimators Robert de Jong and Chirok Han Michigan State University February 2000 Abstract This paper considers Generalized Method of Moment-type estimators for which a criterion
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
Asymptotic Statistics-VI. Changliang Zou
 Asymptotic Statistics-VI Changliang Zou Kolmogorov-Smirnov distance Example (Kolmogorov-Smirnov confidence intervals) We know given α (0, 1), there is a well-defined d = d α,n such that, for any continuous
Asymptotic Statistics-VI Changliang Zou Kolmogorov-Smirnov distance Example (Kolmogorov-Smirnov confidence intervals) We know given α (0, 1), there is a well-defined d = d α,n such that, for any continuous
Wiley. Methods and Applications of Linear Models. Regression and the Analysis. of Variance. Third Edition. Ishpeming, Michigan RONALD R.
 Methods and Applications of Linear Models Regression and the Analysis of Variance Third Edition RONALD R. HOCKING PenHock Statistical Consultants Ishpeming, Michigan Wiley Contents Preface to the Third
Methods and Applications of Linear Models Regression and the Analysis of Variance Third Edition RONALD R. HOCKING PenHock Statistical Consultants Ishpeming, Michigan Wiley Contents Preface to the Third
Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with an Arrhenius rate relationship
 Scholars' Mine Doctoral Dissertations Student Research & Creative Works Spring 01 Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with
Scholars' Mine Doctoral Dissertations Student Research & Creative Works Spring 01 Lifetime prediction and confidence bounds in accelerated degradation testing for lognormal response distributions with
Political Science 236 Hypothesis Testing: Review and Bootstrapping
 Political Science 236 Hypothesis Testing: Review and Bootstrapping Rocío Titiunik Fall 2007 1 Hypothesis Testing Definition 1.1 Hypothesis. A hypothesis is a statement about a population parameter The
Political Science 236 Hypothesis Testing: Review and Bootstrapping Rocío Titiunik Fall 2007 1 Hypothesis Testing Definition 1.1 Hypothesis. A hypothesis is a statement about a population parameter The
A Multiple Testing Approach to the Regularisation of Large Sample Correlation Matrices
 A Multiple Testing Approach to the Regularisation of Large Sample Correlation Matrices Natalia Bailey 1 M. Hashem Pesaran 2 L. Vanessa Smith 3 1 Department of Econometrics & Business Statistics, Monash
A Multiple Testing Approach to the Regularisation of Large Sample Correlation Matrices Natalia Bailey 1 M. Hashem Pesaran 2 L. Vanessa Smith 3 1 Department of Econometrics & Business Statistics, Monash
Unsupervised machine learning
 Chapter 9 Unsupervised machine learning Unsupervised machine learning (a.k.a. cluster analysis) is a set of methods to assign objects into clusters under a predefined distance measure when class labels
Chapter 9 Unsupervised machine learning Unsupervised machine learning (a.k.a. cluster analysis) is a set of methods to assign objects into clusters under a predefined distance measure when class labels
Confidence Intervals in Ridge Regression using Jackknife and Bootstrap Methods
 Chapter 4 Confidence Intervals in Ridge Regression using Jackknife and Bootstrap Methods 4.1 Introduction It is now explicable that ridge regression estimator (here we take ordinary ridge estimator (ORE)
Chapter 4 Confidence Intervals in Ridge Regression using Jackknife and Bootstrap Methods 4.1 Introduction It is now explicable that ridge regression estimator (here we take ordinary ridge estimator (ORE)
A New Combined Approach for Inference in High-Dimensional Regression Models with Correlated Variables
 A New Combined Approach for Inference in High-Dimensional Regression Models with Correlated Variables Niharika Gauraha and Swapan Parui Indian Statistical Institute Abstract. We consider the problem of
A New Combined Approach for Inference in High-Dimensional Regression Models with Correlated Variables Niharika Gauraha and Swapan Parui Indian Statistical Institute Abstract. We consider the problem of
Monte Carlo Studies. The response in a Monte Carlo study is a random variable.
 Monte Carlo Studies The response in a Monte Carlo study is a random variable. The response in a Monte Carlo study has a variance that comes from the variance of the stochastic elements in the data-generating
Monte Carlo Studies The response in a Monte Carlo study is a random variable. The response in a Monte Carlo study has a variance that comes from the variance of the stochastic elements in the data-generating
Multi-objective Quadratic Assignment Problem instances generator with a known optimum solution
 Multi-objective Quadratic Assignment Problem instances generator with a known optimum solution Mădălina M. Drugan Artificial Intelligence lab, Vrije Universiteit Brussel, Pleinlaan 2, B-1050 Brussels,
Multi-objective Quadratic Assignment Problem instances generator with a known optimum solution Mădălina M. Drugan Artificial Intelligence lab, Vrije Universiteit Brussel, Pleinlaan 2, B-1050 Brussels,
SHOTA KATAYAMA AND YUTAKA KANO. Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka , Japan
 A New Test on High-Dimensional Mean Vector Without Any Assumption on Population Covariance Matrix SHOTA KATAYAMA AND YUTAKA KANO Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama,
A New Test on High-Dimensional Mean Vector Without Any Assumption on Population Covariance Matrix SHOTA KATAYAMA AND YUTAKA KANO Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama,
STATS 200: Introduction to Statistical Inference. Lecture 29: Course review
 STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
STATS 200: Introduction to Statistical Inference Lecture 29: Course review Course review We started in Lecture 1 with a fundamental assumption: Data is a realization of a random process. The goal throughout
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
Inference For High Dimensional M-estimates. Fixed Design Results
 : Fixed Design Results Lihua Lei Advisors: Peter J. Bickel, Michael I. Jordan joint work with Peter J. Bickel and Noureddine El Karoui Dec. 8, 2016 1/57 Table of Contents 1 Background 2 Main Results and
: Fixed Design Results Lihua Lei Advisors: Peter J. Bickel, Michael I. Jordan joint work with Peter J. Bickel and Noureddine El Karoui Dec. 8, 2016 1/57 Table of Contents 1 Background 2 Main Results and
Linear Models 1. Isfahan University of Technology Fall Semester, 2014
 Linear Models 1 Isfahan University of Technology Fall Semester, 2014 References: [1] G. A. F., Seber and A. J. Lee (2003). Linear Regression Analysis (2nd ed.). Hoboken, NJ: Wiley. [2] A. C. Rencher and
Linear Models 1 Isfahan University of Technology Fall Semester, 2014 References: [1] G. A. F., Seber and A. J. Lee (2003). Linear Regression Analysis (2nd ed.). Hoboken, NJ: Wiley. [2] A. C. Rencher and
Estimation for state space models: quasi-likelihood and asymptotic quasi-likelihood approaches
 University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 2008 Estimation for state space models: quasi-likelihood and asymptotic
University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 2008 Estimation for state space models: quasi-likelihood and asymptotic
The Slow Convergence of OLS Estimators of α, β and Portfolio. β and Portfolio Weights under Long Memory Stochastic Volatility
 The Slow Convergence of OLS Estimators of α, β and Portfolio Weights under Long Memory Stochastic Volatility New York University Stern School of Business June 21, 2018 Introduction Bivariate long memory
The Slow Convergence of OLS Estimators of α, β and Portfolio Weights under Long Memory Stochastic Volatility New York University Stern School of Business June 21, 2018 Introduction Bivariate long memory
On Markov chain Monte Carlo methods for tall data
 On Markov chain Monte Carlo methods for tall data Remi Bardenet, Arnaud Doucet, Chris Holmes Paper review by: David Carlson October 29, 2016 Introduction Many data sets in machine learning and computational
On Markov chain Monte Carlo methods for tall data Remi Bardenet, Arnaud Doucet, Chris Holmes Paper review by: David Carlson October 29, 2016 Introduction Many data sets in machine learning and computational
Inferences about Parameters of Trivariate Normal Distribution with Missing Data
 Florida International University FIU Digital Commons FIU Electronic Theses and Dissertations University Graduate School 7-5-3 Inferences about Parameters of Trivariate Normal Distribution with Missing
Florida International University FIU Digital Commons FIU Electronic Theses and Dissertations University Graduate School 7-5-3 Inferences about Parameters of Trivariate Normal Distribution with Missing
A Multivariate Two-Sample Mean Test for Small Sample Size and Missing Data
 A Multivariate Two-Sample Mean Test for Small Sample Size and Missing Data Yujun Wu, Marc G. Genton, 1 and Leonard A. Stefanski 2 Department of Biostatistics, School of Public Health, University of Medicine
A Multivariate Two-Sample Mean Test for Small Sample Size and Missing Data Yujun Wu, Marc G. Genton, 1 and Leonard A. Stefanski 2 Department of Biostatistics, School of Public Health, University of Medicine
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
Lessons in Estimation Theory for Signal Processing, Communications, and Control
 Lessons in Estimation Theory for Signal Processing, Communications, and Control Jerry M. Mendel Department of Electrical Engineering University of Southern California Los Angeles, California PRENTICE HALL
Lessons in Estimation Theory for Signal Processing, Communications, and Control Jerry M. Mendel Department of Electrical Engineering University of Southern California Los Angeles, California PRENTICE HALL
A Practitioner s Guide to Cluster-Robust Inference
 A Practitioner s Guide to Cluster-Robust Inference A. C. Cameron and D. L. Miller presented by Federico Curci March 4, 2015 Cameron Miller Cluster Clinic II March 4, 2015 1 / 20 In the previous episode
A Practitioner s Guide to Cluster-Robust Inference A. C. Cameron and D. L. Miller presented by Federico Curci March 4, 2015 Cameron Miller Cluster Clinic II March 4, 2015 1 / 20 In the previous episode
SMOOTHED BLOCK EMPIRICAL LIKELIHOOD FOR QUANTILES OF WEAKLY DEPENDENT PROCESSES
 Statistica Sinica 19 (2009), 71-81 SMOOTHED BLOCK EMPIRICAL LIKELIHOOD FOR QUANTILES OF WEAKLY DEPENDENT PROCESSES Song Xi Chen 1,2 and Chiu Min Wong 3 1 Iowa State University, 2 Peking University and
Statistica Sinica 19 (2009), 71-81 SMOOTHED BLOCK EMPIRICAL LIKELIHOOD FOR QUANTILES OF WEAKLY DEPENDENT PROCESSES Song Xi Chen 1,2 and Chiu Min Wong 3 1 Iowa State University, 2 Peking University and
REALIZING TOURNAMENTS AS MODELS FOR K-MAJORITY VOTING
 California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of Graduate Studies 6-016 REALIZING TOURNAMENTS AS MODELS FOR K-MAJORITY VOTING Gina
California State University, San Bernardino CSUSB ScholarWorks Electronic Theses, Projects, and Dissertations Office of Graduate Studies 6-016 REALIZING TOURNAMENTS AS MODELS FOR K-MAJORITY VOTING Gina
Specification Test for Instrumental Variables Regression with Many Instruments
 Specification Test for Instrumental Variables Regression with Many Instruments Yoonseok Lee and Ryo Okui April 009 Preliminary; comments are welcome Abstract This paper considers specification testing
Specification Test for Instrumental Variables Regression with Many Instruments Yoonseok Lee and Ryo Okui April 009 Preliminary; comments are welcome Abstract This paper considers specification testing
Stat 5101 Lecture Notes
 Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Least Absolute Value vs. Least Squares Estimation and Inference Procedures in Regression Models with Asymmetric Error Distributions
 Journal of Modern Applied Statistical Methods Volume 8 Issue 1 Article 13 5-1-2009 Least Absolute Value vs. Least Squares Estimation and Inference Procedures in Regression Models with Asymmetric Error
Journal of Modern Applied Statistical Methods Volume 8 Issue 1 Article 13 5-1-2009 Least Absolute Value vs. Least Squares Estimation and Inference Procedures in Regression Models with Asymmetric Error
BTRY 4090: Spring 2009 Theory of Statistics
 BTRY 4090: Spring 2009 Theory of Statistics Guozhang Wang September 25, 2010 1 Review of Probability We begin with a real example of using probability to solve computationally intensive (or infeasible)
BTRY 4090: Spring 2009 Theory of Statistics Guozhang Wang September 25, 2010 1 Review of Probability We begin with a real example of using probability to solve computationally intensive (or infeasible)
Institute of Actuaries of India
 Institute of Actuaries of India Subject CT3 Probability and Mathematical Statistics For 2018 Examinations Subject CT3 Probability and Mathematical Statistics Core Technical Syllabus 1 June 2017 Aim The
Institute of Actuaries of India Subject CT3 Probability and Mathematical Statistics For 2018 Examinations Subject CT3 Probability and Mathematical Statistics Core Technical Syllabus 1 June 2017 Aim The
Testing Homogeneity Of A Large Data Set By Bootstrapping
 Testing Homogeneity Of A Large Data Set By Bootstrapping 1 Morimune, K and 2 Hoshino, Y 1 Graduate School of Economics, Kyoto University Yoshida Honcho Sakyo Kyoto 606-8501, Japan. E-Mail: morimune@econ.kyoto-u.ac.jp
Testing Homogeneity Of A Large Data Set By Bootstrapping 1 Morimune, K and 2 Hoshino, Y 1 Graduate School of Economics, Kyoto University Yoshida Honcho Sakyo Kyoto 606-8501, Japan. E-Mail: morimune@econ.kyoto-u.ac.jp
f-divergence Estimation and Two-Sample Homogeneity Test under Semiparametric Density-Ratio Models
 IEEE Transactions on Information Theory, vol.58, no.2, pp.708 720, 2012. 1 f-divergence Estimation and Two-Sample Homogeneity Test under Semiparametric Density-Ratio Models Takafumi Kanamori Nagoya University,
IEEE Transactions on Information Theory, vol.58, no.2, pp.708 720, 2012. 1 f-divergence Estimation and Two-Sample Homogeneity Test under Semiparametric Density-Ratio Models Takafumi Kanamori Nagoya University,
Semi-Nonparametric Inferences for Massive Data
 Semi-Nonparametric Inferences for Massive Data Guang Cheng 1 Department of Statistics Purdue University Statistics Seminar at NCSU October, 2015 1 Acknowledge NSF, Simons Foundation and ONR. A Joint Work
Semi-Nonparametric Inferences for Massive Data Guang Cheng 1 Department of Statistics Purdue University Statistics Seminar at NCSU October, 2015 1 Acknowledge NSF, Simons Foundation and ONR. A Joint Work
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes
 Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Sequential Monte Carlo methods for filtering of unobservable components of multidimensional diffusion Markov processes Ellida M. Khazen * 13395 Coppermine Rd. Apartment 410 Herndon VA 20171 USA Abstract
Comparing Group Means When Nonresponse Rates Differ
 UNF Digital Commons UNF Theses and Dissertations Student Scholarship 2015 Comparing Group Means When Nonresponse Rates Differ Gabriela M. Stegmann University of North Florida Suggested Citation Stegmann,
UNF Digital Commons UNF Theses and Dissertations Student Scholarship 2015 Comparing Group Means When Nonresponse Rates Differ Gabriela M. Stegmann University of North Florida Suggested Citation Stegmann,
Lecture 13: Subsampling vs Bootstrap. Dimitris N. Politis, Joseph P. Romano, Michael Wolf
 Lecture 13: 2011 Bootstrap ) R n x n, θ P)) = τ n ˆθn θ P) Example: ˆθn = X n, τ n = n, θ = EX = µ P) ˆθ = min X n, τ n = n, θ P) = sup{x : F x) 0} ) Define: J n P), the distribution of τ n ˆθ n θ P) under
Lecture 13: 2011 Bootstrap ) R n x n, θ P)) = τ n ˆθn θ P) Example: ˆθn = X n, τ n = n, θ = EX = µ P) ˆθ = min X n, τ n = n, θ P) = sup{x : F x) 0} ) Define: J n P), the distribution of τ n ˆθ n θ P) under
Covariance function estimation in Gaussian process regression
 Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
Covariance function estimation in Gaussian process regression François Bachoc Department of Statistics and Operations Research, University of Vienna WU Research Seminar - May 2015 François Bachoc Gaussian
Reduced [tau]_n-factorizations in Z and [tau]_nfactorizations
![Reduced [tau]_n-factorizations in Z and [tau]_nfactorizations Reduced [tau]_n-factorizations in Z and [tau]_nfactorizations](/thumbs/87/96024068.jpg) University of Iowa Iowa Research Online Theses and Dissertations Summer 2013 Reduced [tau]_n-factorizations in Z and [tau]_nfactorizations in N Alina Anca Florescu University of Iowa Copyright 2013 Alina
University of Iowa Iowa Research Online Theses and Dissertations Summer 2013 Reduced [tau]_n-factorizations in Z and [tau]_nfactorizations in N Alina Anca Florescu University of Iowa Copyright 2013 Alina
Bahadur representations for bootstrap quantiles 1
 Bahadur representations for bootstrap quantiles 1 Yijun Zuo Department of Statistics and Probability, Michigan State University East Lansing, MI 48824, USA zuo@msu.edu 1 Research partially supported by
Bahadur representations for bootstrap quantiles 1 Yijun Zuo Department of Statistics and Probability, Michigan State University East Lansing, MI 48824, USA zuo@msu.edu 1 Research partially supported by
MA 575 Linear Models: Cedric E. Ginestet, Boston University Non-parametric Inference, Polynomial Regression Week 9, Lecture 2
 MA 575 Linear Models: Cedric E. Ginestet, Boston University Non-parametric Inference, Polynomial Regression Week 9, Lecture 2 1 Bootstrapped Bias and CIs Given a multiple regression model with mean and
MA 575 Linear Models: Cedric E. Ginestet, Boston University Non-parametric Inference, Polynomial Regression Week 9, Lecture 2 1 Bootstrapped Bias and CIs Given a multiple regression model with mean and
Lecture 8: Information Theory and Statistics
 Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
A comparison of four different block bootstrap methods
 Croatian Operational Research Review 189 CRORR 5(014), 189 0 A comparison of four different block bootstrap methods Boris Radovanov 1, and Aleksandra Marcikić 1 1 Faculty of Economics Subotica, University
Croatian Operational Research Review 189 CRORR 5(014), 189 0 A comparison of four different block bootstrap methods Boris Radovanov 1, and Aleksandra Marcikić 1 1 Faculty of Economics Subotica, University
Lecture 3. Inference about multivariate normal distribution
 Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Linear Regression. In this problem sheet, we consider the problem of linear regression with p predictors and one intercept,
 Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Linear Regression In this problem sheet, we consider the problem of linear regression with p predictors and one intercept, y = Xβ + ɛ, where y t = (y 1,..., y n ) is the column vector of target values,
Correlated and Interacting Predictor Omission for Linear and Logistic Regression Models
 Clemson University TigerPrints All Dissertations Dissertations 8-207 Correlated and Interacting Predictor Omission for Linear and Logistic Regression Models Emily Nystrom Clemson University, emily.m.nystrom@gmail.com
Clemson University TigerPrints All Dissertations Dissertations 8-207 Correlated and Interacting Predictor Omission for Linear and Logistic Regression Models Emily Nystrom Clemson University, emily.m.nystrom@gmail.com
Stochastic Proximal Gradient Algorithm
 Stochastic Institut Mines-Télécom / Telecom ParisTech / Laboratoire Traitement et Communication de l Information Joint work with: Y. Atchade, Ann Arbor, USA, G. Fort LTCI/Télécom Paristech and the kind
Stochastic Institut Mines-Télécom / Telecom ParisTech / Laboratoire Traitement et Communication de l Information Joint work with: Y. Atchade, Ann Arbor, USA, G. Fort LTCI/Télécom Paristech and the kind
Extended Bayesian Information Criteria for Gaussian Graphical Models
 Extended Bayesian Information Criteria for Gaussian Graphical Models Rina Foygel University of Chicago rina@uchicago.edu Mathias Drton University of Chicago drton@uchicago.edu Abstract Gaussian graphical
Extended Bayesian Information Criteria for Gaussian Graphical Models Rina Foygel University of Chicago rina@uchicago.edu Mathias Drton University of Chicago drton@uchicago.edu Abstract Gaussian graphical
Testing Some Covariance Structures under a Growth Curve Model in High Dimension
 Department of Mathematics Testing Some Covariance Structures under a Growth Curve Model in High Dimension Muni S. Srivastava and Martin Singull LiTH-MAT-R--2015/03--SE Department of Mathematics Linköping
Department of Mathematics Testing Some Covariance Structures under a Growth Curve Model in High Dimension Muni S. Srivastava and Martin Singull LiTH-MAT-R--2015/03--SE Department of Mathematics Linköping
Class 2 & 3 Overfitting & Regularization
 Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
Class 2 & 3 Overfitting & Regularization Carlo Ciliberto Department of Computer Science, UCL October 18, 2017 Last Class The goal of Statistical Learning Theory is to find a good estimator f n : X Y, approximating
EFFICIENT CALCULATION OF FISHER INFORMATION MATRIX: MONTE CARLO APPROACH USING PRIOR INFORMATION. Sonjoy Das
 EFFICIENT CALCULATION OF FISHER INFORMATION MATRIX: MONTE CARLO APPROACH USING PRIOR INFORMATION by Sonjoy Das A thesis submitted to The Johns Hopkins University in conformity with the requirements for
EFFICIENT CALCULATION OF FISHER INFORMATION MATRIX: MONTE CARLO APPROACH USING PRIOR INFORMATION by Sonjoy Das A thesis submitted to The Johns Hopkins University in conformity with the requirements for
STAT 200C: High-dimensional Statistics
 STAT 200C: High-dimensional Statistics Arash A. Amini May 30, 2018 1 / 59 Classical case: n d. Asymptotic assumption: d is fixed and n. Basic tools: LLN and CLT. High-dimensional setting: n d, e.g. n/d
STAT 200C: High-dimensional Statistics Arash A. Amini May 30, 2018 1 / 59 Classical case: n d. Asymptotic assumption: d is fixed and n. Basic tools: LLN and CLT. High-dimensional setting: n d, e.g. n/d
Optimization of new Chinese Remainder theorems using special moduli sets
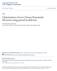 Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2010 Optimization of new Chinese Remainder theorems using special moduli sets Narendran Narayanaswamy Louisiana State
Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2010 Optimization of new Chinese Remainder theorems using special moduli sets Narendran Narayanaswamy Louisiana State
Variable Selection for Highly Correlated Predictors
 Variable Selection for Highly Correlated Predictors Fei Xue and Annie Qu arxiv:1709.04840v1 [stat.me] 14 Sep 2017 Abstract Penalty-based variable selection methods are powerful in selecting relevant covariates
Variable Selection for Highly Correlated Predictors Fei Xue and Annie Qu arxiv:1709.04840v1 [stat.me] 14 Sep 2017 Abstract Penalty-based variable selection methods are powerful in selecting relevant covariates
Central Limit Theorems for Classical Likelihood Ratio Tests for High-Dimensional Normal Distributions
 Central Limit Theorems for Classical Likelihood Ratio Tests for High-Dimensional Normal Distributions Tiefeng Jiang 1 and Fan Yang 1, University of Minnesota Abstract For random samples of size n obtained
Central Limit Theorems for Classical Likelihood Ratio Tests for High-Dimensional Normal Distributions Tiefeng Jiang 1 and Fan Yang 1, University of Minnesota Abstract For random samples of size n obtained
High Dimensional Empirical Likelihood for Generalized Estimating Equations with Dependent Data
 High Dimensional Empirical Likelihood for Generalized Estimating Equations with Dependent Data Song Xi CHEN Guanghua School of Management and Center for Statistical Science, Peking University Department
High Dimensional Empirical Likelihood for Generalized Estimating Equations with Dependent Data Song Xi CHEN Guanghua School of Management and Center for Statistical Science, Peking University Department
Curvature measures for generalized linear models
 University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 1999 Curvature measures for generalized linear models Bernard A.
University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 1999 Curvature measures for generalized linear models Bernard A.
Covering Subsets of the Integers and a Result on Digits of Fibonacci Numbers
 University of South Carolina Scholar Commons Theses and Dissertations 2017 Covering Subsets of the Integers and a Result on Digits of Fibonacci Numbers Wilson Andrew Harvey University of South Carolina
University of South Carolina Scholar Commons Theses and Dissertations 2017 Covering Subsets of the Integers and a Result on Digits of Fibonacci Numbers Wilson Andrew Harvey University of South Carolina
Lawrence D. Brown* and Daniel McCarthy*
 Comments on the paper, An adaptive resampling test for detecting the presence of significant predictors by I. W. McKeague and M. Qian Lawrence D. Brown* and Daniel McCarthy* ABSTRACT: This commentary deals
Comments on the paper, An adaptive resampling test for detecting the presence of significant predictors by I. W. McKeague and M. Qian Lawrence D. Brown* and Daniel McCarthy* ABSTRACT: This commentary deals
Cross-fitting and fast remainder rates for semiparametric estimation
 Cross-fitting and fast remainder rates for semiparametric estimation Whitney K. Newey James M. Robins The Institute for Fiscal Studies Department of Economics, UCL cemmap working paper CWP41/17 Cross-Fitting
Cross-fitting and fast remainder rates for semiparametric estimation Whitney K. Newey James M. Robins The Institute for Fiscal Studies Department of Economics, UCL cemmap working paper CWP41/17 Cross-Fitting
Quantile Regression for Extraordinarily Large Data
 Quantile Regression for Extraordinarily Large Data Shih-Kang Chao Department of Statistics Purdue University November, 2016 A joint work with Stanislav Volgushev and Guang Cheng Quantile regression Two-step
Quantile Regression for Extraordinarily Large Data Shih-Kang Chao Department of Statistics Purdue University November, 2016 A joint work with Stanislav Volgushev and Guang Cheng Quantile regression Two-step
Research Article A Nonparametric Two-Sample Wald Test of Equality of Variances
 Advances in Decision Sciences Volume 211, Article ID 74858, 8 pages doi:1.1155/211/74858 Research Article A Nonparametric Two-Sample Wald Test of Equality of Variances David Allingham 1 andj.c.w.rayner
Advances in Decision Sciences Volume 211, Article ID 74858, 8 pages doi:1.1155/211/74858 Research Article A Nonparametric Two-Sample Wald Test of Equality of Variances David Allingham 1 andj.c.w.rayner
Massive Experiments and Observational Studies: A Linearithmic Algorithm for Blocking/Matching/Clustering
 Massive Experiments and Observational Studies: A Linearithmic Algorithm for Blocking/Matching/Clustering Jasjeet S. Sekhon UC Berkeley June 21, 2016 Jasjeet S. Sekhon (UC Berkeley) Methods for Massive
Massive Experiments and Observational Studies: A Linearithmic Algorithm for Blocking/Matching/Clustering Jasjeet S. Sekhon UC Berkeley June 21, 2016 Jasjeet S. Sekhon (UC Berkeley) Methods for Massive
Multivariate-sign-based high-dimensional tests for sphericity
 Biometrika (2013, xx, x, pp. 1 8 C 2012 Biometrika Trust Printed in Great Britain Multivariate-sign-based high-dimensional tests for sphericity BY CHANGLIANG ZOU, LIUHUA PENG, LONG FENG AND ZHAOJUN WANG
Biometrika (2013, xx, x, pp. 1 8 C 2012 Biometrika Trust Printed in Great Britain Multivariate-sign-based high-dimensional tests for sphericity BY CHANGLIANG ZOU, LIUHUA PENG, LONG FENG AND ZHAOJUN WANG
Random Forests. These notes rely heavily on Biau and Scornet (2016) as well as the other references at the end of the notes.
 Random Forests One of the best known classifiers is the random forest. It is very simple and effective but there is still a large gap between theory and practice. Basically, a random forest is an average
Random Forests One of the best known classifiers is the random forest. It is very simple and effective but there is still a large gap between theory and practice. Basically, a random forest is an average
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
Comparison of Some Improved Estimators for Linear Regression Model under Different Conditions
 Florida International University FIU Digital Commons FIU Electronic Theses and Dissertations University Graduate School 3-24-2015 Comparison of Some Improved Estimators for Linear Regression Model under
Florida International University FIU Digital Commons FIU Electronic Theses and Dissertations University Graduate School 3-24-2015 Comparison of Some Improved Estimators for Linear Regression Model under
Jackknife Empirical Likelihood Test for Equality of Two High Dimensional Means
 Jackknife Empirical Likelihood est for Equality of wo High Dimensional Means Ruodu Wang, Liang Peng and Yongcheng Qi 2 Abstract It has been a long history to test the equality of two multivariate means.
Jackknife Empirical Likelihood est for Equality of wo High Dimensional Means Ruodu Wang, Liang Peng and Yongcheng Qi 2 Abstract It has been a long history to test the equality of two multivariate means.
401 Review. 6. Power analysis for one/two-sample hypothesis tests and for correlation analysis.
 401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
A nonparametric two-sample wald test of equality of variances
 University of Wollongong Research Online Faculty of Informatics - Papers (Archive) Faculty of Engineering and Information Sciences 211 A nonparametric two-sample wald test of equality of variances David
University of Wollongong Research Online Faculty of Informatics - Papers (Archive) Faculty of Engineering and Information Sciences 211 A nonparametric two-sample wald test of equality of variances David
high-dimensional inference robust to the lack of model sparsity
 high-dimensional inference robust to the lack of model sparsity Jelena Bradic (joint with a PhD student Yinchu Zhu) www.jelenabradic.net Assistant Professor Department of Mathematics University of California,
high-dimensional inference robust to the lack of model sparsity Jelena Bradic (joint with a PhD student Yinchu Zhu) www.jelenabradic.net Assistant Professor Department of Mathematics University of California,
Introduction to Self-normalized Limit Theory
 Introduction to Self-normalized Limit Theory Qi-Man Shao The Chinese University of Hong Kong E-mail: qmshao@cuhk.edu.hk Outline What is the self-normalization? Why? Classical limit theorems Self-normalized
Introduction to Self-normalized Limit Theory Qi-Man Shao The Chinese University of Hong Kong E-mail: qmshao@cuhk.edu.hk Outline What is the self-normalization? Why? Classical limit theorems Self-normalized
High-dimensional asymptotic expansions for the distributions of canonical correlations
 Journal of Multivariate Analysis 100 2009) 231 242 Contents lists available at ScienceDirect Journal of Multivariate Analysis journal homepage: www.elsevier.com/locate/jmva High-dimensional asymptotic
Journal of Multivariate Analysis 100 2009) 231 242 Contents lists available at ScienceDirect Journal of Multivariate Analysis journal homepage: www.elsevier.com/locate/jmva High-dimensional asymptotic
Geometry of Goodness-of-Fit Testing in High Dimensional Low Sample Size Modelling
 Geometry of Goodness-of-Fit Testing in High Dimensional Low Sample Size Modelling Paul Marriott 1, Radka Sabolova 2, Germain Van Bever 2, and Frank Critchley 2 1 University of Waterloo, Waterloo, Ontario,
Geometry of Goodness-of-Fit Testing in High Dimensional Low Sample Size Modelling Paul Marriott 1, Radka Sabolova 2, Germain Van Bever 2, and Frank Critchley 2 1 University of Waterloo, Waterloo, Ontario,
Stepwise Searching for Feature Variables in High-Dimensional Linear Regression
 Stepwise Searching for Feature Variables in High-Dimensional Linear Regression Qiwei Yao Department of Statistics, London School of Economics q.yao@lse.ac.uk Joint work with: Hongzhi An, Chinese Academy
Stepwise Searching for Feature Variables in High-Dimensional Linear Regression Qiwei Yao Department of Statistics, London School of Economics q.yao@lse.ac.uk Joint work with: Hongzhi An, Chinese Academy
Permutation-invariant regularization of large covariance matrices. Liza Levina
 Liza Levina Permutation-invariant covariance regularization 1/42 Permutation-invariant regularization of large covariance matrices Liza Levina Department of Statistics University of Michigan Joint work
Liza Levina Permutation-invariant covariance regularization 1/42 Permutation-invariant regularization of large covariance matrices Liza Levina Department of Statistics University of Michigan Joint work
An Approach to Constructing Good Two-level Orthogonal Factorial Designs with Large Run Sizes
 An Approach to Constructing Good Two-level Orthogonal Factorial Designs with Large Run Sizes by Chenlu Shi B.Sc. (Hons.), St. Francis Xavier University, 013 Project Submitted in Partial Fulfillment of
An Approach to Constructing Good Two-level Orthogonal Factorial Designs with Large Run Sizes by Chenlu Shi B.Sc. (Hons.), St. Francis Xavier University, 013 Project Submitted in Partial Fulfillment of
Kernel Methods. Lecture 4: Maximum Mean Discrepancy Thanks to Karsten Borgwardt, Malte Rasch, Bernhard Schölkopf, Jiayuan Huang, Arthur Gretton
 Kernel Methods Lecture 4: Maximum Mean Discrepancy Thanks to Karsten Borgwardt, Malte Rasch, Bernhard Schölkopf, Jiayuan Huang, Arthur Gretton Alexander J. Smola Statistical Machine Learning Program Canberra,
Kernel Methods Lecture 4: Maximum Mean Discrepancy Thanks to Karsten Borgwardt, Malte Rasch, Bernhard Schölkopf, Jiayuan Huang, Arthur Gretton Alexander J. Smola Statistical Machine Learning Program Canberra,
Doubly Indexed Infinite Series
 The Islamic University of Gaza Deanery of Higher studies Faculty of Science Department of Mathematics Doubly Indexed Infinite Series Presented By Ahed Khaleel Abu ALees Supervisor Professor Eissa D. Habil
The Islamic University of Gaza Deanery of Higher studies Faculty of Science Department of Mathematics Doubly Indexed Infinite Series Presented By Ahed Khaleel Abu ALees Supervisor Professor Eissa D. Habil
PRINCIPLES OF STATISTICAL INFERENCE
 Advanced Series on Statistical Science & Applied Probability PRINCIPLES OF STATISTICAL INFERENCE from a Neo-Fisherian Perspective Luigi Pace Department of Statistics University ofudine, Italy Alessandra
Advanced Series on Statistical Science & Applied Probability PRINCIPLES OF STATISTICAL INFERENCE from a Neo-Fisherian Perspective Luigi Pace Department of Statistics University ofudine, Italy Alessandra
Notes on the Multivariate Normal and Related Topics
 Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Multicollinearity and A Ridge Parameter Estimation Approach
 Journal of Modern Applied Statistical Methods Volume 15 Issue Article 5 11-1-016 Multicollinearity and A Ridge Parameter Estimation Approach Ghadban Khalaf King Khalid University, albadran50@yahoo.com
Journal of Modern Applied Statistical Methods Volume 15 Issue Article 5 11-1-016 Multicollinearity and A Ridge Parameter Estimation Approach Ghadban Khalaf King Khalid University, albadran50@yahoo.com
Optimization methods
 Lecture notes 3 February 8, 016 1 Introduction Optimization methods In these notes we provide an overview of a selection of optimization methods. We focus on methods which rely on first-order information,
Lecture notes 3 February 8, 016 1 Introduction Optimization methods In these notes we provide an overview of a selection of optimization methods. We focus on methods which rely on first-order information,
Model Selection Tutorial 2: Problems With Using AIC to Select a Subset of Exposures in a Regression Model
 Model Selection Tutorial 2: Problems With Using AIC to Select a Subset of Exposures in a Regression Model Centre for Molecular, Environmental, Genetic & Analytic (MEGA) Epidemiology School of Population
Model Selection Tutorial 2: Problems With Using AIC to Select a Subset of Exposures in a Regression Model Centre for Molecular, Environmental, Genetic & Analytic (MEGA) Epidemiology School of Population
Economics Division University of Southampton Southampton SO17 1BJ, UK. Title Overlapping Sub-sampling and invariance to initial conditions
 Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Title Overlapping Sub-sampling and invariance to initial conditions By Maria Kyriacou
Inference For High Dimensional M-estimates: Fixed Design Results
 Inference For High Dimensional M-estimates: Fixed Design Results Lihua Lei, Peter Bickel and Noureddine El Karoui Department of Statistics, UC Berkeley Berkeley-Stanford Econometrics Jamboree, 2017 1/49
Inference For High Dimensional M-estimates: Fixed Design Results Lihua Lei, Peter Bickel and Noureddine El Karoui Department of Statistics, UC Berkeley Berkeley-Stanford Econometrics Jamboree, 2017 1/49
Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices
 Article Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices Fei Jin 1,2 and Lung-fei Lee 3, * 1 School of Economics, Shanghai University of Finance and Economics,
Article Lasso Maximum Likelihood Estimation of Parametric Models with Singular Information Matrices Fei Jin 1,2 and Lung-fei Lee 3, * 1 School of Economics, Shanghai University of Finance and Economics,
