The Near-miss Birthday Problem. Gregory Quenell Plattsburgh State
|
|
|
- Betty Dorsey
- 5 years ago
- Views:
Transcription
1 The Near-miss Birthday Problem Gregory Quenell Plattsburgh State 1
2 The Classic Birthday Problem Assuming birthdays are uniformly distributed over 365 days, find P (at least one shared birthday) in a random sample of n people. Solution: Use complementation. P (at least one shared birthday) = 1 P (no shared birthday) = 1 P (n different birthdays) 2
3 Finding P (n different birthdays) 3
4 Finding P (n different birthdays) Birthday of person days {}}{ 4
5 Finding P (n different birthdays) Birthday of person days {}}{ P (n different birthdays) = number of ways to place n 1 birthdays in 364 days with no collision ( ) total number of ways to place n 1 birthdays in 365 days 5
6 Finding P (n different birthdays) Birthday of person days {}}{ P (n different birthdays) = number of ways to place n 1 birthdays in 364 days with no collision ( ) total number of ways to place = = n 1 birthdays in 365 days ( ) 364 (n 1)! n 1 (365) n (364 (n 2)) = (364) n 1 (365) n 1 6
7 Some numbers P (at least one shared birthday) n P (shared birthday) = 1 (364) n 1 (365) n 1 7
8 The Near-miss Birthday Problem Assuming birthdays are uniformly distributed over 365 days, find at least one pair of birthdays P that are either coincident or adjacent in a random sample of n people. Solution: Use complementation. P (at least one near miss) = 1 P (no near misses) = 1 P (n isolated birthdays) 8
9 Finding P (n isolated birthdays) Birthday of person days {}}{ P (n isolated birthdays) = number of ways to place n 1 birthdays in 364 days with no collision and no two birthdays adjacent ( ) total number of ways to place n 1 birthdays in 365 days 9
10 Finding P (n isolated birthdays) Birthday of person days {}}{ P (n isolated birthdays) = This is still (365) n 1 number of ways to place n 1 birthdays in 364 days with no collision and no two birthdays adjacent ( ) total number of ways to place n 1 birthdays in 365 days 10
11 Finding P (n isolated birthdays) Birthday of person days {}}{ P (n isolated birthdays) = This is still (365) n 1 number of ways to place n 1 birthdays in 364 days with no collision and no two birthdays adjacent ( ) total number of ways to place n 1 birthdays in 365 days How do we count these? 11
12 Counting isolated birthdays n 1 isolated birthdays in 364 days {}}{ a 1 a 2 a 3 a 4 a n 1 a n Every arrangement of n 1 isolated birthdays corresponds to a gap sequence a 1, a 2,..., a n in which { a1 + a a n = 364 (n 1) a i 1 for all i 12
13 Aside on counting A sequence a 1, a 2,..., a n of positive integers such that a 1 + a a n = S is called an n-part composition of S. Theorem: The number of n-part compositions of S is ( ) S 1. n 1 Proof: Write down a string of S dots. Then there are S 1 inter-dot spaces. 13
14 Aside on counting A sequence a 1, a 2,..., a n of positive integers such that a 1 + a a n = S is called an n-part composition of S. Theorem: The number of n-part compositions of S is ( ) S 1. n 1 Proof: Write down a string of S dots. Then there are S 1 inter-dot spaces. 3 {}}{ {}}{ 3 {}}{ Placing bars in n 1 of these S 1 spaces determines an n-part composition of S, and conversely. 14
15 Application to birthdays n 1 isolated birthdays in 364 days {}}{ a 1 a 2 a 3 a 4 a n 1 a n There are ( ) [364 (n 1)] 1 n 1 possible gap sequences. = ( ) 364 n n 1 15
16 Application to birthdays n 1 isolated birthdays in 364 days {}}{ a 1 a 2 a 3 a 4 a n 1 a n There are ( ) [364 (n 1)] 1 n 1 possible gap sequences. = ( ) 364 n n 1 Result: ( number of ways to place n 1 isolated birthdays in 364 days ) = ( ) 364 n (n 1)! n 1 = (364 n) n 1 16
17 The near-miss birthday formula P (no near miss) = (364 n) n n 1 The probability of at least one near miss in a random sample of n people is 1 (364 n) n n 1. The least n for which this probability exceeds 0.5 is n = 14: P at least one pair of coincident or adjacent birthdays in a random sample of 14 people
18 More numbers P (shared birthday) = 1 (364) n 1 (365) n 1 n P (shared) P (near miss) P (near miss) = 1 (364 n) n 1 (365) n 1 18
19 Birthdays shared by k or more people Let (X 1, X 2,..., X 365 ) be a random vector in which X i is the number of people in a random sample of size n who were born on day i. Then (X 1, X 2,..., X 365 ) follows a multinomial distribution with n things, 365 bins, and constant probability 1/365. Thus P ((X 1, X 2,..., X 365 ) = (x 1, x 2,..., x 365 )) = ( ) n x 1 x 2 x 365 = n n! x 1! x 2! x 365! ( ) n We want P (max(x 1, X 2,..., X 365 ) k), the probability that some date is the birthday of k or more people in the sample. Again, we use complementation: P (max(x 1, X 2,..., X 365 ) k), = 1 P (max(x 1, X 2,..., X 365 ) k 1) = 1 P (X i k 1) for all i. 19
20 Finding P (X i k 1) for i = 1, 2,..., 365 We need n! 365 n k 1 k 1 k 1 x 1 =0 x 2 =0 x 365 =0 x 1 + x x 365 =n ( 1 x 1! 1 x 2! 1 ) x 365! Consider the product ( 1 0! + 1 ) ( 1! (k 1)! 0! + 1 ) 1! (k 1)! factor for x 1 factor for x 2 ( 1 0! + 1 ) 1! (k 1)! factor for x 365 To pick out the terms with x 1 + x x 365 = n, introduce a tracer variable: ( τ 0 0! + τ 1 1! + + τ ) ( k 1 τ 0 (k 1)! 0! + τ 1 1! + + τ ) ( k 1 τ 0 (k 1)! 0! + τ 1 1! + + τ ) k 1 (k 1)! The coefficient of τ n in this product is exactly the sum that we want. 20
21 The multiple-birthday formula We have P (X i k 1 i) = n! 365 n coeff of τ n in ( τ 0 0! + τ 1 1! + + τ k 1 ) 365 (k 1)! And so P (max(x i ) k) = 1 n! ( τ 365 [τ n 0 ] n 0! + τ 1 1! + + τ k 1 ) 365 (k 1)! 21
22 An example In a random sample of 100 people, what s the probability that there are six (or more) who share a birthday? It s 1 100! ( τ [τ ] 0! + τ 1 1! + τ 2 2! + τ 3 3! + τ 4 4! + τ 5 ) 365 5! Mathematica says the answer is / (This is about ) 22
23 Multiple birthday probabilities Probabilities of at least one date in the calendar being the shared birthday of k people for k = 3, 4, and 5. 23
2 - Strings and Binomial Coefficients
 November 14, 2017 2 - Strings and Binomial Coefficients William T. Trotter trotter@math.gatech.edu Basic Definition Let n be a positive integer and let [n] = {1, 2,, n}. A sequence of length n such as
November 14, 2017 2 - Strings and Binomial Coefficients William T. Trotter trotter@math.gatech.edu Basic Definition Let n be a positive integer and let [n] = {1, 2,, n}. A sequence of length n such as
Attacks on hash functions. Birthday attacks and Multicollisions
 Attacks on hash functions Birthday attacks and Multicollisions Birthday Attack Basics In a group of 23 people, the probability that there are at least two persons on the same day in the same month is greater
Attacks on hash functions Birthday attacks and Multicollisions Birthday Attack Basics In a group of 23 people, the probability that there are at least two persons on the same day in the same month is greater
Probability. Part 1 - Basic Counting Principles. 1. References. (1) R. Durrett, The Essentials of Probability, Duxbury.
 Probability Part 1 - Basic Counting Principles 1. References (1) R. Durrett, The Essentials of Probability, Duxbury. (2) L.L. Helms, Probability Theory with Contemporary Applications, Freeman. (3) J.J.
Probability Part 1 - Basic Counting Principles 1. References (1) R. Durrett, The Essentials of Probability, Duxbury. (2) L.L. Helms, Probability Theory with Contemporary Applications, Freeman. (3) J.J.
Day 2 and 3 Graphing Linear Inequalities in Two Variables.notebook. Formative Quiz. 1) Sketch the graph of the following linear equation.
 Formative Quiz 1) Sketch the graph of the following linear equation. (a) 1 (b) 2 2. Solve for x in the given triangle. 12 53 0 x 47 0 3 3. Solve for x in the given triangle. 87 0 13 9 x 4 5 Graphing Linear
Formative Quiz 1) Sketch the graph of the following linear equation. (a) 1 (b) 2 2. Solve for x in the given triangle. 12 53 0 x 47 0 3 3. Solve for x in the given triangle. 87 0 13 9 x 4 5 Graphing Linear
Lecture 04: Balls and Bins: Birthday Paradox. Birthday Paradox
 Lecture 04: Balls and Bins: Overview In today s lecture we will start our study of balls-and-bins problems We shall consider a fundamental problem known as the Recall: Inequalities I Lemma Before we begin,
Lecture 04: Balls and Bins: Overview In today s lecture we will start our study of balls-and-bins problems We shall consider a fundamental problem known as the Recall: Inequalities I Lemma Before we begin,
L11.P1 Lecture 11. Quantum statistical mechanics: summary
 Lecture 11 Page 1 L11.P1 Lecture 11 Quantum statistical mechanics: summary At absolute zero temperature, a physical system occupies the lowest possible energy configuration. When the temperature increases,
Lecture 11 Page 1 L11.P1 Lecture 11 Quantum statistical mechanics: summary At absolute zero temperature, a physical system occupies the lowest possible energy configuration. When the temperature increases,
CS 210 Foundations of Computer Science
 IIT Madras Dept. of Computer Science & Engineering CS 210 Foundations of Computer Science Debdeep Mukhopadhyay Counting-II Pigeonhole Principle If n+1 or more objects (pigeons) are placed into n boxes,
IIT Madras Dept. of Computer Science & Engineering CS 210 Foundations of Computer Science Debdeep Mukhopadhyay Counting-II Pigeonhole Principle If n+1 or more objects (pigeons) are placed into n boxes,
2016 Canadian Intermediate Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Intermediate Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Intermediate Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November
Testing a Hash Function using Probability
 Testing a Hash Function using Probability Suppose you have a huge square turnip field with 1000 turnips growing in it. They are all perfectly evenly spaced in a regular pattern. Suppose also that the Germans
Testing a Hash Function using Probability Suppose you have a huge square turnip field with 1000 turnips growing in it. They are all perfectly evenly spaced in a regular pattern. Suppose also that the Germans
Carleton University. Final Examination Winter DURATION: 2 HOURS No. of students: 152
 Carleton University Final Examination Winter 2014 DURATION: 2 HOURS No. of students: 152 Department Name & Course Number: Computer Science COMP 2804B Course Instructor: Michiel Smid Authorized memoranda:
Carleton University Final Examination Winter 2014 DURATION: 2 HOURS No. of students: 152 Department Name & Course Number: Computer Science COMP 2804B Course Instructor: Michiel Smid Authorized memoranda:
CS 2336 Discrete Mathematics
 CS 2336 Discrete Mathematics Lecture 8 Counting: Permutations and Combinations 1 Outline Definitions Permutation Combination Interesting Identities 2 Definitions Selection and arrangement of objects appear
CS 2336 Discrete Mathematics Lecture 8 Counting: Permutations and Combinations 1 Outline Definitions Permutation Combination Interesting Identities 2 Definitions Selection and arrangement of objects appear
Discrete Mathematics & Mathematical Reasoning Chapter 6: Counting
 Discrete Mathematics & Mathematical Reasoning Chapter 6: Counting Kousha Etessami U. of Edinburgh, UK Kousha Etessami (U. of Edinburgh, UK) Discrete Mathematics (Chapter 6) 1 / 39 Chapter Summary The Basics
Discrete Mathematics & Mathematical Reasoning Chapter 6: Counting Kousha Etessami U. of Edinburgh, UK Kousha Etessami (U. of Edinburgh, UK) Discrete Mathematics (Chapter 6) 1 / 39 Chapter Summary The Basics
6.8 The Pigeonhole Principle
 6.8 The Pigeonhole Principle Getting Started Are there two leaf-bearing trees on Earth with the same number of leaves if we only consider the number of leaves on a tree at full bloom? Getting Started Are
6.8 The Pigeonhole Principle Getting Started Are there two leaf-bearing trees on Earth with the same number of leaves if we only consider the number of leaves on a tree at full bloom? Getting Started Are
Lecture 4: Counting, Pigeonhole Principle, Permutations, Combinations Lecturer: Lale Özkahya
 BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 4: Counting, Pigeonhole Principle, Permutations, Combinations Lecturer: Lale Özkahya Resources: Kenneth
BBM 205 Discrete Mathematics Hacettepe University http://web.cs.hacettepe.edu.tr/ bbm205 Lecture 4: Counting, Pigeonhole Principle, Permutations, Combinations Lecturer: Lale Özkahya Resources: Kenneth
Glossary. COMMON CORE STATE STANDARDS for MATHEMATICS
 Glossary Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction of two whole numbers with whole number answers, and with sum or minuend in the range 0-5, 0-10, 0-20, or 0-100,
Glossary Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction of two whole numbers with whole number answers, and with sum or minuend in the range 0-5, 0-10, 0-20, or 0-100,
Some Review Problems for Exam 3: Solutions
 Math 3355 Fall 018 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
Math 3355 Fall 018 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
Notes. Combinatorics. Combinatorics II. Notes. Notes. Slides by Christopher M. Bourke Instructor: Berthe Y. Choueiry. Spring 2006
 Combinatorics Slides by Christopher M. Bourke Instructor: Berthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 4.1-4.6 & 6.5-6.6 of Rosen cse235@cse.unl.edu
Combinatorics Slides by Christopher M. Bourke Instructor: Berthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 4.1-4.6 & 6.5-6.6 of Rosen cse235@cse.unl.edu
GLOSSARY & TABLES MATHEMATICS. UTAH CORE STATE STANDARDS for. Education. Utah. UTAH CORE STATE STANDARDS for MATHEMATICS GLOSSARY & TABLES 135
 Utah STATE OFFICE of Education UTAH CORE STATE STANDARDS for MATHEMATICS GLOSSARY & TABLES GLOSSARY & TABLES 135 GLOSSARY Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction
Utah STATE OFFICE of Education UTAH CORE STATE STANDARDS for MATHEMATICS GLOSSARY & TABLES GLOSSARY & TABLES 135 GLOSSARY Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction
Common Core Georgia Performance Standards CCGPS Mathematics
 Common Core Georgia Performance Standards CCGPS Mathematics Glossary Glossary Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction of two whole numbers with whole number answers,
Common Core Georgia Performance Standards CCGPS Mathematics Glossary Glossary Addition and subtraction within 5, 10, 20, 100, or 1000. Addition or subtraction of two whole numbers with whole number answers,
CS Foundations of Computing
 IIT KGP Dept. of Computer Science & Engineering CS 30053 Foundations of Computing Debdeep Mukhopadhyay Pigeon Hole Principle 1 Pigeonhole Principle If n+1 or more objects (pigeons) are placed into n boxes,
IIT KGP Dept. of Computer Science & Engineering CS 30053 Foundations of Computing Debdeep Mukhopadhyay Pigeon Hole Principle 1 Pigeonhole Principle If n+1 or more objects (pigeons) are placed into n boxes,
Solution: By direct calculation, or observe that = = ( ) 2222 = =
 1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
1 Fillins 1. Find the last 4 digits of 3333 6666. Solution: 7778. By direct calculation, or observe that 3333 6666 = 9999 2222 = (10000 1) 2222 = 22220000 2222 = 22217778. 2. How many ways are there to
Counting. Spock's dilemma (Walls and mirrors) call it C(n,k) Rosen, Chapter 5.1, 5.2, 5.3 Walls and Mirrors, Chapter 3 10/11/12
 Counting Rosen, Chapter 5.1, 5.2, 5.3 Walls and Mirrors, Chapter 3 Spock's dilemma (Walls and mirrors) n n planets in the solar system n can only visit k
Counting Rosen, Chapter 5.1, 5.2, 5.3 Walls and Mirrors, Chapter 3 Spock's dilemma (Walls and mirrors) n n planets in the solar system n can only visit k
Discrete Probability
 Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Discrete Probability Counting Permutations Combinations r- Combinations r- Combinations with repetition Allowed Pascal s Formula Binomial Theorem Conditional Probability Baye s Formula Independent Events
Massachusetts Institute of Technology Machine Learning, Fall Problem Set 1 Solutions
 Section A (background questions) Massachusetts Institute of Technology 6.867 Machine Learning, Fall 26 Problem Set 1 Solutions 1. Let s begin with a little math. Let us denote by P n the probability that
Section A (background questions) Massachusetts Institute of Technology 6.867 Machine Learning, Fall 26 Problem Set 1 Solutions 1. Let s begin with a little math. Let us denote by P n the probability that
PROBABILITY VITTORIA SILVESTRI
 PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8 4. Properties of Probability measures Preface These lecture notes are for the course
Warm-up Quantifiers and the harmonic series Sets Second warmup Induction Bijections. Writing more proofs. Misha Lavrov
 Writing more proofs Misha Lavrov ARML Practice 3/16/2014 and 3/23/2014 Warm-up Using the quantifier notation on the reference sheet, and making any further definitions you need to, write the following:
Writing more proofs Misha Lavrov ARML Practice 3/16/2014 and 3/23/2014 Warm-up Using the quantifier notation on the reference sheet, and making any further definitions you need to, write the following:
1 The Basic Counting Principles
 1 The Basic Counting Principles The Multiplication Rule If an operation consists of k steps and the first step can be performed in n 1 ways, the second step can be performed in n ways [regardless of how
1 The Basic Counting Principles The Multiplication Rule If an operation consists of k steps and the first step can be performed in n 1 ways, the second step can be performed in n ways [regardless of how
2013 ΜΑΘ National Convention
 Gemini Mu Test #911 1. In the Name blank, print the names of both members of the Gemini Team; in the Subject blank, print the name of the test; in the Date blank, print your school name (no abbreviations).
Gemini Mu Test #911 1. In the Name blank, print the names of both members of the Gemini Team; in the Subject blank, print the name of the test; in the Date blank, print your school name (no abbreviations).
Discrete Mathematics with Applications MATH236
 Discrete Mathematics with Applications MATH236 Dr. Hung P. Tong-Viet School of Mathematics, Statistics and Computer Science University of KwaZulu-Natal Pietermaritzburg Campus Semester 1, 2013 Tong-Viet
Discrete Mathematics with Applications MATH236 Dr. Hung P. Tong-Viet School of Mathematics, Statistics and Computer Science University of KwaZulu-Natal Pietermaritzburg Campus Semester 1, 2013 Tong-Viet
Combinations and Probabilities
 Combinations and Probabilities Tutor: Zhang Qi Systems Engineering and Engineering Management qzhang@se.cuhk.edu.hk November 2014 Tutor: Zhang Qi (SEEM) Tutorial 7 November 2014 1 / 16 Combination Review
Combinations and Probabilities Tutor: Zhang Qi Systems Engineering and Engineering Management qzhang@se.cuhk.edu.hk November 2014 Tutor: Zhang Qi (SEEM) Tutorial 7 November 2014 1 / 16 Combination Review
Homework every week. Keep up to date or you risk falling behind. Quizzes and Final exam are based on homework questions.
 Week 1 Fall 2016 1 of 25 CISC-102 Fall 2016 Week 1 David Rappaport daver@cs.queensu.ca Goodwin G-532 Office Hours: Monday 1:00-3:00 (or by appointment) Homework Homework every week. Keep up to date or
Week 1 Fall 2016 1 of 25 CISC-102 Fall 2016 Week 1 David Rappaport daver@cs.queensu.ca Goodwin G-532 Office Hours: Monday 1:00-3:00 (or by appointment) Homework Homework every week. Keep up to date or
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 14 October 16, 2013 CPSC 467, Lecture 14 1/45 Message Digest / Cryptographic Hash Functions Hash Function Constructions Extending
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 14 October 16, 2013 CPSC 467, Lecture 14 1/45 Message Digest / Cryptographic Hash Functions Hash Function Constructions Extending
PROBABILITY. Contents Preface 1 1. Introduction 2 2. Combinatorial analysis 5 3. Stirling s formula 8. Preface
 PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction. Combinatorial analysis 5 3. Stirling s formula 8 Preface These lecture notes are for the course Probability IA, given in Lent 09 at the University
PROBABILITY VITTORIA SILVESTRI Contents Preface. Introduction. Combinatorial analysis 5 3. Stirling s formula 8 Preface These lecture notes are for the course Probability IA, given in Lent 09 at the University
CISC-102 Fall 2017 Week 1 David Rappaport Goodwin G-532 Office Hours: Tuesday 1:30-3:30
 Week 1 Fall 2017 1 of 42 CISC-102 Fall 2017 Week 1 David Rappaport daver@cs.queensu.ca Goodwin G-532 Office Hours: Tuesday 1:30-3:30 Homework Homework every week. Keep up to date or you risk falling behind.
Week 1 Fall 2017 1 of 42 CISC-102 Fall 2017 Week 1 David Rappaport daver@cs.queensu.ca Goodwin G-532 Office Hours: Tuesday 1:30-3:30 Homework Homework every week. Keep up to date or you risk falling behind.
Recitation 6. Randomization. 6.1 Announcements. RandomLab has been released, and is due Monday, October 2. It s worth 100 points.
 Recitation 6 Randomization 6.1 Announcements RandomLab has been released, and is due Monday, October 2. It s worth 100 points. FingerLab will be released after Exam I, which is going to be on Wednesday,
Recitation 6 Randomization 6.1 Announcements RandomLab has been released, and is due Monday, October 2. It s worth 100 points. FingerLab will be released after Exam I, which is going to be on Wednesday,
Name: Harry Potter (pothar31) Discrete Math HW#6 Solutions March 9, Added: Chapter 6 Summary/Review: 17(a), 8, 15, 29, 42 and Q1 and Q2 below
 Name: Harry Potter (pothar31 Discrete Math HW#6 Solutions March 9, 2018 Instructions: Do the following problems. Type up those in bold in LaTeX. csf submit them. 6.2: 33, 34, 38, 44 6.3: 18, 20 (explain
Name: Harry Potter (pothar31 Discrete Math HW#6 Solutions March 9, 2018 Instructions: Do the following problems. Type up those in bold in LaTeX. csf submit them. 6.2: 33, 34, 38, 44 6.3: 18, 20 (explain
Recitation 5: Elementary Matrices
 Math 1b TA: Padraic Bartlett Recitation 5: Elementary Matrices Week 5 Caltech 2011 1 Random Question Consider the following two-player game, called Angels and Devils: Our game is played on a n n chessboard,
Math 1b TA: Padraic Bartlett Recitation 5: Elementary Matrices Week 5 Caltech 2011 1 Random Question Consider the following two-player game, called Angels and Devils: Our game is played on a n n chessboard,
Lecture 24: MAC for Arbitrary Length Messages. MAC Long Messages
 Lecture 24: MAC for Arbitrary Length Messages Recall Previous lecture, we constructed MACs for fixed length messages The GGM Pseudo-random Function (PRF) Construction Given. Pseudo-random Generator (PRG)
Lecture 24: MAC for Arbitrary Length Messages Recall Previous lecture, we constructed MACs for fixed length messages The GGM Pseudo-random Function (PRF) Construction Given. Pseudo-random Generator (PRG)
Lecture 6: The Pigeonhole Principle and Probability Spaces
 Lecture 6: The Pigeonhole Principle and Probability Spaces Anup Rao January 17, 2018 We discuss the pigeonhole principle and probability spaces. Pigeonhole Principle The pigeonhole principle is an extremely
Lecture 6: The Pigeonhole Principle and Probability Spaces Anup Rao January 17, 2018 We discuss the pigeonhole principle and probability spaces. Pigeonhole Principle The pigeonhole principle is an extremely
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions
 Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
Lecture 8: Equivalence Relations
 Lecture 8: Equivalence Relations 1 Equivalence Relations Next interesting relation we will study is equivalence relation. Definition 1.1 (Equivalence Relation). Let A be a set and let be a relation on
Lecture 8: Equivalence Relations 1 Equivalence Relations Next interesting relation we will study is equivalence relation. Definition 1.1 (Equivalence Relation). Let A be a set and let be a relation on
Counting Review R 1. R 3 receiver. sender R 4 R 2
 Counting Review Purpose: It is the foundation for many simple yet interesting examples and applications of probability theory. For good counting we need good crutches (fingers?). Hence good images for
Counting Review Purpose: It is the foundation for many simple yet interesting examples and applications of probability theory. For good counting we need good crutches (fingers?). Hence good images for
The arrangement of the fundamental particles on mass levels derived from the Planck Mass
 The arrangement of the fundamental particles on mass levels derived from the Planck Mass B F Riley 1 The most recent evaluations of the Particle Data Group have made it possible to discern with precision
The arrangement of the fundamental particles on mass levels derived from the Planck Mass B F Riley 1 The most recent evaluations of the Particle Data Group have made it possible to discern with precision
Carleton University. Final Examination Winter DURATION: 2 HOURS No. of students: 275
 Carleton University Final Examination Winter 2017 DURATION: 2 HOURS No. of students: 275 Department Name & Course Number: Computer Science COMP 2804B Course Instructor: Michiel Smid Authorized memoranda:
Carleton University Final Examination Winter 2017 DURATION: 2 HOURS No. of students: 275 Department Name & Course Number: Computer Science COMP 2804B Course Instructor: Michiel Smid Authorized memoranda:
Hash Functions. A hash function h takes as input a message of arbitrary length and produces as output a message digest of fixed length.
 Hash Functions 1 Hash Functions A hash function h takes as input a message of arbitrary length and produces as output a message digest of fixed length. 0 1 1 0 1 0 0 1 Long Message Hash Function 1 1 1
Hash Functions 1 Hash Functions A hash function h takes as input a message of arbitrary length and produces as output a message digest of fixed length. 0 1 1 0 1 0 0 1 Long Message Hash Function 1 1 1
MODEL ANSWERS TO THE SEVENTH HOMEWORK. (b) We proved in homework six, question 2 (c) that. But we also proved homework six, question 2 (a) that
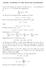 MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
MODEL ANSWERS TO THE SEVENTH HOMEWORK 1. Let X be a finite set, and let A, B and A 1, A 2,..., A n be subsets of X. Let A c = X \ A denote the complement. (a) χ A (x) = A. x X (b) We proved in homework
x n -2.5 Definition A list is a list of objects, where multiplicity is allowed, and order matters. For example, as lists
 Vectors, Linear Combinations, and Matrix-Vector Mulitiplication In this section, we introduce vectors, linear combinations, and matrix-vector multiplication The rest of the class will involve vectors,
Vectors, Linear Combinations, and Matrix-Vector Mulitiplication In this section, we introduce vectors, linear combinations, and matrix-vector multiplication The rest of the class will involve vectors,
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 16 October 30, 2017 CPSC 467, Lecture 16 1/52 Properties of Hash Functions Hash functions do not always look random Relations among
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 16 October 30, 2017 CPSC 467, Lecture 16 1/52 Properties of Hash Functions Hash functions do not always look random Relations among
Math 461 B/C, Spring 2009 Midterm Exam 1 Solutions and Comments
 Math 461 B/C, Spring 2009 Midterm Exam 1 Solutions and Comments 1. Suppose A, B and C are events with P (A) = P (B) = P (C) = 1/3, P (AB) = P (AC) = P (BC) = 1/4 and P (ABC) = 1/5. For each of the following
Math 461 B/C, Spring 2009 Midterm Exam 1 Solutions and Comments 1. Suppose A, B and C are events with P (A) = P (B) = P (C) = 1/3, P (AB) = P (AC) = P (BC) = 1/4 and P (ABC) = 1/5. For each of the following
1 Maintaining a Dictionary
 15-451/651: Design & Analysis of Algorithms February 1, 2016 Lecture #7: Hashing last changed: January 29, 2016 Hashing is a great practical tool, with an interesting and subtle theory too. In addition
15-451/651: Design & Analysis of Algorithms February 1, 2016 Lecture #7: Hashing last changed: January 29, 2016 Hashing is a great practical tool, with an interesting and subtle theory too. In addition
1 Basic Combinatorics
 1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
CMSC 441: Algorithms. NP Completeness
 CMSC 441: Algorithms NP Completeness Intractable & Tractable Problems Intractable problems: As they grow large, we are unable to solve them in reasonable time What constitutes reasonable time? Standard
CMSC 441: Algorithms NP Completeness Intractable & Tractable Problems Intractable problems: As they grow large, we are unable to solve them in reasonable time What constitutes reasonable time? Standard
Ad Placement Strategies
 Case Study 1: Estimating Click Probabilities Tackling an Unknown Number of Features with Sketching Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox 2014 Emily Fox January
Case Study 1: Estimating Click Probabilities Tackling an Unknown Number of Features with Sketching Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox 2014 Emily Fox January
Recursive Definitions
 Recursive Definitions Example: Give a recursive definition of a n. a R and n N. Basis: n = 0, a 0 = 1. Recursion: a n+1 = a a n. Example: Give a recursive definition of n i=0 a i. Let S n = n i=0 a i,
Recursive Definitions Example: Give a recursive definition of a n. a R and n N. Basis: n = 0, a 0 = 1. Recursion: a n+1 = a a n. Example: Give a recursive definition of n i=0 a i. Let S n = n i=0 a i,
CHAPTER 1 NUMBER SYSTEMS. 1.1 Introduction
 N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
Probability, For the Enthusiastic Beginner (Exercises, Version 1, September 2016) David Morin,
 Chapter 8 Exercises Probability, For the Enthusiastic Beginner (Exercises, Version 1, September 2016) David Morin, morin@physics.harvard.edu 8.1 Chapter 1 Section 1.2: Permutations 1. Assigning seats *
Chapter 8 Exercises Probability, For the Enthusiastic Beginner (Exercises, Version 1, September 2016) David Morin, morin@physics.harvard.edu 8.1 Chapter 1 Section 1.2: Permutations 1. Assigning seats *
Carleton University. Final Examination Fall DURATION: 2 HOURS No. of students: 223
 Carleton University Final Examination Fall 2016 DURATION: 2 HOURS No. of students: 223 Department Name & Course Number: Computer Science COMP 2804A Course Instructor: Michiel Smid Authorized memoranda:
Carleton University Final Examination Fall 2016 DURATION: 2 HOURS No. of students: 223 Department Name & Course Number: Computer Science COMP 2804A Course Instructor: Michiel Smid Authorized memoranda:
After that, we will introduce more ideas from Chapter 5: Number Theory. Your quiz in recitation tomorrow will involve writing proofs like those.
 Wednesday, Oct 17 Today we will finish Course Notes 3.2: Methods of Proof. After that, we will introduce more ideas from Chapter 5: Number Theory. The exercise generator Methods of Proof, 3.2 (also includes
Wednesday, Oct 17 Today we will finish Course Notes 3.2: Methods of Proof. After that, we will introduce more ideas from Chapter 5: Number Theory. The exercise generator Methods of Proof, 3.2 (also includes
Unit 4 - Equations and Inequalities - Vocabulary
 12/5/17 Unit 4 Unit 4 - Equations and Inequalities - Vocabulary Begin on a new page Write the date and unit in the top corners of the page Write the title across the top line Review Vocabulary: Absolute
12/5/17 Unit 4 Unit 4 - Equations and Inequalities - Vocabulary Begin on a new page Write the date and unit in the top corners of the page Write the title across the top line Review Vocabulary: Absolute
1 Introduction. n = Key-Words: - Mersenne numbers, prime numbers, Generalized Mersenne numbers, distributions
 Generalized Mersenne prime numbers: characterization and distributions VLADIMIR PLETSER Microgravity Projects Div., European Space Research Technology Centre, European Space Agency Dept MSM-GMM, P.O. Box
Generalized Mersenne prime numbers: characterization and distributions VLADIMIR PLETSER Microgravity Projects Div., European Space Research Technology Centre, European Space Agency Dept MSM-GMM, P.O. Box
The Leech Lattice. Balázs Elek. November 8, Cornell University, Department of Mathematics
 The Leech Lattice Balázs Elek Cornell University, Department of Mathematics November 8, 2016 Consider the equation 0 2 + 1 2 + 2 2 +... + n 2 = m 2. How many solutions does it have? Okay, 0 2 + 1 2 = 1
The Leech Lattice Balázs Elek Cornell University, Department of Mathematics November 8, 2016 Consider the equation 0 2 + 1 2 + 2 2 +... + n 2 = m 2. How many solutions does it have? Okay, 0 2 + 1 2 = 1
Calendar Squares Ten Frames 0-10
 K.CC.A Know number names and the count sequence. K.CC.1 Count to 100 by ones and tens. (0-10) K.CC.3 Write numbers from 0-20. Represent a number of objects with a written numeral 0-20 (with 0 representing
K.CC.A Know number names and the count sequence. K.CC.1 Count to 100 by ones and tens. (0-10) K.CC.3 Write numbers from 0-20. Represent a number of objects with a written numeral 0-20 (with 0 representing
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
Senior Math Circles November 19, 2008 Probability II
 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Senior Math Circles November 9, 2008 Probability II Probability Counting There are many situations where
University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Senior Math Circles November 9, 2008 Probability II Probability Counting There are many situations where
Finite and infinite sets, and cardinality
 (1/17) MA180/186/190 : Semester 2 Calculus http://www.maths.nuigalway.ie/ma180-2 Niall Madden (Niall.Madden@NUIGalway.ie) Finite and infinite sets, and cardinality Lecture 02: Tuesday, 8 January 2013 Today:
(1/17) MA180/186/190 : Semester 2 Calculus http://www.maths.nuigalway.ie/ma180-2 Niall Madden (Niall.Madden@NUIGalway.ie) Finite and infinite sets, and cardinality Lecture 02: Tuesday, 8 January 2013 Today:
Some Review Problems for Exam 3: Solutions
 Math 3355 Spring 017 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
Math 3355 Spring 017 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
CMPUT651: Differential Privacy
 CMPUT65: Differential Privacy Homework assignment # 2 Due date: Apr. 3rd, 208 Discussion and the exchange of ideas are essential to doing academic work. For assignments in this course, you are encouraged
CMPUT65: Differential Privacy Homework assignment # 2 Due date: Apr. 3rd, 208 Discussion and the exchange of ideas are essential to doing academic work. For assignments in this course, you are encouraged
The Law of Averages. MARK FLANAGAN School of Electrical, Electronic and Communications Engineering University College Dublin
 The Law of Averages MARK FLANAGAN School of Electrical, Electronic and Communications Engineering University College Dublin Basic Principle of Inequalities: For any real number x, we have 3 x 2 0, with
The Law of Averages MARK FLANAGAN School of Electrical, Electronic and Communications Engineering University College Dublin Basic Principle of Inequalities: For any real number x, we have 3 x 2 0, with
Introduction to Probability, Fall 2009
 Introduction to Probability, Fall 2009 Math 30530 Review questions for exam 1 solutions 1. Let A, B and C be events. Some of the following statements are always true, and some are not. For those that are
Introduction to Probability, Fall 2009 Math 30530 Review questions for exam 1 solutions 1. Let A, B and C be events. Some of the following statements are always true, and some are not. For those that are
Homework 4 Solutions
 CS 174: Combinatorics and Discrete Probability Fall 01 Homework 4 Solutions Problem 1. (Exercise 3.4 from MU 5 points) Recall the randomized algorithm discussed in class for finding the median of a set
CS 174: Combinatorics and Discrete Probability Fall 01 Homework 4 Solutions Problem 1. (Exercise 3.4 from MU 5 points) Recall the randomized algorithm discussed in class for finding the median of a set
MATH 10B METHODS OF MATHEMATICS: CALCULUS, STATISTICS AND COMBINATORICS
 MATH 10B METHODS OF MATHEMATICS: CALCULUS, STATISTICS AND COMBINATORICS Lior Pachter and Lawrence C. Evans Department of Mathematics University of California Berkeley, CA 94720 January 21, 2013 Lior Pachter
MATH 10B METHODS OF MATHEMATICS: CALCULUS, STATISTICS AND COMBINATORICS Lior Pachter and Lawrence C. Evans Department of Mathematics University of California Berkeley, CA 94720 January 21, 2013 Lior Pachter
Counting. Mukulika Ghosh. Fall Based on slides by Dr. Hyunyoung Lee
 Counting Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Counting Counting The art of counting is known as enumerative combinatorics. One tries to count the number of elements in a set (or,
Counting Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Counting Counting The art of counting is known as enumerative combinatorics. One tries to count the number of elements in a set (or,
Introductory Probability
 Introductory Probability Bernoulli Trials and Binomial Probability Distributions Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK February 04, 2019 Agenda Bernoulli Trials and Probability
Introductory Probability Bernoulli Trials and Binomial Probability Distributions Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK February 04, 2019 Agenda Bernoulli Trials and Probability
In a five-minute period, you get a certain number m of requests. Each needs to be served from one of your n servers.
 Suppose you are a content delivery network. In a five-minute period, you get a certain number m of requests. Each needs to be served from one of your n servers. How to distribute requests to balance the
Suppose you are a content delivery network. In a five-minute period, you get a certain number m of requests. Each needs to be served from one of your n servers. How to distribute requests to balance the
CSCI 150 Discrete Mathematics Homework 5 Solution
 CSCI 150 Discrete Mathematics Homework 5 Solution Saad Mneimneh Computer Science Hunter College of CUNY Problem 1: Happy Birthday (if it applies to you)! Based on the size of the class, there is approximately
CSCI 150 Discrete Mathematics Homework 5 Solution Saad Mneimneh Computer Science Hunter College of CUNY Problem 1: Happy Birthday (if it applies to you)! Based on the size of the class, there is approximately
HW2 Solutions, for MATH441, STAT461, STAT561, due September 9th
 HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
HW2 Solutions, for MATH44, STAT46, STAT56, due September 9th. You flip a coin until you get tails. Describe the sample space. How many points are in the sample space? The sample space consists of sequences
Balls & Bins. Balls into Bins. Revisit Birthday Paradox. Load. SCONE Lab. Put m balls into n bins uniformly at random
 Balls & Bins Put m balls into n bins uniformly at random Seoul National University 1 2 3 n Balls into Bins Name: Chong kwon Kim Same (or similar) problems Birthday paradox Hash table Coupon collection
Balls & Bins Put m balls into n bins uniformly at random Seoul National University 1 2 3 n Balls into Bins Name: Chong kwon Kim Same (or similar) problems Birthday paradox Hash table Coupon collection
arxiv: v1 [math.co] 30 Aug 2017
![arxiv: v1 [math.co] 30 Aug 2017 arxiv: v1 [math.co] 30 Aug 2017](/thumbs/90/101582829.jpg) Parking Cars of Different Sizes arxiv:1708.09077v1 [math.co] 30 Aug 2017 Richard Ehrenborg and Alex Happ Abstract We extend the notion of parking functions to parking sequences, which include cars of different
Parking Cars of Different Sizes arxiv:1708.09077v1 [math.co] 30 Aug 2017 Richard Ehrenborg and Alex Happ Abstract We extend the notion of parking functions to parking sequences, which include cars of different
Computing and Communicating Functions over Sensor Networks
 Computing and Communicating Functions over Sensor Networks Solmaz Torabi Dept. of Electrical and Computer Engineering Drexel University solmaz.t@drexel.edu Advisor: Dr. John M. Walsh 1/35 1 Refrences [1]
Computing and Communicating Functions over Sensor Networks Solmaz Torabi Dept. of Electrical and Computer Engineering Drexel University solmaz.t@drexel.edu Advisor: Dr. John M. Walsh 1/35 1 Refrences [1]
Math-2A Lesson 2-1. Number Systems
 Math-A Lesson -1 Number Systems Natural Numbers Whole Numbers Lesson 1-1 Vocabulary Integers Rational Numbers Irrational Numbers Real Numbers Imaginary Numbers Complex Numbers Closure Why do we need numbers?
Math-A Lesson -1 Number Systems Natural Numbers Whole Numbers Lesson 1-1 Vocabulary Integers Rational Numbers Irrational Numbers Real Numbers Imaginary Numbers Complex Numbers Closure Why do we need numbers?
Homework 1. Spring 2019 (Due Tuesday January 22)
 ECE 302: Probabilistic Methods in Electrical and Computer Engineering Spring 2019 Instructor: Prof. A. R. Reibman Homework 1 Spring 2019 (Due Tuesday January 22) Homework is due on Tuesday January 22 at
ECE 302: Probabilistic Methods in Electrical and Computer Engineering Spring 2019 Instructor: Prof. A. R. Reibman Homework 1 Spring 2019 (Due Tuesday January 22) Homework is due on Tuesday January 22 at
The CS 5 Times. CS 5 Penguin Prepares Revenge
 The CS 5 Times CS 5 Penguin Prepares Revenge The CS5 penguin Claremont (AP): After suffering unmentionably arranges revenge. rude treatment at the trailing end of a physics professor s dog, the CS5 penguin
The CS 5 Times CS 5 Penguin Prepares Revenge The CS5 penguin Claremont (AP): After suffering unmentionably arranges revenge. rude treatment at the trailing end of a physics professor s dog, the CS5 penguin
Set theory background for probability
 Set theory background for probability Defining sets (a very naïve approach) A set is a collection of distinct objects. The objects within a set may be arbitrary, with the order of objects within them having
Set theory background for probability Defining sets (a very naïve approach) A set is a collection of distinct objects. The objects within a set may be arbitrary, with the order of objects within them having
Tracking code for microwave instability
 Tracking code for microwave instability S. Heifets, SLAC ILC Damping Rings R&D Workshop Cornell University September, 2006 To study microwave instability the tracking code is developed. For bench marking,
Tracking code for microwave instability S. Heifets, SLAC ILC Damping Rings R&D Workshop Cornell University September, 2006 To study microwave instability the tracking code is developed. For bench marking,
Name (please print) Mathematics Final Examination December 14, 2005 I. (4)
 Mathematics 513-00 Final Examination December 14, 005 I Use a direct argument to prove the following implication: The product of two odd integers is odd Let m and n be two odd integers Since they are odd,
Mathematics 513-00 Final Examination December 14, 005 I Use a direct argument to prove the following implication: The product of two odd integers is odd Let m and n be two odd integers Since they are odd,
IUPUI Department of Mathematical Sciences High School Math Contest Solutions to problems
 IUPUI Department of Mathematical Sciences 2017 High School Math Contest Solutions to problems Problem 1) Given any arc on a parabola (the part between any two distinct points), use compass and straightedge
IUPUI Department of Mathematical Sciences 2017 High School Math Contest Solutions to problems Problem 1) Given any arc on a parabola (the part between any two distinct points), use compass and straightedge
Combinatorial Proofs and Algebraic Proofs I
 Combinatorial Proofs and Algebraic Proofs I Shailesh A Shirali Shailesh A Shirali is Director of Sahyadri School (KFI), Pune, and also Head of the Community Mathematics Centre in Rishi Valley School (AP).
Combinatorial Proofs and Algebraic Proofs I Shailesh A Shirali Shailesh A Shirali is Director of Sahyadri School (KFI), Pune, and also Head of the Community Mathematics Centre in Rishi Valley School (AP).
Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3)
 1 Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3) On this exam, questions may come from any of the following topic areas: - Union and intersection of sets - Complement of
1 Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3) On this exam, questions may come from any of the following topic areas: - Union and intersection of sets - Complement of
String Art and Calculus
 String Art and Calculus (and Games with Envelopes) Gregory Quenell 1 First example Draw line segments connecting (0, x) with (1 x, 0) for x = 0.1, 0.2,..., 0.9. 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 2 First
String Art and Calculus (and Games with Envelopes) Gregory Quenell 1 First example Draw line segments connecting (0, x) with (1 x, 0) for x = 0.1, 0.2,..., 0.9. 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 2 First
Name: (This only happens every four years or does it?)
 Name: (This only happens every four years or does it?) Calendars: Then and Now Name: 1. What is a leap year? What do you already know about leap years? 2. List at least three questions about leap years
Name: (This only happens every four years or does it?) Calendars: Then and Now Name: 1. What is a leap year? What do you already know about leap years? 2. List at least three questions about leap years
Counting. Math 301. November 24, Dr. Nahid Sultana
 Basic Principles Dr. Nahid Sultana November 24, 2012 Basic Principles Basic Principles The Sum Rule The Product Rule Distinguishable Pascal s Triangle Binomial Theorem Basic Principles Combinatorics: The
Basic Principles Dr. Nahid Sultana November 24, 2012 Basic Principles Basic Principles The Sum Rule The Product Rule Distinguishable Pascal s Triangle Binomial Theorem Basic Principles Combinatorics: The
Number of People Contacted
 Section 7.2 Problem Solving Using Exponential Functions (Exponential Growth and Decay) Key Words: exponential, growth, decay, critical mass Key Concepts: exponential growth, exponential decay, simple interest,
Section 7.2 Problem Solving Using Exponential Functions (Exponential Growth and Decay) Key Words: exponential, growth, decay, critical mass Key Concepts: exponential growth, exponential decay, simple interest,
6. This sum can be rewritten as 4( ). We then recall the formula n =
 . c = 9b = 3 b = 3 a 3 = a = = 6.. (3,, ) = 3 + + 3 = 9 + + 3 = 6 6. 3. We see that this is equal to. 3 = ( +.) 3. Using the fact that (x + ) 3 = x 3 + 3x + 3x + and replacing x with., we find that. 3
. c = 9b = 3 b = 3 a 3 = a = = 6.. (3,, ) = 3 + + 3 = 9 + + 3 = 6 6. 3. We see that this is equal to. 3 = ( +.) 3. Using the fact that (x + ) 3 = x 3 + 3x + 3x + and replacing x with., we find that. 3
Supplementary Information: Three-dimensional quantum photonic elements based on single nitrogen vacancy-centres in laser-written microstructures
 Supplementary Information: Three-dimensional quantum photonic elements based on single nitrogen vacancy-centres in laser-written microstructures Andreas W. Schell, 1, a) Johannes Kaschke, 2 Joachim Fischer,
Supplementary Information: Three-dimensional quantum photonic elements based on single nitrogen vacancy-centres in laser-written microstructures Andreas W. Schell, 1, a) Johannes Kaschke, 2 Joachim Fischer,
Pr[A B] > Pr[A]Pr[B]. Pr[A B C] = Pr[(A B) C] = Pr[A]Pr[B A]Pr[C A B].
![Pr[A B] > Pr[A]Pr[B]. Pr[A B C] = Pr[(A B) C] = Pr[A]Pr[B A]Pr[C A B]. Pr[A B] > Pr[A]Pr[B]. Pr[A B C] = Pr[(A B) C] = Pr[A]Pr[B A]Pr[C A B].](/thumbs/94/121310229.jpg) CS70: Jean Walrand: Lecture 25. Product Rule Product Rule Causality, Independence, Collisions and Collecting 1. Product Rule 2. Correlation and Causality 3. Independence 4. 5. Birthdays 6. Checksums 7.
CS70: Jean Walrand: Lecture 25. Product Rule Product Rule Causality, Independence, Collisions and Collecting 1. Product Rule 2. Correlation and Causality 3. Independence 4. 5. Birthdays 6. Checksums 7.
W3203 Discrete Mathema1cs. Coun1ng. Spring 2015 Instructor: Ilia Vovsha.
 W3203 Discrete Mathema1cs Coun1ng Spring 2015 Instructor: Ilia Vovsha h@p://www.cs.columbia.edu/~vovsha/w3203 Outline Bijec1on rule Sum, product, division rules Permuta1ons and combina1ons Sequences with
W3203 Discrete Mathema1cs Coun1ng Spring 2015 Instructor: Ilia Vovsha h@p://www.cs.columbia.edu/~vovsha/w3203 Outline Bijec1on rule Sum, product, division rules Permuta1ons and combina1ons Sequences with
Supplemental Material : A Unified Framework for Multi-Target Tracking and Collective Activity Recognition
 Supplemental Material : A Unified Framewor for Multi-Target Tracing and Collective Activity Recognition Wongun Choi and Silvio Savarese Electrical and Computer Engineering University of Michigan Ann Arbor
Supplemental Material : A Unified Framewor for Multi-Target Tracing and Collective Activity Recognition Wongun Choi and Silvio Savarese Electrical and Computer Engineering University of Michigan Ann Arbor
Order Statistics and Distributions
 Order Statistics and Distributions 1 Some Preliminary Comments and Ideas In this section we consider a random sample X 1, X 2,..., X n common continuous distribution function F and probability density
Order Statistics and Distributions 1 Some Preliminary Comments and Ideas In this section we consider a random sample X 1, X 2,..., X n common continuous distribution function F and probability density
Lecture 3: Miscellaneous Techniques
 Lecture 3: Miscellaneous Techniques Rajat Mittal IIT Kanpur In this document, we will take a look at few diverse techniques used in combinatorics, exemplifying the fact that combinatorics is a collection
Lecture 3: Miscellaneous Techniques Rajat Mittal IIT Kanpur In this document, we will take a look at few diverse techniques used in combinatorics, exemplifying the fact that combinatorics is a collection
CS221 Practice Midterm #2 Solutions
 CS221 Practice Midterm #2 Solutions Summer 2013 Updated 4:00pm, July 24 2 [Deterministic Search] Pacfamily (20 points) Pacman is trying eat all the dots, but he now has the help of his family! There are
CS221 Practice Midterm #2 Solutions Summer 2013 Updated 4:00pm, July 24 2 [Deterministic Search] Pacfamily (20 points) Pacman is trying eat all the dots, but he now has the help of his family! There are
