Astronomy 8824: Numerical Methods Notes 2 Ordinary Differential Equations
|
|
|
- Cameron Osborne
- 5 years ago
- Views:
Transcription
1 Astronomy 8824: Numerical Methods Notes 2 Ordinary Differential Equations Reading: Numerical Recipes, chapter on Integration of Ordinary Differential Equations (which is ch. 15, 16, or 17 depending on edition). Concentrate on the first three sections. Also look briefly at the first sections of the following chapter on Two Point Boundary Value Problems. For orbit integrations, 3.4 of the current edition of Binney & Tremaine (Galactic Dynamics) is a good discussion, especially on the topics of symplectic integration schemes and individual particle timesteps. We ll discuss some general aspects of integrating ODEs, while the example in the problem set will be a relatively simple case of integrating orbits in a gravitational potential, which is often relevant to astronomers! A Side Note: Systems of Linear Equations Reference: Numerical Recipes, chapter 2. The system of equations a 11 x 1 + a 12 x 2 + a 13 x a 1n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x a 2n x n = b 2... a n1 x 1 + a n2 x 2 + a n3 x a nn x n = b n can be written in matrix form A x = b. If the equations are linearly independent, then the matrix A is non-singular and invertible. The solution to the equations is: x = A 1 A x = A 1 b. The computational task of matrix inversion is discussed in Chapter 2 of NR. For small, non-singular matrices it is straightforward, allowing a straightforward solution to a system of equations. For example, in ipython try import numpy as np a=np.array([[1,9,7],[2,4,12],[3,7,3]]) 1
2 b=np.array([9,-3,7]) ainv=np.linalg.inv(a) np.dot(a,ainv) x=np.dot(ainv,b) np.dot(a,x) The problem becomes more challenging when The solutions have to be done many, many times, in which case it s important to be efficient. The equations are degenerate or nearly so, in which case one needs singular value decomposition. The number of matrix elements is very large. If many of the matrix elements are zero, then one can use sparse matrix methods. Initial Value Problems Higher order differential equations can be reduced to systems of first-order differential equations. For example d 2 y dx + q(x)dy 2 dx = r(x) can be rewritten as dy dx = z(x) dz = r(x) q(x)z(x), dx two first-order equations that can be integrated simultaneously. The generic problem to solve is therefore a system of coupled first-order ODEs, dy i (x) dx = f i (x, y 1, y 2,..., y N ), i = 1,..., N. For the case of an orbit in a gravitational potential we have which can be written d 2 x dt 2 = Φ(x) dx dt = v dv dt = Φ(x). 2
3 This can be written in the dy i (x)/dx form above, though for orbits it is most straightforward to just think in terms of x and v. An initial value problem is one in which all values of y i are specified at the initial value of x. For example, one might specify x and v at t = 0 and integrate forward in time. Runge-Kutta We ll now think about integrating a single ODE for variable y(x). The simplest way to integrate an ODE, like the simplest way to do a numerical integral, is Euler s method: y n+1 = y n + hf(x n, y n ) to advance from x n to x n+1 = x n + h. As with numerical integrals, this is a bad method; one can get higher accuracy and greater stability with only slightly more work. Mid-point method (2nd order Runge-Kutta) Use derivative at x n to advance to x n+1/2. Then use the derivative at x n+1/2 to advance from x n to x n+1. with an error O(h 3 ) per step. k 1 = hf(x n, y n ) k 2 = hf(x n + h/2, y n + k 1 /2) y n+1 = y n + k 2 Since the number of steps is 1/h, the error in the integration should scale as h 2. 4th order Runge-Kutta One can evaluate at more intermediate points and fit a higher order function. This involves more evaluations per step, but it should allow one to take larger steps. The most commonly used scheme is 4th order, which seems to be a good compromise between these two: k 1 = hf(x n, y n ) k 2 = hf(x n + h/2, y n + k 1 /2) k 3 = hf(x n + h/2, y n + k 2 /2) k 4 = hf(x n + h, y n + k 3 ) y n+1 = y n + k 1 /6 + k 2 /3 + k 3 /3 + k 4 /6 + O(h 5 ). 3
4 (See NR, eq ) Adaptive Step Size If computing time is not an issue, you can just integrate your ODE multiple times with steadily decreasing h and check for convergence to your desired accuracy. However, the step size required for an accurate integration may vary by by a large factor through the domain. For example, integrating a highly elliptical orbit requires much smaller timesteps near peri-center than through most of the orbit, so using a fixed timestep may be wasteful. You would also like your code to give you an estimate of the accuracy of its answer. NR discusses strategies for doing this within Runge-Kutta. The most straightforward idea is to advance from x to x + H, where H is macroscopic jump, using small steps h. Keep halving h (doubling the number of steps) until the desired accuracy is achieved. Start with this value of h for the next H-step. If it s more accurate than needed, increase h; if it s less accurate than needed, decrease h. There is a somewhat more efficient way to achieve this effect, described in NR and implemented in their routines. This approach is quite general. For a specific problem, you may have physical intuition about what should guide the size of steps. For example, the accuracy of integration may depend on the ratio of the timestep to the local dynamical time (Gρ) 1/2 for a gravitational calculation or sound-crossing time L/c s for a hydrodynamic calculation. In such situations, you may be able to choose a constant scaling factor that multiplies some function of local conditions, rather than using step-doubling or other Runge-Kutta strategies. Bulirsch-Stoer This is analogous to Romberg integration for numerical integrals. Take a sequence of different numbers of steps, with decreasing h. Using the results for this sequence, extrapolate to the result for h = 0. NR is enthusiastic about this method for cases that require greater efficiency or higher accuracy than Runge-Kutta. 4
5 However, it s more susceptible to problems if the integration isn t smooth everywhere. Leapfrog Integration Leapfrog is a 2nd-order integration scheme for gravitational problems. From initial conditions x 0, v 0, take a half-step to get v 1/2. Then leapfrog the positions over the velocities, then the velocities over the positions, and so forth. x 1 = x 0 + v 1/2 t v 3/2 = v 1/2 Φ(x 1 ) t x 2 = x 1 + v 3/2 t etc. I am almost sure that this is equivalent to 2nd-order Runge-Kutta but for the specific case of equations where ẋ depends only on v and v depends only on x, which makes it possible to do fewer evaluations. Important: You will usually want to output both positions and velocities. If your arrays store positions on the whole steps and velocities on the half-steps, then you must advance the velocities half-a-step before output (but be careful to get them back on the half-step before continuing the integration). You also need to synchronize positions and velocities before computing energy conservation checks. Stiff Equations and Implicit Integration Sometimes you want to integrate a system where there are two or more very different timescales. If you integrate with timesteps short compared to the shorter timescale, your calculation may never finish. A common example is a hydrodynamic system with cooling. You are typically interested in phenomena happening on the sound-crossing timescale L/c s, where L is the scale of the system. But in a dense region, the cooling timescale may become orders-of-magnitude shorter than the sound-crossing timescale. If you have to do the short timescale integration accurately to get the long timescale behavior to be accurate, then your stuck. But sometimes the short timescale behavior doesn t matter too much (e.g., it matters that the gas gets cold, but it doesn t matter exactly what its temperature is), and you just need your integration to be stable. 5
6 In this case, an implicit scheme for the short timescale behavior may be useful. Here is an example from NR: Consider The explicit Euler scheme is y = cy, c > 0. y n+1 = y n + hy n = (1 ch)y n. If h > 2/c, then the method is unstable, with y n as n. One can avoid this behavior by substituting y n+1 for y n, obtaining the implicit equation y n+1 = y n + hy n+1. In this particular case, the implicit equation is trivially solved y n+1 = which gives a stable result even for large h. y n 1 + ch, More generally, the implicit equations may be solved by matrix inversion (if they re linear) or by some form of iteration (which we ll get to in two weeks) if they re non-linear. If you have a stiff set of equations, then sometimes the physics of the problem will suggest an alternative solution. For example, when timescales for ionization are short compared to other timescales in the system, then relative abundances may always be close to ionization equilibrium, where recombination rates balance ionization rates. This gives a set of equations that can be solved as a function of local conditions (e.g., density, temperature), and perhaps stored in a lookup table. If you re interested in evolution of a hierarchical triple star system where the outer orbital period is much longer than the inner orbital period, it may be adequate to treat the inner binary as a ring with mass spread over the orbit according to the amount of time the stars spend there. Two Point Boundary Value Problems Sometimes your boundary conditions aren t all specified at the same point. For example, you might know an initial position but be trying to achieve a specific final velocity. 6
7 Stellar structure is a classic example: some boundary conditions are known at the center of the star, but others are known at the surface. Two general strategies for this kind of problem are the shooting method and relaxation methods. In the simplest version of the shooting method, you take a guess at the initial boundary values and see where you end up. Then you change an initial boundary value and see how that changes where you end up. You can now do some form of iteration (as discussed in two weeks) to try to zero in on the correct initial boundary condition to satisfy your final boundary condition. It s like firing your artillery shell and continuously adjusting the angle of your gun until you hit your desired target. Sometimes it may be very difficult to get to the right final boundary condition. In such cases it may be better to integrate from both sides and try to meet in the middle, e.g., from the center of the star and the surface of the star. In relaxation methods, you start with an approximate guess at the full solution. You then use finite differences to calculate the errors in this guess at every point in the domain. You then try to adjust your solution to eliminate these errors. If your guess is close, then you may be able to reduce the problem of eliminating the errors to a problem of solving simultaneous linear equations. Relaxation methods are most useful when you have a very good guess to start with. For example, you may want to solve for a sequence of main sequence stellar models with increasing mass. The solution at mass M, perhaps scaled in some way, then becomes a good starting guess for the solution at mass M + ǫ. One could do the evolution of a star of fixed M in a similar way, with the composition changing slightly from one time to the next. 7
High performance computing and numerical modeling
 High performance computing and numerical modeling Volker Springel Plan for my lectures Lecture 1: Collisional and collisionless N-body dynamics Lecture 2: Gravitational force calculation Lecture 3: Basic
High performance computing and numerical modeling Volker Springel Plan for my lectures Lecture 1: Collisional and collisionless N-body dynamics Lecture 2: Gravitational force calculation Lecture 3: Basic
Ph 22.1 Return of the ODEs: higher-order methods
 Ph 22.1 Return of the ODEs: higher-order methods -v20130111- Introduction This week we are going to build on the experience that you gathered in the Ph20, and program more advanced (and accurate!) solvers
Ph 22.1 Return of the ODEs: higher-order methods -v20130111- Introduction This week we are going to build on the experience that you gathered in the Ph20, and program more advanced (and accurate!) solvers
Maths III - Numerical Methods
 Maths III - Numerical Methods Matt Probert matt.probert@york.ac.uk 4 Solving Differential Equations 4.1 Introduction Many physical problems can be expressed as differential s, but solving them is not always
Maths III - Numerical Methods Matt Probert matt.probert@york.ac.uk 4 Solving Differential Equations 4.1 Introduction Many physical problems can be expressed as differential s, but solving them is not always
16.7 Multistep, Multivalue, and Predictor-Corrector Methods
 740 Chapter 16. Integration of Ordinary Differential Equations 16.7 Multistep, Multivalue, and Predictor-Corrector Methods The terms multistepand multivaluedescribe two different ways of implementing essentially
740 Chapter 16. Integration of Ordinary Differential Equations 16.7 Multistep, Multivalue, and Predictor-Corrector Methods The terms multistepand multivaluedescribe two different ways of implementing essentially
A Brief Introduction to Numerical Methods for Differential Equations
 A Brief Introduction to Numerical Methods for Differential Equations January 10, 2011 This tutorial introduces some basic numerical computation techniques that are useful for the simulation and analysis
A Brief Introduction to Numerical Methods for Differential Equations January 10, 2011 This tutorial introduces some basic numerical computation techniques that are useful for the simulation and analysis
Logistic Map, Euler & Runge-Kutta Method and Lotka-Volterra Equations
 Logistic Map, Euler & Runge-Kutta Method and Lotka-Volterra Equations S. Y. Ha and J. Park Department of Mathematical Sciences Seoul National University Sep 23, 2013 Contents 1 Logistic Map 2 Euler and
Logistic Map, Euler & Runge-Kutta Method and Lotka-Volterra Equations S. Y. Ha and J. Park Department of Mathematical Sciences Seoul National University Sep 23, 2013 Contents 1 Logistic Map 2 Euler and
Comparison of Numerical Ordinary Differential Equation Solvers
 Adrienne Criss Due: October, 008 Comparison of Numerical Ordinary Differential Equation Solvers Many interesting physical systems can be modeled by ordinary differential equations (ODEs). Since it is always
Adrienne Criss Due: October, 008 Comparison of Numerical Ordinary Differential Equation Solvers Many interesting physical systems can be modeled by ordinary differential equations (ODEs). Since it is always
The family of Runge Kutta methods with two intermediate evaluations is defined by
 AM 205: lecture 13 Last time: Numerical solution of ordinary differential equations Today: Additional ODE methods, boundary value problems Thursday s lecture will be given by Thomas Fai Assignment 3 will
AM 205: lecture 13 Last time: Numerical solution of ordinary differential equations Today: Additional ODE methods, boundary value problems Thursday s lecture will be given by Thomas Fai Assignment 3 will
Butcher tableau Can summarize an s + 1 stage Runge Kutta method using a triangular grid of coefficients
 AM 205: lecture 13 Last time: ODE convergence and stability, Runge Kutta methods Today: the Butcher tableau, multi-step methods, boundary value problems Butcher tableau Can summarize an s + 1 stage Runge
AM 205: lecture 13 Last time: ODE convergence and stability, Runge Kutta methods Today: the Butcher tableau, multi-step methods, boundary value problems Butcher tableau Can summarize an s + 1 stage Runge
Ordinary Differential Equations. Monday, October 10, 11
 Ordinary Differential Equations Monday, October 10, 11 Problems involving ODEs can always be reduced to a set of first order differential equations. For example, By introducing a new variable z, this can
Ordinary Differential Equations Monday, October 10, 11 Problems involving ODEs can always be reduced to a set of first order differential equations. For example, By introducing a new variable z, this can
X i t react. ~min i max i. R ij smallest. X j. Physical processes by characteristic timescale. largest. t diff ~ L2 D. t sound. ~ L a. t flow.
 Physical processes by characteristic timescale Diffusive timescale t diff ~ L2 D largest Sound crossing timescale t sound ~ L a Flow timescale t flow ~ L u Free fall timescale Cooling timescale Reaction
Physical processes by characteristic timescale Diffusive timescale t diff ~ L2 D largest Sound crossing timescale t sound ~ L a Flow timescale t flow ~ L u Free fall timescale Cooling timescale Reaction
Solution of ordinary Differential Equations
 42 Chapter 4 Solution of ordinary Differential Equations Highly suggested Reading Press et al., 1992. Numerical Recipes, 2nd Edition. Chapter 16. (Good description). See also chapter 17. And Matlab help
42 Chapter 4 Solution of ordinary Differential Equations Highly suggested Reading Press et al., 1992. Numerical Recipes, 2nd Edition. Chapter 16. (Good description). See also chapter 17. And Matlab help
AM 205 Final Project The N-Body Problem
 AM 205 Final Project The N-Body Problem Leah Birch Elizabeth Finn Karen Yu December 14, 2012 Abstract The N-Body Problem can be solved using a variety of numeric integrators. Newton s Law of Universal
AM 205 Final Project The N-Body Problem Leah Birch Elizabeth Finn Karen Yu December 14, 2012 Abstract The N-Body Problem can be solved using a variety of numeric integrators. Newton s Law of Universal
Chapter 11 ORDINARY DIFFERENTIAL EQUATIONS
 Chapter 11 ORDINARY DIFFERENTIAL EQUATIONS The general form of a first order differential equations is = f(x, y) with initial condition y(a) = y a We seek the solution y = y(x) for x > a This is shown
Chapter 11 ORDINARY DIFFERENTIAL EQUATIONS The general form of a first order differential equations is = f(x, y) with initial condition y(a) = y a We seek the solution y = y(x) for x > a This is shown
Physically Based Modeling: Principles and Practice Differential Equation Basics
 Physically Based Modeling: Principles and Practice Differential Equation Basics Andrew Witkin and David Baraff Robotics Institute Carnegie Mellon University Please note: This document is 1997 by Andrew
Physically Based Modeling: Principles and Practice Differential Equation Basics Andrew Witkin and David Baraff Robotics Institute Carnegie Mellon University Please note: This document is 1997 by Andrew
Chapter 8. Numerical Solution of Ordinary Differential Equations. Module No. 1. Runge-Kutta Methods
 Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-71309 email: anita.buie@gmail.com 1 . Chapter 8 Numerical Solution of
Numerical Analysis by Dr. Anita Pal Assistant Professor Department of Mathematics National Institute of Technology Durgapur Durgapur-71309 email: anita.buie@gmail.com 1 . Chapter 8 Numerical Solution of
Physically Based Modeling Differential Equation Basics
 Physically Based Modeling Differential Equation Basics Andrew Witkin and David Baraff Pixar Animation Studios Please note: This document is 2001 by Andrew Witkin and David Baraff. This chapter may be freely
Physically Based Modeling Differential Equation Basics Andrew Witkin and David Baraff Pixar Animation Studios Please note: This document is 2001 by Andrew Witkin and David Baraff. This chapter may be freely
Numerical differentiation
 Numerical differentiation Paul Seidel 1801 Lecture Notes Fall 011 Suppose that we have a function f(x) which is not given by a formula but as a result of some measurement or simulation (computer experiment)
Numerical differentiation Paul Seidel 1801 Lecture Notes Fall 011 Suppose that we have a function f(x) which is not given by a formula but as a result of some measurement or simulation (computer experiment)
Chapter 9 Implicit integration, incompressible flows
 Chapter 9 Implicit integration, incompressible flows The methods we discussed so far work well for problems of hydrodynamics in which the flow speeds of interest are not orders of magnitude smaller than
Chapter 9 Implicit integration, incompressible flows The methods we discussed so far work well for problems of hydrodynamics in which the flow speeds of interest are not orders of magnitude smaller than
Review Higher Order methods Multistep methods Summary HIGHER ORDER METHODS. P.V. Johnson. School of Mathematics. Semester
 HIGHER ORDER METHODS School of Mathematics Semester 1 2008 OUTLINE 1 REVIEW 2 HIGHER ORDER METHODS 3 MULTISTEP METHODS 4 SUMMARY OUTLINE 1 REVIEW 2 HIGHER ORDER METHODS 3 MULTISTEP METHODS 4 SUMMARY OUTLINE
HIGHER ORDER METHODS School of Mathematics Semester 1 2008 OUTLINE 1 REVIEW 2 HIGHER ORDER METHODS 3 MULTISTEP METHODS 4 SUMMARY OUTLINE 1 REVIEW 2 HIGHER ORDER METHODS 3 MULTISTEP METHODS 4 SUMMARY OUTLINE
FORTRAN 77 Lesson 7. Reese Haywood Ayan Paul
 FORTRAN 77 Lesson 7 Reese Haywood Ayan Paul 1 Numerical Integration A general all purpose Numerical Integration technique is the Trapezoidal Method. For most functions, this method is fast and accurate.
FORTRAN 77 Lesson 7 Reese Haywood Ayan Paul 1 Numerical Integration A general all purpose Numerical Integration technique is the Trapezoidal Method. For most functions, this method is fast and accurate.
x x2 2 + x3 3 x4 3. Use the divided-difference method to find a polynomial of least degree that fits the values shown: (b)
 Numerical Methods - PROBLEMS. The Taylor series, about the origin, for log( + x) is x x2 2 + x3 3 x4 4 + Find an upper bound on the magnitude of the truncation error on the interval x.5 when log( + x)
Numerical Methods - PROBLEMS. The Taylor series, about the origin, for log( + x) is x x2 2 + x3 3 x4 4 + Find an upper bound on the magnitude of the truncation error on the interval x.5 when log( + x)
Math 225 Differential Equations Notes Chapter 1
 Math 225 Differential Equations Notes Chapter 1 Michael Muscedere September 9, 2004 1 Introduction 1.1 Background In science and engineering models are used to describe physical phenomena. Often these
Math 225 Differential Equations Notes Chapter 1 Michael Muscedere September 9, 2004 1 Introduction 1.1 Background In science and engineering models are used to describe physical phenomena. Often these
Fourth Order RK-Method
 Fourth Order RK-Method The most commonly used method is Runge-Kutta fourth order method. The fourth order RK-method is y i+1 = y i + 1 6 (k 1 + 2k 2 + 2k 3 + k 4 ), Ordinary Differential Equations (ODE)
Fourth Order RK-Method The most commonly used method is Runge-Kutta fourth order method. The fourth order RK-method is y i+1 = y i + 1 6 (k 1 + 2k 2 + 2k 3 + k 4 ), Ordinary Differential Equations (ODE)
Ordinary Differential Equations
 Chapter 13 Ordinary Differential Equations We motivated the problem of interpolation in Chapter 11 by transitioning from analzying to finding functions. That is, in problems like interpolation and regression,
Chapter 13 Ordinary Differential Equations We motivated the problem of interpolation in Chapter 11 by transitioning from analzying to finding functions. That is, in problems like interpolation and regression,
First-Order Ordinary Differntial Equations II: Autonomous Case. David Levermore Department of Mathematics University of Maryland.
 First-Order Ordinary Differntial Equations II: Autonomous Case David Levermore Department of Mathematics University of Maryland 25 February 2009 These notes cover some of the material that we covered in
First-Order Ordinary Differntial Equations II: Autonomous Case David Levermore Department of Mathematics University of Maryland 25 February 2009 These notes cover some of the material that we covered in
Overview spherical accretion
 Spherical accretion - AGN generates energy by accretion, i.e., capture of ambient matter in gravitational potential of black hole -Potential energy can be released as radiation, and (some of) this can
Spherical accretion - AGN generates energy by accretion, i.e., capture of ambient matter in gravitational potential of black hole -Potential energy can be released as radiation, and (some of) this can
ODE Runge-Kutta methods
 ODE Runge-Kutta methods The theory (very short excerpts from lectures) First-order initial value problem We want to approximate the solution Y(x) of a system of first-order ordinary differential equations
ODE Runge-Kutta methods The theory (very short excerpts from lectures) First-order initial value problem We want to approximate the solution Y(x) of a system of first-order ordinary differential equations
Chap. 20: Initial-Value Problems
 Chap. 20: Initial-Value Problems Ordinary Differential Equations Goal: to solve differential equations of the form: dy dt f t, y The methods in this chapter are all one-step methods and have the general
Chap. 20: Initial-Value Problems Ordinary Differential Equations Goal: to solve differential equations of the form: dy dt f t, y The methods in this chapter are all one-step methods and have the general
Integration of Ordinary Differential Equations
 Integration of Ordinary Differential Equations Com S 477/577 Nov 7, 00 1 Introduction The solution of differential equations is an important problem that arises in a host of areas. Many differential equations
Integration of Ordinary Differential Equations Com S 477/577 Nov 7, 00 1 Introduction The solution of differential equations is an important problem that arises in a host of areas. Many differential equations
ES.1803 Topic 13 Notes Jeremy Orloff
 ES.1803 Topic 13 Notes Jeremy Orloff 13 Vector Spaces, matrices and linearity 13.1 Goals 1. Know the definition of a vector space and how to show that a given set is a vector space. 2. Know the meaning
ES.1803 Topic 13 Notes Jeremy Orloff 13 Vector Spaces, matrices and linearity 13.1 Goals 1. Know the definition of a vector space and how to show that a given set is a vector space. 2. Know the meaning
A Hybrid Method for the Wave Equation. beilina
 A Hybrid Method for the Wave Equation http://www.math.unibas.ch/ beilina 1 The mathematical model The model problem is the wave equation 2 u t 2 = (a 2 u) + f, x Ω R 3, t > 0, (1) u(x, 0) = 0, x Ω, (2)
A Hybrid Method for the Wave Equation http://www.math.unibas.ch/ beilina 1 The mathematical model The model problem is the wave equation 2 u t 2 = (a 2 u) + f, x Ω R 3, t > 0, (1) u(x, 0) = 0, x Ω, (2)
Ordinary Differential Equations (ODEs)
 Ordinary Differential Equations (ODEs) NRiC Chapter 16. ODEs involve derivatives wrt one independent variable, e.g. time t. ODEs can always be reduced to a set of firstorder equations (involving only first
Ordinary Differential Equations (ODEs) NRiC Chapter 16. ODEs involve derivatives wrt one independent variable, e.g. time t. ODEs can always be reduced to a set of firstorder equations (involving only first
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES
 MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
Nonlinear Equations. Not guaranteed to have any real solutions, but generally do for astrophysical problems.
 Nonlinear Equations Often (most of the time??) the relevant system of equations is not linear in the unknowns. Then, cannot decompose as Ax = b. Oh well. Instead write as: (1) f(x) = 0 function of one
Nonlinear Equations Often (most of the time??) the relevant system of equations is not linear in the unknowns. Then, cannot decompose as Ax = b. Oh well. Instead write as: (1) f(x) = 0 function of one
1 R.V k V k 1 / I.k/ here; we ll stimulate the action potential another way.) Note that this further simplifies to. m 3 k h k.
 1. The goal of this problem is to simulate a propagating action potential for the Hodgkin-Huxley model and to determine the propagation speed. From the class notes, the discrete version (i.e., after breaking
1. The goal of this problem is to simulate a propagating action potential for the Hodgkin-Huxley model and to determine the propagation speed. From the class notes, the discrete version (i.e., after breaking
Geometric methods for orbit integration. PiTP 2009 Scott Tremaine
 Geometric methods for orbit integration PiTP 2009 Scott Tremaine spacecraft trajectories Cassini-Huygens trajectory around Saturn, 2004-2008 Planetary orbits lines = current orbits of the four inner planets
Geometric methods for orbit integration PiTP 2009 Scott Tremaine spacecraft trajectories Cassini-Huygens trajectory around Saturn, 2004-2008 Planetary orbits lines = current orbits of the four inner planets
Ordinary Differential Equations
 Ordinary Differential Equations Part 4 Massimo Ricotti ricotti@astro.umd.edu University of Maryland Ordinary Differential Equations p. 1/23 Two-point Boundary Value Problems NRiC 17. BCs specified at two
Ordinary Differential Equations Part 4 Massimo Ricotti ricotti@astro.umd.edu University of Maryland Ordinary Differential Equations p. 1/23 Two-point Boundary Value Problems NRiC 17. BCs specified at two
16.7 Multistep, Multivalue, and Predictor-Corrector Methods
 16.7 Multistep, Multivalue, and Predictor-Corrector Methods 747 } free_vector(ysav,1,nv); free_vector(yerr,1,nv); free_vector(x,1,kmaxx); free_vector(err,1,kmaxx); free_matrix(dfdy,1,nv,1,nv); free_vector(dfdx,1,nv);
16.7 Multistep, Multivalue, and Predictor-Corrector Methods 747 } free_vector(ysav,1,nv); free_vector(yerr,1,nv); free_vector(x,1,kmaxx); free_vector(err,1,kmaxx); free_matrix(dfdy,1,nv,1,nv); free_vector(dfdx,1,nv);
Time scales. Notes. Mixed Implicit/Explicit. Newmark Methods [ ] [ ] "!t = O 1 %
![Time scales. Notes. Mixed Implicit/Explicit. Newmark Methods [ ] [ ] !t = O 1 % Time scales. Notes. Mixed Implicit/Explicit. Newmark Methods [ ] [ ] !t = O 1 %](/thumbs/95/124165137.jpg) Notes Time scales! For using Pixie (the renderer) make sure you type use pixie first! Assignment 1 questions?! [work out]! For position dependence, characteristic time interval is "!t = O 1 % $ ' # K &!
Notes Time scales! For using Pixie (the renderer) make sure you type use pixie first! Assignment 1 questions?! [work out]! For position dependence, characteristic time interval is "!t = O 1 % $ ' # K &!
Review for Exam 2 Ben Wang and Mark Styczynski
 Review for Exam Ben Wang and Mark Styczynski This is a rough approximation of what we went over in the review session. This is actually more detailed in portions than what we went over. Also, please note
Review for Exam Ben Wang and Mark Styczynski This is a rough approximation of what we went over in the review session. This is actually more detailed in portions than what we went over. Also, please note
Chapter 6 - Ordinary Differential Equations
 Chapter 6 - Ordinary Differential Equations 7.1 Solving Initial-Value Problems In this chapter, we will be interested in the solution of ordinary differential equations. Ordinary differential equations
Chapter 6 - Ordinary Differential Equations 7.1 Solving Initial-Value Problems In this chapter, we will be interested in the solution of ordinary differential equations. Ordinary differential equations
1 Ordinary differential equations
 Numerical Analysis Seminar Frühjahrssemester 08 Lecturers: Prof. M. Torrilhon, Prof. D. Kressner The Störmer-Verlet method F. Crivelli (flcrivel@student.ethz.ch May 8, 2008 Introduction During this talk
Numerical Analysis Seminar Frühjahrssemester 08 Lecturers: Prof. M. Torrilhon, Prof. D. Kressner The Störmer-Verlet method F. Crivelli (flcrivel@student.ethz.ch May 8, 2008 Introduction During this talk
Multistep Methods for IVPs. t 0 < t < T
 Multistep Methods for IVPs We are still considering the IVP dy dt = f(t,y) t 0 < t < T y(t 0 ) = y 0 So far we have looked at Euler s method, which was a first order method and Runge Kutta (RK) methods
Multistep Methods for IVPs We are still considering the IVP dy dt = f(t,y) t 0 < t < T y(t 0 ) = y 0 So far we have looked at Euler s method, which was a first order method and Runge Kutta (RK) methods
First-Order Differential Equations
 CHAPTER 1 First-Order Differential Equations 1. Diff Eqns and Math Models Know what it means for a function to be a solution to a differential equation. In order to figure out if y = y(x) is a solution
CHAPTER 1 First-Order Differential Equations 1. Diff Eqns and Math Models Know what it means for a function to be a solution to a differential equation. In order to figure out if y = y(x) is a solution
Graded Project #1. Part 1. Explicit Runge Kutta methods. Goals Differential Equations FMN130 Gustaf Söderlind and Carmen Arévalo
 2008-11-07 Graded Project #1 Differential Equations FMN130 Gustaf Söderlind and Carmen Arévalo This homework is due to be handed in on Wednesday 12 November 2008 before 13:00 in the post box of the numerical
2008-11-07 Graded Project #1 Differential Equations FMN130 Gustaf Söderlind and Carmen Arévalo This homework is due to be handed in on Wednesday 12 November 2008 before 13:00 in the post box of the numerical
1 GSW Sets of Systems
 1 Often, we have to solve a whole series of sets of simultaneous equations of the form y Ax, all of which have the same matrix A, but each of which has a different known vector y, and a different unknown
1 Often, we have to solve a whole series of sets of simultaneous equations of the form y Ax, all of which have the same matrix A, but each of which has a different known vector y, and a different unknown
Ordinary Differential Equations
 Ordinary Differential Equations In this lecture, we will look at different options for coding simple differential equations. Start by considering bicycle riding as an example. Why does a bicycle move forward?
Ordinary Differential Equations In this lecture, we will look at different options for coding simple differential equations. Start by considering bicycle riding as an example. Why does a bicycle move forward?
Differential Equations
 Differential Equations Definitions Finite Differences Taylor Series based Methods: Euler Method Runge-Kutta Methods Improved Euler, Midpoint methods Runge Kutta (2nd, 4th order) methods Predictor-Corrector
Differential Equations Definitions Finite Differences Taylor Series based Methods: Euler Method Runge-Kutta Methods Improved Euler, Midpoint methods Runge Kutta (2nd, 4th order) methods Predictor-Corrector
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Basic Concepts Paul Dawkins Table of Contents Preface... Basic Concepts... 1 Introduction... 1 Definitions... Direction Fields... 8 Final Thoughts...19 007 Paul Dawkins i http://tutorial.math.lamar.edu/terms.aspx
DIFFERENTIAL EQUATIONS Basic Concepts Paul Dawkins Table of Contents Preface... Basic Concepts... 1 Introduction... 1 Definitions... Direction Fields... 8 Final Thoughts...19 007 Paul Dawkins i http://tutorial.math.lamar.edu/terms.aspx
Heading for death. q q
 Hubble Photos Credit: NASA, The Hubble Heritage Team (STScI/AURA) Heading for death. q q q q q q Leaving the main sequence End of the Sunlike star The helium core The Red-Giant Branch Helium Fusion Helium
Hubble Photos Credit: NASA, The Hubble Heritage Team (STScI/AURA) Heading for death. q q q q q q Leaving the main sequence End of the Sunlike star The helium core The Red-Giant Branch Helium Fusion Helium
Bindel, Fall 2011 Intro to Scientific Computing (CS 3220) Week 12: Monday, Apr 18. HW 7 is posted, and will be due in class on 4/25.
 Logistics Week 12: Monday, Apr 18 HW 6 is due at 11:59 tonight. HW 7 is posted, and will be due in class on 4/25. The prelim is graded. An analysis and rubric are on CMS. Problem du jour For implicit methods
Logistics Week 12: Monday, Apr 18 HW 6 is due at 11:59 tonight. HW 7 is posted, and will be due in class on 4/25. The prelim is graded. An analysis and rubric are on CMS. Problem du jour For implicit methods
Value Problems Introduction
 Chapter 17. 17.0 Introduction Two Point Boundary Value Problems When ordinary differential equations are to satisfy conditions at more than one of the independent variable, the resulting problem is called
Chapter 17. 17.0 Introduction Two Point Boundary Value Problems When ordinary differential equations are to satisfy conditions at more than one of the independent variable, the resulting problem is called
CS 257: Numerical Methods
 CS 57: Numerical Methods Final Exam Study Guide Version 1.00 Created by Charles Feng http://www.fenguin.net CS 57: Numerical Methods Final Exam Study Guide 1 Contents 1 Introductory Matter 3 1.1 Calculus
CS 57: Numerical Methods Final Exam Study Guide Version 1.00 Created by Charles Feng http://www.fenguin.net CS 57: Numerical Methods Final Exam Study Guide 1 Contents 1 Introductory Matter 3 1.1 Calculus
Newton-Raphson. Relies on the Taylor expansion f(x + δ) = f(x) + δ f (x) + ½ δ 2 f (x) +..
 2008 Lecture 7 starts here Newton-Raphson When the derivative of f(x) is known, and when f(x) is well behaved, the celebrated (and ancient) Newton- Raphson method gives the fastest convergence of all (
2008 Lecture 7 starts here Newton-Raphson When the derivative of f(x) is known, and when f(x) is well behaved, the celebrated (and ancient) Newton- Raphson method gives the fastest convergence of all (
Lec 9: Stellar Evolution and DeathBirth and. Why do stars leave main sequence? What conditions are required for elements. Text
 1 Astr 102 Lec 9: Stellar Evolution and DeathBirth and Evolution Why do stars leave main sequence? What conditions are required for elements Text besides Hydrogen to fuse, and why? How do stars die: white
1 Astr 102 Lec 9: Stellar Evolution and DeathBirth and Evolution Why do stars leave main sequence? What conditions are required for elements Text besides Hydrogen to fuse, and why? How do stars die: white
Section 2.7 Solving Linear Inequalities
 Section.7 Solving Linear Inequalities Objectives In this section, you will learn to: To successfully complete this section, you need to understand: Add and multiply an inequality. Solving equations (.1,.,
Section.7 Solving Linear Inequalities Objectives In this section, you will learn to: To successfully complete this section, you need to understand: Add and multiply an inequality. Solving equations (.1,.,
Ordinary Differential Equations (ODEs)
 Ordinary Differential Equations (ODEs) 1 Computer Simulations Why is computation becoming so important in physics? One reason is that most of our analytical tools such as differential calculus are best
Ordinary Differential Equations (ODEs) 1 Computer Simulations Why is computation becoming so important in physics? One reason is that most of our analytical tools such as differential calculus are best
The Definition and Numerical Method of Final Value Problem and Arbitrary Value Problem Shixiong Wang 1*, Jianhua He 1, Chen Wang 2, Xitong Li 1
 The Definition and Numerical Method of Final Value Problem and Arbitrary Value Problem Shixiong Wang 1*, Jianhua He 1, Chen Wang 2, Xitong Li 1 1 School of Electronics and Information, Northwestern Polytechnical
The Definition and Numerical Method of Final Value Problem and Arbitrary Value Problem Shixiong Wang 1*, Jianhua He 1, Chen Wang 2, Xitong Li 1 1 School of Electronics and Information, Northwestern Polytechnical
Chapter 9 Implicit Methods for Linear and Nonlinear Systems of ODEs
 Chapter 9 Implicit Methods for Linear and Nonlinear Systems of ODEs In the previous chapter, we investigated stiffness in ODEs. Recall that an ODE is stiff if it exhibits behavior on widelyvarying timescales.
Chapter 9 Implicit Methods for Linear and Nonlinear Systems of ODEs In the previous chapter, we investigated stiffness in ODEs. Recall that an ODE is stiff if it exhibits behavior on widelyvarying timescales.
PowerPoints organized by Dr. Michael R. Gustafson II, Duke University
 Part 6 Chapter 20 Initial-Value Problems PowerPoints organized by Dr. Michael R. Gustafson II, Duke University All images copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Part 6 Chapter 20 Initial-Value Problems PowerPoints organized by Dr. Michael R. Gustafson II, Duke University All images copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Maps and differential equations
 Maps and differential equations Marc R. Roussel November 8, 2005 Maps are algebraic rules for computing the next state of dynamical systems in discrete time. Differential equations and maps have a number
Maps and differential equations Marc R. Roussel November 8, 2005 Maps are algebraic rules for computing the next state of dynamical systems in discrete time. Differential equations and maps have a number
PowerPoints organized by Dr. Michael R. Gustafson II, Duke University
 Part 6 Chapter 20 Initial-Value Problems PowerPoints organized by Dr. Michael R. Gustafson II, Duke University All images copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Part 6 Chapter 20 Initial-Value Problems PowerPoints organized by Dr. Michael R. Gustafson II, Duke University All images copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Elliptic Problems / Multigrid. PHY 604: Computational Methods for Physics and Astrophysics II
 Elliptic Problems / Multigrid Summary of Hyperbolic PDEs We looked at a simple linear and a nonlinear scalar hyperbolic PDE There is a speed associated with the change of the solution Explicit methods
Elliptic Problems / Multigrid Summary of Hyperbolic PDEs We looked at a simple linear and a nonlinear scalar hyperbolic PDE There is a speed associated with the change of the solution Explicit methods
Physics 202 Laboratory 3. Root-Finding 1. Laboratory 3. Physics 202 Laboratory
 Physics 202 Laboratory 3 Root-Finding 1 Laboratory 3 Physics 202 Laboratory The fundamental question answered by this week s lab work will be: Given a function F (x), find some/all of the values {x i }
Physics 202 Laboratory 3 Root-Finding 1 Laboratory 3 Physics 202 Laboratory The fundamental question answered by this week s lab work will be: Given a function F (x), find some/all of the values {x i }
16.1 Runge-Kutta Method
 704 Chapter 6. Integration of Ordinary Differential Equations CITED REFERENCES AND FURTHER READING: Gear, C.W. 97, Numerical Initial Value Problems in Ordinary Differential Equations (Englewood Cliffs,
704 Chapter 6. Integration of Ordinary Differential Equations CITED REFERENCES AND FURTHER READING: Gear, C.W. 97, Numerical Initial Value Problems in Ordinary Differential Equations (Englewood Cliffs,
Computational Astrophysics
 Computational Astrophysics Lecture 1: Introduction to numerical methods Lecture 2: The SPH formulation Lecture 3: Construction of SPH smoothing functions Lecture 4: SPH for general dynamic flow Lecture
Computational Astrophysics Lecture 1: Introduction to numerical methods Lecture 2: The SPH formulation Lecture 3: Construction of SPH smoothing functions Lecture 4: SPH for general dynamic flow Lecture
Definition of differential equations and their classification. Methods of solution of first-order differential equations
 Introduction to differential equations: overview Definition of differential equations and their classification Solutions of differential equations Initial value problems Existence and uniqueness Mathematical
Introduction to differential equations: overview Definition of differential equations and their classification Solutions of differential equations Initial value problems Existence and uniqueness Mathematical
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion
 Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 14, 2009) I. INTRODUCTION One frequently obtains detailed dynamical
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 14, 2009) I. INTRODUCTION One frequently obtains detailed dynamical
PH36010: Numerical Methods - Evaluating the Lorenz Attractor using Runge-Kutta methods Abstract
 PH36010: Numerical Methods - Evaluating the Lorenz Attractor using Runge-Kutta methods Mr. Benjamen P. Reed (110108461) IMPACS, Aberystwyth University January 31, 2014 Abstract A set of three coupled ordinary
PH36010: Numerical Methods - Evaluating the Lorenz Attractor using Runge-Kutta methods Mr. Benjamen P. Reed (110108461) IMPACS, Aberystwyth University January 31, 2014 Abstract A set of three coupled ordinary
SYSTEMS OF ODES. mg sin ( (x)) dx 2 =
 SYSTEMS OF ODES Consider the pendulum shown below. Assume the rod is of neglible mass, that the pendulum is of mass m, and that the rod is of length `. Assume the pendulum moves in the plane shown, and
SYSTEMS OF ODES Consider the pendulum shown below. Assume the rod is of neglible mass, that the pendulum is of mass m, and that the rod is of length `. Assume the pendulum moves in the plane shown, and
Ordinary Differential Equations II
 Ordinary Differential Equations II CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Ordinary Differential Equations II 1 / 33 Almost Done! Last
Ordinary Differential Equations II CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Justin Solomon CS 205A: Mathematical Methods Ordinary Differential Equations II 1 / 33 Almost Done! Last
Numerical solution of ODEs
 Numerical solution of ODEs Arne Morten Kvarving Department of Mathematical Sciences Norwegian University of Science and Technology November 5 2007 Problem and solution strategy We want to find an approximation
Numerical solution of ODEs Arne Morten Kvarving Department of Mathematical Sciences Norwegian University of Science and Technology November 5 2007 Problem and solution strategy We want to find an approximation
CHAPTER 7. An Introduction to Numerical Methods for. Linear and Nonlinear ODE s
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
Stars IV Stellar Evolution
 Stars IV Stellar Evolution Attendance Quiz Are you here today? Here! (a) yes (b) no (c) my views are evolving on the subject Today s Topics Stellar Evolution An alien visits Earth for a day A star s mass
Stars IV Stellar Evolution Attendance Quiz Are you here today? Here! (a) yes (b) no (c) my views are evolving on the subject Today s Topics Stellar Evolution An alien visits Earth for a day A star s mass
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion
 Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 17, 23) I. INTRODUCTION One frequently obtains detailed dynamical information
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 17, 23) I. INTRODUCTION One frequently obtains detailed dynamical information
Integration of Differential Equations
 Integration of Differential Equations Gabriel S. Cabrera August 4, 018 Contents 1 Introduction 1 Theory.1 Linear 1 st Order ODEs................................. 3.1.1 Analytical Solution...............................
Integration of Differential Equations Gabriel S. Cabrera August 4, 018 Contents 1 Introduction 1 Theory.1 Linear 1 st Order ODEs................................. 3.1.1 Analytical Solution...............................
Numerical Methods - Initial Value Problems for ODEs
 Numerical Methods - Initial Value Problems for ODEs Y. K. Goh Universiti Tunku Abdul Rahman 2013 Y. K. Goh (UTAR) Numerical Methods - Initial Value Problems for ODEs 2013 1 / 43 Outline 1 Initial Value
Numerical Methods - Initial Value Problems for ODEs Y. K. Goh Universiti Tunku Abdul Rahman 2013 Y. K. Goh (UTAR) Numerical Methods - Initial Value Problems for ODEs 2013 1 / 43 Outline 1 Initial Value
Lecture 9 Approximations of Laplace s Equation, Finite Element Method. Mathématiques appliquées (MATH0504-1) B. Dewals, C.
 Lecture 9 Approximations of Laplace s Equation, Finite Element Method Mathématiques appliquées (MATH54-1) B. Dewals, C. Geuzaine V1.2 23/11/218 1 Learning objectives of this lecture Apply the finite difference
Lecture 9 Approximations of Laplace s Equation, Finite Element Method Mathématiques appliquées (MATH54-1) B. Dewals, C. Geuzaine V1.2 23/11/218 1 Learning objectives of this lecture Apply the finite difference
Ordinary Differential Equations
 Ordinary Differential Equations We call Ordinary Differential Equation (ODE) of nth order in the variable x, a relation of the kind: where L is an operator. If it is a linear operator, we call the equation
Ordinary Differential Equations We call Ordinary Differential Equation (ODE) of nth order in the variable x, a relation of the kind: where L is an operator. If it is a linear operator, we call the equation
Chapter 5. Formulation of FEM for Unsteady Problems
 Chapter 5 Formulation of FEM for Unsteady Problems Two alternatives for formulating time dependent problems are called coupled space-time formulation and semi-discrete formulation. The first one treats
Chapter 5 Formulation of FEM for Unsteady Problems Two alternatives for formulating time dependent problems are called coupled space-time formulation and semi-discrete formulation. The first one treats
Review. Numerical Methods Lecture 22. Prof. Jinbo Bi CSE, UConn
 Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
Review Taylor Series and Error Analysis Roots of Equations Linear Algebraic Equations Optimization Numerical Differentiation and Integration Ordinary Differential Equations Partial Differential Equations
EXAMPLES OF PROOFS BY INDUCTION
 EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
EXAMPLES OF PROOFS BY INDUCTION KEITH CONRAD 1. Introduction In this handout we illustrate proofs by induction from several areas of mathematics: linear algebra, polynomial algebra, and calculus. Becoming
Outline - March 18, H-R Diagram Review. Protostar to Main Sequence Star. Midterm Exam #2 Tuesday, March 23
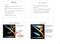 Midterm Exam #2 Tuesday, March 23 Outline - March 18, 2010 Closed book Will cover Lecture 8 (Special Relativity) through Lecture 14 (Star Formation) only If a topic is in the book, but was not covered
Midterm Exam #2 Tuesday, March 23 Outline - March 18, 2010 Closed book Will cover Lecture 8 (Special Relativity) through Lecture 14 (Star Formation) only If a topic is in the book, but was not covered
Getting Started with Communications Engineering
 1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
1 Linear algebra is the algebra of linear equations: the term linear being used in the same sense as in linear functions, such as: which is the equation of a straight line. y ax c (0.1) Of course, if we
NUMERICAL METHODS FOR ENGINEERING APPLICATION
 NUMERICAL METHODS FOR ENGINEERING APPLICATION Second Edition JOEL H. FERZIGER A Wiley-Interscience Publication JOHN WILEY & SONS, INC. New York / Chichester / Weinheim / Brisbane / Singapore / Toronto
NUMERICAL METHODS FOR ENGINEERING APPLICATION Second Edition JOEL H. FERZIGER A Wiley-Interscience Publication JOHN WILEY & SONS, INC. New York / Chichester / Weinheim / Brisbane / Singapore / Toronto
Lecture 4. Magic Numbers
 Lecture 4 In last lecture we discussed how one can solve the Schroedinger equation to determine the allowed energies of a particle trapped in a spherically symmetric potential. We will apply these methods
Lecture 4 In last lecture we discussed how one can solve the Schroedinger equation to determine the allowed energies of a particle trapped in a spherically symmetric potential. We will apply these methods
A First Course on Kinetics and Reaction Engineering Supplemental Unit S5. Solving Initial Value Differential Equations
 Supplemental Unit S5. Solving Initial Value Differential Equations Defining the Problem This supplemental unit describes how to solve a set of initial value ordinary differential equations (ODEs) numerically.
Supplemental Unit S5. Solving Initial Value Differential Equations Defining the Problem This supplemental unit describes how to solve a set of initial value ordinary differential equations (ODEs) numerically.
(f(x) P 3 (x)) dx. (a) The Lagrange formula for the error is given by
 1. QUESTION (a) Given a nth degree Taylor polynomial P n (x) of a function f(x), expanded about x = x 0, write down the Lagrange formula for the truncation error, carefully defining all its elements. How
1. QUESTION (a) Given a nth degree Taylor polynomial P n (x) of a function f(x), expanded about x = x 0, write down the Lagrange formula for the truncation error, carefully defining all its elements. How
NUMERICAL SOLUTION OF ODE IVPs. Overview
 NUMERICAL SOLUTION OF ODE IVPs 1 Quick review of direction fields Overview 2 A reminder about and 3 Important test: Is the ODE initial value problem? 4 Fundamental concepts: Euler s Method 5 Fundamental
NUMERICAL SOLUTION OF ODE IVPs 1 Quick review of direction fields Overview 2 A reminder about and 3 Important test: Is the ODE initial value problem? 4 Fundamental concepts: Euler s Method 5 Fundamental
Spiral Structure Formed in a Pair of Interacting Galaxies
 J. Astrophys. Astr. (1993) 14, 19 35 Spiral Structure Formed in a Pair of Interacting Galaxies Ch. L. Vozikis & Ν. D.Caranicolas Department of Physics, Section of Astrophysics, Astronomy and Mechanics,
J. Astrophys. Astr. (1993) 14, 19 35 Spiral Structure Formed in a Pair of Interacting Galaxies Ch. L. Vozikis & Ν. D.Caranicolas Department of Physics, Section of Astrophysics, Astronomy and Mechanics,
Numerical Methods for Ordinary Differential Equations
 Numerical Methods for Ordinary Differential Equations By Brian D. Storey 1. Introduction Differential equations can describe nearly all systems undergoing change. They are ubiquitous is science and engineering
Numerical Methods for Ordinary Differential Equations By Brian D. Storey 1. Introduction Differential equations can describe nearly all systems undergoing change. They are ubiquitous is science and engineering
CHAPTER 4. Basics of Fluid Dynamics
 CHAPTER 4 Basics of Fluid Dynamics What is a fluid? A fluid is a substance that can flow, has no fixed shape, and offers little resistance to an external stress In a fluid the constituent particles (atoms,
CHAPTER 4 Basics of Fluid Dynamics What is a fluid? A fluid is a substance that can flow, has no fixed shape, and offers little resistance to an external stress In a fluid the constituent particles (atoms,
3.4 Numerical orbit integration
 196 Chapter 3: The Orbits of Stars about the center of the galaxy. For small-amplitude librations, the libration frequency is p, consistent with our assumption that the oscillation frequency is of order
196 Chapter 3: The Orbits of Stars about the center of the galaxy. For small-amplitude librations, the libration frequency is p, consistent with our assumption that the oscillation frequency is of order
Efficient solution of stationary Euler flows with critical points and shocks
 Efficient solution of stationary Euler flows with critical points and shocks Hans De Sterck Department of Applied Mathematics University of Waterloo 1. Introduction consider stationary solutions of hyperbolic
Efficient solution of stationary Euler flows with critical points and shocks Hans De Sterck Department of Applied Mathematics University of Waterloo 1. Introduction consider stationary solutions of hyperbolic
NUMERICAL METHODS IN ASTROPHYSICS An Introduction
 -1 Series in Astronomy and Astrophysics NUMERICAL METHODS IN ASTROPHYSICS An Introduction Peter Bodenheimer University of California Santa Cruz, USA Gregory P. Laughlin University of California Santa Cruz,
-1 Series in Astronomy and Astrophysics NUMERICAL METHODS IN ASTROPHYSICS An Introduction Peter Bodenheimer University of California Santa Cruz, USA Gregory P. Laughlin University of California Santa Cruz,
Differential Equations
 This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
This document was written and copyrighted by Paul Dawkins. Use of this document and its online version is governed by the Terms and Conditions of Use located at. The online version of this document is
3 Hydrostatic Equilibrium
 3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
2. Equations of Stellar Structure
 2. Equations of Stellar Structure We already discussed that the structure of stars is basically governed by three simple laws, namely hyostatic equilibrium, energy transport and energy generation. In this
2. Equations of Stellar Structure We already discussed that the structure of stars is basically governed by three simple laws, namely hyostatic equilibrium, energy transport and energy generation. In this
Physics 115/242 Romberg Integration
 Physics 5/242 Romberg Integration Peter Young In this handout we will see how, starting from the trapezium rule, we can obtain much more accurate values for the integral by repeatedly eliminating the leading
Physics 5/242 Romberg Integration Peter Young In this handout we will see how, starting from the trapezium rule, we can obtain much more accurate values for the integral by repeatedly eliminating the leading
