Gassner Representation of the Pure Braid Group P 4
|
|
|
- Griselda Henderson
- 5 years ago
- Views:
Transcription
1 International Journal of Algebra, Vol. 3, 2009, no. 16, Gassner Representation of the Pure Braid Group P 4 Mohammad N. Abdulrahim Department of Mathematics Beirut Arab University P.O. Box , Beirut, Lebanon mna@bau.edu.lb Abstract. The reduced Gassner representation is a multi-parameter representation of P n, the pure braid group on n strings. Specializing the parameters t 1,t 2,...,t n to nonzero complex numbers z 1,z 2,...,z n gives a representation G n (z 1,...,z n ) : P n GL(C n 1 ) = GL n 1 (C). It was proved that the representation is irreducible if and only if z 1...z n 1. In our work, we consider the case n = 4 and we determine the composition factors of G 4 (z 1,...,z 4 ) when it is reducible. Our main theorem shows that the reduced Gassner representation G 4 (z 1,...,z 4 ) of degree three is either a direct sum of one-dimensional representations or it has a composition factor of degree 2, namely, Ĝ4(z 1,...,z 4 ), which is an extension of the irreducible representation G 3 (z 1,z 2,z 3 ) to P 4. Mathematics Subject Classification: Primary: 20F36 Keywords: braid group, pure braid group, Gassner representation 1. Introduction. The pure braid group, P n, is a normal subgroup of the braid group, B n, on n strings. It has a lot of linear representations. One of them is the Gassner representation which comes from the embedding P n Aut(F n ), by means of Magnus representation [2, p.119]. According to Artin, the automorphism corresponding to the braid generator σ i takes x i to x i x i+1 x 1 i,x i+1 to x i, and fixes all other free generators. Applying this standard Artin representation to the generator of the pure braid group, we get a representation of the pure braid group by automorphisms. Such a representation has a composition factor, the reduced Gassner representation G n (t 1,...,t n ) : P n GL n 1 (Z[t ±1 1,...,t ±1 n ]), where t 1,...,t n are indeterminates. Unlike the Burau representation of the braid group, B n, that also arises as a
2 794 M. N. Abdulrahim subgroup of the automorphism group of a free group with n generators, there is no explicit representation which is agreed to be the reduced Gassner representation of the pure braid group. In our work, we define the reduced Gassner representation up to equivalence. Specializing the indeterminates t 1,...,t n to nonzero complex numbers z 1,...,z n, we get a representation G n (z 1,...,z n ) : P n GL n 1 (C) = GL(C n 1 ) which is irreducible if and only if z 1...z n 1 (see [1]). It was shown that the reduced Burau representation β n (z) :B n GL n 1 (C) is either irreducible or it has a composition factor of degree n 2 that is irreducible. The composition factor is β n (z) :B n GL n 2 (C) =GL(C n 2 ) where β n (z) B n 1 = β n 1 (z). In our work, we get a similar result concerning the pure braid group on 4 strings. We consider the representation G 4 (z 1,...,z 4 ):P 4 GL 3 (C) =GL(C 3 ) and we describe the composition factors of G 4 (z 1,...,z 4 ) when it is reducible. In section two, we present the reduced Gassner representation of P 4 by choosing a free generating set with n generators to be our basis and by applying the Magnus representation as was suggested by J. Birman in [2]. In section three, we diagonalize the matrix corresponding to some element in P 4 by an invertible matrix, say T, and conjugate the reduced Gassner representation of P 4 by the same matrix T. Diagonalizing one of the matrices means that the eigen vectors of this diagonal matrix are the standard unit vectors in C 3 or a linear combination of some of them in case of equal eigenvalues. Our objective is to look for invariant subspaces, if exist. Then we present our main theorem that shows that if G 4 (z 1,...,z 4 ):P 4 GL 3 (C) =GL(C 3 ) is reducible then either the representation is a direct sum of one-dimensional representations or its composition factor Ĝ4(z 1,...,z 4 ):P 4 GL 2 (C) =GL(C 2 )isan extension of the (irreducible) reduced Gasssner representation G 3 (z 1,...,z 3 ) to P Definitions Definition 1. The braid group on n strings, B n, is an abstract group which has a presentation with generators: and defining relations : σ 1,...,σ n 1 σ i σ i+1 σ i = σ i+1 σ i σ i+1, for i =1, 2,..., n 2 σ i σ j = σ j σ i if i j 2 The generators σ 1,...,σ n 1 are called the standard generators of B n. Let t be an indeterminate and C[t ±1 ] represent the Laurent polynomial ring over complex numbers. Definition 2. The pure braid group, P n, is defined as the kernel of the homomorphism B n S n, defined by σ i (i, i +1), 1 i n 1. It has the
3 Gassner representation 795 following generators: A i,j = σ j 1 σ j 2...σ i+1 σ i 2 σ 1 i+1...σ 1 j 2 σ 1 j 1, 1 i<j n We will construct for each j =1,...,n a free normal subgroup of rank n 1, namely, U j. Let U j be the subgroup generated by the elements A 1,j,A 2,j,...,A j 1,j,A j,j+1,...,a j,n, where A i,j are those generators of P n. In other words, the generators of U j are A i,j where A i,j = A j,i whenever i>jand j =1, 2,...,n. It is known that U j generates a free subgroup of P n which is isomorphic to the subgroup U n freely generated by {A 1,n,A 2,n,...,A n 1,n }. This is intuitively clear because it is quite arbitrary how we assign indices to the braid strings. We will follow the idea suggested by J. Birman to define our reduced Gassner representation of the pure braid group. Let F 4 be the free group of rank 4, with free basis x 1,...,x 4. In F 4, we introduce the free generating set g 1,...,g 4 with g i = x 1...x i. The Jacobian matrix is defined as follows: D 1 (A i,j (g 1 ))... D 4 (A i,j (g 1 )) J(A i,j )=.. D 1 (A i,j (g 4 ))... D 4 (A i,j (g 4 )) where D j = φd j. Here d j is the Fox derivative defined in [2] and φ(g i )= t 1...t i. The action of the braid generator σ i on the basis {g 1,...,g 4 } is defined as follows: g k g k, k i σ i : g i g i+1 g i 1 g i 1, i 1 g 1 g 2 g 1 1, i =1 Under the action of the pure braid generators on the basis {g 1,g 2,g 3,g 4 }, we determine the Gassner representation of P 4. Having done this, we observe that the last row of these 4 4 matrices is (0, 0, 0, 1). Hence the last row and column may be deleted to obtain a 3 3 representation of P 4 and is denoted by G 4 (t 1,...,t 4 ). Definition 3. The reduced Gassner representation G 4 (t 1,...,t 4 ): P 4 GL 3 (Z[t 1 ±1,...,t n ±1 ]) is given by A 1,2 = t 1t 2 1 t A 1,3 = t 3 t 3 (t 1 1) 1 t 1 t 3 1 t 3 + t 1 t t 1
4 796 M. N. Abdulrahim A 2,3 = t 2 (1 t 3 ) t 2 t 3 1 t 2 A 1,4 = t 4 0 t 4 (t 1 1) t t 4 (t 1 1) t t 4 + t 1 t 4 +1 A 2,4 = t 2 (1 t 4 ) t 4 t 4 (t 2 1) t 2 (1 t 4 ) t 4 1 t 4 + t 2 t 4 +1 A 3,4 = t 3 (1 t 4 ) t 3 t 4 Here A i,j means G 4 (t 1,...,t 4 )(A i,j ). For simplicity, we still denote the matrix for A i,j by A i,j. 3. Composition Factors of G 4 (z 1,...,z 4 ) Specialize the indeterminates t 1,t 2,t 3 and t 4 to nonzero complex numbers a, b, c and d respectively. For z =(a, b, c, d) (C ) 4, it was proved in [1] that the complex specialization of the reduced Gassner representation of P 4, namely, G 4 (z) :P 4 GL 3 (C) is irreducible if and only if abcd 1. Now, we suppose that G 4 (z) is reducible and abcd = 1. Our main work is to determine the composition factors of the reducible representation. Theorem 1. Let G 4 (z) :P 4 GL 3 (C) =GL(C 3 ) be the complex specialization of the reduced Gassner representation. Let z =(a, b, c, d) (C ) 4 and abcd =1. (i) If a = 1 or d = 1 then G 4 (a,...,d) is the direct sum of onedimensional representations. (ii) If a 1 and d 1 then the irreducible representation G 3 (a, b, c) : P 3 GL 2 (C) =GL(C 2 ) extends to a ( necessarily irreducible) representation Ĝ 4 (a,...,d):p 4 GL 2 (C) =GL(C 2 ). Proof. (i) Let a =1. Under the assumption that abcd = 1, we get that bcd = 1. Making this substitution in Definition 3, we obtain a 3 3 representation of P 4 where the (1, 2) and (1, 3) entries of each of the matrices are zeros. Therefore, we may delete the first row and the first column to obtain a 2 2 representation. This is true because the subspace generated by e 2 and e 3 is invariant. Here, we regard M 3 (C) as acting from the left on column vectors and acting from right on row vectors. The 2 2 representation is reduced further to one-dimensional representations since the subspace generated by the column vector (1 b, 1 bc) is invariant and the subspace generated by the row vector (1 bc, b 1) is also invariant. Thus, by Theorem 4 of [1], Ĝ 4 (a,...,d):p 4 GL 2 (C) =GL(C 2 ) is the direct sum of one-dimensional representations. Let d =1. As above, we have that abc = 1. After substitution in Definition 3, we get 3 3 matrices whose (3, 1) and (3, 2) entries are zeros. The subspace
5 Gassner representation 797 generated by e 1 and e 2 is invariant and we may delete the last row and the last column to obtain a 2 2 representation. Again, the subspace generated by the column vector (1 a, 1 ab) and the subspace generated by the row vector (1 ab, a 1) are invariant under the 2 2 representation. Therefore, Ĝ 4 (a,...,d):p 4 GL 2 (C) =GL(C 2 ) is the direct sum of one-dimensional representations. (ii) Let d 1, and a 1. We diagonalize the matrix that corresponds to the pure braid A 1,4 A 1,3 A 1,2 by a matrix T. The diagonal form becomes A 1,4 A 1,3 A 1,2 = a a abcd Since abcd = 1 and a 1, it follows that any non-zero invariant subspace of all the matrices of P 4 should contain at least one of e 3 or ue 1 + ve 2, where (u, v) (0, 0). The conjugating matrix T is 0 0 bc(d 1) T = cd c(d 1) We observe that det(t )= 1 bcd bc(d 1) = a 1 0. Now we conjugate abc(d 1) the reduced Gassner representation, G 4 (a,...,d), by the invertible matrix T to get an equivalent representation of degree 3. The matrices are T 1 A 1,2 T = 1 abc ab 0 0 bc(a 1)(d 1) bcd(1 a) T 1 A 1,3 T = abc c(1 abc) 0 a(b 1) 1 + ac abc 0 bc 2 (a 1)(d 1) bc(a 1)(d 1) T 1 A 2,3 T = b bc 0 bcd(1 a)
6 798 M. N. Abdulrahim T 1 A 1,4 T = ad 0 0 ad(1 b) 1 0 bcd(a 1)(d 1) 0 bcd(1 a) T 1 A 2,4 T = 1 d + bd d 1 0 (b 1)d d 0 and T 1 A 3,4 T = cd c(d 1) We observe that the subspace generated by the eigenvector e 3 =(0, 0, 1) is invariant under this representation. This is due to the fact that the (1, 3) and (2, 3) entries in all of the matrices are zeros. Here, we used the hypothesis that abcd = 1. Therefore, we may delete the last row and the last column to obtain a2 2 representation of P 4. On the other hand, we consider the complex specialization of the Gassner representation P 3 GL 3 (C) =GL(C 3 ), which is obtained by having the generators of P 3 act on the basis g 1,g 2,g 3 and applying the Magnus representation. Then we conjugate the representation by the invertible matrix T, defined above. We observe that the (1, 3) and (2, 3) entries of all the matrices are zeros. Therefore, we may delete the last row and column to obtain a 2 2 representation which is exactly the same representation as Ĝ4(a,...,d) restricted to the subgroup P 3. Since abcd = 1 and d 1, it follows that abc 1 which implies the irreducibility of the 2 2 matrix representation of P 3 (see [1]). As a result, the irreducibility on P 4 follows. References [1] M. Abdulrahim,Complex Specializations of the reduced Gassner Representation of the Pure Braid Group, Proc of AMS 125 (no.6) (1997), [2] J. S. Birman, Braids, Links and Mapping Class Groups, Annals of Mathematical Studies 82, Princeton University Press, New Jersey ( 1975). [3] E. Formanek, Braid group representations of low degree, Proc. London Math. Soc. 73 (1996), Received: February, 2009
Pure Braid Group Representations of Low Degree
 International Journal of Algebra, Vol 5, 2011, no 21, 1011-1020 Pure Braid Group Representations of Low Degree Mohammad N Abdulrahim and Ghenwa H Abboud Department of Mathematics Beirut Arab University
International Journal of Algebra, Vol 5, 2011, no 21, 1011-1020 Pure Braid Group Representations of Low Degree Mohammad N Abdulrahim and Ghenwa H Abboud Department of Mathematics Beirut Arab University
On the Irreducibility of Perron Representations of Degrees 4 and 5
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. No. 28 25-237 ISSN 37-5543 www.ejpam.com Published by New York Business Global On the Irreducibility of Perron Representations of Degrees 4 and 5 Malak
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. No. 28 25-237 ISSN 37-5543 www.ejpam.com Published by New York Business Global On the Irreducibility of Perron Representations of Degrees 4 and 5 Malak
Research Article Another Proof of the Faithfulness of the Lawrence-Krammer Representation of the Braid Group B 3
 International Scholarly Research Network ISRN Algebra Volume 01, Article ID 858959, 13 pages doi:10.540/01/858959 Research Article Another Proof of the Faithfulness of the Lawrence-Krammer Representation
International Scholarly Research Network ISRN Algebra Volume 01, Article ID 858959, 13 pages doi:10.540/01/858959 Research Article Another Proof of the Faithfulness of the Lawrence-Krammer Representation
arxiv: v1 [math.ra] 10 Nov 2018
![arxiv: v1 [math.ra] 10 Nov 2018 arxiv: v1 [math.ra] 10 Nov 2018](/thumbs/94/121048279.jpg) arxiv:1811.04243v1 [math.ra] 10 Nov 2018 BURNSIDE S THEOREM IN THE SETTING OF GENERAL FIELDS HEYDAR RADJAVI AND BAMDAD R. YAHAGHI Abstract. We extend a well-known theorem of Burnside in the setting of
arxiv:1811.04243v1 [math.ra] 10 Nov 2018 BURNSIDE S THEOREM IN THE SETTING OF GENERAL FIELDS HEYDAR RADJAVI AND BAMDAD R. YAHAGHI Abstract. We extend a well-known theorem of Burnside in the setting of
Solutions of exercise sheet 8
 D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 8 1. In this exercise, we will give a characterization for solvable groups using commutator subgroups. See last semester s (Algebra
D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 8 1. In this exercise, we will give a characterization for solvable groups using commutator subgroups. See last semester s (Algebra
18.S34 linear algebra problems (2007)
 18.S34 linear algebra problems (2007) Useful ideas for evaluating determinants 1. Row reduction, expanding by minors, or combinations thereof; sometimes these are useful in combination with an induction
18.S34 linear algebra problems (2007) Useful ideas for evaluating determinants 1. Row reduction, expanding by minors, or combinations thereof; sometimes these are useful in combination with an induction
GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory.
 GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory. Linear Algebra Standard matrix manipulation to compute the kernel, intersection of subspaces, column spaces,
GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory. Linear Algebra Standard matrix manipulation to compute the kernel, intersection of subspaces, column spaces,
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Group Theory. 1. Show that Φ maps a conjugacy class of G into a conjugacy class of G.
 Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
Practice Algebra Qualifying Exam Solutions
 Practice Algebra Qualifying Exam Solutions 1. Let A be an n n matrix with complex coefficients. Define tr A to be the sum of the diagonal elements. Show that tr A is invariant under conjugation, i.e.,
Practice Algebra Qualifying Exam Solutions 1. Let A be an n n matrix with complex coefficients. Define tr A to be the sum of the diagonal elements. Show that tr A is invariant under conjugation, i.e.,
(a) II and III (b) I (c) I and III (d) I and II and III (e) None are true.
 1 Which of the following statements is always true? I The null space of an m n matrix is a subspace of R m II If the set B = {v 1,, v n } spans a vector space V and dimv = n, then B is a basis for V III
1 Which of the following statements is always true? I The null space of an m n matrix is a subspace of R m II If the set B = {v 1,, v n } spans a vector space V and dimv = n, then B is a basis for V III
18.312: Algebraic Combinatorics Lionel Levine. Lecture 22. Smith normal form of an integer matrix (linear algebra over Z).
 18.312: Algebraic Combinatorics Lionel Levine Lecture date: May 3, 2011 Lecture 22 Notes by: Lou Odette This lecture: Smith normal form of an integer matrix (linear algebra over Z). 1 Review of Abelian
18.312: Algebraic Combinatorics Lionel Levine Lecture date: May 3, 2011 Lecture 22 Notes by: Lou Odette This lecture: Smith normal form of an integer matrix (linear algebra over Z). 1 Review of Abelian
CSL361 Problem set 4: Basic linear algebra
 CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA
 ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
235 Final exam review questions
 5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
January 2016 Qualifying Examination
 January 2016 Qualifying Examination If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems, in principle,
January 2016 Qualifying Examination If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems, in principle,
Introduction to Matrix Algebra
 Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
Homework 5 M 373K Mark Lindberg and Travis Schedler
 Homework 5 M 373K Mark Lindberg and Travis Schedler 1. Artin, Chapter 3, Exercise.1. Prove that the numbers of the form a + b, where a and b are rational numbers, form a subfield of C. Let F be the numbers
Homework 5 M 373K Mark Lindberg and Travis Schedler 1. Artin, Chapter 3, Exercise.1. Prove that the numbers of the form a + b, where a and b are rational numbers, form a subfield of C. Let F be the numbers
Remark By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Solutions to Final Exam
 Solutions to Final Exam. Let A be a 3 5 matrix. Let b be a nonzero 5-vector. Assume that the nullity of A is. (a) What is the rank of A? 3 (b) Are the rows of A linearly independent? (c) Are the columns
Solutions to Final Exam. Let A be a 3 5 matrix. Let b be a nonzero 5-vector. Assume that the nullity of A is. (a) What is the rank of A? 3 (b) Are the rows of A linearly independent? (c) Are the columns
arxiv:math/ v1 [math.gt] 27 Oct 2000
![arxiv:math/ v1 [math.gt] 27 Oct 2000 arxiv:math/ v1 [math.gt] 27 Oct 2000](/thumbs/88/115451538.jpg) arxiv:math/0010267v1 [math.gt] 27 Oct 2000 ON THE LINEARITY OF CERTAIN MAPPING CLASS GROUPS MUSTAFA KORKMAZ Abstract. S. Bigelow proved that the braid groups are linear. That is, there is a faithful representation
arxiv:math/0010267v1 [math.gt] 27 Oct 2000 ON THE LINEARITY OF CERTAIN MAPPING CLASS GROUPS MUSTAFA KORKMAZ Abstract. S. Bigelow proved that the braid groups are linear. That is, there is a faithful representation
Dimension. Eigenvalue and eigenvector
 Dimension. Eigenvalue and eigenvector Math 112, week 9 Goals: Bases, dimension, rank-nullity theorem. Eigenvalue and eigenvector. Suggested Textbook Readings: Sections 4.5, 4.6, 5.1, 5.2 Week 9: Dimension,
Dimension. Eigenvalue and eigenvector Math 112, week 9 Goals: Bases, dimension, rank-nullity theorem. Eigenvalue and eigenvector. Suggested Textbook Readings: Sections 4.5, 4.6, 5.1, 5.2 Week 9: Dimension,
MATRIX LIE GROUPS AND LIE GROUPS
 MATRIX LIE GROUPS AND LIE GROUPS Steven Sy December 7, 2005 I MATRIX LIE GROUPS Definition: A matrix Lie group is a closed subgroup of Thus if is any sequence of matrices in, and for some, then either
MATRIX LIE GROUPS AND LIE GROUPS Steven Sy December 7, 2005 I MATRIX LIE GROUPS Definition: A matrix Lie group is a closed subgroup of Thus if is any sequence of matrices in, and for some, then either
Practice Final Exam Solutions
 MAT 242 CLASS 90205 FALL 206 Practice Final Exam Solutions The final exam will be cumulative However, the following problems are only from the material covered since the second exam For the material prior
MAT 242 CLASS 90205 FALL 206 Practice Final Exam Solutions The final exam will be cumulative However, the following problems are only from the material covered since the second exam For the material prior
Algebra Exam Syllabus
 Algebra Exam Syllabus The Algebra comprehensive exam covers four broad areas of algebra: (1) Groups; (2) Rings; (3) Modules; and (4) Linear Algebra. These topics are all covered in the first semester graduate
Algebra Exam Syllabus The Algebra comprehensive exam covers four broad areas of algebra: (1) Groups; (2) Rings; (3) Modules; and (4) Linear Algebra. These topics are all covered in the first semester graduate
Q N id β. 2. Let I and J be ideals in a commutative ring A. Give a simple description of
 Additional Problems 1. Let A be a commutative ring and let 0 M α N β P 0 be a short exact sequence of A-modules. Let Q be an A-module. i) Show that the naturally induced sequence is exact, but that 0 Hom(P,
Additional Problems 1. Let A be a commutative ring and let 0 M α N β P 0 be a short exact sequence of A-modules. Let Q be an A-module. i) Show that the naturally induced sequence is exact, but that 0 Hom(P,
Problem Set (T) If A is an m n matrix, B is an n p matrix and D is a p s matrix, then show
 MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Representations and Linear Actions
 Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
A PRIMER ON SESQUILINEAR FORMS
 A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
A PRIMER ON SESQUILINEAR FORMS BRIAN OSSERMAN This is an alternative presentation of most of the material from 8., 8.2, 8.3, 8.4, 8.5 and 8.8 of Artin s book. Any terminology (such as sesquilinear form
Again we return to a row of 1 s! Furthermore, all the entries are positive integers.
 Lecture Notes Introduction to Cluster Algebra Ivan C.H. Ip Updated: April 4, 207 Examples. Conway-Coxeter frieze pattern Frieze is the wide central section part of an entablature, often seen in Greek temples,
Lecture Notes Introduction to Cluster Algebra Ivan C.H. Ip Updated: April 4, 207 Examples. Conway-Coxeter frieze pattern Frieze is the wide central section part of an entablature, often seen in Greek temples,
Representations. 1 Basic definitions
 Representations 1 Basic definitions If V is a k-vector space, we denote by Aut V the group of k-linear isomorphisms F : V V and by End V the k-vector space of k-linear maps F : V V. Thus, if V = k n, then
Representations 1 Basic definitions If V is a k-vector space, we denote by Aut V the group of k-linear isomorphisms F : V V and by End V the k-vector space of k-linear maps F : V V. Thus, if V = k n, then
Problem 1.1. Classify all groups of order 385 up to isomorphism.
 Math 504: Modern Algebra, Fall Quarter 2017 Jarod Alper Midterm Solutions Problem 1.1. Classify all groups of order 385 up to isomorphism. Solution: Let G be a group of order 385. Factor 385 as 385 = 5
Math 504: Modern Algebra, Fall Quarter 2017 Jarod Alper Midterm Solutions Problem 1.1. Classify all groups of order 385 up to isomorphism. Solution: Let G be a group of order 385. Factor 385 as 385 = 5
UNIVERSAL IDENTITIES. b = det
 UNIVERSAL IDENTITIES KEITH CONRAD 1 Introduction We want to describe an idea which reduces the verification of algebraic identities valid over all commutative rings to the verification over the complex
UNIVERSAL IDENTITIES KEITH CONRAD 1 Introduction We want to describe an idea which reduces the verification of algebraic identities valid over all commutative rings to the verification over the complex
Math 594. Solutions 5
 Math 594. Solutions 5 Book problems 6.1: 7. Prove that subgroups and quotient groups of nilpotent groups are nilpotent (your proof should work for infinite groups). Give an example of a group G which possesses
Math 594. Solutions 5 Book problems 6.1: 7. Prove that subgroups and quotient groups of nilpotent groups are nilpotent (your proof should work for infinite groups). Give an example of a group G which possesses
Problems in Linear Algebra and Representation Theory
 Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Math 396. An application of Gram-Schmidt to prove connectedness
 Math 396. An application of Gram-Schmidt to prove connectedness 1. Motivation and background Let V be an n-dimensional vector space over R, and define GL(V ) to be the set of invertible linear maps V V
Math 396. An application of Gram-Schmidt to prove connectedness 1. Motivation and background Let V be an n-dimensional vector space over R, and define GL(V ) to be the set of invertible linear maps V V
On the Rothenberg Steenrod spectral sequence for the mod 3 cohomology of the classifying space of the exceptional Lie group E 8
 213 226 213 arxiv version: fonts, pagination and layout may vary from GTM published version On the Rothenberg Steenrod spectral sequence for the mod 3 cohomology of the classifying space of the exceptional
213 226 213 arxiv version: fonts, pagination and layout may vary from GTM published version On the Rothenberg Steenrod spectral sequence for the mod 3 cohomology of the classifying space of the exceptional
Remark 1 By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
MATH 240 Spring, Chapter 1: Linear Equations and Matrices
 MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
Topics in linear algebra
 Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld.
![ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld. ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld.](/thumbs/90/104374286.jpg) ENTRY GROUP THEORY [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld Group theory [Group theory] is studies algebraic objects called groups.
ENTRY GROUP THEORY [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld Group theory [Group theory] is studies algebraic objects called groups.
Braid Groups, Hecke Algebras, Representations, and Anyons
 Braid Groups, Hecke Algebras, Representations, and Anyons Andreas Blass University of Michigan Ann Arbor, MI 4809 ablass@umich.edu Joint work with Yuri Gurevich 9 November, 206 Anyons Anyons are particle-like
Braid Groups, Hecke Algebras, Representations, and Anyons Andreas Blass University of Michigan Ann Arbor, MI 4809 ablass@umich.edu Joint work with Yuri Gurevich 9 November, 206 Anyons Anyons are particle-like
Linear Algebra Review
 Chapter 1 Linear Algebra Review It is assumed that you have had a beginning course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc I will review some of these terms here,
Chapter 1 Linear Algebra Review It is assumed that you have had a beginning course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc I will review some of these terms here,
IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1
 IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1 Let Σ be the set of all symmetries of the plane Π. 1. Give examples of s, t Σ such that st ts. 2. If s, t Σ agree on three non-collinear points, then
IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1 Let Σ be the set of all symmetries of the plane Π. 1. Give examples of s, t Σ such that st ts. 2. If s, t Σ agree on three non-collinear points, then
Math 1060 Linear Algebra Homework Exercises 1 1. Find the complete solutions (if any!) to each of the following systems of simultaneous equations:
 Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
Di-eigenals. Jennifer Galovich St. John s University/College of St. Benedict JMM 11 January, 2018
 Di-eigenals Jennifer Galovich St. John s University/College of St. Benedict JMM 11 January, 2018 Geometric Interpretation of Eigenvalues in R 2 Suppose M = It is easy to check that the eigenvalues of M
Di-eigenals Jennifer Galovich St. John s University/College of St. Benedict JMM 11 January, 2018 Geometric Interpretation of Eigenvalues in R 2 Suppose M = It is easy to check that the eigenvalues of M
Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop. Eric Sommers
 Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop Eric Sommers 17 July 2009 2 Contents 1 Background 5 1.1 Linear algebra......................................... 5 1.1.1
Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop Eric Sommers 17 July 2009 2 Contents 1 Background 5 1.1 Linear algebra......................................... 5 1.1.1
Linear Algebra Review
 Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Math 215 HW #9 Solutions
 Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
ALGORITHMS FOR COMPUTING QUARTIC GALOIS GROUPS OVER FIELDS OF CHARACTERISTIC 0
 ALGORITHMS FOR COMPUTING QUARTIC GALOIS GROUPS OVER FIELDS OF CHARACTERISTIC 0 CHAD AWTREY, JAMES BEUERLE, AND MICHAEL KEENAN Abstract. Let f(x) beanirreducibledegreefourpolynomialdefinedover afieldf and
ALGORITHMS FOR COMPUTING QUARTIC GALOIS GROUPS OVER FIELDS OF CHARACTERISTIC 0 CHAD AWTREY, JAMES BEUERLE, AND MICHAEL KEENAN Abstract. Let f(x) beanirreducibledegreefourpolynomialdefinedover afieldf and
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T. KEMP)
 MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
REPRESENTATION THEORY WEEK 5. B : V V k
 REPRESENTATION THEORY WEEK 5 1. Invariant forms Recall that a bilinear form on a vector space V is a map satisfying B : V V k B (cv, dw) = cdb (v, w), B (v 1 + v, w) = B (v 1, w)+b (v, w), B (v, w 1 +
REPRESENTATION THEORY WEEK 5 1. Invariant forms Recall that a bilinear form on a vector space V is a map satisfying B : V V k B (cv, dw) = cdb (v, w), B (v 1 + v, w) = B (v 1, w)+b (v, w), B (v, w 1 +
NONCOMMUTATIVE POLYNOMIAL EQUATIONS. Edward S. Letzter. Introduction
 NONCOMMUTATIVE POLYNOMIAL EQUATIONS Edward S Letzter Introduction My aim in these notes is twofold: First, to briefly review some linear algebra Second, to provide you with some new tools and techniques
NONCOMMUTATIVE POLYNOMIAL EQUATIONS Edward S Letzter Introduction My aim in these notes is twofold: First, to briefly review some linear algebra Second, to provide you with some new tools and techniques
Kac-Moody Algebras. Ana Ros Camacho June 28, 2010
 Kac-Moody Algebras Ana Ros Camacho June 28, 2010 Abstract Talk for the seminar on Cohomology of Lie algebras, under the supervision of J-Prof. Christoph Wockel Contents 1 Motivation 1 2 Prerequisites 1
Kac-Moody Algebras Ana Ros Camacho June 28, 2010 Abstract Talk for the seminar on Cohomology of Lie algebras, under the supervision of J-Prof. Christoph Wockel Contents 1 Motivation 1 2 Prerequisites 1
Spectrally arbitrary star sign patterns
 Linear Algebra and its Applications 400 (2005) 99 119 wwwelseviercom/locate/laa Spectrally arbitrary star sign patterns G MacGillivray, RM Tifenbach, P van den Driessche Department of Mathematics and Statistics,
Linear Algebra and its Applications 400 (2005) 99 119 wwwelseviercom/locate/laa Spectrally arbitrary star sign patterns G MacGillivray, RM Tifenbach, P van den Driessche Department of Mathematics and Statistics,
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES
 MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
Part IV. Rings and Fields
 IV.18 Rings and Fields 1 Part IV. Rings and Fields Section IV.18. Rings and Fields Note. Roughly put, modern algebra deals with three types of structures: groups, rings, and fields. In this section we
IV.18 Rings and Fields 1 Part IV. Rings and Fields Section IV.18. Rings and Fields Note. Roughly put, modern algebra deals with three types of structures: groups, rings, and fields. In this section we
Mirror Reflections on Braids and the Higher Homotopy Groups of the 2-sphere
 Mirror Reflections on Braids and the Higher Homotopy Groups of the 2-sphere A gift to Professor Jiang Bo Jü Jie Wu Department of Mathematics National University of Singapore www.math.nus.edu.sg/ matwujie
Mirror Reflections on Braids and the Higher Homotopy Groups of the 2-sphere A gift to Professor Jiang Bo Jü Jie Wu Department of Mathematics National University of Singapore www.math.nus.edu.sg/ matwujie
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 2011
 UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
UNIVERSITY OF MICHIGAN UNDERGRADUATE MATH COMPETITION 28 APRIL 7, 20 Instructions. Write on the front of your blue book your student ID number. Do not write your name anywhere on your blue book. Each question
Math 121 Homework 5: Notes on Selected Problems
 Math 121 Homework 5: Notes on Selected Problems 12.1.2. Let M be a module over the integral domain R. (a) Assume that M has rank n and that x 1,..., x n is any maximal set of linearly independent elements
Math 121 Homework 5: Notes on Selected Problems 12.1.2. Let M be a module over the integral domain R. (a) Assume that M has rank n and that x 1,..., x n is any maximal set of linearly independent elements
Abstract Algebra Study Sheet
 Abstract Algebra Study Sheet This study sheet should serve as a guide to which sections of Artin will be most relevant to the final exam. When you study, you may find it productive to prioritize the definitions,
Abstract Algebra Study Sheet This study sheet should serve as a guide to which sections of Artin will be most relevant to the final exam. When you study, you may find it productive to prioritize the definitions,
Eigenvalues and Eigenvectors
 Eigenvalues and Eigenvectors Definition 0 Let A R n n be an n n real matrix A number λ R is a real eigenvalue of A if there exists a nonzero vector v R n such that A v = λ v The vector v is called an eigenvector
Eigenvalues and Eigenvectors Definition 0 Let A R n n be an n n real matrix A number λ R is a real eigenvalue of A if there exists a nonzero vector v R n such that A v = λ v The vector v is called an eigenvector
Noetherian property of infinite EI categories
 Noetherian property of infinite EI categories Wee Liang Gan and Liping Li Abstract. It is known that finitely generated FI-modules over a field of characteristic 0 are Noetherian. We generalize this result
Noetherian property of infinite EI categories Wee Liang Gan and Liping Li Abstract. It is known that finitely generated FI-modules over a field of characteristic 0 are Noetherian. We generalize this result
Solution. That ϕ W is a linear map W W follows from the definition of subspace. The map ϕ is ϕ(v + W ) = ϕ(v) + W, which is well-defined since
 MAS 5312 Section 2779 Introduction to Algebra 2 Solutions to Selected Problems, Chapters 11 13 11.2.9 Given a linear ϕ : V V such that ϕ(w ) W, show ϕ induces linear ϕ W : W W and ϕ : V/W V/W : Solution.
MAS 5312 Section 2779 Introduction to Algebra 2 Solutions to Selected Problems, Chapters 11 13 11.2.9 Given a linear ϕ : V V such that ϕ(w ) W, show ϕ induces linear ϕ W : W W and ϕ : V/W V/W : Solution.
A Little Beyond: Linear Algebra
 A Little Beyond: Linear Algebra Akshay Tiwary March 6, 2016 Any suggestions, questions and remarks are welcome! 1 A little extra Linear Algebra 1. Show that any set of non-zero polynomials in [x], no two
A Little Beyond: Linear Algebra Akshay Tiwary March 6, 2016 Any suggestions, questions and remarks are welcome! 1 A little extra Linear Algebra 1. Show that any set of non-zero polynomials in [x], no two
Eigenvectors. Prop-Defn
 Eigenvectors Aim lecture: The simplest T -invariant subspaces are 1-dim & these give rise to the theory of eigenvectors. To compute these we introduce the similarity invariant, the characteristic polynomial.
Eigenvectors Aim lecture: The simplest T -invariant subspaces are 1-dim & these give rise to the theory of eigenvectors. To compute these we introduce the similarity invariant, the characteristic polynomial.
Definition (T -invariant subspace) Example. Example
 Eigenvalues, Eigenvectors, Similarity, and Diagonalization We now turn our attention to linear transformations of the form T : V V. To better understand the effect of T on the vector space V, we begin
Eigenvalues, Eigenvectors, Similarity, and Diagonalization We now turn our attention to linear transformations of the form T : V V. To better understand the effect of T on the vector space V, we begin
Spectral Theorem for Self-adjoint Linear Operators
 Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Symmetries, Fields and Particles 2013 Solutions
 Symmetries, Fields and Particles 03 Solutions Yichen Shi July 9, 04. a Define the groups SU and SO3, and find their Lie algebras. Show that these Lie algebras, including their bracket structure, are isomorphic.
Symmetries, Fields and Particles 03 Solutions Yichen Shi July 9, 04. a Define the groups SU and SO3, and find their Lie algebras. Show that these Lie algebras, including their bracket structure, are isomorphic.
Quantum Computing Lecture 2. Review of Linear Algebra
 Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Background on Chevalley Groups Constructed from a Root System
 Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Solutions to the August 2008 Qualifying Examination
 Solutions to the August 2008 Qualifying Examination Any student with questions regarding the solutions is encouraged to contact the Chair of the Qualifying Examination Committee. Arrangements will then
Solutions to the August 2008 Qualifying Examination Any student with questions regarding the solutions is encouraged to contact the Chair of the Qualifying Examination Committee. Arrangements will then
Contents. Preface for the Instructor. Preface for the Student. xvii. Acknowledgments. 1 Vector Spaces 1 1.A R n and C n 2
 Contents Preface for the Instructor xi Preface for the Student xv Acknowledgments xvii 1 Vector Spaces 1 1.A R n and C n 2 Complex Numbers 2 Lists 5 F n 6 Digression on Fields 10 Exercises 1.A 11 1.B Definition
Contents Preface for the Instructor xi Preface for the Student xv Acknowledgments xvii 1 Vector Spaces 1 1.A R n and C n 2 Complex Numbers 2 Lists 5 F n 6 Digression on Fields 10 Exercises 1.A 11 1.B Definition
Eigenvalues and Eigenvectors: An Introduction
 Eigenvalues and Eigenvectors: An Introduction The eigenvalue problem is a problem of considerable theoretical interest and wide-ranging application. For example, this problem is crucial in solving systems
Eigenvalues and Eigenvectors: An Introduction The eigenvalue problem is a problem of considerable theoretical interest and wide-ranging application. For example, this problem is crucial in solving systems
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Algebra Exam Topics. Updated August 2017
 Algebra Exam Topics Updated August 2017 Starting Fall 2017, the Masters Algebra Exam will have 14 questions. Of these students will answer the first 8 questions from Topics 1, 2, and 3. They then have
Algebra Exam Topics Updated August 2017 Starting Fall 2017, the Masters Algebra Exam will have 14 questions. Of these students will answer the first 8 questions from Topics 1, 2, and 3. They then have
2 b 3 b 4. c c 2 c 3 c 4
 OHSx XM511 Linear Algebra: Multiple Choice Questions for Chapter 4 a a 2 a 3 a 4 b b 1. What is the determinant of 2 b 3 b 4 c c 2 c 3 c 4? d d 2 d 3 d 4 (a) abcd (b) abcd(a b)(b c)(c d)(d a) (c) abcd(a
OHSx XM511 Linear Algebra: Multiple Choice Questions for Chapter 4 a a 2 a 3 a 4 b b 1. What is the determinant of 2 b 3 b 4 c c 2 c 3 c 4? d d 2 d 3 d 4 (a) abcd (b) abcd(a b)(b c)(c d)(d a) (c) abcd(a
ACM 104. Homework Set 4 Solutions February 14, 2001
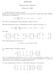 ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
A connection between number theory and linear algebra
 A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
Name: Solutions Final Exam
 Instructions. Answer each of the questions on your own paper, and be sure to show your work so that partial credit can be adequately assessed. Put your name on each page of your paper. 1. [10 Points] For
Instructions. Answer each of the questions on your own paper, and be sure to show your work so that partial credit can be adequately assessed. Put your name on each page of your paper. 1. [10 Points] For
1 Linear Algebra Problems
 Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
ALGEBRAIC GROUPS J. WARNER
 ALGEBRAIC GROUPS J. WARNER Let k be an algebraically closed field. varieties unless otherwise stated. 1. Definitions and Examples For simplicity we will work strictly with affine Definition 1.1. An algebraic
ALGEBRAIC GROUPS J. WARNER Let k be an algebraically closed field. varieties unless otherwise stated. 1. Definitions and Examples For simplicity we will work strictly with affine Definition 1.1. An algebraic
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Lemma 1.3. The element [X, X] is nonzero.
![Lemma 1.3. The element [X, X] is nonzero. Lemma 1.3. The element [X, X] is nonzero.](/thumbs/93/117947057.jpg) Math 210C. The remarkable SU(2) Let G be a non-commutative connected compact Lie group, and assume that its rank (i.e., dimension of maximal tori) is 1; equivalently, G is a compact connected Lie group
Math 210C. The remarkable SU(2) Let G be a non-commutative connected compact Lie group, and assume that its rank (i.e., dimension of maximal tori) is 1; equivalently, G is a compact connected Lie group
Representations of algebraic groups and their Lie algebras Jens Carsten Jantzen Lecture III
 Representations of algebraic groups and their Lie algebras Jens Carsten Jantzen Lecture III Lie algebras. Let K be again an algebraically closed field. For the moment let G be an arbitrary algebraic group
Representations of algebraic groups and their Lie algebras Jens Carsten Jantzen Lecture III Lie algebras. Let K be again an algebraically closed field. For the moment let G be an arbitrary algebraic group
Since G is a compact Lie group, we can apply Schur orthogonality to see that G χ π (g) 2 dg =
 Problem 1 Show that if π is an irreducible representation of a compact lie group G then π is also irreducible. Give an example of a G and π such that π = π, and another for which π π. Is this true for
Problem 1 Show that if π is an irreducible representation of a compact lie group G then π is also irreducible. Give an example of a G and π such that π = π, and another for which π π. Is this true for
Study Guide for Linear Algebra Exam 2
 Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
MATH 320: PRACTICE PROBLEMS FOR THE FINAL AND SOLUTIONS
 MATH 320: PRACTICE PROBLEMS FOR THE FINAL AND SOLUTIONS There will be eight problems on the final. The following are sample problems. Problem 1. Let F be the vector space of all real valued functions on
MATH 320: PRACTICE PROBLEMS FOR THE FINAL AND SOLUTIONS There will be eight problems on the final. The following are sample problems. Problem 1. Let F be the vector space of all real valued functions on
REPRESENTATIONS OF U(N) CLASSIFICATION BY HIGHEST WEIGHTS NOTES FOR MATH 261, FALL 2001
 9 REPRESENTATIONS OF U(N) CLASSIFICATION BY HIGHEST WEIGHTS NOTES FOR MATH 261, FALL 21 ALLEN KNUTSON 1 WEIGHT DIAGRAMS OF -REPRESENTATIONS Let be an -dimensional torus, ie a group isomorphic to The we
9 REPRESENTATIONS OF U(N) CLASSIFICATION BY HIGHEST WEIGHTS NOTES FOR MATH 261, FALL 21 ALLEN KNUTSON 1 WEIGHT DIAGRAMS OF -REPRESENTATIONS Let be an -dimensional torus, ie a group isomorphic to The we
ALGEBRA PH.D. QUALIFYING EXAM September 27, 2008
 ALGEBRA PH.D. QUALIFYING EXAM September 27, 2008 A passing paper consists of four problems solved completely plus significant progress on two other problems; moreover, the set of problems solved completely
ALGEBRA PH.D. QUALIFYING EXAM September 27, 2008 A passing paper consists of four problems solved completely plus significant progress on two other problems; moreover, the set of problems solved completely
Representations of the singular braid monoid and group invariants of singular knots
 Topology and its Applications 114 2001) 117 140 Representations of the singular braid monoid and group invariants of singular knots Bernd Gemein Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf,
Topology and its Applications 114 2001) 117 140 Representations of the singular braid monoid and group invariants of singular knots Bernd Gemein Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf,
TEST CODE: PMB SYLLABUS
 TEST CODE: PMB SYLLABUS Convergence and divergence of sequence and series; Cauchy sequence and completeness; Bolzano-Weierstrass theorem; continuity, uniform continuity, differentiability; directional
TEST CODE: PMB SYLLABUS Convergence and divergence of sequence and series; Cauchy sequence and completeness; Bolzano-Weierstrass theorem; continuity, uniform continuity, differentiability; directional
Math Bootcamp An p-dimensional vector is p numbers put together. Written as. x 1 x =. x p
 Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
POLYNOMIAL EQUATIONS OVER MATRICES. Robert Lee Wilson. Here are two well-known facts about polynomial equations over the complex numbers
 POLYNOMIAL EQUATIONS OVER MATRICES Robert Lee Wilson Here are two well-known facts about polynomial equations over the complex numbers (C): (I) (Vieta Theorem) For any complex numbers x,..., x n (not necessarily
POLYNOMIAL EQUATIONS OVER MATRICES Robert Lee Wilson Here are two well-known facts about polynomial equations over the complex numbers (C): (I) (Vieta Theorem) For any complex numbers x,..., x n (not necessarily
PHYS 705: Classical Mechanics. Rigid Body Motion Introduction + Math Review
 1 PHYS 705: Classical Mechanics Rigid Body Motion Introduction + Math Review 2 How to describe a rigid body? Rigid Body - a system of point particles fixed in space i r ij j subject to a holonomic constraint:
1 PHYS 705: Classical Mechanics Rigid Body Motion Introduction + Math Review 2 How to describe a rigid body? Rigid Body - a system of point particles fixed in space i r ij j subject to a holonomic constraint:
MAT 2037 LINEAR ALGEBRA I web:
 MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
Representations of Matrix Lie Algebras
 Representations of Matrix Lie Algebras Alex Turzillo REU Apprentice Program, University of Chicago aturzillo@uchicago.edu August 00 Abstract Building upon the concepts of the matrix Lie group and the matrix
Representations of Matrix Lie Algebras Alex Turzillo REU Apprentice Program, University of Chicago aturzillo@uchicago.edu August 00 Abstract Building upon the concepts of the matrix Lie group and the matrix
