Roberta Parreiras * and Petr Ekel
|
|
|
- Erika Alexander
- 5 years ago
- Views:
Transcription
1 Pesquisa Operacional (2013) 33(2): Brazilian Operations Research Society Printed version ISSN / Online version ISSN CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS WITH THE USE OF PREFERENCE FUNCTIONS Roberta Parreiras * and Petr Ekel Received October 22, 2010 / Accepted December 12, 2011 ABSTRACT. In order to model the preferences of a decision-maker (DM) by means of fuzzy preference relations, a DM can utilize different preference formats (such as ordering of the alternatives, utility values, multiplicative preference relations, fuzzy estimates, and reciprocal as well as nonreciprocal fuzzy preference relations) to express his/her judgments. Afterward, the obtained information is utilized to construct fuzzy preference relations. Here we introduce a procedure that allows the use of so-called preference functions (which is a preference format utilized in the methods of PROMETHEE family) to construct nonreciprocal fuzzy preference relations. With diverse preference formats being offered, a DM can select the one that is the most convenient to articulate his/her preferences. In order to demonstrate the applicability of the proposed procedure a multicriteria decision-making problem related to the site selection for constructing a new hospital is considered here. Keywords: multicriteria decision-making, fuzzy preference relations, preference functions. 1 INTRODUCTION The approaches to dealing with multicriteria (multiattribute) decision-making problems, which, for instance, are discussed in Orlovsky (1978), Chiclana et al. (1998), Ekel et al. (1998), Chiclana et al. (2001), are directed at processing the individual preferences as a pair X, R, X = {X 1, X 2,..., X n } represents a finite and discrete set of alternatives, which are to be evaluated, compared, ordered, and/or prioritized under the consideration of a set of fuzzy nonstrict preference relations R = {R 1, R 2,..., R q }, given in accordance with a set of criteria F = {F 1, F 2,..., F q } being considered. A fuzzy nonstrict preference relation (Orlovsky, 1978) consists of a binary fuzzy relation (BFR), which is a fuzzy set with bi-dimensional membership function R p (X k, X l ): X X [0, 1]. In essence, the membership function of the pth fuzzy preference relation indicates in the unit interval the degree to which the alternative X k is at least as good as X l, when the criterion F p, *Corresponding author Post-Graduate Program in Electrical Engineering, Pontifical Catholic University of Minas Gerais, Brazil. s: rop.asotech@gmail.com; pekel@superig.com.br
2 306 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS is considered by a particular decision-maker (DM). In a somewhat loose sense R p (X k, X l ) also represents the degree of truth of the statement X k is at least as good as X l (Kulshreshtha & Shekar, 2000). In dealing with X, R models, a fundamental question arises on how one can construct fuzzy preference relations to reflect the preferences of a DM. In practice, a DM can use different formats to establish preferences for the alternatives under consideration (Herrera-Viedma et al., 2002; Zhang et al., 2007; Pedrycz et al., 2011), including, the ordering of the alternatives, the utility values, multiplicative preference relations, fuzzy estimates, and fuzzy preference relations (additive reciprocal and nonreciprocal). In real world applications, several factors may lead a DM to select a different way for expressing his/her preferences about each criterion. Among these factors we can list the following (Pedrycz et al., 2011): each criterion comes with its significance (a fundamental feature which provides significance to the difference between two degrees evaluated on this criterion). Depending whether this significance has a qualitative or quantitative character, the use of certain preference formats can make the preference elicitation process easier and also more reliable; each criterion is associated with information arising from different sources and with information having different levels of uncertainty; a DM may find that his/her preference strengths can be better reflected or quantified by a specific preference format; a fact that a DM may posses previous knowledge or experience in expressing a specific preference format can motivate him/her to choose using it again. The information captured by those different preference formats can be utilized to construct fuzzy preference relations by means of applying adequate transformation functions (Chiclana et al., 1998, 2001; Herrera-Viedma et al., 2002; Pedrycz et al., 2011). Alternatively, a DM can directly assess the fuzzy nonstrict preference relation by determining the preference strength of one alternative over another as a number in the unit interval. Current literature contains different encoding schemes which can be utilized in the construction of fuzzy preference relations (refer to (Wang, 1997) for instances of fuzzy preference relations based on different encoding schemes). In this paper, we consider a particular encoding scheme which can be utilized to construct a nonreciprocal fuzzy preference relation (NRFPR) (Orlovsky, 1978; Fodor & Roubens, 1994a; Ekel & Schuffner Neto, 2006; Pedrycz et al., 2011). Such encoding scheme allows one to construct a NRFPR which is compatible with: a rational approach (Ekel et al., 1998) for deriving fuzzy preference relations, which is based on the comparison of the fuzzy estimates provided by a DM to evaluate each alternative (a discussion of the advantages of such rational approach can be found in (Pedrycz et al., 2011)); the notion of fuzzy nonstrict preference relation belonging to fuzzy preference structures with incomparability relation (Fodor & Roubens, 1994a). In this way, the use of a NRFPR
3 ROBERTA PARREIRAS and PETR EKEL 307 permits one to capture the preference degree of each pairwise comparison and the confidence degree of each pairwise comparison as well. A DM should assign a low credibility degree to a paired comparison whenever he/she can not define with conviction the preference degree for one alternative over another. The lack of conviction may be associated with missing information or to the occurrence of contradictory information about one alternative or both alternatives belonging to the pair (Fodor & Roubens, 1994a,b). Motivated by a demand for different preference formats to choose it as comfortable as possible for a DM to articulate his/her preferences (Zhang et al., 2007; Pedrycz et al., 2011), here we introduce a procedure that allows the use of preference functions to construct NRFPRs. In the methods of PROMETHEE family (Brans & Vincke, 1985), a DM must define the shape of the preference functions in accordance with his/her preferences so that they can be utilized to compare the alternatives and to construct outranking relations for each criterion being considered in the multicriteria analysis. Here, the preference functions are implemented as part of a general framework for preference modeling in a fuzzy environment, which offers six preference formats for preference articulation. They are: the ordering of the alternatives, the utility values, the multiplicative preference relations, the fuzzy estimates, the fuzzy preference relations (reciprocal and nonreciprocal), and the preference functions. With the availability of several preference formats, the choice of the most suitable one is a prerogative of a DM. The applicability of the preference functions to construct NRFPRs, within such general framework for preference modeling, is demonstrated through the solution of a decision-making problem related to the site selection for constructing a new hospital (Vahidnia et al., 2009). 2 JUDGMENTS OF STRICT PREFERENCE, INDIFFERENCE, AND INCOMPARABILITY Let us consider that a DM is asked to compare two alternatives X k X, X l X for a given criterion and determine which, between these two, he/she prefers. One of the following answers is expected (Fodor & Roubens, 1994a): X k and X l are indifferent; X k is strictly better than X l ; X l is strictly better than X k ; X k and X l are incomparable (a DM may not be able to compare the alternatives due to missing or uncertain information or as a consequence of the existence of conflicting information). Accordingly, in order to realistically characterize this comparison between two alternatives, three main types of judgments can be distinguished, namely indifference, strict preference, and incomparability. Given the pth criterion, these judgments can be modeled by means of three specific BFRs, namely the fuzzy indifference relation I p, the fuzzy strict preference relation P p, and the fuzzy incomparability relation J p, in such a way that the membership function of each BFR quantifies in the interval [0, 1], the credibility or the intensity of the observed judgment.
4 308 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS In fuzzy preference models based on BFRs, given De Morgan triplet (T, S, N), it is possible to define I p, P p, and J p exclusively in terms of the fuzzy nonstrict preference relation R p. It is important to indicate that the fuzzy nonstrict preference relation, by definition, can be expressed as (Fodor & Roubens, 1994a): R p = P p I p. (1) By considering that I p corresponds to all pairs of alternatives that simultaneously satisfy R p (X k, X l ) and R p (X l, X k ), the indifference relation can be stated as where R 1 p 1981). I p = R p R 1 p, (2) is the inverse relation of R p, that is R 1 p (X k, X l ) = R p (X l, X k ) (Orlovsky, 1978, Similarly, as P p (X k, X l ) implies that R p (X k, X l ) and N(R p (X l, X k )), the strict preference can be specified as P p = R p R d p, (3) where R d corresponds to the dual relation of R p, that is (Fodor & Roubens, 1994a). R d p (X k, X l ) = 1 R p (X l, X k )) Finally, as the relation J p (X k, X l ) implies that N(R p (X k, X l )) and N(R p (X l, X k )), the incomparability relation is given by J p = ˉR p R d p, (4) where ˉR p corresponds to the complementary relation of R p that is (Fodor & Roubens, 1994a). R p (X k, X l ) = 1 R p (X k, X l ) Therefore, once we have at hand the values of R p (X k, X l ) and R p (X l, X k ), the estimation of I p, P p, and J p is realized on the basis of (2), (3), and (4), respectively. As one can note, those three expressions require the selection of a t-norm operator. Unfortunately, as it has been discussed, for instance, in De Baets & Fodor (1997), it is not simple to select a t-norm to implement (2)-(4), if we want to preserve certain desirable properties of a fuzzy preference structure. Indeed, a negative result demonstrated in Alsina (1985) indicates that, if a De Morgan triplet is utilized to represent the complement, the intersection and the union of BFRs, then the equality Z = (Z W ) (Z ˉW ) (5) is not satisfied for any binary fuzzy relations Z and W. If we consider Z as being R p and W as R d p, then it implies that the relationships (2), (3), and (1) are inconsistent for any reflexive fuzzy binary relation, if we use the same intersection operator to implement the two intersection operations in (5).
5 ROBERTA PARREIRAS and PETR EKEL 309 Among the admissible t-norms to be utilized in this context (Fodor & Roubens, 1994b), we selected the min operator to implement the intersection in (2) and in (4) and the Lukasiewicz t-norm to implement the intersection in (3), as given by the following expressions: I p (X k, X l ) = min{r p (X k, X l ), R p (X l, X k )}, (6) P p (X k, X l ) = min{r p (X k, X l ) R p (X l, X k ), 0}, (7) J p (X k, X l ) = min{1 R p (X k, X l ), 1 R p (X l, X k )}. (8) It should be indicated that the definition of the fuzzy strict preference relation as given by (7) is in conformity with the Orlovsky choice procedure (Orlovsky, 1978), which is described in Section 5. 3 DIRECT ASSESSMENT OF NONRECIPROCAL FUZZY NONSTRICT PREFERENCE RELATIONS In real applications, a DM is usually asked to pick up the values in the unit interval that reflect the level of credibility or just the strength of his/her nonstrict preference for one alternative over the other. The encoding scheme considered here is reflected by a NRFPR which verifies the following conditions (Pedrycz et al., 2011): if R p (X k, X l ) = 1 and R p (X l, X k ) = 1, then X k is indifferent to X l ; if R p (X k, X l ) = 1 and R p (X l, X k ) = 0, then X k is strictly preferred to X l ; if R p (X k, X l ) = 0 and R p (X l, X k ) = 1, then X l is strictly preferred to X k ; if R p (X k, X l ) = 0 and R p (X l, X k ) = 0, then X k and X l are not comparable; the entries of the main diagonal are filled with 1, due to the reflexivity of R p (X k, X l ). Intermediate judgments among the situations described above are also allowed. They can be interpreted as follows: if 0 < R p (X k, X l ) < 1 and R p (X l, X k ) = 1, then X l is weakly preferred to X k ; if R p (X k, X l ) = 1 and 0 < R p (X l, X k ) < 1, then X k is weakly preferred to X l ; if 0 < R p (X k, X l ) < 1 and R p (X l, X k ) = 0, then X k is weakly preferred to X l and, at the same time, X k and X l are to a degree considered incomparable; if R p (X k, X l ) = 0 and 0 < R p (X l, X k ) < 1, then X l is weakly preferred to X k and, at the same time, X k and X l are to a degree considered incomparable.
6 310 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS It is important to indicate that relations (6) and (7) determine a clear relationship between the values of R p (X k, X l ) and R p (X l, X k ). If (6) and (7) are utilized for defining the fuzzy indifference relation and the fuzzy strict preference relation, respectively, then the difference between R p (X k, X l ) and R p (X l, X k ) reflects the level of strict preference between the alternatives X k and X l. Besides, the minimum value between R p (X k, X l ) and R p (X l, X k ) reflects the level of indifference between the alternatives X k and X l. With reference to the consistency of NRFPRs, the weak transitivity, which is given by (Herrera- Viedma et al., 2004). If R p (X k, X j ) > R p (X j, X k ) and R p (X j, X l ) > R p (X l, X j ), then R p (X k, X l ) > R p (X l, X k ), X k, X j, X l X (9) leads to the minimum requirement that should be satisfied by rational preference judgments. It implies that if someone says that X k is preferred to X j and that X j is preferred to X l, then X k is preferred to X l, without considering the strength of the preferences. It is also the minimum requirement for the application of decision-making methods based on the Orlovsky choice function (Orlovsky, 1978), if one wants some rational properties to be attained (Sengupta, 1998). 4 INDIRECT ASSESSMENT OF NONRECIPROCAL FUZZY NONSTRICT PREFERENCE RELATIONS In individual (as well as in group decision-making), when different preference formats are utilized by a DM to express his/her preferences, the information must be made uniform under adequate transformation functions, before being analyzed. These transformation functions can convert heterogeneous preference information, which may be qualitative or quantitative, two-valued or fuzzy, ordered or non-ordered, ordinal or cardinal into fuzzy preference relations, which form a more general preference model (Chiclana et al., 1998, 2001; Herrera-Viedma et al., 2002; Pedrycz et al., 2011). As it was indicated above, the five main formats, that can be utilize by a DM to articulate his/her preferences, in addition to the NRFPRs, are: Vector with the ordering of all alternatives. The ordering of alternatives from best to worst can be represented as an array O p = [O p (X 1 ),..., O p (X n )], with O p (X k ) being a permutation function, which returns the position of alternative X k among the integer values {1, 2,..., n} (Chiclana et al., 1998). Vector of the utility values. A measurable utility function U p (x): X [0, 1], founded on differences in preference strengths (Belton, 1999; Farquhar & Keller, 1989), allows a DM to assign a utility value from the unity interval [0, 1] to each alternative belonging to X. Multiplicative preference relation. The multiplicative preference relation can be represented as a n n positive reciprocal matrix M p reflecting the preference intensity ratio between the alternatives in accordance with the Analytic Hierarchy Process approach
7 ROBERTA PARREIRAS and PETR EKEL 311 (Saaty, 1980). Each entry M p (X k, X l ) of this reciprocal matrix represents a preference intensity ratio and can be interpreted as X k is M p (X k, X l ) times more dominant than X l (Saaty, 1980) or as X k is M p (X k, X l ) times as good as X l (Chiclana et al., 2001). Under the condition of multiplicative reciprocity, once a DM provides M p (X k, X l ), the value of M p (X l, X k ) is automatically inferred as M p (X l, X k ) = 1/M p (X k, X l ). Fuzzy estimates. The elements of X can be evaluated with the use of fuzzy estimates L p = {l p (X 1 ),..., l p (X n )}, being l p (X k ) the fuzzy estimate associated with alternative X k from the point of view of a given criterion F p. The fuzzy estimate l p (X k ) refers to a fuzzy number that can be directly specified by a DM or indirectly expressed by means of linguistic terms from some set S such as, for instance, S(F p ) = {low quality, average quality, high quality}. In the latter case, the linguistic terms must be converted into fuzzy estimates, as required to perform the analysis of the problem. Additive reciprocal fuzzy preference relation (ARFPR). An ARFPR consists of a specific type of fuzzy preference relation which satisfies the additive reciprocity condition: R R p (X k, X l ) + R R p (X l, X k ) = 1, X k, X l X, (10) where R R p represents the ARFPR (here, NRFPR is denoted as R p and ARFPR is denoted as R R p ). The encoding scheme usually associated with ARFPRs can be summarized as the following rules: R R p (X k, X l ) = 0.5 means that X k is indifferent to X l ; 0 R R p (X k, X l ) < 0.5 means that X l is preferred to X k ; 0.5 < R R(X k, X l ) 1 means that X k is preferred to X l ; the entries of the main diagonal are filled with 0.5, as each element is equal to itself and, as a result, indifferent to itself. In (Chiclana et al., 1998), one can find different transformation functions for converting a vector with the ordering of all alternatives or a vector of the utility values associated with each alternative into an ARFPR. A transformation function for converting multiplicative preference relations into an ARFPR is proposed in (Chiclana et al., 2001). In (Pedrycz et al., 2011), new transformation functions are proposed. They convert preference information expressed in those five different formats described above into NRFPRs. Some of the transformation functions proposed in (Queiroz, 2009; Pedrycz et al., 2011) are summarized in Table 1. It should be indicated that they are defined for the case of maximization criteria (if the criterion being considered has a minimization character, then the direction of the signs of all the inequalities appearing in the transformation functions should be reversed).
8 312 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS Table 1 Transformation functions for the conversion of preference information expressed in different formats into a NRFPR (Pedrycz et al., 2011). Original preference format Vector with the ordering of all alternatives Vector of the utility values based on an interval scale Multiplicative preference relation Additive reciprocal fuzzy preference relation Transformation function R(X k, X l ) = H 1 (O(X k ), O(X l )) = O(X l) O(X k ), if O(X k ) > O(X l ) 2(n 1) 1, if O(X k ) O(X l ) { R(X k, X l ) = H 2 (U(X k ), U(X l )) = 1 + U(X k ) U(X l ), if U(X k ) < U(X l ) 1, if U(X k ) U(X l ) R(X k, X l ) = H 3 (M(X k, X l ), M(X l, X l )) = log M(X k, X l ) m M(X l, X k ), if log m M(X k, X l ) < 0 1, if log m M(X k, X l ) 0 { R(X k, X l ) = H 4 (R R(X k, X l ), R R(X l, X k )) = 1 + R R(X k, X l ) R R(X l, X k ), if R R(X k, X l ) < 0.5 1, if R R(X k, X l ) 0.5 In this paper, those transformation functions summarized in Table 1 are utilized to create a general framework for constructing NRFPRs on the basis of preference information which may be expressed in different formats. Given a set X of alternatives, a DM can express his/her preferences by ordering the alternatives from best to worst, by constructing a utility function or by performing pairwise comparisons between the alternatives to construct a multiplicative preference relation, a ARFPR or a NRFPR. At the same time, in order to increase the flexibility of such general framework, the results of (Ekel et al., 1998) are utilized to derive NRFPRs from the fuzzy estimates given by a DM to evaluate the alternatives. In this way, once a DM provides fuzzy estimates F p (X k ), k = 1, 2,..., n to evaluate all the alternatives for a criterion F p which can be measured on a numerical scale, if the essence of preference is coherent with the natural order ( ) along the axis of measurable values of F p, then the following expressions can be utilized to construct a NRFPR: R p (X k, X l ) = sup f p (X k ), f p (X l ) F p f p (X k ) f p (X l ) min ( F p ( f p (X k )), F p ( f p (X l )) ), (11) R p (X l, X k ) = sup f p (X k ), f p (X l ) F p f p (X l ) f p (X k ) min ( F p ( f p (X k )), F p ( f p (X l )) ), (12) where f p (X k ) and f p (X l ) are real numbers reflecting the evaluation of the attribute F p (with a maximization character) for the alternatives X k and X l ; F p ( f p (X k )) and F p ( f p (X l )) represent the membership functions of the fuzzy sets F p (X k ) and F p (X l ) evaluated at f p (X k ) and f p (X l ), respectively. It should be indicated that (11) and (12) are defined for maximization criteria. The direction of the signs of the inequalities in (11) and (12) should be reversed, if a minimization criterion is being considered.
9 ROBERTA PARREIRAS and PETR EKEL CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS WITH THE USE OF PREFERENCE FUNCTIONS The results of (Brans & Vincke, 1985) permit one to apply preference functions as an additional format that can be used by a DM to express his/her preferences. In particular, in the family of PROMETHEE methods, the preferences being restricted to a single criterion F p, are modeled through a preference function s p (X k, X l ), in such a way that it reflects the preference level of X k over X l, according to the following rules: if s p (X k, X l ) = 0, both alternatives are considered indifferent to each other; if s p (X k, X l ) = 1, X k is strictly preferred to X l ; if 0 < s p (X k, X l ) < 1, X k is weakly preferred to X l. The preference functions are usually defined in terms of the difference d p (X k, X l ) = f p (X k ) f p (X l ) (13) in such a way that they transform the difference in the evaluations of two alternatives into a preference intensity between 0 and 1. The preference functions can have different shapes, as long as they are nondecreasing functions of the difference d p (X k, X l ) (Brans & Vincke, 1985). The methods PROMETHEE I and PROMETHEE II admit six different generalized models for the preference function, which cover most part of the scenarios encountered in real applications (Brans & Vincke, 1985). They are: the usual criterion, the quasi-criterion, the level-criterion, the linear criterion, the linear criterion with indifference region, and the Gaussian criterion. With the availability of those generalized functions, it may be easier for a DM to define a preference function reflecting his/her preferences. Next, we describe how one can construct NRFPRs based on each one of those preference functions. It should be indicated that, here we consider the criteria as being of maximization type (without loss of generality). Let us begin by considering three preference functions that are particularly easy to define: the usual criterion, the quasi-criterion, and the level-criterion. Figure 1 shows the graphical representation of the usual criterion, which may be considered as being the simplest type of preference function, since it does not require any parameter to be set by a DM. As it can be seen in Figure 1, the level of strict preference of X k over X l is equal to 1 for d p (X k, X l ) > 0 and is null for d p (X k, X l ) < 0. If a DM wants to construct a NRFPR based on the usual criterion, the following rules must be applied to the comparison of each pair of alternatives: if d p (X k, X l ) < 0, then R p (X k, X l ) = 0 and R p (X l, X k ) = 1; if d p (X k, X l ) = 0, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1; if d p (X k, X l ) > 0, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0.
10 314 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS Left side: Preference function based on the usual criterion; Right side: NRF Figure 1 Left side: Preference function based on the usual criterion; Right side: NRFPR based on the usual criterion, expressed in function of the difference d p (X k, X l ). Figure 2 shows a graphical representation of the preference function corresponding to the quasicriterion and of the NRFPR based on the quasi-criterion. It is worth noting that the usual criterion can be seen as a particular case of the quasi-criterion where the bounds of the indifference interval [ a p, a p ] are null, that is a p = 0. If a DM wants to construct a NRFPR coherently with the quasi-criterion, the pairwise comparisons must attain the following conditions: if d p (X k, X l ) < a p, then R p (X k, X l ) = 0 and R p (X l, X k ) = 1; if a p d p (X k, X l ) a p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1; if d p (X k, X l ) > a p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0.. Left side: Preference function based on the quasi-criterion; Right side: NRFP Figure 2 Left side: Preference function based on the quasi-criterion; Right side: NRFPR based on the quasi-criterion, expressed in function of the difference d p (X k, X l ). The level-criterion allows discriminating an indifference interval [ a p, a p ] and a weak preference interval [a p, b p ] (and [ b p, a p ]). The pairwise comparisons must satisfy the following conditions in order to construct a NRFPR coherently with the level-criterion: if d p (X k, X l ) b p, then R p (X k, X l ) = 0 and R p (X l, X k ) = 1; if b p < d p (X k, X l ) a p, then R p (X k, X l ) = 0.5 and R p (X l, X k ) = 1; if a p < d p (X k, X l ) < a p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1; if a p < d p (X k, X l ) < b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0.5; if d p (X k, X l ) b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0.
11 ROBERTA PARREIRAS and PETR EKEL 315 Left side: Preference function based on the level criterion; Right side: NRFPR base Figure 3 Left side: Preference function based on the level criterion; Right side: NRFPR based on the level criterion, expressed in function of the difference d p (X k, X l ). The preference functions of the linear criterion, the linear criterion with an indifference region, and the Gaussian criterion present a smooth transition between indifference and strict preference, which permits a DM to make judgments at different levels of weak preference. The graphical representations of those preference functions are shown in the Figures 4, 5, and 6, respectively. In the visualization of the linear criterion (refer to Fig. 4), the slope of the preference function depend on the value of the preference threshold b p. Thus, in order to define a NRFPR coherently with the linear criterion, the pairwise comparisons must be in accordance with the following conditions: if d p (X k, X l ) < b p, then R p (X k, X l ) = 0 and R p (X l, X k ) = 1; if b p d p (X k, X l ) < 0, then R p (X k, X l ) = 1 d p (X k, X l ) /b p and R p (X l, X k ) = 1; if 0 d p (X k, X l ) < b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1 d p (X k, X l ) /b p ; if d p (X k, X l ) > b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0. Left side: Preference function based on the linear criterion; Right side: NR Figure 4 Left side: Preference function based on the linear criterion; Right side: NRFPR based on the linear criterion, expressed in function of the difference d p (X k, X l ). The Linear criterion with indifference region can be considered an extension of the linear criterion to deal with judgments of indifference when the pair of alternatives have similar evaluations and their difference lies in an indifference interval [ a p, a p ]. A NRFPR is coherent with this definition of linear criterion with indifference region if it is in accordance with the following conditions (refer to Fig. 5):
12 316 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS if d p (X k, X l ) < b p, then R p (X k, X l ) = 0 and R p (X l, X k ) = 1; if b p d p (X k, X l ) < a p, then R p (X k, X l ) = 1 d p (X k, X l ) /b p and R p (X l, X k ) = 1; if a p d p (X k, X l ) a p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1; if a p < d p (X k, X l ) b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 1 d p (X k, X l ) /b p ; if d p (X k, X l ) > b p, then R p (X k, X l ) = 1 and R p (X l, X k ) = 0. Left side: Preference function based on the linear criterion with indifference region Figure 5 Left side: Preference function based on the linear criterion with indifference region; Right side: NRFPR based on the linear criterion with indifference region, expressed in function of the difference d p (X k, X l ). Finally, in the case of the Gaussian criterion, σ p is the distance between the origin and the inflexion point of the curve s p (X k, X l ). The Gaussian Criterion allows a transition (without discontinuities) between judgments of indifference and strict preference. In order to define a NRFPR coherently with the Gaussian criterion, the pairwise comparisons must be in accordance with the following conditions: if d p (X k, X l ) < 0, then R p (X k, X l ) = exp( d p (X k, X l ) /2σ 2 p ) and R p(x l, X k ) = 1; if d p (X k, X l ) 0, then R p (X k, X l ) = 1 and R p (X l, X k ) = exp( d p (X k, X l ) /2σ 2 p ), where σ p is the distance between the origin and the inflexion point of the preference function. Left side: Preference function based on the Gaussian criterion; Right side: NR Figure 6 Left side: Preference function based on the Gaussian criterion; Right side: NRFPR based on the Gaussian criterion, expressed in function of the difference d p (X k, X l ).
13 ROBERTA PARREIRAS and PETR EKEL 317 It is not difficult to demonstrate that NRFPRs constructed coherently with those six types of preference functions always satisfy weak transitivity (refer to expression (9)). For this demonstration, it is worth noting that R p (X k, X l ) R p (X l, X k ) only if s p (X k, X l ) 0 (which the reader can easily verify for each type of preference function) and that a nondecreasing preference function satisfies s p (X k, X l ) 0 only if d p (X k, X l ) 0. In this way, if R p (X k, X j ) R p (X j, X k ) and R p (X j, X l ) R p (X l, X j ), then d p (X k, X j ) 0 (which means that f p (X k ) > f p (X j )) and, at the same time, d p (X j, X l ) 0 (which means that f p (X j ) > f p (X l )). It is also possible to infer that f p (X k ) > f p (X j ) > f p (X l ), which results in d p (X k, X l ) 0, s p (X k, X l ) 0, and R p (X k, X l ) > R p (X l, X k ). 6 A METHOD FOR MULTICRITERIA DECISION MAKING BASED ON THE ORLOVSKY CHOICE PROCEDURE The Orlovsky choice procedure makes use of a fuzzy strict preference relation given by (7) to carry out the choice of alternatives (Orlovsky, 1978, 1981). Considering the pth criterion, as P p (X l, X k ) describes the set of all alternatives X k that are strictly dominated by X l, its compliment P p (X l, X k ) corresponds to the set of alternatives that are not dominated by X l. Therefore, in order to meet the set of alternatives from X that are not dominated by any other alternative, it suffices to obtain for each alternative X k belonging to X the intersection of P p (X l, X k ) for all X l belonging to X. This intersection is the set of nondominated alternatives with the membership function N D p (X k ) = inf {1 P p(x l, X k )} = 1 sup P p (X l, X k ), (14) X l X X l X which reflects the level of nondominance of each alternative X k. A natural choice for a monocriteria problem based on this model should be the alternatives providing: { } X R N D p = Xk N D X R p N D (Xk N D ) = sup N D p (X k ). (15) X k X It is worth emphasizing that the alternatives satisfying { } X R N D p = Xk N D X R p N D (Xk N D ) = 1 are actually nonfuzzy nondominated and can be considered as the nonfuzzy solution for the choice problem (Orlovsky, 1978, 1981). Expressions (7), (14), and (15) may be used to solve choice or ranking problems not only with a single criterion, but also with multiple criteria. In particular, several procedures that allow one to include multiple criteria in the analysis of a decision making problem are discussed in Orlovsky (1981), Ekel & Schuffner Neto (2006). Let us consider one of them. Having at hand nonstrict preference relations for each criterion, one possible procedure for solving multicriteria problems consists in obtaining a global relation through the intersection of those relations as follows: G = R 1... R q. (17) (16)
14 318 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS The use of intersection to aggregate all criteria is suitable, when it is a necessary condition that a good alternative X k must simultaneously satisfy F 1 and F 2 and... and F q. Among the t-norm operators, the use of the min operator, as proposed in (Orlovsky, 1981), allows one to construct the global fuzzy nonstrict preference relation G(X k, X l ) = min { R 1 (X k, X l ),..., R q (X k, X l ) } (18) under a completely non-compensatory approach for multicriteria decision-making, in the sense that the high satisfaction of some criteria does not relieve the remaining ones from the requirement of being satisfied (there is no compensation among the criteria). Such approach is also considered pessimistic, since it gives emphasis to the worst evaluations of each alternative. Having at hand the global fuzzy nonstrict preference relation, equations (7), (14) and (15) can be subsequently applied directly to G and the result corresponds to a fuzzy set of nondominated alternatives fulfilling the role of a Pareto set (Orlovsky, 1981). However, in case of not being possible to distinguish two or more alternatives, the contraction of (18) is possible by differentiating the importance of R p, p = 1,..., q with the use of the weighted sum: q T (X k, X l ) = λ p R p (X k, X l ), (19) p=1 where λ p, p = 1,..., q are importance factors of the corresponding criteria, defined as w p [0, 1] and q p=1 w p = 1. The construction of T (X k, X l ), allows one to obtain the membership function N DT (X k ) of the fuzzy set of nondominated alternatives by subsequently applying (7) and (14) to (19). The intersection Q(X k ) = min ( N D(X k ), N DT (X k ) ), (20) provides us with a set of alternatives with the highest level of nondominance { } X N D = Xk N D Xk N D X, Q(Xk N D ) = sup Q(X k ). (21) X k K 7 APPLICATION EXAMPLE The multicriteria decision-making problem related to the site selection for constructing a new hospital is studied in Vahidnia et al. (2009). Here, we consider a simplified version of this problem, in which six sites are to be ranked, taking into account the following four criteria: 1. Distance from the arterial routes (minimization criterion); 2. Land cost (minimization criterion); 3. Population density (maximization criterion); 4. Average travel time to the nearest existing hospital (maximization criterion).
15 ROBERTA PARREIRAS and PETR EKEL 319 Hospitals should be located close to main public transport routes. Here, criterion F 1 allows one to evaluate the distance from each site to the closest arterial route. Besides, for social convenience, it is important to guarantee that every person lives in an area with accessible hospital service. Criterion F 4 evaluates the average time one would take to travel between the site and the nearest existing hospital. The fifth criterion which could be considered is associated with the pollution level present at each site. However, as the sites considered here do not significantly differ with respect to this criterion, the DM decided to eliminate it from the subsequent multicriteria analysis. Figure 7 presents the fuzzy scores utilized for evaluating the third criterion, F 3 -population density. Table 2 shows the evaluation matrix of the alternatives. Figure 7 Valuation of criterion F 3 (population density). Table 2 Evaluation matrix of the alternatives. F 1 (X k ) F 2 (X k ) F F 3 (X k ) 4 (X k ) (m) ($/m 2 ) (minutes) X middle 22 X high 17 X high 12 X middle 10 X low 7 X very high 5 When the criterion F 1 was considered by the DM, he decided not to infer the degrees of his preferences directly from those distances listed in Table 2. The DM felt more comfortable with utilizing the multiplicative preference relation to articulate his preferences as follows: /4 1 1/ / /3 1/2 M 1 =. (22) 1/4 1/3 1/4 1 1/4 1/2 1/3 1/ / /4 1 Indeed, it is worth noting in (22) that the degrees of preference of the DM can not be directly inferred from the distances from arterial streets. For instance, although the distance of X 4 is ten
16 320 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS times larger than the distance of X 5, X 5 is not considered ten times better than X 4. At the same time, the distance of X 2 is higher than the distance of X 6. However, the DM judged X 2 and X 6 as being indifferent to each other. Besides, it is important to indicate that although (22) does not satisfy the multiplicative transitivity, the NRFPR R 1 = (23) constructed with the use of H 3 (refer to Table 1) satisfies the weak transitivity and this is a satisfactory level of consistency for the application of the decision-making method to be used. In the case of criterion F 2, the DM decided to use a preference function corresponding to a Linear criterion with b 2 = 5($/m 2 ). The obtained NRFPR is as follows: R 2 =. (24) The population density of each alternative, which is related to criterion F 3, was estimated by him, by the linguistic terms shown in Table 2. By applying the expressions (11) and (12) to construct a NRFPR from the comparison of fuzzy estimates, the following NRFPR is obtained: R 3 =. (25) Finally, in the case of criterion F 4, a preference relation corresponding to a Quasi-criterion, with a 4 = 3 min. The obtained NRFPR is as follows: R 4 =. (26)
17 ROBERTA PARREIRAS and PETR EKEL 321 Having at hand the NRFPRs (23)-(26), the multicriteria analysis begins by applying (18) to obtain a global relation under a pessimistic approach through the intersection: G =. (27) Afterward, expression (7) provides the strict preference relation P =. (28) Finally, with the use of (14), we obtain the nondominance degrees of each alternative N D = [ ]. (29) We can order them from best to worst as (X 1 X 3 X 6 ) X 2 X 5 X 4. In order to distinguish alternatives X 1, X 3, and X 6, a subsequent analysis is performed by applying (19) and (20). Considering that the DM defined the weights of the criteria as λ 1 = λ 2 = 0.2 and λ 3 = λ 4 = 0.3, the convolution (19) provides the following matrix of pairwise comparisons: T =. (30) In this way, by processing (30) with the use of (7) and (14), it is possible to obtain the following fuzzy set of nondominated alternatives: N DT = [ ]. (31) Finally, the intersection of (29) and (30), obtained in accordance with (20), makes it possible to contract the fuzzy set of nondominated alternatives as follows: N D = [ ]. (32) The final ranking of the alternatives can be defined on the basis of (32) as X 6 X 1 X 3 X 2 X 5 X 4.
18 322 CONSTRUCTION OF NONRECIPROCAL FUZZY PREFERENCE RELATIONS CONCLUSIONS In this paper we showed how the preference functions can be utilized to construct NRFPRs. The preference functions correspond to a well established preference format which has been utilized to model the preferences of a DM in the methods PROMETHEE I and PROMETHEE II. The results of this paper allow a more flexible input of preferences in the decision-making process based on the analysis of X, R models (now, it is possible to offer to a DM the following formats: the ordering of the alternatives, the utility values, the multiplicative preference relations, the fuzzy estimates, the reciprocal as well as the nonreciprocal fuzzy preference relations and the preference functions). The applicability of the proposed procedure is demonstrated through the solution of a multicriteria decision-making problem related to the site selection for constructing a new hospital. ACKNOWLEDGMENTS This research is supported by the National Council for Scientific and Technological Development of Brazil (CNPq) grants PQ: / and PQ: / REFERENCES [1] ALSINA C On a family of connectives for fuzzy sets. Fuzzy Sets and Systems, 16: [2] BELTON V Multiple-criteria problem structuring and analysis in a value theory framework. In: Multicriteria decision making: advances in MCDM models, algorithms, theory [edited by GAL T, STEWART T & HANNE T], Kluwer Academic Publishers, Dordrecht, [3] BRANS JP & VINCKE PH A preference ranking organization method (the PROMETHEE method for multiple criteria decision-making. Management Science, 31: [4] DE BAETS B & FODOR JC Twenty years of fuzzy preference structures. Rivista di Matematica per le Scienze Economiche e Sociali, 20: [5] CHICLANA F, HERRERA F & HERRERA-VIEDMA E Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations. Fuzzy Sets and Systems, 97: [6] CHICLANA F, HERRERA F & HERRERA-VIEDMA E Integrating multiplicative preference relations rain a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets and Systems, 122: [7] EKEL P, PEDRYCZ W & SCHINZINGER R A general approach to solving a wide class of fuzzy optimization problems. Fuzzy Sets and Systems, 97: [8] EKEL P.YA. & SCHUFFNER NETO FH Algorithms of discrete optimization and their application to problems with fuzzy coefficients. Information Sciences, 176: [9] FARQUHAR PH & KELLER LR Preference intensity measurement. Annals of Operations Research, 19: [10] FODOR JC & ROUBENS M. 1994a. Fuzzy preference modelling and multicriteria decision support, Kluwer, Boston.
19 ROBERTA PARREIRAS and PETR EKEL 323 [11] FODOR JC & ROUBENS M. 1994b. Valued preference structures. European Journal of Operational Research, 79: [12] HERRERA-VIEDMA E, HERRERA F & CHICLANA F A consensus model for multiperson decision making with different preference structures. IEEE Transactions on Systems, Man and Cybernetics Part A: Systems and Humans, 32: [13] HERRERA-VIEDMA E, HERRERA F, CHICLANA F & LUQUE M Some issues on consistency of fuzzy preference relations. European Journal of Operational Research, 154: [14] KULSHRESHTHA P & SHEKAR B Interrelations among fuzzy preference-based choice functions and significance of rationality conditions: A taxonomic and intuitive perspective. Fuzzy Sets and Systems, 109: [15] LU J, ZHANG G, RUAN D & WU F Multi-objective Group Decision Making: Methods, Software and Applications with Fuzzy Set Techniques. Imperial College Press, London. [16] ORLOVSKY SA Decision-making with a fuzzy preference relation. Fuzzy Sets and Systems, 1: [17] ORLOVSKY SA Problems of Decision Making with Fuzzy Information (in Russian), Nauka, Moscow. [18] PEDRYCZ W, EKEL P & PARREIRAS R Fuzzy Multicriteria Decision-Making: Models, Methods, and Applications. Wiley, Chichester. [19] QUEIROZ JCB Models and Methods of Decision Making Support for Strategic Management: PhD thesis (in Portuguese), Federal University of Minas Gerais, Belo Horizonte. [20] SAATY T The Analytic Hierarchy Process. McGraw Hill, New York. [21] SENGUPTA K Fuzzy preference and Orlovsky choice procedure. Fuzzy Sets and Systems, 93: [22] VAHIDNIA MH, ALESHEIKH AA & ALIMOHAMMADI A Hospital site selection using fuzzy AHP and its derivatives. Journal of Environmental Management, 90: [23] WANG X An investigation into relations between some transitivity-related concepts. Fuzzy Sets and Systems, 89: [24] ZHANG Q, WANG Y & YANG Y Fuzzy multiple attribute decision making with eight types of preference information on alternatives. In: Proc. of the 2007 IEEE Symposium on Computational Intelligence in Multicriteria Decision Making, Honolulu,
Additive Consistency of Fuzzy Preference Relations: Characterization and Construction. Extended Abstract
 Additive Consistency of Fuzzy Preference Relations: Characterization and Construction F. Herrera a, E. Herrera-Viedma a, F. Chiclana b Dept. of Computer Science and Artificial Intelligence a University
Additive Consistency of Fuzzy Preference Relations: Characterization and Construction F. Herrera a, E. Herrera-Viedma a, F. Chiclana b Dept. of Computer Science and Artificial Intelligence a University
Group Decision-Making with Incomplete Fuzzy Linguistic Preference Relations
 Group Decision-Making with Incomplete Fuzzy Linguistic Preference Relations S. Alonso Department of Software Engineering University of Granada, 18071, Granada, Spain; salonso@decsai.ugr.es, F.J. Cabrerizo
Group Decision-Making with Incomplete Fuzzy Linguistic Preference Relations S. Alonso Department of Software Engineering University of Granada, 18071, Granada, Spain; salonso@decsai.ugr.es, F.J. Cabrerizo
A Consistency Based Procedure to Estimate Missing Pairwise Preference Values
 A Consistency Based Procedure to Estimate Missing Pairwise Preference Values S. Alonso F. Chiclana F. Herrera E. Herrera-Viedma J. Alcalá-Fernádez C. Porcel Abstract In this paper, we present a procedure
A Consistency Based Procedure to Estimate Missing Pairwise Preference Values S. Alonso F. Chiclana F. Herrera E. Herrera-Viedma J. Alcalá-Fernádez C. Porcel Abstract In this paper, we present a procedure
Multicriteria Decision Making Based on Fuzzy Relations
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 8, No 4 Sofia 2008 Multicriteria Decision Maing Based on Fuzzy Relations Vania Peneva, Ivan Popchev Institute of Information
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 8, No 4 Sofia 2008 Multicriteria Decision Maing Based on Fuzzy Relations Vania Peneva, Ivan Popchev Institute of Information
Comparison of two versions of the Ferrers property of fuzzy interval orders
 Comparison of two versions of the Ferrers property of fuzzy interval orders Susana Díaz 1 Bernard De Baets 2 Susana Montes 1 1.Dept. Statistics and O. R., University of Oviedo 2.Dept. Appl. Math., Biometrics
Comparison of two versions of the Ferrers property of fuzzy interval orders Susana Díaz 1 Bernard De Baets 2 Susana Montes 1 1.Dept. Statistics and O. R., University of Oviedo 2.Dept. Appl. Math., Biometrics
An Analysis on Consensus Measures in Group Decision Making
 An Analysis on Consensus Measures in Group Decision Making M. J. del Moral Statistics and Operational Research Email: delmoral@ugr.es F. Chiclana CCI Faculty of Technology De Montfort University Leicester
An Analysis on Consensus Measures in Group Decision Making M. J. del Moral Statistics and Operational Research Email: delmoral@ugr.es F. Chiclana CCI Faculty of Technology De Montfort University Leicester
Chapter 2 An Overview of Multiple Criteria Decision Aid
 Chapter 2 An Overview of Multiple Criteria Decision Aid Abstract This chapter provides an overview of the multicriteria decision aid paradigm. The discussion covers the main features and concepts in the
Chapter 2 An Overview of Multiple Criteria Decision Aid Abstract This chapter provides an overview of the multicriteria decision aid paradigm. The discussion covers the main features and concepts in the
Advances in the Use of MCDA Methods in Decision-Making
 Advances in the Use of MCDA Methods in Decision-Making JOSÉ RUI FIGUEIRA CEG-IST, Center for Management Studies, Instituto Superior Técnico, Lisbon LAMSADE, Université Paris-Dauphine (E-mail : figueira@ist.utl.pt)
Advances in the Use of MCDA Methods in Decision-Making JOSÉ RUI FIGUEIRA CEG-IST, Center for Management Studies, Instituto Superior Técnico, Lisbon LAMSADE, Université Paris-Dauphine (E-mail : figueira@ist.utl.pt)
International Journal of Information Technology & Decision Making c World Scientific Publishing Company
 International Journal of Information Technology & Decision Making c World Scientific Publishing Company A MIN-MAX GOAL PROGRAMMING APPROACH TO PRIORITY DERIVATION IN AHP WITH INTERVAL JUDGEMENTS DIMITRIS
International Journal of Information Technology & Decision Making c World Scientific Publishing Company A MIN-MAX GOAL PROGRAMMING APPROACH TO PRIORITY DERIVATION IN AHP WITH INTERVAL JUDGEMENTS DIMITRIS
Measuring transitivity of fuzzy pairwise comparison matrix
 Measuring transitivity of fuzzy pairwise comparison matrix Jaroslav Ramík 1 Abstract. A pair-wise comparison matrix is the result of pair-wise comparison a powerful method in multi-criteria optimization.
Measuring transitivity of fuzzy pairwise comparison matrix Jaroslav Ramík 1 Abstract. A pair-wise comparison matrix is the result of pair-wise comparison a powerful method in multi-criteria optimization.
A New Fuzzy Positive and Negative Ideal Solution for Fuzzy TOPSIS
 A New Fuzzy Positive and Negative Ideal Solution for Fuzzy TOPSIS MEHDI AMIRI-AREF, NIKBAKHSH JAVADIAN, MOHAMMAD KAZEMI Department of Industrial Engineering Mazandaran University of Science & Technology
A New Fuzzy Positive and Negative Ideal Solution for Fuzzy TOPSIS MEHDI AMIRI-AREF, NIKBAKHSH JAVADIAN, MOHAMMAD KAZEMI Department of Industrial Engineering Mazandaran University of Science & Technology
Fuzzy Integral Multiple Criteria Decision Making Method Based on Fuzzy Preference Relation on Alternatives
 Journal of Systems Science and Information Jun., 2016, Vol. 4, No. 3, pp. 280 290 DOI: 10.21078/JSSI-2016-280-11 Fuzzy Integral Multiple Criteria Decision Making Method Based on Fuzzy Preference Relation
Journal of Systems Science and Information Jun., 2016, Vol. 4, No. 3, pp. 280 290 DOI: 10.21078/JSSI-2016-280-11 Fuzzy Integral Multiple Criteria Decision Making Method Based on Fuzzy Preference Relation
Preferences and Consistency Issues in Group Decision Making
 Preferences and Consistency Issues in Group Decision Making Francisco Chiclana 1, Enrique Herrera-Viedma 2, Sergio Alonso 2, and Ricardo Alberto Marques Pereira 3 1 Centre for Computational Intelligence
Preferences and Consistency Issues in Group Decision Making Francisco Chiclana 1, Enrique Herrera-Viedma 2, Sergio Alonso 2, and Ricardo Alberto Marques Pereira 3 1 Centre for Computational Intelligence
New Reference-Neighbourhood Scalarization Problem for Multiobjective Integer Programming
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 3 No Sofia 3 Print ISSN: 3-97; Online ISSN: 34-48 DOI:.478/cait-3- New Reference-Neighbourhood Scalariation Problem for Multiobjective
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 3 No Sofia 3 Print ISSN: 3-97; Online ISSN: 34-48 DOI:.478/cait-3- New Reference-Neighbourhood Scalariation Problem for Multiobjective
Construction of Interval-valued Fuzzy Preference Relations from Ignorance Functions and Fuzzy Preference Relations. Application to Decision Making
 Construction of Interval-valued Fuzzy Preference Relations from Ignorance Functions and Fuzzy Preference Relations. Application to Decision Making Edurne Barrenechea a, Javier Fernandez a, Miguel Pagola
Construction of Interval-valued Fuzzy Preference Relations from Ignorance Functions and Fuzzy Preference Relations. Application to Decision Making Edurne Barrenechea a, Javier Fernandez a, Miguel Pagola
Ranking Multicriteria Alternatives: the method ZAPROS III. Institute for Systems Analysis, 9, pr. 60 let Octjabrja, Moscow, , Russia.
 Ranking Multicriteria Alternatives: the method ZAPROS III Oleg I. Larichev, Institute for Systems Analysis, 9, pr. 60 let Octabra, Moscow, 117312, Russia. Abstract: The new version of the method for the
Ranking Multicriteria Alternatives: the method ZAPROS III Oleg I. Larichev, Institute for Systems Analysis, 9, pr. 60 let Octabra, Moscow, 117312, Russia. Abstract: The new version of the method for the
Intuitionistic Fuzzy Sets - An Alternative Look
 Intuitionistic Fuzzy Sets - An Alternative Look Anna Pankowska and Maciej Wygralak Faculty of Mathematics and Computer Science Adam Mickiewicz University Umultowska 87, 61-614 Poznań, Poland e-mail: wygralak@math.amu.edu.pl
Intuitionistic Fuzzy Sets - An Alternative Look Anna Pankowska and Maciej Wygralak Faculty of Mathematics and Computer Science Adam Mickiewicz University Umultowska 87, 61-614 Poznań, Poland e-mail: wygralak@math.amu.edu.pl
Mathematical foundations of the methods for multicriterial decision making
 Mathematical Communications 2(1997), 161 169 161 Mathematical foundations of the methods for multicriterial decision making Tihomir Hunjak Abstract In this paper the mathematical foundations of the methods
Mathematical Communications 2(1997), 161 169 161 Mathematical foundations of the methods for multicriterial decision making Tihomir Hunjak Abstract In this paper the mathematical foundations of the methods
REMOVING INCONSISTENCY IN PAIRWISE COMPARISON MATRIX IN THE AHP
 MULTIPLE CRITERIA DECISION MAKING Vol. 11 2016 Sławomir Jarek * REMOVING INCONSISTENCY IN PAIRWISE COMPARISON MATRIX IN THE AHP DOI: 10.22367/mcdm.2016.11.05 Abstract The Analytic Hierarchy Process (AHP)
MULTIPLE CRITERIA DECISION MAKING Vol. 11 2016 Sławomir Jarek * REMOVING INCONSISTENCY IN PAIRWISE COMPARISON MATRIX IN THE AHP DOI: 10.22367/mcdm.2016.11.05 Abstract The Analytic Hierarchy Process (AHP)
Favoring Consensus and Penalizing Disagreement in Group Decision Making
 Favoring Consensus and Penalizing Disagreement in Group Decision Making Paper: jc*-**-**-**** Favoring Consensus and Penalizing Disagreement in Group Decision Making José Luis García-Lapresta PRESAD Research
Favoring Consensus and Penalizing Disagreement in Group Decision Making Paper: jc*-**-**-**** Favoring Consensus and Penalizing Disagreement in Group Decision Making José Luis García-Lapresta PRESAD Research
Normalized priority vectors for fuzzy preference relations
 Normalized priority vectors for fuzzy preference relations Michele Fedrizzi, Matteo Brunelli Dipartimento di Informatica e Studi Aziendali Università di Trento, Via Inama 5, TN 38100 Trento, Italy e mail:
Normalized priority vectors for fuzzy preference relations Michele Fedrizzi, Matteo Brunelli Dipartimento di Informatica e Studi Aziendali Università di Trento, Via Inama 5, TN 38100 Trento, Italy e mail:
A characterization of the 2-additive Choquet integral
 A characterization of the 2-additive Choquet integral Brice Mayag Thales R & T University of Paris I brice.mayag@thalesgroup.com Michel Grabisch University of Paris I Centre d Economie de la Sorbonne 106-112
A characterization of the 2-additive Choquet integral Brice Mayag Thales R & T University of Paris I brice.mayag@thalesgroup.com Michel Grabisch University of Paris I Centre d Economie de la Sorbonne 106-112
B best scales 51, 53 best MCDM method 199 best fuzzy MCDM method bound of maximum consistency 40 "Bridge Evaluation" problem
 SUBJECT INDEX A absolute-any (AA) critical criterion 134, 141, 152 absolute terms 133 absolute-top (AT) critical criterion 134, 141, 151 actual relative weights 98 additive function 228 additive utility
SUBJECT INDEX A absolute-any (AA) critical criterion 134, 141, 152 absolute terms 133 absolute-top (AT) critical criterion 134, 141, 151 actual relative weights 98 additive function 228 additive utility
IN ORDER to reach a decision, experts have to express their
 14 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 17, NO. 1, FEBRUARY 2009 Cardinal Consistency of Reciprocal Preference Relations: A Characterization of Multiplicative Transitivity Francisco Chiclana, Enrique
14 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 17, NO. 1, FEBRUARY 2009 Cardinal Consistency of Reciprocal Preference Relations: A Characterization of Multiplicative Transitivity Francisco Chiclana, Enrique
ORDER STABILITY ANALYSIS OF RECIPROCAL JUDGMENT MATRIX
 ISAHP 003, Bali, Indonesia, August 7-9, 003 ORDER STABILITY ANALYSIS OF RECIPROCAL JUDGMENT MATRIX Mingzhe Wang a Danyi Wang b a Huazhong University of Science and Technology, Wuhan, Hubei 430074 - P.
ISAHP 003, Bali, Indonesia, August 7-9, 003 ORDER STABILITY ANALYSIS OF RECIPROCAL JUDGMENT MATRIX Mingzhe Wang a Danyi Wang b a Huazhong University of Science and Technology, Wuhan, Hubei 430074 - P.
Preservation of t-norm and t-conorm based properties of fuzzy relations during aggregation process
 8th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT 2013) Preservation of t-norm and t-conorm based properties of fuzzy relations during aggregation process Urszula Dudziak Institute
8th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT 2013) Preservation of t-norm and t-conorm based properties of fuzzy relations during aggregation process Urszula Dudziak Institute
On tolerant or intolerant character of interacting criteria in aggregation by the Choquet integral
 On tolerant or intolerant character of interacting criteria in aggregation by the Choquet integral Jean-Luc Marichal Department of Mathematics, Brigham Young University 292 TMCB, Provo, Utah 84602, U.S.A.
On tolerant or intolerant character of interacting criteria in aggregation by the Choquet integral Jean-Luc Marichal Department of Mathematics, Brigham Young University 292 TMCB, Provo, Utah 84602, U.S.A.
On measuring and testing the ordinal correlation between valued outranking relations
 On measuring and testing the ordinal correlation between valued outranking relations Raymond Bisdorff University of Luxembourg, FSTC/CSC/ILIAS raymond.bisdorff@uni.lu Abstract. We generalize Kendall s
On measuring and testing the ordinal correlation between valued outranking relations Raymond Bisdorff University of Luxembourg, FSTC/CSC/ILIAS raymond.bisdorff@uni.lu Abstract. We generalize Kendall s
Strategic Manipulation and Regular Decomposition of Fuzzy Preference Relations
 Strategic Manipulation and Regular Decomposition of Fuzzy Preference Relations Olfa Meddeb, Fouad Ben Abdelaziz, José Rui Figueira September 27, 2007 LARODEC, Institut Supérieur de Gestion, 41, Rue de
Strategic Manipulation and Regular Decomposition of Fuzzy Preference Relations Olfa Meddeb, Fouad Ben Abdelaziz, José Rui Figueira September 27, 2007 LARODEC, Institut Supérieur de Gestion, 41, Rue de
Fusing Interval Preferences
 Fusing Interval Preferences Taner Bilgiç Department of Industrial Engineering Boğaziçi University Bebek, İstanbul, 80815 Turkey taner@boun.edu.tr Appeared in Proceedings of EUROFUSE Workshop on Preference
Fusing Interval Preferences Taner Bilgiç Department of Industrial Engineering Boğaziçi University Bebek, İstanbul, 80815 Turkey taner@boun.edu.tr Appeared in Proceedings of EUROFUSE Workshop on Preference
Comparison of Judgment Scales of the Analytical Hierarchy Process - A New Approach
 Comparison of Judgment Scales of the Analytical Hierarchy Process - A New Approach Klaus D. Goepel a a BPMSG Business Performance Management Singapore 2 Bedok Reservoir View #17-02, Singapore 479232 E-mail
Comparison of Judgment Scales of the Analytical Hierarchy Process - A New Approach Klaus D. Goepel a a BPMSG Business Performance Management Singapore 2 Bedok Reservoir View #17-02, Singapore 479232 E-mail
A risk attitudinal ranking method for interval-valued intuitionistic fuzzy numbers based on novel attitudinal expected score and accuracy functions
 A risk attitudinal ranking method for interval-valued intuitionistic fuzzy numbers based on novel attitudinal expected score and accuracy functions Jian Wu a,b, Francisco Chiclana b a School of conomics
A risk attitudinal ranking method for interval-valued intuitionistic fuzzy numbers based on novel attitudinal expected score and accuracy functions Jian Wu a,b, Francisco Chiclana b a School of conomics
A Comparative Study of Different Order Relations of Intervals
 A Comparative Study of Different Order Relations of Intervals Samiran Karmakar Department of Business Mathematics and Statistics, St. Xavier s College, Kolkata, India skmath.rnc@gmail.com A. K. Bhunia
A Comparative Study of Different Order Relations of Intervals Samiran Karmakar Department of Business Mathematics and Statistics, St. Xavier s College, Kolkata, India skmath.rnc@gmail.com A. K. Bhunia
Fuzzy relation equations with dual composition
 Fuzzy relation equations with dual composition Lenka Nosková University of Ostrava Institute for Research and Applications of Fuzzy Modeling 30. dubna 22, 701 03 Ostrava 1 Czech Republic Lenka.Noskova@osu.cz
Fuzzy relation equations with dual composition Lenka Nosková University of Ostrava Institute for Research and Applications of Fuzzy Modeling 30. dubna 22, 701 03 Ostrava 1 Czech Republic Lenka.Noskova@osu.cz
The modeling of the preference structure of a decision maker can, grosso mode, be 263
 ARGUS - A NEW MULTIPLE CRITERIA METHOD BASED ON THE GENERAL IDEA OF OUTRANKING 1. Introduction W.S.M. DE KEYSER and P.H.M. PEETERS Vrije Universiteit Brussel Centrum voor Statistiek en Operationeel Onderzoek
ARGUS - A NEW MULTIPLE CRITERIA METHOD BASED ON THE GENERAL IDEA OF OUTRANKING 1. Introduction W.S.M. DE KEYSER and P.H.M. PEETERS Vrije Universiteit Brussel Centrum voor Statistiek en Operationeel Onderzoek
The possible and the necessary for multiple criteria group decision
 The possible and the necessary for multiple criteria group decision Salvatore Greco 1, Vincent Mousseau 2 and Roman S lowiński 3 1 Faculty of Economics, University of Catania, Italy, salgreco@unict.it,
The possible and the necessary for multiple criteria group decision Salvatore Greco 1, Vincent Mousseau 2 and Roman S lowiński 3 1 Faculty of Economics, University of Catania, Italy, salgreco@unict.it,
Jian Wu a,b, Francisco Chiclana b,c. Abstract
 *Manuscript (including abstract Click here to view linked References Visual information feedback mechanism and attitudinal prioritisation method for group decision making with triangular fuzzy complementary
*Manuscript (including abstract Click here to view linked References Visual information feedback mechanism and attitudinal prioritisation method for group decision making with triangular fuzzy complementary
THE IMPACT ON SCALING ON THE PAIR-WISE COMPARISON OF THE ANALYTIC HIERARCHY PROCESS
 ISAHP 200, Berne, Switzerland, August 2-4, 200 THE IMPACT ON SCALING ON THE PAIR-WISE COMPARISON OF THE ANALYTIC HIERARCHY PROCESS Yuji Sato Department of Policy Science, Matsusaka University 846, Kubo,
ISAHP 200, Berne, Switzerland, August 2-4, 200 THE IMPACT ON SCALING ON THE PAIR-WISE COMPARISON OF THE ANALYTIC HIERARCHY PROCESS Yuji Sato Department of Policy Science, Matsusaka University 846, Kubo,
Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC - Coimbra
 Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC - Coimbra Claude Lamboray Luis C. Dias Pairwise support maximization methods to exploit
Instituto de Engenharia de Sistemas e Computadores de Coimbra Institute of Systems Engineering and Computers INESC - Coimbra Claude Lamboray Luis C. Dias Pairwise support maximization methods to exploit
LOCATION OF PREHOSPITAL CARE BASIS THROUGH COMBINED FUZZY AHP AND GIS METHOD
 ISAHP Article: Mu, Saaty/A Style Guide for Paper Proposals To Be Submitted to the LOCATION OF PREHOSPITAL CARE BASIS THROUGH COMBINED FUZZY AHP AND GIS METHOD Marco Tiznado Departamento de Ingeniería Industrial,
ISAHP Article: Mu, Saaty/A Style Guide for Paper Proposals To Be Submitted to the LOCATION OF PREHOSPITAL CARE BASIS THROUGH COMBINED FUZZY AHP AND GIS METHOD Marco Tiznado Departamento de Ingeniería Industrial,
Lecture 04 Decision Making under Certainty: The Tradeoff Problem
 Lecture 04 Decision Making under Certainty: The Tradeoff Problem Jitesh H. Panchal ME 597: Decision Making for Engineering Systems Design Design Engineering Lab @ Purdue (DELP) School of Mechanical Engineering
Lecture 04 Decision Making under Certainty: The Tradeoff Problem Jitesh H. Panchal ME 597: Decision Making for Engineering Systems Design Design Engineering Lab @ Purdue (DELP) School of Mechanical Engineering
Similarity-based Classification with Dominance-based Decision Rules
 Similarity-based Classification with Dominance-based Decision Rules Marcin Szeląg, Salvatore Greco 2,3, Roman Słowiński,4 Institute of Computing Science, Poznań University of Technology, 60-965 Poznań,
Similarity-based Classification with Dominance-based Decision Rules Marcin Szeląg, Salvatore Greco 2,3, Roman Słowiński,4 Institute of Computing Science, Poznań University of Technology, 60-965 Poznań,
Towards Decision Making under Interval Uncertainty
 Journal of Uncertain Systems Vol.1, No.3, pp.00-07, 018 Online at: www.us.org.uk Towards Decision Making under Interval Uncertainty Andrze Pownuk, Vladik Kreinovich Computational Science Program, University
Journal of Uncertain Systems Vol.1, No.3, pp.00-07, 018 Online at: www.us.org.uk Towards Decision Making under Interval Uncertainty Andrze Pownuk, Vladik Kreinovich Computational Science Program, University
Research Article Deriving Weights of Criteria from Inconsistent Fuzzy Comparison Matrices by Using the Nearest Weighted Interval Approximation
 Advances in Operations Research Volume 202, Article ID 57470, 7 pages doi:0.55/202/57470 Research Article Deriving Weights of Criteria from Inconsistent Fuzzy Comparison Matrices by Using the Nearest Weighted
Advances in Operations Research Volume 202, Article ID 57470, 7 pages doi:0.55/202/57470 Research Article Deriving Weights of Criteria from Inconsistent Fuzzy Comparison Matrices by Using the Nearest Weighted
A Group Analytic Network Process (ANP) for Incomplete Information
 A Group Analytic Network Process (ANP) for Incomplete Information Kouichi TAJI Yousuke Sagayama August 5, 2004 Abstract In this paper, we propose an ANP framework for group decision-making problem with
A Group Analytic Network Process (ANP) for Incomplete Information Kouichi TAJI Yousuke Sagayama August 5, 2004 Abstract In this paper, we propose an ANP framework for group decision-making problem with
POSET-VALUED PREFERENCE RELATIONS
 K Y B E R N E T I K A V O L U M E?? (???? ), N U M B E R?, P A G E S 1 1 8 POSET-VALUED PREFERENCE RELATIONS Vladimír Janiš, Susana Montes, Branimir Šešelja and Andreja Tepavčević In decision processes
K Y B E R N E T I K A V O L U M E?? (???? ), N U M B E R?, P A G E S 1 1 8 POSET-VALUED PREFERENCE RELATIONS Vladimír Janiš, Susana Montes, Branimir Šešelja and Andreja Tepavčević In decision processes
Left-continuous t-norms in Fuzzy Logic: an Overview
 Left-continuous t-norms in Fuzzy Logic: an Overview János Fodor Dept. of Biomathematics and Informatics, Faculty of Veterinary Sci. Szent István University, István u. 2, H-1078 Budapest, Hungary E-mail:
Left-continuous t-norms in Fuzzy Logic: an Overview János Fodor Dept. of Biomathematics and Informatics, Faculty of Veterinary Sci. Szent István University, István u. 2, H-1078 Budapest, Hungary E-mail:
Compenzational Vagueness
 Compenzational Vagueness Milan Mareš Institute of information Theory and Automation Academy of Sciences of the Czech Republic P. O. Box 18, 182 08 Praha 8, Czech Republic mares@utia.cas.cz Abstract Some
Compenzational Vagueness Milan Mareš Institute of information Theory and Automation Academy of Sciences of the Czech Republic P. O. Box 18, 182 08 Praha 8, Czech Republic mares@utia.cas.cz Abstract Some
Axioms of the Analytic Hierarchy Process (AHP) and its Generalization to Dependence and Feedback: The Analytic Network Process (ANP)
 Axioms of the Analytic Hierarchy Process (AHP) and its Generalization to Dependence and Feedback: The Analytic Network Process (ANP) Thomas L. Saaty Distinguished University Professor, University of Pittsburgh;
Axioms of the Analytic Hierarchy Process (AHP) and its Generalization to Dependence and Feedback: The Analytic Network Process (ANP) Thomas L. Saaty Distinguished University Professor, University of Pittsburgh;
Interactive Multi-Objective Optimization (MOO) using a Set of Additive Value Functions
 Interactive Multi-Objective Optimization (MOO) using a Set of Additive Value Functions José Rui Figueira 1, Salvatore Greco 2, Vincent Mousseau 3, and Roman Słowiński 4 1 CEG-IST, Center for Management
Interactive Multi-Objective Optimization (MOO) using a Set of Additive Value Functions José Rui Figueira 1, Salvatore Greco 2, Vincent Mousseau 3, and Roman Słowiński 4 1 CEG-IST, Center for Management
Chapter 6. Intuitionistic Fuzzy PROMETHEE Technique. AIDS stands for acquired immunodeficiency syndrome. AIDS is the final stage. 6.
 Chapter 6 Intuitionistic Fuzzy PROMETHEE Technique 6.1 Introduction AIDS stands for acquired immunodeficiency syndrome. AIDS is the final stage of HIV infection, and not everyone who has HIV advances to
Chapter 6 Intuitionistic Fuzzy PROMETHEE Technique 6.1 Introduction AIDS stands for acquired immunodeficiency syndrome. AIDS is the final stage of HIV infection, and not everyone who has HIV advances to
A minimum adjustment cost feedback mechanism based consensus model for group decision making under social network with distributed linguistic trust
 A minimum adjustment cost feedback mechanism based consensus model for group decision making under social network with distributed linguistic trust Jian Wu a, Lifang Dai b, Francisco Chiclana c, Hamido
A minimum adjustment cost feedback mechanism based consensus model for group decision making under social network with distributed linguistic trust Jian Wu a, Lifang Dai b, Francisco Chiclana c, Hamido
TIES598 Nonlinear Multiobjective Optimization A priori and a posteriori methods spring 2017
 TIES598 Nonlinear Multiobjective Optimization A priori and a posteriori methods spring 2017 Jussi Hakanen jussi.hakanen@jyu.fi Contents A priori methods A posteriori methods Some example methods Learning
TIES598 Nonlinear Multiobjective Optimization A priori and a posteriori methods spring 2017 Jussi Hakanen jussi.hakanen@jyu.fi Contents A priori methods A posteriori methods Some example methods Learning
An axiomatic approach of the discrete Sugeno integral as a tool to aggregate interacting criteria in a qualitative framework
 An axiomatic approach of the discrete Sugeno integral as a tool to aggregate interacting criteria in a qualitative framework Jean-Luc Marichal Revised version, September 20, 2000 Abstract We present a
An axiomatic approach of the discrete Sugeno integral as a tool to aggregate interacting criteria in a qualitative framework Jean-Luc Marichal Revised version, September 20, 2000 Abstract We present a
Econ 2148, spring 2019 Statistical decision theory
 Econ 2148, spring 2019 Statistical decision theory Maximilian Kasy Department of Economics, Harvard University 1 / 53 Takeaways for this part of class 1. A general framework to think about what makes a
Econ 2148, spring 2019 Statistical decision theory Maximilian Kasy Department of Economics, Harvard University 1 / 53 Takeaways for this part of class 1. A general framework to think about what makes a
Why pairwise comparison methods may fail in MCDM rankings
 Why pairwise comparison methods may fail in MCDM rankings PL Kunsch Abstract This article is based on previous author s articles on a correct way for ranking alternatives in Multi-criteria Decision-Making
Why pairwise comparison methods may fail in MCDM rankings PL Kunsch Abstract This article is based on previous author s articles on a correct way for ranking alternatives in Multi-criteria Decision-Making
Incomplete Pairwise Comparison Matrices and Weighting Methods
 Incomplete Pairwise Comparison Matrices and Weighting Methods László Csató Lajos Rónyai arxiv:1507.00461v2 [math.oc] 27 Aug 2015 August 28, 2015 Abstract A special class of preferences, given by a directed
Incomplete Pairwise Comparison Matrices and Weighting Methods László Csató Lajos Rónyai arxiv:1507.00461v2 [math.oc] 27 Aug 2015 August 28, 2015 Abstract A special class of preferences, given by a directed
Decomposition of the transitivity for additive fuzzy preference structures
 Decomposition of the transitivity for additive fuzzy preference structures Susana Díaz, Susana Montes 1 Bernard De Baets 1.Dept. of Statistics and O.R., University of Oviedo Oviedo, Spain.Dept. of Applied
Decomposition of the transitivity for additive fuzzy preference structures Susana Díaz, Susana Montes 1 Bernard De Baets 1.Dept. of Statistics and O.R., University of Oviedo Oviedo, Spain.Dept. of Applied
Group Decision Making with Incomplete Reciprocal Preference Relations Based on Multiplicative Consistency
 Group Decision Making with Incomplete Reciprocal Preference Relations Based on Multiplicative Consistency Etienne E Kerre, Ati-ur-Rehman, Samina Ashraf 3 Department of Applied Mathematics, Computer Science
Group Decision Making with Incomplete Reciprocal Preference Relations Based on Multiplicative Consistency Etienne E Kerre, Ati-ur-Rehman, Samina Ashraf 3 Department of Applied Mathematics, Computer Science
IN GROUP-decision-making (GDM) analysis, the preference
 http://wwwpapereducn IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS PART B: CYBERNETICS, VOL 0, NO 5, OCTOBER 00 An Approach to Solve Group-Decision-Making Problems With Ordinal Interval Numbers Zhi-Ping
http://wwwpapereducn IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS PART B: CYBERNETICS, VOL 0, NO 5, OCTOBER 00 An Approach to Solve Group-Decision-Making Problems With Ordinal Interval Numbers Zhi-Ping
Nonlinear Optimization Subject to a System of Fuzzy Relational Equations with Max-min Composition
 The 7th International Symposium on Operations Research and Its Applications (ISORA 08) Lijiang, China, October 31 Novemver 3, 2008 Copyright 2008 ORSC & APORC, pp. 1 9 Nonlinear Optimization Subject to
The 7th International Symposium on Operations Research and Its Applications (ISORA 08) Lijiang, China, October 31 Novemver 3, 2008 Copyright 2008 ORSC & APORC, pp. 1 9 Nonlinear Optimization Subject to
Set-based Min-max and Min-min Robustness for Multi-objective Robust Optimization
 Proceedings of the 2017 Industrial and Systems Engineering Research Conference K. Coperich, E. Cudney, H. Nembhard, eds. Set-based Min-max and Min-min Robustness for Multi-objective Robust Optimization
Proceedings of the 2017 Industrial and Systems Engineering Research Conference K. Coperich, E. Cudney, H. Nembhard, eds. Set-based Min-max and Min-min Robustness for Multi-objective Robust Optimization
PREFERENCE MATRICES IN TROPICAL ALGEBRA
 PREFERENCE MATRICES IN TROPICAL ALGEBRA 1 Introduction Hana Tomášková University of Hradec Králové, Faculty of Informatics and Management, Rokitanského 62, 50003 Hradec Králové, Czech Republic e-mail:
PREFERENCE MATRICES IN TROPICAL ALGEBRA 1 Introduction Hana Tomášková University of Hradec Králové, Faculty of Informatics and Management, Rokitanského 62, 50003 Hradec Králové, Czech Republic e-mail:
Preservation of graded properties of fuzzy relations by aggregation functions
 Preservation of graded properties of fuzzy relations by aggregation functions Urszula Dudziak Institute of Mathematics, University of Rzeszów, 35-310 Rzeszów, ul. Rejtana 16a, Poland. e-mail: ududziak@univ.rzeszow.pl
Preservation of graded properties of fuzzy relations by aggregation functions Urszula Dudziak Institute of Mathematics, University of Rzeszów, 35-310 Rzeszów, ul. Rejtana 16a, Poland. e-mail: ududziak@univ.rzeszow.pl
Previous Accomplishments. Focus of Research Iona College. Focus of Research Iona College. Publication List Iona College. Journals
 Network-based Hard/Soft Information Fusion: Soft Information and its Fusion Ronald R. Yager, Tel. 212 249 2047, E-Mail: yager@panix.com Objectives: Support development of hard/soft information fusion Develop
Network-based Hard/Soft Information Fusion: Soft Information and its Fusion Ronald R. Yager, Tel. 212 249 2047, E-Mail: yager@panix.com Objectives: Support development of hard/soft information fusion Develop
Theoretical Foundation of Uncertain Dominance
 Theoretical Foundation of Uncertain Dominance Yang Zuo, Xiaoyu Ji 2 Uncertainty Theory Laboratory, Department of Mathematical Sciences Tsinghua University, Beijing 84, China 2 School of Business, Renmin
Theoretical Foundation of Uncertain Dominance Yang Zuo, Xiaoyu Ji 2 Uncertainty Theory Laboratory, Department of Mathematical Sciences Tsinghua University, Beijing 84, China 2 School of Business, Renmin
VI Fuzzy Optimization
 VI Fuzzy Optimization 1. Fuzziness, an introduction 2. Fuzzy membership functions 2.1 Membership function operations 3. Optimization in fuzzy environments 3.1 Water allocation 3.2 Reservoir storage and
VI Fuzzy Optimization 1. Fuzziness, an introduction 2. Fuzzy membership functions 2.1 Membership function operations 3. Optimization in fuzzy environments 3.1 Water allocation 3.2 Reservoir storage and
Uncertain Quadratic Minimum Spanning Tree Problem
 Uncertain Quadratic Minimum Spanning Tree Problem Jian Zhou Xing He Ke Wang School of Management Shanghai University Shanghai 200444 China Email: zhou_jian hexing ke@shu.edu.cn Abstract The quadratic minimum
Uncertain Quadratic Minimum Spanning Tree Problem Jian Zhou Xing He Ke Wang School of Management Shanghai University Shanghai 200444 China Email: zhou_jian hexing ke@shu.edu.cn Abstract The quadratic minimum
MADM method Input Output Decision types DM interaction Assumptions MCDM software Attribute scores, Moderate Nonrestrictive Spreadsheets 7eights
 Aggregation methods This document is made of excerpts extracted from: Malcze7ski, :. (1>>>) GIS and multicriteria decision analysis. :ohn Diley E Sons Inc. Ne7 Gork These methods are only for attribute
Aggregation methods This document is made of excerpts extracted from: Malcze7ski, :. (1>>>) GIS and multicriteria decision analysis. :ohn Diley E Sons Inc. Ne7 Gork These methods are only for attribute
Linguistic-Valued Approximate Reasoning With Lattice Ordered Linguistic-Valued Credibility
 International Journal of Computational Intelligence Systems, Vol. 8, No. 1 (2015) 53-61 Linguistic-Valued Approximate Reasoning With Lattice Ordered Linguistic-Valued Credibility Li Zou and Yunxia Zhang
International Journal of Computational Intelligence Systems, Vol. 8, No. 1 (2015) 53-61 Linguistic-Valued Approximate Reasoning With Lattice Ordered Linguistic-Valued Credibility Li Zou and Yunxia Zhang
An hybrid model of Mathematical Programming and analytic hierarchy process for the GISMR: The Industrial localization
 6th WSEAS International Conference on CIRCUITS, SYSTEMS, ELECTRONICS,CONTROL & SIGNAL PROCESSING, Cairo, Egypt, Dec 29-31, 2007 559 An hybrid model of Mathematical Programming and analytic hierarchy process
6th WSEAS International Conference on CIRCUITS, SYSTEMS, ELECTRONICS,CONTROL & SIGNAL PROCESSING, Cairo, Egypt, Dec 29-31, 2007 559 An hybrid model of Mathematical Programming and analytic hierarchy process
Comparison between Interval and Fuzzy Load Flow Methods Considering Uncertainty
 Comparison between Interval and Fuzzy Load Flow Methods Considering Uncertainty T.Srinivasarao, 2 P.Mallikarajunarao Department of Electrical Engineering, College of Engineering (A), Andhra University,
Comparison between Interval and Fuzzy Load Flow Methods Considering Uncertainty T.Srinivasarao, 2 P.Mallikarajunarao Department of Electrical Engineering, College of Engineering (A), Andhra University,
Fuzzy if-then rules for modeling interdependences in FMOP problems
 Fuzzy if-then rules for modeling interdependences in FMOP problems Christer Carlsson Institute for Advanced Management Systems Research, Åbo Akademi University, DataCity A 3210, SF-20520 Åbo, Finland Robert
Fuzzy if-then rules for modeling interdependences in FMOP problems Christer Carlsson Institute for Advanced Management Systems Research, Åbo Akademi University, DataCity A 3210, SF-20520 Åbo, Finland Robert
DECISION MAKING SUPPORT AND EXPERT SYSTEMS
 325 ITHEA DECISION MAKING SUPPORT AND EXPERT SYSTEMS UTILITY FUNCTION DESIGN ON THE BASE OF THE PAIRED COMPARISON MATRIX Stanislav Mikoni Abstract: In the multi-attribute utility theory the utility functions
325 ITHEA DECISION MAKING SUPPORT AND EXPERT SYSTEMS UTILITY FUNCTION DESIGN ON THE BASE OF THE PAIRED COMPARISON MATRIX Stanislav Mikoni Abstract: In the multi-attribute utility theory the utility functions
Uninorm trust propagation and aggregation methods for group decision making in social network with four tuple information
 Uninorm trust propagation and aggregation methods for group decision making in social network with four tuple information Jian Wu a,b, Ruoyun Xiong a, Francisco Chiclana b a School of Economics and Management,
Uninorm trust propagation and aggregation methods for group decision making in social network with four tuple information Jian Wu a,b, Ruoyun Xiong a, Francisco Chiclana b a School of Economics and Management,
Chapter 1 - Preference and choice
 http://selod.ensae.net/m1 Paris School of Economics (selod@ens.fr) September 27, 2007 Notations Consider an individual (agent) facing a choice set X. Definition (Choice set, "Consumption set") X is a set
http://selod.ensae.net/m1 Paris School of Economics (selod@ens.fr) September 27, 2007 Notations Consider an individual (agent) facing a choice set X. Definition (Choice set, "Consumption set") X is a set
INTEGRATION OF GIS AND MULTICRITORIAL HIERARCHICAL ANALYSIS FOR AID IN URBAN PLANNING: CASE STUDY OF KHEMISSET PROVINCE, MOROCCO
 Geography Papers 2017, 63 DOI: http://dx.doi.org/10.6018/geografia/2017/280211 ISSN: 1989-4627 INTEGRATION OF GIS AND MULTICRITORIAL HIERARCHICAL ANALYSIS FOR AID IN URBAN PLANNING: CASE STUDY OF KHEMISSET
Geography Papers 2017, 63 DOI: http://dx.doi.org/10.6018/geografia/2017/280211 ISSN: 1989-4627 INTEGRATION OF GIS AND MULTICRITORIAL HIERARCHICAL ANALYSIS FOR AID IN URBAN PLANNING: CASE STUDY OF KHEMISSET
Valued relations aggregation with the Borda method.
 Valued relations aggregation with the Borda method. Thierry Marchant* Service de mathématiques de la gestion, Université Libre de Bruxelles, Boulevard du Triomphe CP210-01, 1050 Bruxelles, Belgium. Tél
Valued relations aggregation with the Borda method. Thierry Marchant* Service de mathématiques de la gestion, Université Libre de Bruxelles, Boulevard du Triomphe CP210-01, 1050 Bruxelles, Belgium. Tél
New Weighted Sum Model
 Filomat 31:10 (2017), 2991 2998 https://doi.org/10.2298/fil1710991m Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat New Weighted
Filomat 31:10 (2017), 2991 2998 https://doi.org/10.2298/fil1710991m Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat New Weighted
A general unified framework for interval pairwise comparison matrices
 A general unified framework for interval pairwise comparison matrices Bice Cavallo a and Matteo Brunelli b a Department of Architecture, University of Naples Federico II, Italy e mail: bice.cavallo@unina.it
A general unified framework for interval pairwise comparison matrices Bice Cavallo a and Matteo Brunelli b a Department of Architecture, University of Naples Federico II, Italy e mail: bice.cavallo@unina.it
Adapting the DF-QuAD Algorithm to Bipolar Argumentation
 Adapting the DF-QuAD Algorithm to Bipolar Argumentation Antonio RAGO a,1, Kristijonas ČYRAS a and Francesca TONI a a Department of Computing, Imperial College London, UK Abstract. We define a quantitative
Adapting the DF-QuAD Algorithm to Bipolar Argumentation Antonio RAGO a,1, Kristijonas ČYRAS a and Francesca TONI a a Department of Computing, Imperial College London, UK Abstract. We define a quantitative
Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ]
![Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ] Definitions: A binary relation R on a set X is (a) reflexive if x X : xrx; (f) asymmetric if x, x X : [x Rx xr c x ]](/thumbs/72/67754492.jpg) Binary Relations Definition: A binary relation between two sets X and Y (or between the elements of X and Y ) is a subset of X Y i.e., is a set of ordered pairs (x, y) X Y. If R is a relation between X
Binary Relations Definition: A binary relation between two sets X and Y (or between the elements of X and Y ) is a subset of X Y i.e., is a set of ordered pairs (x, y) X Y. If R is a relation between X
On Decision Making under Interval Uncertainty: A New Justification of Hurwicz Optimism-Pessimism Approach and Its Use in Group Decision Making
 On Decision Making under Interval Uncertainty: A New Justification of Hurwicz Optimism-Pessimism Approach and Its Use in Group Decision Making Van Nam Huynh 1, Chenyi Hu, Yoshiteru Nakamori 1, and Vladik
On Decision Making under Interval Uncertainty: A New Justification of Hurwicz Optimism-Pessimism Approach and Its Use in Group Decision Making Van Nam Huynh 1, Chenyi Hu, Yoshiteru Nakamori 1, and Vladik
Weighting Expert Opinions in Group Decision Making for the Influential Effects between Variables in a Bayesian Network Model
 Weighting Expert Opinions in Group Decision Making for the Influential Effects between Variables in a Bayesian Network Model Nipat Jongsawat 1, Wichian Premchaiswadi 2 Graduate School of Information Technology
Weighting Expert Opinions in Group Decision Making for the Influential Effects between Variables in a Bayesian Network Model Nipat Jongsawat 1, Wichian Premchaiswadi 2 Graduate School of Information Technology
Lecture notes on statistical decision theory Econ 2110, fall 2013
 Lecture notes on statistical decision theory Econ 2110, fall 2013 Maximilian Kasy March 10, 2014 These lecture notes are roughly based on Robert, C. (2007). The Bayesian choice: from decision-theoretic
Lecture notes on statistical decision theory Econ 2110, fall 2013 Maximilian Kasy March 10, 2014 These lecture notes are roughly based on Robert, C. (2007). The Bayesian choice: from decision-theoretic
Research Article A Fictitious Play Algorithm for Matrix Games with Fuzzy Payoffs
 Abstract and Applied Analysis Volume 2012, Article ID 950482, 12 pages doi:101155/2012/950482 Research Article A Fictitious Play Algorithm for Matrix Games with Fuzzy Payoffs Emrah Akyar Department of
Abstract and Applied Analysis Volume 2012, Article ID 950482, 12 pages doi:101155/2012/950482 Research Article A Fictitious Play Algorithm for Matrix Games with Fuzzy Payoffs Emrah Akyar Department of
Non Additive Measures for Group Multi Attribute Decision Models
 Non Additive Measures for Group Multi Attribute Decision Models Marta Cardin, Silvio Giove Dept. of Applied Mathematics, University of Venice Venice, Italy Email: mcardin@unive.it, sgiove@unive.it Abstract
Non Additive Measures for Group Multi Attribute Decision Models Marta Cardin, Silvio Giove Dept. of Applied Mathematics, University of Venice Venice, Italy Email: mcardin@unive.it, sgiove@unive.it Abstract
IN many real-life situations we come across problems with
 Algorithm for Interval Linear Programming Involving Interval Constraints Ibraheem Alolyan Abstract In real optimization, we always meet the criteria of useful outcomes increasing or expenses decreasing
Algorithm for Interval Linear Programming Involving Interval Constraints Ibraheem Alolyan Abstract In real optimization, we always meet the criteria of useful outcomes increasing or expenses decreasing
arxiv: v2 [math.co] 14 Apr 2011
![arxiv: v2 [math.co] 14 Apr 2011 arxiv: v2 [math.co] 14 Apr 2011](/thumbs/94/118914939.jpg) Complete Characterization of Functions Satisfying the Conditions of Arrow s Theorem Elchanan Mossel and Omer Tamuz arxiv:0910.2465v2 [math.co] 14 Apr 2011 April 15, 2011 Abstract Arrow s theorem implies
Complete Characterization of Functions Satisfying the Conditions of Arrow s Theorem Elchanan Mossel and Omer Tamuz arxiv:0910.2465v2 [math.co] 14 Apr 2011 April 15, 2011 Abstract Arrow s theorem implies
Computations Under Time Constraints: Algorithms Developed for Fuzzy Computations can Help
 Journal of Uncertain Systems Vol.6, No.2, pp.138-145, 2012 Online at: www.jus.org.uk Computations Under Time Constraints: Algorithms Developed for Fuzzy Computations can Help Karen Villaverde 1, Olga Kosheleva
Journal of Uncertain Systems Vol.6, No.2, pp.138-145, 2012 Online at: www.jus.org.uk Computations Under Time Constraints: Algorithms Developed for Fuzzy Computations can Help Karen Villaverde 1, Olga Kosheleva
First-Level Transitivity Rule Method for Filling in Incomplete Pair-Wise Comparison Matrices in the Analytic Hierarchy Process
 Appl. Math. Inf. Sci. 8, No. 2, 459-467 (2014) 459 Applied Mathematics & Information Sciences An International Journal http://dx.doi.org/10.12785/amis/080202 First-Level Transitivity Rule Method for Filling
Appl. Math. Inf. Sci. 8, No. 2, 459-467 (2014) 459 Applied Mathematics & Information Sciences An International Journal http://dx.doi.org/10.12785/amis/080202 First-Level Transitivity Rule Method for Filling
POL502: Foundations. Kosuke Imai Department of Politics, Princeton University. October 10, 2005
 POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
Włodzimierz Ogryczak. Warsaw University of Technology, ICCE ON ROBUST SOLUTIONS TO MULTI-OBJECTIVE LINEAR PROGRAMS. Introduction. Abstract.
 Włodzimierz Ogryczak Warsaw University of Technology, ICCE ON ROBUST SOLUTIONS TO MULTI-OBJECTIVE LINEAR PROGRAMS Abstract In multiple criteria linear programming (MOLP) any efficient solution can be found
Włodzimierz Ogryczak Warsaw University of Technology, ICCE ON ROBUST SOLUTIONS TO MULTI-OBJECTIVE LINEAR PROGRAMS Abstract In multiple criteria linear programming (MOLP) any efficient solution can be found
CREDIBILITY THEORY ORIENTED PREFERENCE INDEX FOR RANKING FUZZY NUMBERS
 Iranian Journal of Fuzzy Systems Vol. 4, No. 6, (27) pp. 3-7 3 CREDIBILITY THEORY ORIENTED PREFERENCE INDEX FOR RANKING FUZZY NUMBERS G. HESAMIAN AND F. BAHRAMI Abstract. This paper suggests a novel approach
Iranian Journal of Fuzzy Systems Vol. 4, No. 6, (27) pp. 3-7 3 CREDIBILITY THEORY ORIENTED PREFERENCE INDEX FOR RANKING FUZZY NUMBERS G. HESAMIAN AND F. BAHRAMI Abstract. This paper suggests a novel approach
Best Guaranteed Result Principle and Decision Making in Operations with Stochastic Factors and Uncertainty
 Stochastics and uncertainty underlie all the processes of the Universe. N.N.Moiseev Best Guaranteed Result Principle and Decision Making in Operations with Stochastic Factors and Uncertainty by Iouldouz
Stochastics and uncertainty underlie all the processes of the Universe. N.N.Moiseev Best Guaranteed Result Principle and Decision Making in Operations with Stochastic Factors and Uncertainty by Iouldouz
Transportation, Transshipment, and Assignment Problems
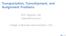 Transportation, Transshipment, and Assignment Problems Prof. Yongwon Seo (seoyw@cau.ac.kr) College of Business Administration, CAU Transportation, Transshipment, and Assignment Problems TRANSPORTATION
Transportation, Transshipment, and Assignment Problems Prof. Yongwon Seo (seoyw@cau.ac.kr) College of Business Administration, CAU Transportation, Transshipment, and Assignment Problems TRANSPORTATION
The PROMTHEE II Method Based on Probabilistic Linguistic Information and Their Application to Decision Making
 INFORMATICA, 2018, Vol. 29, No. 2, 303 320 303 2018 Vilnius University DOI: http://dx.doi.org/10.15388/informatica.2018.169 The PROMTHEE II Method Based on Probabilistic Linguistic Information and Their
INFORMATICA, 2018, Vol. 29, No. 2, 303 320 303 2018 Vilnius University DOI: http://dx.doi.org/10.15388/informatica.2018.169 The PROMTHEE II Method Based on Probabilistic Linguistic Information and Their
Towards Morphological Design of GSM Network
 !"$#%#'&(&)*+,.-0/%1(2(3/(45&(- #&5&)87:9;= @:
!"$#%#'&(&)*+,.-0/%1(2(3/(45&(- #&5&)87:9;= @:
A soft computing logic method for agricultural land suitability evaluation
 A soft computing logic method for agricultural land suitability evaluation B. Montgomery 1, S. Dragićević 1* and J. Dujmović 2 1 Geography Department, Simon Fraser University, 8888 University Drive, Burnaby,
A soft computing logic method for agricultural land suitability evaluation B. Montgomery 1, S. Dragićević 1* and J. Dujmović 2 1 Geography Department, Simon Fraser University, 8888 University Drive, Burnaby,
Pairing Transitive Closure and Reduction to Efficiently Reason about Partially Ordered Events
 Pairing Transitive Closure and Reduction to Efficiently Reason about Partially Ordered Events Massimo Franceschet Angelo Montanari Dipartimento di Matematica e Informatica, Università di Udine Via delle
Pairing Transitive Closure and Reduction to Efficiently Reason about Partially Ordered Events Massimo Franceschet Angelo Montanari Dipartimento di Matematica e Informatica, Università di Udine Via delle
