MA : Introductory Probability
|
|
|
- Ellen Gilmore
- 5 years ago
- Views:
Transcription
1 MA : Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky Spring 2017 David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
2 Suppose X and Y are two independent discrete random variables with distribution functions f 1 (x) and f 2 (x). Let Z = X + Y. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
3 Suppose X and Y are two independent discrete random variables with distribution functions f 1 (x) and f 2 (x). Let Z = X + Y. Suppose that X = k, where k is some integer. Then Z = z if and only if Y = z k. So the event Z = z is the union of the pairwise disjoint events {X = k} and {Y = z k} where k runs over the integers. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
4 Suppose X and Y are two independent discrete random variables with distribution functions f 1 (x) and f 2 (x). Let Z = X + Y. Suppose that X = k, where k is some integer. Then Z = z if and only if Y = z k. So the event Z = z is the union of the pairwise disjoint events {X = k} and {Y = z k} where k runs over the integers. Since these events are pairwise disjoint, we have P(Z = z) = k= P(X = k) P(Y = z k) Thus, we have found the distribution function of the random variable Z. This leads to the following definition. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
5 Definition (Convolutions) Let X and Y be two independent integer-valued random variables, with density functions f 1 (x) and f 2 (x) respectively. Then the convolution of f 1 (x) and f 2 (x) is the distribution function f 3 = f 1 f 2 given by f 3 (j) = (f 1 f 2 )(j) = k f 1 (k) f 2 (j k) for j =..., 2, 1, 0, 1, 2,... The function f 3 (x) is the distribution function of the random variable Z = X + Y. It is easy to see that the convolution operation is commutative, and it is straightforward to show that it is also associative. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
6 Let S n = X 1 + X X n be the sum of n independent random variables of an independent trials process with common distribution function f defined on the integers. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
7 Let S n = X 1 + X X n be the sum of n independent random variables of an independent trials process with common distribution function f defined on the integers. Then the distribution function of S 1 is f. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
8 Let S n = X 1 + X X n be the sum of n independent random variables of an independent trials process with common distribution function f defined on the integers. Then the distribution function of S 1 is f. And we can write S n = S n 1 + X n Thus, since we know the distribution function of X n is f, we can find the distribution function of S n by induction. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
9 Example (Homework12: Problem 1) Let X and Y be independent discrete random variables: X can be wither 1, 2, or 3, while Y can be either 4, 5, or 6. They have the following probability distributions: (a) Find P(X = 1 and Y = 4). (b) Find P(X + Y = 5). (c) Find P(X + Y = 6). (d) Find P(X + Y = 7). x P(X = x) y P(Y = y) (e) Find P(X + Y = 7 and X = 2). (f) Find P(X + Y = 7 given X = 2). (g) Find P(X + Y = 10). David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
10 Example (Example 7.1) A die is rolled twice. Let X 1 and X 2 be the outcomes, and let S 2 = X 1 + X 2 be the sum of these outcomes. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
11 Example (Example 7.1) A die is rolled twice. Let X 1 and X 2 be the outcomes, and let S 2 = X 1 + X 2 be the sum of these outcomes. Then X 1 and X 2 have the common distribution function: f (j) = 1/6 for j = 1,..., 6. Find the distribution function f S2 of S 2. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
12 Example (Example 7.1) A die is rolled twice. Let X 1 and X 2 be the outcomes, and let S 2 = X 1 + X 2 be the sum of these outcomes. Then X 1 and X 2 have the common distribution function: f (j) = 1/6 for j = 1,..., 6. Find the distribution function f S2 of S 2. Solution: The distribution function of S 2 is then the convolution of f with itself. f S2 (j) = (f f )(j) = 6 f (k) f (j k) for j = 2,..., 12. k=1 David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
13 Figure: Density of S 10 for rolling a die 10 times. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
14 Figure: Density of S 20 for rolling a die 20 times. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
15 Figure: Density of S 30 for rolling a die 30 times. David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
16 Section 7.2 Sums of Continuous Random Variables Definition (Convolutions) Let X and Y be two continuous random variables with density functions f (x) and g(y), respectively. Assume that both f (x) and g(y) are defined for all real numbers. Then the convolution f g of f and g is the function given by (f g)(z) = f (z y)g(y) dx = g(z y)f (y) dx David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
17 Section 7.2 Sums of Continuous Random Variables Theorem (Theorem 7.1) Let X and Y be two independent random variables with density Let X and Y be two continuous random variables with density functions f (x) and g(y), respectively. Then the sum Z = X + Y is a random variable with density function f Z (z), where f Z (z) is the convolution of f (x) and g(y). David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
18 Section 7.2 Sums of Continuous Random Variables Example (Example 7.3) Suppose we choose independently two numbers at random from the interval [0, 1] with uniform probability density. What is the density of their sum? David Murrugarra (University of Kentucky) MA 320: Section 7.1 Spring / 12
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
Continuous Random Variables
 1 Continuous Random Variables Example 1 Roll a fair die. Denote by X the random variable taking the value shown by the die, X {1, 2, 3, 4, 5, 6}. Obviously the probability mass function is given by (since
1 Continuous Random Variables Example 1 Roll a fair die. Denote by X the random variable taking the value shown by the die, X {1, 2, 3, 4, 5, 6}. Obviously the probability mass function is given by (since
A&S 320: Mathematical Modeling in Biology
 A&S 320: Mathematical Modeling in Biology David Murrugarra Department of Mathematics, University of Kentucky http://www.ms.uky.edu/~dmu228/as320/ Spring 2016 David Murrugarra (University of Kentucky) A&S
A&S 320: Mathematical Modeling in Biology David Murrugarra Department of Mathematics, University of Kentucky http://www.ms.uky.edu/~dmu228/as320/ Spring 2016 David Murrugarra (University of Kentucky) A&S
CSC Discrete Math I, Spring Discrete Probability
 CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
CSC 125 - Discrete Math I, Spring 2017 Discrete Probability Probability of an Event Pierre-Simon Laplace s classical theory of probability: Definition of terms: An experiment is a procedure that yields
Mathematics 426 Robert Gross Homework 9 Answers
 Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
Let X and Y be two real valued stochastic variables defined on (Ω, F, P). Theorem: If X and Y are independent then. . p.1/21
 Multivariate transformations The remaining part of the probability course is centered around transformations t : R k R m and how they transform probability measures. For instance tx 1,...,x k = x 1 +...
Multivariate transformations The remaining part of the probability course is centered around transformations t : R k R m and how they transform probability measures. For instance tx 1,...,x k = x 1 +...
Introductory Probability
 Introductory Probability Joint Probability with Independence; Binomial Distributions Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Comparing Two Variables with Joint Random
Introductory Probability Joint Probability with Independence; Binomial Distributions Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Comparing Two Variables with Joint Random
Let us think of the situation as having a 50 sided fair die; any one number is equally likely to appear.
 Probability_Homework Answers. Let the sample space consist of the integers through. {, 2, 3,, }. Consider the following events from that Sample Space. Event A: {a number is a multiple of 5 5, 0, 5,, }
Probability_Homework Answers. Let the sample space consist of the integers through. {, 2, 3,, }. Consider the following events from that Sample Space. Event A: {a number is a multiple of 5 5, 0, 5,, }
Probabilistic Systems Analysis Spring 2018 Lecture 6. Random Variables: Probability Mass Function and Expectation
 EE 178 Probabilistic Systems Analysis Spring 2018 Lecture 6 Random Variables: Probability Mass Function and Expectation Probability Mass Function When we introduce the basic probability model in Note 1,
EE 178 Probabilistic Systems Analysis Spring 2018 Lecture 6 Random Variables: Probability Mass Function and Expectation Probability Mass Function When we introduce the basic probability model in Note 1,
MATHEMATICS 154, SPRING 2009 PROBABILITY THEORY Outline #11 (Tail-Sum Theorem, Conditional distribution and expectation)
 MATHEMATICS 154, SPRING 2009 PROBABILITY THEORY Outline #11 (Tail-Sum Theorem, Conditional distribution and expectation) Last modified: March 7, 2009 Reference: PRP, Sections 3.6 and 3.7. 1. Tail-Sum Theorem
MATHEMATICS 154, SPRING 2009 PROBABILITY THEORY Outline #11 (Tail-Sum Theorem, Conditional distribution and expectation) Last modified: March 7, 2009 Reference: PRP, Sections 3.6 and 3.7. 1. Tail-Sum Theorem
Sec$on Summary. Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability
 Section 7.2 Sec$on Summary Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability Independence Bernoulli Trials and the Binomial Distribution Random Variables
Section 7.2 Sec$on Summary Assigning Probabilities Probabilities of Complements and Unions of Events Conditional Probability Independence Bernoulli Trials and the Binomial Distribution Random Variables
Introductory Probability
 Introductory Probability Conditional Probability: Bayes Probabilities Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Computing Bayes Probabilities Conditional Probability and
Introductory Probability Conditional Probability: Bayes Probabilities Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Computing Bayes Probabilities Conditional Probability and
MA 320 Introductory Probability, Section 1 Spring 2017 Final Exam Practice May. 1, Exam Scores. Question Score Total. Name:
 MA 320 Introductory Probability, Section 1 Spring 2017 Final Exam Practice May. 1, 2017 Exam Scores Question Score Total 1 10 Name: Last 4 digits of student ID #: No books or notes may be used. Turn off
MA 320 Introductory Probability, Section 1 Spring 2017 Final Exam Practice May. 1, 2017 Exam Scores Question Score Total 1 10 Name: Last 4 digits of student ID #: No books or notes may be used. Turn off
MATH 151, FINAL EXAM Winter Quarter, 21 March, 2014
 Time: 3 hours, 8:3-11:3 Instructions: MATH 151, FINAL EXAM Winter Quarter, 21 March, 214 (1) Write your name in blue-book provided and sign that you agree to abide by the honor code. (2) The exam consists
Time: 3 hours, 8:3-11:3 Instructions: MATH 151, FINAL EXAM Winter Quarter, 21 March, 214 (1) Write your name in blue-book provided and sign that you agree to abide by the honor code. (2) The exam consists
MA 138: Calculus II for the Life Sciences
 MA 138: Calculus II for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky. Spring 2016 David Murrugarra (University of Kentucky) MA 138: Section 11.4.2 Spring 2016 1
MA 138: Calculus II for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky. Spring 2016 David Murrugarra (University of Kentucky) MA 138: Section 11.4.2 Spring 2016 1
4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio
 4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Wrong is right. Thelonious Monk 4.1 Three Definitions of
4 Lecture 4 Notes: Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Wrong is right. Thelonious Monk 4.1 Three Definitions of
MA 137: Calculus I for the Life Sciences
 MA 137: Calculus I for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky http://www.ms.uky.edu/~ma137/ Spring 2018 David Murrugarra (University of Kentucky) MA 137: Lecture
MA 137: Calculus I for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky http://www.ms.uky.edu/~ma137/ Spring 2018 David Murrugarra (University of Kentucky) MA 137: Lecture
Probability- describes the pattern of chance outcomes
 Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Expectations and Entropy
 Expectations and Entropy Data Science: Jordan Boyd-Graber University of Maryland SLIDES ADAPTED FROM DAVE BLEI AND LAUREN HANNAH Data Science: Jordan Boyd-Graber UMD Expectations and Entropy 1 / 9 Expectation
Expectations and Entropy Data Science: Jordan Boyd-Graber University of Maryland SLIDES ADAPTED FROM DAVE BLEI AND LAUREN HANNAH Data Science: Jordan Boyd-Graber UMD Expectations and Entropy 1 / 9 Expectation
Probability Basics. Part 3: Types of Probability. INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder
 Probability Basics Part 3: Types of Probability INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder September 30, 2016 Prof. Michael Paul Prof. William Aspray Example A large government
Probability Basics Part 3: Types of Probability INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder September 30, 2016 Prof. Michael Paul Prof. William Aspray Example A large government
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15. Lecture 2: Random Experiments. Prof. Vince Calhoun
 ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
Brief Review of Probability
 Brief Review of Probability Nuno Vasconcelos (Ken Kreutz-Delgado) ECE Department, UCSD Probability Probability theory is a mathematical language to deal with processes or experiments that are non-deterministic
Brief Review of Probability Nuno Vasconcelos (Ken Kreutz-Delgado) ECE Department, UCSD Probability Probability theory is a mathematical language to deal with processes or experiments that are non-deterministic
Name: Firas Rassoul-Agha
 Midterm 1 - Math 5010 - Spring 016 Name: Firas Rassoul-Agha Solve the following 4 problems. You have to clearly explain your solution. The answer carries no points. Only the work does. CALCULATORS ARE
Midterm 1 - Math 5010 - Spring 016 Name: Firas Rassoul-Agha Solve the following 4 problems. You have to clearly explain your solution. The answer carries no points. Only the work does. CALCULATORS ARE
Multivariate distributions
 CHAPTER Multivariate distributions.. Introduction We want to discuss collections of random variables (X, X,..., X n ), which are known as random vectors. In the discrete case, we can define the density
CHAPTER Multivariate distributions.. Introduction We want to discuss collections of random variables (X, X,..., X n ), which are known as random vectors. In the discrete case, we can define the density
More on Distribution Function
 More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
More on Distribution Function The distribution of a random variable X can be determined directly from its cumulative distribution function F X. Theorem: Let X be any random variable, with cumulative distribution
1 INFO Sep 05
 Events A 1,...A n are said to be mutually independent if for all subsets S {1,..., n}, p( i S A i ) = p(a i ). (For example, flip a coin N times, then the events {A i = i th flip is heads} are mutually
Events A 1,...A n are said to be mutually independent if for all subsets S {1,..., n}, p( i S A i ) = p(a i ). (For example, flip a coin N times, then the events {A i = i th flip is heads} are mutually
The integers. Chapter 3
 Chapter 3 The integers Recall that an abelian group is a set A with a special element 0, and operation + such that x +0=x x + y = y + x x +y + z) =x + y)+z every element x has an inverse x + y =0 We also
Chapter 3 The integers Recall that an abelian group is a set A with a special element 0, and operation + such that x +0=x x + y = y + x x +y + z) =x + y)+z every element x has an inverse x + y =0 We also
X 1 ((, a]) = {ω Ω : X(ω) a} F, which leads us to the following definition:
![X 1 ((, a]) = {ω Ω : X(ω) a} F, which leads us to the following definition: X 1 ((, a]) = {ω Ω : X(ω) a} F, which leads us to the following definition:](/thumbs/89/98839224.jpg) nna Janicka Probability Calculus 08/09 Lecture 4. Real-valued Random Variables We already know how to describe the results of a random experiment in terms of a formal mathematical construction, i.e. the
nna Janicka Probability Calculus 08/09 Lecture 4. Real-valued Random Variables We already know how to describe the results of a random experiment in terms of a formal mathematical construction, i.e. the
Example 1. The sample space of an experiment where we flip a pair of coins is denoted by:
 Chapter 8 Probability 8. Preliminaries Definition (Sample Space). A Sample Space, Ω, is the set of all possible outcomes of an experiment. Such a sample space is considered discrete if Ω has finite cardinality.
Chapter 8 Probability 8. Preliminaries Definition (Sample Space). A Sample Space, Ω, is the set of all possible outcomes of an experiment. Such a sample space is considered discrete if Ω has finite cardinality.
5. Conditional Distributions
 1 of 12 7/16/2009 5:36 AM Virtual Laboratories > 3. Distributions > 1 2 3 4 5 6 7 8 5. Conditional Distributions Basic Theory As usual, we start with a random experiment with probability measure P on an
1 of 12 7/16/2009 5:36 AM Virtual Laboratories > 3. Distributions > 1 2 3 4 5 6 7 8 5. Conditional Distributions Basic Theory As usual, we start with a random experiment with probability measure P on an
The probability of an event is viewed as a numerical measure of the chance that the event will occur.
 Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
Chapter 5 This chapter introduces probability to quantify randomness. Section 5.1: How Can Probability Quantify Randomness? The probability of an event is viewed as a numerical measure of the chance that
Introductory Probability
 Introductory Probability Bernoulli Trials and Binomial Probability Distributions Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK February 04, 2019 Agenda Bernoulli Trials and Probability
Introductory Probability Bernoulli Trials and Binomial Probability Distributions Dr. Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK February 04, 2019 Agenda Bernoulli Trials and Probability
Combinatorics & Discrete Probability Theory
 & Discrete Probability Theory CIS008-2 Logic and Foundations of Mathematics David Goodwin david.goodwin@perisic.com 11:00, Tuesday 28 th February 2012 Outline 1 Combinatorics Enumeration Permutations Combinations
& Discrete Probability Theory CIS008-2 Logic and Foundations of Mathematics David Goodwin david.goodwin@perisic.com 11:00, Tuesday 28 th February 2012 Outline 1 Combinatorics Enumeration Permutations Combinations
Deviations from the Mean
 Deviations from the Mean The Markov inequality for non-negative RVs Variance Definition The Bienaymé Inequality For independent RVs The Chebyeshev Inequality Markov s Inequality For any non-negative random
Deviations from the Mean The Markov inequality for non-negative RVs Variance Definition The Bienaymé Inequality For independent RVs The Chebyeshev Inequality Markov s Inequality For any non-negative random
Chapter 1 : The language of mathematics.
 MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis
![UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis](/thumbs/90/103872711.jpg) UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Lecture 10 Class URL: http://vlsicad.ucsd.edu/courses/cse21-s14/ Lecture 10 Notes Midterm Good job overall! = 81; =
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Lecture 10 Class URL: http://vlsicad.ucsd.edu/courses/cse21-s14/ Lecture 10 Notes Midterm Good job overall! = 81; =
2.2 Grouping Data. Tom Lewis. Fall Term Tom Lewis () 2.2 Grouping Data Fall Term / 6
 2.2 Grouping Data Tom Lewis Fall Term 2009 Tom Lewis () 2.2 Grouping Data Fall Term 2009 1 / 6 Outline 1 Quantitative methods 2 Qualitative methods Tom Lewis () 2.2 Grouping Data Fall Term 2009 2 / 6 Test
2.2 Grouping Data Tom Lewis Fall Term 2009 Tom Lewis () 2.2 Grouping Data Fall Term 2009 1 / 6 Outline 1 Quantitative methods 2 Qualitative methods Tom Lewis () 2.2 Grouping Data Fall Term 2009 2 / 6 Test
ELEG 3143 Probability & Stochastic Process Ch. 1 Probability
 Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
Department of Electrical Engineering University of Arkansas ELEG 3143 Probability & Stochastic Process Ch. 1 Probability Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Applications Elementary Set Theory Random
3. DISCRETE RANDOM VARIABLES
 IA Probability Lent Term 3 DISCRETE RANDOM VARIABLES 31 Introduction When an experiment is conducted there may be a number of quantities associated with the outcome ω Ω that may be of interest Suppose
IA Probability Lent Term 3 DISCRETE RANDOM VARIABLES 31 Introduction When an experiment is conducted there may be a number of quantities associated with the outcome ω Ω that may be of interest Suppose
Lecture 10: Probability distributions TUESDAY, FEBRUARY 19, 2019
 Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Lecture 10: Probability distributions DANIEL WELLER TUESDAY, FEBRUARY 19, 2019 Agenda What is probability? (again) Describing probabilities (distributions) Understanding probabilities (expectation) Partial
Math 3215 Intro. Probability & Statistics Summer 14. Homework 5: Due 7/3/14
 Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
Discrete Structures for Computer Science
 Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #24: Probability Theory Based on materials developed by Dr. Adam Lee Not all events are equally likely
Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #24: Probability Theory Based on materials developed by Dr. Adam Lee Not all events are equally likely
SDS 321: Introduction to Probability and Statistics
 SDS 321: Introduction to Probability and Statistics Lecture 2: Conditional probability Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/ psarkar/teaching
SDS 321: Introduction to Probability and Statistics Lecture 2: Conditional probability Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/ psarkar/teaching
AMS7: WEEK 2. CLASS 2
 AMS7: WEEK 2. CLASS 2 Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Friday April 10, 2015 Probability: Introduction Probability:
AMS7: WEEK 2. CLASS 2 Introduction to Probability. Probability Rules. Independence and Conditional Probability. Bayes Theorem. Risk and Odds Ratio Friday April 10, 2015 Probability: Introduction Probability:
MA 250 Probability and Statistics. Nazar Khan PUCIT Lecture 15
 MA 250 Probability and Statistics Nazar Khan PUCIT Lecture 15 RANDOM VARIABLES Random Variables Random variables come in 2 types 1. Discrete set of outputs is real valued, countable set 2. Continuous set
MA 250 Probability and Statistics Nazar Khan PUCIT Lecture 15 RANDOM VARIABLES Random Variables Random variables come in 2 types 1. Discrete set of outputs is real valued, countable set 2. Continuous set
M378K In-Class Assignment #1
 The following problems are a review of M6K. M7K In-Class Assignment # Problem.. Complete the definition of mutual exclusivity of events below: Events A, B Ω are said to be mutually exclusive if A B =.
The following problems are a review of M6K. M7K In-Class Assignment # Problem.. Complete the definition of mutual exclusivity of events below: Events A, B Ω are said to be mutually exclusive if A B =.
Communication Theory II
 Communication Theory II Lecture 4: Review on Fourier analysis and probabilty theory Ahmed Elnakib, PhD Assistant Professor, Mansoura University, Egypt Febraury 19 th, 2015 1 Course Website o http://lms.mans.edu.eg/eng/
Communication Theory II Lecture 4: Review on Fourier analysis and probabilty theory Ahmed Elnakib, PhD Assistant Professor, Mansoura University, Egypt Febraury 19 th, 2015 1 Course Website o http://lms.mans.edu.eg/eng/
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
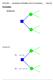 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Deep Learning for Computer Vision
 Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
Deep Learning for Computer Vision Lecture 3: Probability, Bayes Theorem, and Bayes Classification Peter Belhumeur Computer Science Columbia University Probability Should you play this game? Game: A fair
Attempt QUESTIONS 1 and 2, and THREE other questions. penalised if you attempt additional questions.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Series UG Examination 2017 18 SETS, NUMBERS AND PROBABILITY MTHA4001Y Time allowed: 2 Hours Attempt QUESTIONS 1 and 2, and THREE other questions. penalised
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Series UG Examination 2017 18 SETS, NUMBERS AND PROBABILITY MTHA4001Y Time allowed: 2 Hours Attempt QUESTIONS 1 and 2, and THREE other questions. penalised
The Theory behind PageRank
 The Theory behind PageRank Mauro Sozio Telecom ParisTech May 21, 2014 Mauro Sozio (LTCI TPT) The Theory behind PageRank May 21, 2014 1 / 19 A Crash Course on Discrete Probability Events and Probability
The Theory behind PageRank Mauro Sozio Telecom ParisTech May 21, 2014 Mauro Sozio (LTCI TPT) The Theory behind PageRank May 21, 2014 1 / 19 A Crash Course on Discrete Probability Events and Probability
CS 441 Discrete Mathematics for CS Lecture 19. Probabilities. CS 441 Discrete mathematics for CS. Probabilities
 CS 441 Discrete Mathematics for CS Lecture 19 Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Experiment: a procedure that yields one of the possible outcomes Sample space: a set of possible outcomes
CS 441 Discrete Mathematics for CS Lecture 19 Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Experiment: a procedure that yields one of the possible outcomes Sample space: a set of possible outcomes
Recap of Basic Probability Theory
 02407 Stochastic Processes Recap of Basic Probability Theory Uffe Høgsbro Thygesen Informatics and Mathematical Modelling Technical University of Denmark 2800 Kgs. Lyngby Denmark Email: uht@imm.dtu.dk
02407 Stochastic Processes Recap of Basic Probability Theory Uffe Høgsbro Thygesen Informatics and Mathematical Modelling Technical University of Denmark 2800 Kgs. Lyngby Denmark Email: uht@imm.dtu.dk
Random experiments may consist of stages that are performed. Example: Roll a die two times. Consider the events E 1 = 1 or 2 on first roll
 Econ 514: Probability and Statistics Lecture 4: Independence Stochastic independence Random experiments may consist of stages that are performed independently. Example: Roll a die two times. Consider the
Econ 514: Probability and Statistics Lecture 4: Independence Stochastic independence Random experiments may consist of stages that are performed independently. Example: Roll a die two times. Consider the
I - Probability. What is Probability? the chance of an event occuring. 1classical probability. 2empirical probability. 3subjective probability
 What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
What is Probability? the chance of an event occuring eg 1classical probability 2empirical probability 3subjective probability Section 2 - Probability (1) Probability - Terminology random (probability)
Recap of Basic Probability Theory
 02407 Stochastic Processes? Recap of Basic Probability Theory Uffe Høgsbro Thygesen Informatics and Mathematical Modelling Technical University of Denmark 2800 Kgs. Lyngby Denmark Email: uht@imm.dtu.dk
02407 Stochastic Processes? Recap of Basic Probability Theory Uffe Høgsbro Thygesen Informatics and Mathematical Modelling Technical University of Denmark 2800 Kgs. Lyngby Denmark Email: uht@imm.dtu.dk
Statistics for Economists. Lectures 3 & 4
 Statistics for Economists Lectures 3 & 4 Asrat Temesgen Stockholm University 1 CHAPTER 2- Discrete Distributions 2.1. Random variables of the Discrete Type Definition 2.1.1: Given a random experiment with
Statistics for Economists Lectures 3 & 4 Asrat Temesgen Stockholm University 1 CHAPTER 2- Discrete Distributions 2.1. Random variables of the Discrete Type Definition 2.1.1: Given a random experiment with
Lecture 3. David Aldous. 31 August David Aldous Lecture 3
 Lecture 3 David Aldous 31 August 2015 This size-bias effect occurs in other contexts, such as class size. If a small Department offers two courses, with enrollments 90 and 10, then average class (faculty
Lecture 3 David Aldous 31 August 2015 This size-bias effect occurs in other contexts, such as class size. If a small Department offers two courses, with enrollments 90 and 10, then average class (faculty
2.1 Elementary probability; random sampling
 Chapter 2 Probability Theory Chapter 2 outlines the probability theory necessary to understand this text. It is meant as a refresher for students who need review and as a reference for concepts and theorems
Chapter 2 Probability Theory Chapter 2 outlines the probability theory necessary to understand this text. It is meant as a refresher for students who need review and as a reference for concepts and theorems
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Conditional distributions (discrete case)
 Conditional distributions (discrete case) The basic idea behind conditional distributions is simple: Suppose (XY) is a jointly-distributed random vector with a discrete joint distribution. Then we can
Conditional distributions (discrete case) The basic idea behind conditional distributions is simple: Suppose (XY) is a jointly-distributed random vector with a discrete joint distribution. Then we can
Sum and Product Rules
 Sum and Product Rules Exercise. Consider tossing a coin five times. What is the probability of getting the same result on the first two tosses or the last two tosses? Solution. Let E be the event that
Sum and Product Rules Exercise. Consider tossing a coin five times. What is the probability of getting the same result on the first two tosses or the last two tosses? Solution. Let E be the event that
HW Solution 3 Due: July 15
 ECS 315: Probability and Random Processes 2010/1 HW Solution 3 Due: July 15 Lecturer: Prapun Suksompong, Ph.D. Instructions (a) A part of ONE question will be graded. Of course, you do not know which problem
ECS 315: Probability and Random Processes 2010/1 HW Solution 3 Due: July 15 Lecturer: Prapun Suksompong, Ph.D. Instructions (a) A part of ONE question will be graded. Of course, you do not know which problem
Problem set 5, Real Analysis I, Spring, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, 1 x (log 1/ x ) 2 dx 1
 Problem set 5, Real Analysis I, Spring, 25. (5) Consider the function on R defined by f(x) { x (log / x ) 2 if x /2, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, R f /2
Problem set 5, Real Analysis I, Spring, 25. (5) Consider the function on R defined by f(x) { x (log / x ) 2 if x /2, otherwise. (a) Verify that f is integrable. Solution: Compute since f is even, R f /2
MATH 3C: MIDTERM 1 REVIEW. 1. Counting
 MATH 3C: MIDTERM REVIEW JOE HUGHES. Counting. Imagine that a sports betting pool is run in the following way: there are 20 teams, 2 weeks, and each week you pick a team to win. However, you can t pick
MATH 3C: MIDTERM REVIEW JOE HUGHES. Counting. Imagine that a sports betting pool is run in the following way: there are 20 teams, 2 weeks, and each week you pick a team to win. However, you can t pick
Probability. Carlo Tomasi Duke University
 Probability Carlo Tomasi Due University Introductory concepts about probability are first explained for outcomes that tae values in discrete sets, and then extended to outcomes on the real line 1 Discrete
Probability Carlo Tomasi Due University Introductory concepts about probability are first explained for outcomes that tae values in discrete sets, and then extended to outcomes on the real line 1 Discrete
Math 151. Rumbos Fall Solutions to Review Problems for Exam 2. Pr(X = 1) = ) = Pr(X = 2) = Pr(X = 3) = p X. (k) =
 Math 5. Rumbos Fall 07 Solutions to Review Problems for Exam. A bowl contains 5 chips of the same size and shape. Two chips are red and the other three are blue. Draw three chips from the bowl at random,
Math 5. Rumbos Fall 07 Solutions to Review Problems for Exam. A bowl contains 5 chips of the same size and shape. Two chips are red and the other three are blue. Draw three chips from the bowl at random,
MAT PS4 Solutions
 MAT 394 - PS4 Solutions 1.) Suppose that a fair six-sided die is rolled three times and let X 1, X 2 and X 3 be the three numbers obtained, in order of occurrence. (a) Calculate the probability that X
MAT 394 - PS4 Solutions 1.) Suppose that a fair six-sided die is rolled three times and let X 1, X 2 and X 3 be the three numbers obtained, in order of occurrence. (a) Calculate the probability that X
Classical Probability
 Chapter 1 Classical Probability Probability is the very guide of life. Marcus Thullius Cicero The original development of probability theory took place during the seventeenth through nineteenth centuries.
Chapter 1 Classical Probability Probability is the very guide of life. Marcus Thullius Cicero The original development of probability theory took place during the seventeenth through nineteenth centuries.
Review of Basic Probability
 Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
Review of Basic Probability Erik G. Learned-Miller Department of Computer Science University of Massachusetts, Amherst Amherst, MA 01003 September 16, 2009 Abstract This document reviews basic discrete
6.041/6.431 Fall 2010 Quiz 2 Solutions
 6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
1 Chapter 1: SETS. 1.1 Describing a set
 1 Chapter 1: SETS set is a collection of objects The objects of the set are called elements or members Use capital letters :, B, C, S, X, Y to denote the sets Use lower case letters to denote the elements:
1 Chapter 1: SETS set is a collection of objects The objects of the set are called elements or members Use capital letters :, B, C, S, X, Y to denote the sets Use lower case letters to denote the elements:
HOMEWORK ASSIGNMENT 6
 HOMEWORK ASSIGNMENT 6 DUE 15 MARCH, 2016 1) Suppose f, g : A R are uniformly continuous on A. Show that f + g is uniformly continuous on A. Solution First we note: In order to show that f + g is uniformly
HOMEWORK ASSIGNMENT 6 DUE 15 MARCH, 2016 1) Suppose f, g : A R are uniformly continuous on A. Show that f + g is uniformly continuous on A. Solution First we note: In order to show that f + g is uniformly
Sample Exam #1 Probability and Statistics I
 Sample Exam # Probability and Statistics I Instructions. Show all work. No need to simplify answers.. 0 points Jack and Jill, along with four other students chosen from the same class of ten students,
Sample Exam # Probability and Statistics I Instructions. Show all work. No need to simplify answers.. 0 points Jack and Jill, along with four other students chosen from the same class of ten students,
Math 463/563 Homework #2 - Solutions
 Math 463/563 Homework #2 - Solutions 1. How many 5-digit numbers can be formed with the integers 1, 2,..., 9 if no digit can appear exactly once? (For instance 43443 is OK, while 43413 is not allowed.)
Math 463/563 Homework #2 - Solutions 1. How many 5-digit numbers can be formed with the integers 1, 2,..., 9 if no digit can appear exactly once? (For instance 43443 is OK, while 43413 is not allowed.)
CMPSCI 240: Reasoning about Uncertainty
 CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
Homework 1 Due: Wednesday, September 28, 2016
 0-704 Information Processing and Learning Fall 06 Homework Due: Wednesday, September 8, 06 Notes: For positive integers k, [k] := {,..., k} denotes te set of te first k positive integers. Wen p and Y q
0-704 Information Processing and Learning Fall 06 Homework Due: Wednesday, September 8, 06 Notes: For positive integers k, [k] := {,..., k} denotes te set of te first k positive integers. Wen p and Y q
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006
 Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
Properties of Probability
 Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Theorem 1.7 [Bayes' Law]: Assume that,,, are mutually disjoint events in the sample space s.t.. Then Pr( )
![Theorem 1.7 [Bayes' Law]: Assume that,,, are mutually disjoint events in the sample space s.t.. Then Pr( ) Theorem 1.7 [Bayes' Law]: Assume that,,, are mutually disjoint events in the sample space s.t.. Then Pr( )](/thumbs/95/125074181.jpg) Theorem 1.7 [Bayes' Law]: Assume that,,, are mutually disjoint events in the sample space s.t.. Then Pr Pr = Pr Pr Pr() Pr Pr. We are given three coins and are told that two of the coins are fair and the
Theorem 1.7 [Bayes' Law]: Assume that,,, are mutually disjoint events in the sample space s.t.. Then Pr Pr = Pr Pr Pr() Pr Pr. We are given three coins and are told that two of the coins are fair and the
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018
 Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
Mathematical Foundations of Computer Science Lecture Outline October 18, 2018 The Total Probability Theorem. Consider events E and F. Consider a sample point ω E. Observe that ω belongs to either F or
Probability: Terminology and Examples Class 2, Jeremy Orloff and Jonathan Bloom
 1 Learning Goals Probability: Terminology and Examples Class 2, 18.05 Jeremy Orloff and Jonathan Bloom 1. Know the definitions of sample space, event and probability function. 2. Be able to organize a
1 Learning Goals Probability: Terminology and Examples Class 2, 18.05 Jeremy Orloff and Jonathan Bloom 1. Know the definitions of sample space, event and probability function. 2. Be able to organize a
Bivariate distributions
 Bivariate distributions 3 th October 017 lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.) Bivariate Distributions of the Discrete Type The Correlation Coefficient
Bivariate distributions 3 th October 017 lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.) Bivariate Distributions of the Discrete Type The Correlation Coefficient
Why study probability? Set theory. ECE 6010 Lecture 1 Introduction; Review of Random Variables
 ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
Dept. of Linguistics, Indiana University Fall 2015
 L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
L645 Dept. of Linguistics, Indiana University Fall 2015 1 / 34 To start out the course, we need to know something about statistics and This is only an introduction; for a fuller understanding, you would
Math 127 Homework. Mary Radcliffe. Due 29 March Complete the following problems. Fully justify each response.
 Math 17 Homework Mary Radcliffe Due 9 March 018 Complete the following problems Fully justify each response NOTE: due to the Spring Break, this homework set is a bit longer than is typical You only need
Math 17 Homework Mary Radcliffe Due 9 March 018 Complete the following problems Fully justify each response NOTE: due to the Spring Break, this homework set is a bit longer than is typical You only need
3 Multiple Discrete Random Variables
 3 Multiple Discrete Random Variables 3.1 Joint densities Suppose we have a probability space (Ω, F,P) and now we have two discrete random variables X and Y on it. They have probability mass functions f
3 Multiple Discrete Random Variables 3.1 Joint densities Suppose we have a probability space (Ω, F,P) and now we have two discrete random variables X and Y on it. They have probability mass functions f
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis
![UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis](/thumbs/83/87821691.jpg) UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Lecture 10 Class URL: http://vlsicad.ucsd.edu/courses/cse21-s14/ Lecture 10 Notes Midterm Good job overall! = 81; =
UCSD CSE 21, Spring 2014 [Section B00] Mathematics for Algorithm and System Analysis Lecture 10 Class URL: http://vlsicad.ucsd.edu/courses/cse21-s14/ Lecture 10 Notes Midterm Good job overall! = 81; =
Lecture Notes 1 Probability and Random Variables. Conditional Probability and Independence. Functions of a Random Variable
 Lecture Notes 1 Probability and Random Variables Probability Spaces Conditional Probability and Independence Random Variables Functions of a Random Variable Generation of a Random Variable Jointly Distributed
Lecture Notes 1 Probability and Random Variables Probability Spaces Conditional Probability and Independence Random Variables Functions of a Random Variable Generation of a Random Variable Jointly Distributed
Edexcel past paper questions
 Edexcel past paper questions Statistics 1 Discrete Random Variables Past examination questions Discrete Random variables Page 1 Discrete random variables Discrete Random variables Page 2 Discrete Random
Edexcel past paper questions Statistics 1 Discrete Random Variables Past examination questions Discrete Random variables Page 1 Discrete random variables Discrete Random variables Page 2 Discrete Random
Recitation 2: Probability
 Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Lecture Notes 1 Probability and Random Variables. Conditional Probability and Independence. Functions of a Random Variable
 Lecture Notes 1 Probability and Random Variables Probability Spaces Conditional Probability and Independence Random Variables Functions of a Random Variable Generation of a Random Variable Jointly Distributed
Lecture Notes 1 Probability and Random Variables Probability Spaces Conditional Probability and Independence Random Variables Functions of a Random Variable Generation of a Random Variable Jointly Distributed
A Probability Primer. A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes.
 A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
Bayes Classifiers. CAP5610 Machine Learning Instructor: Guo-Jun QI
 Bayes Classifiers CAP5610 Machine Learning Instructor: Guo-Jun QI Recap: Joint distributions Joint distribution over Input vector X = (X 1, X 2 ) X 1 =B or B (drinking beer or not) X 2 = H or H (headache
Bayes Classifiers CAP5610 Machine Learning Instructor: Guo-Jun QI Recap: Joint distributions Joint distribution over Input vector X = (X 1, X 2 ) X 1 =B or B (drinking beer or not) X 2 = H or H (headache
Lecture Lecture 5
 Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Lecture 4 --- Lecture 5 A. Basic Concepts (4.1-4.2) 1. Experiment: A process of observing a phenomenon that has variation in its outcome. Examples: (E1). Rolling a die, (E2). Drawing a card form a shuffled
Chapter 5: Probability in Our Daily Lives
 Chapter 5: in Our Daily Lives These notes reflect material from our text, Statistics: The Art and Science of Learning from Data, Third Edition, by Alan Agresti and Catherine Franklin, published by Pearson,
Chapter 5: in Our Daily Lives These notes reflect material from our text, Statistics: The Art and Science of Learning from Data, Third Edition, by Alan Agresti and Catherine Franklin, published by Pearson,
