Functions. Ex. f : R 0 Ñ R 0 defined by x fiñ x 2.
|
|
|
- Rudolph Simmons
- 5 years ago
- Views:
Transcription
1 Functions Let f : X Ñ Y be a function. Recall, the image of f is fpxq ty P Y fpxq y for some x P Xu. Further, f is... injective if at most one x P X maps to each y P Y,i.e. if fpx q fpx q then x x. Ex. f : R 0 Ñ R defined by x fiñ x. Non-ex. f : R Ñ R defined by x fiñ x. surjective if every y P Y gets mapped to, i.e. for all y P Y,thereexistsxPX such that fpxq y. Ex. f : R Ñ R 0 defined by x fiñ x. Non-ex. f : R Ñ R defined by x fiñ x. bijective if it s both injective and surjective. Ex. f : R 0 Ñ R 0 defined by x fiñ x. Non-ex. f : R Ñ R defined by x fiñ x. Injective, not surjective: f c b a 0 X Y Surjective, not injective: f c b a X Y To show f : X Ñ Y is injective: Start: Suppose fpx q fpx q... Goal: Show x x. To show f : X Ñ Y is surjective: Start: Let y P Y... Goal: Find x P X such that fpxq y.
2 For a function f : X Ñ Y,andanelementy P Y,let f pyq tx P X fpxq yu Ä X, called the inverse image or preimage of y. Note that this is abusing notation: we write f whether or not f is invertible; and f pyq is a set, not an element. c f f pq H b f pq tb, cu a X Y f pq tau We say f is invertible if for all y P Y, f pyq has exactly one element (no more, no fewer). Thm. For nonempty sets X and Y, a function f : X Ñ Y is invertible if and only if it is bijective. We say f is invertible if for all y P Y, f pyq has exactly one element (no more, no fewer). Thm. For nonempty sets X and Y, a function f : X Ñ Y is invertible if and only if it is bijective. Proof. Suppose f is bijective. Since f is surjective, for all y P Y,wehave f pyq. Andsincef is injective, for any x,x P f pyq, we have x x.so f pyq. Therefore,forally P Y,wehave f pyq, sothatf is invertible. Now suppose f is invertible. Thus for all y P Y,wehave f pyq. Therefore,forally P Y, fpyq H,sothatf is surjective. And for all y P Y,sincef pyq has exactly one element, it has at most one element. So f is injective. Therefore, f is bijective.
3 Cardinality of sets Two sets A and B have the same size, or cardinality, ifthereisa bijection f : A Ñ B. Example: We know that set ta, b, cu has elements because we can count them: : a : b : c But this is essentially the same as the bijection f c b a A B Cardinality of sets Definition: Two sets A and B have the same size, orsame cardinality, ifand only if there is a bijection f : A Ñ B. (This allows us to measure the relative sizes of sets, even if they happen to be infinite!) Example: The sets Z 0 and Z 0 have the same cardinality since is a bijective map. f : Z 0 Ñ Z 0 x fiñ x
4 Countably infinite sets A set is countable if it is either finite or the same cardinality as the natural numbers (N Z 0 ). If a set A is not finite but is countable, we say A is countably infinite and write 0 (pronounced aleph naught or aleph null ). To show that 0 :showa is not finite, and give a bijection f : Z 0 Ñ A. Examples:. Z 0 is countably infinite: It is not finite, and f : Z 0 Ñ Z 0 by x fiñ x is a bijection.. Z 0 is countably infinite: It is not finite, and f : Z 0 Ñ Z 0 by x fiñ x is a bijection.. Z is countably infinite: Not finite, and f : Z 0 Ñ Z by x fiñ p q x tx{u is a bijection. Z 0 : Z: More on this last example, 0 : We started with the picture Z 0 : Z: This at least gives us a list of integers, :0, :, :, 4:, 5:,... If I know that every integer appears on this list somewhere, then I know that the integers are countable. (Ok answer) The next step in giving a more sophisticated, more robust, answer is to try to get the formula # written down: x{ if x is even, f : Z 0 Ñ Z x fiñ (Better answer) px q{ if x is odd. To be even more sophisticated, we used the floor function to get a closed form # answer: x{ if x is even, px q{ if x is odd p qx tx{u, for x P Z 0.(Best answer)
5 Recall that A B if and only if there is a bijection f : A Ñ B. If we know that 0 and f : A Ñ B is a bijection, then B 0. Example: To show that Z teven integers u is countably infinite, we could construct a bijection like in the previous example. But it s a little more straightforward to note that f : Z Ñ Z is a bijection, x fiñ x so that Z 0. Examples: For each of the following, show that the set is countably infinite. (Define a bijective function to something that we know to be countably infinite if it s not too hard; otherwise, explain how to make the list.). The set of negative integers (Z 0 ).. The set of integers less than 00 (Z 00 ).. The set of integers that are integer multiples of ( Z). 4. The set of integers that are not integer multiples of (Z Z). The rational numbers Claim: Q 0 is countably infinite. Make a table: 4 5 { { 5 { 6 4{ 5{ { { 7 { 4{ 5{ 4 { 8 { { 4{ 5{ (skip prev. counted fractions) 4 9 {4 {4 {4 4{4 5{ {5 {5 {5 4{5 5{5 Then use the same alternating map that we did for Z 0 Ñ Z to build a bijection Q 0 Ñ Q, yielding a bijection Z 0 Ñ Q 0 Ñ Q.
6 Are there sets that are not countable? Theorem. The set of real numbers in the interval r0, q is not countable. Proof outline: We will prove this by contradiction. Suppose that the set r0, q is countable, so that the real numbers in r0, q can be listed. Take one such list. Goal: Show that the list isn t complete. Namely, algorithmically produce an element of r0, q that isn t on any fixed list. Take this is the supposedly complete list of real numbers in r0, q. For example: Algorithm for producing a number that is not on the list: In the ith number in the list, highlight the ith digit. Build a new number as follows: i. If the highlighted digit of the ith number is a 0, then make the corresponding digit of the new number a ii. If the highlighted digit of the ith number is not a 0, then make the corresponding digit of the new number a Example: In this way, this new number di ers from every item in the list in at least one digit!
7 Theorem. The set of real numbers in the interval r0, q is not countable. Proof outline: We will prove this by contradiction. Suppose that the set r0, q is countable, so that the real numbers in r0, q can be listed. Show that any list isn t complete. Namely, algorithmically produce an element of r0, q that isn t on any fixed list. Proof. For x Pr0, q, denote the ith digit of x by xris. Note that for x, y Pr0, q, wehavex y if and only if xris yris for all i P Z 0. Now, suppose f : Z 0 Ñr0, q is a bijection. Define x f Pr0, q so that the ith digit of x f is # if fpiqris 0, x f ris 0 if fpiqris. Then, for all i P Z 0,wehavefpiqris x f ris, sothatfpiq x f. Therefore x f R fpz 0,sothatf is not surjective. This contradicts f being bijective, so no such bijection exists. Therefore r0, q is not countable. Theorem. The set of real numbers in the interval r0, q is not countable. Proof outline: We will prove this by contradiction. Suppose that the set r0, q is countable, so that the real numbers in r0, q can be listed. Show that any list isn t complete. Namely, algorithmically produce an element of r0, q that isn t on any fixed list. Proof. For x Pr0, q, denote the ith digit of x by xris. Note that for x, y Pr0, q, wehavex y if and only if xris yris for all i P Z 0. Now, suppose f : Z 0 Ñr0, q is a bijection let f : Z 0 Ñr0, q. Define x f Pr0, q so that the ith digit of x f is # if fpiqris 0, x f ris 0 if fpiqris. Then, for all i P Z 0,wehavefpiqris x f ris, sothatfpiq x f. Therefore x f R fpz 0,sothatf is not surjective. This contradicts f being bijective, so no such bijection exists. Thus, since no function f : Z 0 Ñr0, q can be surjective, no bijection between Z 0 and r0, q exists. Therefore r0, q is not countable.
8 For sets X and Y,wesay X Y if there exists an injective function f : X Ñ Y.Andwrite X Y if X Y and X Y. Recall, the power set of as set A is the set of subsets of A, given by Theorem. A PpAq. Outline: PpAq ts S Ñ Au.. Show A PpAq by showing an injective map exists (give one example).. Show A PpAq by showing that any map (not just the example from before) cannot be surjective. Hint. For any f : A Ñ PpAq, showf is not surjective; i.e. construct a set S Ñ A such that S fpaq for all a P A. (Need for care: is a there exists statement; is a for all statement.) Relations A binary relation on a set A is a subset R Ñ A ˆ A, where elements pa, bq are written as a b. Example: A Z and R ta b a bu. In words: Let be the relation on Z given by a b if a b. (Note that we use language like in definitions, where if actually means if and only if.) Example: A R and R ta b a bu. In words: Let be the relation on R given by a b if a b. Example: A Z and R ta b a b pmod qu. In words: Let be the relation on Z given by a b if a b pmod q.
9 More examples of (binary) relations:. For A anumbersystem,leta b if a b. R, S, T. For A anumbersystem,leta b if a b. not R, not S, T. For A R, leta b if ab 0. not R, S, not T 4. For A a set of people, let a b if a is a (full) sibling of b. not R, S, T 5. For A a set of people, let a b if a and b speak a common language. R, S, not T A binary relation on a set A is... (R) reflexive if a a for all a P A; (S) symmetric if a b implies b a; (T) transitive if a b and b c implies a c, i.e. pa b ^ b cq ña c An equivalence relation on a set A is a binary relation that is reflexive, symmetric, and transitive. (Only #) Fix n P Z 0 and define the relation on Z given by Is is an equivalence relation? a b if a b pmod nq. Check: we have a b pmod nq if and only if a b kn for some k P Z. reflexivity: symmetry: transitivity: a a 0 0 n X If a b kn, thenb a kn p kqn. X If a b kn and b c `n, then a c pa bq`pb cq kn ` `n pk ` `qn.x Yes! This is an equivalence relation!
10 Let A be a set. Consider the relation on PpAq by Is is an equivalence relation? S T if S Ñ T Check: This is reflexive and transitive, but not symmetric. So no, it is not an equivalence relation. Is S T if S Ñ T or S Ñ T an equivalence relation on PpAq? Check: This is reflexive and symmetric, but not transitive. So still no, it is not an equivalence relation. Is S T if S T an equivalence relation on PpAq? Read: Why reflexivity doesn t follow from symmetry and transitivity. Let be an equivalence relation on a set A, andleta P A. The set of all elements b P A such that a b is called the equivalence class of a, denoted by ras. Example: Consider the equivalence relation on A ta, b, cu given by Then a a, b b, c c, a c, and c a. ras ta, cu rcs, rbs tbu and are the two equivalence classes in A (with respect to this relation). (We say there are two, not three, since the equivalence classes refers to the sets themselves, not to the elements that generate them.)
11 Let be an equivalence relation on a set A, andleta P A. The set of all elements b P A such that a b is called the equivalence class of a, denoted by ras. Example: We showed that a b if a b pmod 5q is an equivalence relation on Z. Then r0s t5n n P Zu 5Z rs t5n ` n P Zu 5Z ` rs t5n ` n P Zu 5Z ` rs t5n ` n P Zu 5Z ` r4s t5n ` 4 n P Zu 5Z ` 4 r5s t5n ` 5 n P Zu t5m m P Zu r0s r 5s r0s r6s t5n ` 6 n P Zu t5m ` m P Zu rs r 4s rs. In general, if x Prys, thatmeansy x. So x y. So y Prxs. Claim: x Prys if and only if rxs rys. We call any element a of a class C representative of C (since we can write C ras for any a P C). Theorem. The equivalence classes of A partition A into subsets, meaning. the equivalence classes are subsets of A: ras Ñ A for all a P A;. any two equivalence classes are either equal or disjoint: for all a, b P A, eitherras rbs or rasxrbs H; and. the union of all the equivalence classes is all of A: A aparas. We say that A is the disjoint union of equivalency classes, written A ß aparas, L A TEX: \bigsqcup, \sqcup For example, in our last example, there are exactly 5 equivalence classes: r0s, rs, rs, rs, and r4s. Any other seemingly di erent class is actually one of these (for example, r5s r0s). And r0syrsyrsyrsyr4s Z. So Z r0s\rs\rs\rs\r4s.
Cardinality of sets. Cardinality of sets
 Cardinality of sets Two sets A and B have the same size, or cardinality, if and only if there is a bijection f : A Ñ B. Example: We know that set ta, b, cu has elements because we can count them: 1: a
Cardinality of sets Two sets A and B have the same size, or cardinality, if and only if there is a bijection f : A Ñ B. Example: We know that set ta, b, cu has elements because we can count them: 1: a
9 < Ways to place n distinguishable objects= S(n, k) = into k indistinguishable boxes so that no box is left empty We stated in section 6.
 Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
In words: Let be the relation on Z given by a b if a b. (Note that we use language like in definitions, where if actually means if and only if.
 Reltions A binry reltion on set A is subset R Ñ A ˆ A, where elements p, bq re written s b. Exmple: A Z nd R t b bu. In words: Let be the reltion on Z given by b if b. (Note tht we use lnguge like in definitions,
Reltions A binry reltion on set A is subset R Ñ A ˆ A, where elements p, bq re written s b. Exmple: A Z nd R t b bu. In words: Let be the reltion on Z given by b if b. (Note tht we use lnguge like in definitions,
CITS2211 Discrete Structures (2017) Cardinality and Countability
 CITS2211 Discrete Structures (2017) Cardinality and Countability Highlights What is cardinality? Is it the same as size? Types of cardinality and infinite sets Reading Sections 45 and 81 84 of Mathematics
CITS2211 Discrete Structures (2017) Cardinality and Countability Highlights What is cardinality? Is it the same as size? Types of cardinality and infinite sets Reading Sections 45 and 81 84 of Mathematics
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017
 MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
MATH 220 (all sections) Homework #12 not to be turned in posted Friday, November 24, 2017 Definition: A set A is finite if there exists a nonnegative integer c such that there exists a bijection from A
SETS AND FUNCTIONS JOSHUA BALLEW
 SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
SETS AND FUNCTIONS JOSHUA BALLEW 1. Sets As a review, we begin by considering a naive look at set theory. For our purposes, we define a set as a collection of objects. Except for certain sets like N, Z,
INFINITY: CARDINAL NUMBERS
 INFINITY: CARDINAL NUMBERS BJORN POONEN 1 Some terminology of set theory N := {0, 1, 2, 3, } Z := {, 2, 1, 0, 1, 2, } Q := the set of rational numbers R := the set of real numbers C := the set of complex
INFINITY: CARDINAL NUMBERS BJORN POONEN 1 Some terminology of set theory N := {0, 1, 2, 3, } Z := {, 2, 1, 0, 1, 2, } Q := the set of rational numbers R := the set of real numbers C := the set of complex
Functions. Definition 1 Let A and B be sets. A relation between A and B is any subset of A B.
 Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
Chapter 4 Functions Definition 1 Let A and B be sets. A relation between A and B is any subset of A B. Definition 2 Let A and B be sets. A function from A to B is a relation f between A and B such that
A Short Review of Cardinality
 Christopher Heil A Short Review of Cardinality November 14, 2017 c 2017 Christopher Heil Chapter 1 Cardinality We will give a short review of the definition of cardinality and prove some facts about the
Christopher Heil A Short Review of Cardinality November 14, 2017 c 2017 Christopher Heil Chapter 1 Cardinality We will give a short review of the definition of cardinality and prove some facts about the
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 27
 CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
CS 70 Discrete Mathematics for CS Spring 007 Luca Trevisan Lecture 7 Infinity and Countability Consider a function f that maps elements of a set A (called the domain of f ) to elements of set B (called
Discussion Summary 10/16/2018
 Discussion Summary 10/16/018 1 Quiz 4 1.1 Q1 Let r R and r > 1. Prove the following by induction for every n N, assuming that 0 N as in the book. r 1 + r + r 3 + + r n = rn+1 r r 1 Proof. Let S n = Σ n
Discussion Summary 10/16/018 1 Quiz 4 1.1 Q1 Let r R and r > 1. Prove the following by induction for every n N, assuming that 0 N as in the book. r 1 + r + r 3 + + r n = rn+1 r r 1 Proof. Let S n = Σ n
PRINCIPLES OF ANALYSIS - LECTURE NOTES
 PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
Section 0. Sets and Relations
 0. Sets and Relations 1 Section 0. Sets and Relations NOTE. Mathematics is the study of ideas, not of numbers!!! The idea from modern algebra which is the focus of most of this class is that of a group
0. Sets and Relations 1 Section 0. Sets and Relations NOTE. Mathematics is the study of ideas, not of numbers!!! The idea from modern algebra which is the focus of most of this class is that of a group
Section 7.5: Cardinality
 Section 7: Cardinality In this section, we shall consider extend some of the ideas we have developed to infinite sets One interesting consequence of this discussion is that we shall see there are as many
Section 7: Cardinality In this section, we shall consider extend some of the ideas we have developed to infinite sets One interesting consequence of this discussion is that we shall see there are as many
Mathematics 220 Workshop Cardinality. Some harder problems on cardinality.
 Some harder problems on cardinality. These are two series of problems with specific goals: the first goal is to prove that the cardinality of the set of irrational numbers is continuum, and the second
Some harder problems on cardinality. These are two series of problems with specific goals: the first goal is to prove that the cardinality of the set of irrational numbers is continuum, and the second
Example. The sequence defined by the function. a : Z 0 Ñ Q defined by n fiñ 1{n
 Sequences A sequence is a function a from a subset of the set of integers (usually Z 0 or Z 0 )toasets, a : Z 0 Ñ S or a : Z 0 Ñ S. We write a n apnq, andcalla n the nth term of the sequence. Example The
Sequences A sequence is a function a from a subset of the set of integers (usually Z 0 or Z 0 )toasets, a : Z 0 Ñ S or a : Z 0 Ñ S. We write a n apnq, andcalla n the nth term of the sequence. Example The
S15 MA 274: Exam 3 Study Questions
 S15 MA 274: Exam 3 Study Questions You can find solutions to some of these problems on the next page. These questions only pertain to material covered since Exam 2. The final exam is cumulative, so you
S15 MA 274: Exam 3 Study Questions You can find solutions to some of these problems on the next page. These questions only pertain to material covered since Exam 2. The final exam is cumulative, so you
NOTES WEEK 02 DAY 1. THEOREM 0.3. Let A, B and C be sets. Then
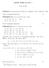 NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
Week 4-5: Binary Relations
 1 Binary Relations Week 4-5: Binary Relations The concept of relation is common in daily life and seems intuitively clear. For instance, let X be the set of all living human females and Y the set of all
1 Binary Relations Week 4-5: Binary Relations The concept of relation is common in daily life and seems intuitively clear. For instance, let X be the set of all living human females and Y the set of all
Lecture 8: Equivalence Relations
 Lecture 8: Equivalence Relations 1 Equivalence Relations Next interesting relation we will study is equivalence relation. Definition 1.1 (Equivalence Relation). Let A be a set and let be a relation on
Lecture 8: Equivalence Relations 1 Equivalence Relations Next interesting relation we will study is equivalence relation. Definition 1.1 (Equivalence Relation). Let A be a set and let be a relation on
Math 300: Final Exam Practice Solutions
 Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Chapter Summary. Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.
 Chapter 2 Chapter Summary Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.6) Section 2.1 Section Summary Definition of sets Describing
Chapter 2 Chapter Summary Sets (2.1) Set Operations (2.2) Functions (2.3) Sequences and Summations (2.4) Cardinality of Sets (2.5) Matrices (2.6) Section 2.1 Section Summary Definition of sets Describing
Week 4-5: Binary Relations
 1 Binary Relations Week 4-5: Binary Relations The concept of relation is common in daily life and seems intuitively clear. For instance, let X be the set of all living human females and Y the set of all
1 Binary Relations Week 4-5: Binary Relations The concept of relation is common in daily life and seems intuitively clear. For instance, let X be the set of all living human females and Y the set of all
Name (print): Question 4. exercise 1.24 (compute the union, then the intersection of two sets)
 MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
Lecture Notes 1 Basic Concepts of Mathematics MATH 352
 Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Chapter 1 : The language of mathematics.
 MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
MAT 200, Logic, Language and Proof, Fall 2015 Summary Chapter 1 : The language of mathematics. Definition. A proposition is a sentence which is either true or false. Truth table for the connective or :
Definition: Let S and T be sets. A binary relation on SxT is any subset of SxT. A binary relation on S is any subset of SxS.
 4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
4 Functions Before studying functions we will first quickly define a more general idea, namely the notion of a relation. A function turns out to be a special type of relation. Definition: Let S and T be
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X.
 MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
MATH 215 Sets (S) Definition 1 A set is a collection of objects. The objects in a set X are called elements of X. Notation 2 A set can be described using set-builder notation. That is, a set can be described
Final Exam Review. 2. Let A = {, { }}. What is the cardinality of A? Is
 1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
1. Describe the elements of the set (Z Q) R N. Is this set countable or uncountable? Solution: The set is equal to {(x, y) x Z, y N} = Z N. Since the Cartesian product of two denumerable sets is denumerable,
MATH 13 SAMPLE FINAL EXAM SOLUTIONS
 MATH 13 SAMPLE FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers.
MATH 13 SAMPLE FINAL EXAM SOLUTIONS WINTER 2014 Problem 1 (15 points). For each statement below, circle T or F according to whether the statement is true or false. You do NOT need to justify your answers.
1.4 Cardinality. Tom Lewis. Fall Term Tom Lewis () 1.4 Cardinality Fall Term / 9
 1.4 Cardinality Tom Lewis Fall Term 2006 Tom Lewis () 1.4 Cardinality Fall Term 2006 1 / 9 Outline 1 Functions 2 Cardinality 3 Cantor s theorem Tom Lewis () 1.4 Cardinality Fall Term 2006 2 / 9 Functions
1.4 Cardinality Tom Lewis Fall Term 2006 Tom Lewis () 1.4 Cardinality Fall Term 2006 1 / 9 Outline 1 Functions 2 Cardinality 3 Cantor s theorem Tom Lewis () 1.4 Cardinality Fall Term 2006 2 / 9 Functions
Introduction to Applied Algebraic Topology
 Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a
![Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a Thus, X is connected by Problem 4. Case 3: X = (a, b]. This case is analogous to Case 2. Case 4: X = (a, b). Choose ε < b a](/thumbs/93/112528193.jpg) Solutions to Homework #6 1. Complete the proof of the backwards direction of Theorem 12.2 from class (which asserts the any interval in R is connected). Solution: Let X R be a closed interval. Case 1:
Solutions to Homework #6 1. Complete the proof of the backwards direction of Theorem 12.2 from class (which asserts the any interval in R is connected). Solution: Let X R be a closed interval. Case 1:
Math 105A HW 1 Solutions
 Sect. 1.1.3: # 2, 3 (Page 7-8 Math 105A HW 1 Solutions 2(a ( Statement: Each positive integers has a unique prime factorization. n N: n = 1 or ( R N, p 1,..., p R P such that n = p 1 p R and ( n, R, S
Sect. 1.1.3: # 2, 3 (Page 7-8 Math 105A HW 1 Solutions 2(a ( Statement: Each positive integers has a unique prime factorization. n N: n = 1 or ( R N, p 1,..., p R P such that n = p 1 p R and ( n, R, S
Basic counting techniques. Periklis A. Papakonstantinou Rutgers Business School
 Basic counting techniques Periklis A. Papakonstantinou Rutgers Business School i LECTURE NOTES IN Elementary counting methods Periklis A. Papakonstantinou MSIS, Rutgers Business School ALL RIGHTS RESERVED
Basic counting techniques Periklis A. Papakonstantinou Rutgers Business School i LECTURE NOTES IN Elementary counting methods Periklis A. Papakonstantinou MSIS, Rutgers Business School ALL RIGHTS RESERVED
Chapter Summary. Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability
 Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
Chapter 2 1 Chapter Summary Sets The Language of Sets Set Operations Set Identities Functions Types of Functions Operations on Functions Computability Sequences and Summations Types of Sequences Summation
ABOUT THE CLASS AND NOTES ON SET THEORY
 ABOUT THE CLASS AND NOTES ON SET THEORY About the Class Evaluation. Final grade will be based 25%, 25%, 25%, 25%, on homework, midterm 1, midterm 2, final exam. Exam dates. Midterm 1: Oct 4. Midterm 2:
ABOUT THE CLASS AND NOTES ON SET THEORY About the Class Evaluation. Final grade will be based 25%, 25%, 25%, 25%, on homework, midterm 1, midterm 2, final exam. Exam dates. Midterm 1: Oct 4. Midterm 2:
Principles of Real Analysis I Fall I. The Real Number System
 21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
21-355 Principles of Real Analysis I Fall 2004 I. The Real Number System The main goal of this course is to develop the theory of real-valued functions of one real variable in a systematic and rigorous
Any Wizard of Oz fans? Discrete Math Basics. Outline. Sets. Set Operations. Sets. Dorothy: How does one get to the Emerald City?
 Any Wizard of Oz fans? Discrete Math Basics Dorothy: How does one get to the Emerald City? Glynda: It is always best to start at the beginning Outline Sets Relations Proofs Sets A set is a collection of
Any Wizard of Oz fans? Discrete Math Basics Dorothy: How does one get to the Emerald City? Glynda: It is always best to start at the beginning Outline Sets Relations Proofs Sets A set is a collection of
Sets are one of the basic building blocks for the types of objects considered in discrete mathematics.
 Section 2.1 Introduction Sets are one of the basic building blocks for the types of objects considered in discrete mathematics. Important for counting. Programming languages have set operations. Set theory
Section 2.1 Introduction Sets are one of the basic building blocks for the types of objects considered in discrete mathematics. Important for counting. Programming languages have set operations. Set theory
Last time: Cyclic groups. Proposition
 Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx` ` P Zu xxy, Additive notation: H t`x `
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx` ` P Zu xxy, Additive notation: H t`x `
Fundamentals of Pure Mathematics - Problem Sheet
 Fundamentals of Pure Mathematics - Problem Sheet ( ) = Straightforward but illustrates a basic idea (*) = Harder Note: R, Z denote the real numbers, integers, etc. assumed to be real numbers. In questions
Fundamentals of Pure Mathematics - Problem Sheet ( ) = Straightforward but illustrates a basic idea (*) = Harder Note: R, Z denote the real numbers, integers, etc. assumed to be real numbers. In questions
CS 125 Section #10 (Un)decidability and Probability November 1, 2016
 CS 125 Section #10 (Un)decidability and Probability November 1, 2016 1 Countability Recall that a set S is countable (either finite or countably infinite) if and only if there exists a surjective mapping
CS 125 Section #10 (Un)decidability and Probability November 1, 2016 1 Countability Recall that a set S is countable (either finite or countably infinite) if and only if there exists a surjective mapping
Random Variables. Andreas Klappenecker. Texas A&M University
 Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
Lecture 10: Everything Else
 Math 94 Professor: Padraic Bartlett Lecture 10: Everything Else Week 10 UCSB 2015 This is the tenth week of the Mathematics Subject Test GRE prep course; here, we quickly review a handful of useful concepts
Math 94 Professor: Padraic Bartlett Lecture 10: Everything Else Week 10 UCSB 2015 This is the tenth week of the Mathematics Subject Test GRE prep course; here, we quickly review a handful of useful concepts
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations
 Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Mathematics Course 111: Algebra I Part I: Algebraic Structures, Sets and Permutations D. R. Wilkins Academic Year 1996-7 1 Number Systems and Matrix Algebra Integers The whole numbers 0, ±1, ±2, ±3, ±4,...
Notes on counting. James Aspnes. December 13, 2010
 Notes on counting James Aspnes December 13, 2010 1 What counting is Recall that in set theory we formally defined each natural number as the set of all smaller natural numbers, so that n = {0, 1, 2,...,
Notes on counting James Aspnes December 13, 2010 1 What counting is Recall that in set theory we formally defined each natural number as the set of all smaller natural numbers, so that n = {0, 1, 2,...,
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS
 ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
Discrete Mathematics and Probability Theory Spring 2014 Anant Sahai Note 20. To Infinity And Beyond: Countability and Computability
 EECS 70 Discrete Mathematics and Probability Theory Spring 014 Anant Sahai Note 0 To Infinity And Beyond: Countability and Computability This note ties together two topics that might seem like they have
EECS 70 Discrete Mathematics and Probability Theory Spring 014 Anant Sahai Note 0 To Infinity And Beyond: Countability and Computability This note ties together two topics that might seem like they have
MATH 101: ALGEBRA I WORKSHEET, DAY #1. We review the prerequisites for the course in set theory and beginning a first pass on group. 1.
 MATH 101: ALGEBRA I WORKSHEET, DAY #1 We review the prerequisites for the course in set theory and beginning a first pass on group theory. Fill in the blanks as we go along. 1. Sets A set is a collection
MATH 101: ALGEBRA I WORKSHEET, DAY #1 We review the prerequisites for the course in set theory and beginning a first pass on group theory. Fill in the blanks as we go along. 1. Sets A set is a collection
Functions and cardinality (solutions) sections A and F TA: Clive Newstead 6 th May 2014
 Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Functions and cardinality (solutions) 21-127 sections A and F TA: Clive Newstead 6 th May 2014 What follows is a somewhat hastily written collection of solutions for my review sheet. I have omitted some
Erdinç Dündar, Celal Çakan
 DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
DEMONSTRATIO MATHEMATICA Vol. XLVII No 3 2014 Erdinç Dündar, Celal Çakan ROUGH I-CONVERGENCE Abstract. In this work, using the concept of I-convergence and using the concept of rough convergence, we introduced
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS
 UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
Finite and Infinite Sets
 Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
Chapter 9 Finite and Infinite Sets 9. Finite Sets Preview Activity (Equivalent Sets, Part ). Let A and B be sets and let f be a function from A to B..f W A! B/. Carefully complete each of the following
Lecture 3: Sizes of Infinity
 Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
Math/CS 20: Intro. to Math Professor: Padraic Bartlett Lecture 3: Sizes of Infinity Week 2 UCSB 204 Sizes of Infinity On one hand, we know that the real numbers contain more elements than the rational
Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability.
 Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability. Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon
Today. Wrapup of Polynomials...and modular arithmetic. Coutability and Uncountability. Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon
Exercises for Unit VI (Infinite constructions in set theory)
 Exercises for Unit VI (Infinite constructions in set theory) VI.1 : Indexed families and set theoretic operations (Halmos, 4, 8 9; Lipschutz, 5.3 5.4) Lipschutz : 5.3 5.6, 5.29 5.32, 9.14 1. Generalize
Exercises for Unit VI (Infinite constructions in set theory) VI.1 : Indexed families and set theoretic operations (Halmos, 4, 8 9; Lipschutz, 5.3 5.4) Lipschutz : 5.3 5.6, 5.29 5.32, 9.14 1. Generalize
Cardinality and ordinal numbers
 Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
Cardinality and ordinal numbers The cardinality A of a finite set A is simply the number of elements in it. When it comes to infinite sets, we no longer can speak of the number of elements in such a set.
Lecture 2: Period Three Implies Chaos
 Dynamical Systems Instructor: Padraic Bartlett Lecture 2: Period Three Implies Chaos Week 3 Mathcamp 2014 We ended our last class by proving the following result (whose name I found while doing some research
Dynamical Systems Instructor: Padraic Bartlett Lecture 2: Period Three Implies Chaos Week 3 Mathcamp 2014 We ended our last class by proving the following result (whose name I found while doing some research
Scott Taylor 1. EQUIVALENCE RELATIONS. Definition 1.1. Let A be a set. An equivalence relation on A is a relation such that:
 Equivalence MA Relations 274 and Partitions Scott Taylor 1. EQUIVALENCE RELATIONS Definition 1.1. Let A be a set. An equivalence relation on A is a relation such that: (1) is reflexive. That is, (2) is
Equivalence MA Relations 274 and Partitions Scott Taylor 1. EQUIVALENCE RELATIONS Definition 1.1. Let A be a set. An equivalence relation on A is a relation such that: (1) is reflexive. That is, (2) is
Isomorphisms and Well-definedness
 Isomorphisms and Well-definedness Jonathan Love October 30, 2016 Suppose you want to show that two groups G and H are isomorphic. There are a couple of ways to go about doing this depending on the situation,
Isomorphisms and Well-definedness Jonathan Love October 30, 2016 Suppose you want to show that two groups G and H are isomorphic. There are a couple of ways to go about doing this depending on the situation,
2.1 Sets. Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R.
 2. Basic Structures 2.1 Sets Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R. Definition 2 Objects in a set are called elements or members of the set. A set is
2. Basic Structures 2.1 Sets Definition 1 A set is an unordered collection of objects. Important sets: N, Z, Z +, Q, R. Definition 2 Objects in a set are called elements or members of the set. A set is
One-to-one functions and onto functions
 MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
MA 3362 Lecture 7 - One-to-one and Onto Wednesday, October 22, 2008. Objectives: Formalize definitions of one-to-one and onto One-to-one functions and onto functions At the level of set theory, there are
Reed-Solomon code. P(n + 2k)
 Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon Code: 1. Make a polynomial, P(x) of degree n 1, that encodes message: coefficients,
Reed-Solomon code. Problem: Communicate n packets m 1,...,m n on noisy channel that corrupts k packets. Reed-Solomon Code: 1. Make a polynomial, P(x) of degree n 1, that encodes message: coefficients,
Week Some Warm-up Questions
 1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
1 Some Warm-up Questions Week 1-2 Abstraction: The process going from specific cases to general problem. Proof: A sequence of arguments to show certain conclusion to be true. If... then... : The part after
Countable and uncountable sets. Matrices.
 Lecture 11 Countable and uncountable sets. Matrices. Instructor: Kangil Kim (CSE) E-mail: kikim01@konkuk.ac.kr Tel. : 02-450-3493 Room : New Milenium Bldg. 1103 Lab : New Engineering Bldg. 1202 Next topic:
Lecture 11 Countable and uncountable sets. Matrices. Instructor: Kangil Kim (CSE) E-mail: kikim01@konkuk.ac.kr Tel. : 02-450-3493 Room : New Milenium Bldg. 1103 Lab : New Engineering Bldg. 1202 Next topic:
0 Sets and Induction. Sets
 0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
0 Sets and Induction Sets A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a A to denote that a is an element of the set
CHAPTER 8: EXPLORING R
 CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
Chapter 1. Sets and Mappings
 Chapter 1. Sets and Mappings 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
Chapter 1. Sets and Mappings 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
REVIEW FOR THIRD 3200 MIDTERM
 REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
REVIEW FOR THIRD 3200 MIDTERM PETE L. CLARK 1) Show that for all integers n 2 we have 1 3 +... + (n 1) 3 < 1 n < 1 3 +... + n 3. Solution: We go by induction on n. Base Case (n = 2): We have (2 1) 3 =
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes
 Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
Foundations of Mathematics MATH 220 FALL 2017 Lecture Notes These notes form a brief summary of what has been covered during the lectures. All the definitions must be memorized and understood. Statements
3. Only sequences that were formed by using finitely many applications of rules 1 and 2, are propositional formulas.
 1 Chapter 1 Propositional Logic Mathematical logic studies correct thinking, correct deductions of statements from other statements. Let us make it more precise. A fundamental property of a statement is
1 Chapter 1 Propositional Logic Mathematical logic studies correct thinking, correct deductions of statements from other statements. Let us make it more precise. A fundamental property of a statement is
a + b = b + a and a b = b a. (a + b) + c = a + (b + c) and (a b) c = a (b c). a (b + c) = a b + a c and (a + b) c = a c + b c.
 Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Solutions to Tutorial for Week 4
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial for Week 4 MATH191/1931: Calculus of One Variable (Advanced) Semester 1, 018 Web Page: sydneyeduau/science/maths/u/ug/jm/math191/
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial for Week 4 MATH191/1931: Calculus of One Variable (Advanced) Semester 1, 018 Web Page: sydneyeduau/science/maths/u/ug/jm/math191/
Properties of the Integers
 Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Economics 204 Summer/Fall 2017 Lecture 1 Monday July 17, 2017
 Economics 04 Summer/Fall 07 Lecture Monday July 7, 07 Section.. Methods of Proof We begin by looking at the notion of proof. What is a proof? Proof has a formal definition in mathematical logic, and a
Economics 04 Summer/Fall 07 Lecture Monday July 7, 07 Section.. Methods of Proof We begin by looking at the notion of proof. What is a proof? Proof has a formal definition in mathematical logic, and a
Lecture 21: Midterm 2 Review.
 Lecture 21: Midterm 2 Review. Professor Walrand. Wrapping up his lectures for other course this week. Will take over lectures next week. Rao will continue co-teaching. Office hours. See you on Piazza.
Lecture 21: Midterm 2 Review. Professor Walrand. Wrapping up his lectures for other course this week. Will take over lectures next week. Rao will continue co-teaching. Office hours. See you on Piazza.
Automata and Languages
 Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Mathematical Background Mathematical Background Sets Relations Functions Graphs Proof techniques Sets
Automata and Languages Prof. Mohamed Hamada Software Engineering Lab. The University of Aizu Japan Mathematical Background Mathematical Background Sets Relations Functions Graphs Proof techniques Sets
Foundations Revision Notes
 oundations Revision Notes hese notes are designed as an aid not a substitute for revision. A lot of proofs have not been included because you should have them in your notes, should you need them. Also,
oundations Revision Notes hese notes are designed as an aid not a substitute for revision. A lot of proofs have not been included because you should have them in your notes, should you need them. Also,
MATH 3300 Test 1. Name: Student Id:
 Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
Name: Student Id: There are nine problems (check that you have 9 pages). Solutions are expected to be short. In the case of proofs, one or two short paragraphs should be the average length. Write your
Warm-up Quantifiers and the harmonic series Sets Second warmup Induction Bijections. Writing more proofs. Misha Lavrov
 Writing more proofs Misha Lavrov ARML Practice 3/16/2014 and 3/23/2014 Warm-up Using the quantifier notation on the reference sheet, and making any further definitions you need to, write the following:
Writing more proofs Misha Lavrov ARML Practice 3/16/2014 and 3/23/2014 Warm-up Using the quantifier notation on the reference sheet, and making any further definitions you need to, write the following:
1 Partitions and Equivalence Relations
 Today we re going to talk about partitions of sets, equivalence relations and how they are equivalent. Then we are going to talk about the size of a set and will see our first example of a diagonalisation
Today we re going to talk about partitions of sets, equivalence relations and how they are equivalent. Then we are going to talk about the size of a set and will see our first example of a diagonalisation
Discrete Mathematics 2007: Lecture 5 Infinite sets
 Discrete Mathematics 2007: Lecture 5 Infinite sets Debrup Chakraborty 1 Countability The natural numbers originally arose from counting elements in sets. There are two very different possible sizes for
Discrete Mathematics 2007: Lecture 5 Infinite sets Debrup Chakraborty 1 Countability The natural numbers originally arose from counting elements in sets. There are two very different possible sizes for
6 Cosets & Factor Groups
 6 Cosets & Factor Groups The course becomes markedly more abstract at this point. Our primary goal is to break apart a group into subsets such that the set of subsets inherits a natural group structure.
6 Cosets & Factor Groups The course becomes markedly more abstract at this point. Our primary goal is to break apart a group into subsets such that the set of subsets inherits a natural group structure.
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative
 Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
RELATIONS AND FUNCTIONS
 For more important questions visit : www.4ono.com CHAPTER 1 RELATIONS AND FUNCTIONS IMPORTANT POINTS TO REMEMBER Relation R from a set A to a set B is subset of A B. A B = {(a, b) : a A, b B}. If n(a)
For more important questions visit : www.4ono.com CHAPTER 1 RELATIONS AND FUNCTIONS IMPORTANT POINTS TO REMEMBER Relation R from a set A to a set B is subset of A B. A B = {(a, b) : a A, b B}. If n(a)
Chapter 1. Sets and Numbers
 Chapter 1. Sets and Numbers 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
Chapter 1. Sets and Numbers 1. Sets A set is considered to be a collection of objects (elements). If A is a set and x is an element of the set A, we say x is a member of A or x belongs to A, and we write
Math /Foundations of Algebra/Fall 2017 Foundations of the Foundations: Proofs
 Math 4030-001/Foundations of Algebra/Fall 017 Foundations of the Foundations: Proofs A proof is a demonstration of the truth of a mathematical statement. We already know what a mathematical statement is.
Math 4030-001/Foundations of Algebra/Fall 017 Foundations of the Foundations: Proofs A proof is a demonstration of the truth of a mathematical statement. We already know what a mathematical statement is.
Modular Arithmetic Inverses and GCD
 Lecture 21: Midterm 2 Review. Professor Walrand. Wrapping up his lectures for other course this week. Will take over lectures next week. Rao will continue co-teaching. Office hours. See you on Piazza.
Lecture 21: Midterm 2 Review. Professor Walrand. Wrapping up his lectures for other course this week. Will take over lectures next week. Rao will continue co-teaching. Office hours. See you on Piazza.
Math 42, Discrete Mathematics
 c Fall 2018 last updated 10/10/2018 at 23:28:03 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
c Fall 2018 last updated 10/10/2018 at 23:28:03 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
Proofs. Chapter 2 P P Q Q
 Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
Countable and uncountable sets. Matrices.
 CS 441 Discrete Mathematics for CS Lecture 11 Countable and uncountable sets. Matrices. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Arithmetic series Definition: The sum of the terms of the
CS 441 Discrete Mathematics for CS Lecture 11 Countable and uncountable sets. Matrices. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Arithmetic series Definition: The sum of the terms of the
MATH FINAL EXAM REVIEW HINTS
 MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
MATH 109 - FINAL EXAM REVIEW HINTS Answer: Answer: 1. Cardinality (1) Let a < b be two real numbers and define f : (0, 1) (a, b) by f(t) = (1 t)a + tb. (a) Prove that f is a bijection. (b) Prove that any
Math 3361-Modern Algebra Lecture 08 9/26/ Cardinality
 Math 336-Modern Algebra Lecture 08 9/26/4. Cardinality I started talking about cardinality last time, and you did some stuff with it in the Homework, so let s continue. I said that two sets have the same
Math 336-Modern Algebra Lecture 08 9/26/4. Cardinality I started talking about cardinality last time, and you did some stuff with it in the Homework, so let s continue. I said that two sets have the same
1. A Little Set Theory
 . A Little Set Theory I see it, but I don t believe it. Cantor to Dedekind 29 June 877 Functions are the single most important idea pervading modern mathematics. We will assume the informal definition
. A Little Set Theory I see it, but I don t believe it. Cantor to Dedekind 29 June 877 Functions are the single most important idea pervading modern mathematics. We will assume the informal definition
Supplementary Material for MTH 299 Online Edition
 Supplementary Material for MTH 299 Online Edition Abstract This document contains supplementary material, such as definitions, explanations, examples, etc., to complement that of the text, How to Think
Supplementary Material for MTH 299 Online Edition Abstract This document contains supplementary material, such as definitions, explanations, examples, etc., to complement that of the text, How to Think
PRODUCT MEASURES AND FUBINI S THEOREM
 CHAPTER 6 PRODUCT MEASURES AND FUBINI S THEOREM All students learn in elementary calculus to evaluate a double integral by iteration. The theorem justifying this process is called Fubini s theorem. However,
CHAPTER 6 PRODUCT MEASURES AND FUBINI S THEOREM All students learn in elementary calculus to evaluate a double integral by iteration. The theorem justifying this process is called Fubini s theorem. However,
Sets and Functions. (As we will see, in describing a set the order in which elements are listed is irrelevant).
 Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
Sets and Functions 1. The language of sets Informally, a set is any collection of objects. The objects may be mathematical objects such as numbers, functions and even sets, or letters or symbols of any
