Lesson 19: Understanding Variability When Estimating a Population Proportion
|
|
|
- Alison Pope
- 6 years ago
- Views:
Transcription
1 Lesson 19: Understanding Variability When Estimating a Population Proportion Student Outcomes Students understand the term sampling variability in the context of estimating a population proportion. Students know that increasing the sample size decreases sampling variability. Lesson Notes In a previous lesson, students investigated sampling variability in the sample mean for numerical data. In this lesson, they will investigate sampling variability in the sample proportion for categorical data. Distinguishing between the sample mean for numerical data and the sample proportion for categorical data is important. This lesson begins with students investigating these differences. It is important that students see the similarity between working with a proportion and what they did in the previous lessons when working with the mean; that is, as the sample size increases, the sampling variability of sample proportions decreases. The dot plots provide students a visual representation of sampling variability. Dot plots are also used to show the connection between sampling variability and sample size. Before students start the exercises, prepare bags containing 100 cubes (or beads or slips of paper, etc.) for each group of four students. Forty cubes should be red, and the remaining 60 cubes can be any other color (e.g., orange, blue, green, yellow). Also, prepare a number line (illustrated in Example 1) that is visible on the board or on poster paper. Classwork Opening (3 minutes) As a warm-up activity, discuss how the data used to calculate a proportion (such as the proportion of gym members that are female) is different from the data used to determine a mean (such as the mean time people spend in the gym or the mean number of words in a children s literature book). Other examples of a proportion are the proportion of people at a particular school who run a marathon or the proportion of Great Lake perch that are 5 cm or less. Understanding what a proportion is and how the type of data used to calculate a proportion is different from the type of data they used to calculate a mean is important for the next couple of lessons. This difference is not always easy for students to see, so be deliberate in pointing this out with each new data scenario that is introduced. Before students begin working with the example in their lesson, discuss the following statistical questions with students. Ask students what data they would collect to answer the questions and what they would do with the data. Point out to the students those situations in which they would find the average or mean of the data and those situations in which they would find a proportion or a percent. Question 1: How many hours of sleep do seventh graders get on a night in which there is school the next day? Data on the number of hours students in a sample of seventh graders sleep would be collected. This would be numerical data, and the mean of the numbers would be used to answer this statistical question. Date: 2/6/15 210
2 Question 2: What proportion of the students in our school participate in band or orchestra? A sample of students could be asked to indicate whether or not they participate in band or orchestra. This data would not be numerical. The proportion of the students participating in band or orchestra for the sample would be used to answer this statistical question. (Point out that it would not be possible to calculate a mean based on this data.) Question 3: What is the typical weight of a backpack for students at our school? Data from a sample of students at the school on the weight of backpacks would be collected. This data would be numerical, and the mean of the weights would be used to answer this statistical question. Question 4: What is the likelihood that voters in a certain city will vote for building a new high school? A sample of voters could be obtained. Each voter in the sample would be asked whether or not they would vote for building a new high school. This data is not numerical. The proportion of the voters who indicated they would vote yes for the sample would be used to answer this question. After the warm-up, proceed with the example in the student lesson. In a previous lesson, you selected several random samples from a population. You recorded values of a numerical variable. You then calculated the mean for each sample, saw that there was variability in the sample means, and created a distribution of sample means to better see the sampling variability. You then considered larger samples and saw that the variability in the distribution decreases when the sample size increases. In this lesson, you will use a similar process to investigate variability in sample proportions. Example 1 (15 minutes): Sample Proportion Prior to the start of the lesson, prepare the following: A bag containing 100 cubes (or beads or slips of paper, etc.) for each group of four students. Forty should be red, and the remaining 60 cubes can be any other color. On the board, draw a number line similar to the one shown below Begin the lesson by saying, Today we are going to learn something about the population of cubes in this bag. It is full of cubes. Based on your previous work, how could you learn something about the whole bag of cubes? After this discussion, instruct each student to take a random sample of 10 cubes from the bag. This sample should be taken with replacement. You may want to begin by taking a sample as a demonstration. Example 1: Sample Proportion Your teacher will give your group a bag that contains colored cubes, some of which are red. With your classmates, you are going to build a distribution of sample proportions. Each student should record the color of each draw and then calculate the proportion of red in her sample of 10. Date: 2/6/15 211
3 How would you determine the sample proportion of red cubes? number of successes in the sample Sample proportion = total number of observations in the sample Have students place post-it notes on the number line to build a dot plot. After all of the post-it notes have been placed, explain to students that the graph is the sampling distribution of the sample proportions. Allow students to work with their groups on parts (a) (f). Then, discuss as a class. As students discuss the answers to parts (d) and (e), note that the shape of the distribution of sample proportions is often mound shaped. For the variability, students need to focus on the overall spread in the sample proportions and the main cluster around the center of the distribution. a. Each person in your group should randomly select a sample of 1111 cubes from the bag. Record the data for your sample in the table below. Students tables will vary based on their samples. Cube Outcome (Color) Green Orange Red Red Blue Orange Red Green Blue Blue b. What is the proportion of red cubes in your sample of 1111? This value is called the sample proportion. The sample proportion is found by dividing the number of successes (in this example, the number of red cubes) by the total number of observations in the sample. Student results will be around In this example, the sample proportion is Date: 2/6/15 212
4 c. Write your sample proportion on a post-it note, and place it on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion. The graph of all the students sample proportions is called a sampling distribution of the sample proportions. This is an example of a dot plot of the sampling distribution. d. Describe the shape of the distribution. Nearly symmetrical distribution that is clustered around e. Describe the variability in the sample proportions. The spread of the data is from to Much of the data clusters between and Based on the distribution, answer the following: f. What do you think is the population proportion? Based on the dot plot, an estimate of the population proportion is approximately g. How confident are you of your estimate? Because there is a lot of variability from sample to sample ( to ), there is not a lot of confidence in the estimate. Example 2 (14 minutes): Sampling Variability This example parallels Example 1. Students now take a random sample of 30 cubes from the bag. This sample should be taken with replacement. Example 2: Sampling Variablity What do you think would happen to the sampling distribution if everyone in class took a random sample of 3333 cubes from the bag? To help answer this question, you will repeat the random sampling you did in part (a) of Example 1, except now you will draw a random sample of 3333 cubes instead of Students record their sample results and find the sample proportion of red cubes in the bag. Again, they should record the proportion on a post-it note. Date: 2/6/15 213
5 Draw another number line on the board using the same scale as in Example 1. Allow students to work with their groups on Example 2. Then, discuss the answers as a class. a. Take a random sample of 3333 cubes from the bag. Carefully record the outcome of each draw. Answers will vary. An example follows: Blue Green Red Yellow Blue Red Red Green Blue Red Green Red Red Green Yellow Blue Blue Yellow Red Blue Red Green Red Red Blue Red Yellow Green Green Yellow b. What is the proportion of red cubes in your sample of 3333? Answers will vary. In this example, the sample proportion is 1111, or approximately c. Write your sample proportion on a post-it note, and place the note on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion. An example of a dot plot: d. Describe the shape of the distribution. Mound-shaped, centered around Date: 2/6/15 214
6 Exercises 1 5 (5 minutes) Students should work independently on Exercises 1 5. Then, discuss as a class. Exercises Describe the variability in the sample proportions. Spread of the data is from to Most of the data clusters between and Based on the distribution, answer the following: a. What do you think is the population proportion? Based on the dot plot, an estimate of the population proportion is approximately b. How confident are you of your estimate? Because there is less variability from sample to sample ( to ), there is more confidence in the estimate. c. If you were taking a random sample of 3333 cubes and determined the proportion that was red, do you think your sample proportion will be within of the population proportion? Explain. Answers depend on the dot plots prepared by students. If the dot plot in Example 2, part (c) is used as an example, note that only about half of the dots are between and There are several samples that had sample proportions that were farther away from the center than , so the sample proportion might not be within of the population proportion. 3. Compare the sampling distribution based on samples of size 1111 to the sampling distribution based on samples of size Both distributions are mound-shaped and center around Variability is less in the sampling distribution of sample sizes of 3333 versus sample sizes of As the sample size increased from 1111 to 3333, describe what happened to the sampling variability of the sample proportions. The sampling variability decreased as the sample size increased. MP.2 5. What do you think would happen to the sampling variability of the sample proportions if the sample size for each sample was 5555 instead of 3333? Explain. The sampling variability in the sampling distribution for samples of size 5555 will be less than the sampling variability of the sampling distribution for samples of size Closing (3 minutes) To highlight the Lesson Summary, ask students the following questions: How do you know if the data collected is summarized by a mean or by a proportion? Anticipate responses that indicate the different types of data collected and how the data is summarized. Examples similar to those discussed in the lesson would indicate an understanding of when a mean is calculated and when a proportion is calculated. Date: 2/6/15 215
7 What would a dot plot of a sampling distribution of the sample proportion look like if proportions from many different random samples were used to create the plot? Anticipate responses that describe a dot plot in which each dot represents the sample proportion of one sample. The graph would show variability (or sampling variability) with a cluster around a value close to the value of the proportion for the population. Consider asking students to sketch a dot plot that they might get for one of the examples in which a proportion is used to answer the statistical question. What happens to the sampling distribution as the sample size increases? Anticipate responses that indicate the sampling variability (spread of the dots in the dot plot) decreases as the sample size increases. Lesson Summary The sampling distribution of the sample proportion is a graph of the sample proportions for many different samples. The mean of the sample proportions will be approximately equal to the value of the population proportion. As the sample size increases, the sampling variability decreases. Exit Ticket (5 minutes) Date: 2/6/15 216
8 Name Date Lesson 19: Understanding Variability When Estimating a Population Proportion Exit Ticket A group of seventh graders took repeated samples of size 20 from a bag of colored cubes. The dot plot below shows the sampling distribution of the sample proportion of blue cubes in the bag. 1. Describe the shape of the distribution. 2. Describe the variability of the distribution. 3. Predict how the dot plot would look differently if the sample sizes had been 40 instead of 20. Date: 2/6/15 217
9 Exit Ticket Sample Solutions A group of seventh graders took repeated samples of size 2222 from a bag of colored cubes. The dot plot below shows the sampling distribution of the sample proportion of blue cubes in the bag. 1. Describe the shape of the distribution. Mound-shaped, centered around Describe the variability of the distribution. The spread of the data is from to , with much of the data between and Predict how the dot plot would look differently if the sample sizes had been 4444 instead of The variability will decrease as the sample size increases. The dot plot will be centered in a similar place but will be less spread out. Problem Set Sample Solutions 1. A class of seventh graders wanted to find the proportion of M&M s that are red. Each seventh grader took a random sample of 2222 M&M s from a very large container of M&M s. Following is the proportion of red M&M s each student found a. Construct a dot plot of the sample proportions. b. Describe the shape of the distribution. Somewhat mound-shaped, slightly skewed to the right. Date: 2/6/15 218
10 c. Describe the variability of the distribution. Spread of the data is from to Most of the data clusters between and d. Suppose the seventh-grade students had taken random samples of size Describe how the sampling distribution would change from the one you constructed in part (a). The sampling variability would decrease. 2. A group of seventh graders wanted to estimate the proportion of middle school students who suffer from allergies. The members of one group of seventh graders each took a random sample of 1111 middle school students, and the members of another group of seventh graders each took a random sample of 4444 middle school students. Below are two sampling distributions of the sample proportions of middle school students who said that they suffer from allergies. Which dot plot is based on random samples of size 4444? How can you tell? Dot Plot A Dot Plot B Dot Plot A because the variability of the distribution is less than the variability in Dot Plot B. 3. The nurse in your school district would like to study the proportion of middle school students who usually get at least eight hours of sleep on school nights. Suppose each student in your class plans on taking a random sample of 2222 middle school students from your district, and each calculates a sample proportion of students who said that they usually get at least eight hours of sleep on school nights. a. Do you expect everyone in your class to get the same value for their sample proportion? Explain. No, we expect sample variability. b. Suppose each student in class increased the sample size from 2222 to Describe how you could reduce the sampling variability. I could reduce the sampling variability by using the larger sample size. Date: 2/6/15 219
Lesson 7: The Mean as a Balance Point
 Student Outcomes Students characterize the center of a distribution by its mean in the sense of a balance point. Students understand that the mean is a balance point by calculating the distances of the
Student Outcomes Students characterize the center of a distribution by its mean in the sense of a balance point. Students understand that the mean is a balance point by calculating the distances of the
Lesson 23: The Defining Equation of a Line
 Student Outcomes Students know that two equations in the form of and graph as the same line when and at least one of or is nonzero. Students know that the graph of a linear equation, where,, and are constants
Student Outcomes Students know that two equations in the form of and graph as the same line when and at least one of or is nonzero. Students know that the graph of a linear equation, where,, and are constants
Lesson 8: Graphs of Simple Non Linear Functions
 Student Outcomes Students examine the average rate of change for non linear functions and learn that, unlike linear functions, non linear functions do not have a constant rate of change. Students determine
Student Outcomes Students examine the average rate of change for non linear functions and learn that, unlike linear functions, non linear functions do not have a constant rate of change. Students determine
Lesson 28: Another Computational Method of Solving a Linear System
 Lesson 28: Another Computational Method of Solving a Linear System Student Outcomes Students learn the elimination method for solving a system of linear equations. Students use properties of rational numbers
Lesson 28: Another Computational Method of Solving a Linear System Student Outcomes Students learn the elimination method for solving a system of linear equations. Students use properties of rational numbers
Lesson 5: Measuring Variability for Symmetrical Distributions
 1. : Measuring Variability for Symmetrical Distributions Student Outcomes Students calculate the standard deviation for a set of data. Students interpret the standard deviation as a typical distance from
1. : Measuring Variability for Symmetrical Distributions Student Outcomes Students calculate the standard deviation for a set of data. Students interpret the standard deviation as a typical distance from
Lesson 10: Describing Distributions Using the Mean and MAD
 Lesson 10: Describing Distributions Using the Mean and MAD Student Outcomes Students calculate the mean and MAD for a data distribution. Students use the mean and MAD to describe a data distribution in
Lesson 10: Describing Distributions Using the Mean and MAD Student Outcomes Students calculate the mean and MAD for a data distribution. Students use the mean and MAD to describe a data distribution in
Lesson 26: Characterization of Parallel Lines
 Student Outcomes Students know that when a system of linear equations has no solution, i.e., no point of intersection of the lines, then the lines are parallel. Lesson Notes The discussion that begins
Student Outcomes Students know that when a system of linear equations has no solution, i.e., no point of intersection of the lines, then the lines are parallel. Lesson Notes The discussion that begins
Lesson 18: Recognizing Equations of Circles
 Student Outcomes Students complete the square in order to write the equation of a circle in center-radius form. Students recognize when a quadratic in xx and yy is the equation for a circle. Lesson Notes
Student Outcomes Students complete the square in order to write the equation of a circle in center-radius form. Students recognize when a quadratic in xx and yy is the equation for a circle. Lesson Notes
Lesson 24: True and False Number Sentences
 NYS COMMON CE MATHEMATICS CURRICULUM Lesson 24 6 4 Student Outcomes Students identify values for the variables in equations and inequalities that result in true number sentences. Students identify values
NYS COMMON CE MATHEMATICS CURRICULUM Lesson 24 6 4 Student Outcomes Students identify values for the variables in equations and inequalities that result in true number sentences. Students identify values
Using Dice to Introduce Sampling Distributions Written by: Mary Richardson Grand Valley State University
 Using Dice to Introduce Sampling Distributions Written by: Mary Richardson Grand Valley State University richamar@gvsu.edu Overview of Lesson In this activity students explore the properties of the distribution
Using Dice to Introduce Sampling Distributions Written by: Mary Richardson Grand Valley State University richamar@gvsu.edu Overview of Lesson In this activity students explore the properties of the distribution
Eureka Lessons for 6th Grade Unit FIVE ~ Equations & Inequalities
 Eureka Lessons for 6th Grade Unit FIVE ~ Equations & Inequalities These 2 lessons can easily be taught in 2 class periods. If you like these lessons, please consider using other Eureka lessons as well.
Eureka Lessons for 6th Grade Unit FIVE ~ Equations & Inequalities These 2 lessons can easily be taught in 2 class periods. If you like these lessons, please consider using other Eureka lessons as well.
Lesson 7: Classification of Solutions
 Student Outcomes Students know the conditions for which a linear equation will have a unique solution, no solution, or infinitely many solutions. Lesson Notes Part of the discussion on the second page
Student Outcomes Students know the conditions for which a linear equation will have a unique solution, no solution, or infinitely many solutions. Lesson Notes Part of the discussion on the second page
Chapter 9: Equations and Inequalities
 Chapter 9: Equations and Inequalities Lesson Objectives Class Periods Tetbook & Workbook Teacher's Guide Page Additional Materials Needed Determine whether a given number makes an equation true. TB: 28
Chapter 9: Equations and Inequalities Lesson Objectives Class Periods Tetbook & Workbook Teacher's Guide Page Additional Materials Needed Determine whether a given number makes an equation true. TB: 28
2275 Speedway, Mail Code C9000 Austin, TX (512) Weather and Climate
 Lesson Plan for Grades: Middle School Length of Lesson: 90 minutes Authored by: UT Environmental Science Institute Date created: 05/10/2017 Subject area/course: Mathematics Materials: Fun size bags of
Lesson Plan for Grades: Middle School Length of Lesson: 90 minutes Authored by: UT Environmental Science Institute Date created: 05/10/2017 Subject area/course: Mathematics Materials: Fun size bags of
Objective: Recognize halves within a circular clock face and tell time to the half hour.
 Lesson 13 1 5 Lesson 13 Objective: Recognize halves within a circular clock face and tell time to the half Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Lesson 13 1 5 Lesson 13 Objective: Recognize halves within a circular clock face and tell time to the half Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Five people were asked approximately how many hours of TV they watched per week. Their responses were as follows.
 Exit icket Sample Solutions Five people were asked approximately how many hours of V they watched per week. heir responses were as follows. 1. Find the mean number of hours of V watched for these five
Exit icket Sample Solutions Five people were asked approximately how many hours of V they watched per week. heir responses were as follows. 1. Find the mean number of hours of V watched for these five
Student Outcomes. Lesson Notes. Classwork. Example 1 (5 minutes) Students apply knowledge of geometry to writing and solving linear equations.
 Student Outcomes Students apply knowledge of geometry to writing and solving linear equations. Lesson Notes All of the problems in this lesson relate to what students have learned about geometry in recent
Student Outcomes Students apply knowledge of geometry to writing and solving linear equations. Lesson Notes All of the problems in this lesson relate to what students have learned about geometry in recent
Student Outcomes. Classwork. Example 1 (6 minutes)
 Student Outcomes Students know the definition of constant rate in varied contexts as expressed using two variables where one is representing a time interval. Students graph points on a coordinate plane
Student Outcomes Students know the definition of constant rate in varied contexts as expressed using two variables where one is representing a time interval. Students graph points on a coordinate plane
Lesson 24: Modeling with Quadratic Functions
 Student Outcomes Students create a quadratic function from a data set based on a contextual situation, sketch its graph, and interpret both the function and the graph in context. They answer questions
Student Outcomes Students create a quadratic function from a data set based on a contextual situation, sketch its graph, and interpret both the function and the graph in context. They answer questions
Chapter 18. Sampling Distribution Models. Copyright 2010, 2007, 2004 Pearson Education, Inc.
 Chapter 18 Sampling Distribution Models Copyright 2010, 2007, 2004 Pearson Education, Inc. Normal Model When we talk about one data value and the Normal model we used the notation: N(μ, σ) Copyright 2010,
Chapter 18 Sampling Distribution Models Copyright 2010, 2007, 2004 Pearson Education, Inc. Normal Model When we talk about one data value and the Normal model we used the notation: N(μ, σ) Copyright 2010,
Lesson 12: Overcoming Obstacles in Factoring
 Lesson 1: Overcoming Obstacles in Factoring Student Outcomes Students factor certain forms of polynomial expressions by using the structure of the polynomials. Lesson Notes Students have factored polynomial
Lesson 1: Overcoming Obstacles in Factoring Student Outcomes Students factor certain forms of polynomial expressions by using the structure of the polynomials. Lesson Notes Students have factored polynomial
Lesson 28: A Focus on Square Roots
 now Lesson 28: A Focus on Square Roots Student Outcomes Students solve simple radical equations and understand the possibility of extraneous solutions. They understand that care must be taken with the
now Lesson 28: A Focus on Square Roots Student Outcomes Students solve simple radical equations and understand the possibility of extraneous solutions. They understand that care must be taken with the
Student Outcomes. Lesson Notes. Classwork. Opening Exercise (5 minutes)
 Student Outcomes Students know that truncated cones and pyramids are solids obtained by removing the top portion above a plane parallel to the base. Students find the volume of truncated cones. Lesson
Student Outcomes Students know that truncated cones and pyramids are solids obtained by removing the top portion above a plane parallel to the base. Students find the volume of truncated cones. Lesson
Lesson 12. Student Outcomes. Classwork. Opening Exercise (4 minutes) Discussion (4 minutes)
 Student Outcomes Students are introduced to the formal process of solving an equation: starting from the assumption that the original equation has a solution. Students explain each step as following from
Student Outcomes Students are introduced to the formal process of solving an equation: starting from the assumption that the original equation has a solution. Students explain each step as following from
Measuring Keepers S E S S I O N 1. 5 A
 S E S S I O N 1. 5 A Measuring Keepers Math Focus Points Naming, notating, and telling time to the hour on a digital and an analog clock Understanding the meaning of at least in the context of linear measurement
S E S S I O N 1. 5 A Measuring Keepers Math Focus Points Naming, notating, and telling time to the hour on a digital and an analog clock Understanding the meaning of at least in the context of linear measurement
Lesson 8: Using If-Then Moves in Solving Equations
 Student Outcomes Students understand and use the addition, subtraction, multiplication, division, and substitution properties of equality to solve word problems leading to equations of the form and where,,
Student Outcomes Students understand and use the addition, subtraction, multiplication, division, and substitution properties of equality to solve word problems leading to equations of the form and where,,
Lesson 11: The Special Role of Zero in Factoring
 Lesson 11: The Special Role of Zero in Factoring Student Outcomes Students find solutions to polynomial equations where the polynomial expression is not factored into linear factors. Students construct
Lesson 11: The Special Role of Zero in Factoring Student Outcomes Students find solutions to polynomial equations where the polynomial expression is not factored into linear factors. Students construct
Objective: Construct a paper clock by partitioning a circle and tell time to the hour. (10 minutes)
 Lesson 10 1 Lesson 10 Objective: Construct a paper clock by partitioning a circle and tell time to the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Lesson 10 1 Lesson 10 Objective: Construct a paper clock by partitioning a circle and tell time to the Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Lesson 12: Solving Equations
 Student Outcomes Students are introduced to the formal process of solving an equation: starting from the assumption that the original equation has a solution. Students explain each step as following from
Student Outcomes Students are introduced to the formal process of solving an equation: starting from the assumption that the original equation has a solution. Students explain each step as following from
Lesson 5: Criterion for Perpendicularity
 Student Outcomes Students explain the connection between the Pythagorean theorem and the criterion for perpendicularity. Lesson Notes It is the goal of this lesson to justify and prove the following: Theorem:
Student Outcomes Students explain the connection between the Pythagorean theorem and the criterion for perpendicularity. Lesson Notes It is the goal of this lesson to justify and prove the following: Theorem:
Two-Color Counters. KEY TERM additive inverses
 Two-Color Counters Adding Integers, Part II 3 WARM UP Use a number line to determine each sum. Then write a sentence to describe the movement you used on the number line to compute the sum of the two integers.
Two-Color Counters Adding Integers, Part II 3 WARM UP Use a number line to determine each sum. Then write a sentence to describe the movement you used on the number line to compute the sum of the two integers.
Lesson 8: Complex Number Division
 Student Outcomes Students determine the modulus and conjugate of a complex number. Students use the concept of conjugate to divide complex numbers. Lesson Notes This is the second day of a two-day lesson
Student Outcomes Students determine the modulus and conjugate of a complex number. Students use the concept of conjugate to divide complex numbers. Lesson Notes This is the second day of a two-day lesson
THE SAMPLING DISTRIBUTION OF THE MEAN
 THE SAMPLING DISTRIBUTION OF THE MEAN COGS 14B JANUARY 26, 2017 TODAY Sampling Distributions Sampling Distribution of the Mean Central Limit Theorem INFERENTIAL STATISTICS Inferential statistics: allows
THE SAMPLING DISTRIBUTION OF THE MEAN COGS 14B JANUARY 26, 2017 TODAY Sampling Distributions Sampling Distribution of the Mean Central Limit Theorem INFERENTIAL STATISTICS Inferential statistics: allows
Lesson 12: The Relationship Between Absolute Value and Order
 Lesson 12: The Relationship Between Absolute Value and Order Student Outcomes Students understand that the order of positive numbers is the same as the order of their absolute values. Students understand
Lesson 12: The Relationship Between Absolute Value and Order Student Outcomes Students understand that the order of positive numbers is the same as the order of their absolute values. Students understand
Student Outcomes. Lesson Notes. Classwork. Opening Exercises 1 3 (5 minutes)
 Student Outcomes Students calculate the decimal expansion of using basic properties of area. Students estimate the value of expressions such as. Lesson Notes For this lesson, students will need grid paper
Student Outcomes Students calculate the decimal expansion of using basic properties of area. Students estimate the value of expressions such as. Lesson Notes For this lesson, students will need grid paper
Objective: Construct a paper clock by partitioning a circle into halves and quarters, and tell time to the half hour or quarter hour.
 Lesson 13 Objective: Suggested Lesson Structure Fluency Practice Concept Development Student Debrief Total Time (10 minutes) (40 minutes) (10 minutes) (60 minutes) Fluency Practice (10 minutes) Rename
Lesson 13 Objective: Suggested Lesson Structure Fluency Practice Concept Development Student Debrief Total Time (10 minutes) (40 minutes) (10 minutes) (60 minutes) Fluency Practice (10 minutes) Rename
Lesson 9: Radicals and Conjugates
 Lesson 9: Radicals and Conjugates Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert
Lesson 9: Radicals and Conjugates Student Outcomes Students understand that the sum of two square roots (or two cube roots) is not equal to the square root (or cube root) of their sum. Students convert
Objective: Recognize halves within a circular clock face and tell time to the half hour. (60 minutes) (2 minutes) (5 minutes)
 Lesson 11 1 Lesson 11 Objective: Recognize halves within a circular clock face and tell time to the half Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Lesson 11 1 Lesson 11 Objective: Recognize halves within a circular clock face and tell time to the half Suggested Lesson Structure Fluency Practice Application Problem Concept Development Student Debrief
Lesson 3: Advanced Factoring Strategies for Quadratic Expressions
 Advanced Factoring Strategies for Quadratic Expressions Student Outcomes Students develop strategies for factoring quadratic expressions that are not easily factorable, making use of the structure of the
Advanced Factoring Strategies for Quadratic Expressions Student Outcomes Students develop strategies for factoring quadratic expressions that are not easily factorable, making use of the structure of the
Lesson 4: Numbers Raised to the Zeroth Power
 Student Outcomes Students know that a number raised to the zeroth power is equal to one. Students recognize the need for the definition to preserve the properties of exponents. Classwork Concept Development
Student Outcomes Students know that a number raised to the zeroth power is equal to one. Students recognize the need for the definition to preserve the properties of exponents. Classwork Concept Development
Lesson 14: From Ratio Tables, Equations, and Double Number Line Diagrams to Plots on the Coordinate Plane
 Lesson 14: From Ratio Tables, Equations, and Double Number Line Diagrams to Student Outcomes Students associate with each ratio : the ordered pair (, ) and plot it in the coordinate plane. Students represent
Lesson 14: From Ratio Tables, Equations, and Double Number Line Diagrams to Student Outcomes Students associate with each ratio : the ordered pair (, ) and plot it in the coordinate plane. Students represent
23.3. Sampling Distributions. Engage Sampling Distributions. Learning Objective. Math Processes and Practices. Language Objective
 23.3 Sampling Distributions Essential Question: How is the mean of a sampling distribution related to the corresponding population mean or population proportion? Explore 1 Developing a Distribution of
23.3 Sampling Distributions Essential Question: How is the mean of a sampling distribution related to the corresponding population mean or population proportion? Explore 1 Developing a Distribution of
Warm Up. Current: CST Released Test Question. Draw three different models to solve 3 x 5 =.
 Warm Up CST Released Test Question What number can be multiplied by 5768 to give the answer 5768? Current: Draw three different models to solve 3 x 5 =. 5768 = 5768 A 0 B 1 C 2 D 10 Challenge: Find product.
Warm Up CST Released Test Question What number can be multiplied by 5768 to give the answer 5768? Current: Draw three different models to solve 3 x 5 =. 5768 = 5768 A 0 B 1 C 2 D 10 Challenge: Find product.
The Shape, Center and Spread of a Normal Distribution - Basic
 The Shape, Center and Spread of a Normal Distribution - Basic Brenda Meery, (BrendaM) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version
The Shape, Center and Spread of a Normal Distribution - Basic Brenda Meery, (BrendaM) Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) To access a customizable version
L I T T L E L I O N C H A L L E N G E
 L I T T L E L I O N C H A L L E N G E Dear Teacher: We are excited to have you and your students participate in Little Lion Challenge Day this year! Little Lion Challenge Day is February 11th and it is
L I T T L E L I O N C H A L L E N G E Dear Teacher: We are excited to have you and your students participate in Little Lion Challenge Day this year! Little Lion Challenge Day is February 11th and it is
Lesson 4: Strategies for Solving Simultaneous Equations (Substitution)
 Lesson 4: Strategies for Solving Simultaneous Equations (Substitution) Brief Overview of Lesson: In this lesson students explore an alternate strategy for solving simultaneous linear equations known as
Lesson 4: Strategies for Solving Simultaneous Equations (Substitution) Brief Overview of Lesson: In this lesson students explore an alternate strategy for solving simultaneous linear equations known as
5E Lesson Plan Template
 Handout Authors: Ashley Thornburg Austin Ross Title of Lesson: The Life Cycle of Stars Date of Lesson: Wednesday March 14, 2012 Length of Lesson: 40-45 minutes Name/Level of Course: Science 8 th Source
Handout Authors: Ashley Thornburg Austin Ross Title of Lesson: The Life Cycle of Stars Date of Lesson: Wednesday March 14, 2012 Length of Lesson: 40-45 minutes Name/Level of Course: Science 8 th Source
Classwork. Example 1: Describing Distributions. Exercises 1 4
 Classwork Example 1: Describing Distributions In Lesson 9, Sabina developed the mean absolute deviation (MAD) as a number that measures variability in a data distribution. Using the mean and MAD with a
Classwork Example 1: Describing Distributions In Lesson 9, Sabina developed the mean absolute deviation (MAD) as a number that measures variability in a data distribution. Using the mean and MAD with a
What Is a Sampling Distribution? DISTINGUISH between a parameter and a statistic
 Section 8.1A What Is a Sampling Distribution? Learning Objectives After this section, you should be able to DISTINGUISH between a parameter and a statistic DEFINE sampling distribution DISTINGUISH between
Section 8.1A What Is a Sampling Distribution? Learning Objectives After this section, you should be able to DISTINGUISH between a parameter and a statistic DEFINE sampling distribution DISTINGUISH between
Lesson 8: Representing Proportional Relationships with Equations
 Lesson 8: Representing Proportional Relationships with Equations Student Outcomes Students use the constant of proportionality to represent proportional relationships by equations in real world contexts
Lesson 8: Representing Proportional Relationships with Equations Student Outcomes Students use the constant of proportionality to represent proportional relationships by equations in real world contexts
Lesson 15: Structure in Graphs of Polynomial Functions
 150 Lesson 15: Structure in Graphs of Polynomial Functions Student Outcomes Students graph polynomial functions and describe end behavior based upon the degree of the polynomial. Lesson Notes So far in
150 Lesson 15: Structure in Graphs of Polynomial Functions Student Outcomes Students graph polynomial functions and describe end behavior based upon the degree of the polynomial. Lesson Notes So far in
Lesson 8: Complex Number Division
 Student Outcomes Students determine the modulus and conjugate of a complex number. Students use the concept of conjugate to divide complex numbers. Lesson Notes This is the second day of a two-day lesson
Student Outcomes Students determine the modulus and conjugate of a complex number. Students use the concept of conjugate to divide complex numbers. Lesson Notes This is the second day of a two-day lesson
Math 31 Lesson Plan. Day 2: Sets; Binary Operations. Elizabeth Gillaspy. September 23, 2011
 Math 31 Lesson Plan Day 2: Sets; Binary Operations Elizabeth Gillaspy September 23, 2011 Supplies needed: 30 worksheets. Scratch paper? Sign in sheet Goals for myself: Tell them what you re going to tell
Math 31 Lesson Plan Day 2: Sets; Binary Operations Elizabeth Gillaspy September 23, 2011 Supplies needed: 30 worksheets. Scratch paper? Sign in sheet Goals for myself: Tell them what you re going to tell
3 PROBABILITY TOPICS
 Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Probability Distributions
 Probability Distributions Probability This is not a math class, or an applied math class, or a statistics class; but it is a computer science course! Still, probability, which is a math-y concept underlies
Probability Distributions Probability This is not a math class, or an applied math class, or a statistics class; but it is a computer science course! Still, probability, which is a math-y concept underlies
Balancing Chemical Equations
 Lesson Created by: Lauryn Atwood Length of lesson: 1 week Description of the class: Heterogeneous Name of course: Chemistry Grade level: 10-12 Honors or regular: Regular Balancing Chemical Equations Source
Lesson Created by: Lauryn Atwood Length of lesson: 1 week Description of the class: Heterogeneous Name of course: Chemistry Grade level: 10-12 Honors or regular: Regular Balancing Chemical Equations Source
Lesson 14: Solving Inequalities
 Student Outcomes Students learn if-then moves using the addition and multiplication properties of inequality to solve inequalities and graph the solution sets on the number line. Classwork Exercise 1 (5
Student Outcomes Students learn if-then moves using the addition and multiplication properties of inequality to solve inequalities and graph the solution sets on the number line. Classwork Exercise 1 (5
Lesson 29: Solving Radical Equations
 Lesson 29: Solving Radical Equations Student Outcomes Students develop facility in solving radical equations. Lesson Notes In the previous lesson, students were introduced to the notion of solving radical
Lesson 29: Solving Radical Equations Student Outcomes Students develop facility in solving radical equations. Lesson Notes In the previous lesson, students were introduced to the notion of solving radical
Chapter 12 Learning to Reason About Samples and Sampling Distributions
 Chapter 12 Learning to Reason About Samples and Sampling Distributions Why is the role of sample size in sampling distributions so hard to grasp? One consideration is that...the rule that the variability
Chapter 12 Learning to Reason About Samples and Sampling Distributions Why is the role of sample size in sampling distributions so hard to grasp? One consideration is that...the rule that the variability
Probability and Inference. POLI 205 Doing Research in Politics. Populations and Samples. Probability. Fall 2015
 Fall 2015 Population versus Sample Population: data for every possible relevant case Sample: a subset of cases that is drawn from an underlying population Inference Parameters and Statistics A parameter
Fall 2015 Population versus Sample Population: data for every possible relevant case Sample: a subset of cases that is drawn from an underlying population Inference Parameters and Statistics A parameter
6 THE NORMAL DISTRIBUTION
 CHAPTER 6 THE NORMAL DISTRIBUTION 341 6 THE NORMAL DISTRIBUTION Figure 6.1 If you ask enough people about their shoe size, you will find that your graphed data is shaped like a bell curve and can be described
CHAPTER 6 THE NORMAL DISTRIBUTION 341 6 THE NORMAL DISTRIBUTION Figure 6.1 If you ask enough people about their shoe size, you will find that your graphed data is shaped like a bell curve and can be described
Lesson 9: Analyzing Standard Deviation
 Exploratory Challenge 1 - Analyzing Standard Deviation 1. A group of people attended a talk at a conference. At the end of the talk, ten of the attendees were given a questionnaire that consisted of four
Exploratory Challenge 1 - Analyzing Standard Deviation 1. A group of people attended a talk at a conference. At the end of the talk, ten of the attendees were given a questionnaire that consisted of four
Bag RED ORANGE GREEN YELLOW PURPLE Candies per Bag
 Skittles Project For this project our entire class when out and bought a standard 2.17 ounce bag of skittles. Before we ate them, we recorded all of our data, the amount of skittles in our bag and the
Skittles Project For this project our entire class when out and bought a standard 2.17 ounce bag of skittles. Before we ate them, we recorded all of our data, the amount of skittles in our bag and the
Lesson Plan by: Stephanie Miller
 Lesson: Pythagorean Theorem and Distance Formula Length: 45 minutes Grade: Geometry Academic Standards: MA.G.1.1 2000 Find the lengths and midpoints of line segments in one- or two-dimensional coordinate
Lesson: Pythagorean Theorem and Distance Formula Length: 45 minutes Grade: Geometry Academic Standards: MA.G.1.1 2000 Find the lengths and midpoints of line segments in one- or two-dimensional coordinate
Mathematics Level D: Lesson 2 Representations of a Line
 Mathematics Level D: Lesson 2 Representations of a Line Targeted Student Outcomes Students graph a line specified by a linear function. Students graph a line specified by an initial value and rate of change
Mathematics Level D: Lesson 2 Representations of a Line Targeted Student Outcomes Students graph a line specified by a linear function. Students graph a line specified by an initial value and rate of change
Today I will write and explain inequality statements involving rational numbers
 Today I will write and explain inequality statements involving rational numbers Lesson 0: Writing and Interpreting Inequality Statements Involving Rational Numbers Classwork: The amount of money I have
Today I will write and explain inequality statements involving rational numbers Lesson 0: Writing and Interpreting Inequality Statements Involving Rational Numbers Classwork: The amount of money I have
Lesson Plan: Star Gazing By: Darby Feldwinn
 Lesson Plan: Star Gazing By: Darby Feldwinn Target Grade: 5 th Teacher Prep Time: 10 (1 hour if you need to print and laminate star cards.) Lesson Time: 3 hours (we recommend doing this lesson over three
Lesson Plan: Star Gazing By: Darby Feldwinn Target Grade: 5 th Teacher Prep Time: 10 (1 hour if you need to print and laminate star cards.) Lesson Time: 3 hours (we recommend doing this lesson over three
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson.1 Name Date A Little Dash of Logic Two Methods of Logical Reasoning Vocabulary Define each term in your own words. 1. inductive reasoning 2. deductive reasoning
Skills Practice Skills Practice for Lesson.1 Name Date A Little Dash of Logic Two Methods of Logical Reasoning Vocabulary Define each term in your own words. 1. inductive reasoning 2. deductive reasoning
Lesson 13: Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology
 Lesson 13: Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology Student Outcomes Students compare numbers expressed in scientific notation. Students
Lesson 13: Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology Student Outcomes Students compare numbers expressed in scientific notation. Students
a. Do you think the function is linear or non-linear? Explain using what you know about powers of variables.
 8.5.8 Lesson Date: Graphs of Non-Linear Functions Student Objectives I can examine the average rate of change for non-linear functions and learn that they do not have a constant rate of change. I can determine
8.5.8 Lesson Date: Graphs of Non-Linear Functions Student Objectives I can examine the average rate of change for non-linear functions and learn that they do not have a constant rate of change. I can determine
Life on other planets Life in space
 Life on other planets Life in space V 59 time 80 minutes learning outcomes To: discover that different celestial bodies have different conditions regarding temperature, gravity, atmosphere, and oxygen
Life on other planets Life in space V 59 time 80 minutes learning outcomes To: discover that different celestial bodies have different conditions regarding temperature, gravity, atmosphere, and oxygen
Cells [6th grade] Digital Trinity. Trinity University. Roxanne Hammonds Trinity University
![Cells [6th grade] Digital Trinity. Trinity University. Roxanne Hammonds Trinity University Cells [6th grade] Digital Trinity. Trinity University. Roxanne Hammonds Trinity University](/thumbs/74/70194968.jpg) Trinity University Digital Commons @ Trinity Understanding by Design: Complete Collection Understanding by Design 7-2-2008 Cells [6th grade] Roxanne Hammonds Trinity University Follow this and additional
Trinity University Digital Commons @ Trinity Understanding by Design: Complete Collection Understanding by Design 7-2-2008 Cells [6th grade] Roxanne Hammonds Trinity University Follow this and additional
Unit 22: Sampling Distributions
 Unit 22: Sampling Distributions Summary of Video If we know an entire population, then we can compute population parameters such as the population mean or standard deviation. However, we generally don
Unit 22: Sampling Distributions Summary of Video If we know an entire population, then we can compute population parameters such as the population mean or standard deviation. However, we generally don
ACTIVITY 2: Motion and Energy
 Developing Ideas ACTIVITY 2: Motion and Purpose We use the idea of energy in many ways in everyday life. For example, there is sometimes talk of an energy crisis when fuel supplies run low; people eat
Developing Ideas ACTIVITY 2: Motion and Purpose We use the idea of energy in many ways in everyday life. For example, there is sometimes talk of an energy crisis when fuel supplies run low; people eat
Lesson 7: Patterns in Scatter Plots
 Lesson 7: Patterns in Scatter Plots Classwork Example In the previous lesson, you learned that when data is collected on two numerical variables, a good place to start is to look at a scatter plot of the
Lesson 7: Patterns in Scatter Plots Classwork Example In the previous lesson, you learned that when data is collected on two numerical variables, a good place to start is to look at a scatter plot of the
Two-Digit Number Times Two-Digit Number
 Lesson Two-Digit Number Times Two-Digit Number Common Core State Standards 4.NBT.B.5 Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using
Lesson Two-Digit Number Times Two-Digit Number Common Core State Standards 4.NBT.B.5 Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using
6 TH GRADE ACCURATE PLANET SIZES AND DISTANCE FROM THE SUN ACTIVITY
 6 TH GRADE ACCURATE PLANET SIZES AND DISTANCE FROM THE SUN ACTIVITY Summary: Accurate planet size and distance from the Sun is studied in this lesson. Each student constructs a correctly scaled diagram
6 TH GRADE ACCURATE PLANET SIZES AND DISTANCE FROM THE SUN ACTIVITY Summary: Accurate planet size and distance from the Sun is studied in this lesson. Each student constructs a correctly scaled diagram
Pea Patch Pollination Game
 Pea Patch Pollination Game Classroom Activity: 5-8 Time: One 45-60-minute class period Overview: In this activity, students play a simulation game modeling changes in a plant population (a Pea Patch) caused
Pea Patch Pollination Game Classroom Activity: 5-8 Time: One 45-60-minute class period Overview: In this activity, students play a simulation game modeling changes in a plant population (a Pea Patch) caused
Lesson 8: Why Stay with Whole Numbers?
 Student Outcomes Students use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context. Students create functions that
Student Outcomes Students use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context. Students create functions that
Lesson 13: Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology
 m Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology Student Outcomes Students compare numbers expressed in scientific notation. Students apply the
m Comparison of Numbers Written in Scientific Notation and Interpreting Scientific Notation Using Technology Student Outcomes Students compare numbers expressed in scientific notation. Students apply the
Mathematics Curriculum
 Common Core Mathematics Curriculum Table of Contents 1 Similarity GRADE 8 MODULE 3 Module Overview... 2 Topic A: Dilation (8.G.A.3)... 7 Lesson 1: What Lies Behind Same Shape?... 9 Lesson 2: Properties
Common Core Mathematics Curriculum Table of Contents 1 Similarity GRADE 8 MODULE 3 Module Overview... 2 Topic A: Dilation (8.G.A.3)... 7 Lesson 1: What Lies Behind Same Shape?... 9 Lesson 2: Properties
Lesson 8: Informally Fitting a Line
 Classwork Example 1: Housing Costs Let s look at some data from one midwestern city that indicates the sizes and sale prices of various houses sold in this city. Size (square feet) Price (dollars) Size
Classwork Example 1: Housing Costs Let s look at some data from one midwestern city that indicates the sizes and sale prices of various houses sold in this city. Size (square feet) Price (dollars) Size
Giant Traveling Map Lesson
 Giant Traveling Map Lesson TITLE / AUTHOR: Idahoans on the Move / Rebecca Theobald IDAHO ACADEMIC STANDARDS / SUITABLE DISCIPLINES: OBJECTIVES: Students will: Learn about major cities in Idaho during three
Giant Traveling Map Lesson TITLE / AUTHOR: Idahoans on the Move / Rebecca Theobald IDAHO ACADEMIC STANDARDS / SUITABLE DISCIPLINES: OBJECTIVES: Students will: Learn about major cities in Idaho during three
Do not copy, post, or distribute
 14 CORRELATION ANALYSIS AND LINEAR REGRESSION Assessing the Covariability of Two Quantitative Properties 14.0 LEARNING OBJECTIVES In this chapter, we discuss two related techniques for assessing a possible
14 CORRELATION ANALYSIS AND LINEAR REGRESSION Assessing the Covariability of Two Quantitative Properties 14.0 LEARNING OBJECTIVES In this chapter, we discuss two related techniques for assessing a possible
Chapter 18 Sampling Distribution Models
 Chapter 18 Sampling Distribution Models The histogram above is a simulation of what we'd get if we could see all the proportions from all possible samples. The distribution has a special name. It's called
Chapter 18 Sampling Distribution Models The histogram above is a simulation of what we'd get if we could see all the proportions from all possible samples. The distribution has a special name. It's called
Lesson 8: Variability in a Data Distribution
 Classwork Example 1: Comparing Two Distributions Robert s family is planning to move to either New York City or San Francisco. Robert has a cousin in San Francisco and asked her how she likes living in
Classwork Example 1: Comparing Two Distributions Robert s family is planning to move to either New York City or San Francisco. Robert has a cousin in San Francisco and asked her how she likes living in
Mathematics (Project Maths Phase 1)
 L.20 NAME SCHOOL TEACHER Pre-Leaving Certificate Examination, 2012 Mathematics (Project Maths Phase 1) Paper 2 Higher Level Time: 2 hours, 30 minutes 300 marks For examiner Question Mark 1 2 3 Centre stamp
L.20 NAME SCHOOL TEACHER Pre-Leaving Certificate Examination, 2012 Mathematics (Project Maths Phase 1) Paper 2 Higher Level Time: 2 hours, 30 minutes 300 marks For examiner Question Mark 1 2 3 Centre stamp
Problem statement, Standards, Data and Technology
 Lesson Plan Title: Cellular Energy Transfer Teacher Name: Leigh-Ann Cruz Subject: Biology STEM Energy Lesson Plan Elements Inclusion School: Cardinal Ritter High School Grade Level: 8 th through 10 th
Lesson Plan Title: Cellular Energy Transfer Teacher Name: Leigh-Ann Cruz Subject: Biology STEM Energy Lesson Plan Elements Inclusion School: Cardinal Ritter High School Grade Level: 8 th through 10 th
Phases of the Moon. Phenomenon: The appearance of the moon changes every night. 1. What questions do you have about this phenomenon?
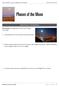 THE EARTH-SUN-MOON SYSTEM Phases of the Moon OBSERVING PHENOMENA Phenomenon: The appearance of the moon changes every night. 1. What questions do you have about this phenomenon? 2. Sketch a simple model
THE EARTH-SUN-MOON SYSTEM Phases of the Moon OBSERVING PHENOMENA Phenomenon: The appearance of the moon changes every night. 1. What questions do you have about this phenomenon? 2. Sketch a simple model
Lesson 22: Equivalent Rational Expressions
 0 Lesson 22: Equivalent Rational Expressions Student Outcomes Students define rational expressions and write them in equivalent forms. Lesson Notes In this module, students have been working with polynomial
0 Lesson 22: Equivalent Rational Expressions Student Outcomes Students define rational expressions and write them in equivalent forms. Lesson Notes In this module, students have been working with polynomial
Heat Transfer Lesson Plan
 Heat Transfer Lesson Plan I. Benchmarks: P.EN.M.4 Energy Transfer- Energy is transferred from a source to a receiver by radiation, conduction, and convection. When energy is transferred from one system
Heat Transfer Lesson Plan I. Benchmarks: P.EN.M.4 Energy Transfer- Energy is transferred from a source to a receiver by radiation, conduction, and convection. When energy is transferred from one system
Flags of the Sea. Standards : Numbers and Operations, Geometry, Data Analysis and Probability, Problem Solving, Communication, and Connections.
 Part 1 Standards : Numbers and Operations, Geometry, Data Analysis and Probability, Problem Solving, Communication, and Connections. There are flags everywhere you go. You see them in front of buildings.
Part 1 Standards : Numbers and Operations, Geometry, Data Analysis and Probability, Problem Solving, Communication, and Connections. There are flags everywhere you go. You see them in front of buildings.
Bay Area Scientists in Schools Presentation Plan
 Bay Area Scientists in Schools Presentation Plan Lesson Name: We Love Gravity! Presenter(s) Virginia Lehr, Laura Hidrobo Grade Level 5 Standards Connection(s) Solar System and Gravity Teaser: Gravity is
Bay Area Scientists in Schools Presentation Plan Lesson Name: We Love Gravity! Presenter(s) Virginia Lehr, Laura Hidrobo Grade Level 5 Standards Connection(s) Solar System and Gravity Teaser: Gravity is
Students write, add and subtract numbers in scientific notation and understand what is meant by the term leading digit.
 Student Outcomes Students write, add and subtract numbers in scientific notation and understand what is meant by the term leading digit. Classwork Discussion (5 minutes) Our knowledge of the integer powers
Student Outcomes Students write, add and subtract numbers in scientific notation and understand what is meant by the term leading digit. Classwork Discussion (5 minutes) Our knowledge of the integer powers
For Exercises 1 and 2, use the table below. It shows the height and stride distance for 10 students.
 A C E Applications Connections Extensions Applications For Exercises 1 and 2, use the table below. It shows the height and stride distance for 10 students. For humans, walking is the most basic form of
A C E Applications Connections Extensions Applications For Exercises 1 and 2, use the table below. It shows the height and stride distance for 10 students. For humans, walking is the most basic form of
Unit Plan: Matrices (4 weeks or 20 instructional Days)
 Unit Plan: Matrices (4 weeks or 20 instructional Days) Day 1: Review of Systems of Equations in 2 and 3 Variables Objectives: (M.4HS.CVM.18 )(CCSS.Math.Content.HSF-IF.B.6) Students will be able to solve
Unit Plan: Matrices (4 weeks or 20 instructional Days) Day 1: Review of Systems of Equations in 2 and 3 Variables Objectives: (M.4HS.CVM.18 )(CCSS.Math.Content.HSF-IF.B.6) Students will be able to solve
Mathematics Success Grade 8
 T538 Mathematics Success Grade 8 [OBJECTIVE] The student will compare functions represented algebraically, graphically, with verbal descriptions or in tables and identify functions as linear or non-linear.
T538 Mathematics Success Grade 8 [OBJECTIVE] The student will compare functions represented algebraically, graphically, with verbal descriptions or in tables and identify functions as linear or non-linear.
Talking feet: Scatterplots and lines of best fit
 Talking feet: Scatterplots and lines of best fit Student worksheet What does your foot say about your height? Can you predict people s height by how long their feet are? If a Grade 10 student s foot is
Talking feet: Scatterplots and lines of best fit Student worksheet What does your foot say about your height? Can you predict people s height by how long their feet are? If a Grade 10 student s foot is
Comparing Planet Sizes
 Target Standard Measurement Recognize the attributes of length, volume, weight, area, and time Compare and order objects according to these attributes Understand how to measure using nonstandard and standard
Target Standard Measurement Recognize the attributes of length, volume, weight, area, and time Compare and order objects according to these attributes Understand how to measure using nonstandard and standard
Unit Title: Weather, Climate, Climate Change Lesson Title: Will It Rain Tomorrow?
 OVERVIEW Unit Title: Weather, Climate, Climate Change Lesson Title: Will It Rain Tomorrow? Length of Lesson in # of Hours: 3 # of Classes: 2 How does this lesson connect to previous or future work as exemplified
OVERVIEW Unit Title: Weather, Climate, Climate Change Lesson Title: Will It Rain Tomorrow? Length of Lesson in # of Hours: 3 # of Classes: 2 How does this lesson connect to previous or future work as exemplified
