Improved Soil-Water Characteristic Curves and Permeability Functions for Unsaturated Soils
|
|
|
- Holly Lambert
- 6 years ago
- Views:
Transcription
1 Ipovd SoilWat haactitic uv ad Pailit Fuctio fo Uatuatd Soil Shada H. Kihapillai, Nadaajah Ravichada ivil Egiig Dpatt lo Uivit, lo, S, USA ABSTRAT Soilwat chaactitic cuv (SW) which pt th oituuctio latio of oil i o of th ipotat cotitutiv odl dd to iulat th havio of uatuatd oil. A ffctiv SW odl hould capal of calculatig th oituuctio vaiatio fo th ti ag of dg of atuatio. Applicailit of popula SW odl uch a Book ad o, va Gucht, ad Fdlud ad Xig i liitd, pciall i low (<2%) dg of atuatio ag. I thi tud, all th odl a odifid, o that th odl ca ffctivl ud i ti ag of dg of atuatio. Th Fdlud t al (994) pailit fuctio i alo odifid ad o th odifid Fdlud ad Xig SW odl. Th applicailit of th ipovd odl i ivtigatd caliatig th SW of vaiou tp of oil ad ptd i thi pap. Bad o thi tud it ca cocludd that th odifid odl a flxil ough to fit th xpital data fo th ti ag of dg of atuatio. RÉSUMÉ olau cou caactéitiqu d qui pét l d'huidité t d'apiatio latio d t l'u d odèl ipotat écai pou iul l copott d ol o atué. U odèl fficac dvait êt capal d calcul la vaiatio d l'huidité d'apiatio da tout l ga dgé d atuatio. L'applicailité d olau cou caactéitiqu odèl tl qu Book t o (B), va Gucht (vg), t Fdlud t Xig (FX) t liité, paticuli da la fouchtt d dgé d atuatio fail. Da ctt étud, tou c odèl ot odifié ou aélioé, d ot qu c odèl puvt êt utilié tout l ga dgé d atuatio. L Fdlud t al foctio d péailité t égalt odifié u l aélioé odèl. L'applicailité d odèl aélioé d'u quêt appofodi t caliat l cou caactéitiqu olau d div tp d ol t pété da l pét l papi. Baé u ctt étud, o put coclu qu l odèl odifié ot uffiat oupl pou 'adapt aux doé xpéital pou da tout l ga du dgé d atuatio. INTRODUTION Th Soil Wat haactitic uv (SW) i a latiohip tw th aout of wat pt i th oil (oitu) ad th uctio chaactitic of th oil atix. Th aout of wat pt i th oil ca xpd i t of dg of atuatio (S), volutic wat cott (ϴ), o gavitic wat cott (u). Ma ach hav idtifid th facto which ifluc th hap of th SW ad ad o that, a athatical SW odl w dvlopd. Gad (956), Book ad o (964), va Gucht (9), Kougi (994), ad Fdlud ad Xig (994) a o of th odl foud i th litatu. All th odl cofi a iv popotioal latiohip tw S ad uctio (ψ). Thi ca xplaid with th fudatal icu tho a follow. Wh th S ica, th adiu (R ) of th icu will ica. Wh R ica, th pu diffc tw th po ai pu ad th po wat pu (uctio) will dca ( Eq. ). g l 2T = p p [] R wh ψ i th uctio, p g i po ga pu, p l i po liquid pu, ad T i ufac tio. Th ait uctio that i alo kow a ulig pu ad po iz ditiutio a two aic paat icopoatd i ot of th SW odl. I odl uch a Book ad o (B), va Gucht (vg), ad Fdlud ad Xig (FX), th two paat a ptd a ad, pctivl. Th Book ad o odl (Eq. 2) i o of th aic SW odl dvlopd with two paat. Thi odl do ot povid a cotiuou athatical fuctio fo th ti ag of S. if ψ a / a if ψ a wh a ad a th fittig paat. Th paat a i latd to th ait uctio of th oil ad th i latd to th po iz ditiutio of th oil. ψ i uctio, θ i volutic wat cott, θ i idual wat cott, ad θ i atuatd wat cott. Th vg odl (Eq. 3) povid a igl quatio fo th ti ag of S. Thi odl ha a additioal fittig paat, th akig thi odl o flxil copad to th B odl. [3] ( a ) wh th fittig paat i latd to idual wat cott. All th oth paat a a a i th B odl. Th FX odl i ptd i Eq. 4. Th ailit of thi odl to pdict th SW fo ti ag of S i [2]
2 coidd a th ajo advatag of thi odl. Th F X odl au a axiu uctio of,, kpa at d coditio, whil th B ad th vg odl au ifiit valu of axiu uctio. Th FX odl i ath iila to th vg odl oth tha th coctio facto ( ) ad lt i th quatio. Th lt i v ffctiv i kpig th SW without achig zo oalizd wat cott i low uctio ag, pciall fo ad oil. Fdlud ad Xig (994) hav alo uggtd aoth fo of th odl (Eq. 5) which ca ud if a idual wat cott i kow. ( ) l ( ψ / a) = l ( ψ / a) ( ψ) l ( ψ ) 6 l ( ) wh i a paat latd to idual wat cott ad oth paat a a a i th vg odl. Th popti which affct th oil wat chaactitic cuv alo affct th pailit cofficit of po fluid i uatuatd oil. Thfo, SW ca ffctivl ud to calculat pailituctio latio, which i cool fd a pailit fuctio. Bad o FX SW odl, a pailit fuctio (Eq. 6) i popod Fdlud t al. (994). K l l av wh ψ i uctio, K (ψ) i th lativ pailit at uctio ψ, ψ av i th ait uctio, i a du vaial of itgatio, = l(l,,), θ i volutic wat cott giv i Eq. 4 ad θ i it divativ. a,, ad a fittig paat of th FX odl (Eq. 4). Th B, vg, ad FX odl a ig widl ud to calculat th oituuctio latio of uatuatd oil. Fo th B ad vg odl, a idual wat cott valu ha to pcifid. Howv th two odl calculat ualitic uctio wh th oalizd wat cott i zo o l, i.. wat cott of th oil i l tha o qual to th idual wat cott. I th FX odl, th axiu uctio i aud to,, kpa. Although th a thodaic cocpt to ack up thi axiu uctio, it i a coc to u a fixd valu fo all tp of oil. I additio, wh d d [4] [5] [6] th actual axiu uctio i low, uag of uch lag axiu uctio valu ight ov pdict ha tgth i uical iulatio. Siila to th B ad vg odl, th cod fo of th FX odl (Eq. 5) alo calculat a ualitic uctio wh th oalizd wat cott i zo o l. Thfo, to avoid a ualitic uctio valu at zo oalizd wat cott, th axiu uctio valu hould pcifid v with a idual wat cott pcifid. I additio, th fouth odl paat i th FX odl i cho fo a wid ag ( to,, kpa) ad it cat difficulti i achivig a uiqu t of caliatd odl paat. Alo, th affct th iitial potio of th cuv wh th valu of i lativl low ad it i coidd a aoth diadvatag (Log ad Rahadjo, 997). Th pia ojctiv of thi tud i to ica th flxiilit of th B ad vg odl o that th odl ca pdict alitic high uctio i low dg of atuatio without cauig uical itailiti i fiit lt iulatio. It i v challgig to odl th oil havio fo a full d coditio to a full atuatd coditio uig a igl full coupld fiit lt coput cod. Th cut tat of th at uggt that th a th ajo difficulti i dvlopig uicall tal iulatio capailit. Th a: difficulti i dalig with ultipl odal/lt vaial i fiit lt foulatio of poou dia at th xt coditio, difficulti i dvlopig ttai havio with appopiat t tat vaial at th xt coditio, ad difficulti i accuatl calculatig th uctio ov th ti ag of dg of atuatio. Th odifid odl ca icopoatd i fiit lt iulatio without itoducig uical itailiti ai fo SW. I thi tud, th B ad vg odl a odifid icopoatig coctio facto. Alo, th coctio facto i th FX odl i odifid to avoid th ffct of additioal fittig paat. Icopoatig th axiu uctio a pat of th odl icad it flxiilit i fittig aud data of vaiou oil ov th full ag of S. All th odl a ipovd with th fatu to pcif oth idual wat cott ad axiu uctio valu. Th capailit of th ipovd odl i vifid atchig with th xpital data ad pdictio of oigial odl. Bad o th ipovd FX odl, th pailit fuctio popod Fdlud t al. (994) i odifid ad ptd. 2 IMPROVED SW MODELS AND OMPARISONS Although th a uou SW odl availal i th litatu, thi tud i itdd to ipov th popula B, vg, ad FX odl. Th B ad vg odl a odifid piail to ak u that th odl o log calculat high uctio wh th oalizd wat cott i zo o l. Ad alo th odifid odl hav th fatu to pcif oth idual wat cott ad axiu uctio valu. 2. Th Ipovd Book ad o (IB) Modl
3 Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) Th ipovd Book ad o (IB) odl i giv i Equatio 7. To pv th advatag of th B odl, o additioal fittig paat i itoducd. Ev though th axiu uctio ψ ax i icopoatd i th quatio, it caot coidd to a fittig paat, a th hap of th SW caot chagd adjutig th ψ ax. Th IB odl do ot povid a cotiuou athatical fuctio fo th ti ag of S. / a if if ψ ψ a ax wh ψ ax i axiu uctio ad oth paat a a a i th B odl. 2.. opaio of th B ad th IB Modl apailit of th ipovd B (IB) odl i pdictig th oituuctio latio i ivtigatd ad copad with th B odl fo fou difft oil. Th copaio of B ad IB Modl fo oluia ad loa (data Book & o 964) i how i Figu. Th Figu 2 ad 3 how th copaio fo Madid cla ad ad Aligto oil, pctivl. Th Figu 4 how th copaio fo Idia had till (data Vaapalli t al. 999). It hould otd that th xpital SW data a ot availal fo th full ag of S (%). Bad o th xpital data, th axiu uctio of,, kpa i cho fo all fou oil. Th idual wat cott i aud to zo fo all fou oil. A how i th figu, th IB odl i capal of calculatig th oituuctio latio fo full ag of S, wha th B odl i ot ffctiv. Th B, IB odl a ot ffctiv fo ad oil ad it i vidtl how i Figu a th odl faild to kp th SW without achig zo oalizd wat cott i low uctio ag a B IB oluia ad loa B (a = 5 kpa, =.8) IB (a = 5 kpa, =.8) [7] Figu. B ad IB SW fo oluia ad loa 4 2 B IB B (a = 32 kpa, =.3) IB (a = 32 kpa, =.3) Madid cla ad Figu 2. B ad IB SW fo Madid cla ad 4 2 B IB B (a = 68 kpa, =.5) IB (a = 68 kpa, =.45) Aligto oil Figu 3. B ad IB SW fo Aligto oil 4 2 B IB B (a = 23 kpa, =.23) IB (a = 22 kpa, =.25) Idia had till Figu 4. B ad IB SW fo Idia had till 2.2 Th Ipovd va Gucht (IvG) Modl Th ipovd va Gucht (IvG) odl i giv i Equatio 8. Sic th paat a i latd to th ait uctio, th odl i vid o that th paat a ha th uit of uctio. Th IvG odl i dvlopd with th fatu to pcif oth idual wat cott ad axiu uctio valu with o additioal fittig paat.
4 Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) a [8] Aligto oil vg IvG ax wh ψ ax i axiu uctio ad oth paat a a a i th vg odl Pdictiv apailit of th IvG Modl apailit of th ipovd vg (I vg) odl i pdictig th oituuctio latio i ptd fo oluia ad loa, Madid cla ad, Aligto oil, ad Idia had till i figu 5 though 8, pctivl. Siila to th IB odl, axiu uctio of,, kpa ad idual wat cott of zo a ud fo all fou oil. A how i figu 5 though 8, th IvG odl i capal of calculatig th oituuctio latio fo full ag of S, wha th vg odl i ot ffctiv. A how i Figu 5, th vg, IvG odl a alo ot uital fo ad oil a th odl alo faild to kp th SW without achig zo oalizd wat cott i low uctio ag Figu 5. vg ad IvG SW fo oluia ad loa oluia ad loa vg IvG vg (a =.8 kpa, =, =.) vg IvG IvG (a = 6 kpa, =, =.) vg (a =.3 kpa, = 2.85, =.) IvG (a = 33 kpa, = 2.9, =.5) Madid cla ad Figu 6. vg ad IvG SW fo Madid cla ad 4 2 vg (a =.2 kpa, = 2., =.77) IvG (a = 85 kpa, = 2, =.77) Figu 7. vg ad IvG SW fo Aligto oil Idia had till vg IvG 4 vg (a =.3 kpa, =., =.23) 2 IvG (a = 37 kpa, =., =.2) Figu 8. vg ad IvG SW fo Idia had till 2.3 Th Ipovd Fdlud ad Xig (IFX) Modl Th ipovd Fdlud ad Xig (IFX) odl i giv i Equatio 9. Th IFX odl i dvlopd with th fatu to pcif oth idual wat cott ad axiu uctio valu without th paat, i.. with ol th fittig paat. Thfo, th ffct of i th iitial potio of th FX odl (Log ad Rahadjo, 997) i avoidd i th IFX odl. ( ) = l a ax wh all th paat a a a i th IvG odl Pdictiv apailit of th IFX Modl Th pdictiv capailit of th IFX odl i pdictig th oituuctio latio i ptd i figu 9 though 2. Siila to th IB, IvG odl,,, kpa axiu uctio ad zo idual wat cott.5 [9]
5 Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) Dg of atuatio (%) a ud. It ca otd that th IFX odl i alo ffctiv i full ag of S. Howv th IFX odl ca coidd tt a it ha ol th fittig paat, wha th FX odl ha fou. FX IFX FX (a = 6.2 kpa, = 8.5, 4 =.49, = 4 kpa) IFX (a = 6.2 kpa, = 8.5, 2 =.5) oluia ad loa Figu 9. FX ad IFX SW fo oluia ad loa 4 2 FX IFX Madid cla ad FX (a = kpa, =.8, =.64, = 4 kpa) IFX (a = 64 kpa, =.6, =.7) Figu. FX ad IFX SW fo Madid cla ad Aligto oil FX IFX 4 FX (a =.25 kpa, =.6, 2 =.3, = 4 kpa) IFX (a = kpa, =.3, =.43) Figu. FX ad IFX SW fo Aligto oil 4 Idia Had till FX (a = 3 kpa, =, =.46, = 3 kpa) FX IFX 2 IFX (a = 575 kpa, =.95, =.72) Figu 2. FX ad IFX SW fo Idia had till 3 MODIFIED PERMEABILITY FUNTION AND OMPARISONS Bad o FX SW odl, a pailit fuctio i popod Fdlud t al. (994) ad it i ig widl ud. Thfo, it i ipotat to odif th Fdlud t al pailit fuctio (FAll odl) ad o th IFX SW odl. Th FAll odl i odifid ad o th IFX SW odl, ad ptd a IFAll odl i Equatio. Th ol diffc tw th FAll ad I FAll odl, i th coctio facto ( ψ ). K l l av Th fuctio ad a giv ( ψ) l ( ψ / a) ax ad.5 d d [] wh ax i axiu uctio ad oth paat a a a i th FAll odl. 3. Pdictiv apailit of th IFAll Modl Th pailit cofficit of wat i fou difft oil a pdictd with FAll ad IFAll odl ad ptd i Figu 3 though 6. Figu 3 illutat th pdictio fo Suptitio ad ad th copaio with xpital data (fo Richad, 952). A how i Figu 3, th FAll ad IFAll odl how tt atch with th xpital data. Howv, cau of
6 Rlativ pailit Rlativ pailit Rlativ pailit Rlativ pailit th lack of xpital data, th accuac of th two odl i th high uctio ag could ot vifid. Th Figu 4 how th copaio of pdictd ult ad xpital data fo oluia ad loa (xpital data fo Book & o 964). Siila to th Suptitio ad, th pdictio of FAll ad IFAll odl atch wll with th xpital data i th low uctio ag. A how i Figu 5, iila pdictio a otaid fo th Toucht ilt loa (xpital data fo Book & o, 964). Figu 6 how th pdictio ad copaio fo Yolo light cla (data fo Moo 939). A how th, th diffc tw th xpital data ad th pdictio of FAll ad IFAll odl ica a th uctio ica. I additio, th pdictio of FAll odl lightl dviat fo th pdictio of IFAll odl at high uctio ag FAll IFAll FX (a = 2.6 kpa = 9 =.46 = 3 kpa) IFX (a = 2.6 kpa = 9 =.46) 2 3 Figu 3. FAll ad IFAll odl fo Suptitio ad FX (a = 6.2 kpa = 8.5 =.49 = 4 kpa) IFX (a = 6.2 kpa = 8.5 =.5) FAll IFAll 2 3 Figu 4. FAll ad IFAll odl fo oluia ad loa FX (a = 8.4 kpa = =.5 = 3 kpa) IFX (a = 8.4 kpa = =.5) FAll IFAll 2 3 Figu 5. FAll ad IFAll odl fo Toucht ilt loa FX (a = 2.9 kpa =.9 =.4 = kpa) IFX (a = 2.9 kpa =.9 =.4) FAll IFAll 2 3 Figu 6. FAll ad IFAll odl fo Yolo light cla 4 ONLUSION Th Book ad o, va Gucht, ad Fdlud & Xig odl a odifid to captu th high uctio at low dg of atuatio. Both axiu uctio ad idual wat cott ca ud a iput i th odifid odl. Sic th i o data availal to vif it capailit i high uctio ag, th flxiilit of th odifid odl ha vifid fittig xpital data fo fou difft oil i high uctio ag ad th pdictio fo oigial odl. REFERENES Book R.H., o A.T Hdaulic popti of poou dia. Hdolog Pap, oloado Stat Uivit. Fot olli, 27(3). Fdlud D.G., Xig A Equatio fo th oilwat chaactitic cuv. aadia Gotchical Joua, 3: Fdlud D.G., Xig A., Huag S Pdictig th pailit fuctio fo uatuatd oil uig th oilwat chaactitic cuv. aadia Gotchical Joual, 3: Kougi, K Th paat logoal ditiutio odl fo oil wat ttio. Wat Rouc Rach, 3: 899. Log, E.., ad Rahadjo, H Rviw of oilwat chaactitic cuv quatio. Joual of Gotchical ad Goviotal Egiig, 23:67. Moo R.E Wat coductio fo hallow wat tal. Hilgadia, 2: Richad L.A Wat coductig ad taiig popti of oil i latio to iigatio. Pocdig, Itatioal Spoiu o Dt Rach, Jual, va Gucht M.Th. 9. A clod fo quatio fo pdictig th hdaulic coductivit of uatuatd oil. Soil Scic Socit of Aica Joual, 44: Vaapalli, S. K., Pufahl, D. E., ad Fdlud, D. G Th ifluc of oil tuctu ad t hito o th oilwat chaactitic of a copactd till. Gotchiqu, 49(2): 4359.
Improving the Predictive Capability of Popular SWCCs by Incorporating Maximum Possible Suction
 Itatioal Joual of Gocic, 2011, 2, 468-475 doi:10.4236/ijg.2011.24049 Publihd Oli Novb 2011 (http://www.scirp.og/joual/ijg) Ipovig th Pdictiv Capabilit of Popula SWCC b Icopoatig Maxiu Poibl Suctio Abtact
Itatioal Joual of Gocic, 2011, 2, 468-475 doi:10.4236/ijg.2011.24049 Publihd Oli Novb 2011 (http://www.scirp.og/joual/ijg) Ipovig th Pdictiv Capabilit of Popula SWCC b Icopoatig Maxiu Poibl Suctio Abtact
The tight-binding method
 Th tight-idig thod Wa ottial aoach: tat lcto a a ga of aly f coductio lcto. ow aout iulato? ow aout d-lcto? d Tight-idig thod: gad a olid a a collctio of wa itactig utal ato. Ovla of atoic wav fuctio i
Th tight-idig thod Wa ottial aoach: tat lcto a a ga of aly f coductio lcto. ow aout iulato? ow aout d-lcto? d Tight-idig thod: gad a olid a a collctio of wa itactig utal ato. Ovla of atoic wav fuctio i
ENGG 1203 Tutorial. Difference Equations. Find the Pole(s) Finding Equations and Poles
 ENGG 03 Tutoial Systms ad Cotol 9 Apil Laig Obctivs Z tasfom Complx pols Fdbac cotol systms Ac: MIT OCW 60, 6003 Diffc Equatios Cosid th systm pstd by th followig diffc quatio y[ ] x[ ] (5y[ ] 3y[ ]) wh
ENGG 03 Tutoial Systms ad Cotol 9 Apil Laig Obctivs Z tasfom Complx pols Fdbac cotol systms Ac: MIT OCW 60, 6003 Diffc Equatios Cosid th systm pstd by th followig diffc quatio y[ ] x[ ] (5y[ ] 3y[ ]) wh
Galaxy Photometry. Recalling the relationship between flux and luminosity, Flux = brightness becomes
 Galaxy Photomty Fo galaxis, w masu a sufac flux, that is, th couts i ach pixl. Though calibatio, this is covtd to flux dsity i Jaskys ( Jy -6 W/m/Hz). Fo a galaxy at som distac, d, a pixl of sid D subtds
Galaxy Photomty Fo galaxis, w masu a sufac flux, that is, th couts i ach pixl. Though calibatio, this is covtd to flux dsity i Jaskys ( Jy -6 W/m/Hz). Fo a galaxy at som distac, d, a pixl of sid D subtds
Ch. 6 Free Electron Fermi Gas
 Ch. 6 lcto i Gas Coductio lctos i a tal ov fl without scattig b io cos so it ca b cosidd as if walitactig o f paticls followig idiac statistics. hfo th coductio lctos a fqutl calld as f lcto i gas. Coductio
Ch. 6 lcto i Gas Coductio lctos i a tal ov fl without scattig b io cos so it ca b cosidd as if walitactig o f paticls followig idiac statistics. hfo th coductio lctos a fqutl calld as f lcto i gas. Coductio
Noise in electronic components.
 No lto opot5098, JDS No lto opot Th PN juto Th ut thouh a PN juto ha fou opot t: two ffuo ut (hol fo th paa to th aa a lto th oppot to) a thal at oty ha a (hol fo th aa to th paa a lto th oppot to, laka
No lto opot5098, JDS No lto opot Th PN juto Th ut thouh a PN juto ha fou opot t: two ffuo ut (hol fo th paa to th aa a lto th oppot to) a thal at oty ha a (hol fo th aa to th paa a lto th oppot to, laka
rad / sec min rev 60sec. 2* rad / sec s
 EE 559, Exa 2, Spig 26, D. McCalley, 75 iute allowed. Cloed Book, Cloed Note, Calculato Peitted, No Couicatio Device. (6 pt) Coide a.5 MW, 69 v, 5 Hz, 75 p DFG wid eegy yt. he paaete o the geeato ae give
EE 559, Exa 2, Spig 26, D. McCalley, 75 iute allowed. Cloed Book, Cloed Note, Calculato Peitted, No Couicatio Device. (6 pt) Coide a.5 MW, 69 v, 5 Hz, 75 p DFG wid eegy yt. he paaete o the geeato ae give
The Hydrogen Atom. Chapter 7
 Th Hyog Ato Chapt 7 Hyog ato Th vy fist pobl that Schöig hislf tackl with his w wav quatio Poucig th oh s gy lvls a o! lctic pottial gy still plays a ol i a subatoic lvl btw poto a lcto V 4 Schöig q. fo
Th Hyog Ato Chapt 7 Hyog ato Th vy fist pobl that Schöig hislf tackl with his w wav quatio Poucig th oh s gy lvls a o! lctic pottial gy still plays a ol i a subatoic lvl btw poto a lcto V 4 Schöig q. fo
( ) L = D e. e e. Example:
 xapl: A Si p juctio diod av acoss sctioal aa of, a accpto coctatio of 5 0 8 c -3 o t p-sid ad a doo coctatio of 0 6 c -3 o t -sid. T lif ti of ols i -gio is 47 s ad t lif ti of lctos i t p-gio is 5 s.
xapl: A Si p juctio diod av acoss sctioal aa of, a accpto coctatio of 5 0 8 c -3 o t p-sid ad a doo coctatio of 0 6 c -3 o t -sid. T lif ti of ols i -gio is 47 s ad t lif ti of lctos i t p-gio is 5 s.
Chapter 11 Solutions ( ) 1. The wavelength of the peak is. 2. The temperature is found with. 3. The power is. 4. a) The power is
 Chapt Solutios. Th wavlgth of th pak is pic 3.898 K T 3.898 K 373K 885 This cospods to ifad adiatio.. Th tpatu is foud with 3.898 K pic T 3 9.898 K 50 T T 5773K 3. Th pow is 4 4 ( 0 ) P σ A T T ( ) ( )
Chapt Solutios. Th wavlgth of th pak is pic 3.898 K T 3.898 K 373K 885 This cospods to ifad adiatio.. Th tpatu is foud with 3.898 K pic T 3 9.898 K 50 T T 5773K 3. Th pow is 4 4 ( 0 ) P σ A T T ( ) ( )
Today s topic 2 = Setting up the Hydrogen Atom problem. Schematic of Hydrogen Atom
 Today s topic Sttig up th Hydog Ato pobl Hydog ato pobl & Agula Motu Objctiv: to solv Schödig quatio. st Stp: to dfi th pottial fuctio Schatic of Hydog Ato Coulob s aw - Z 4ε 4ε fo H ato Nuclus Z What
Today s topic Sttig up th Hydog Ato pobl Hydog ato pobl & Agula Motu Objctiv: to solv Schödig quatio. st Stp: to dfi th pottial fuctio Schatic of Hydog Ato Coulob s aw - Z 4ε 4ε fo H ato Nuclus Z What
GAUSS PLANETARY EQUATIONS IN A NON-SINGULAR GRAVITATIONAL POTENTIAL
 GAUSS PLANETARY EQUATIONS IN A NON-SINGULAR GRAVITATIONAL POTENTIAL Ioannis Iaklis Haanas * and Michal Hany# * Dpatmnt of Physics and Astonomy, Yok Univsity 34 A Pti Scinc Building Noth Yok, Ontaio, M3J-P3,
GAUSS PLANETARY EQUATIONS IN A NON-SINGULAR GRAVITATIONAL POTENTIAL Ioannis Iaklis Haanas * and Michal Hany# * Dpatmnt of Physics and Astonomy, Yok Univsity 34 A Pti Scinc Building Noth Yok, Ontaio, M3J-P3,
Homework 1: Solutions
 Howo : Solutos No-a Fals supposto tst but passs scal tst lthouh -f th ta as slowss [S /V] vs t th appaac of laty alty th path alo whch slowss s to b tat to obta tavl ts ps o th ol paat S o V as a cosquc
Howo : Solutos No-a Fals supposto tst but passs scal tst lthouh -f th ta as slowss [S /V] vs t th appaac of laty alty th path alo whch slowss s to b tat to obta tavl ts ps o th ol paat S o V as a cosquc
Solutions to Supplementary Problems
 Solution to Supplmntay Poblm Chapt Solution. Fomula (.4): g d G + g : E ping th void atio: G d 2.7 9.8 0.56 (56%) 7 mg Fomula (.6): S Fomula (.40): g d E ping at contnt: S m G 0.56 0.5 0. (%) 2.7 + m E
Solution to Supplmntay Poblm Chapt Solution. Fomula (.4): g d G + g : E ping th void atio: G d 2.7 9.8 0.56 (56%) 7 mg Fomula (.6): S Fomula (.40): g d E ping at contnt: S m G 0.56 0.5 0. (%) 2.7 + m E
STRIPLINES. A stripline is a planar type transmission line which is well suited for microwave integrated circuitry and photolithographic fabrication.
 STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
STIPLINES A tiplin i a plana typ tanmiion lin hih i ll uitd fo mioav intgatd iuity and photolithogaphi faiation. It i uually ontutd y thing th nt onduto of idth, on a utat of thikn and thn oving ith anoth
ELEC9721: Digital Signal Processing Theory and Applications
 ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
ELG3150 Assignment 3
 ELG350 Aigmt 3 Aigmt 3: E5.7; P5.6; P5.6; P5.9; AP5.; DP5.4 E5.7 A cotrol ytm for poitioig th had of a floppy dik driv ha th clodloop trafr fuctio 0.33( + 0.8) T ( ) ( + 0.6)( + 4 + 5) Plot th pol ad zro
ELG350 Aigmt 3 Aigmt 3: E5.7; P5.6; P5.6; P5.9; AP5.; DP5.4 E5.7 A cotrol ytm for poitioig th had of a floppy dik driv ha th clodloop trafr fuctio 0.33( + 0.8) T ( ) ( + 0.6)( + 4 + 5) Plot th pol ad zro
The Reign of Grace and Life. Romans 5:12-21 (5:12-14, 17 focus)
 Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
COMMUNITY LEGAL CLINIC OF YORK REGION 21 DUNLOP ST., SUITE 200 RICHMOND HILL, ON., L4C 2M6
 B T T D I G 1 0 D o u g l a s o a d U x b r i d g e, O. L 9 P 1 9 HHAngus & Associates Limited Consulting ngineers 1127 Leslie treet, Toronto, O, M3C 2J6 Canada GAL OT THI DAWIG I TH POPTY OF BTT DIG AOCIAT
B T T D I G 1 0 D o u g l a s o a d U x b r i d g e, O. L 9 P 1 9 HHAngus & Associates Limited Consulting ngineers 1127 Leslie treet, Toronto, O, M3C 2J6 Canada GAL OT THI DAWIG I TH POPTY OF BTT DIG AOCIAT
On Jackson's Theorem
 It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform
![and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform](/thumbs/90/103666297.jpg) NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
Explicit scheme. Fully implicit scheme Notes. Fully implicit scheme Notes. Fully implicit scheme Notes. Notes
 Explicit cheme So far coidered a fully explicit cheme to umerically olve the diffuio equatio: T + = ( )T + (T+ + T ) () with = κ ( x) Oly table for < / Thi cheme i ometime referred to a FTCS (forward time
Explicit cheme So far coidered a fully explicit cheme to umerically olve the diffuio equatio: T + = ( )T + (T+ + T ) () with = κ ( x) Oly table for < / Thi cheme i ometime referred to a FTCS (forward time
STATISTICAL PARAMETER ESTIMATION FROM MODAL DATA USING A VARIABLE TRANSFORMATION AND TWO WEIGHTING MATRICES
 SAISICAL PARAMEER ESIMAION FROM MODAL DAA USING A VARIABLE RANSFORMAION AND WO WEIGHING MARICES Haddad Khodapaast, H., Mottshad, J. E., Badcock, K. J. ad Mas, C. Dpatt of Egiig, Uivsity of Livpool, Livpool
SAISICAL PARAMEER ESIMAION FROM MODAL DAA USING A VARIABLE RANSFORMAION AND WO WEIGHING MARICES Haddad Khodapaast, H., Mottshad, J. E., Badcock, K. J. ad Mas, C. Dpatt of Egiig, Uivsity of Livpool, Livpool
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
(( ) ( ) ( ) ( ) ( 1 2 ( ) ( ) ( ) ( ) Two Stage Cluster Sampling and Random Effects Ed Stanek
 Two ag ampling and andom ffct 8- Two Stag Clu Sampling and Random Effct Ed Stank FTE POPULATO Fam Labl Expctd Rpon Rpon otation and tminology Expctd Rpon: y = and fo ach ; t = Rpon: k = y + Wk k = indx
Two ag ampling and andom ffct 8- Two Stag Clu Sampling and Random Effct Ed Stank FTE POPULATO Fam Labl Expctd Rpon Rpon otation and tminology Expctd Rpon: y = and fo ach ; t = Rpon: k = y + Wk k = indx
Control Systems. Lecture 8 Root Locus. Root Locus. Plant. Controller. Sensor
 Cotol Syt ctu 8 Root ocu Clacal Cotol Pof. Eugo Schut hgh Uvty Root ocu Cotoll Plat R E C U Y - H C D So Y C C R C H Wtg th loo ga a w a ttd tackg th clod-loo ol a ga va Clacal Cotol Pof. Eugo Schut hgh
Cotol Syt ctu 8 Root ocu Clacal Cotol Pof. Eugo Schut hgh Uvty Root ocu Cotoll Plat R E C U Y - H C D So Y C C R C H Wtg th loo ga a w a ttd tackg th clod-loo ol a ga va Clacal Cotol Pof. Eugo Schut hgh
Revised Variational Iteration Method for Solving Systems of Ordinary Differential Equations
 Availabl at http://pvau.du/aa Appl. Appl. Math. ISSN: 9-9 Spcial Iu No. Augut 00 pp. 0 Applicatio ad Applid Mathatic: A Itratioal Joural AAM Rvid Variatioal Itratio Mthod for Solvig St of Ordiar Diffrtial
Availabl at http://pvau.du/aa Appl. Appl. Math. ISSN: 9-9 Spcial Iu No. Augut 00 pp. 0 Applicatio ad Applid Mathatic: A Itratioal Joural AAM Rvid Variatioal Itratio Mthod for Solvig St of Ordiar Diffrtial
2. SIMPLE SOIL PROPETIES
 2. SIMPLE SOIL PROPETIES 2.1 EIGHT-OLUME RELATIONSHIPS It i oft rquir of th gotchical gir to collct, claify a ivtigat oil ampl. B it for ig of fouatio or i calculatio of arthork volum, trmiatio of oil
2. SIMPLE SOIL PROPETIES 2.1 EIGHT-OLUME RELATIONSHIPS It i oft rquir of th gotchical gir to collct, claify a ivtigat oil ampl. B it for ig of fouatio or i calculatio of arthork volum, trmiatio of oil
1985 AP Calculus BC: Section I
 985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
Instrumentation for Characterization of Nanomaterials (v11) 11. Crystal Potential
 Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
STA 4032 Final Exam Formula Sheet
 Chapter 2. Probability STA 4032 Fial Eam Formula Sheet Some Baic Probability Formula: (1) P (A B) = P (A) + P (B) P (A B). (2) P (A ) = 1 P (A) ( A i the complemet of A). (3) If S i a fiite ample pace
Chapter 2. Probability STA 4032 Fial Eam Formula Sheet Some Baic Probability Formula: (1) P (A B) = P (A) + P (B) P (A B). (2) P (A ) = 1 P (A) ( A i the complemet of A). (3) If S i a fiite ample pace
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
u t u 0 ( 7) Intuitively, the maximum principles can be explained by the following observation. Recall
 Oct. Heat Equatio M aximum priciple I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
Oct. Heat Equatio M aximum priciple I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
THE CONCEPT OF THE ROOT LOCUS. H(s) THE CONCEPT OF THE ROOT LOCUS
 So far i the tudie of cotrol yte the role of the characteritic equatio polyoial i deteriig the behavior of the yte ha bee highlighted. The root of that polyoial are the pole of the cotrol yte, ad their
So far i the tudie of cotrol yte the role of the characteritic equatio polyoial i deteriig the behavior of the yte ha bee highlighted. The root of that polyoial are the pole of the cotrol yte, ad their
Digital Signal Processing, Fall 2006
 Digital Sigal Procssig, Fall 6 Lctur 9: Th Discrt Fourir Trasfor Zhg-Hua Ta Dpartt of Elctroic Systs Aalborg Uivrsity, Dar zt@o.aau.d Digital Sigal Procssig, I, Zhg-Hua Ta, 6 Cours at a glac MM Discrt-ti
Digital Sigal Procssig, Fall 6 Lctur 9: Th Discrt Fourir Trasfor Zhg-Hua Ta Dpartt of Elctroic Systs Aalborg Uivrsity, Dar zt@o.aau.d Digital Sigal Procssig, I, Zhg-Hua Ta, 6 Cours at a glac MM Discrt-ti
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Relation (12.1) states that if two points belong to the convex subset Ω then all the points on the connecting line also belong to Ω.
 Lectue 6. Poectio Opeato Deiitio A.: Subset Ω R is cove i [ y Ω R ] λ + λ [ y = z Ω], λ,. Relatio. states that i two poits belog to the cove subset Ω the all the poits o the coectig lie also belog to Ω.
Lectue 6. Poectio Opeato Deiitio A.: Subset Ω R is cove i [ y Ω R ] λ + λ [ y = z Ω], λ,. Relatio. states that i two poits belog to the cove subset Ω the all the poits o the coectig lie also belog to Ω.
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Comparisons of the Variance of Predictors with PPS sampling (update of c04ed26.doc) Ed Stanek
 Coparo o th Varac o Prdctor wth PPS aplg (updat o c04d6doc Ed Sta troducto W copar prdctor o a PSU a or total bad o PPS aplg Th tratgy to ollow that o Sta ad Sgr (JASA, 004 whr w xpr th prdctor a a lar
Coparo o th Varac o Prdctor wth PPS aplg (updat o c04d6doc Ed Sta troducto W copar prdctor o a PSU a or total bad o PPS aplg Th tratgy to ollow that o Sta ad Sgr (JASA, 004 whr w xpr th prdctor a a lar
Helping you learn to save. Pigby s tips and tricks
 Hlpg yu lan t av Pigby tip and tick Hlpg vy littl av Pigby ha bn tachg hi find all abut ny and hw t av f what ty want. Tuffl i avg f a nw tappy bubbl d and Pi can t wait t b abl t buy nw il pat. Pigby
Hlpg yu lan t av Pigby tip and tick Hlpg vy littl av Pigby ha bn tachg hi find all abut ny and hw t av f what ty want. Tuffl i avg f a nw tappy bubbl d and Pi can t wait t b abl t buy nw il pat. Pigby
Lecture 24: Observability and Constructibility
 ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
ectue 24: Obsevability ad Costuctibility 7 Obsevability ad Costuctibility Motivatio: State feedback laws deped o a kowledge of the cuet state. I some systems, xt () ca be measued diectly, e.g., positio
EXACT MODEL MATCHING AND DISTURBANCE REJECTION FOR GENERAL LINEAR TIME DELAY SYSTEMS VIA MEASUREMENT OUTPUT FEEDBACK
 EXACT ODEL ATCHIN AND DISTURBANCE REJECTION FOR ENERAL LINEAR TIE DELAY SYSTES VIA EASUREENT OUTUT FEEDBACK Fotis N. Kouboulis Halkis Istitut of Tchology Dpatt of Autoatio saha Evoia Halki 344, c kouboulis@tihal.g
EXACT ODEL ATCHIN AND DISTURBANCE REJECTION FOR ENERAL LINEAR TIE DELAY SYSTES VIA EASUREENT OUTUT FEEDBACK Fotis N. Kouboulis Halkis Istitut of Tchology Dpatt of Autoatio saha Evoia Halki 344, c kouboulis@tihal.g
Lecture 7 Diffusion. Our fluid equations that we developed before are: v t v mn t
 Cla ot fo EE6318/Phy 6383 Spg 001 Th doumt fo tutoal u oly ad may ot b opd o dtbutd outd of EE6318/Phy 6383 tu 7 Dffuo Ou flud quato that w dvlopd bfo a: f ( )+ v v m + v v M m v f P+ q E+ v B 13 1 4 34
Cla ot fo EE6318/Phy 6383 Spg 001 Th doumt fo tutoal u oly ad may ot b opd o dtbutd outd of EE6318/Phy 6383 tu 7 Dffuo Ou flud quato that w dvlopd bfo a: f ( )+ v v m + v v M m v f P+ q E+ v B 13 1 4 34
Math 7409 Homework 2 Fall from which we can calculate the cycle index of the action of S 5 on pairs of vertices as
 Math 7409 Hoewok 2 Fall 2010 1. Eueate the equivalece classes of siple gaphs o 5 vetices by usig the patte ivetoy as a guide. The cycle idex of S 5 actig o 5 vetices is 1 x 5 120 1 10 x 3 1 x 2 15 x 1
Math 7409 Hoewok 2 Fall 2010 1. Eueate the equivalece classes of siple gaphs o 5 vetices by usig the patte ivetoy as a guide. The cycle idex of S 5 actig o 5 vetices is 1 x 5 120 1 10 x 3 1 x 2 15 x 1
Chapter Taylor Theorem Revisited
 Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Tidal forces. m r. m 1 m 2. x r 2. r 1
 Tidal foces Befoe we look at fee waves on the eath, let s fist exaine one class of otion that is diectly foced: astonoic tides. Hee we will biefly conside soe of the tidal geneating foces fo -body systes.
Tidal foces Befoe we look at fee waves on the eath, let s fist exaine one class of otion that is diectly foced: astonoic tides. Hee we will biefly conside soe of the tidal geneating foces fo -body systes.
Physics 111. Lecture 38 (Walker: ) Phase Change Latent Heat. May 6, The Three Basic Phases of Matter. Solid Liquid Gas
 Physics 111 Lctu 38 (Walk: 17.4-5) Phas Chang May 6, 2009 Lctu 38 1/26 Th Th Basic Phass of Matt Solid Liquid Gas Squnc of incasing molcul motion (and ngy) Lctu 38 2/26 If a liquid is put into a sald contain
Physics 111 Lctu 38 (Walk: 17.4-5) Phas Chang May 6, 2009 Lctu 38 1/26 Th Th Basic Phass of Matt Solid Liquid Gas Squnc of incasing molcul motion (and ngy) Lctu 38 2/26 If a liquid is put into a sald contain
Last time: Completed solution to the optimum linear filter in real-time operation
 6.3 tochatic Etimatio ad Cotrol, Fall 4 ecture at time: Completed olutio to the oimum liear filter i real-time operatio emi-free cofiguratio: t D( p) F( p) i( p) dte dp e π F( ) F( ) ( ) F( p) ( p) 4444443
6.3 tochatic Etimatio ad Cotrol, Fall 4 ecture at time: Completed olutio to the oimum liear filter i real-time operatio emi-free cofiguratio: t D( p) F( p) i( p) dte dp e π F( ) F( ) ( ) F( p) ( p) 4444443
Figure 7: Boat Houses in the Thousand Islands. Sheet 1 of 1. March 2015
 T f Alxaia/Villag f Alxaia cal af vializai Pla T f Alxaia & Villag f Alxaia Jff u, N Y Figu 7: a u i h Thua Ila h f ach 5 N: Thi figu a a f h N Y a a f a ih fu vi u Til f h Evial Pci Fu. uc:. c-ea Oai
T f Alxaia/Villag f Alxaia cal af vializai Pla T f Alxaia & Villag f Alxaia Jff u, N Y Figu 7: a u i h Thua Ila h f ach 5 N: Thi figu a a f h N Y a a f a ih fu vi u Til f h Evial Pci Fu. uc:. c-ea Oai
(( )( )) = = S p S p = S p p m ( )
 36 Chapt 3. Rnoalization Toolit Poof of th oiginal Wad idntity o w nd O p Σ i β = idβ γ is p γ d p p π π π p p S p = id i d = id i S p S p d π β γ γ γ i β i β β γ γ β γ γ γ p = id is p is p d = Λ p, p.
36 Chapt 3. Rnoalization Toolit Poof of th oiginal Wad idntity o w nd O p Σ i β = idβ γ is p γ d p p π π π p p S p = id i d = id i S p S p d π β γ γ γ i β i β β γ γ β γ γ γ p = id is p is p d = Λ p, p.
Buoyancy effect control in multi legged robot locomotion on seabed using integrated impedance-fuzzy logic approach
 Idia Joual of Go-Mai Scic Vol. 44(), Dcm 5, pp. 937-945 Buoyacy ffct cotol i multi lggd oot locomotio o ad uig itgatd impdac-fuzzy logic appoach Md. Moktadi Alam, Addi Iawa* & Ta Y Yi ootic ad Umad Sytm
Idia Joual of Go-Mai Scic Vol. 44(), Dcm 5, pp. 937-945 Buoyacy ffct cotol i multi lggd oot locomotio o ad uig itgatd impdac-fuzzy logic appoach Md. Moktadi Alam, Addi Iawa* & Ta Y Yi ootic ad Umad Sytm
DIGITAL SIGNAL PROCESSING LECTURE 3
 DIGITAL SIGNAL PROCESSING LECTURE 3 Fall 2 2K8-5 th Semester Tahir Muhammad tmuhammad_7@yahoo.com Cotet ad Figures are from Discrete-Time Sigal Processig, 2e by Oppeheim, Shafer, ad Buc, 999-2 Pretice
DIGITAL SIGNAL PROCESSING LECTURE 3 Fall 2 2K8-5 th Semester Tahir Muhammad tmuhammad_7@yahoo.com Cotet ad Figures are from Discrete-Time Sigal Processig, 2e by Oppeheim, Shafer, ad Buc, 999-2 Pretice
SOLUTION: The 95% confidence interval for the population mean µ is x ± t 0.025; 49
 C22.0103 Sprig 2011 Homework 7 olutio 1. Baed o a ample of 50 x-value havig mea 35.36 ad tadard deviatio 4.26, fid a 95% cofidece iterval for the populatio mea. SOLUTION: The 95% cofidece iterval for the
C22.0103 Sprig 2011 Homework 7 olutio 1. Baed o a ample of 50 x-value havig mea 35.36 ad tadard deviatio 4.26, fid a 95% cofidece iterval for the populatio mea. SOLUTION: The 95% cofidece iterval for the
PESIT Bangalore South Campus Hosur road, 1km before Electronic City, Bengaluru -100 Department of Basic Science and Humanities
 P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
CHAPTER 5 CIRCULAR MOTION
 CHAPTER 5 CIRCULAR MOTION and GRAVITATION 5.1 CENTRIPETAL FORCE It is known that if a paticl mos with constant spd in a cicula path of adius, it acquis a cntiptal acclation du to th chang in th diction
CHAPTER 5 CIRCULAR MOTION and GRAVITATION 5.1 CENTRIPETAL FORCE It is known that if a paticl mos with constant spd in a cicula path of adius, it acquis a cntiptal acclation du to th chang in th diction
( ) ( ) ( ) 2011 HSC Mathematics Solutions ( 6) ( ) ( ) ( ) π π. αβ = = 2. α β αβ. Question 1. (iii) 1 1 β + (a) (4 sig. fig.
 HS Mathmatics Solutios Qustio.778.78 ( sig. fig.) (b) (c) ( )( + ) + + + + d d (d) l ( ) () 8 6 (f) + + + + ( ) ( ) (iii) β + + α α β αβ 6 (b) si π si π π π +,π π π, (c) y + dy + d 8+ At : y + (,) dy 8(
HS Mathmatics Solutios Qustio.778.78 ( sig. fig.) (b) (c) ( )( + ) + + + + d d (d) l ( ) () 8 6 (f) + + + + ( ) ( ) (iii) β + + α α β αβ 6 (b) si π si π π π +,π π π, (c) y + dy + d 8+ At : y + (,) dy 8(
On Gaussian Distribution
 Ppad b Çağata ada MU lctical gi. Dpt. Dc. documt vio. Gauia ditibutio i did a ollow O Gauia Ditibutio π h uctio i clal poitiv valud. Bo callig thi uctio a a pobabilit dit uctio w hould chc whth th aa ud
Ppad b Çağata ada MU lctical gi. Dpt. Dc. documt vio. Gauia ditibutio i did a ollow O Gauia Ditibutio π h uctio i clal poitiv valud. Bo callig thi uctio a a pobabilit dit uctio w hould chc whth th aa ud
An Unknown Physical Constant Missing from Physics
 Applid Phyic Rach; Vol 7, No 5; 5 ISSN 96-9639 -ISSN 96-967 Publihd by Caadia Ct of Scic ad ducatio A Ukow Phyical Cotat Miig fom Phyic Chudaiji Buddhit Tmpl, Iaki, Japa Kohu Suto Copodc: Kohu Suto, Chudaiji
Applid Phyic Rach; Vol 7, No 5; 5 ISSN 96-9639 -ISSN 96-967 Publihd by Caadia Ct of Scic ad ducatio A Ukow Phyical Cotat Miig fom Phyic Chudaiji Buddhit Tmpl, Iaki, Japa Kohu Suto Copodc: Kohu Suto, Chudaiji
International Symposium on Room Acoustics Satellite Symposium of the 19 th International Congress on Acoustics Seville, September 2007
 Itatioal Sypoiu o Roo Acoutic Satllit Sypoiu of th 9 th Itatioal Cog o Acoutic Svill, - Sptb 7 A THEORETICA AAYSIS OF UTI-ODA BASS-TRAPPIG RESOATORS COUPED TO COTRO-ROO ACOUSTICS PACS: 43.55.C Atu, Joé
Itatioal Sypoiu o Roo Acoutic Satllit Sypoiu of th 9 th Itatioal Cog o Acoutic Svill, - Sptb 7 A THEORETICA AAYSIS OF UTI-ODA BASS-TRAPPIG RESOATORS COUPED TO COTRO-ROO ACOUSTICS PACS: 43.55.C Atu, Joé
The Performance of Feedback Control Systems
 The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
CDS 101: Lecture 9.1 PID and Root Locus
 CS : Lct 9. P ad Root Loc Richad M. Ma 5 Novmb Goal: fi P cotoll ad dcib how to thm todc th oot loc tchiq ad dcib how to it to choo loop gai Show om of th limitatio of fdback d to RHP pol ad zo Radig:
CS : Lct 9. P ad Root Loc Richad M. Ma 5 Novmb Goal: fi P cotoll ad dcib how to thm todc th oot loc tchiq ad dcib how to it to choo loop gai Show om of th limitatio of fdback d to RHP pol ad zo Radig:
SOLVED PROBLEMS IN FOUNDATION ENGINEERING
 Probl # (6) rctagular footig is actd by a vrtical load of 8060 kn ad two horizotal forcs of 500 kn i both th log ad th short dirctios with a distac of 0.6 fro th groud surfac. Dtri:. Th bas prssur at th
Probl # (6) rctagular footig is actd by a vrtical load of 8060 kn ad two horizotal forcs of 500 kn i both th log ad th short dirctios with a distac of 0.6 fro th groud surfac. Dtri:. Th bas prssur at th
Magnetic effects and the peculiarity of the electron spin in Atoms
 Magtic ffcts ad t pculiaity of t lcto spi i Atos Pit Za Hdik otz Nobl Piz 90 Otto t Nobl 9 Wolfgag Pauli Nobl 95 ctu Nots tuctu of Matt: Atos ad Molculs; W. Ubacs T obital agula otu of a lcto i obit iclassical
Magtic ffcts ad t pculiaity of t lcto spi i Atos Pit Za Hdik otz Nobl Piz 90 Otto t Nobl 9 Wolfgag Pauli Nobl 95 ctu Nots tuctu of Matt: Atos ad Molculs; W. Ubacs T obital agula otu of a lcto i obit iclassical
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
 Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
A Simple Proof that e is Irrational
 Two of th most bautiful ad sigificat umbrs i mathmatics ar π ad. π (approximatly qual to 3.459) rprsts th ratio of th circumfrc of a circl to its diamtr. (approximatly qual to.788) is th bas of th atural
Two of th most bautiful ad sigificat umbrs i mathmatics ar π ad. π (approximatly qual to 3.459) rprsts th ratio of th circumfrc of a circl to its diamtr. (approximatly qual to.788) is th bas of th atural
Handout on. Crystal Symmetries and Energy Bands
 dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
z 1+ 3 z = Π n =1 z f() z = n e - z = ( 1-z) e z e n z z 1- n = ( 1-z/2) 1+ 2n z e 2n e n -1 ( 1-z )/2 e 2n-1 1-2n -1 1 () z
 Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Test 2 phy a) How is the velocity of a particle defined? b) What is an inertial reference frame? c) Describe friction.
 Tet phy 40 1. a) How i the velocity of a paticle defined? b) What i an inetial efeence fae? c) Decibe fiction. phyic dealt otly with falling bodie. d) Copae the acceleation of a paticle in efeence fae
Tet phy 40 1. a) How i the velocity of a paticle defined? b) What i an inetial efeence fae? c) Decibe fiction. phyic dealt otly with falling bodie. d) Copae the acceleation of a paticle in efeence fae
APPENDIX: STATISTICAL TOOLS
 I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
I. Nots o radom samplig Why do you d to sampl radomly? APPENDI: STATISTICAL TOOLS I ordr to masur som valu o a populatio of orgaisms, you usually caot masur all orgaisms, so you sampl a subst of th populatio.
Worksheet: Taylor Series, Lagrange Error Bound ilearnmath.net
 Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Chapter 4 : Laplace Transform
 4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
New Advanced Higher Mathematics: Formulae
 Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
UNIVERSITY OF BOLTON SCHOOL OF ENGINEERING BENG (HONS) IN MECHANICAL ENGINEERING SEMESTER 1 EXAMINATION 2016/2017
 UNIVERSITY OF BOLTON TW30 SCHOOL OF ENGINEERING BENG (HONS) IN MECHANICAL ENGINEERING SEMESTER EXAMINATION 06/07 ADVANCED THERMOFLUIDS & CONTROL SYSTEMS MODULE NO: AME6005 Date: Thursday Jauary 07 Time:
UNIVERSITY OF BOLTON TW30 SCHOOL OF ENGINEERING BENG (HONS) IN MECHANICAL ENGINEERING SEMESTER EXAMINATION 06/07 ADVANCED THERMOFLUIDS & CONTROL SYSTEMS MODULE NO: AME6005 Date: Thursday Jauary 07 Time:
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
MM1. Introduction to State-Space Method
 MM Itroductio to Stt-Spc Mthod Wht tt-pc thod? How to gt th tt-pc dcriptio? 3 Proprty Alyi Bd o SS Modl Rdig Mtril: FC: p469-49 C: p- /4/8 Modr Cotrol Wht th SttS tt-spc Mthod? I th tt-pc thod th dyic
MM Itroductio to Stt-Spc Mthod Wht tt-pc thod? How to gt th tt-pc dcriptio? 3 Proprty Alyi Bd o SS Modl Rdig Mtril: FC: p469-49 C: p- /4/8 Modr Cotrol Wht th SttS tt-spc Mthod? I th tt-pc thod th dyic
8(4 m0) ( θ ) ( ) Solutions for HW 8. Chapter 25. Conceptual Questions
 Solutios for HW 8 Captr 5 Cocptual Qustios 5.. θ dcrass. As t crystal is coprssd, t spacig d btw t plas of atos dcrass. For t first ordr diffractio =. T Bragg coditio is = d so as d dcrass, ust icras for
Solutios for HW 8 Captr 5 Cocptual Qustios 5.. θ dcrass. As t crystal is coprssd, t spacig d btw t plas of atos dcrass. For t first ordr diffractio =. T Bragg coditio is = d so as d dcrass, ust icras for
Motivation. We talk today for a more flexible approach for modeling the conditional probabilities.
 Baysia Ntworks Motivatio Th coditioal idpdc assuptio ad by aïv Bays classifirs ay s too rigid spcially for classificatio probls i which th attributs ar sowhat corrlatd. W talk today for a or flibl approach
Baysia Ntworks Motivatio Th coditioal idpdc assuptio ad by aïv Bays classifirs ay s too rigid spcially for classificatio probls i which th attributs ar sowhat corrlatd. W talk today for a or flibl approach
Two-Dimensional Modeling of Thermoelectric Cells
 udu Uivit udu -ub Itatioal Rfigatio ad i Coditioig Cofc School of Mchaical Egiig 2014 o-dimioal Modlig of hmolctic Cll Klaudio S. M. Olivia UFR, Bazil, klaudio@uol.com.b Rodigo. Cadoo UFR, Bazil, odigo.pito@ufp.b
udu Uivit udu -ub Itatioal Rfigatio ad i Coditioig Cofc School of Mchaical Egiig 2014 o-dimioal Modlig of hmolctic Cll Klaudio S. M. Olivia UFR, Bazil, klaudio@uol.com.b Rodigo. Cadoo UFR, Bazil, odigo.pito@ufp.b
A novel analytic potential function applied to neutral diatomic molecules and charged lons
 Vol., No., 84-89 (00 http://dx.doi.o/0.46/s.00.08 Natual Scic A ovl aalytic pottial fuctio applid to utal diatomic molculs ad chad los Cha-F Yu, Cha-Ju Zhu, Cho-Hui Zha, Li-Xu So, Qiu-Pi Wa Dpatmt of physics,
Vol., No., 84-89 (00 http://dx.doi.o/0.46/s.00.08 Natual Scic A ovl aalytic pottial fuctio applid to utal diatomic molculs ad chad los Cha-F Yu, Cha-Ju Zhu, Cho-Hui Zha, Li-Xu So, Qiu-Pi Wa Dpatmt of physics,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science. BACKGROUND EXAM September 30, 2004.
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.34 Discrete Time Sigal Processig Fall 24 BACKGROUND EXAM September 3, 24. Full Name: Note: This exam is closed
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.34 Discrete Time Sigal Processig Fall 24 BACKGROUND EXAM September 3, 24. Full Name: Note: This exam is closed
[ ] 1+ lim G( s) 1+ s + s G s s G s Kacc SYSTEM PERFORMANCE. Since. Lecture 10: Steady-state Errors. Steady-state Errors. Then
![[ ] 1+ lim G( s) 1+ s + s G s s G s Kacc SYSTEM PERFORMANCE. Since. Lecture 10: Steady-state Errors. Steady-state Errors. Then [ ] 1+ lim G( s) 1+ s + s G s s G s Kacc SYSTEM PERFORMANCE. Since. Lecture 10: Steady-state Errors. Steady-state Errors. Then](/thumbs/79/79716622.jpg) SYSTEM PERFORMANCE Lctur 0: Stady-tat Error Stady-tat Error Lctur 0: Stady-tat Error Dr.alyana Vluvolu Stady-tat rror can b found by applying th final valu thorm and i givn by lim ( t) lim E ( ) t 0 providd
SYSTEM PERFORMANCE Lctur 0: Stady-tat Error Stady-tat Error Lctur 0: Stady-tat Error Dr.alyana Vluvolu Stady-tat rror can b found by applying th final valu thorm and i givn by lim ( t) lim E ( ) t 0 providd
The angle between L and the z-axis is found from
 Poblm 6 This is not a ifficult poblm but it is a al pain to tansf it fom pap into Mathca I won't giv it to you on th quiz, but know how to o it fo th xam Poblm 6 S Figu 6 Th magnitu of L is L an th z-componnt
Poblm 6 This is not a ifficult poblm but it is a al pain to tansf it fom pap into Mathca I won't giv it to you on th quiz, but know how to o it fo th xam Poblm 6 S Figu 6 Th magnitu of L is L an th z-componnt
Hydrogen atom. Energy levels and wave functions Orbital momentum, electron spin and nuclear spin Fine and hyperfine interaction Hydrogen orbitals
 Hydogn atom Engy lvls and wav functions Obital momntum, lcton spin and nucla spin Fin and hypfin intaction Hydogn obitals Hydogn atom A finmnt of th Rydbg constant: R ~ 109 737.3156841 cm -1 A hydogn mas
Hydogn atom Engy lvls and wav functions Obital momntum, lcton spin and nucla spin Fin and hypfin intaction Hydogn obitals Hydogn atom A finmnt of th Rydbg constant: R ~ 109 737.3156841 cm -1 A hydogn mas
ME 410 MECHANICAL ENGINEERING SYSTEMS LABORATORY REGRESSION ANALYSIS
 ME 40 MECHANICAL ENGINEERING REGRESSION ANALYSIS Regreio problem deal with the relatiohip betwee the frequec ditributio of oe (depedet) variable ad aother (idepedet) variable() which i (are) held fied
ME 40 MECHANICAL ENGINEERING REGRESSION ANALYSIS Regreio problem deal with the relatiohip betwee the frequec ditributio of oe (depedet) variable ad aother (idepedet) variable() which i (are) held fied
Define a Markov chain on {1,..., 6} with transition probability matrix P =
 Pla Group Work 0. The title says it all Next Tie: MCMC ad Geeral-state Markov Chais Midter Exa: Tuesday 8 March i class Hoework 4 due Thursday Uless otherwise oted, let X be a irreducible, aperiodic Markov
Pla Group Work 0. The title says it all Next Tie: MCMC ad Geeral-state Markov Chais Midter Exa: Tuesday 8 March i class Hoework 4 due Thursday Uless otherwise oted, let X be a irreducible, aperiodic Markov
Estimation of a Random Variable
 Estimation of a andom Vaiabl Obsv and stimat. ˆ is an stimat of. ζ : outcom Estimation ul ˆ Sampl Spac Eampl: : Pson s Hight, : Wight. : Ailin Company s Stock Pic, : Cud Oil Pic. Cost of Estimation Eo
Estimation of a andom Vaiabl Obsv and stimat. ˆ is an stimat of. ζ : outcom Estimation ul ˆ Sampl Spac Eampl: : Pson s Hight, : Wight. : Ailin Company s Stock Pic, : Cud Oil Pic. Cost of Estimation Eo
S U E K E AY S S H A R O N T IM B E R W IN D M A R T Z -PA U L L IN. Carlisle Franklin Springboro. Clearcreek TWP. Middletown. Turtlecreek TWP.
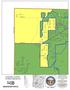 F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
MA1200 Exercise for Chapter 7 Techniques of Differentiation Solutions. First Principle 1. a) To simplify the calculation, note. Then. lim h.
 MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
ES 330 Electronics II Homework # 5 (Fall 2016 Due Wednesday, October 4, 2017)
 Pag1 Na olutions E 33 Elctonics II Howok # 5 (Fall 216 Du Wdnsday, Octob 4, 217) Pobl 1 (25 pots) A coon-itt aplifi uss a BJT with cunt ga = 1 whn biasd at I =.5 A. It has a collcto sistanc of = 1 k. (a)
Pag1 Na olutions E 33 Elctonics II Howok # 5 (Fall 216 Du Wdnsday, Octob 4, 217) Pobl 1 (25 pots) A coon-itt aplifi uss a BJT with cunt ga = 1 whn biasd at I =.5 A. It has a collcto sistanc of = 1 k. (a)
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Estimating the Variance in a Simulation Study of Balanced Two Stage Predictors of Realized Random Cluster Means Ed Stanek
 Etatg th Varac a Sulato Study of Balacd Two Stag Prdctor of Ralzd Rado Clutr Ma Ed Stak Itroducto W dcrb a pla to tat th varac copot a ulato tudy N ( µ µ W df th varac of th clutr paratr a ug th N ulatd
Etatg th Varac a Sulato Study of Balacd Two Stag Prdctor of Ralzd Rado Clutr Ma Ed Stak Itroducto W dcrb a pla to tat th varac copot a ulato tudy N ( µ µ W df th varac of th clutr paratr a ug th N ulatd
Shor s Algorithm. Motivation. Why build a classical computer? Why build a quantum computer? Quantum Algorithms. Overview. Shor s factoring algorithm
 Motivation Sho s Algoith It appas that th univs in which w liv is govnd by quantu chanics Quantu infoation thoy givs us a nw avnu to study & tst quantu chanics Why do w want to build a quantu coput? Pt
Motivation Sho s Algoith It appas that th univs in which w liv is govnd by quantu chanics Quantu infoation thoy givs us a nw avnu to study & tst quantu chanics Why do w want to build a quantu coput? Pt
Option 3. b) xe dx = and therefore the series is convergent. 12 a) Divergent b) Convergent Proof 15 For. p = 1 1so the series diverges.
 Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Engineering Differential Equations Practice Final Exam Solutions Fall 2011
 9.6 Enginring Diffrntial Equation Practic Final Exam Solution Fall 0 Problm. (0 pt.) Solv th following initial valu problm: x y = xy, y() = 4. Thi i a linar d.. bcau y and y appar only to th firt powr.
9.6 Enginring Diffrntial Equation Practic Final Exam Solution Fall 0 Problm. (0 pt.) Solv th following initial valu problm: x y = xy, y() = 4. Thi i a linar d.. bcau y and y appar only to th firt powr.
Physics 202, Lecture 5. Today s Topics. Announcements: Homework #3 on WebAssign by tonight Due (with Homework #2) on 9/24, 10 PM
 Physics 0, Lctu 5 Today s Topics nnouncmnts: Homwok #3 on Wbssign by tonight Du (with Homwok #) on 9/4, 10 PM Rviw: (Ch. 5Pat I) Elctic Potntial Engy, Elctic Potntial Elctic Potntial (Ch. 5Pat II) Elctic
Physics 0, Lctu 5 Today s Topics nnouncmnts: Homwok #3 on Wbssign by tonight Du (with Homwok #) on 9/4, 10 PM Rviw: (Ch. 5Pat I) Elctic Potntial Engy, Elctic Potntial Elctic Potntial (Ch. 5Pat II) Elctic
Formula overview. Halit Eroglu, 04/2014 With the base formula the following fundamental constants and significant physical parameters were derived.
 Foula ovviw Halit Eolu, 0/0 With th bas foula th followin fundantal onstants and sinifiant physial paats w divd. aiabl usd: Spd of liht G Gavitational onstant h lank onstant α Fin stutu onstant h dud lank
Foula ovviw Halit Eolu, 0/0 With th bas foula th followin fundantal onstants and sinifiant physial paats w divd. aiabl usd: Spd of liht G Gavitational onstant h lank onstant α Fin stutu onstant h dud lank
ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS
 Joual of Pue ad Alied Mathematics: Advaces ad Alicatios Volume 0 Numbe 03 Pages 5-58 ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS ALI H HAKAMI Deatmet of Mathematics
Joual of Pue ad Alied Mathematics: Advaces ad Alicatios Volume 0 Numbe 03 Pages 5-58 ON EUCLID S AND EULER S PROOF THAT THE NUMBER OF PRIMES IS INFINITE AND SOME APPLICATIONS ALI H HAKAMI Deatmet of Mathematics
HONDA 4 cylinder Goldwing. Instruction manual with visual guide for the Gen 5 Goldwing GL1000 & GL1100
 HONDA 4 cylinder Goldwing Instruction manual with visual guide for the Gen 5 Goldwing GL1000 & GL1100 Please ead this i po ta t i fo atio BEFORE i stallatio : This ig itio kit epla es all o igi al Ho da
HONDA 4 cylinder Goldwing Instruction manual with visual guide for the Gen 5 Goldwing GL1000 & GL1100 Please ead this i po ta t i fo atio BEFORE i stallatio : This ig itio kit epla es all o igi al Ho da
ASSERTION AND REASON
 ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
