10-1 Study Guide and Intervention
|
|
|
- Harold Conley
- 5 years ago
- Views:
Transcription
1 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are a given distance, called the radius, from a given point called the center. segment or line can intersect a circle in several ways. segment with endpoints that are the center of the circle and a point of the circle is a radius. segment with endpoints that lie on the circle is a chord. chord that contains the circle s center is a diameter. F chord:, radius: F, F, F diameter: ample a. Name the circle. he name of the circle is. b. Name radii of the circle.,,, and are radii. c. Name chords of the circle. and are chords. d. Name a diameter of the circle. is a diameter. ercises 1. Name the circle. X. Name radii of the circle. 3. Name chords of the circle. Y 4. Name diameters of the circle. 5. Find if is 1 millimeters.. Find and if Y is 10 inches. 7. Is XY? plain. hapter 10 Glencoe Geometry
2 NM I 10-1 tudy Guide and Intervention (continued) ircles and ircumference ircumference he circumference of a circle is the distance around the circle. ircumference For a circumference of units and a diameter of d units or a radius of r units, d or r. ample Find the circumference of the circle to the nearest hundredth. r ircumference formula (13) r Use a calculator. he circumference is about 1. centimeters. ercises 13 cm Lesson 10-1 Find the circumference of a circle with the given radius or diameter. ound to the nearest hundredth. 1. r cm. r 3 ft 3. r 4.1 cm 4. d 10 in. opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. 5. d 1 m. d 1 yd 3 he radius, diameter, or circumference of a circle is given. Find the missing measures to the nearest hundredth. 7. r 4 cm. d ft d, r, 9. r 1 cm 10. d 15 in. d, r, Find the eact circumference of each circle cm cm 1 cm cm hapter 10 7 Glencoe Geometry
3 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. 10- tudy Guide and Intervention ample In, m 4 and is a diameter. Find m and m. is a central angle and m 4, so m 4. hus m 30 4 or 31. ercises NM I Measuring ngles and rcs ngles and rcs central angle is an angle whose verte is at the center of a circle and whose sides are radii. central angle separates a circle into two arcs, a major arc and a minor arc. G Here are some properties of central angles and arcs. he sum of the measures of the central angles of mh mf mfg mgh 30 a circle with no interior points in common is 30. he measure of a minor arc equals the measure of its central angle. he measure of a major arc is 30 minus the measure of the minor arc. wo arcs are congruent if and only if their corresponding central angles are congruent. he measure of an arc formed by two adjacent arcs is the sum of the measures of the two arcs. (rc ddition ostulate) Find each measure. 1. m. mu 3. m 4. m In, m 44. Find each measure. 5. m. m 7. m. m 9. m 10. m H mf mf mgf 30 mf F FG if and only if F FG. mf mfg mg 45 0 F GF is a minor arc. HG is a major arc. U GF is a central angle. Lesson 10- hapter Glencoe Geometry
4 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10- tudy Guide and Intervention (continued) Measuring ngles and rcs rc Length n arc is part of a circle and its length is a part of the circumference of the circle. ample In, m 135,, and is a diameter. Find the length of. m 135, so m 135. Using the formula r, the circumference is () or 1. o find the length of, write a proportion to compare each part to its whole. length of degree measure of arc circumference degree measure of circle roportion ubstitution (1 )( 135) 30 Multiply each side by 1. implify. he length of is or about 1.5 units. ercises he diameter of is 4 units long. Find the length of each arc for the given angle measure. ound to the nearest tenth. 1. if m 10. if m if m if m 45 he diameter of is 15 units long and. Find the length of each arc for the given angle measure. ound to the nearest tenth. 5. if m 70 M. N if m 50 N 7. M. M if mm 140 hapter Glencoe Geometry
5 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-3 tudy Guide and Intervention (continued) rcs and hords rcs and hords oints on a circle determine both chords and arcs. everal properties are related to points on a circle. In a circle or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent. If all the vertices of a polygon lie on a circle, the polygon is said to be inscribed in the circle and the circle is circumscribed about the polygon. V V if and only if V. V is inscribed in. is circumscribed about V. ample rapezoid is inscribed in. If and m 50, what is m? hords,, and are congruent, so,, and are congruent. m 50, so m m m hen m or 10. ercises ach regular polygon is inscribed in a circle. etermine the measure of each arc that corresponds to a side of the polygon. 1. heagon. pentagon 3. triangle 4. square 5. octagon. 3-gon etermine the measure of each arc of the circle circumscribed about the polygon U 9. V U 4 V 7 U hapter 10 0 Glencoe Geometry
6 NM I 10-3 tudy Guide and Intervention (continued) rcs and hords iameters and hords In a circle, if a diameter is perpendicular to a chord, then it bisects the chord and its arc. In a circle or in congruent circles, two chords are congruent if and only if they are equidistant from the center. W Z X Y If WZ, then X X and W W. If X Y, then. If, then and are equidistant from point. ample In,, 15, and 4. Find. diameter or radius perpendicular to a chord bisects the chord, so is half of. 1 (4) 1 Use the ythagorean heorem to find in. () () () ythagorean heorem ubstitution Multiply. ubtract 144 from each side. ake the square root of each side. opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. ercises In, 4 and my 45. Find each measure my 7. mx. mx. m 9. m In G, G GU and. Find each measure. 10. U m G 15. m 5 G 3 U X Y Lesson chord of a circle 0 inches long is 4 inches from the center of a circle. Find the length of the radius. hapter 10 1 Glencoe Geometry
7 NM I 10-4 tudy Guide and Intervention Inscribed ngles Inscribed ngles n inscribed angle is an angle whose verte is on a circle and whose sides contain chords of the circle. In G, inscribed F intercepts F. G Inscribed ngle heorem If an angle is inscribed in a circle, then the measure of the angle equals one-half the measure of its intercepted arc. F mf 1 mf ample In G above, mf 90. Find mf. F is an inscribed angle so its measure is half of the intercepted arc. mf 1 mf 1 (90) or 45 ercises Use for ercises In, V and V. opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. 1. Name the intercepted arc for.. Name an inscribed angle that intercepts V. In, mv 10 and m 7. Find each measure. 3. m 4. mv 5. m. mv 7. m. mv 9. mv 10. mv V Lesson 10-4 hapter 10 7 Glencoe Geometry
8 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-4 tudy Guide and Intervention (continued) Inscribed ngles ngles of Inscribed olygons n inscribed polygon is one whose sides are chords of a circle and whose vertices are points on the circle. Inscribed polygons have several properties. If an angle of an inscribed polygon intercepts a semicircle, the angle is a right angle. If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary. If is a semicircle, then m 90. For inscribed quadrilateral, m m 10 and m m 10. ample a. m In above, 3 and 5. Find each measure. intercepts a semicircle. herefore is a right angle and m 90. b. is a right triangle, so use the ythagorean heorem to find. () () () () 3 5 () 5 9 () 1 4 ercises Find the measure of each angle or segment for each figure. 1. mx, my. 3. m1, m X G W 10 Y 5 F Z 1 J H 4. m1, m 5.,. m1, m K U M N 30 Z L 5 30 W 1 V hapter 10 Glencoe Geometry
9 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-5 tudy Guide and Intervention (continued) angents angents tangent to a circle intersects the circle in eactly one point, called the point of tangency. here are three important relationships involving tangents. If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency. If a line is perpendicular to a radius of a circle at its endpoint on the circle, then the line is a tangent to the circle. If two segments from the same eterior point are tangent to a circle, then they are congruent. if and only if is tangent to. If and are tangent to, then. ample is tangent to. Find. is tangent to, so is perpendicular to radius. is a radius, so and 9 or 17. Use the ythagorean heorem with right. 9 () () () ythagorean heorem ubstitution Multiply. ubtract 4 from each side. ake the positive square root of each side. ercises Find. ssume that segments that appear to be tangent are tangent. 1.. J 0 K H G F 3. N 4. 1 M U Y Z 5 F hapter Glencoe Geometry
10 NM I 10-5 tudy Guide and Intervention (continued) angents ircumscribed olygons When a polygon is circumscribed about a circle, all of the sides of the polygon are tangent to the circle. G H F Heagon F is circumscribed about.,,,, F, and F are tangent to. K J quare GHJK is circumscribed about. GH, JH, JK, and KG are tangent to. ample is circumscribed about. Find the perimeter of. is circumscribed about, so points,, and F are points of tangency. herefore F,, and F. F F F he perimeter is 5 units. opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. ercises Find. ssume that segments that appear to be tangent are tangent. 1.. square square regular heagon 4 4 equilateral triangle Lesson 10-5 hapter Glencoe Geometry
11 NM I 10- tudy Guide and Intervention ecants, angents, and ngle Measures Intersections n or Inside a ircle line that intersects a circle in eactly two points is called a secant. he measures of angles formed by secants and tangents are related to intercepted arcs. If two secants intersect in the interior of a circle, then the measure of the angle formed is one-half the sum of the measure of the arcs intercepted by the angle and its vertical angle. 1 m1 1 (m m ) If a secant and a tangent intersect at the point of tangency, then the measure of each angle formed is one-half the measure of its intercepted arc. X Y U V mxv 1 muv myv 1 mv Lesson 10- ample 1 Find. ample Find y. 30 he two secants intersect he secant and the inside the circle, so is tangent intersect at the equal to one-half the sum point of tangency, so the of the measures of the arcs 55 measure of the angle is intercepted by the angle one-half the measure of and its vertical angle. its intercepted arc. 1 y 1 (30 55) y 1 (1) opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. 1 (5) 4.5 ercises Find each measure m1. m 3. m m4 5. m5. m 3 0 U 10 4 V W X hapter Glencoe Geometry
12 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10- tudy Guide and Intervention (continued) ecants, angents, and ngle Measures Intersections utside a ircle If secants and tangents intersect outside a circle, they form an angle whose measure is related to the intercepted arcs. If two secants, a secant and a tangent, or two tangents intersect in the eterior of a circle, then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs. H G J K N M and are secants. G is a tangent. J is a secant. mgh m 1 (m m ) m 1 (mgkj ) m 1 M and N are tangents. (mmn mmn ) ample Find mmn. MN is formed by two secants that intersect in the eterior of a circle. mmn 1 (mmn m) M 34 N 1 1 (34 1) 1 (1) or he measure of the angle is. ercises Find each measure. 1. m1. m m hapter Glencoe Geometry
13 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-7 tudy Guide and Intervention pecial egments in a ircle egments Intersecting Inside a ircle If two chords intersect in a circle, then the products of the measures of the chords are equal. a c d b a b c d ample Find. he two chords intersect inside the circle, so the products and are equal. 3 ubstitution 4 implify. 4 ivide each side by. 3 ercises Find to the nearest tenth hapter Glencoe Geometry
14 NM I 10-7 tudy Guide and Intervention (continued) pecial egments in a ircle egments Intersecting utside a ircle If secants and tangents intersect outside a circle, then two products are equal. If two secant segments are drawn to a circle from an eterior point, then the product of the measures of one secant segment and its eternal secant segment is equal to the product of the measures of the other secant segment and its eternal secant segment. and are secant segments. and are eternal secant segments. If a tangent segment and a secant segment are drawn to a circle from an eterior point, then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its eternal secant segment. is a tangent segment. is a secant segment. is an eternal secant segment. () Lesson 10-7 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. ample Find to the nearest tenth. he tangent segment is, the secant segment is, and the eternal secant segment is. () (1) 15(15 ) ercises Find to the nearest tenth. ssume segments that appear to be tangent are tangent W Y 3 V hapter Glencoe Geometry
15 NM I 10- tudy Guide and Intervention quations of ircles quation of a ircle circle is the locus of points in a plane equidistant from a given point. You can use this definition to write an equation of a circle. tandard quation n equation for a circle with center at (h, k) of a ircle and a radius of r units is ( h) (y k) r. y r (h, k) ample Write an equation for a circle with center (1, 3) and radius. Use the formula ( h) ( y k) r with h 1, k 3, and r. ( h) ( y k) r quation of a circle ( (1)) ( y 3) ubstitution ( 1) ( y 3) 3 implify. ercises Write an equation for each circle. 1. center at (0, 0), r. center at (, 3), r 5 Lesson 10- opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. 3. center at (, 4), r 1 4. center at (1, 4), r 5. center at (, ), diameter. center at 1, 1 4, r 3 7. center at the origin, diameter 4. center at 1, 5, r 5 9. Find the center and radius of a circle with equation y Find the center and radius of a circle with equation ( 4) (y 3) 1. hapter Glencoe Geometry
16 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10- tudy Guide and Intervention (continued) quations of ircles Graph ircles If you are given an equation of a circle, you can find information to help you graph the circle. ample Graph ( 3) (y 1) 9. Use the parts of the equation to find (h, k) and r. y ( h) ( y k) r ( h) ( 3) ( y k) ( y 1) r 9 h 3 y k y 1 r 3 h 3 k 1 h 3 k 1 (3, 1) he center is at (3, 1) and the radius is 3. Graph the center. Use a compass set at a radius of 3 grid squares to draw the circle. ercises Graph each equation. 1. y 1. ( ) ( y 1) 9 y y 3. ( ) y 1 4. ( 1) ( y ).5 y y 5. 1 y ( y 1) 9 y y hapter 10 5 Glencoe Geometry
Geometry. Chapter 10 Resource Masters
 Geometry hapter 10 esource Masters onsumable Workbooks Many of the worksheets contained in the hapter esource Masters booklets are available as consumable workbooks. tudy Guide and Intervention Workbook
Geometry hapter 10 esource Masters onsumable Workbooks Many of the worksheets contained in the hapter esource Masters booklets are available as consumable workbooks. tudy Guide and Intervention Workbook
Study Guide. Exploring Circles. Example: Refer to S for Exercises 1 6.
 9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
Using Properties of Segments that Intersect Circles
 ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
radii: AP, PR, PB diameter: AB chords: AB, CD, AF secant: AG or AG tangent: semicircles: ACB, ARB minor arcs: AC, AR, RD, BC,
 h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
Geometry. Chapter 10 Resource Masters
 Geometry hapter 10 esource Masters 10 eading to Learn Mathematics Vocabulary uilder This is an alphabetical list of the key vocabulary terms you will learn in hapter 10. s you study the chapter, complete
Geometry hapter 10 esource Masters 10 eading to Learn Mathematics Vocabulary uilder This is an alphabetical list of the key vocabulary terms you will learn in hapter 10. s you study the chapter, complete
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
 10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
Solve problems involving tangents to a circle. Solve problems involving chords of a circle
 8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
 Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Geometry: A Complete Course
 eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
SM2H Unit 6 Circle Notes
 Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Indicate whether the statement is true or false.
 PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
Chords and Arcs. Objectives To use congruent chords, arcs, and central angles To use perpendicular bisectors to chords
 - hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
- hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
Unit 10 Geometry Circles. NAME Period
 Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Replacement for a Carpenter s Square
 Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Lesson 12.1 Skills Practice
 Lesson 12.1 Skills Practice Introduction to ircles ircle, Radius, and iameter Vocabulary efine each term in your own words. 1. circle circle is a collection of points on the same plane equidistant from
Lesson 12.1 Skills Practice Introduction to ircles ircle, Radius, and iameter Vocabulary efine each term in your own words. 1. circle circle is a collection of points on the same plane equidistant from
11. Concentric Circles: Circles that lie in the same plane and have the same center.
 Circles Definitions KNOW THESE TERMS 1. Circle: The set of all coplanar points equidistant from a given point. 2. Sphere: The set of all points equidistant from a given point. 3. Radius of a circle: The
Circles Definitions KNOW THESE TERMS 1. Circle: The set of all coplanar points equidistant from a given point. 2. Sphere: The set of all points equidistant from a given point. 3. Radius of a circle: The
What is the longest chord?.
 Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
Chapter-wise questions
 hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
Mth 076: Applied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE
 Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
Example 1: Finding angle measures: I ll do one: We ll do one together: You try one: ML and MN are tangent to circle O. Find the value of x
 Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
 Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
UNIT OBJECTIVES. unit 9 CIRCLES 259
 UNIT 9 ircles Look around whatever room you are in and notice all the circular shapes. Perhaps you see a clock with a circular face, the rim of a cup or glass, or the top of a fishbowl. ircles have perfect
UNIT 9 ircles Look around whatever room you are in and notice all the circular shapes. Perhaps you see a clock with a circular face, the rim of a cup or glass, or the top of a fishbowl. ircles have perfect
Ready To Go On? Skills Intervention 11-1 Lines That Intersect Circles
 Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Riding a Ferris Wheel
 Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
 ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
Riding a Ferris Wheel. Students should be able to answer these questions after Lesson 10.1:
 .1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
.1 Riding a Ferris Wheel Introduction to ircles Students should be able to answer these questions after Lesson.1: What are the parts of a circle? How are the parts of a circle drawn? Read Question 1 and
10.4 Explore Inscribed Angles
 Investigating g eometry IIY se before esson 0.4 0.4 Eplore Inscribed ngles E I compass straightedge protractor Q E I O N How are inscribed angles related to central angles? he verte of a central angle
Investigating g eometry IIY se before esson 0.4 0.4 Eplore Inscribed ngles E I compass straightedge protractor Q E I O N How are inscribed angles related to central angles? he verte of a central angle
Geometry Honors Homework
 Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Skills Practice Skills Practice for Lesson 11.1
 Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Chapter 10. Properties of Circles
 Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Name Date Period. Notes - Tangents. 1. If a line is a tangent to a circle, then it is to the
 Name ate Period Notes - Tangents efinition: tangent is a line in the plane of a circle that intersects the circle in eactly one point. There are 3 Theorems for Tangents. 1. If a line is a tangent to a
Name ate Period Notes - Tangents efinition: tangent is a line in the plane of a circle that intersects the circle in eactly one point. There are 3 Theorems for Tangents. 1. If a line is a tangent to a
10.3 Start Thinking Warm Up Cumulative Review Warm Up
 10.3 tart hinking etermine if the statement is always true, sometimes true, or never true. plain your reasoning. 1. chord is a diameter. 2. diameter is a chord. 3. chord and a radius have the same measure.
10.3 tart hinking etermine if the statement is always true, sometimes true, or never true. plain your reasoning. 1. chord is a diameter. 2. diameter is a chord. 3. chord and a radius have the same measure.
Circles and Arcs. Objectives To find the measures of central angles and arcs To find the circumference and arc length
 10-6 ircles and rcs ommon ore tate tandards G-..1 Know precise definitions of... circle... G-..1 rove that all circles are similar. lso G-..2, G-..5 M 1, M 3, M 4, M 6, M 8 bjectives o find the measures
10-6 ircles and rcs ommon ore tate tandards G-..1 Know precise definitions of... circle... G-..1 rove that all circles are similar. lso G-..2, G-..5 M 1, M 3, M 4, M 6, M 8 bjectives o find the measures
Use Properties of Tangents
 6.1 Georgia Performance Standard(s) MM2G3a, MM2G3d Your Notes Use Properties of Tangents Goal p Use properties of a tangent to a circle. VOULRY ircle enter Radius hord iameter Secant Tangent Example 1
6.1 Georgia Performance Standard(s) MM2G3a, MM2G3d Your Notes Use Properties of Tangents Goal p Use properties of a tangent to a circle. VOULRY ircle enter Radius hord iameter Secant Tangent Example 1
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
Chapter 12 Practice Test
 hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
hapter 12 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. ssume that lines that appear to be tangent are tangent. is the center of the circle.
Arcs and Inscribed Angles of Circles
 Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Click on a topic to go to that section. Euclid defined a circle and its center in this way: Euclid defined figures in this way:
 lide 1 / 59 lide / 59 New Jersey enter for eaching and Learning Progressive Mathematics Initiative his material is made freely available at www.njctl.org and is intended for the non-commercial use of students
lide 1 / 59 lide / 59 New Jersey enter for eaching and Learning Progressive Mathematics Initiative his material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Find the area of the triangle. You try: D C. Determine whether each of the following statements is true or false. Solve for the variables.
 lameda USD Geometr enchmark Stud Guide ind the area of the triangle. 9 4 5 D or all right triangles, a + b c where c is the length of the hpotenuse. 5 4 a + b c 9 + b 5 + b 5 b 5 b 44 b 9 he area of a
lameda USD Geometr enchmark Stud Guide ind the area of the triangle. 9 4 5 D or all right triangles, a + b c where c is the length of the hpotenuse. 5 4 a + b c 9 + b 5 + b 5 b 5 b 44 b 9 he area of a
Circles and Volume. Circle Theorems. Essential Questions. Module Minute. Key Words. What To Expect. Analytical Geometry Circles and Volume
 Analytical Geometry Circles and Volume Circles and Volume There is something so special about a circle. It is a very efficient shape. There is no beginning, no end. Every point on the edge is the same
Analytical Geometry Circles and Volume Circles and Volume There is something so special about a circle. It is a very efficient shape. There is no beginning, no end. Every point on the edge is the same
Lesson 1.7 circles.notebook. September 19, Geometry Agenda:
 Geometry genda: Warm-up 1.6(need to print of and make a word document) ircle Notes 1.7 Take Quiz if you were not in class on Friday Remember we are on 1.7 p.72 not lesson 1.8 1 Warm up 1.6 For Exercises
Geometry genda: Warm-up 1.6(need to print of and make a word document) ircle Notes 1.7 Take Quiz if you were not in class on Friday Remember we are on 1.7 p.72 not lesson 1.8 1 Warm up 1.6 For Exercises
( ) ( ) Geometry Team Solutions FAMAT Regional February = 5. = 24p.
 . A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
. A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
Tangent Lines Unit 10 Lesson 1 Example 1: Tell how many common tangents the circles have and draw them.
 Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Name. Chapter 12: Circles
 Name Chapter 12: Circles Chapter 12 Calendar Sun Mon Tue Wed Thu Fri Sat May 13 12.1 (Friday) 14 Chapter 10/11 Assessment 15 12.2 12.1 11W Due 16 12.3 12.2 HW Due 17 12.1-123 Review 12.3 HW Due 18 12.1-123
Name Chapter 12: Circles Chapter 12 Calendar Sun Mon Tue Wed Thu Fri Sat May 13 12.1 (Friday) 14 Chapter 10/11 Assessment 15 12.2 12.1 11W Due 16 12.3 12.2 HW Due 17 12.1-123 Review 12.3 HW Due 18 12.1-123
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
 ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to Circles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. Chord b.
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to Circles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. Chord b.
Introduction Circle Some terms related with a circle
 141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
Geo - CH11 Practice Test
 Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
Mid-Chapter Quiz: Lessons 10-1 through Refer to. 1. Name the circle. SOLUTION: The center of the circle is A. Therefore, the circle is ANSWER:
 Refer to. 1. Name the circle. The center of the circle is A. Therefore, the circle is 2. Name a diameter. ; since is a chord that passes through the center, it is a diameter. 3. Name a chord that is not
Refer to. 1. Name the circle. The center of the circle is A. Therefore, the circle is 2. Name a diameter. ; since is a chord that passes through the center, it is a diameter. 3. Name a chord that is not
So, PQ is about 3.32 units long Arcs and Chords. ALGEBRA Find the value of x.
 ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
Honors Geometry Circle Investigation - Instructions
 Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
If the measure ofaacb is less than 180, then A, B, and all the points on C that lie in the
 age 1 of 7 11.3 rcs and entral ngles oal Use properties of arcs of circles. Key Words minor arc major arc semicircle congruent circles congruent arcs arc length ny two points and on a circle determine
age 1 of 7 11.3 rcs and entral ngles oal Use properties of arcs of circles. Key Words minor arc major arc semicircle congruent circles congruent arcs arc length ny two points and on a circle determine
Using Chords. Essential Question What are two ways to determine when a chord is a diameter of a circle?
 10.3 Using hords ssential uestion What are two ways to determine when a chord is a diameter of a circle? rawing iameters OOKI O UU o be proficient in math, you need to look closely to discern a pattern
10.3 Using hords ssential uestion What are two ways to determine when a chord is a diameter of a circle? rawing iameters OOKI O UU o be proficient in math, you need to look closely to discern a pattern
Chapter 10 Worksheet 1 Name: Honors Accelerated Geometry Hour:
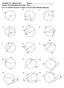 hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
Seismograph (p. 582) Car (p. 554) Dartboard (p. 547) Bicycle Chain (p. 539)
 10 ircles 10.1 ines and egments hat Intersect ircles 10. inding rc easures 10.3 Using hords 10.4 Inscribed ngles and olygons 10.5 ngle elationships in ircles 10.6 egment elationships in ircles 10.7 ircles
10 ircles 10.1 ines and egments hat Intersect ircles 10. inding rc easures 10.3 Using hords 10.4 Inscribed ngles and olygons 10.5 ngle elationships in ircles 10.6 egment elationships in ircles 10.7 ircles
NAME DATE PERIOD. 4. If m ABC x and m BAC m BCA 2x 10, is B F an altitude? Explain. 7. Find x if EH 16 and FH 6x 5. G
 5- NM IO ractice isectors, Medians, and ltitudes LG In, is the angle bisector of,,, and are medians, and is the centroid.. ind x if 4x and 0.. ind y if y and 8.. ind z if 5z 0 and 4. 4. If m x and m m
5- NM IO ractice isectors, Medians, and ltitudes LG In, is the angle bisector of,,, and are medians, and is the centroid.. ind x if 4x and 0.. ind y if y and 8.. ind z if 5z 0 and 4. 4. If m x and m m
Practice For use with pages
 Name ate ON 0. ractice For use with pages 678 686 se ( to draw the described part of the circle.. raw a diameter and label it }.. raw a tangent ra and label it ###$. 3. raw a secant and label it } F. 4.
Name ate ON 0. ractice For use with pages 678 686 se ( to draw the described part of the circle.. raw a diameter and label it }.. raw a tangent ra and label it ###$. 3. raw a secant and label it } F. 4.
Understand and Apply Theorems about Circles
 UNIT 4: CIRCLES AND VOLUME This unit investigates the properties of circles and addresses finding the volume of solids. Properties of circles are used to solve problems involving arcs, angles, sectors,
UNIT 4: CIRCLES AND VOLUME This unit investigates the properties of circles and addresses finding the volume of solids. Properties of circles are used to solve problems involving arcs, angles, sectors,
10.1 circles and circumference 2017 ink.notebook. March 13, Page 91. Page 92. Page 90. Ch 10 Circles Circles and Circumference.
 Page 90 Page 91 Page 92 Ch 10 Circles 10.1 Circles and Circumference Lesson Objectives Page 93 Standards Lesson Notes Page 94 10.1 Circles and Circumference Press the tabs to view details. 1 Lesson Objectives
Page 90 Page 91 Page 92 Ch 10 Circles 10.1 Circles and Circumference Lesson Objectives Page 93 Standards Lesson Notes Page 94 10.1 Circles and Circumference Press the tabs to view details. 1 Lesson Objectives
( ) Chapter 10 Review Question Answers. Find the value of x mhg. m B = 1 2 ( 80 - x) H x G. E 30 = 80 - x. x = 50. Find m AXB and m Y A D X 56
 hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
Objectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord
 1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS.
 ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS. A B X Z Y A MINOR arc is LESS than 1/2 way around the circle. A MAJOR arc is MORE than 1/2 way around
ARCS An ARC is any unbroken part of the circumference of a circle. It is named using its ENDPOINTS. A B X Z Y A MINOR arc is LESS than 1/2 way around the circle. A MAJOR arc is MORE than 1/2 way around
MODULE. (40 + 8x) + (5x -16) = 180. STUDY GUIDE REVIEW Angles and Segments in Circles. Key Vocabulary
 STUDY GUIDE REVIEW Angles and Segments in ircles ODULE 15 Essential Question: How can you use angles and segments in circles to solve real-world problems? EY EXALE (Lesson 15.1) Determine m DE, m BD, m
STUDY GUIDE REVIEW Angles and Segments in ircles ODULE 15 Essential Question: How can you use angles and segments in circles to solve real-world problems? EY EXALE (Lesson 15.1) Determine m DE, m BD, m
NAME DATE PERIOD. Study Guide and Intervention
 7-1 tudy Guide and Intervention atios and Proportions Write and Use atios ratio is a comparison of two quantities by divisions. The ratio a to b, where b is not zero, can be written as a b or a:b. ample
7-1 tudy Guide and Intervention atios and Proportions Write and Use atios ratio is a comparison of two quantities by divisions. The ratio a to b, where b is not zero, can be written as a b or a:b. ample
2 Explain 1 Proving the Intersecting Chords Angle Measure Theorem
 xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
10-3 Arcs and Chords. ALGEBRA Find the value of x.
 ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
UNIT 3 CIRCLES AND VOLUME Lesson 1: Introducing Circles Instruction
 Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Prerequisite Skills This lesson requires the use of the following skills: performing operations with fractions understanding slope, both algebraically and graphically understanding the relationship of
Page 1 Central Angles & Arc Measures
 Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
Circles. Exercise 9.1
 9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
Properties of Circles
 10 10.1 roperties of ircles Use roperties of Tangents 10.2 ind rc Measures 10.3 pply roperties of hords 10.4 Use Inscribed ngles and olygons 10.5 pply Other ngle elationships in ircles 10.6 ind egment
10 10.1 roperties of ircles Use roperties of Tangents 10.2 ind rc Measures 10.3 pply roperties of hords 10.4 Use Inscribed ngles and olygons 10.5 pply Other ngle elationships in ircles 10.6 ind egment
Name two radii in Circle E.
 A C E B D Name two radii in Circle E. Unit 4: Prerequisite Terms A C E B D ECandED Unit 4: Prerequisite Terms A C E B D Name all chords in Circle E. Unit 4: Prerequisite Terms A C E B D AD, CD, AB Unit
A C E B D Name two radii in Circle E. Unit 4: Prerequisite Terms A C E B D ECandED Unit 4: Prerequisite Terms A C E B D Name all chords in Circle E. Unit 4: Prerequisite Terms A C E B D AD, CD, AB Unit
1. Draw and label a diagram to illustrate the property of a tangent to a circle.
 Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
Master 8.17 Extra Practice 1 Lesson 8.1 Properties of Tangents to a Circle 1. Draw and label a diagram to illustrate the property of a tangent to a circle. 2. Point O is the centre of the circle. Points
DO NOW #1. Please: Get a circle packet
 irclengles.gsp pril 26, 2013 Please: Get a circle packet Reminders: R #10 due Friday Quiz Monday 4/29 Quiz Friday 5/3 Quiz Wednesday 5/8 Quiz Friday 5/10 Initial Test Monday 5/13 ctual Test Wednesday 5/15
irclengles.gsp pril 26, 2013 Please: Get a circle packet Reminders: R #10 due Friday Quiz Monday 4/29 Quiz Friday 5/3 Quiz Wednesday 5/8 Quiz Friday 5/10 Initial Test Monday 5/13 ctual Test Wednesday 5/15
Answers. Chapter10 A Start Thinking. and 4 2. Sample answer: no; It does not pass through the center.
 hapter10 10.1 Start Thinking 6. no; is not a right triangle because the side lengths do not satisf the Pthagorean Theorem (Thm. 9.1). 1. (3, ) 7. es; is a right triangle because the side lengths satisf
hapter10 10.1 Start Thinking 6. no; is not a right triangle because the side lengths do not satisf the Pthagorean Theorem (Thm. 9.1). 1. (3, ) 7. es; is a right triangle because the side lengths satisf
0610ge. Geometry Regents Exam The diagram below shows a right pentagonal prism.
 0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
Liberal High School Lesson Plans
 Monday, 5/8/2017 Liberal High School Lesson Plans er:david A. Hoffman Class:Algebra III 5/8/2017 To 5/12/2017 Students will perform math operationsto solve rational expressions and find the domain. How
Monday, 5/8/2017 Liberal High School Lesson Plans er:david A. Hoffman Class:Algebra III 5/8/2017 To 5/12/2017 Students will perform math operationsto solve rational expressions and find the domain. How
Pre-Test. Use the following figure to answer Questions 1 through 6. B C. 1. What is the center of the circle? The center of the circle is point G.
 Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
West Haven Public Schools Unit Planning Organizer
 West Haven Public Schools Unit Planning Organizer Subject: Circles and Other Conic Sections Grade 10 Unit: Five Pacing: 4 weeks + 1 week Essential Question(s): 1. What is the relationship between angles
West Haven Public Schools Unit Planning Organizer Subject: Circles and Other Conic Sections Grade 10 Unit: Five Pacing: 4 weeks + 1 week Essential Question(s): 1. What is the relationship between angles
0114ge. Geometry Regents Exam 0114
 0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
10.6 Investigate Segment Lengths
 Investigating g Geometry TIVITY. Investigate Segment Lengths M T R I LS graphing calculator or computer Use before Lesson. classzone.com Keystrokes Q U S T I O N What is the relationship between the lengths
Investigating g Geometry TIVITY. Investigate Segment Lengths M T R I LS graphing calculator or computer Use before Lesson. classzone.com Keystrokes Q U S T I O N What is the relationship between the lengths
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Reteaching , or 37.5% 360. Geometric Probability. Name Date Class
 Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Chapter 19 Exercise 19.1
 hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
14.3 Tangents and Circumscribed Angles
 Name lass Date 14.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? Explore G.5. Investigate patterns to make conjectures about geometric relationships,
Name lass Date 14.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? Explore G.5. Investigate patterns to make conjectures about geometric relationships,
Mu Alpha Theta State 2007 Euclidean Circles
 Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
15.3 Tangents and Circumscribed Angles
 Name lass ate 15.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? esource Locker Explore Investigating the Tangent-adius Theorem tangent is a line
Name lass ate 15.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? esource Locker Explore Investigating the Tangent-adius Theorem tangent is a line
( ) Find the value of x mhg. H x G. Find m AXB and m Y A D X 56. Baroody Page 1 of 18
 1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
Name Grp Pd Date. Circles Test Review 1
 ircles est eview 1 1. rc 2. rea 3. entral ngle 4. hord 5. ircumference 6. Diameter 7. Inscribed 8. Inscribed ngle 9. Intercepted rc 10. Pi 11. adius 12. ector 13. emicircle 14. angent 15. πr 2 16. 2πr
ircles est eview 1 1. rc 2. rea 3. entral ngle 4. hord 5. ircumference 6. Diameter 7. Inscribed 8. Inscribed ngle 9. Intercepted rc 10. Pi 11. adius 12. ector 13. emicircle 14. angent 15. πr 2 16. 2πr
Review for Grade 9 Math Exam - Unit 8 - Circle Geometry
 Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
10.6 Find Segment Lengths
 10. Find Segment Lengths in ircles Goal p Find segment lengths in circles. Your Notes VOULRY Segments of a chord Secant segment Eternal segment THEOREM 10.14: SEGMENTS OF HORS THEOREM If two chords intersect
10. Find Segment Lengths in ircles Goal p Find segment lengths in circles. Your Notes VOULRY Segments of a chord Secant segment Eternal segment THEOREM 10.14: SEGMENTS OF HORS THEOREM If two chords intersect
Circles-Tangent Properties
 15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
~ 1 ~ Geometry 2 nd Semester Review Find the value for the variable for each of the following situations
 Geometry nd Semester Review 018 Find the value for the variable for each of the following situations. 7. 400 m 1. 7 8. y. 8.9 cm 0 0 9.. 19 6 60 1 11 10. 45 4. 58 5 11. 5. 11 6. 18 1 slide 4.1 meters long
Geometry nd Semester Review 018 Find the value for the variable for each of the following situations. 7. 400 m 1. 7 8. y. 8.9 cm 0 0 9.. 19 6 60 1 11 10. 45 4. 58 5 11. 5. 11 6. 18 1 slide 4.1 meters long
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
Geometry. Circles. Name Period
 Geometry Circles Name Period 1 Date: Section 10 1 & 10 2: Circumference, Arcs, and Angles Notes Circle a set of equidistant from a given point called the of the circle Circumference: Example #1: a.) Find
Geometry Circles Name Period 1 Date: Section 10 1 & 10 2: Circumference, Arcs, and Angles Notes Circle a set of equidistant from a given point called the of the circle Circumference: Example #1: a.) Find
Copy Material. Geometry Unit 5. Circles With and Without Coordinates. Eureka Math. Eureka Math
 Copy Material Geometry Unit 5 Circles With and Without Coordinates Eureka Math Eureka Math Lesson 1 Lesson 1: Thales Theorem Circle A is shown below. 1. Draw two diameters of the circle. 2. Identify the
Copy Material Geometry Unit 5 Circles With and Without Coordinates Eureka Math Eureka Math Lesson 1 Lesson 1: Thales Theorem Circle A is shown below. 1. Draw two diameters of the circle. 2. Identify the
02)
 GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
Circles in Neutral Geometry
 Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Geometry H Ch. 10 Test
 Geometry H Ch. 10 est 1. In the diagram, point is a point of tangency,, and. What is the radius of? M N J a. 76 c. 72 b. 70 d. 64 2. In the diagram, is tangent to at, is tangent to at,, and. Find the value
Geometry H Ch. 10 est 1. In the diagram, point is a point of tangency,, and. What is the radius of? M N J a. 76 c. 72 b. 70 d. 64 2. In the diagram, is tangent to at, is tangent to at,, and. Find the value
0809ge. Geometry Regents Exam Based on the diagram below, which statement is true?
 0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
